quadratic transformations assignment

Study Guides > College Algebra CoRequisite Course

Transformations of quadratic functions, learning outcomes.

• Graph vertical and horizontal shifts of quadratic functions
• Graph vertical compressions and stretches of quadratic functions
• Write the equation of a transformed quadratic function using the vertex form
• Identify the vertex and axis of symmetry for a given quadratic function in vertex form

The standard form of a quadratic function presents the function in the form

[latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]

where [latex]\left(h,\text{ }k\right)[/latex] is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function .

Shift Up and Down by Changing the Value of [latex]k[/latex]

You can represent a vertical (up, down) shift of the graph of [latex]f(x)=x^2[/latex] by adding or subtracting a constant, [latex]k[/latex].

[latex]f(x)=x^2 + k[/latex]

Answer: The equation for the graph of [latex]f(x)=x^2[/latex] that has been shifted up 4 units is [latex-display]f(x)=x^2+4[/latex-display] The equation for the graph of [latex]f(x)=x^2[/latex] that has been shifted down 4 units is [latex-display]f(x)=x^2-4[/latex-display]

Shift left and right by changing the value of [latex]h[/latex]

You can represent a horizontal (left, right) shift of the graph of [latex]f(x)=x^2[/latex] by adding or subtracting a constant, [latex]h[/latex], to the variable [latex]x[/latex], before squaring.

[latex]f(x)=(x-h)^2 [/latex]

tip for success

[latex]f(x)=(x-2)^2[/latex]

The equation for the graph of [latex]f(x)=^2[/latex] that has been shifted left 2 units is

[latex]f(x)=(x+2)^2[/latex]

Stretch or compress by changing the value of [latex]a[/latex].

You can represent a stretch or compression (narrowing, widening) of the graph of [latex]f(x)=x^2[/latex] by multiplying the squared variable by a constant, [latex]a[/latex].

[latex]f(x)=ax^2 [/latex]

[latex]f(x)=\frac{1}{2}x^2[/latex]

[latex]f(x)=3x^2[/latex]

This is the [latex]x[/latex] coordinate of the vertexr and [latex]x=-\dfrac{b}{2a}[/latex] is the  axis of symmetry we defined earlier. Setting the constant terms equal gives us:

Answer: There is only one [latex](h,k)[/latex] pair that will satisfy these conditions, [latex](-3,2)[/latex].  The value of [latex]a[/latex] does not affect the line of symmetry or the vertex of a quadratic graph, so [latex]a[/latex] can take on any value.

 Challenge Problem

Answer: The path passes through the origin and has vertex at [latex]\left(-4,\text{ }7\right)[/latex], so [latex]\left(h\right)x=-\frac{7}{16}{\left(x+4\right)}^{2}+7[/latex]. To make the shot, [latex]h\left(-7.5\right)[/latex] would need to be about 4 but [latex]h\left(-7.5\right)\approx 1.64[/latex]; he doesn’t make it.

Licenses & Attributions

Cc licensed content, original.

• Interactive: Transform Quadratic 1. Provided by: Lumen Learning (with Desmos) Located at: https://www.desmos.com/calculator/fpatj6tbcn. License: CC BY: Attribution .
• Interactive: Transform Quadratic 2. Provided by: Lumen Learning (with Desmos) Located at: https://www.desmos.com/calculator/5g3xfhkklq. License: CC BY: Attribution .
• Interactive: Transform Quadratic 3. Provided by: Lumen Learning (with Desmos) Located at: https://www.desmos.com/calculator/ha6gh59rq7. License: CC BY: Attribution .
• Interactive: Transform Quadratic 4. Provided by: Lumen Learning (with Desmos) Located at: https://www.desmos.com/calculator/pimelalx4i. License: CC BY: Attribution .
• Revision and Adaptation. Provided by: Lumen Learning License: CC BY: Attribution .

CC licensed content, Shared previously

• College Algebra. Provided by: OpenStax Authored by: Abramson, Jay et al.. Located at: https://openstax.org/books/college-algebra/pages/1-introduction-to-prerequisites. License: CC BY: Attribution . License terms: Download for free at http://cnx.org/contents/ [email protected] .

Please add a message.

Message received. Thanks for the feedback.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 9: Transformations of functions

About this unit.

We can think graphs of absolute value and quadratic functions as transformations of the parent functions |x| and x². Importantly, we can extend this idea to include transformations of any function whatsoever! This fascinating concept allows us to graph many other types of functions, like square/cube root, exponential and logarithmic functions.

Shifting functions

• Shifting functions introduction (Opens a modal)
• Shifting functions examples (Opens a modal)
• Graphing shifted functions (Opens a modal)
• Shift functions Get 3 of 4 questions to level up!

Reflecting functions

• Reflecting functions introduction (Opens a modal)
• Reflecting functions: examples (Opens a modal)
• Reflect functions Get 3 of 4 questions to level up!

Symmetry of functions

• Function symmetry introduction (Opens a modal)
• Even and odd functions: Graphs (Opens a modal)
• Even and odd functions: Tables (Opens a modal)
• Even and odd functions: Equations (Opens a modal)
• Even and odd functions: Find the mistake (Opens a modal)
• Symmetry of polynomials (Opens a modal)
• Even and odd functions: Graphs and tables Get 3 of 4 questions to level up!
• Even & odd functions: Equations Get 3 of 4 questions to level up!

Scaling functions

• Scaling functions introduction (Opens a modal)
• Scaling functions vertically: examples (Opens a modal)
• Scaling functions horizontally: examples (Opens a modal)
• Identifying horizontal squash from graph (Opens a modal)
• Scale functions vertically Get 3 of 4 questions to level up!
• Scale functions horizontally Get 3 of 4 questions to level up!

Putting it all together

• Identifying function transformations (Opens a modal)
• Identify function transformations Get 3 of 4 questions to level up!

Graphs of square and cube root functions

• Graphing square and cube root functions (Opens a modal)
• Radical functions & their graphs (Opens a modal)
• Graphs of square and cube root functions Get 3 of 4 questions to level up!

Graphs of exponential functions

• Transforming exponential graphs (Opens a modal)
• Transforming exponential graphs (example 2) (Opens a modal)
• Graphing exponential functions (Opens a modal)
• Graphs of exponential functions Get 3 of 4 questions to level up!

Graphs of logarithmic functions

• Graphical relationship between 2ˣ and log₂(x) (Opens a modal)
• Graphing logarithmic functions (example 1) (Opens a modal)
• Graphing logarithmic functions (example 2) (Opens a modal)
• Transformations of functions: FAQ (Opens a modal)
• Graphs of logarithmic functions Get 3 of 4 questions to level up!

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Algebra >
• Functions >
• Quadratic >

Transformation of Quadratic Functions Worksheets

This compilation of well-researched printable worksheets has been designed to help high school learners strengthen their understanding on transformation of quadratic functions, transforming the graphs, finding the transformation function g(x) from its parents function f(x) and identifying the various types of shifts. Knowledge of the rules of transformation is a prerequisite to solve pdf worksheets based on horizontal shift, vertical shift and reflection. Begin your practice with our free worksheets!

Printing Help - Please do not print worksheets with grids directly from the browser. Kindly download them and print.

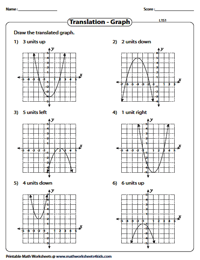
Translation of the Graph: Level 1

Translate each quadratic function according to the indicated shift. Students should draw the new position of the graph after translation. Right, left, up and down shifts are included. Use the answer key to verify your responses.

• Download the set

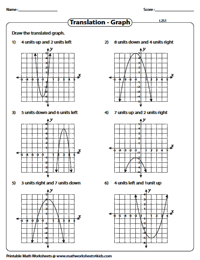
Translation of the Graph: Level 2

In this series of second level of worksheets, translate f(x) as per a combination of two subsequent translations provided. Shift them as indicated to get the translated graph g(x).

Translation of the Function: Level 1

Translate each given quadratic function f(x) in the series of high school worksheets provided here. Follow the relevant rules f(x) + c or f(x) - c to make up or down shifts and f(x + c) or f(x - c) to make left or right shifts.

Translation of the Function: Level 2

Use the relevant rules to shift each quadratic function f(x) left/ right and up/ down. This set of transformation worksheets will require students to make two consecutive translations to obtain g(x).

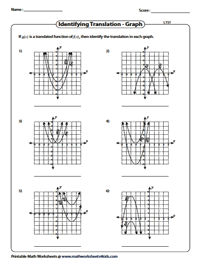
Identify the Translation from the Graph: Level 1

This batch of quadratic transformation worksheet pdfs contains the graph of the function f(x) and its translation g(x). Read the graphs and identify the number of units up / down / left / right that g(x) is translated from f(x).

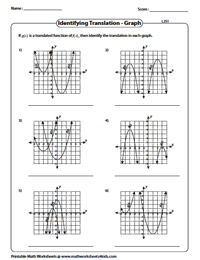
Identify the Translation from the Graph: Level 2

These printable worksheets comprise the graph of the parent function f(x) and its translation g(x). Students will need to identify two consecutive shifts (right/ left and up/ down) for every grid provided.

Reflection of the Function

Write the reflection of each quadratic function f(x) provided in this set of transformation worksheets. A reflection on the x-axis will be obtained by multiplying the function by -1 i.e. -f(x). To find the Reflection of the Function across y-axis, find f(-x).

Related Worksheets

» Graphing Quadratic Function

» Quadratic Equation

» Linear Transformation

» Transformations

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

• Get started
• Pre-Algebra

A quicker path to better grades

We have gathered all your curriculum-based courses, assignments, hints, tests, and solutions in one easy-to-use place

• Integrated I
• Integrated II
• Integrated III

Can't find your textbook?

More math. less studying.

A personal private tutor for each student. Free from preassure and study anxiety.

Transformations of Quadratic Functions

Catch-up and review.

Here are a few recommended readings before getting started with this lesson.

• Graphing Quadratic Functions in Standard Form
• Graphing Quadratic Functions in Vertex Form and Intercept Form
• Translation of a Function
• Vertical Stretch and Shrink of a Function
• Horizontal Stretch and Shrink of a Function
• Reflection of a Function

Transforming the Graph of a Function

The graph of the quadratic function f(x)=- x^2+2x+1 is drawn on the coordinate plane . By applying transformations to the parabola that corresponds to f, draw the graph of g(x)=- x^2+4x.

Reflection of Quadratic Functions

Reflecting a quadratic function.

Kriz is given an extra credit math assignment about quadratic functions and parabolas . The assignment consists of four tasks. For the first task, Kriz is given the graph of the function y= 12(x+2)^2+1.

Help Kriz with their extra credit assignment.

Equation: y=- 1/2(x+2)^2-1

Equation: y=1/2(x-2)^2+1

(- a)^2 = a^2

Distribute - 1

Stretching and Shrinking a Parabola

In the coordinate plane , the parabola that corresponds to the quadratic function y=af(bx) can be seen. Observe how the graph is vertically and horizontally stretched and shrunk by changing the values of a and b.

Stretch and Shrink of Quadratic Functions

Finding the equation of a stretch and a shrink.

Kriz's second task is about horizontal and vertical stretches and shrinks of parabolas .

They are given the quadratic function y=x^2-3 and want to write the function rules of two related functions .

Stating the Factor of a Stretch or a Shrink

The graph of the quadratic function y=x^2 is shown in the coordinate plane . The graph of a horizontal or vertical stretch or shrink is also shown.

Combining Transformations of Quadratic Functions

Kriz's assignment is getting more interesting, as the third task is about combining reflections with vertical and horizontal stretches and shrinks.

This time, they are given the quadratic function y=(x-1)^2 and want to write the function rules of two other functions .

Distribute -1

(a+b)^2=a^2+2ab+b^2

Identity Property of Multiplication

Distribute 3

(a-b)^2=a^2-2ab+b^2

(a b)^m=a^m b^m

Translating a Graph

In the coordinate plane , the graph of the quadratic function y=(x-h)^2+k can be seen. Observe how the graph is horizontally and vertically translated by changing the values of h and k.

Translation of Quadratic Functions

Translating a quadratic function.

To finally finish the assignment and get the extra credit they need, Kriz has to finish the fourth task of the math assignment. This time, the graph of the quadratic parent function y=x^2 is given.

By translating this quadratic function , Kriz wants to draw the graphs and write the equations of the following functions .

Commutative Property of Multiplication

Calculate power

Subtract term

Stating the Translation

The graph of the quadratic function y=x^2 and a vertical or horizontal translation are shown in the coordinate plane .

With the topics learned in this lesson, the challenge presented at the beginning can be solved. The parabola that corresponds to the quadratic function f(x)=- x^2+2x+1 is given.

Rewrite the function whose graph is to be drawn to clearly identify the transformations.

Write as a difference

Factor out 3

(- a)^2=a^2

a+(- b)=a-b

• Reflection in the y-axis.
• Vertical stretch by a factor of 3.
• Translation 2 units down.

Recommended exercises

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.1: Quadratic Functions

• Last updated
• Save as PDF
• Page ID 32519

Learning Objectives

• Recognize characteristics of parabolas.
• Understand how the graph of a parabola is related to its quadratic function.
• Determine a quadratic function’s minimum or maximum value.
• Solve problems involving a quadratic function’s minimum or maximum value.

Curved antennas, such as the ones shown in Figure \(\PageIndex{1}\), are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.

In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior.

Recognizing Characteristics of Parabolas

The graph of a quadratic function is a U-shaped curve called a parabola. One important feature of the graph is that it has an extreme point, called the vertex . If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value . In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry . These features are illustrated in Figure \(\PageIndex{2}\).

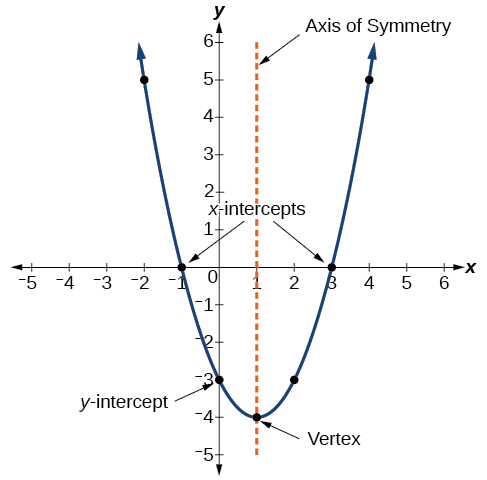
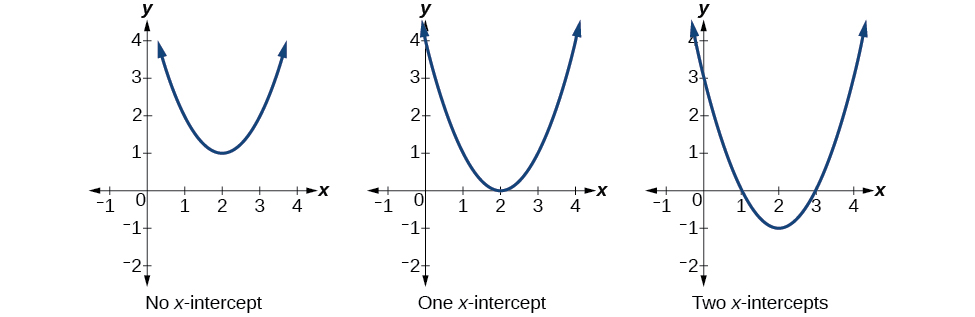
The y-intercept is the point at which the parabola crosses the \(y\)-axis. The x-intercepts are the points at which the parabola crosses the \(x\)-axis. If they exist, the x-intercepts represent the zeros , or roots , of the quadratic function, the values of \(x\) at which \(y=0\).

Example \(\PageIndex{1}\): Identifying the Characteristics of a Parabola

Determine the vertex, axis of symmetry, zeros, and y-intercept of the parabola shown in Figure \(\PageIndex{3}\).

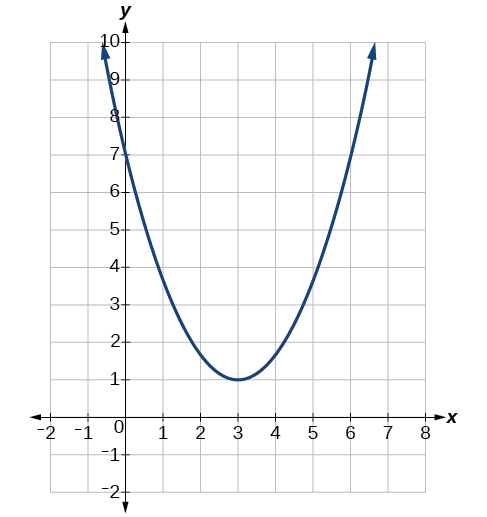
The vertex is the turning point of the graph. We can see that the vertex is at \((3,1)\). Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is \(x=3\). This parabola does not cross the x-axis, so it has no zeros. It crosses the \(y\)-axis at \((0,7)\) so this is the y-intercept.

Understanding How the Graphs of Parabolas are Related to Their Quadratic Functions

The general form of a quadratic function presents the function in the form

\[f(x)=ax^2+bx+c\]

where \(a\), \(b\), and \(c\) are real numbers and \(a{\neq}0\). If \(a>0\), the parabola opens upward. If \(a<0\), the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.

The axis of symmetry is defined by \(x=−\frac{b}{2a}\). If we use the quadratic formula, \(x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}\), to solve \(ax^2+bx+c=0\) for the x-intercepts, or zeros, we find the value of \(x\) halfway between them is always \(x=−\frac{b}{2a}\), the equation for the axis of symmetry.

Figure \(\PageIndex{4}\) represents the graph of the quadratic function written in general form as \(y=x^2+4x+3\). In this form, \(a=1\), \(b=4\), and \(c=3\). Because \(a>0\), the parabola opens upward. The axis of symmetry is \(x=−\frac{4}{2(1)}=−2\). This also makes sense because we can see from the graph that the vertical line \(x=−2\) divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, \((−2,−1)\). The x-intercepts, those points where the parabola crosses the x-axis, occur at \((−3,0)\) and \((−1,0)\).

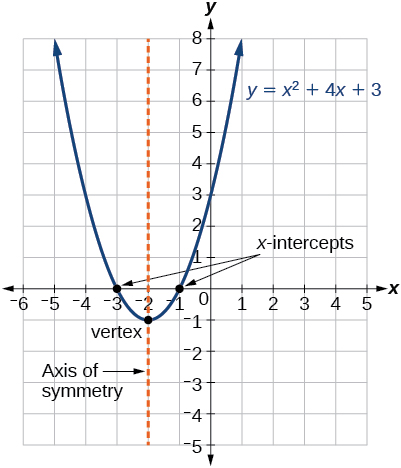
The standard form of a quadratic function presents the function in the form

\[f(x)=a(x−h)^2+k\]

where \((h, k)\) is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function .

As with the general form, if \(a>0\), the parabola opens upward and the vertex is a minimum. If \(a<0\), the parabola opens downward, and the vertex is a maximum. Figure \(\PageIndex{5}\) represents the graph of the quadratic function written in standard form as \(y=−3(x+2)^2+4\). Since \(x–h=x+2\) in this example, \(h=–2\). In this form, \(a=−3\), \(h=−2\), and \(k=4\). Because \(a<0\), the parabola opens downward. The vertex is at \((−2, 4)\).

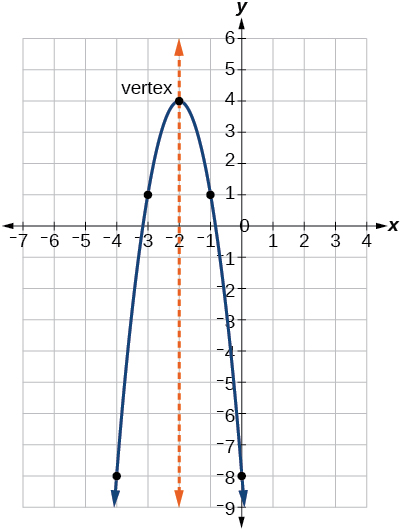
The standard form is useful for determining how the graph is transformed from the graph of \(y=x^2\). Figure \(\PageIndex{6}\) is the graph of this basic function.

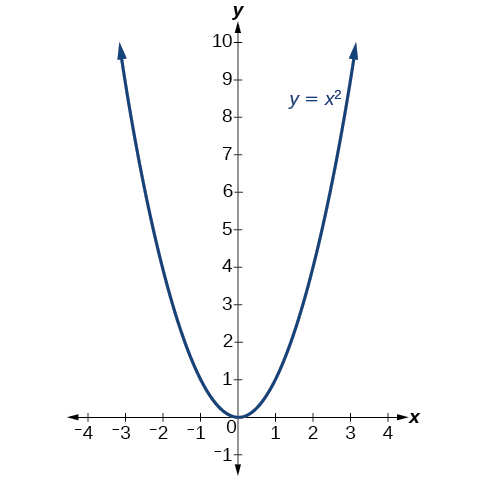
If \(k>0\), the graph shifts upward, whereas if \(k<0\), the graph shifts downward. In Figure \(\PageIndex{5}\), \(k>0\), so the graph is shifted 4 units upward. If \(h>0\), the graph shifts toward the right and if \(h<0\), the graph shifts to the left. In Figure \(\PageIndex{5}\), \(h<0\), so the graph is shifted 2 units to the left. The magnitude of \(a\) indicates the stretch of the graph. If \(|a|>1\), the point associated with a particular x-value shifts farther from the x-axis, so the graph appears to become narrower, and there is a vertical stretch. But if \(|a|<1\), the point associated with a particular x-value shifts closer to the x-axis, so the graph appears to become wider, but in fact there is a vertical compression. In Figure \(\PageIndex{5}\), \(|a|>1\), so the graph becomes narrower.

The standard form and the general form are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the standard form.

\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]

For the linear terms to be equal, the coefficients must be equal.

\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]

This is the axis of symmetry we defined earlier. Setting the constant terms equal:

\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a\cdot\Big(-\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\]

In practice, though, it is usually easier to remember that \(k\) is the output value of the function when the input is \(h\), so \(f(h)=k\).

Definitions: Forms of Quadratic Functions

A quadratic function is a function of degree two. The graph of a quadratic function is a parabola.

• The general form of a quadratic function is \(f(x)=ax^2+bx+c\) where \(a\), \(b\), and \(c\) are real numbers and \(a{\neq}0\).
• The standard form of a quadratic function is \(f(x)=a(x−h)^2+k\).
• The vertex \((h,k)\) is located at \[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]

HOWTO: Write a quadratic function in a general form

Given a graph of a quadratic function, write the equation of the function in general form.

• Identify the horizontal shift of the parabola; this value is \(h\). Identify the vertical shift of the parabola; this value is \(k\).
• Substitute the values of the horizontal and vertical shift for \(h\) and \(k\). in the function \(f(x)=a(x–h)^2+k\).
• Substitute the values of any point, other than the vertex, on the graph of the parabola for \(x\) and \(f(x)\).
• Solve for the stretch factor, \(|a|\).
• If the parabola opens up, \(a>0\). If the parabola opens down, \(a<0\) since this means the graph was reflected about the x-axis.
• Expand and simplify to write in general form.

Example \(\PageIndex{2}\): Writing the Equation of a Quadratic Function from the Graph

Write an equation for the quadratic function \(g\) in Figure \(\PageIndex{7}\) as a transformation of \(f(x)=x^2\), and then expand the formula, and simplify terms to write the equation in general form.

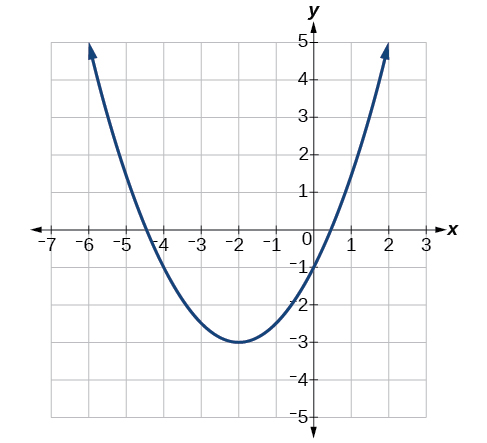
We can see the graph of \(g\) is the graph of \(f(x)=x^2\) shifted to the left 2 and down 3, giving a formula in the form \(g(x)=a(x+2)^2–3\).

Substituting the coordinates of a point on the curve, such as \((0,−1)\), we can solve for the stretch factor.

\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]

In standard form, the algebraic model for this graph is \(g(x)=\dfrac{1}{2}(x+2)^2–3\).

To write this in general polynomial form, we can expand the formula and simplify terms.

\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]

Notice that the horizontal and vertical shifts of the basic graph of the quadratic function determine the location of the vertex of the parabola; the vertex is unaffected by stretches and compressions.

We can check our work using the table feature on a graphing utility. First enter \(\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}\). Next, select \(\mathrm{TBLSET}\), then use \(\mathrm{TblStart=–6}\) and \(\mathrm{ΔTbl = 2}\), and select \(\mathrm{TABLE}\). See Table \(\PageIndex{1}\)

The ordered pairs in the table correspond to points on the graph.

Exercise \(\PageIndex{2}\)

A coordinate grid has been superimposed over the quadratic path of a basketball in Figure \(\PageIndex{8}\). Find an equation for the path of the ball. Does the shooter make the basket?

Figure \(\PageIndex{8}\): Stop motioned picture of a boy throwing a basketball into a hoop to show the parabolic curve it makes. (credit: modification of work by Dan Meyer)

The path passes through the origin and has vertex at \((−4, 7)\), so \(h(x)=–\frac{7}{16}(x+4)^2+7\). To make the shot, \(h(−7.5)\) would need to be about 4 but \(h(–7.5){\approx}1.64\); he doesn’t make it.

• Identify \(a\), \(b\), and \(c\).
• Find \(h\), the x-coordinate of the vertex, by substituting \(a\) and \(b\) into \(h=–\frac{b}{2a}\).
• Find \(k\), the y-coordinate of the vertex, by evaluating \(k=f(h)=f\Big(−\frac{b}{2a}\Big)\).

Example \(\PageIndex{3}\): Finding the Vertex of a Quadratic Function

Find the vertex of the quadratic function \(f(x)=2x^2–6x+7\). Rewrite the quadratic in standard form (vertex form).

The horizontal coordinate of the vertex will be at

\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]

The vertical coordinate of the vertex will be at

\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]

Rewriting into standard form, the stretch factor will be the same as the \(a\) in the original quadratic.

\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]

Using the vertex to determine the shifts,

\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]

One reason we may want to identify the vertex of the parabola is that this point will inform us what the maximum or minimum value of the function is, \((k)\),and where it occurs, \((h)\).

Exercise \(\PageIndex{3}\)

Given the equation \(g(x)=13+x^2−6x\), write the equation in general form and then in standard form.

\(g(x)=x^2−6x+13\) in general form; \(g(x)=(x−3)^2+4\) in standard form.

Finding the Domain and Range of a Quadratic Function

Any number can be the input value of a quadratic function. Therefore, the domain of any quadratic function is all real numbers. Because parabolas have a maximum or a minimum point, the range is restricted. Since the vertex of a parabola will be either a maximum or a minimum, the range will consist of all y-values greater than or equal to the y-coordinate at the turning point or less than or equal to the y-coordinate at the turning point, depending on whether the parabola opens up or down.

Definition: Domain and Range of a Quadratic Function

The domain of any quadratic function is all real numbers.

The range of a quadratic function written in general form \(f(x)=ax^2+bx+c\) with a positive \(a\) value is \(f(x){\geq}f ( −\frac{b}{2a}\Big)\), or \([ f(−\frac{b}{2a}),∞ ) \); the range of a quadratic function written in general form with a negative a value is \(f(x) \leq f(−\frac{b}{2a})\), or \((−∞,f(−\frac{b}{2a})]\).

The range of a quadratic function written in standard form \(f(x)=a(x−h)^2+k\) with a positive \(a\) value is \(f(x) \geq k;\) the range of a quadratic function written in standard form with a negative \(a\) value is \(f(x) \leq k\).

• Identify the domain of any quadratic function as all real numbers.
• Determine whether \(a\) is positive or negative. If \(a\) is positive, the parabola has a minimum. If \(a\) is negative, the parabola has a maximum.
• Determine the maximum or minimum value of the parabola, \(k\).
• If the parabola has a minimum, the range is given by \(f(x){\geq}k\), or \(\left[k,\infty\right)\). If the parabola has a maximum, the range is given by \(f(x){\leq}k\), or \(\left(−\infty,k\right]\).

Example \(\PageIndex{4}\): Finding the Domain and Range of a Quadratic Function

Find the domain and range of \(f(x)=−5x^2+9x−1\).

As with any quadratic function, the domain is all real numbers.

Because \(a\) is negative, the parabola opens downward and has a maximum value. We need to determine the maximum value. We can begin by finding the x-value of the vertex.

\[\begin{align} h&=−\dfrac{b}{2a} \\ &=−\dfrac{9}{2(-5)} \\ &=\dfrac{9}{10} \end{align}\]

The maximum value is given by \(f(h)\).

\[\begin{align} f(\dfrac{9}{10})&=5(\dfrac{9}{10})^2+9(\dfrac{9}{10})-1 \\&= \dfrac{61}{20}\end{align}\]

The range is \(f(x){\leq}\frac{61}{20}\), or \(\left(−\infty,\frac{61}{20}\right]\).

Exercise \(\PageIndex{4}\)

Find the domain and range of \(f(x)=2\Big(x−\frac{4}{7}\Big)^2+\frac{8}{11}\).

The domain is all real numbers. The range is \(f(x){\geq}\frac{8}{11}\), or \(\left[\frac{8}{11},\infty\right)\).

Determining the Maximum and Minimum Values of Quadratic Functions

The output of the quadratic function at the vertex is the maximum or minimum value of the function, depending on the orientation of the parabola . We can see the maximum and minimum values in Figure \(\PageIndex{9}\).

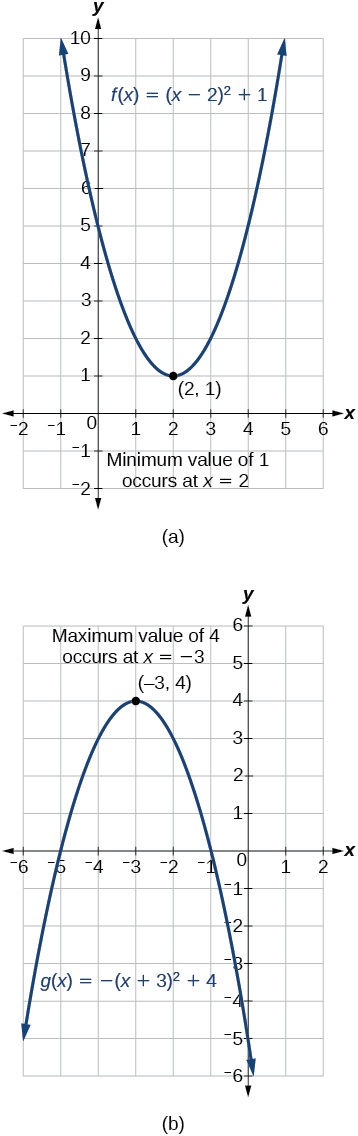
There are many real-world scenarios that involve finding the maximum or minimum value of a quadratic function, such as applications involving area and revenue.

Example \(\PageIndex{5}\): Finding the Maximum Value of a Quadratic Function

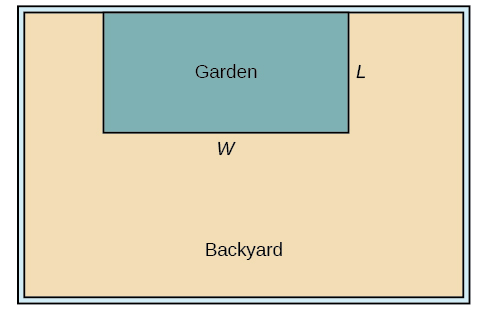
A backyard farmer wants to enclose a rectangular space for a new garden within her fenced backyard. She has purchased 80 feet of wire fencing to enclose three sides, and she will use a section of the backyard fence as the fourth side.

• Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length \(L\).
• What dimensions should she make her garden to maximize the enclosed area?

Let’s use a diagram such as Figure \(\PageIndex{10}\) to record the given information. It is also helpful to introduce a temporary variable, \(W\), to represent the width of the garden and the length of the fence section parallel to the backyard fence.

a. We know we have only 80 feet of fence available, and \(L+W+L=80\), or more simply, \(2L+W=80\). This allows us to represent the width, \(W\), in terms of \(L\).

\[W=80−2L\]

Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so

\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]

This formula represents the area of the fence in terms of the variable length \(L\). The function, written in general form, is

\[A(L)=−2L^2+80L\].

The quadratic has a negative leading coefficient, so the graph will open downward, and the vertex will be the maximum value for the area. In finding the vertex, we must be careful because the equation is not written in standard polynomial form with decreasing powers. This is why we rewrote the function in general form above. Since \(a\) is the coefficient of the squared term, \(a=−2\), \(b=80\), and \(c=0\).

To find the vertex:

\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]

The maximum value of the function is an area of 800 square feet, which occurs when \(L=20\) feet. When the shorter sides are 20 feet, there is 40 feet of fencing left for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet and the longer side parallel to the existing fence has length 40 feet.

This problem also could be solved by graphing the quadratic function. We can see where the maximum area occurs on a graph of the quadratic function in Figure \(\PageIndex{11}\).

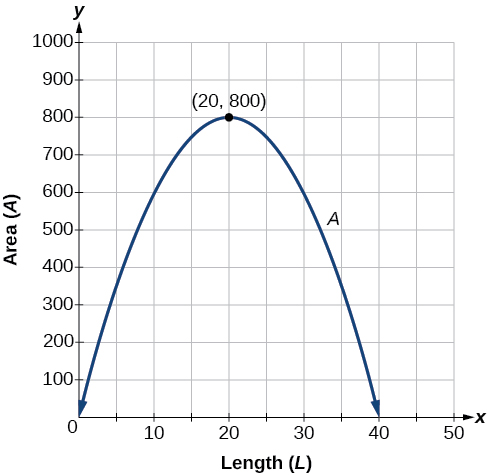
• Write a quadratic equation for revenue.
• Find the vertex of the quadratic equation.
• Determine the y-value of the vertex.

Example \(\PageIndex{6}\): Finding Maximum Revenue

The unit price of an item affects its supply and demand. That is, if the unit price goes up, the demand for the item will usually decrease. For example, a local newspaper currently has 84,000 subscribers at a quarterly charge of $30. Market research has suggested that if the owners raise the price to $32, they would lose 5,000 subscribers. Assuming that subscriptions are linearly related to the price, what price should the newspaper charge for a quarterly subscription to maximize their revenue?

Revenue is the amount of money a company brings in. In this case, the revenue can be found by multiplying the price per subscription times the number of subscribers, or quantity. We can introduce variables, \(p\) for price per subscription and \(Q\) for quantity, giving us the equation \(\text{Revenue}=pQ\).

Because the number of subscribers changes with the price, we need to find a relationship between the variables. We know that currently \(p=30\) and \(Q=84,000\). We also know that if the price rises to $32, the newspaper would lose 5,000 subscribers, giving a second pair of values, \(p=32\) and \(Q=79,000\). From this we can find a linear equation relating the two quantities. The slope will be

\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]

This tells us the paper will lose 2,500 subscribers for each dollar they raise the price. We can then solve for the y-intercept.

\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]

This gives us the linear equation \(Q=−2,500p+159,000\) relating cost and subscribers. We now return to our revenue equation.

\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]

We now have a quadratic function for revenue as a function of the subscription charge. To find the price that will maximize revenue for the newspaper, we can find the vertex.

\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]

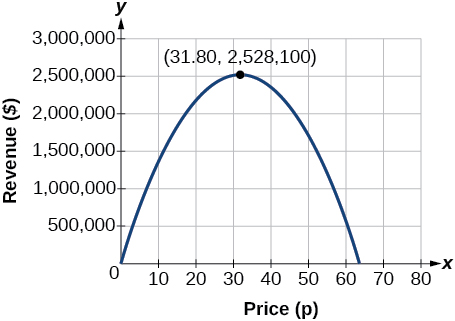
The model tells us that the maximum revenue will occur if the newspaper charges $31.80 for a subscription. To find what the maximum revenue is, we evaluate the revenue function.

\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]

This could also be solved by graphing the quadratic as in Figure \(\PageIndex{12}\). We can see the maximum revenue on a graph of the quadratic function.

Finding the x- and y-Intercepts of a Quadratic Function

Much as we did in the application problems above, we also need to find intercepts of quadratic equations for graphing parabolas. Recall that we find the y-intercept of a quadratic by evaluating the function at an input of zero, and we find the x-intercepts at locations where the output is zero. Notice in Figure \(\PageIndex{13}\) that the number of x-intercepts can vary depending upon the location of the graph.

• Evaluate \(f(0)\) to find the y-intercept.
• Solve the quadratic equation \(f(x)=0\) to find the x-intercepts.

Example \(\PageIndex{7}\): Finding the y- and x-Intercepts of a Parabola

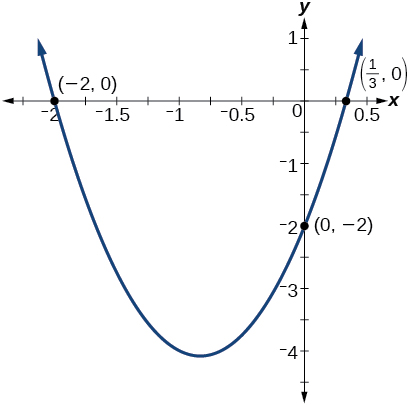
Find the y- and x-intercepts of the quadratic \(f(x)=3x^2+5x−2\).

We find the y-intercept by evaluating \(f(0)\).

\[\begin{align} f(0)&=3(0)^2+5(0)−2 \\ &=−2 \end{align}\]

So the y-intercept is at \((0,−2)\).

For the x-intercepts, we find all solutions of \(f(x)=0\).

\[0=3x^2+5x−2\]

In this case, the quadratic can be factored easily, providing the simplest method for solution.

\[0=(3x−1)(x+2)\]

\[\begin{align} 0&=3x−1 & 0&=x+2 \\ x&= \frac{1}{3} &\text{or} \;\;\;\;\;\;\;\; x&=−2 \end{align}\]

So the x-intercepts are at \((\frac{1}{3},0)\) and \((−2,0)\).

By graphing the function, we can confirm that the graph crosses the \(y\)-axis at \((0,−2)\). We can also confirm that the graph crosses the x-axis at \(\Big(\frac{1}{3},0\Big)\) and \((−2,0)\). See Figure \(\PageIndex{14}\).

Rewriting Quadratics in Standard Form

In Example \(\PageIndex{7}\), the quadratic was easily solved by factoring. However, there are many quadratics that cannot be factored. We can solve these quadratics by first rewriting them in standard form.

• Substitute a and \(b\) into \(h=−\frac{b}{2a}\).
• Substitute \(x=h\) into the general form of the quadratic function to find \(k\).
• Rewrite the quadratic in standard form using \(h\) and \(k\).
• Solve for when the output of the function will be zero to find the x-intercepts.

Example \(\PageIndex{8}\): Finding the x-Intercepts of a Parabola

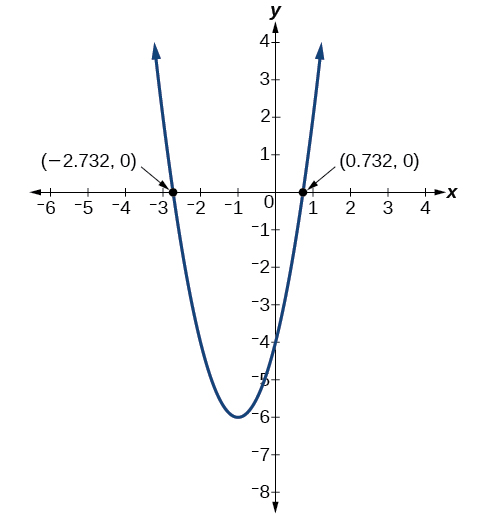
Find the x-intercepts of the quadratic function \(f(x)=2x^2+4x−4\).

We begin by solving for when the output will be zero.

\[0=2x^2+4x−4 \nonumber\]

Because the quadratic is not easily factorable in this case, we solve for the intercepts by first rewriting the quadratic in standard form.

\[f(x)=a(x−h)^2+k\nonumber\]

We know that \(a=2\). Then we solve for \(h\) and \(k\).

\[\begin{align*} h&=−\dfrac{b}{2a} & k&=f(−1) \\ &=−\dfrac{4}{2(2)} & &=2(−1)^2+4(−1)−4 \\ &=−1 & &=−6 \end{align*}\]

So now we can rewrite in standard form.

\[f(x)=2(x+1)^2−6\nonumber\]

We can now solve for when the output will be zero.

\[\begin{align*} 0&=2(x+1)^2−6 \\ 6&=2(x+1)^2 \\ 3&=(x+1)^2 \\ x+1&={\pm}\sqrt{3} \\ x&=−1{\pm}\sqrt{3} \end{align*}\]

The graph has x-intercepts at \((−1−\sqrt{3},0)\) and \((−1+\sqrt{3},0)\).

We can check our work by graphing the given function on a graphing utility and observing the x-intercepts. See Figure \(\PageIndex{15}\).

Exercise \(\PageIndex{1}\)

In Try It \(\PageIndex{1}\), we found the standard and general form for the function \(g(x)=13+x^2−6x\). Now find the y- and x-intercepts (if any).

y-intercept at \((0, 13)\), No x-intercepts

Example \(\PageIndex{9}\): Solving a Quadratic Equation with the Quadratic Formula

Solve \(x^2+x+2=0\).

Let’s begin by writing the quadratic formula: \(x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}\).

When applying the quadratic formula, we identify the coefficients \(a\), \(b\) and \(c\). For the equation \(x^2+x+2=0\), we have \(a=1\), \(b=1\), and \(c=2\). Substituting these values into the formula we have:

\[\begin{align*} x&=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a} \\ &=\dfrac{−1{\pm}\sqrt{1^2−4⋅1⋅(2)}}{2⋅1} \\ &=\dfrac{−1{\pm}\sqrt{1−8}}{2} \\ &=\dfrac{−1{\pm}\sqrt{−7}}{2} \\ &=\dfrac{−1{\pm}i\sqrt{7}}{2} \end{align*}\]

The solutions to the equation are \(x=\frac{−1+i\sqrt{7}}{2}\) and \(x=\frac{−1-i\sqrt{7}}{2}\) or \(x=−\frac{1}{2}+\frac{i\sqrt{7}}{2}\) and \(x=\frac{-1}{2}−\frac{i\sqrt{7}}{2}\).

Example \(\PageIndex{10}\): Applying the Vertex and x-Intercepts of a Parabola

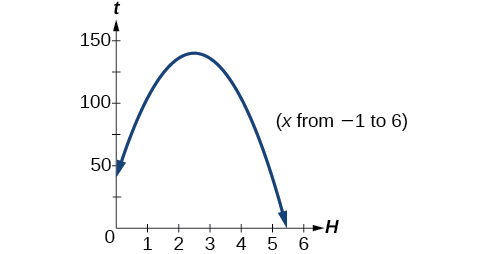
A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation \(H(t)=−16t^2+80t+40\).

When does the ball reach the maximum height? What is the maximum height of the ball? When does the ball hit the ground?

The ball reaches the maximum height at the vertex of the parabola. \[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]

The ball reaches a maximum height after 2.5 seconds.

To find the maximum height, find the y-coordinate of the vertex of the parabola. \[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]

The ball reaches a maximum height of 140 feet.

To find when the ball hits the ground, we need to determine when the height is zero, \(H(t)=0\).

We use the quadratic formula.

\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]

Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.

\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]

The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds. See Figure \(\PageIndex{16}\).

• When does the rock reach the maximum height?
• What is the maximum height of the rock?
• When does the rock hit the ocean?

a. 3 seconds b. 256 feet c. 7 seconds

Key Equations

• general form of a quadratic function: \(f(x)=ax^2+bx+c\)
• the quadratic formula: \(x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}\)
• standard form of a quadratic function: \(f(x)=a(x−h)^2+k\)

Key Concepts

• A polynomial function of degree two is called a quadratic function.
• The graph of a quadratic function is a parabola. A parabola is a U-shaped curve that can open either up or down.
• The axis of symmetry is the vertical line passing through the vertex. The zeros, or x-intercepts, are the points at which the parabola crosses the x-axis. The y-intercept is the point at which the parabola crosses the \(y\)-axis.
• Quadratic functions are often written in general form. Standard or vertex form is useful to easily identify the vertex of a parabola. Either form can be written from a graph.
• The vertex can be found from an equation representing a quadratic function. .
• The domain of a quadratic function is all real numbers. The range varies with the function.
• A quadratic function’s minimum or maximum value is given by the y-value of the vertex.
• The minimum or maximum value of a quadratic function can be used to determine the range of the function and to solve many kinds of real-world problems, including problems involving area and revenue.
• Some quadratic equations must be solved by using the quadratic formula.
• The vertex and the intercepts can be identified and interpreted to solve real-world problems.

axis of symmetry a vertical line drawn through the vertex of a parabola around which the parabola is symmetric; it is defined by \(x=−\frac{b}{2a}\).

general form of a quadratic function the function that describes a parabola, written in the form \(f(x)=ax^2+bx+c\), where \(a,b,\) and \(c\) are real numbers and a≠0.

standard form of a quadratic function the function that describes a parabola, written in the form \(f(x)=a(x−h)^2+k\), where \((h, k)\) is the vertex.

vertex the point at which a parabola changes direction, corresponding to the minimum or maximum value of the quadratic function

vertex form of a quadratic function another name for the standard form of a quadratic function

zeros in a given function, the values of \(x\) at which \(y=0\), also called roots

Transformations of Quadratic Functions

Learning outcomes.

• Graph vertical and horizontal shifts of quadratic functions
• Graph vertical compressions and stretches of quadratic functions
• Write the equation of a transformed quadratic function using the vertex form
• Identify the vertex and axis of symmetry for a given quadratic function in vertex form

The standard form of a quadratic function presents the function in the form

[latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]

where [latex]\left(h,\text{ }k\right)[/latex] is the vertex. Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function .

The standard form is useful for determining how the graph is transformed from the graph of [latex]y={x}^{2}[/latex]. The figure below is the graph of this basic function.

Shift Up and Down by Changing the Value of [latex]k[/latex]

You can represent a vertical (up, down) shift of the graph of [latex]f(x)=x^2[/latex] by adding or subtracting a constant, [latex]k[/latex].

[latex]f(x)=x^2 + k[/latex]

 If [latex]k>0[/latex], the graph shifts upward, whereas if [latex]k<0[/latex], the graph shifts downward.

Using an online graphing calculator, plot the function [latex]f(x)=x^2+k[/latex]. Now change the [latex]k[/latex] value to shift the graph down 4 units, then up 4 units.

The equation for the graph of [latex]f(x)=x^2[/latex] that has been shifted up 4 units is

[latex]f(x)=x^2+4[/latex]

The equation for the graph of [latex]f(x)=x^2[/latex] that has been shifted down 4 units is

[latex]f(x)=x^2-4[/latex]

Shift left and right by changing the value of [latex]h[/latex]

You can represent a horizontal (left, right) shift of the graph of [latex]f(x)=x^2[/latex] by adding or subtracting a constant, [latex]h[/latex], to the variable [latex]x[/latex], before squaring.

[latex]f(x)=(x-h)^2 [/latex]

If [latex]h>0[/latex], the graph shifts toward the right and if [latex]h<0[/latex], the graph shifts to the left.

tip for success

Remember that the negative sign inside the argument of the vertex form of a parabola (in the parentheses with the variable [latex]x[/latex] ) is part of the formula [latex]f(x)=(x-h)^2 +k[/latex].

If [latex]h>0[/latex], we have [latex]f(x)=(x-h)^2 +k[/latex]. You’ll see the negative sign, but the graph will shift right.

If  [latex]h<0[/latex], we have [latex]f(x)=(x-(-h))^2 +k \rightarrow f(x)=(x+h)^2+k[/latex]. You’ll see the positive sign, but the graph will shift left.

Using an online graphing calculator, plot the function [latex]f(x)=(x-h)^2[/latex]. Now change the [latex]h[/latex] value to shift the graph 2 units to the right, then 2 units to the left.

The equation for the graph of [latex]f(x)=x^2[/latex] that has been shifted right 2 units is

[latex]f(x)=(x-2)^2[/latex]

The equation for the graph of [latex]f(x)=^2[/latex] that has been shifted left 2 units is

[latex]f(x)=(x+2)^2[/latex]

Stretch or compress by changing the value of [latex]a[/latex].

You can represent a stretch or compression (narrowing, widening) of the graph of [latex]f(x)=x^2[/latex] by multiplying the squared variable by a constant, [latex]a[/latex].

[latex]f(x)=ax^2 [/latex]

The magnitude of [latex]a[/latex] indicates the stretch of the graph. If [latex]|a|>1[/latex], the point associated with a particular [latex]x[/latex]-value shifts farther from the [latex]x[/latex] – axis, so the graph appears to become narrower, and there is a vertical stretch. But if [latex]|a|<1[/latex], the point associated with a particular [latex]x[/latex]-value shifts closer to the [latex]x[/latex] – axis, so the graph appears to become wider, but in fact there is a vertical compression.

Using an online graphing calculator plot the function [latex]f(x)=ax^2[/latex]. Now adjust the [latex]a[/latex] value to create a graph that has been compressed vertically by a factor of [latex]\frac{1}{2}[/latex] and another that has been vertically stretched by a factor of 3. What are the equations of the two graphs?

The equation for the graph of [latex]f(x)=x^2[/latex] that has been compressed vertically by a factor of [latex]\frac{1}{2}[/latex] is

[latex]f(x)=\frac{1}{2}x^2[/latex]

The equation for the graph of [latex]f(x)=x^2[/latex] that has been vertically stretched by a factor of 3 is

[latex]f(x)=3x^2[/latex]

The standard form and the general form are equivalent methods of describing the same function. We can see this by expanding out the general form and setting it equal to the standard form.

This is the [latex]x[/latex] coordinate of the vertexr and [latex]x=-\dfrac{b}{2a}[/latex] is the  axis of symmetry we defined earlier. Setting the constant terms equal gives us:

In practice, though, it is usually easier to remember that [latex]h[/latex] is the output value of the function when the input is [latex]h[/latex], so [latex]f\left(h\right)=f\left(-\dfrac{b}{2a}\right)=k[/latex].

Using an online graphing calculator plot the function [latex]f\left(x\right)\ =\ a\left(x-h\right)^2+k[/latex]. Now adjust the variables [latex]a,h,k[/latex] to define two quadratic functions whose axis of symmetry is [latex]x=-3[/latex], and whose vertex is [latex](-3, 2)[/latex].

How many potential values are there for [latex]h[/latex] in this scenario? How about [latex]k[/latex]? How about [latex]a[/latex]

There is only one [latex](h,k)[/latex] pair that will satisfy these conditions, [latex](-3,2)[/latex].  The value of [latex]a[/latex] does not affect the line of symmetry or the vertex of a quadratic graph, so [latex]a[/latex] can take on any value.

 Challenge Problem

Define a function whose axis of symmetry is [latex]x = -3[/latex], and whose vertex is [latex](-3,2)[/latex] and has an average rate of change of 2 on the interval [latex][-2,0][/latex].

Use the online graphing calculator where you plotted [latex]f\left(x\right)\ =\ a\left(x-h\right)^2+k[/latex] to help with this.

A coordinate grid has been superimposed over the quadratic path of a basketball in the picture below. Find an equation for the path of the ball. Does the shooter make the basket?

(credit: modification of work by Dan Meyer)

The path passes through the origin and has vertex at [latex]\left(-4,\text{ }7\right)[/latex], so [latex]\left(h\right)x=-\frac{7}{16}{\left(x+4\right)}^{2}+7[/latex]. To make the shot, [latex]h\left(-7.5\right)[/latex] would need to be about 4 but [latex]h\left(-7.5\right)\approx 1.64[/latex]; he doesn’t make it.

• Interactive: Transform Quadratic 1. Provided by : Lumen Learning (with Desmos). Located at : https://www.desmos.com/calculator/fpatj6tbcn . License : CC BY: Attribution
• Interactive: Transform Quadratic 2. Provided by : Lumen Learning (with Desmos). Located at : https://www.desmos.com/calculator/5g3xfhkklq . License : CC BY: Attribution
• Interactive: Transform Quadratic 3. Provided by : Lumen Learning (with Desmos). Located at : https://www.desmos.com/calculator/ha6gh59rq7 . License : CC BY: Attribution
• Interactive: Transform Quadratic 4. Provided by : Lumen Learning (with Desmos). Located at : https://www.desmos.com/calculator/pimelalx4i . License : CC BY: Attribution
• Revision and Adaptation. Provided by : Lumen Learning. License : CC BY: Attribution
• College Algebra. Authored by : Abramson, Jay et al.. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]

Privacy Policy

The Federal Register

The daily journal of the united states government, request access.

Due to aggressive automated scraping of FederalRegister.gov and eCFR.gov, programmatic access to these sites is limited to access to our extensive developer APIs.

If you are human user receiving this message, we can add your IP address to a set of IPs that can access FederalRegister.gov & eCFR.gov; complete the CAPTCHA (bot test) below and click "Request Access". This process will be necessary for each IP address you wish to access the site from, requests are valid for approximately one quarter (three months) after which the process may need to be repeated.

An official website of the United States government.

If you want to request a wider IP range, first request access for your current IP, and then use the "Site Feedback" button found in the lower left-hand side to make the request.