High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:

Triangular pyramid
Here you will learn about triangular pyramids, including what a triangular pyramid is and how to find the volume and surface area of triangular pyramids.
Students will first learn about triangular pyramids as part of geometry in 1 st grade. In middle school and high school, students will expand their knowledge of triangular pyramids when they learn to find the volume and the surface area of a triangular pyramid.
What is a triangular pyramid?
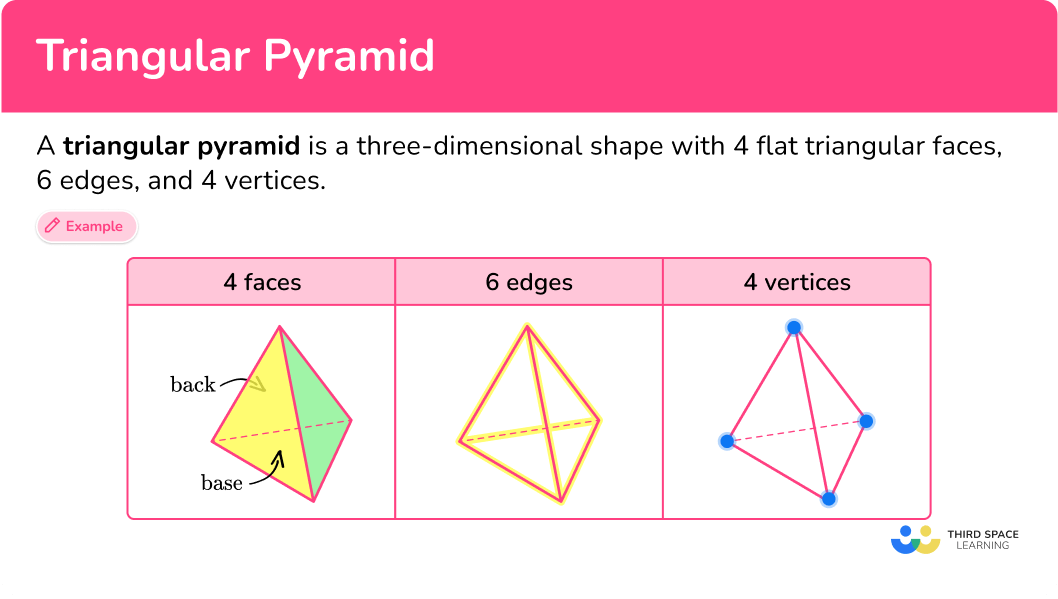
A triangular pyramid is a three-dimensional shape with 4 flat triangular faces, 6 edges and 4 vertices. Another name for a triangular pyramid is tetrahedron .
| faces | edges | vertices |
|---|---|---|
Types of triangular pyramids
There are two main types of triangular pyramids, right triangular pyramids and irregular pyramids.
A right triangular pyramid is a triangular pyramid which has an equilateral triangle as its base and the apex is directly above the center of the triangle base, forming a right angle. The other 3 faces are congruent isosceles triangles. If all of the faces are congruent equilateral triangles it is a regular triangular pyramid or regular tetrahedron .
An irregular triangular pyramid is a triangular pyramid where its base is not an equilateral triangle.
Net of a triangular pyramid
The net of a triangular pyramid is made of 4 triangles. This net shows 4 equilateral triangles, therefore, this is the net of a regular tetrahedron. The prefix “tetra” comes from the 4 triangular faces.

Volume of a triangular pyramid
The volume of a triangular pyramid can be found by using the formula,
\text{Volume}=\cfrac{1}{3}\times \text{area of base} \times \text{height}.
You may be given the area of the triangular base or be asked to work it out. The pyramid height should be perpendicular to its base.
This can be written as,
V=\cfrac{1}{3} \, Bh
- V represents the volume of the pyramid.
- B represents the area of the base of the pyramid.
- h represents the perpendicular height of the pyramid.
Surface area of a triangular pyramid
The surface area of a triangular pyramid is calculated by finding the area of each of the triangular faces and adding them together.
If the faces of the triangular pyramid are all the same size, you can find the area of one face and multiply it by 4.
If the faces are different, you will need to work out the area of each face and add them together.
For example, find the surface area of the regular tetrahedron.
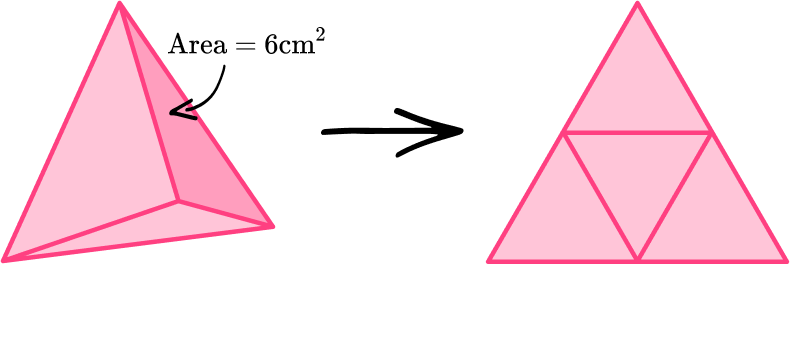
Area of each triangular face = 6 \mathrm{~cm}^2
There are 4 triangular faces, so multiply 6 \mathrm{~cm}^2 by 4 to give 24 \mathrm{~cm}^2.
Total surface area = 24 \mathrm{~cm}^2
Common Core State Standards
How does this relate to 1 st grade, 6 th grade and 7 th grade math?
- Grade 1: Geometry (1.G.A.2) Compose two-dimensional shapes (rectangles, squares, trapezoids, triangles, half-circles, and quarter-circles) or three-dimensional shapes (cubes, right rectangular prisms, right circular cones, and right circular cylinders) to create a composite shape, and compose new shapes from the composite shape.
- Grade 6: Geometry (6.G.A.4) Represent three-dimensional figures using nets made up of rectangles and triangles, and use the nets to find the surface area of these figures. Apply these techniques in the context of solving real-world and mathematical problems.
- Grade 7: Geometry (7.G.B.6) Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.
How to identify a triangular pyramid
In order to identify a triangular pyramid, you will:
Look for the characteristics of a triangular pyramid.
State whether or not the shape is a triangular pyramid.
- If the shape is not a triangular pyramid, explain what characteristics are different.
![triangular pyramid problem solving [FREE] 3D Shape Check for Understanding (Grade 1, 5 and 6)](https://thirdspacelearning.com/wp-content/uploads/2023/11/3D-Shape-listing-image.png)
[FREE] 3D Shape Check for Understanding (Grade 1, 5 and 6)
Use this quiz to check your grade 1, 5 and 6 students’ understanding of 3D shape. 10+ questions with answers covering a range of 1st, 5th and 6th grade 3D shape topics to identify areas of strength and support!
Triangular pyramid examples
Example 1: identifying triangular pyramids.
Look at the image below and determine if it’s a triangular pyramid or not.

- Look for the characteristics of a triangular pyramid.
A triangular pyramid is a 3D shape with 4 triangular faces, 6 edges and 4 vertices.
This shape has 2 triangular faces, 3 rectangular faces, 9 edges and 6 vertices.
2 State whether or not the shape is a triangular pyramid.
This shape is not a triangular pyramid, it is a triangular prism.
3 If the shape is not a triangular pyramid, explain what characteristics are different.
The triangular prism has 2 triangular side faces and 3 rectangular faces, 9 edges and 6 vertices.
Example 2: identifying triangular pyramids

This shape has 4 triangular faces, 6 edges and 4 vertices.
This shape is a triangular pyramid.
How to calculate the volume of a triangular pyramid
In order to calculate the volume of a triangular pyramid:
Calculate the area of the base.
Substitute values into the formula and solve.
Write the answer, including the units.
Example 3: calculating the volume
Find the volume of the pyramid. The area of the base is 20 \mathrm{~cm}^2.
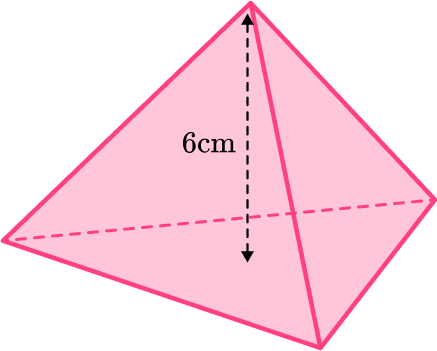
The area of the base is given to you and is 20 \mathrm{~cm}^2.
The volume of the triangular pyramid can be found by using the formula,
V=\cfrac{1}{3} \, Bh.
\begin{aligned}& B=20 \mathrm{~cm}^2 \text { and } \\\\ & h=6 \mathrm{~cm}\end{aligned}
Substitute the values that have been given into the formula:
V=\cfrac{1}{3}\times 20 \times 6.
\text {Volume}=\cfrac{1}{3}\times 20 \times 6 =40.
The volume of the triangular pyramid is 40 \mathrm{~cm}^3.
Example 4: calculating height given the volume and area
Find the height of the pyramid with volume 150 \mathrm{~cm}^3 and the base area of 60 \mathrm{~cm}^2.
The area of the base is given to you and is 60 \mathrm{~cm}^2.
B=60 \mathrm{~cm}^2 , and h is unknown.
Substitute the values that have been given into the formula,
150=\cfrac{1}{3}\times 60 \times h.
This can be rearranged to give,
h=\cfrac{150\times 3}{60}=7.5.
The height of the pyramid is 7.5 \mathrm{~cm}.
Example 5: calculating base area given the height of the pyramid
The volume of the pyramid below is 40 \mathrm{~m}^3. Find the base area.
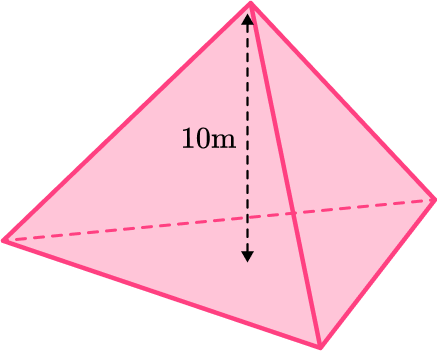
Use the formula for the volume of a pyramid.
40=\cfrac{1}{3}\times B\times 10.
Work out the answer.
B=\cfrac{40\times 3}{10}=12.
The area of the base of the pyramid is 12 \mathrm{~cm}^2.
How to calculate the surface area of a triangular pyramid
In order to find the surface area of a triangular pyramid:
Calculate the area of each face.
Add the area of each face together.
Include the units.
Example 6: working out the total surface area
Find the total surface area of a triangular pyramid made of equilateral triangles. The area of each face is 20 \mathrm{~cm}^2.
This step is not needed, because you are given the area of each face, which is 20 \mathrm{~cm}^2.
A triangular pyramid is made of 4 triangular faces.
You are told that all 4 faces are the same and each face has an area of 20 \mathrm{~cm}^2.
Therefore, the total surface area can be found by multiplying 20 by 4.

4\times 20=80
The total surface area is 80 \mathrm{~cm}^2.
Teaching tips for triangular pyramid
- Provide students with manipulatives, such as pyramid-shaped blocks or cut-outs, that they can hold and manipulate. Encourage them to examine the different faces, edges, and vertices of the pyramid.
- Help students make connections between triangular pyramids and other geometric shapes. For example, discuss how a triangular pyramid can be seen as a combination of a triangle and a point (vertex), or how it relates to the concept of a tetrahedron. This helps deepen their understanding of geometric relationships.
- Provide students with problem-solving activities that involve triangular pyramids, instead of practice worksheets. For example, give them a scenario where they need to calculate the height of a pyramid or find the dimensions of a base given the volume.
Easy mistakes to make
- Not using the perpendicular height The height of the pyramid needs to be the perpendicular height. This is the height that is at a right-angle to the base.
- Using the wrong units Remember to use cubic units for volume such as \mathrm{cm}^3 \text { or } \mathrm{m}^3. Square units are for area, for example \mathrm{cm}^2 or \mathrm{m}^2.
- Mixing up the different triangular pyramid formulas There are many different volume formulas in math. Make sure that you use the correct one to work out the volume of a pyramid. \text{Volume}=\cfrac{1}{3}\times \text{area of base} \times \text{height} Or V=\cfrac{1}{3} \, Bh.
Related 3D shapes lessons
- Hemisphere shape
- Sphere shape
- Pyramid shape
- Square pyramid
- 3D shape names
- Angles of elevation and depression
Practice triangular pyramid questions
1. Which shape is a triangular pyramid?

2. Which shape is a triangular pyramid?

3. The area of the base of this triangular pyramid is 40 \mathrm{~cm}^2. Find its volume.
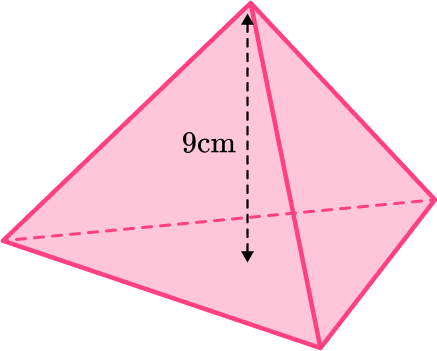
You can find the volume of a pyramid by using the formula:
B=40 \mathrm{~cm}^2 \text { and } h=9 \mathrm{~cm}.
Substitute the values that have been given into the formula and work out the volume,
V=\cfrac{1}{3}\times 40 \times 9=120.
The volume of the triangular pyramid is 120 \mathrm{~cm}^3.
4. The volume of a triangular pyramid is 100 \mathrm{~cm}^3. The area of its base is 25 \mathrm{~cm}^2. Find the height of the triangular pyramid.
Use the formula for volume of a pyramid:
V=100 \mathrm{~cm}^3 \text { and } B=25 \mathrm{~cm}^2.
100=\cfrac{1}{3}\times 25 \times h.
You can rearrange this to find the height,
h=\cfrac{100\times 3}{25}=12.
The height of the triangular pyramid is 12 \mathrm{~cm}.
5. The volume of a triangular pyramid is 80 \mathrm{~cm}^3. The height is 9.7 \mathrm{~cm}. Find the area of the base of the triangular pyramid. Round your answer to the tenths place.
Use the formula for volume of a pyramid,
V=80 \mathrm{~cm}^3 \text { and } h=9.7 \mathrm{~cm}.
80=\cfrac{1}{3}\times B \times 9.7
You can rearrange this to find the base area,
B=\cfrac{80\times 3}{9.7}=24.742…
The area of the base is 24.7 \mathrm{~cm}^2 when rounded to the tenths place.
6. A triangular pyramid is made from 4 equilateral triangles. If the area of one of the faces is 21 \mathrm{~cm}^2, find the total surface area of the triangular pyramid.
A triangular pyramid has 4 faces. If all the faces are the same, you can find the total surface area by multiplying by 4.
You are told that the pyramid is made up of 4 equilateral triangles with an area of 21 \mathrm{~cm}^2.
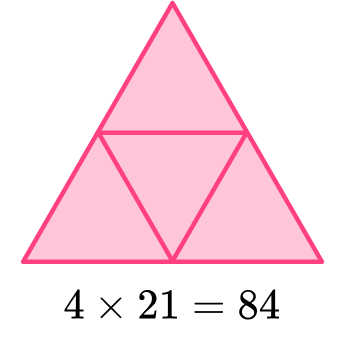
The total surface area is 84 \mathrm{~cm}^2.
Triangular pyramid FAQs
A triangular pyramid, also known as a tetrahedron, is a polyhedron with a triangular base and three triangular faces that converge at a single point called the vertex.
A pyramid is a polyhedra with a flat base and triangular sides which meet at the apex. The flat base can be any polygon. Pyramids can come in different forms such as a square pyramid, a rectangular pyramid or even a pentagonal pyramid.
To calculate the volume of a triangular pyramid, you need to multiply the base area by the height and divide the result by 3. The formula is: \text { Volume }=\cfrac{1}{3} \times \text { Base Area } \times \text { Height } The base area is the area of the triangular base, and the height is the perpendicular distance from the base to the apex.
To calculate the surface area of a triangular pyramid, you need to find the area of each triangular face and sum them up. You can use the surface area of a triangular pyramid formula: \text { Surface Area }=\cfrac{1}{2} \times \text { Base Perimeter } \times \text { Slant Height }+ \text { Base Area } The base perimeter is the sum of the lengths of the base triangle’s sides, and the slant height is the distance from the apex to the base along one of the triangular faces.
The next lessons are
- Surface area
- Area of a quadrilateral
- Range in math
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview
Triangular Pyramid — How To Find Volume & Surface Area (Formulas)
Triangular pyramid.
A triangular pyramid is a three-dimensional solid – a polyhedron – with a triangular base and three triangular faces meeting at the pyramid’s apex.
The base of a pyramid can be any two-dimensional geometric shape:
There are many types of pyramids, and all pyramids are named by the shape of their bases.
Just as you can have a triangular pyramid, you can also have a rectangular pyramid, a pentagonal pyramid, etc.

The Great Pyramids of Egypt in Giza, for example, is a square pyramid because its base (bottom) is a square. A triangular pyramid is a pyramid with a triangular base.
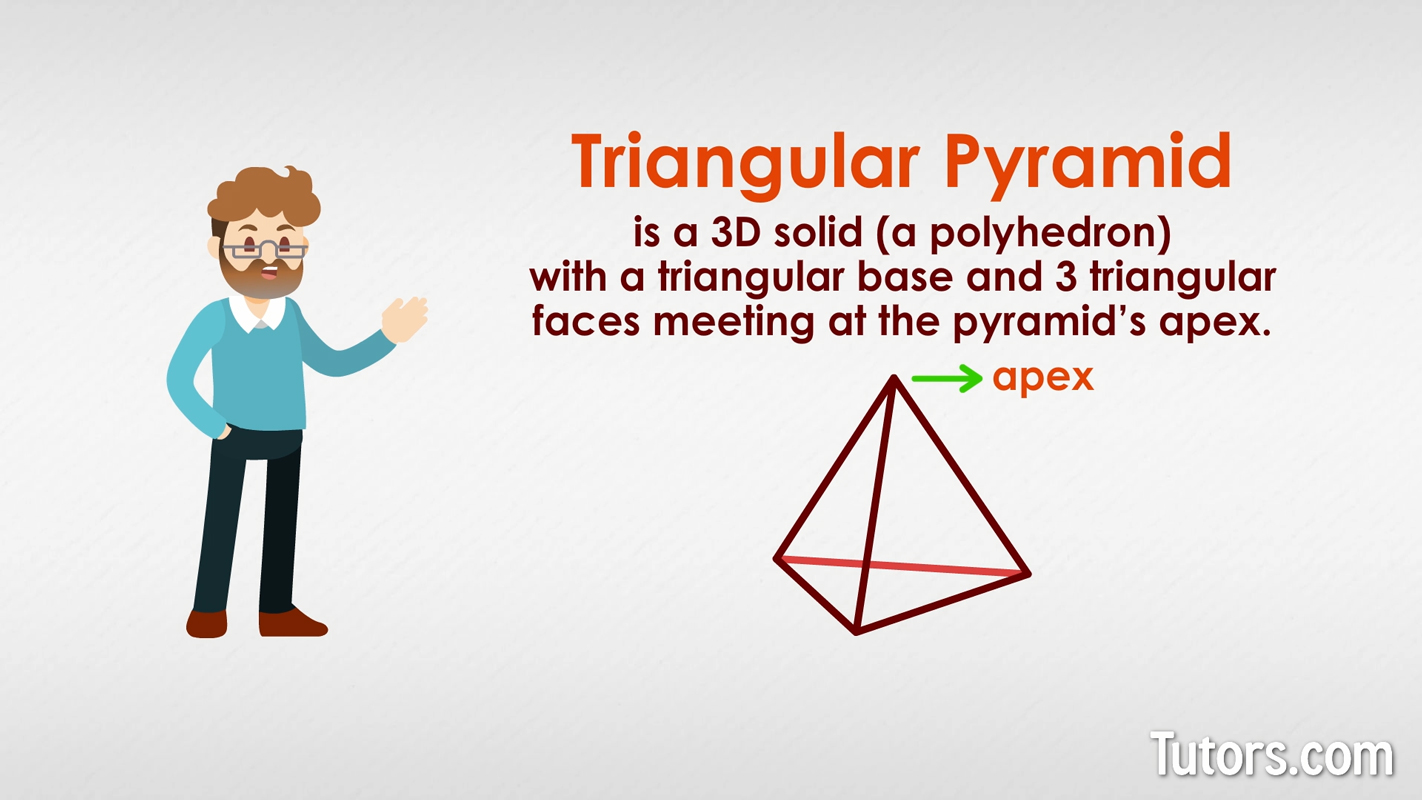
Triangular pyramid faces, edges, and vertices
A triangular pyramid has:
Triangular base
3 triangular faces

Regular triangular pyramid
A pyramid with an equilateral triangle base is a regular triangular pyramid . If a scalene or isosceles triangle forms the base, then the pyramid is a non-regular triangular pyramid .
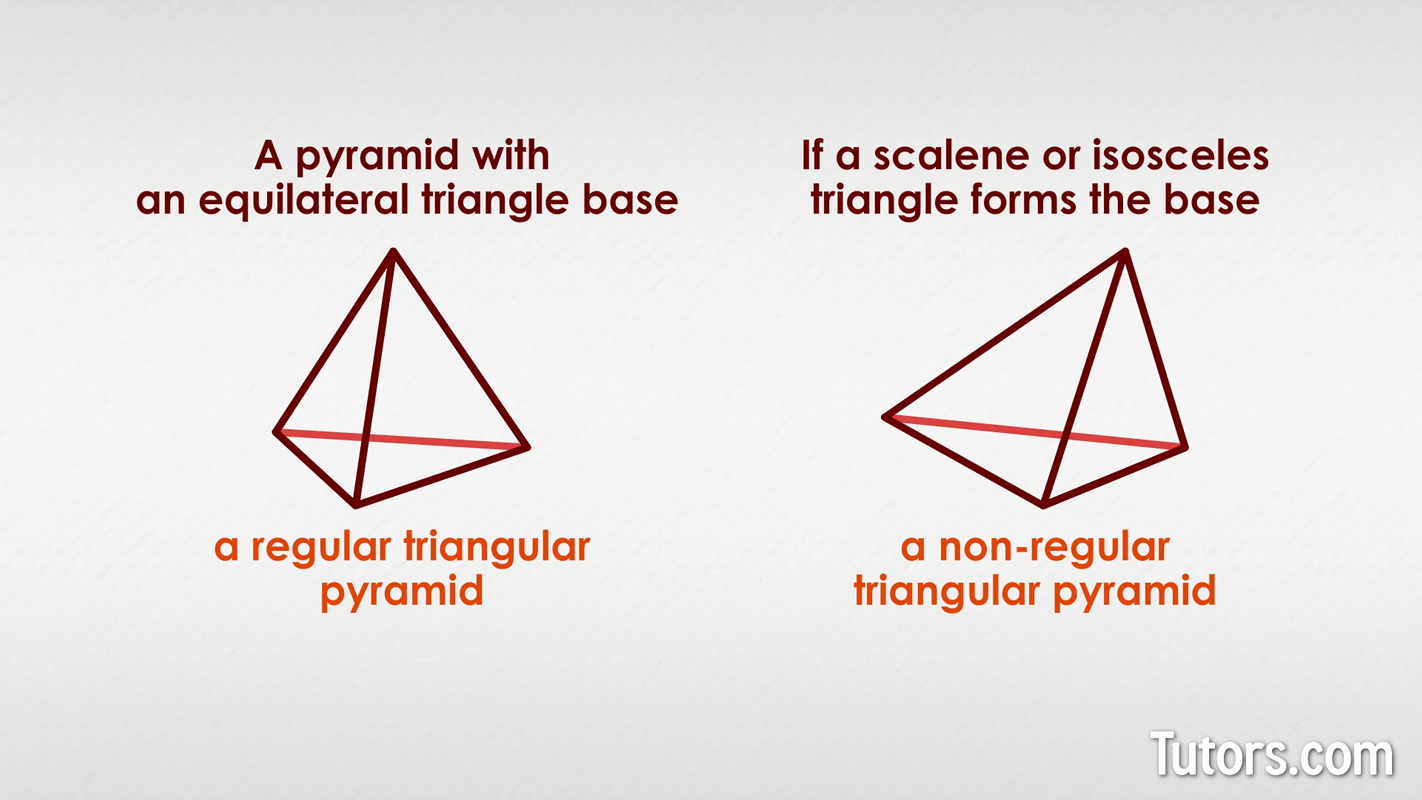
No rule requires the base of a triangular pyramid to be an equilateral triangle, though constructing scalene or isosceles triangular pyramids is far harder than constructing an equilateral triangular pyramid.
Surface area of a triangular pyramid
Two different surface area measurements can be taken for any 3D solid: the lateral surface area and the surface area .
Lateral surface area, LSA , does not include the base for our pyramid. The surface area of a pyramid, SA , includes the base.

The surface area of a triangular pyramid with three congruent, visible faces is the area of those three triangular faces, plus the area of the triangular base.
The formula for calculating the surface area involves the area of the base, the perimeter of the base, and the slant height of any side.
Surface area of a triangular pyramid formula
This formula works because you are adding the base area to the area of all three slanted faces. The perimeter gives you the sum of all three bases. You multiply that sum times the slant height of the triangular pyramid as though you had one big rectangle, and then you take one-half of that as the area of the three triangles.
How to find the surface area of a triangular pyramid
Suppose you have this triangular pyramid:
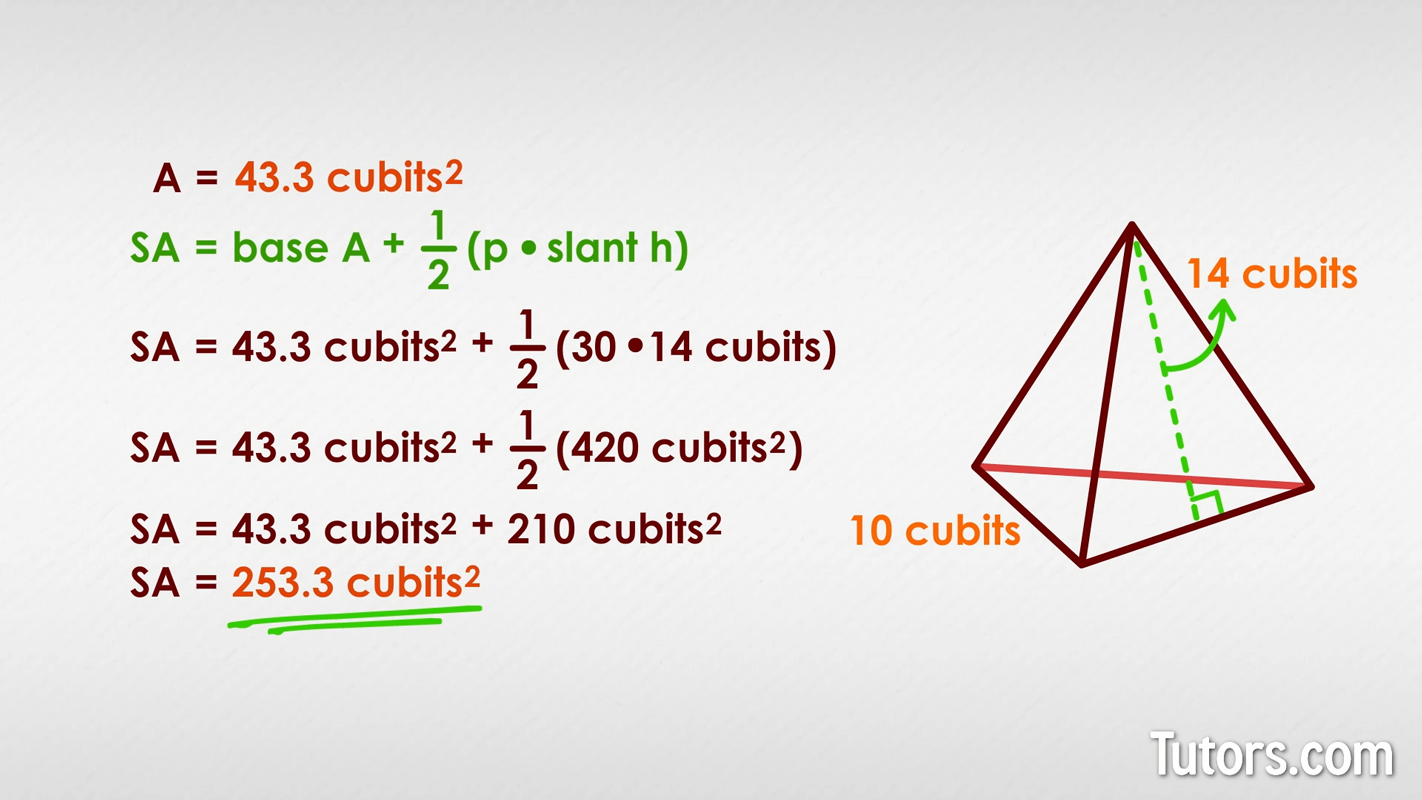
The base of the pyramid is an equilateral triangle since all three of its sides are 10 cubits . To find the area of the base triangle, use this formula for the area of an equilateral triangle with sides a :
For this particular triangular pyramid, the formula works out as:
We have now found the area of the base. We already know the perimeter of the base is 30 cubits (the three sides are each 10 cubits ), and we are given the slant height, 14 cubits .
Area is always measured in square units, whether they are c m 2 c{m}^{2} c m 2 , m 2 {m}^{2} m 2 , f t 2 f{t}^{2} f t 2 , or c u b i t s 2 cubit{s}^{2} c u bi t s 2 .
How to calculate lateral surface area of a triangular pyramid
You may have needed to take your time getting through all that, finding the area of the base, finding the perimeter, adding everything.
To find the area of just the slanted sides – the lateral surface area ( LSA ) – you need to do a lot less work:
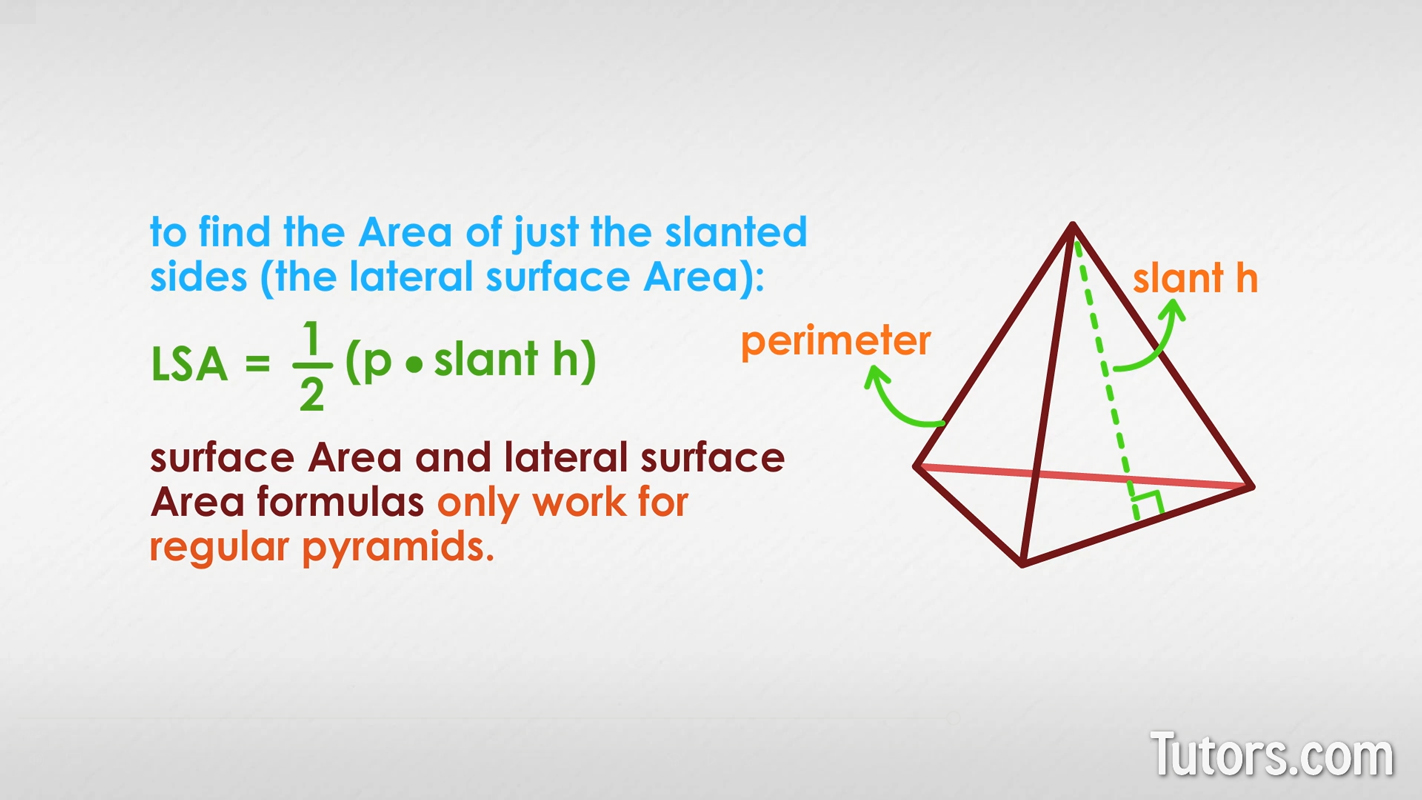
These formulas only work for regular pyramids. If you have a non-regular triangular pyramid, calculate the area of each of the four faces individually (three slanted faces and the base) and add them together.
Volume of a triangular pyramid
Volume is the amount of space a 3D solid takes up, so, with a triangular pyramid, we are finding how much room it has inside it. It is always measured in cubic units. Though the pyramid rapidly diminishes to an apex, the calculation is not hard.
Triangular pyramid volume formula
In the volume of a triangular pyramid formula, A is the area of the base and h is the height from base to apex.
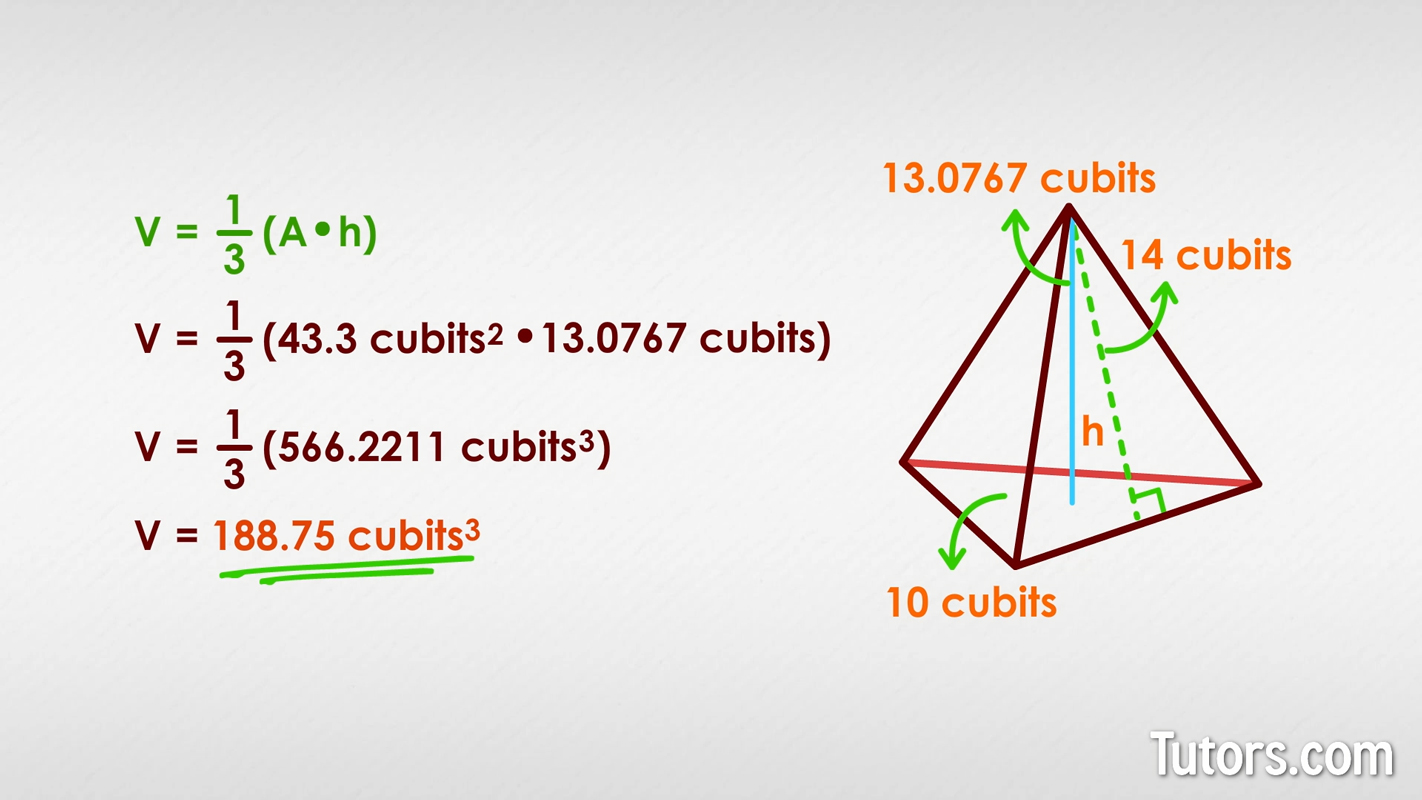
For our pyramid with a base 10 cubits and slant height of 14 cubits , the height, h , works out to 13.0767 cubits . We already know the area from our earlier calculations, so we can plug the know numbers in to get the volume in cubic cubits:
Please note that, with the fraction as a factor in our multiplication, we do not have a precise decimal answer, so we have an approximate value.

- Math Formulas
Triangular Pyramid Formula

When you think about a Pyramid, the first thing that comes to your mind is the Great Pyramids of Egypt. If you observe the shape of the Great Pyramid of Egypt, then you will notice that the pyramid has a base, that is square shaped. Hence, those pyramids are called Square Pyramid. Similarly, in the triangular pyramid the base of the same is triangular .
When a base is constructed to connect to the apex , a pyramid is formed. A pyramid that had a triangular base is a triangular pyramid. It is also known as the tetrahedron which has equilateral triangles for each of its faces. The illustration below will make it clear what the triangular pyramid looks like.
There are majorly two formulas for triangular pyramid:
Surface area of triangular pyramid = A + 3a
where A is the base area and ‘a’ is the area of one of pyramid’s faces.
Examples of Triangular Pyramid
Question 1: Find the volume of a triangular pyramid when base area is \(\begin{array}{l}9\;cm^{2}\end{array} \) and height is 4 cm ?
Solution: Given, Base area = \(\begin{array}{l}9\;cm^{2}\end{array} \) Height = 4 cm
\(\begin{array}{l}Volume\;of\;a\;triangular\;pyramid=\frac{1}{3}\;Base\;Area\times Height\end{array} \)
| FORMULAS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
- Scientific Notation
Table of Contents
Last modified on August 3rd, 2023
#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline
Surface area of a triangular pyramid.
The surface area, or total surface area (TSA), of a triangular pyramid, is the entire space occupied by its four faces. It is measured in square units such as m 2 , cm 2 , mm 2 , and in 2 .
The formula is:
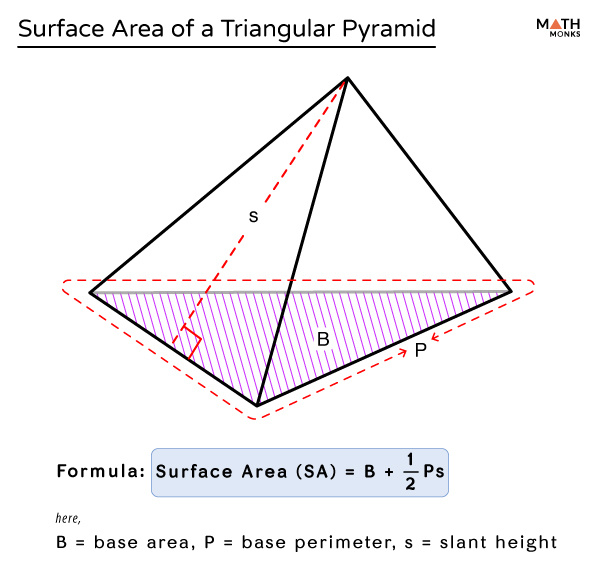
The formula to calculate the surface area of a triangular pyramid also includes its lateral surface area (LSA).
Lateral Surface Area (LSA) = ${\dfrac{1}{2}Ps}$ , here P = base perimeter, s = slant height
∴ Total Surface Area ( TSA ) = B + LSA
Let us solve some example to understand the above concept better.
Solved Examples
Find the surface area of a regular triangular pyramid with a base area of 43 cm 2 , a base perimeter of 30 cm, and a slant height of 8 cm.
As we know, Total Surface Area ( TSA ) = ${B+\dfrac{1}{2}Ps}$, here B = 43 cm 2 , P = 30 cm, s = 8 cm ∴ TSA = ${43+\dfrac{1}{2}\times 30\times 8}$, = 163 cm 2
Calculate the lateral and total surface area of a triangular-based pyramid with a base of 20 cm, a base height of 12 cm, and a slant height of 19 cm.
As we know, Lateral Surface Area ( LSA ) = ${\dfrac{1}{2}Ps}$, P = 3 × b, here b = 20 cm ∴ LSA = ${\dfrac{3}{2}bs}$, here b = 20 cm, s = 14 cm = ${\dfrac{3}{2}\times 20\times 14}$ = 570 cm 2 Total Surface Area ( TSA ) = B + LSA Now, B = ${\dfrac{1}{2}bH}$, here b = 20 cm, H = 12 cm ∴ ${TSA=\dfrac{1}{2}bH+LSA}$, here b = 20 cm, H = 12 cm, LSA = 570 cm 2 ∴ ${TSA=\dfrac{1}{2}\times 20\times 12+570}$ = 690 cm 2
Finding the surface area of a regular (equilateral) triangular pyramid when the BASE and SLANT HEIGHT are known
Find the surface area of a regular triangular pyramid with a base of 16 cm and a slant height of 19 cm.
Here, we will use an alternative formula. Total Surface Area ( TSA ) = ${\dfrac{\sqrt{3}}{4}b^{2}+\dfrac{1}{2}\times 3bs}$, here b = 16 cm, s = 19 cm ∴ TSA = ${\dfrac{\sqrt{3}}{4}\times 16^{2}+\dfrac{1}{2}\times 3\times 16\times 19}$ = 566.85 cm 2
Leave a comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Privacy Policy
- Trigonometry
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.

Surface Area of Triangular Pyramid
Surface area of triangular pyramid: introduction, what is a triangular pyramid, how to find the surface area of a triangular pyramid, solved examples, practice problems, frequently asked questions.
The surface area, or total surface area (TSA), of a triangular pyramid, is the total area of its 4 faces. Even though we have formulas to find the surface area of a pyramid with a triangular base, the basic idea of finding the surface is to add the areas of all the faces. It is measured in square units such as $in^{2}$, $ft^{2}$, etc.
There are many types of pyramids, and all pyramids are named by the shape of their bases. For example, a pyramid, which has a rectangular base is a rectangular pyramid; the one that has a pentagon as a base is a pentagonal pyramid, and so on. So, a triangular pyramid has a base that is triangular in shape. Let’s first learn about triangular pyramids.

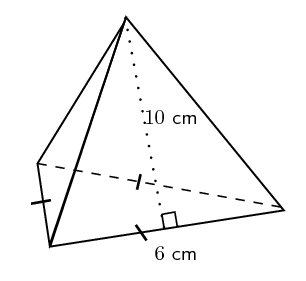
A triangular pyramid is a pyramid with a triangle as a base and 3 triangular faces. These 3 lateral triangular faces meet at one vertex. All triangular-based pyramids, either regular or irregular, have 4 vertices. They have 6 edges, out of which 3 are along the base and 3 are extending up from the base. Take a look at the image given below to understand its components.
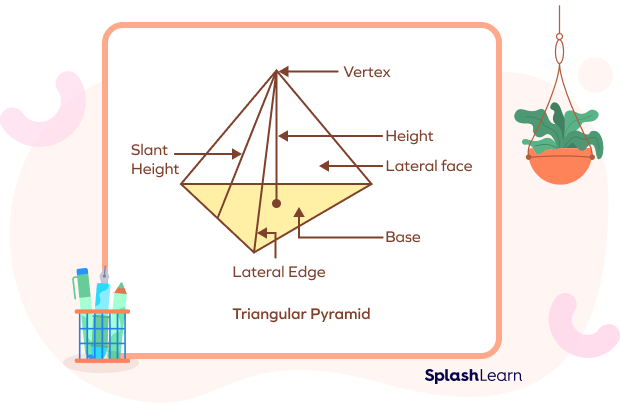
Related Worksheets

A triangular pyramid has two types of surface areas: The lateral surface area and the total surface area. You can find the surface area of a triangular pyramid by adding the lateral area of the pyramid (three triangles) to the area of the pyramid’s base (a triangle again). Let us study both in detail.
Lateral Surface Area
The lateral surface area is the area of the side faces, or we can say lateral surface area (LSA) does not include the base. It can be calculated by subtracting the base from the total surface area.
Lateral Surface Area of a Triangular Pyramid Formula

The lateral surface area of a triangular pyramid is calculated using the following formula:
The lateral surface area of a triangular pyramid $= \frac{1}{2}$ (Perimeter of the base $\times$ Slant height)
We know that the base is a triangle. So, the perimeter of the base would be, $3 \times$ side for equilateral triangles.
The lateral surface area of a triangular pyramid $= \frac{3}{2}$ (side slant $\times$ height)
$= \frac{3}{2}(b \times l)$
Where, $b =$ side of the base triangular base
$s =$ slant height
Total Surface Area
The total surface area of an object is the total area of the object’s surface. Thus, the total surface area is the sum of the base area and lateral surface area of the pyramid.
Total Surface Area of a Triangular Pyramid Formula

Here, h is the height of the pyramid. l is the slant height of the pyramid.
The total surface area of a triangular pyramid is calculated using the following formula:
The total surface area of a triangular pyramid $=$ Base Area $+$ Lateral Surface Area
As we know, Area of a triangle $= 1\frac{2} \times$ base $\times$ height
Total surface area of triangular pyramid $= (\frac{1}{2} \times$ Side of base $\times$ Height of base) $+ \frac{3}{2}$ (b $\times$ l)
$= \frac{1}{2} \times$ (b $\times$ h) $+ \frac{3}{2}$ (b $\times$ l)
where, $h =$ the height of the base triangle
$b =$ the side of the triangular base
$l =$ slant height
- A triangle-based pyramid is unique in comparison to other pyramids, as it only consists of one kind of 2D shape, a triangle.
- A triangular pyramid has 4 triangular faces, 6 edges, and 4 vertices.
- Triangular pyramids can be regular, irregular, and right-angled.
- The base of a triangle pyramid can be any type of triangle, but is usually an equilateral triangle. This means that all sides and faces are the same.
- The net of a triangle-based pyramid folds out to a large triangle made up of 4 smaller triangles.
- The base of a right triangular pyramid is a right triangle.
In this article, we learned in detail about the triangular pyramid definition, and formulas and facts. Let’s solve some examples and practice problems to understand it better.
1. Determine the total surface area of a triangular pyramid whose base area is 36 sq. in, the perimeter of the triangle is 24 in, and the slant height of the pyramid is 28 in.
Given data:
Area of the triangular base $= 36\; in^{2}$
The slant height (l) $= 28$ in
Perimeter (P) $= 24$ in
We know that,
Total surface area (TSA) of a triangular pyramid $= \frac{1}{2}$ perimeter of the base $\times$ slant height $+$ base area
Thus, TSA $= (\frac{1}{2} \times 24 \times 28 ) + 36$
$= 12 \times 28 + 36$
$= 336 + 36$
$= 372\; in^{2}$
Hence, the total surface area of the given pyramid is $372\; in^{2}$.
2. Find the total surface area of a triangular pyramid with base lengths of 10 and base height of 8.7 and slant height of 14. (Note: Base is an equilateral triangle.)
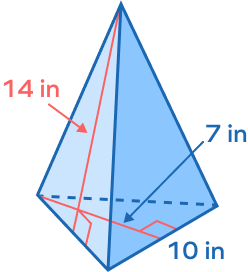
Base length $= 10$ in
Base height $= 7$ in
Slant height $= 14$ in
Firstly, we need to find the perimeter and the area of the base.
We know that, Area of base (triangle) $= \frac{1}{2} \times$ base $\times$ height
$= \frac{1}{2} \times 10 \times 7$
$= 35\; in^{2}$
Now, perimeter of the base of triangle $= 10 + 10 + 10$
$= 30$ in.
The total surface area (TSA) of a triangular pyramid $= (\frac{1}{2} \times$ perimeter of the base $\times$ slant height$) +$ Base area
Thus, TSA $= \frac{1}{2} \times 30 \times 14 + 35$
$= 15 \times 14 + 35$
$= 210 + 35$
$= 245\; in^{2}$
The total surface area of a triangular pyramid is $245\; in^{2}$.
3. Find the lateral surface area of a triangular pyramid with slant height 10 inch and base perimeter 24 inch.
Solution:
Base perimeter $= 24$ in
Slant height $= 10$
The lateral surface area of a triangular pyramid $= \frac{1}{2} ($Perimeter of the base $\times$ Slant height$)$
$= \frac{1}{2} \times 24 \times 10$
$= 120\; in^{2}$
The lateral surface area of a triangular pyramid is $120\; in^{2}$.
4. Find the base length of a triangular pyramid with a slant height of 16 ft and a lateral area of 360 sq. ft.
Lateral surface area = 360 sq. ft
Slant height = 16 ft
The lateral surface area of a triangular pyramid (LSA ) $= \frac{3}{2} (b \times l)$
$360 = \frac{3}{2} (b \times 16)$
$360 = \frac{48 \times b}{2}$
$720 = 48 \times b$
$b = \frac{720}{48}$
$b = 15$ ft.
The base length of a triangular pyramid shaped museum is 15 ft.
5. Find the slant length of a triangular pyramid with a base of 8 units and a lateral area of 120 sq. units.
Base side $= 8$ units
Lateral Surface Area ( LSA) $= 120$ sq. units
We know that, the lateral surface area of a triangular pyramid $= \frac{3}{2} (b \times s)$
$120 = \frac{3}{2} \times 8 \times s$
$120 = \frac{24 \times s}{2}$
$240 = 24 \times s$
$s = \frac{240}{24}$
$s = 10$ sq. units
The slant length of a triangular pyramid is 10 sq. units.
Attend this quiz & Test your knowledge.

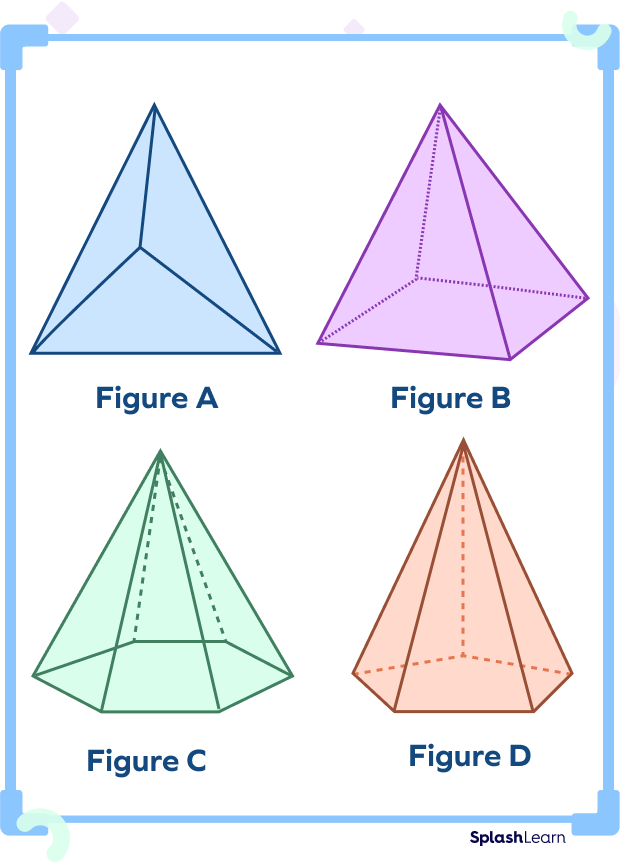
Identify the triangular pyramid from the shapes given below.
The base of a right triangular pyramid is a __________.
A triangular pyramid _________ vertices., the formula to calculate the total surface area of a triangular pyramid is ________., which of the following is an incorrect statement about a triangular pyramid.
Is a triangular pyramid called a tetrahedron?
A tetrahedron is a triangular pyramid in which all the faces are triangles of equal size. All the triangles of the tetrahedron are congruent and when all the sides of all the triangles are equal, then it is a triangular pyramid with an equilateral triangle and is called a tetrahedron.
How do you find the volume of a triangular pyramid?
The volume of a 3D figure refers to its capacity, or the space occupied by it. It is measured in cubic units. Knowing the base area and height of a triangular pyramid is enough to calculate its volume. The volume of a triangular pyramid is given by the formula $\frac{1}{3} \times$ base area $\times$ height
Now consider a regular triangular pyramid made of equilateral triangles of side “$a$.”Regular Triangular Pyramid Volume $= \frac{a^{3}}{6\sqrt{2}}$ cubic units.
What are some real-life examples of a triangular pyramid?
A common example of a triangular pyramid is the pyramix or the Rubik’s triangle. It has a triangular base and 3 other triangular faces.

What are the types of triangular pyramids?
There are three types of triangular pyramids.They are as follows:
- Regular triangular pyramids.
- Irregular triangular pyramids.
- Right-angled triangular pyramids.
What does a net of a triangular pyramid look like?
The image below shows what a net of a triangular pyramid looks like.
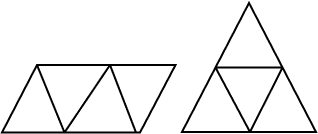
The net of a 3D shape is what it looks like if it is opened out flat. The net of a triangular pyramid has 3 triangular faces and 1 triangular base.
RELATED POSTS
- Positive Rational Numbers – Definition, Reciprocal, Examples, FAQs
- Parallelepiped: Definition, Formula, Volume, Examples, FAQs
- Perfect Squares – Definition, Formula, List, Examples
- Surface Area of Sphere

Math & ELA | PreK To Grade 5
Kids see fun., you see real learning outcomes..
Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.
Parents, Try for Free Teachers, Use for Free
Surface Area of Triangular Pyramid Formula
The surface area of a triangular pyramid is the total area of all faces of a triangular pyramid. Basically, a triangular pyramid has a triangular base and is bounded by three lateral triangular faces that meet at one vertex. A triangular pyramid has all faces as triangles. This pyramid has 4 faces, 6 edges, and 4 corners or vertices. Few types of the triangular pyramid are given below:
- Regular triangular pyramid - all faces are equilateral triangles and are known as tetrahedrons.
- Right triangular pyramid - the base is an equilateral triangle while other faces are isosceles triangles.
- An irregular triangular pyramid - a scalene or isosceles triangle forms the base.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
What Is The Surface Area of a Triangular Pyramid?
The surface area of any three-dimensional geometrical shape is the sum of the areas of all of the faces or surfaces of that enclosed solid. A triangular pyramid has four triangular faces. Thus, The formula for calculating the surface area of a triangular pyramid involves the area of the base, the perimeter of the base, and the slant height of any side of the pyramid. The surface area is always measured in square units like cm 2 , m 2 , ft 2 , or cubits 2 . The surface area of a triangular pyramid is \(\begin{align} \text {Base Area}+\!\frac{1}{2} \text {(Perimeter}\!\times\!\text {Slant Height}) \end{align}\).

The Formula for the surface area of a triangular pyramid is calculated by adding up the area of all triangular faces of a pyramid. The surface area of a right triangular pyramid formula is \(\begin{align} \text {Base Area}+\!\frac{1}{2} \text {(Perimeter}\!\times\!\text {Slant Height}) \end{align}\).
After putting the values we get an expression of the surface area of the triangular pyramid formula as 1⁄2(a × b) + 3⁄2(b × s).
- b is the side of the triangle pyramid.
- a is the height of the base triangle
- s is the slant height of a triangular pyramid.
- 1⁄2(a × b) is the base area of the triangular faces.
- 3⁄2(b × s) is the product of the perimeter and slant height of a pyramid.
How to Calculate the Surface Area of Triangular Pyramids?
The surface area of a triangular pyramid can be calculated by representing the 3D shape into a 2D net, to make the shapes easier to see. After expanding the 3D shape into 2D shape we will get four triangles. The following steps are used to calculate the surface area of a triangular pyramid:
- Step 1: Find the area of the base triangles: The area of the base triangles is (1/2 × base of the triangle × height of the triangle) which becomes base × height.
- Step 2: Find the perimeter of triangular faces: The perimeter of a triangle is the sum of all sides of a triangle which is \((side)_{1}\) + \((side)_{2}\) + \((side)_{3}\).
- Step 3: Find the slant height of triangular faces: The slant height of a triangular pyramid is generally represented by 's'.
- Step 4: Add all the areas together. Thus, the surface area of a triangular pyramid formula is 1⁄2(a × b) + 3⁄2(b × s) in squared units.
Lateral Surface Area of Triangular Pyramid
The lateral surface area is the area of the non-base faces or we can say that only the lateral surface area of any object is calculated by removing the base area. The lateral area of a triangular pyramid can be calculated by removing the base area of a triangle from the product of the perimeter of the base and the slant height of a pyramid.
Thus, the lateral surface area of a right triangular pyramid is 1⁄2(perimeter of the base × slant height) which further becomes 3⁄2(side × slant height).
- b is the side of a pyramid.
- s is the slant height of the base.
Examples on Surface Area of Triangular Pyramid Formula
Example 1: Each side of a triangular pyramid is of length 3 units, the height of the base triangle is 6, and the slant height is 5. Find its total surface area.
The surface area of a triangular pyramid of side a is
Surface Area = 1⁄2(a × b) + 3⁄2(b × s)
On Substituting the values, we get,
Surface Area = 1⁄2(6 × 3) + 3⁄2(3 × 5)
Surface Area = (9) + (22.5) = 31.5 units 2
Answer: The total Surface Area of the triangular pyramid is 31.5 units 2 .
Example 2: Find the surface area of a triangular pyramid whose area of the base triangle is 24 units 2 , the perimeter is 12 units, and the slant height of the pyramid is 18.
The surface area of a triangular pyramid = \(\begin{align} \text {Base Area}+\!\frac{1}{2} \text {(Perimeter}\!\times\!\text {Slant Height}) \end{align}\)
Putting the values in the formula,
The surface area of a triangular pyramid = \(\begin{align} \text {24}+\!\frac{1}{2} \text {(12}\!\times\!\text {18}) \end{align}\)
= 132 square units.
Answer: The surface area of a triangular pyramid is 96 units 2 .
go to slide go to slide

Book a Free Trial Class
Practice Questions on Surface Area of Triangular Pyramid Formula
Faqs on surface area of triangular pyramid formula, how do you find the surface area of a triangular pyramid.
The Formula for the surface area of a pyramid is calculated by adding up the area of all triangular faces of a pyramid. which is 1⁄2(a × b) + 3⁄2(b × s). Where b is the side of a pyramid, a is the height of a base triangle, and s is the slant height of a pyramid.
What Is the Formula for the Volume of a Triangular Pyramid?
The volume of a triangular pyramid can be found by using the formula, 1/3 × Base Area × Height.
How Do You Find the Area of the Base of a Right Triangular Pyramid?
The area of the base of a right triangular pyramid is 1/2 × height of a base triangle × the bottom edge of the base triangle.
What Is the Lateral Surface of a Triangular Pyramid?
The lateral surface of a triangular pyramid is calculated following the steps given below.
- Step 1: Look for the given parameters.
- Step 2: Multiply 1/3 with the perimeter of the base triangle and the slant height of a triangular pyramid.
- Step 3: Write the result in squared units.
How To Find the Total Surface Area of a Triangular Pyramid When Its Lateral Surface Area and Base area are Given?
The formula to calculate the total surface area of a triangular pyramid is 1⁄2(a × b) + 3⁄2(b × s).
- Step 1: Check for the given parameters.
- Step 2: Add the value of its lateral surface area and the base area.
- Step 3: Write the sum so obtained in squared units.
Triangular Pyramid
Go to Surface Area or Volume .
Notice these interesting things:
- It has 4 Faces
- The 3 Side Faces are Triangles
- The Base is also a Triangle
- It has 4 Vertices (corner points)
- It has 6 Edges
- It is also a Tetrahedron
Surface Area
When side faces are the same :
Surface Area = [Base Area] + 1 2 × Perimeter × [Slant Length]
Example: Base Area is 28, Perimeter is 20, Slant length is 5
When side faces are different we can calculate the area of the base and each triangular face separately and then add them up.
Volume = 1 3 × [Base Area] × Height
Example: base area is 28, height is 4.5

Calculating the Surface Area of a Triangular Pyramid: A Comprehensive Guide
- Author: Noreen Niazi
- Last Updated on: November 16, 2023

As a student or professional in mathematics or engineering, you may need to find the surface area of a triangular pyramid. The surface area of a triangular pyramid is the total area that covers all the faces of the pyramid, including the base and the lateral faces. This guide will help you understand the formula for finding a triangular pyramid’s surface area, provide step-by-step instructions, and offer tips and tricks to help you avoid common mistakes.
Introduction to the Surface Area of a Triangular Pyramid
.webp)
Before we dive into the formula for finding the surface area of a triangular pyramid, let’s first understand what a triangular pyramid is. A triangular pyramid is a four-faced solid figure with a triangular base and three triangular faces at a common vertex. The triangular faces are called the lateral faces, and the pyramid height is the perpendicular distance from the vertex to the base.
The surface area of a triangular pyramid is the sum of the areas of its faces, including the area of the base. The formula for finding the surface area of a triangular pyramid is:
Surface Area = Base Area + (1/2 x Perimeter of Base x Slant Height)
Understanding the Formula for the Surface Area of a Triangular Pyramid
To understand the formula for finding the surface area of a triangular pyramid, let’s break it down into its components. The surface area is the sum of the base area and the lateral area. The base area is simply the area of the triangular base, which can be found using the formula for the area of a triangle:
Base Area = 1/2 x Base x Height
The lateral area is the sum of the areas of the three triangular lateral faces. The lateral faces are congruent triangles, so they all have the same area. The area of one of the lateral faces can be found using the formula:
Lateral Area = 1/2 x Perimeter of Base x Slant Height
The slant height is the distance from the vertex to the midpoint of one of the sides of the base, and the perimeter of the base is the sum of the lengths of all the sides.
Step-by-Step Guide on How to Find the Surface Area of a Triangular Pyramid

Now that we understand the formula for finding the surface area of a triangular pyramid, let’s go through a step-by-step guide to help you calculate it. Let’s use the following dimensions for our example:
- Base length: 4 cm
- Base height: 3 cm
- Slant height: 5 cm
- Step 1: Find the area of the base
Using the formula for the area of a triangle, we can find the area of the base:
- Base Area = 1/2 x Base x Height = 1/2 x 4 cm x 3 cm = 6 cm^2
- Step 2: Find the perimeter of the base.
- The perimeter of the base is simply the sum of the lengths of all the sides. Since we have a triangular base, the perimeter is:
- Perimeter of Base = Side 1 + Side 2 + Side 3 = 4 cm + 4 cm + 4 cm = 12 cm
- Step 3: Find the lateral area
Using the formula for the lateral area, we can find the area of one of the lateral faces:
Lateral Area = 1/2 x Perimeter of Base x Slant Height = 1/2 x 12 cm x 5 cm = 30 cm^2
Since there are three lateral faces, the total lateral area is:
Total Lateral Area = 3 x Lateral Area = 3 x 30 cm^2 = 90 cm^2
- Step 4: Find the surface area
Now that we have the area of the base and the total lateral area, we can find the surface area of the triangular pyramid:
- Surface Area = Base Area + Total Lateral Area = 6 cm^2 + 90 cm^2 = 96 cm^2
Therefore, the surface area of the triangular pyramid with the given dimensions is 96 cm^2
Example Problems and Solutions for Finding the Surface Area of a Triangular Pyramid
Let’s go through some more example problems to help you practice finding the surface area of a triangular pyramid.
Example 1: Find the surface area of a triangular pyramid with base length 6 cm, base height 4 cm, and slant height 8 cm.
Base Area = 1/2 x Base x Height = 1/2 x 6 cm x 4 cm = 12 cm^2
- Step 2: Find the perimeter of the base
Perimeter of Base = Side 1 + Side 2 + Side 3 = 6 cm + 6 cm + 6 cm = 18 cm
Lateral Area = 1/2 x Perimeter of Base x Slant Height = 1/2 x 18 cm x 8 cm = 72 cm^2
Surface Area = Base Area + Total Lateral Area = 12 cm^2 + 72 cm^2 = 84 cm^2
Therefore, the surface area of the triangular pyramid with the given dimensions is 84 cm^2.
- Example 2: Find the surface area of a triangular pyramid with base length 3 cm, base height 2 cm, and slant height 4 cm.
Base Area = 1/2 x Base x Height = 1/2 x 3 cm x 2 cm = 3 cm^2
Perimeter of Base = Side 1 + Side 2 + Side 3 = 3 cm + 3 cm + 3 cm = 9 cm
Lateral Area = 1/2 x Perimeter of Base x Slant Height = 1/2 x 9 cm x 4 cm = 18 cm^2
Surface Area = Base Area + Total Lateral Area = 3 cm^2 + 18 cm^2 = 21 cm^2
Therefore, the surface area of the triangular pyramid with the given dimensions is 21 cm^2.
Tips and Tricks for Solving Surface Area of a Triangular Pyramid Problems
Solving problems related to the surface area of a triangular pyramid can be challenging. Here are some tips and tricks that can help you:
- Draw a diagram: Drawing a diagram can help you visualize the problem and identify the dimensions of the triangular pyramid.
- Label the dimensions: Labeling the dimensions in your diagram can help you keep track of the variables in the formula.
- Use the correct formula: Make sure you use the correct formula for the surface area of a triangular pyramid.
- Check your units: Make sure your units are consistent throughout the problem.
- Practice, practice, practice: The more practice problems you solve, the more comfortable you will be with the formula and the process.
Common Mistakes to Avoid When Calculating the Surface Area of a Triangular Pyramid
When calculating the surface area of a triangular pyramid, there are some common mistakes that you should avoid:
- Need to include the area of the base in the total surface area.
- Using the wrong formula for the lateral area.
- Using the wrong dimensions in the formula.
- Forgetting to convert units to the same system before calculating.
- Rounding too early in the calculation process.
Applications of the Surface Area of a Triangular Pyramid in Real Life
The s urface area of a triangular pyramid has many applications in real life. Here are some examples:
Architecture: The surface area of a triangular pyramid is used in the design and construction of roofs and buildings with pyramid-shaped structures.
Packaging: The surface area of a triangular pyramid is used in the design and manufacturing of triangular pyramid-shaped packages and boxes.
Geometry: The surface area of a triangular pyramid is used in the study of geometry and calculus.
Surface Area of Pyramid Worksheet for Practice
In addition to the formula we discussed earlier, there are alternative methods for finding the surface area of a triangular pyramid. One such method involves using the Pythagorean theorem to find the slant height and then using the formula for the area of an isosceles triangle to find the area of the lateral faces. However, the formula we discussed earlier is more commonly used and straightforward.
Alternative Methods for Finding the Surface Area of a Triangular Pyramid
Conclusion and summary of key takeaways.
In conclusion, the surface area of a triangular pyramid is the sum of the areas of its faces, including the area of the base. The formula for finding the surface area of a triangular pyramid is Surface Area = Base Area + (1/2 x Perimeter of Base x Slant Height). To find the surface area, you need to find the area of the base, the perimeter of the base, and the slant height. Practice is key to mastering the formula, and avoid common mistakes such as using the wrong formula or dimensions. The surface area of a triangular pyramid has many real-life applications in architecture, packaging, and geometry. We hope this comprehensive guide has helped you understand and master the surface area of a triangular pyramid.
- Math Tutorials
- Trigonometry
- Cookie Policy
- Privacy Policy and Terms of Use
Connect With Us
- LearnAboutMath Newsletter
The Best Math Website for Learning and Practice
By signing up you are agreeing to receive emails according to our privacy policy.
Stay tuned with our latest math posts
Lesson Solved problems on surface area of pyramids
- Problems on Pyramid
Solved word problems on pyramid are shown below using step-by-step explanation with the help of the exact diagram in finding surface area and volume of a pyramid.
Worked-out problems on pyramid: 1. The base of a right pyramid is a square of side 24 cm. and its height is 16 cm.
(i) the area of its slant surface
(ii) area of its whole surface and
(iii) its volume.
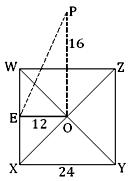
Let, the square WXYZ be the base of the right pyramid and its diagonals WY and XZ intersect at O. If OP be perpendicular to the plane of the square at O, then OP is the height of the pyramid.
Draw OE ┴ WX Then, E is the mid - point of WX .
By question, OP = 16 cm. and WX = 24 cm. Therefore, OE = EX = 1/2 ∙ WX = 12 cm Clearly, PE is the slant height of the pyramid. Since OP ┴ OE , hence from ∆ POE we get, PE² = OP² + OE²
or,PE² = 16² + 12²
or, PE² = 256 + 144
or, PE² = 400
PE = √400
Therefore, PE = 20. Therefore, (i) the required area of slant surface of the right pyramid
= 1/2 × perimeter of the base × slant height.
= 1/2 × 4 × 24× 20 square cm.
= 960 square cm.
(ii) The area of the whole surface of the right pyramid = area of slant surface + area of the base
= (960 + 24 × 24) square cm
= 1536 square cm.
(iii) the volume of the right pyramid
= 1/3 × area of the base × height
= 1/3 × 24 × 24 × 16 cubic cm
= 3072 cubic cm.
2. The base of a right pyramid 8 m high, is an equilateral triangle of side 12√3 m. Find its volume and the slant surface. Solution:
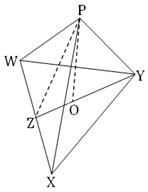
Let equilateral ∆ WXY be the base and P, the vertex of the right pyramid.
In the plane of the ∆ WXY draw YZ perpendicular to WX and let OZ = 1/3 YZ . Then, O is the centroid of ∆ WXY. Let OP be perpendicular to the plane of ∆ WXY at O; then OP is the height of the pyramid. By question, WX = XY = YW = 8√3 m and OP = 8 m. Since ∆ WXY is equilateral and YZ ┴ WX Hence, Z bisects WX .
Therefore, XZ = 1/2 ∙ WX = 1/2 ∙ 12√3 = 6√3 m. Now, from right - angled ∆ XYZ we get,
YZ² = XY² - XZ²
or, YZ² = (12√3) ² - (6√3)²
or, YZ² = 6² (12 - 3)
or, YZ² = 6² ∙ 9
or, YZ² = 324
Therefore, YZ = 18
Therefore, OZ = 1/3 ∙ 18 = 6. Join PZ . Then, PZ is the slant height of the pyramid. Since OP is perpendicular to the plane of ∆ WXY at O, hence OP ┴ OZ . Therefore, from the right angled ∆ POZ we get,
PZ² = OZ² + OP²
or, PZ ² = 6² + 8²
or, PZ² = 36 + 64
or, PZ² = 100
Therefore, PZ = 10 Therefore, the required slant surface of the right pyramid
= 1/2 × perimetre of the base × slant height
= 1/2 × 3 × 12√3 × PZ
= 1/2 × 36√3 × 10
= 180√3 square meter.
and its volume = 1/3 × area of the base × height
= 1/3 × (√3)/4 (12√3)² × 8
[Since, area of equilateral triangle
= (√3)/4 × (length of a side)² and height = OP = 8]
= 288√3 cubic meter.
● Mensuration
- Formulas for 3D Shapes
- Volume and Surface Area of the Prism
- Worksheet on Volume and Surface Area of Prism
- Volume and Whole Surface Area of Right Pyramid
- Volume and Whole Surface Area of Tetrahedron
- Volume of a Pyramid
- Volume and Surface Area of a Pyramid
- Worksheet on Volume and Surface Area of a Pyramid
- Worksheet on Volume of a Pyramid
11 and 12 Grade Math From Problems on Pyramid to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
|
What’s this? | Facebook X Pinterest WhatsApp Messenger |
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 9th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy
| E-mail Address | |
| First Name | |
| to send you Math Only Math. |
Recent Articles
Worksheet on adding integers | integers worksheets | answers |addition.
Jun 11, 24 07:15 PM

Properties of Adding Integers | Closure |Commutative | Associative ...
Jun 11, 24 07:04 PM

Roman Numerals | System of Numbers | Symbol of Roman Numerals |Numbers
Jun 11, 24 01:18 PM

Rules to Add Integers | Rules For Addition of Integers | Examples |
Jun 11, 24 11:46 AM
Addition of Integers | Adding Integers on a Number Line | Examples
Jun 10, 24 06:46 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Free Mathematics Tutorials
Pyramid problems.
Surface area and volume of pyramid problems along with with detailed solutions are presented.
where L and W are the length and width of the base and h is the height of the pyramid. Find a formula for the total area of the surface of the pyramid shown above
H = sqrt [ h + (L/2) ] A(DOC) = (1 / 2) * W * sqrt [ h + (L/2) ] H' = sqrt [ h + (W/2) ] A(AOD) = (1 / 2) * L * sqrt [ h + (W/2) ] A(lateral surface) = W * sqrt [ h + (L/2) ] + L * sqrt [ h + (W/2) ] + (L/2) ] + L * sqrt [ h + (W/2) ] + W * L Below is shown a pyramid with square base, side x, and height h. Find the value of x so that the volume of the pyramid is 1000 cm the surface area is minimum.
(1 / 3) h x = 1000 S = x * sqrt [ h + (x/2) ] + x * sqrt [ h + (x/2) ] + x * x = 2 x sqrt [ h + (x/2) ] + x = 1000 for h to obtain: h = 3000 / x to obtain a formula in terms of x only: S = 2 x sqrt [ (3000 / x ) + (x/2) ] + x x = 12.9 cm. (approximated to 1 decimal place). on the graph of S above can be done rigorously using calculus methods.
Online calculator to calculate the surface area, the volume and many other parameters of a pyramid given the dimensions of its rectangular base and its height. |
Popular Pages
- Use First Derivative to Minimize Area of Pyramid
- Free Geometry Tutorials, Problems and Interactive Applets
- Cone Problems
- Geometry Problems with Answers and Solutions - Grade 10
- Mathematics Applied to Physics/Engineering
Stay In Touch
- Privacy Policy
IB Maths Resources from Intermathematics
IB Maths Resources: 300 IB Maths Exploration ideas, video tutorials and Exploration Guides
Stacking cannonballs – solving maths with code
Numberphile have recently done a video looking at the maths behind stacking cannonballs – so in this post I’ll look at the code needed to solve this problem.
Triangular based pyramid.

A triangular based pyramid would have:
1 ball on the top layer
1 + 3 balls on the second layer
1 + 3 + 6 balls on the third layer
1 + 3 + 6 + 10 balls on the fourth layer.
Therefore a triangular based pyramid is based on the sum of the first n triangular numbers.
The formula for the triangular numbers is:

and the formula for the sum of the first n triangular numbers is:

We can simplify this by using the identity for the sum of the first n square numbers and also the identity for the sum of the first n natural numbers:

and the question we want to find out is whether there is triangular based pyramid with a certain number of cannonballs which can be rearranged into a triangular number i.e.:

here n and m can be any natural number. For example if we choose n = 3 and m = 4 we see that we have the following:

Therefore we can have a triangular pyramid of height 3, which has 10 cannonballs. There 10 cannonballs can then be rearranged into a triangular number.
Square based pyramids and above.

For a square based pyramid we would have:
1 + 4 balls on the second layer
1 + 4 + 9 balls on the third layer
1 + 4 + 9 + 16 balls on the fourth layer.
This is the sum of the first n square numbers. So the formula for the square numbers is:

and the sum of the first n square numbers is:

For a pentagonal based pyramid we have:
1 + 5 balls on the second layer
1 + 5 + 12 balls on the third layer
1 + 5 + 12 + 22 balls on the fourth layer.
This is the sum of the first n pentagonal numbers. So the formula for the pentagonal numbers is:

and the formula for the first n pentagonal numbers is:

For a hexagonal based pyramid we have:
The formula for the first n hexagonal numbers:

and the formula for the sum of the first n hexagonal numbers:

For a k-agon based pyramid we have

and the formula for the sum of the first n k-agon numbers:

Therefore the general case is to ask if a k-agonal pyramid can be rearranged into a k-agon number i.e:
Computers to the rescue
We can then use some coding to brute force some solutions by running through large numbers of integers and seeing if any values give a solution. Here is the Python code. Type it (taking care with the spacing) into a Python editor and you can run it yourself.

You can then change the k range to check larger k-agons and also change the range for a and b. Running this we can find the following. (The first number is the value of k, the second the height of a k-agonal pyramid, the third number the k-agon number and the last number the number of cannonballs used).
3 , 3 , 4 , 10 3 , 8 , 15 , 120 3 , 20 , 55 , 1540 3 , 34 , 119 , 7140 4 , 24 , 70 , 4900 6 , 11 , 22 , 946 8 , 10 , 19 , 1045 8 , 18 , 45 , 5985 10 , 5 , 7 , 175 11 , 25 , 73 , 23725 14 , 6 , 9 , 441 14 , 46 , 181 , 195661 17 , 73 , 361 , 975061 20 , 106 , 631 , 3578401 23 , 145 , 1009 , 10680265 26 , 190 , 1513 , 27453385 29 , 241 , 2161 , 63016921 30 , 17 , 41 , 23001 32 , 298 , 2971 , 132361021 35 , 361 , 3961 , 258815701 38 , 430 , 5149 , 477132085 41 , 204 , 1683 , 55202400 41 , 505 , 6553 , 837244045 43 , 33 , 110 , 245905 44 , 586 , 8191 , 1408778281 50 , 34 , 115 , 314755 88 , 15 , 34 , 48280 145, 162, 1191, 101337426 276, 26, 77, 801801) 322, 28, 86, 1169686 823, 113, 694, 197427385 2378, 103, 604, 432684460 31265, 259, 2407, 90525801730

For example we can see a graphical representation of this. When k is 6, we have a hexagonal pyramid with height 11 or the 22nd hexagonal number – both of which give a solution of 946. These are all the solutions I can find – can you find any others? Leave a comment below if you do find any others and I’ll add them to the list!
Share this:
Leave a reply cancel reply.
Powered by WordPress.com .
Discover more from IB Maths Resources from Intermathematics
Subscribe now to keep reading and get access to the full archive.
Type your email…
Continue reading
Volume Of A Pyramid
In these lessons, we will learn
- what is a pyramid?
- how to find the volume of a pyramid with rectangular or square bases.
- how to find the volume of a pyramid with different types of bases.
- how to solve word problems about pyramids.
- how to demonstrate the relationship between the volume of a pyramid and the volume of a prism with the same base and height.
Related Pages Volume Formulas Volume Of Cylinders Explanations For The Surface Area Formulas More Geometry Lessons
Solid geometry is concerned with three-dimensional shapes.
A pyramid is a solid with a polygon base and connected by triangular faces to its vertex. The lateral faces meet at a common vertex . The height of the pyramid is the perpendicular distance from the base to the vertex.
A pyramid is a regular pyramid if its base is a regular polygon and the triangular faces are all congruent isosceles triangles. The pyramid is named after the shape of its base. A rectangular pyramid has a rectangle base. A triangular pyramid has a triangle base.
Volume Of Pyramids
The volume of a pyramid is equal to one-third the product of the area of the base and the height.
The volume of a pyramid is given by the formula:
Worksheet: calculate the volumes of square pyramids
Worksheet: calculate the volumes of prisms & pyramids
Example: Find the volume of a pyramid with a rectangular base measuring 6 cm by 4 cm and height 10 cm.
Example: The following figure is a right pyramid with an isosceles triangle base. Find the volume of the pyramid if the height is 20 cm.
Solution: First, we have to calculate the area of the base.
To do that, we would need to get the height of the isosceles triangle that forms the base.
Volume of a Pyramid with Rectangular or Square Base
This video gives the formula to find the volume of a pyramid and uses it to find the volume of a pyramid with a rectangular base.
How to find the volume of a pyramid?
Example: Find the volume of a pyramid given s = 9ft, h = 5ft, l = 8ft.
How to calculate the volume of a pyramid?
Example: The base of the following pyramid is a square. What is the volume of the pyramid?
Volume of a pyramid: Calculate height using Pythagorean Theorem
Volume Of Pyramid With Different Types Of Bases
Volume Of A Triangular And Square Pyramid
How to find the volume of a square pyramid and a triangular pyramid and compare how they are the same and how they are different?
Volume of a Hexagonal Pyramid
Example: Find the volume of a hexagonal pyramid that has a height of 8 and a base edge of 10.
Word Problems About The Volume Of Pyramids
Find the height of a pyramid given the volume and base dimensions.
Example: The base of the following pyramid is a square. If the volume of the pyramid is 360 ft 3 , what is the missing length?
Example: The volume of a pyramid is 80cm 3 , base is a triangle, find the height.
Volume of a Pentagonal Pyramid
Example: Find the surface area of a regular pentagonal pyramid given an altitude of 4 and a slant height of 5. Given the altitude and slant height we can find the apothem. Using the apothem, we can find the area of the base. The volume of the pyramid is 1/3 the area of the base multiply by the height.
- A square pyramid has a height of 7 m and a base that measures 2 m on each side. Find the volume of the pyramid. Explain whether doubling the height would double the volume of the pyramid.
- The volume of a prism is 27 in 3 . What is the volume of a pyramid with the same base and height?
Demonstrate the formula of the volume of a pyramid
This video will demonstrate that the volume of a pyramid is one-third that of a prism with the same base and height and that the volume of a cone is on-third that of a cylinder with the same base and height. This is not a formal proof.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Surface Area Of Prisms And Pyramids Problems
# 1 of 3 : medium.
Surface Area of Prisms and Pyramids
# 2 of 3 : Medium
# 3 of 3 : medium.
In this exercise, students will practice finding the surface area of a rectangular prism. They will be given the dimensions of a rectangular prism and asked to use the formula for surface area to find the total area of all six faces. This activity will help students develop their understanding o...
What teachers are saying about Bytelearn What teachers are saying

Finding The Area Of A Parallelogram Nets Of Solids Finding The Area Of A Triangle Solve For Missing Dimension Of A Rectangle Given Area Solve For Missing Dimension Of A Rectangle Given Perimeter Find Area Of A Parallelogram
1973 AHSME Problems/Problem 32
| ( • • ) | ||
| Preceded by | Followed by | |
- Introductory Geometry Problems
Something appears to not have loaded correctly.
Click to refresh .

IMAGES
VIDEO
COMMENTS
Provide students with problem-solving activities that involve triangular pyramids, instead of practice worksheets. For example, give them a scenario where they need to calculate the height of a pyramid or find the dimensions of a base given the volume. ... Mixing up the different triangular pyramid formulas There are many different volume ...
Example 2: Find the volume of a triangular pyramid with a base area is 28cm, height is 4.5cm. Solution: Volume = ⅓ × Base Area × Height. = ⅓ × 28 × 4.5. = ⅓ × 126. = 42 cubic.cm. Example 3: Find the volume of the following triangular pyramid, rounding your answer to two decimal places. Solution: V = ⅓ × AH.
A triangular pyramid has: Triangular base. 3 triangular faces. 6 edges. 4 vertices. Triangular pyramid - faces, edges, and vertices Regular triangular pyramid. A pyramid with an equilateral triangle base is a regular triangular pyramid. If a scalene or isosceles triangle forms the base, then the pyramid is a non-regular triangular pyramid.
The formula is: Volume (V) = 1 3 B h, here B = base area, h = height. Let us solve some examples involving the above formula. Find the volume of a regular triangular pyramid with a base area of 97 cm2 and a height of 26 cm. Solution: As we know, Volume ( V) = 1 3 B h, here B = 97 cm 2, h = 26 cm. ∴ V = 1 3 × 97 × 26. = 840.6 cm 3.
Example 2: Find the volume of a regular triangular pyramid with a side length measuring 5 units. (Round off the answer to 2 decimal places) Solution: We know that for a triangular pyramid whose side is a volume is: a 3 /6√2. Substituting a = 5, we get. Volume = 5 3 /6√2.
The illustration below will make it clear what the triangular pyramid looks like. There are majorly two formulas for triangular pyramid: \ [\large Volume\;of\;a\;triangular\;pyramid=\frac {1} {3}Base\;Area\times Height\] Surface area of triangular pyramid = A + 3a. where A is the base area and 'a' is the area of one of pyramid's faces.
Using the formula for the volume of a triangular pyramid. Volume =1/3 × Base area × Height. = 1/3 × 10 × 5. = 16.67 cm 3. Therefore, the volume of the triangular pyramid is 16.67 cm 3. Example 2: A triangular pyramid has a base area of 15 units2 and a sum of the lengths of the edges 60 units.
The formula is: The formula to calculate the surface area of a triangular pyramid also includes its lateral surface area (LSA). Lateral Surface Area (LSA) = 1 2 P s, here P = base perimeter, s = slant height. ∴ Total Surface Area (TSA) = B + LSA. Let us solve some example to understand the above concept better.
Find the slant length of a triangular pyramid with a base of 8 units and a lateral area of 120 sq. units. Solution: Base side = 8 units. Lateral Surface Area ( LSA) = 120 sq. units. We know that, the lateral surface area of a triangular pyramid = 3 2 ( b × s) 120 = 3 2 × 8 × s. 120 = 24 × s 2. 240 = 24 × s. s = 240 24.
Tetrahedron. The tetrahedron (plural tetrahedra) or triangular pyramid is the simplest polyhedron. Tetrahedra have four vertices, four triangular faces and six edges. Three faces and three edges meet at each vertex. Any four points chosen in space will be the vertices of a tetrahedron as long as they do not all lie on a single plane .
The surface area of a triangular pyramid = Base Area+ 1 2(Perimeter×Slant Height) Base Area + 1 2 (Perimeter × Slant Height) Putting the values in the formula, The surface area of a triangular pyramid = 24+ 1 2(12×18) 24 + 1 2 (12 × 18) = 132 square units. Answer: The surface area of a triangular pyramid is 96 units 2.
A pyramid is a 3-dimensional geometric solid. It consists of a base that is a polygon and a point not on the plane of the polygon, called the vertex. The edges of the pyramid are the sides of the polygonal base together with line segments which join the vertex of the pyramid to each vertex of the polygon. The volume of a pyramid is given by the ...
Example: Base Area is 28, Perimeter is 20, Slant length is 5. Surface Area = [Base Area] + 1 2 × Perimeter × [Slant Length] = 28 + 1 2 × 20 × 5. = 28 + 50. = 78. When side faces are different we can calculate the area of the base and each triangular face separately and then add them up.
Solution 2. We can start by finding the total volume of the parallelepiped. It is , because a rectangular parallelepiped is a rectangular prism. Next, we can consider the wedge-shaped section made when the plane cuts the figure. We can find the volume of the triangular pyramid with base and apex . The area of is .
Example 1: Find the surface area of a triangular pyramid with base length 6 cm, base height 4 cm, and slant height 8 cm. Step 1: Find the area of the base. Base Area = 1/2 x Base x Height = 1/2 x 6 cm x 4 cm = 12 cm^2. Step 2: Find the perimeter of the base. Perimeter of Base = Side 1 + Side 2 + Side 3 = 6 cm + 6 cm + 6 cm = 18 cm.
Solution Three faces of the given triangular pyramid are right-angled triangles ABD, ACD and ABC. The area of the triangle ABD is .. = 24 . The area of the triangle ACD is the same: .. = 24 . The area of the triangle ABC is .. = 18 . The triangle BCD is an isosceles triangle with the lateral sides BD and CD of = = 10 cm long and the base BC of = = cm long.
Solved word problems on pyramid are shown below using step-by-step explanation with the help of the exact diagram in finding surface area and volume of a pyramid. Worked-out problems on pyramid: 1. The base of a right pyramid is a square of side 24 cm. and its height is 16 cm. Find: (i) the area of its slant surface (ii) area of its whole ...
Problem 2. Below is shown a pyramid with square base, side x, and height h. Find the value of x so that the volume of the pyramid is 1000 cm 3 the surface area is minimum. Solution to Problem 2: We first use the formula of the volume given above to write the equation: (1 / 3) h x 2 = 1000. We now use the formula for the surface area found in ...
Numberphile have recently done a video looking at the maths behind stacking cannonballs - so in this post I'll look at the code needed to solve this problem. Triangular based pyramid. A triangular based pyramid would have: 1 ball on the top layer. 1 + 3 balls on the second layer. 1 + 3 + 6 balls on the third layer.
Problem. A pyramid has a triangular base with side lengths , , and . The three edges of the pyramid from the three corners of the base to the fourth vertex of the pyramid all have length . The volume of the pyramid is , where and are positive integers, and is not divisible by the square of any prime. Find . Solution. Let the triangular base be ...
The volume of the pyramid is 1/3 the area of the base multiply by the height. Examples: A square pyramid has a height of 7 m and a base that measures 2 m on each side. Find the volume of the pyramid. Explain whether doubling the height would double the volume of the pyramid. The volume of a prism is 27 in 3.
The base of the pyramid is an equilateral triangle. What is the surface area of the triangular pyramid? Write your answer as a whole number, simplified fraction, or exact decimal. 7.8 ft 9 ft 7.8 ft. # 2 of 3: Medium. Surface Area of Prisms and Pyramids.
Problem. The volume of a pyramid whose base is an equilateral triangle of side length 6 and whose other edges are each of length is Solution. Draw an altitude towards the equilateral triangle base. By symmetry (this can also be proved by HL), the base of the altitude is equidistant from the three points of the equilateral triangle.
Introduction. In this comprehensive guide, we'll delve into the world of pattern programming using Python, a fundamental exercise for mastering nested loops and output formatting.This article covers a wide array of patterns, including basic star and number patterns, such as right triangles and pyramids, as well as more intricate designs like Pascal's Triangle, spiral number patterns, and ...