representation definition in math

Representation Theory

Symmetries occur throughout mathematics and science. Representation theory seeks to understand all the possible ways that an abstract collection of symmetries can arise. Nineteenth-century representation theory helped to explain the structure of electron orbitals, and 1920s representation theory is at the heart of quantum chromodynamics. In number theory, p -adic representation theory is central the Langlands program, a family of conjectures that have guided a large part of number theory for the past forty years.

One fundamental problem involves describing all the irreducible unitary representations of each Lie group, the continuous symmetries of a finite-dimensional geometry. Doing so corresponds to identifying all finite-dimensional symmetries of a quantum-mechanical system. We've made great progress on this important problem, including work by MIT's strong faculty in this area. The representation theory of infinite-dimensional groups and supergroups is vital to string theory, statistical mechanics, integrable systems, tomography, and many other areas of mathematics and its applications.

Research interests of this group include vertex algebras, quantum groups, infinite-dimensional Lie algebras, representations of real and p -adic groups, Hecke algebras and symmetric spaces.

Department Members in This Field

• Roman Bezrukavnikov Representation Theory, Algebraic Geometry
• Alexei Borodin Integrable Probability
• Pavel Etingof Representation Theory, Quantum Groups, Noncommutative Algebra
• Victor Kac Algebra, Mathematical Physics
• Ju-Lee Kim Representation Theory of p-adic groups
• George Lusztig Group Representations, Algebraic Groups
• Andrei Neguț Algebraic Geometry, Representation Theory
• Leonid Rybnikov Representation Theory, Integrable Systems, Quantization, Kashiwara Crystals
• David Vogan Group Representations, Lie Theory
• Zhiwei Yun Representation Theory, Number Theory, Algebraic Geometry

Instructors & Postdocs

• Elijah Bodish Representation theory, Link homology
• Hunter Dinkins Algebraic Geometry, Representation Theory
• Yuchen Fu Geometric Representation Theory
• Artem Kalmykov Representation theory, quantum groups
• Siyan Daniel Li-Huerta Arithmetic Geometry, Langlands Program
• Thomas Rüd Number theory, representation theory of p-adic groups, algebraic geometry
• Minh-Tâm Trinh
• Kent Vashaw Noncommutative Algebra, Representation Theory, Tensor Triangular Geometry.
• Robin Zhang Number Theory, Automorphic Forms, Diophantine Geometry

Researchers & Visitors

• David Roe Computational number theory, Arithmetic geometry, local Langlands correspondence

Graduate Students*

• Anlong Chua Geometric representation theory
• Ilya Dumanski Geometric and combinatorial methods in representation theory
• Marisa Gaetz Group Representations, Lie Theory
• Svetlana Gavrilova
• Arun Kannan
• Daniil Kliuev
• Vasily Krylov Geometric Representation Theory
• Calder Morton-Ferguson Geometric representation theory
• Ivan Motorin Cluster Algebras, Resolution of Singularities, Representation Theory, Integrable Systems
• Andrew Riesen
• Hamilton Wan

*Only a partial list of graduate students

Mathematical Representations

• Living reference work entry
• First Online: 28 July 2018
• Cite this living reference work entry

• Gerald A. Goldin 2  

328 Accesses

2 Citations

Definitions

As most commonly interpreted in education, mathematical representations are visible or tangible productions – such as diagrams, number lines, graphs, arrangements of concrete objects or manipulatives, physical models, written words, mathematical expressions, formulas and equations, or depictions on the screen of a computer or calculator – that encode, stand for, or embody mathematical ideas or relationships. Such a production is sometimes called an inscription when the intent is to focus on a specific instance without referring, even tacitly, to any interpretation of it. To call something a representation thus includes reference to some meaning or signification it is taken to have. Such representations are called external – i.e., they are external to the individual who produced them and accessible to others for observation, discussion, interpretation, and/or manipulation. Spoken language, interjections, gestures, facial expressions, movements, and postures may sometimes...

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Institutional subscriptions

Anderson C, Scheuer N, Pérez Echeverría MP, Teubal EV (eds) (2009) Representational systems and practices as learning tools. Sense, Rotterdam

Google Scholar  

Bruner JS (1966) Toward a theory of instruction. The Belknap Press – Harvard University Press, Cambridge, MA

Common Core State Standards Initiative (2018) Preparing America’s students for success. Retrieved June 2018 from http://www.corestandards.org/

Cuoco AA, Curcio FR (2001) The roles of representation in school mathematics: NCTM 2001 yearbook. National Council of Teachers of Mathematics, Reston

Davis RB (1984) Learning mathematics: the cognitive science approach to mathematics education. Ablex, Norwood

Duval R (2006) A cognitive analysis of problems of comprehension in a learning of mathematics. Educ Stud Math 61:103–131

Article   Google Scholar  

Goldin GA (1998) Representational systems, learning, and problem solving in mathematics. J Math Behav 17:137–165

Goldin GA (2008) Perspectives on representation in mathematical learning and problem solving. In: English LD (ed) Handbook of international research in mathematics education, 2nd edn. Routledge – Taylor and Francis, London, pp 176–201

Goldin GA, Janvier, C (eds) (1998) Representations and the psychology of mathematics education: parts I and II (special issues). J Math Behav 17(1 & 2)

Goldin GA, Kaput JJ (1996) A joint perspective on the idea of representation in learning and doing mathematics. In: Steffe L, Nesher P, Cobb P, Goldin GA, Greer B (eds) Theories of mathematical learning. Erlbaum, Hillsdale, pp 397–430

Gravemeijer K, Doorman M, Drijvers P (2010) Symbolizing and the development of meaning in computer-supported algebra education. In: Verschaffel L, De Corte E, de Jong T, Elen J (eds) Use of representations in reasoning and problem solving: analysis and improvement. Routledge – Taylor and Francis, London, pp 191–208

Heinze A, Star JR, Verschaffel L (2009) Flexible and adaptive use of strategies and representations in mathematics education. ZDM 41:535–540

Hitt F (ed) (2002) Representations and mathematics visualization. Departamento de Matemática Educativa del Cinvestav – IPN, México

Janvier C (ed) (1987) Problems of representation in the teaching and learning of mathematics. Erlbaum, Hillsdale

Kaput J, Noss R, Hoyles C (2002) Developing new notations for a learnable mathematics in the computational era. In: English LD (ed) Handbook of international research in mathematics education. Erlbaum, Mahwah, pp 51–75

Lesh RA, Doerr HM (eds) (2003) Beyond constructivism: models and modeling perspectives on mathematics problem solving, learning, and teaching. Erlbaum, Mahwah

McClelland JL, Mickey K, Hansen S, Yuan A, Lu Q (2016) A parallel-distributed processing approach to mathematical cognition. Manuscript, Stanford University. Retrieved June 2018 from https://stanford.edu/~jlmcc/papers/

Moreno-Armella L, Sriraman B (2010) Symbols and mediation in mathematics education. In: Sriraman B, English L (eds) Advances in mathematics education: seeking new frontiers. Springer, Berlin, pp 213–232

Moreno-Armella L, Hegedus SJ, Kaput JJ (2008) From static to dynamic mathematics: historical and representational perspectives. Educ Stud Math 68:99–111

National Council of Teachers of Mathematics (2000) Principles and standards for school mathematics. NCTM, Reston

Newell A, Simon HA (1972) Human problem solving. Prentice-Hall, Englewood Cliffs

Novack MA, Congdon EL, Hermani-Lopez N, Goldin-Meadow S (2014) From action to abstraction: using the hands to learn math. Psychol Sci 25:903–910

Palmer SE (1978) Fundamental aspects of cognitive representation. In: Rosch E, Lloyd B (eds) Cognition and categorization. Erlbaum, Hillsdale, pp 259–303

Roth W-M (ed) (2009) Mathematical representation at the interface of body and culture. Information Age, Charlotte

Skemp RR (ed) (1982) Understanding the symbolism of mathematics (special issue). Visible Language 26(3)

van Garderen D, Scheuermann A, Poch A, Murray MM (2018) Visual representation in mathematics: special education teachers’ knowledge and emphasis for instruction. Teach Educ Spec Educ 41:7–23

Download references

Author information

Authors and affiliations.

Graduate School of Education, Rutgers University, New Brunswick, NJ, USA

Gerald A. Goldin

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Gerald A. Goldin .

Editor information

Editors and affiliations.

South Bank University Centre for Mathematics Education, London, United Kingdom

Steve Lerman

Section Editor information

Department of Science Teaching, The Weizmann Institute of Science, Rehovot, Israel

Ruhama Even

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer Nature Switzerland AG

About this entry

Cite this entry.

Goldin, G.A. (2018). Mathematical Representations. In: Lerman, S. (eds) Encyclopedia of Mathematics Education. Springer, Cham. https://doi.org/10.1007/978-3-319-77487-9_103-4

Download citation

DOI : https://doi.org/10.1007/978-3-319-77487-9_103-4

Received : 15 June 2018

Accepted : 02 July 2018

Published : 28 July 2018

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-77487-9

Online ISBN : 978-3-319-77487-9

eBook Packages : Springer Reference Education Reference Module Humanities and Social Sciences Reference Module Education

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Representation Theory

Representation theory is fundamental in the study of objects with symmetry. 

It arises in contexts as diverse as card shuffling and quantum mechanics. An early success was the work of Schur and Weyl, who computed the representation theory of the symmetric and unitary groups; the answer is closely related to the classical theory of symmetric functions and deeper study leads to intricate questions in combinatorics.

More recently, methods from geometry and topology have greatly enhanced our understanding of these questions (“geometric representation theory”). The study of affine Lie algebras and quantum groups has brought many new ideas and viewpoints, and representation theory now furnishes a basic language for other fields, including the modern theory of automorphic forms.

All of these aspects are studied by Stanford faculty.  Topics of recent seminars include combinatorial representation theory as well as quantum groups.

Daniel Bump

Persi Diaconis

Search form

• Travel & Maps
• Our Building
• Supporting Mathematics
• Art and Oxford Mathematics
• Equality, Diversity & Inclusion
• Undergraduate Study
• Postgraduate Study
• Current Students
• Research Groups
• Case Studies
• Faculty Books
• Oxford Mathematics Alphabet
• Oxford Online Maths Club
• Oxford Maths Festival 2023
• It All Adds Up
• Problem Solving Matters
• PROMYS Europe
• Oxfordshire Maths Masterclasses
• Outreach Information
• Mailing List
• Key Contacts
• People List
• A Global Department
• Research Fellowship Programmes
• Professional Services Teams
• Conference Facilities
• Public Lectures & Events
• Departmental Seminars & Events
• Special Lectures
• Conferences
• Summer Schools
• Past Events
• Alumni Newsletters
• Info for Event Organisers & Attendees

What is Representation Theory and how is it used? Oxford Mathematics Research investigates

Oxford Mathematician Karin Erdmann  specializes in the areas of algebra known as representation theory (especially modular representation theory) and homological algebra (especially Hochschild cohomology). Here she discusses her latest work.

"Roughly speaking, representation theory investigates how algebraic systems can act on vector spaces. When the vector spaces are finite-dimensional this allows one to explicitly express the elements of the algebraic system by matrices, hence one can exploit linear algebra to study 'abstract' algebraic systems. In this way one can study symmetry, via group actions. One can also study irreversible processes. Algebras and their representations provide a natural frame for this.

An algebra is a ring which also is a vector space such that scalars commute with everything. An important construction are path algebras: Take a directed graph $Q$, which we call a quiver, and take a coefficient field $K$. Then the path algebra $KQ$ is the vector space over $K$ with basis all paths in $Q$. This becomes an algebra, where the product of two basis elements is either its concatenation if this exists, or is zero otherwise.

Algebras generalize groups, namely if we start with a group, we get naturally an algebra: take the vector space with basis labelled by the group, and extend the group multiplication to a ring structure.

When the coefficients are contained in the complex numbers, representations of groups have been studied for a long time, and have many applications. With coefficients in the integers modulo $2$, for example, the algebras and their representations are much harder to understand. For some groups, the representations have 'finite type'. These are well-understood but almost always they have 'infinite type'. With a few exceptional 'tame' cases, these are usually 'wild', that is there is no hope of a classification of the representations.

The same cases occur precisely for modulo 2 arithmetic and when the symmetry is based on dihedral or semidihedral or quaternion 2-groups. Dihedral 2-groups are symmetries of regular $n$-gons when $n$ is a power of 2. The smallest quaternion group is the famous one discovered by Hamilton.

Viewing these symmetries from groups in the wider context of algebras was used (a while ago) to classify such tame situations. Recently it was discovered that this is part of a much larger universe. Namely one can construct algebras from surface triangulations, in which the ones from the group setting occur as special cases.

One starts with a surface triangulation, and constructs from this a quiver, that is, a directed graph: Replace each edge of the triangulation by a vertex, and for each triangle

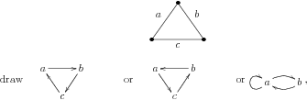
where in the last case $a=c\neq b$. At any boundary edge, draw a loop.

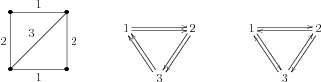
For example, consider triangulation of the torus with two triangles, as shown below. Then there are, up to labelling, two possible orientations of triangles and two possible quivers:

The tetrahedral triangulation of the sphere

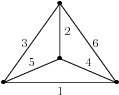
gives rise to several quivers, depending on the orientation of each triangle, for example:

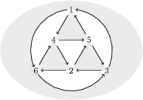
The crystal in the north wing of the Andrew Wiles Building, home of Oxford Mathematics (image drawn above) can be viewed as a triangulation of a surface with boundary. We leave drawing the quiver to the reader.

Starting with the path algebra of such a quiver, we construct algebras by imposing explicit relations, which mimic the triangulation. Although the quiver can be arbitrarily large and complicated, there is an easy description of the algebras. We call these 'weighted surface algebras.' This is joint work with A. Skowronski .

We show that these algebras place group representations in a wider context. The starting point is that (with one exception) the cohomology of a weighted surface algebra is periodic of period four, which means that these algebras generalize group algebras with quaternion symmetry.

The relations which mimic triangles can be degenerated, so that the product of two arrows around a triangle become zero in the algebra. This gives rise to many new algebras. When all such relations are degenerated, the resulting algebras are very similar to group algebras with dihedral symmetry. If we degenerate relations around some but not all triangles, we obtain algebras which share properties of group algebras with semidihedral symmetry. Work on these is in progress."

Initial Thoughts

Perspectives & resources, what is high-quality mathematics instruction and why is it important.

• Page 1: The Importance of High-Quality Mathematics Instruction
• Page 2: A Standards-Based Mathematics Curriculum
• Page 3: Evidence-Based Mathematics Practices

What evidence-based mathematics practices can teachers employ?

• Page 4: Explicit, Systematic Instruction

Page 5: Visual Representations

• Page 6: Schema Instruction
• Page 7: Metacognitive Strategies
• Page 8: Effective Classroom Practices
• Page 9: References & Additional Resources
• Page 10: Credits

Research Shows

• Students who use accurate visual representations are six times more likely to correctly solve mathematics problems than are students who do not use them. However, students who use inaccurate visual representations are less likely to correctly solve mathematics problems than those who do not use visual representations at all. (Boonen, van Wesel, Jolles, & van der Schoot, 2014)
• Students with a learning disability (LD) often do not create accurate visual representations or use them strategically to solve problems. Teaching students to systematically use a visual representation to solve word problems has led to substantial improvements in math achievement for students with learning disabilities. (van Garderen, Scheuermann, & Jackson, 2012; van Garderen, Scheuermann, & Poch, 2014)
• Students who use visual representations to solve word problems are more likely to solve the problems accurately. This was equally true for students who had LD, were low-achieving, or were average-achieving. (Krawec, 2014)

Visual representations are flexible; they can be used across grade levels and types of math problems. They can be used by teachers to teach mathematics facts and by students to learn mathematics content. Visual representations can take a number of forms. Click on the links below to view some of the visual representations most commonly used by teachers and students.

How does this practice align?

High-leverage practice (hlp).

• HLP15 : Provide scaffolded supports

CCSSM: Standards for Mathematical Practice

• MP1 : Make sense of problems and persevere in solving them.

Number Lines

Definition : A straight line that shows the order of and the relation between numbers.

Common Uses : addition, subtraction, counting

Strip Diagrams

Definition : A bar divided into rectangles that accurately represent quantities noted in the problem.

Common Uses : addition, fractions, proportions, ratios

Definition : Simple drawings of concrete or real items (e.g., marbles, trucks).

Common Uses : counting, addition, subtraction, multiplication, division

Graphs/Charts

Definition : Drawings that depict information using lines, shapes, and colors.

Common Uses : comparing numbers, statistics, ratios, algebra

Graphic Organizers

Definition : Visual that assists students in remembering and organizing information, as well as depicting the relationships between ideas (e.g., word webs, tables, Venn diagrams).

Common Uses : algebra, geometry

Before they can solve problems, however, students must first know what type of visual representation to create and use for a given mathematics problem. Some students—specifically, high-achieving students, gifted students—do this automatically, whereas others need to be explicitly taught how. This is especially the case for students who struggle with mathematics and those with mathematics learning disabilities. Without explicit, systematic instruction on how to create and use visual representations, these students often create visual representations that are disorganized or contain incorrect or partial information. Consider the examples below.

Elementary Example

Mrs. Aldridge ask her first-grade students to add 2 + 4 by drawing dots.

Notice that Talia gets the correct answer. However, because Colby draws his dots in haphazard fashion, he fails to count all of them and consequently arrives at the wrong solution.

High School Example

Mr. Huang asks his students to solve the following word problem:

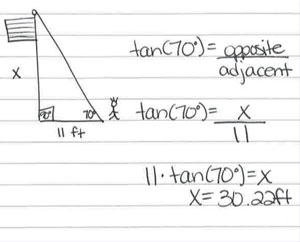
The flagpole needs to be replaced. The school would like to replace it with the same size pole. When Juan stands 11 feet from the base of the pole, the angle of elevation from Juan’s feet to the top of the pole is 70 degrees. How tall is the pole?

Compare the drawings below created by Brody and Zoe to represent this problem. Notice that Brody drew an accurate representation and applied the correct strategy. In contrast, Zoe drew a picture with partially correct information. The 11 is in the correct place, but the 70° is not. As a result of her inaccurate representation, Zoe is unable to move forward and solve the problem. However, given an accurate representation developed by someone else, Zoe is more likely to solve the problem correctly.

Manipulatives

Some students will not be able to grasp mathematics skills and concepts using only the types of visual representations noted in the table above. Very young children and students who struggle with mathematics often require different types of visual representations known as manipulatives. These concrete, hands-on materials and objects—for example, an abacus or coins—help students to represent the mathematical idea they are trying to learn or the problem they are attempting to solve. Manipulatives can help students develop a conceptual understanding of mathematical topics. (For the purpose of this module, the term concrete objects refers to manipulatives and the term visual representations refers to schematic diagrams.)

It is important that the teacher make explicit the connection between the concrete object and the abstract concept being taught. The goal is for the student to eventually understand the concepts and procedures without the use of manipulatives. For secondary students who struggle with mathematics, teachers should show the abstract along with the concrete or visual representation and explicitly make the connection between them.

A move from concrete objects or visual representations to using abstract equations can be difficult for some students. One strategy teachers can use to help students systematically transition among concrete objects, visual representations, and abstract equations is the Concrete-Representational-Abstract (CRA) framework.

If you would like to learn more about this framework, click here.

Concrete-Representational-Abstract Framework

• Concrete —Students interact and manipulate three-dimensional objects, for example algebra tiles or other algebra manipulatives with representations of variables and units.
• Representational — Students use two-dimensional drawings to represent problems. These pictures may be presented to them by the teacher, or through the curriculum used in the class, or students may draw their own representation of the problem.
• Abstract — Students solve problems with numbers, symbols, and words without any concrete or representational assistance.

CRA is effective across all age levels and can assist students in learning concepts, procedures, and applications. When implementing each component, teachers should use explicit, systematic instruction and continually monitor student work to assess their understanding, asking them questions about their thinking and providing clarification as needed. Concrete and representational activities must reflect the actual process of solving the problem so that students are able to generalize the process to solve an abstract equation. The illustration below highlights each of these components.

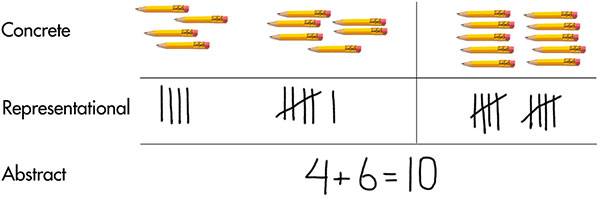
For Your Information

One promising practice for moving secondary students with mathematics difficulties or disabilities from the use of manipulatives and visual representations to the abstract equation quickly is the CRA-I strategy . In this modified version of CRA, the teacher simultaneously presents the content using concrete objects, visual representations of the concrete objects, and the abstract equation. Studies have shown that this framework is effective for teaching algebra to this population of students (Strickland & Maccini, 2012; Strickland & Maccini, 2013; Strickland, 2017).

Kim Paulsen discusses the benefits of manipulatives and a number of things to keep in mind when using them (time: 2:35).

Kim Paulsen, EdD Associate Professor, Special Education Vanderbilt University

View Transcript

Transcript: Kim Paulsen, EdD

Manipulatives are a great way of helping kids understand conceptually. The use of manipulatives really helps students see that conceptually, and it clicks a little more with them. Some of the things, though, that we need to remember when we’re using manipulatives is that it is important to give students a little bit of free time when you’re using a new manipulative so that they can just explore with them. We need to have specific rules for how to use manipulatives, that they aren’t toys, that they really are learning materials, and how students pick them up, how they put them away, the right time to use them, and making sure that they’re not distracters while we’re actually doing the presentation part of the lesson. One of the important things is that we don’t want students to memorize the algorithm or the procedures while they’re using the manipulatives. It really is just to help them understand conceptually. That doesn’t mean that kids are automatically going to understand conceptually or be able to make that bridge between using the concrete manipulatives into them being able to solve the problems. For some kids, it is difficult to use the manipulatives. That’s not how they learn, and so we don’t want to force kids to have to use manipulatives if it’s not something that is helpful for them. So we have to remember that manipulatives are one way to think about teaching math.

I think part of the reason that some teachers don’t use them is because it takes a lot of time, it takes a lot of organization, and they also feel that students get too reliant on using manipulatives. One way to think about using manipulatives is that you do it a couple of lessons when you’re teaching a new concept, and then take those away so that students are able to do just the computation part of it. It is true we can’t walk around life with manipulatives in our hands. And I think one of the other reasons that a lot of schools or teachers don’t use manipulatives is because they’re very expensive. And so it’s very helpful if all of the teachers in the school can pool resources and have a manipulative room where teachers can go check out manipulatives so that it’s not so expensive. Teachers have to know how to use them, and that takes a lot of practice.

Representations in our primary video lessons

Mathematical structure, manipulatives and myth-busting

Representations are used in lessons to expose the mathematical structure being taught. They are not new – we can probably all remember using counters when we were children. The history of mathematics uncovers many examples of objects, pictures or symbols used in early maths to represent concepts. Nowadays it’s not unusual to find tens frames, Dienes blocks, Cuisenaire® rods, bar models and other representations in frequent use in primary classrooms.

In recent years, teaching for mastery has encouraged the use of representations to deepen understanding, and encouraged teachers to question their purpose, and which representation to use and when.

In this piece, we bust some myths about representations and encourage you to watch them being used in a teaching for mastery context. Can you see what each representation used in the video below exposes about the mathematical structure of multiples of two?

Secondary maths teachers may find Using mathematical representations at KS3 helpful.

Myth: Manipulatives and pictures are for younger children and low prior-attainers

Representations are useful for all learners, whatever their age. Research mathematicians often use representations to explain their thinking. Teaching for mastery suggests that representations should be used throughout primary and secondary school to promote a deep understanding of mathematical structure. Once learners have a deep understanding of the maths being represented, the aim is to work with the maths without recourse to the representation, though they will often continue to work with visuals in their mind’s eye.

Myth: Representations help children to do calculations

Objects can assist children in performing calculations – for example, a child might use three groups of five counters to then count all the counters to find the product 15. However, using the representations in this way can encourage a child to become dependent on them. Teaching for mastery encourages the use of representations to demonstrate the structure (e.g. three groups of five counters). The child’s understanding of the structure is then built on to teach efficient calculation methods.

Myth: Children should always be able to choose their own representations

When teaching for mastery, the teacher will often have a clear idea of the particular structure s/he is trying to illuminate and will choose the most appropriate representations for doing this. Children given free rein with manipulatives may use them to do, rather than see, the maths.

Myth: A particular concept calls for a particular representation (e.g. fractions as pizzas)

Teaching for mastery uses multiple representations of a concept to expose different aspects of the structure.

Watch the video lessons below and see how the teacher uses many different representations to build the concept of units of two. You might like to see if you can identify the purpose of each representation, before you check in the dropdowns:

Numicon is used to expose the pairs and evenness in multiples of two. The non-example (five) is used to expose how this is different from odd numbers.

The ten Numicon is used greyed out to expose the ‘10 and’ nature of the teen numbers.

The number line is used alongside the Numicon to help the transition to a more abstract representation.

The number line shows the linear relationship of odd and even numbers. The odd numbers are shown in grey to expose the alternateness of even numbers. Skip counting out loud in twos embeds this. Skip counting is chanted backwards and forwards to develop fluency, so the knowledge of adjacent multiples of two is easily retrievable for use.

The bicycles are used as familiar concrete objects, to group the wheels into units of two so that children can start to unitise two. The bikes can be counted in ones; the wheels, pedals, brakes etc. in twos.

The pairs of shoes are used to help identify groups of two and connect the word ‘pair’ with groups of two. They are arranged in the layout of a tens frame to make a connection the children may be familiar with.

The counters with two dots are a more abstract representation of units of two than the bikes or shoes. This representation connects with future lessons in the sequence where pre-money tokens are used to represent 2p coins.

The subsequent video in the sequence goes on to introduce other representations to deepen children’s understanding of two-ness:

The hedgehogs are objects that don’t generally come in pairs but are used to show that any group of objects can be grouped into units of two. Again they are arranged in the familiar tens-frame format.

Pebbles are then used to show that two-ness can be used with any group of objects, and children are encouraged to go and find their own objects and identify the groups of two by circling them, to then count in twos.

The representations, now familiar from the lessons, can then be used to enable counting on in twos from a multiple of two and beginning to touch on the two times table.

Teachers may want to use the slides in these videos to teach their own lessons. These are available, along with teacher guides, on the Key Stage 1, Multiplication 1 page .

However, our Primary Team warns against teaching individual lessons in isolation. ‘Each lesson is part of a carefully planned sequence’ says the NCETM Director for Primary, Debbie Morgan. ‘The learning builds over the sequence of lessons’.

The lesson sequences were collaboratively planned by groups of Mastery Specialists and members of the NCETM Primary Team for the purpose of home learning, during the first lockdown in 2020.

You can watch all 17 lessons in the Multiplication 1 sequence or find other lesson sequences for all year groups .

Related Pages

Is there anything wrong with this page?

Subscribe to our newsletter

• Skip to main content

Welcome, Fellow Math Enthusiast! I’m so happy you’re here!

• Counting & Cardinality
• Addition & Subtraction
• Multiplication & Division
• Place Value & Base Ten
• Measurement & Data
• Geometry & Fractions
• Vocabulary & Discourse
• Math Manipulatives
• Classroom Management
• Classroom Organization
• Holidays & Seasonal
• Social-Emotional Learning
• Privacy Policy
• Terms of Use
• SHOP RESOURCES
• BECOME A MEMBER
• Search this website

Teaching with Jillian Starr

teaching little stars to shine brightly

Grab Your FREE Gift

Addition Centers Freebie

Looking for fun and engaging centers to help your students practice their addition fact fluency? Be sure to grab these freebies!

Mathematical Representations Series Part 3: Symbolic Representation

Welcome back to our deep dive into mathematical representations! Today, we are taking a look at symbolic representations and how we can translate between symbolic, concrete, and visual representations. First, let’s do a two-sentence recap of this series so far:

We have already focused on concrete representations and the immense value of manipulatives, as well as the range of visual representations we want to encourage with our students. We are centering our conversation around Lesh’s Translation Model, which encompasses the range of ways we represent our thinking, and stresses the importance of making connections between representations.

Symbolic Representation

Now, that we’re all caught up, let’s take a peek at Symbolic Representations. You may have heard it called Abstract Representation, especially if you’re familiar with the Concrete-Pictorial-Abstract model (also called CRA model).

So what are symbolic representations? Well, symbolic representation is when mathematical symbols (like numerals and operation signs) are used to show a mathematical concept. They are using symbolic, mathematical language to express their understanding of a math concept.

Let’s go back to the example from concrete representation . In that example, the student used 5 yellow counters, and 4 red counters to concretely show their understanding of 5 + 4 = 9.

Then in their visual representation , they were able to create a sketch of their concrete representation. This was our first example of translating between two different representations (connecting visual to concrete).

Now, we can support students even further by helping them represent their understanding with symbols. Here the student counts the collection of five counters and writes the numeral “5” below it. They do the same for the four counters.

Finally, they count all of the counters together and write down “9”. We can help them with the operations symbols if needed, showing that “+” means that we are putting the 5 and the 4 together and that the “=” means “4+5” has the same value as “9”.

When we guide students to using numerals and operations, they are connecting their manipulatives, their sketches, AND the symbolic representation. This is such a powerful move to help deepen student understanding!

Connecting Two Symbolic Representations

It’s a fairly straightforward representation, but how do abstract representations connect to themselves in Lesh’s translation model? 

Well, this student actually wanted to write 4 + 4 +1 because that is how they solved the problem. They knew 4 + 4 = 8, so 4 + 5 = 9 because it’s 4 + 4 + 1 more. Understanding that both expressions can describe the same concept is just one example of how to translate within the symbolic representation.

What’s Up Next?

This series is going to dive deep into each of the representations discussed in Lesh’s Translation Model, and then we are going to put it all together so we can make a big impact on your math teaching this year.

If you missed Part One about Concrete Representations or Part Two about Visual Representations , check them out so you have all of the info you need before we move on!

Addition & Subtraction Resources

You May Also Enjoy These Posts:

Reader Interactions

Great post! I completely agree that symbolic representations can help students understand complex mathematical concepts more easily. I’ve seen firsthand how visual aids and manipulatives can make a difference in a student’s learning journey. Thanks for sharing your insights and experiences!

Leave a Comment

Your email address will not be published. Required fields are marked *

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Ready to go deeper?

JOIN MEANINGFUL MATH

hello I'm Jillian

I’m so happy you’re here. I want every child to feel confident in their math abilities, and that happens when every teacher feels confident in their ability to teach math.

In my fifteen years of teaching, I sought every opportunity to learn more about teaching math. I wanted to know HOW students develop math concepts, just like I had been taught how students learn to read. I want every teacher to experience the same math transformation I did, and have the confidence to teach any student that steps foot in their classroom. I’m excited to be alongside you in your math journey!

Follow Me on Instagram!

Factor Tree – Definition with Examples

What is a factor tree, what is splitting numbers and branching, how to draw a factor tree of a number, solved examples on factor trees, practice problems on factor trees, frequently asked questions about factor trees.

A factor tree is a diagram that breaks down a composite number into its prime factors. It starts with the given number at the top and branches out, with each branch representing a factor of the previous number. This process continues until all the branches reach prime numbers. The last numbers (leaf nodes) represent the prime factorization of the original number. 

The general method to find the prime factorization can be tedious for large numbers. Factor tree provides a quick, simple, and systematic way to understand the prime factorization of numbers.

What Are Factors?

A factor is a number that divides a given number evenly without leaving a remainder. 

When we multiply two numbers to find the product, both the numbers being multiplied are called factors of the product.

1 × 15 = 15

3 × 5 = 15 

So, 15 has four factors: 1, 3, 5, and 15. 

However, this method can be inconvenient for larger numbers. That’s where the factor tree method comes in.

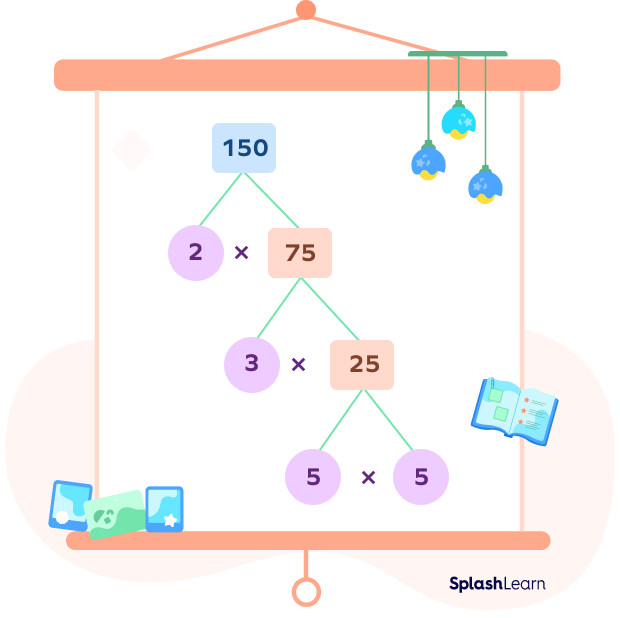
Factor Tree: Definition

A factor tree is a visual representation or a diagram that breaks down a given number into its prime factors. It is a prime factorization method, which expresses a composite number as a product of prime numbers.

Related Worksheets

• Splitting Numbers in a Factor Tree:

Splitting numbers in a factor tree refers to breaking down a composite number into its factors.

When you start with a composite number as the root of the factor tree, you split it into two or more factors along branches.

These factors can be prime or composite, and the process continues until you reach prime factors at the end of the branches.

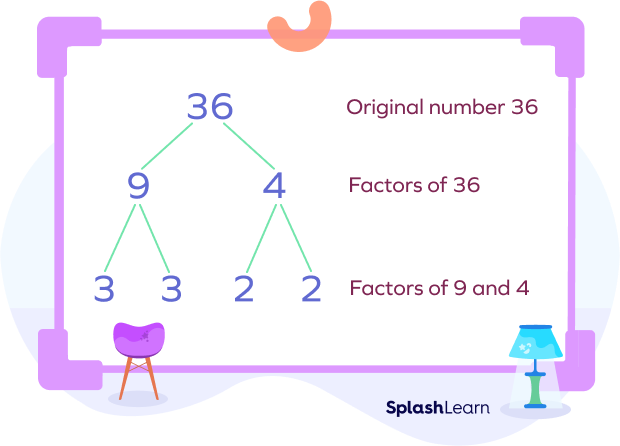
• Branching in a Factor Tree:

Branching in a factor tree involves extending lines or branches from a number to represent its factors or divisors. Each branch represents one of the factors of the number from which it originates. The branching process continues until all factors are expressed as prime numbers, creating a visual representation of the prime factorization of the original composite number.

In summary, splitting numbers involves breaking down a composite number into its factors, while branching represents the visual connections between these factors in a factor tree, ultimately leading to the prime factorization of the original number.

Example: We can express 120 as the product of 12 and 10. 

120 = 12 × 10 

Both 12 and 10 are, again, composite numbers. 

12 = 4 × 3

10 = 2 × 5

Next, we can write 4 as

4 = 2 × 2

Now, we have reached the end since we obtained all the prime factors, 2, 3, 4, and 5.

Step 1: Write the composite number at the top of the tree. (This number is often termed as the root number of the factor tree.)

Step 2: Identify two numbers that multiply together to give the root number. These factors can be prime or composite. 

Step 3 : Determine if the factor is prime or composite for each branch.

If it’s composite, continue branching until you reach prime factors.

Step 4: Continue this process for each composite factor, branching out and factoring until you have expressed all factors as primes. 

Step 5: The factor tree is complete when there are prime numbers at the end of each branch.

Note: To create a systematic pattern, encircle the prime factors and draw a box around the composite factors.

Factor Tree Examples:

Example 1: Factor tree of 120

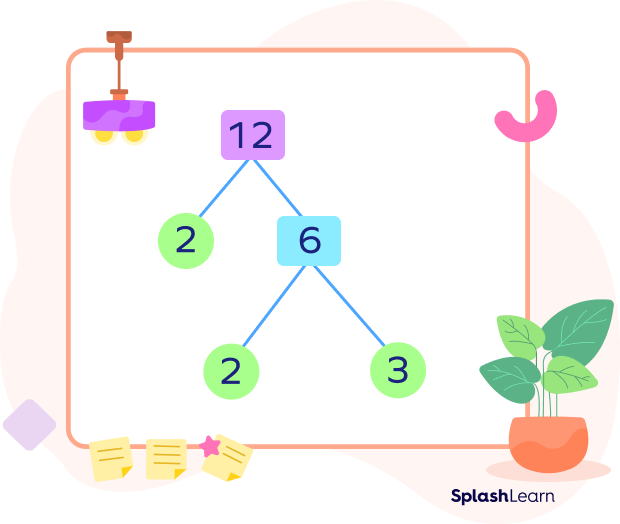
Example 2: Factor tree of 12

Find the factor tree of 12.

12 = 2 × 6

2 is prime. 6 is composite.

12 = 2 × (2 × 3)

Thus, 12 = 2 × 2 × 3

12 = 2 2 × 3

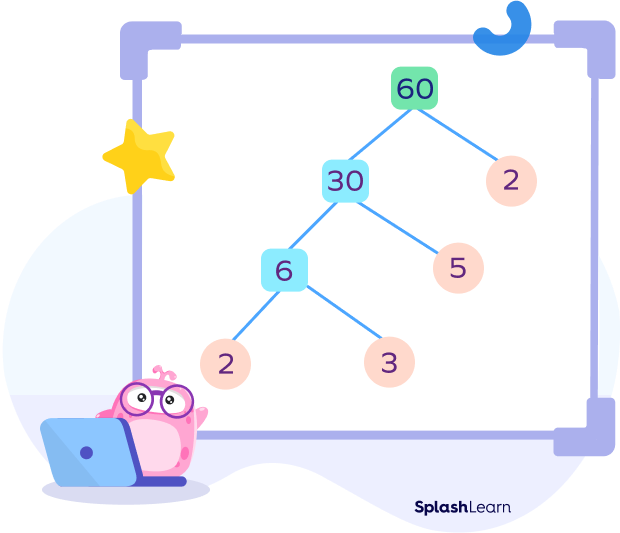
Example 3 : Factor tree of 60

60 = 2 × 30

60 = 2 × 3 × 5 × 2

60 = 2 × 2 × 3 × 5

Prime Factor Tree

A prime factor tree specifically aims to find the prime factorization of a composite number. The focus is solely on breaking down the number into its prime components. 

The primary purpose of a prime factor tree is to express a composite number as a product of its prime factors, simplifying it to its prime form.

A prime number is a natural number with only two factors: 1 and the number itself. 

Examples: 2, 3, 5, 7,…

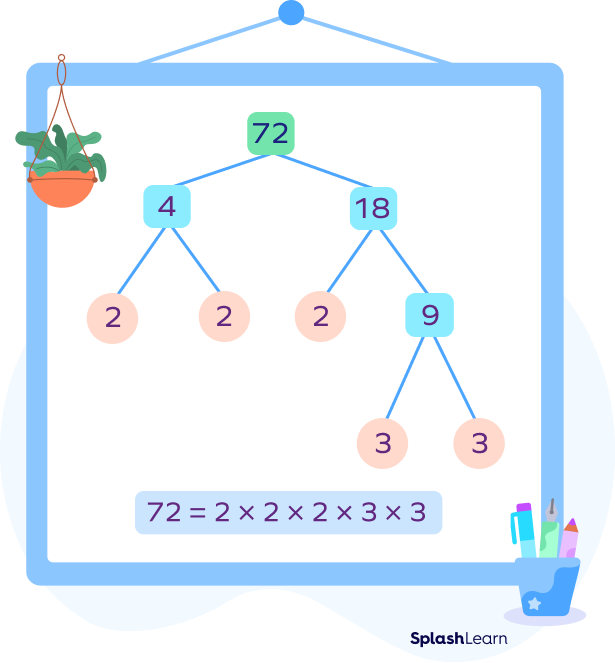
Example 1: Find the prime factorization of 72

Example 2: Factor tree of 180

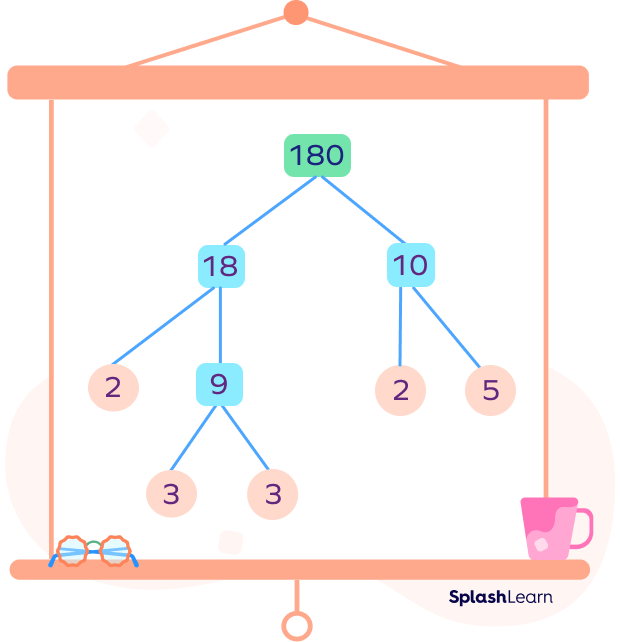
NOTE: A number can have multiple factor trees, which ultimately give the same prime factorization. The prime factorization is unique, but a factor tree can have different forms depending on how you break down the number.

Here are two different factor trees of 64:

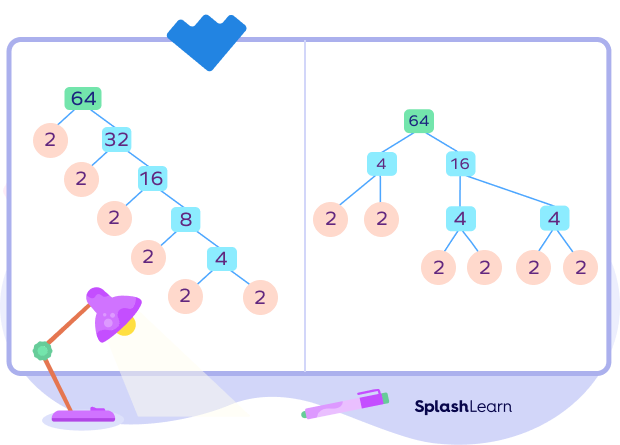
Prime factorization of 64 = 2 6

Applications of a Factor Tree

1) To find the prime factors of a number

2) To write the prime factorization of a number

3) To find the GCD (Greatest Common Divisor) of a number

4) to find the LCM (Least Common Multiple) of a number

Facts about Factor Trees

• The endpoints of the tree represent prime factors, as they cannot be further factored. They are also called “leaf nodes.”
• The prime factorization of any number is always unique. However, the factor

In this article, we learned about Factor Trees, a method for finding a number’s prime factors. We discussed how to draw a factor tree, its applications, and associated concepts. Let’s solve a few examples for better comprehension and reinforcement.

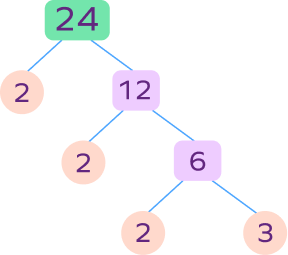
1. Draw a factor tree for 24.

Solution: 

24 = 2 × 1 2

24 = 2 × 2 × 6

24 = 2 × 2 × 2 × 3

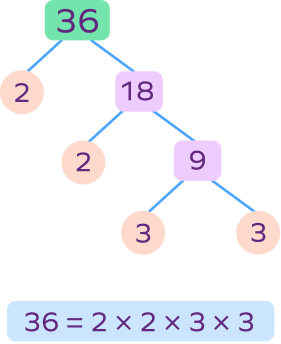
2. Write the prime factorization of 36 using a factor tree.

Here’s the factor tree and prime factorization of 36:

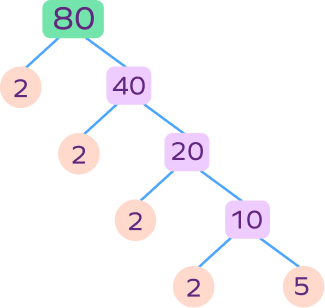
3. Draw a factor tree for 80.

Solution:  

Factor tree of 80:

4. Write the prime factors of 156 using the factor tree method.

Here’s a factor tree of 156:

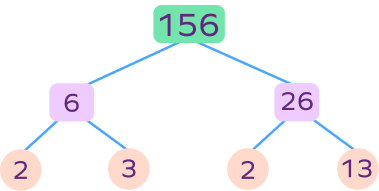
Prime factors of 156: 2, 3, and 13

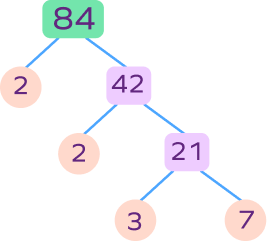
5. Draw a factor tree of 84.

Factor tree of 84:

Factor Tree – Definition with Examples

Attend this quiz & Test your knowledge.

Find the missing number in the factor tree of 125.

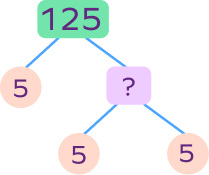
A prime number has ___ factors.

Which of the following prime factorizations are correct.

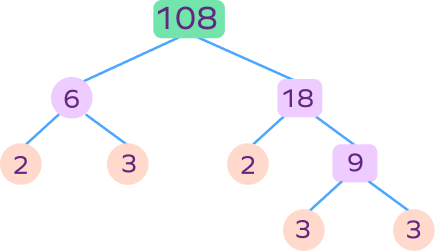
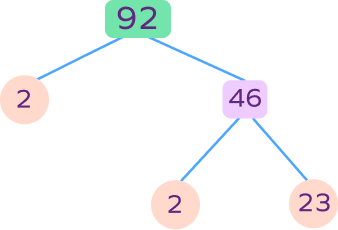
Write the prime factorization of 92 using the given factor tree.

What are factor trees?

Factor trees are a visual way to show how numbers can be broken down into their prime factors (numbers divisible only by 1 and themselves).

How do I make a factor tree?

• Start with your number at the top. Find two factors that multiply to make that number. Write them below, branching out like a tree.
• Repeat for each factor, breaking them down further until you reach prime numbers.

What are prime numbers?

Prime numbers are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11).

What are some uses of factor trees?

• Finding prime factors of a number.
• Checking if a number is prime.
• Finding the least common multiple (LCM) or greatest common factor (GCF) of two numbers (more advanced).

RELATED POSTS

• Prime Factorization: Definition, Methods, Examples, FAQs
• Prime Numbers – Definition, Chart, Examples, Practice Problems
• Factor in Math – Definition, Types, Properties, Examples, Facts
• Relatively Prime
• Composite Numbers – Definition with Examples

Math & ELA | PreK To Grade 5

Kids see fun., you see real learning outcomes..

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free