4 2 problem solving angle relationships in triangles answers

Calcworkshop

Angle Relationships Simply Explained w/ 11+ Step-by-Step Examples!

// Last Updated: January 21, 2020 - Watch Video //

In today’s lesson, you’re going to learn all about angle relationships and their measures.

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

We’ll walk through 11 step-by-step examples to ensure mastery.

Let’s dive in!

Angle Pair Relationship Names

In Geometry , there are five fundamental angle pair relationships:

• Complementary Angles
• Supplementary Angles
• Adjacent Angles
• Linear Pair
• Vertical Angles

1. Complementary Angles

Complementary angles are two positive angles whose sum is 90 degrees.

For example, complementary angles can be adjacent, as seen in with ∠ABD and ∠CBD in the image below. Or they can be two acute angles, like ∠MNP and ∠EFG, whose sum is equal to 90 degrees. Both of these graphics represent pairs of complementary angles.

Complementary Angles Example

2. Supplementary Angles

Supplementary angles are two positive angles whose sum is 180 degrees.

For example, supplementary angles may be adjacent, as seen in with ∠ABD and ∠CBD in the image below. Or they can be two angles, like ∠MNP and ∠KLR, whose sum is equal to 180 degrees. Both of these graphics represent pairs of supplementary angles.

Supplementary Angles Example

What is important to note is that both complementary and supplementary angles don’t always have to be adjacent angles.

3. Adjacent Angles

Adjacent angles are two angles in a plane that have a common vertex and a common side but no common interior points.

Angles 1 and 2 are adjacent angles because they share a common side.

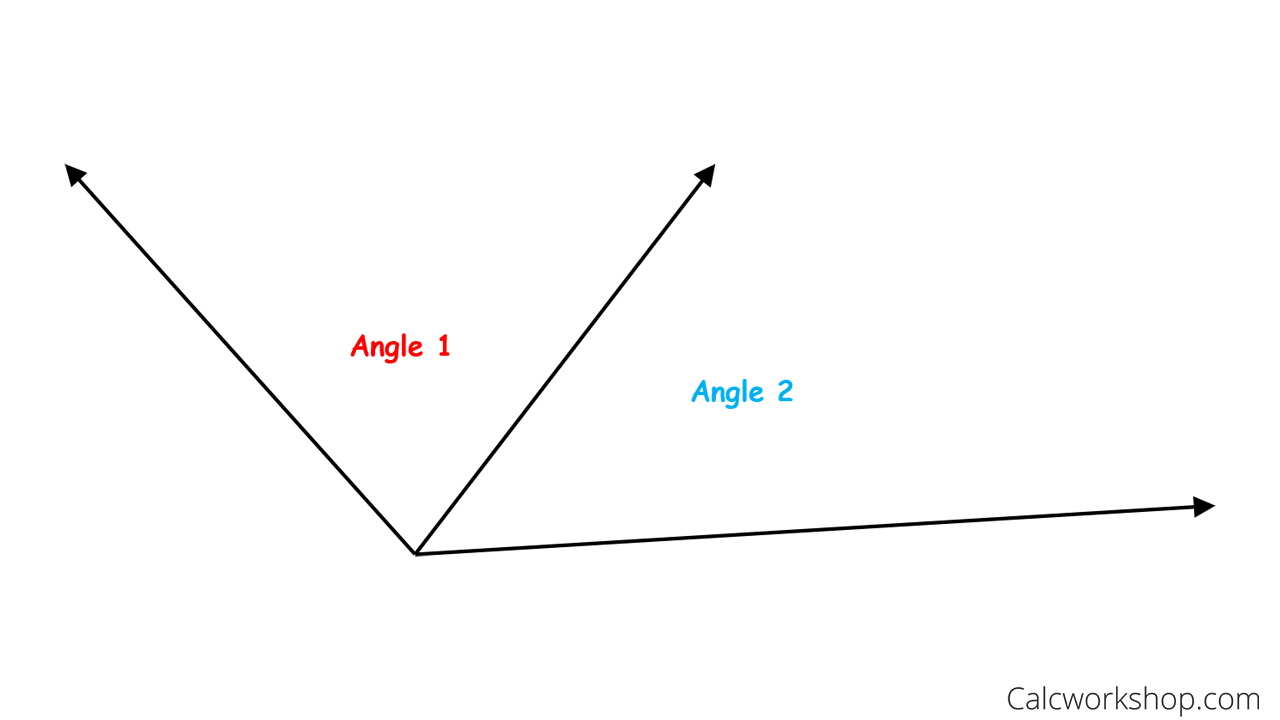
Adjacent Angles Examples

And as Math is Fun so nicely points out, a straightforward way to remember Complementary and Supplementary measures is to think:

C is for Corner of a Right Angle (90 degrees) S is for Straight Angle (180 degrees)

Now it’s time to talk about my two favorite angle-pair relationships: Linear Pair and Vertical Angles.

4. Linear Pair

A linear pair is precisely what its name indicates. It is a pair of angles sitting on a line! In fact, a linear pair forms supplementary angles.

Because, we know that the measure of a straight angle is 180 degrees, so a linear pair of angles must also add up to 180 degrees.

∠ABD and ∠CBD form a linear pair and are also supplementary angles, where ∠1 + ∠2 = 180 degrees.

Linear Pair Example

5. Vertical Angles

Vertical angles are two nonadjacent angles formed by two intersecting lines or opposite rays.

Think of the letter X. These two intersecting lines form two sets of vertical angles (opposite angles). And more importantly, these vertical angles are congruent.

In the accompanying graphic, we see two intersecting lines, where ∠1 and ∠3 are vertical angles and are congruent. And ∠2 and ∠4 are vertical angles and are also congruent.

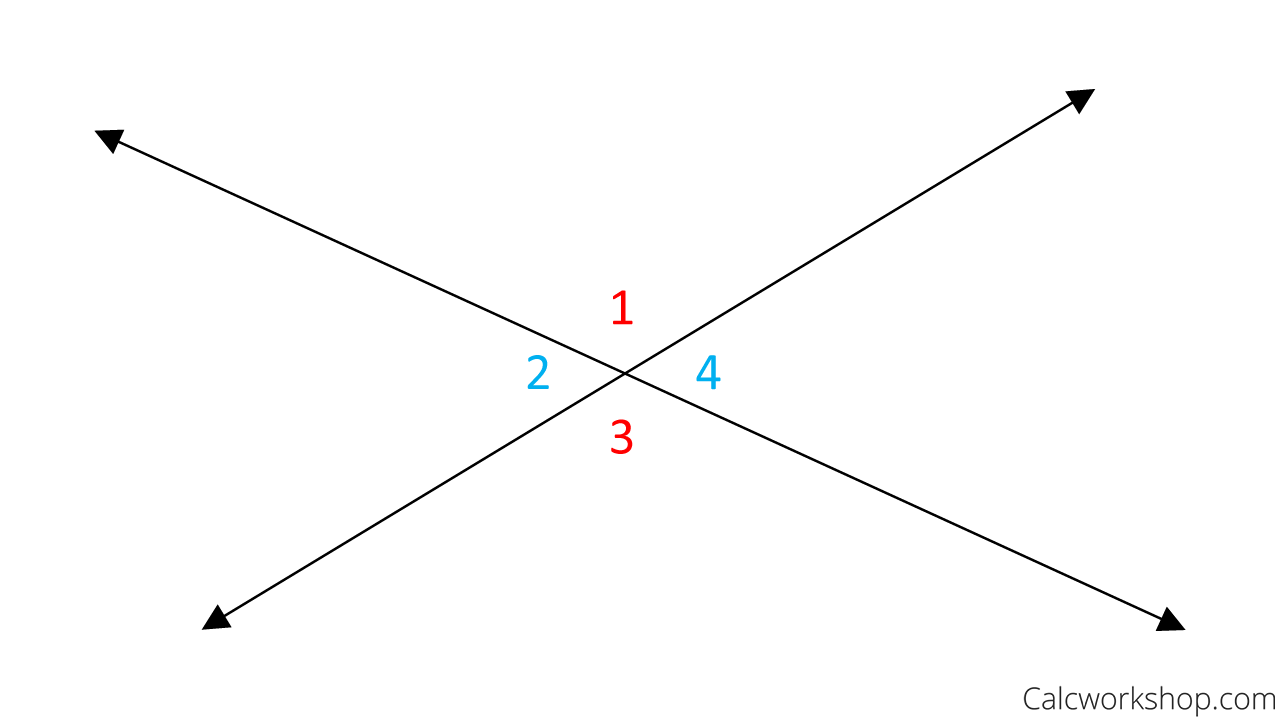
Vertical Angles Examples

Together we are going to use our knowledge of Angle Addition, Adjacent Angles, Complementary and Supplementary Angles, as well as Linear Pair and Vertical Angles to find the values of unknown measures.

Angle Relationships – Lesson & Examples (Video)

• Introduction to Angle Pair Relationships
• 00:00:15 – Overview of Complementary, Supplementary, Adjacent, and Vertical Angles and Linear Pair
• Exclusive Content for Member’s Only
• 00:06:29 – Use the diagram to solve for the unknown angle measures (Examples #1-8)
• 00:19:05 – Find the measure of each variable involving Linear Pair and Vertical Angles (Examples #9-12)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.0: Side and Angle Relationships

• Last updated
• Save as PDF
• Page ID 112415

• Katherine Yoshiwara
• Los Angeles Pierce College

Introduction

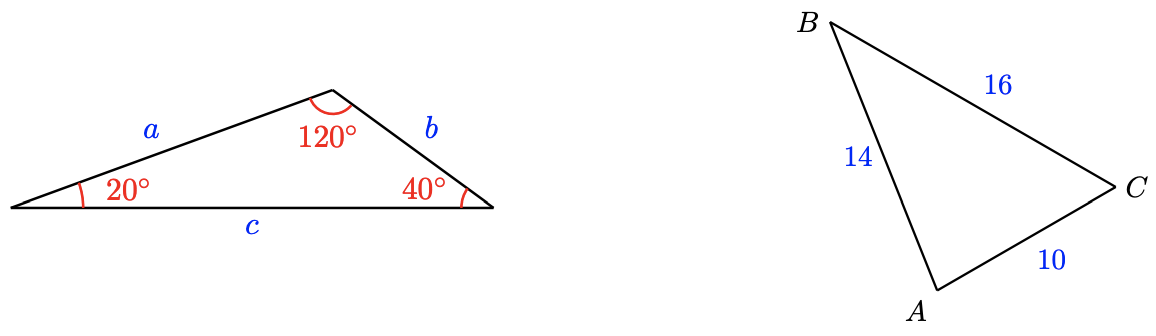
From geometry we know that the sum of the angles in a triangle is \(180^{\circ}\). Are there any relationships between the angles of a triangle and its sides?

First of all, you have probably observed that the longest side in a triangle is always opposite the largest angle, and the shortest side is opposite the smallest angle, as illustrated below.

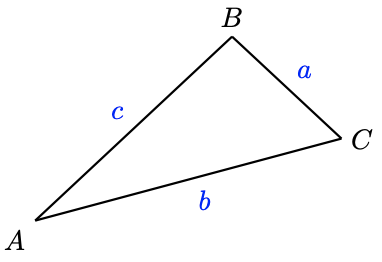
It is usual to label the angles of a triangle with capital letters, and the side opposite each angle with the corresponding lower-case letter, as shown at right. We will follow this practice unless indicated otherwise.

Example 2.2

In \(\triangle F G H, \angle F=48^{\circ}\), and \(\angle G\) is obtuse. Side \(f\) is 6 feet long. What can you conclude about the other sides?

Because \(\angle G\) is greater than \(90^{\circ}\), we know that \(\angle F+\angle G\) is greater than \(90^{\circ}+48^{\circ}=138^{\circ}\), so \(\angle F\) is less than \(180^{\circ}-138^{\circ}=42^{\circ}\). Thus, \(\angle H<\angle F<\angle G\), and consequently \(h<f<g\). We can conclude that \(h<6\) feet long, and \(g>6\) feet long.

Checkpoint 2.3

In isosceles triangle \(\triangle R S T\), the vertex angle \(\angle S=72^{\circ}\). Which side is longer, \(s\) or \(t\)?

\(s\) is longer

The Triangle Inequality

It is also true that the sum of the lengths of any two sides of a triangle must be greater than the third side, or else the two sides will not meet to form a triangle. This fact is called the triangle inequality.

Triangle Inequality.

In any triangle, we must have that

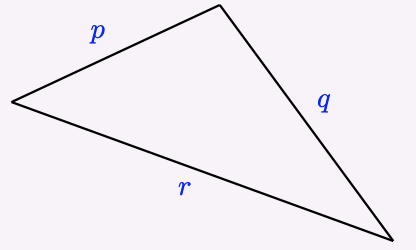
\(p + q > r\)

where \(p, q\), and \(r\) are the lengths of the sides of the triangle.

We cannot use the triangle inequality to find the exact lengths of the sides of a triangle, but we can find largest and smallest possible values for the length.

Example 2.4

Two sides of a triangle have lengths 7 inches and 10 inches, as shown at right. What can you say about the length of the third side?

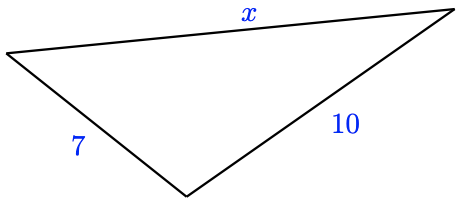
We let \(x\) represent the length of the third side of the triangle. By looking at each side in turn, we can apply the triangle inequality three different ways, to get

\[7<x+10, \quad 10<x+7, \quad \text { and } \quad x<10+7 \nonumber\]

We solve each of these inequalities to find

\[-3<x, \quad 3<x, \quad \text { and } \quad x<17 \nonumber\]

We already know that \(x>-3\) because \(x\) must be positive, but the other two inequalities do give us new information. The third side must be greater than 3 inches but less than 17 inches long.

Checkpoint 2.5

Can you make a triangle with three wooden sticks of lengths 14 feet, 26 feet, and 10 feet? Sketch a picture, and explain why or why not.

No, \(10+14\) is not greater than 26 .

Right Triangles: The Pythagorean Theorem

In Chapter 1 we used the Pythagorean theorem to derive the distance formula. We can also use the Pythagorean theorem to find one side of a right triangle if we know the other two sides.

Pythagorean Theorem

In a right triangle, if \(c\) stands for the length of the hypotenuse, and the lengths of the two legs are denoted by \(a\) and \(b\), then

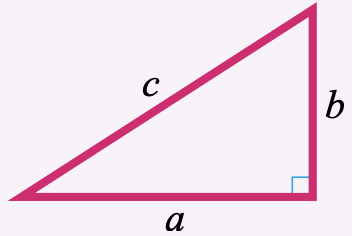
\(a^2 + b^2 = c^2\)

Example 2.6

A 25 -foot ladder is placed against a wall so that its foot is 7 feet from the base of the wall. How far up the wall does the ladder reach?

We make a sketch of the situation, as shown below, and label any known dimensions. We'll call the unknown height \(h\).

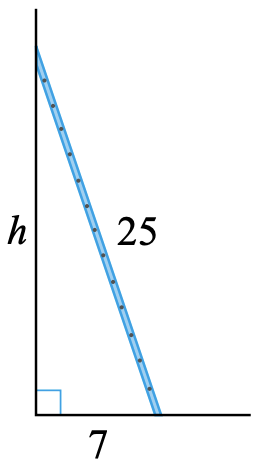
The ladder forms the hypotenuse of a right triangle, so we can apply the Pythagorean theorem, substituting 25 for \(c, 7\) for \(b\), and \(h\) for \(a\).

\begin{gathered} a^2+b^2=c^2 \\ h^2+7^2=25^2 \end{gathered}

Now solve by extraction of roots:

\begin{aligned} h^2+49 &=625 &&\text{Subtract 49 from both sides.} \\ h^2 &=576 &&\text{Extract roots.}\\ h &=\pm \sqrt{576} &&\text{Simplify the radical.}\\ h &=\pm 24 \end{aligned}

The height must be a positive number, so the solution \(-24\) does not make sense for this problem. The ladder reaches 24 feet up the wall.

Checkpoint 2.7

A baseball diamond is a square whose sides are 90 feet long. The catcher at home plate sees a runner on first trying to steal second base, and throws the ball to the second-baseman. Find the straight-line distance from home plate to second base.

\(90 \sqrt{2} \approx 127.3\) feet

Keep in mind that the Pythagorean theorem is true only for right triangles, so the converse of the theorem is also true. In other words, if the sides of a triangle satisfy the relationship \(a^2+b^2=c^2\), then the triangle must be a right triangle. We can use this fact to test whether or not a given triangle has a right angle.

Example 2.9

Delbert is paving a patio in his back yard, and would like to know if the corner at \(C\) is a right angle.

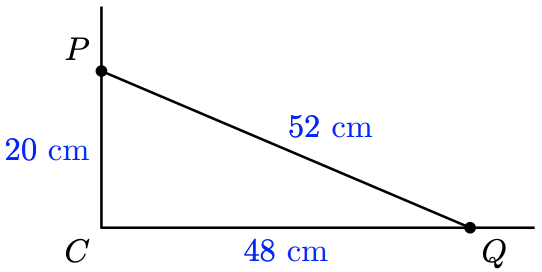
He measures 20 cm along one side from the corner, and 48 cm along the other side, placing pegs \(P\) and \(Q\) at each position, as shown at right. The line joining those two pegs is 52 cm long. Is the corner a right angle?

If is a right triangle, then its sides must satisfy \(p^2+q^2=c^2\). We find

\begin{aligned} p^2+q^2 &=20^2+48^2=400+2304=2704 \\ c^2 &=52^2=2704 \end{aligned}

Yes, because \(p^2+q^2=c^2\), the corner at \(C\) is a right angle.

Checkpoint 2.10

The sides of a triangle measure 15 inches, 25 inches, and 30 inches long. Is the triangle a right triangle?

The Pythagorean theorem relates the sides of right triangles. However, for information about the sides of other triangles, the best we can do (without trigonometry!) is the triangle inequality. Nor does the Pythagorean theorem help us find the angles in a triangle. In the next section we discover relationships between the angles and the sides of a right triangle.

Review the following skills you will need for this section.

Algebra Refresher 2.2

Solve the inequality.

1. \(6-x>3\)

2. \(\dfrac{-3 x}{4} \geq-6\)

3. \(3 x-7 \leq-10\)

4. \(4-3 x<2 x+9\)

If \(x<0\), which of the following expressions are positive, and which are negative?

6. \(-(-x)\)

8. \(-|x|\)

9. \(-|-x|\)

10. \(x^{-1}\)

1 \(x<3\)

2 \(x \leq 8\)

3 \(x \leq -1\)

4 \(x > -1\)

10 Negative

Section 2.1 Summary

• Converse • Extraction of roots • Inequality

1 The longest side in a triangle is opposite the largest angle, and the shortest side is opposite the smallest angle.

2 Triangle Inequality: In any triangle, the sum of the lengths of any two sides is greater than the length of the third side.

3 Pythagorean Theorem: In a right triangle with hypotenuse \(c\), \(a^2 + b^2 = c^2\).

4 If the sides of a triangle satisfy the relationship \(a^2 + b^2 = c^2\), then the triangle is a right triangle.

Study Questions

1 Is it always true that the hypotenuse is the longest side in a right triangle? Why or why not?

2 In \(\triangle D E F\), is it possible that \(d+e>f\) and \(e+f>d\) are both true? Explain your answer.

3 In a right triangle with hypotenuse \(c\), we know that \(a^2+b^2=c^2\). Is it also true that \(a+b=c\)? Why or why not?

4 The two shorter sides of an obtuse triangle are 3 in and 4 in. What are the possible lengths for the third side?

1 Identify inconsistencies in figures #1-12

2 Use the triangle inequality to put bounds on the lengths of sides #13-16

3 Use the Pythagorean theorem to find the sides of a right triangle #17-26

4 Use the Pythagorean theorem to identify right triangles #27-32

5 Solve problems using the Pythagorean theorem #33-42

Homework 2.1

For Problems 1–12, explain why the measurements shown cannot be accurate.

13. If two sides of a triangle are 6 feet and 10 feet long, what are the largest and smallest possible values for the length of the third side?

14. Two adjacent sides of a parallelogram are 3 cm and 4 cm long. What are the largest and smallest possible values for the length of the diagonal?

15. If one of the equal sides of an isosceles triangle is 8 millimeters long, what are the largest and smallest possible values for the length of the base?

16. The town of Madison is 15 miles from Newton, and 20 miles from Lewis. What are the possible values for the distance from Lewis to Newton?

For Problems 17–22,

a Make a sketch of the situation described, and label a right triangle.

b Use the Pythagorean Theorem to solve each problem.

17. The size of a TV screen is the length of its diagonal. If the width of a 35-inch TV screen is 28 inches, what is its height?

18. If a 30-meter pine tree casts a shadow of 30 meters, how far is the tip of the shadow from the top of the tree?

19. The diagonal of a square is 12 inches long. How long is the side of the square?

20. The length of a rectangle is twice its width, and its diagonal is meters long. Find the dimensions of the rectangle.

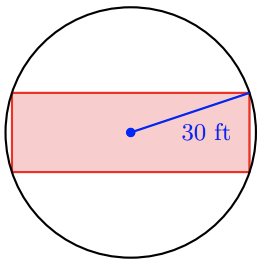
21. What size rectangle can be inscribed in a circle of radius 30 feet if the length of the rectangle must be three times its width?

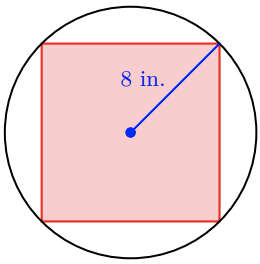
22. What size square can be inscribed inside a circle of radius 8 inches, so that its vertices just touch the circle?

For Problems 23–26, find the unknown side of the triangle.

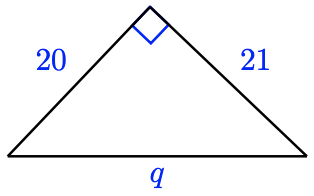
For Problems 27–32, decide whether a triangle with the given sides is a right triangle.

27. 9 in, 16 in, 25 in

28. 12 m, 16 m, 20 m

29. 5 m, 12 m, 13 m

30. 5 ft, 8 ft, 13 ft

31. \(5^2\) ft, \(8^2\) ft, \(13^2\) ft

32. \(\sqrt{5}\) ft, \(\sqrt{8}\) ft, \(\sqrt{13}\) ft

33. Show that the triangle with vertices (0, 0), (6, 0) and (3, 3) is an isosceles right triangle, that is, a right triangle with two sides of the same length.

34. Two opposite vertices of a square are \(A(−9, −5)\) and \(C(3, 3)\).

a Find the length of a diagonal of the square.

b Find the length of the side of the square.

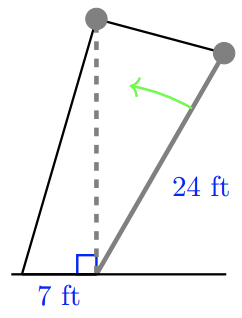
35. A 24-foot flagpole is being raised by a rope and pulley, as shown in the figure. The loose end of the rope can be secured to a ring on the ground 7 feet from the base of the pole. From the ring to the top of the pulley, how long should the rope be when the flagpole is vertical?

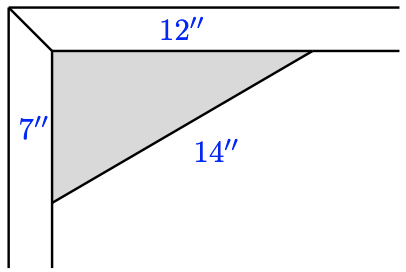
36. To check whether the corners of a frame are square, carpenters sometimes measure the sides of a triangle, with two sides meeting at the join of the boards. Is the corner shown in the figure square?

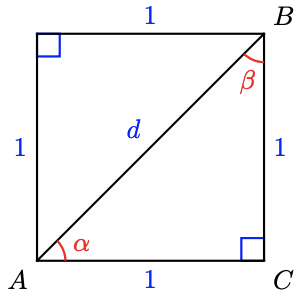
37. Find \(\alpha, \beta\) and \(h\).

38. Find \(\alpha, \beta\) and \(d\).

39. Find the diagonal of a cube of side 8 inches. Hint: Find the diagonal of the base first.

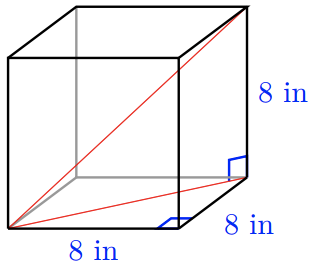
40. Find the diagonal of a rectangular box whose sides are 6 cm by 8 cm by 10 cm. Hint: Find the diagonal of the base first.

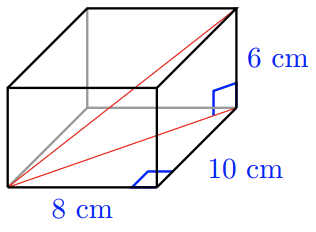
For Problems 41 and 42, make a sketch and solve.

a The back of Brian’s pickup truck is five feet wide and seven feet long. He wants to bring home a 9-foot length of copper pipe. Will it lie flat on the floor of the truck?

42. What is the longest curtain rod that will fit inside a box 60 inches long by 10 inches wide by 4 inches tall?

43. In this problem, we’ll show that any angle inscribed in a semi-circle must be a right angle. The figure shows a triangle inscribed in a unit circle, one side lying on the diameter of the circle and the opposite vertex at point \((p, q)\) on the circle.

a What are the coordinates of the other two vertices of the triangle? What is the length of the side joining those vertices?

b Use the distance formula to compute the lengths of the other two sides of the triangle.

c Show that the sides of the triangle satisfy the Pythagorean theorem, \(a^2 + b^2 = c^2\).

44. There are many proofs of the Pythagorean theorem. Here is a simple visual argument.

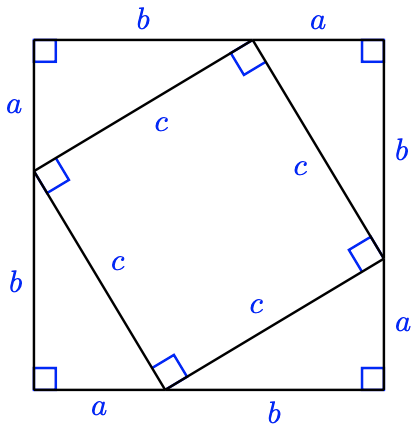
a What is the length of the side of the large square in the figure? Write an expression for its area.

b Write another expression for the area of the large square by adding the areas of the four right triangles and the smaller central square.

c Equate your two expressions for the area of the large square, and deduce the Pythagorean theorem.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 6: Angle relationships

Complementary, supplementary, & vertical angles.

• Angles: introduction (Opens a modal)
• Complementary & supplementary angles (Opens a modal)
• Vertical angles (Opens a modal)
• Complementary and supplementary angles review (Opens a modal)
• Identifying supplementary, complementary, and vertical angles Get 5 of 7 questions to level up!
• Complementary and supplementary angles (visual) Get 3 of 4 questions to level up!
• Complementary and supplementary angles (no visual) Get 5 of 7 questions to level up!
• Vertical angles Get 3 of 4 questions to level up!
• Finding angle measures between intersecting lines Get 3 of 4 questions to level up!

Finding missing angles

• Find measure of vertical angles (Opens a modal)
• Find measure of angles word problem (Opens a modal)
• Equation practice with complementary angles (Opens a modal)
• Equation practice with supplementary angles (Opens a modal)
• Equation practice with vertical angles (Opens a modal)
• Finding missing angles Get 5 of 7 questions to level up!
• Create equations to solve for missing angles Get 5 of 7 questions to level up!
• Unknown angle problems (with algebra) Get 5 of 7 questions to level up!
• Equation practice with angle addition Get 3 of 4 questions to level up!

Triangle angles

• Angles in a triangle sum to 180° proof (Opens a modal)
• Isosceles & equilateral triangles problems (Opens a modal)
• Triangle exterior angle example (Opens a modal)
• Triangle angles review (Opens a modal)
• Find angles in triangles Get 5 of 7 questions to level up!
• Find angles in isosceles triangles Get 3 of 4 questions to level up!
• Triangle exterior angle property problems Get 3 of 4 questions to level up!

Polygon angles

• Sum of interior angles of a polygon (Opens a modal)
• Angles of a polygon Get 3 of 4 questions to level up!

Chapter 2: Trigonometric Ratios

2.1 Side and Angle Relationships

Algebra refresher.

Solve the inequality.

1. [latex]6-x >  3[/latex]

2. [latex]\dfrac{-3x}{4} \geq -6[/latex]

3. [latex]3x-7 \leq -10[/latex]

4. [latex]2x+9 > 4-3x[/latex]

If [latex]0> x[/latex], which of the following expressions are positive, and which are negative?

5. [latex]- x[/latex]

6. [latex]-(-x)[/latex]

7. [latex]|x|[/latex]

8. [latex]-|x|[/latex]

9. [latex]-|-x|[/latex]

10. [latex]x^{-1}[/latex]

• [latex]\displaystyle \:x \lt 3[/latex]
• [latex]\displaystyle \:x \le 8[/latex]
• [latex]\displaystyle \:x \le -1[/latex]
• [latex]\displaystyle \:x \gt -1[/latex]

Learning Objectives

• Identify inconsistencies in figures
• Use the triangle inequality to put bounds on the lengths of sides
• Use the Pythagorean theorem to find the sides of a right triangle
• Use the Pythagorean theorem to identify right triangles
• Solve problems using the Pythagorean theorem

Introduction

From geometry, we know that the sum of the angles in a triangle is [latex]180°.[/latex] Are there any relationships between the angles of a triangle and its sides? First of all, you have probably observed that the longest side in a triangle is always opposite the largest angle, and the shortest side is opposite the smallest angle, as illustrated below.

It is usual to label the angles of a triangle with capital letters, and the side opposite each angle with the corresponding lower-case letter, as shown at right. We will follow this practice unless indicated otherwise.

Example 2.2.

In [latex]\triangle FGH, \angle F=48^o,[/latex] and [latex]\angle G[/latex] is obtuse. Side [latex]f[/latex] is [latex]6[/latex] feet long. What can you conclude about the other sides?

Because [latex]\angle G[/latex] is greater than [latex]90^o\text{,}[/latex] we know that [latex]\angle F +\angle G[/latex] is greater than [latex]90^o + 48^o = 138^o\text{,}[/latex] so [latex]\angle F[/latex] is less than [latex]180^o-138^o = 42^o.[/latex] Thus, [latex]\angle H \lt \angle F \lt \angle G,[/latex] and consequently, [latex]h \lt f \lt g\text{.}[/latex] We can conclude that [latex]h \lt 6[/latex] feet long, and [latex]g \gt 6[/latex] feet long.

Checkpoint 2.3.

In isosceles triangle [latex]\triangle RST\text{,}[/latex] the vertex angle [latex]\angle S = 72^o\text{.}[/latex] Which side is longer, [latex]s[/latex] or [latex]t\text{?}[/latex]

[latex]s[/latex] is longer

The Triangle Inequality

It is also true that the sum of the lengths of any two sides of a triangle must be greater than the third side, or else the two sides will not meet to form a triangle. This fact is called the triangle inequality.

Triangle Inequality.

In any triangle, we must have that [latex]\begin{equation*} p+q \gt r \end{equation*}[/latex] where [latex]p, q, \text{and}~ r[/latex] are the lengths of the sides of the triangle.

We cannot use the triangle inequality to find the exact lengths of the sides of a triangle, but we can find the largest and smallest possible values for the length.

Example 2.4.

Two sides of a triangle have lengths [latex]7[/latex] inches and [latex]10[/latex] inches, as shown at right. What can you say about the length of the third side?

We let [latex]x[/latex] represent the length of the third side of the triangle. By looking at each side in turn, we can apply the triangle inequality three different ways to get [latex]\begin{equation*} 7 \lt x+10, ~~~ 10 \lt x+7, ~~~ \text{and} ~~~ x \lt 10+7 \end{equation*}[/latex] We solve each of these inequalities to find [latex]\begin{equation*} -3 \lt x, ~~~ 3 \lt x, ~~~ \text{and} ~~~ x \lt 17 \end{equation*}[/latex] We already know that [latex]x \gt -3[/latex] because [latex]x[/latex] must be positive, but the other two inequalities do give us new information. The third side must be greater than [latex]3[/latex] inches but less than [latex]17[/latex] inches long.

Checkpoint 2.5.

Can you make a triangle with three wooden sticks of lengths [latex]14[/latex] feet, [latex]26[/latex] feet, and [latex]10[/latex] feet? Sketch a picture, and explain why or why not.

No, [latex]10+14[/latex] is not greater than [latex]26[/latex].

Right Triangles: The Pythagorean Theorem

In Chapter 1 we used the Pythagorean theorem to derive the distance formula. We can also use the Pythagorean theorem to find one side of a right triangle if we know the other two sides.

Pythagorean Theorem.

In a right triangle, if [latex]c[/latex] stands for the length of the hypotenuse, and the lengths of the two legs are denoted by [latex]a[/latex] and [latex]b\text{,}[/latex] then [latex]\begin{equation*} a^2 + b^2 = c^2 \end{equation*}[/latex]

Example 2.6.

A [latex]25[/latex]-foot ladder is placed against a wall so that its foot is [latex]7[/latex] feet from the base of the wall. How far up the wall does the ladder reach?

We make a sketch of the situation, as shown below, and label any known dimensions. We’ll call the unknown height [latex]h\text{.}[/latex]

The ladder forms the hypotenuse of a right triangle, so we can apply the Pythagorean theorem, substituting [latex]25[/latex] for [latex]c\text{,}[/latex] [latex]7[/latex] for [latex]b\text{,}[/latex] and [latex]h[/latex] for [latex]a\text{.}[/latex] [latex]\begin{align*} a^2 + b^2 = c^2\\ h^2 + 7^2 = 25^2 \end{align*}[/latex] Now solve by extraction of roots:

[latex]\begin{align*} h^2 + 49 = 625 \ \ \text{Subtract 49 from both sides.}\\ h^2 = 576 \ \ \text{Extract roots.}\\ h = \pm \sqrt{576}\ \ \text{Simplify the radical.}\\ h = \pm 24 \end{align*}[/latex] The height must be a positive number, so the solution [latex]-24[/latex] does not make sense for this problem. The ladder reaches [latex]24[/latex] feet up the wall.

Checkpoint 2.7.

A baseball diamond is a square whose sides are [latex]90[/latex] feet long. The catcher at home plate sees a runner on first trying to steal second base, and throws the ball to the second baseman. Find the straight-line distance from home plate to second base.

[latex]90\sqrt{2} \approx 127.3[/latex] feet

Keep in mind that the Pythagorean theorem is true only for right triangles, so the converse of the theorem is also true. In other words, if the sides of a triangle satisfy the relationship [latex]a^2 + b^2 = c^2\text{,}[/latex] then the triangle must be a right triangle. We can use this fact to test whether or not a given triangle has a right angle.

Example 2.9.

Delbert is paving a patio in his backyard and would like to know if the corner at [latex]C[/latex] is a right angle.

He measures [latex]20[/latex] cm along one side from the corner and [latex]48[/latex] cm along the other side, placing pegs [latex]P[/latex] and [latex]Q[/latex] at each position, as shown at right. The line joining those two pegs is [latex]52[/latex] cm long. Is the corner a right angle?

If is a right triangle, then its sides must satisfy [latex]p^2 + q^2 = c^2\text{.}[/latex] We find [latex]\begin{align*} p^2 + q^2 = 20^2 + 48^2 = 400 + 2304 = 2704\\ c^2 = 52^2 = 2704 \end{align*}[/latex] Yes, because [latex]p^2 + q^2 = c^2\text{,}[/latex] the corner at [latex]C[/latex] is a right angle.

Checkpoint 2.10.

The sides of a triangle measure 15 inches, 25 inches, and 30 inches long. Is the triangle a right triangle?

The Pythagorean theorem relates the sides of right triangles. However, for information about the sides of other triangles, the best we can do (without trigonometry!) is the triangle inequality. Nor does the Pythagorean theorem help us find the angles in a triangle. In the next section, we discover relationships between the angles and the sides of a right triangle.

Section 2.1 Summary

• Extraction of roots
• The longest side in a triangle is opposite the largest angle, and the shortest side is opposite the smallest angle.
• Triangle Inequality: In any triangle, the sum of the lengths of any two sides is greater than the length of the third side.
• Pythagorean Theorem: In a right triangle with hypotenuse [latex]c,~~ a^2 +b^2 = c^2\text{.}[/latex]
• If the sides of a triangle satisfy the relationship [latex]~a^2 +b^2 = c^2~\text{,}[/latex] then the triangle is a right triangle.

 Study Questions

• Is it always true that the hypotenuse is the longest side in a right triangle? Why or why not?
• In [latex]\triangle DEF\text{,}[/latex] is it possible that [latex]~d+e\gt f~[/latex] and [latex]~e+f\gt d~[/latex] are both true? Explain your answer.
• In a right triangle with hypotenuse [latex]c\text{,}[/latex] we know that [latex]~a^2 +b^2 = c^2~\text{.}[/latex] Is it also true that [latex]~a + b = c~\text{?}[/latex] Why or why not?
• The two shorter sides of an obtuse triangle are [latex]3[/latex] in and [latex]4[/latex] in. What are the possible lengths for the third side?

The converse of a statement is a proposition obtained by reversing its terms. For example, the converse of the statement “If it is raining, then the streets are wet” is “If the streets are wet, then it is raining.” Note that the converse may or may not be true, even if the original statement is true.

Extraction of roots refers to the process of finding the value of a root (usually square, cube, or higher) of a number or expression, either by using a numerical method or by solving an equation.

An inequality is a mathematical statement that compares two values, expressions, or quantities using an inequality symbol (such as “>” for greater than, “>=” for greater than or equal to), indicating that one value is not equal to the other.

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

Angle relationships and unknown angle problems

This lesson first explains supplementary and vertical angles. Then we look at a variety of "angle puzzles", or problems with an unknown angle, and solve those using these basic principles. I also write an equation for each problem, to help students learn to both write and solve equations, since this lesson belongs to my pre-algebra course .

Angles in a triangle — video lesson

Math Mammoth Geometry 3 — a self-teaching worktext with explanations & exercises (grades 4-5)

Back to the geometry videos index

Back to pre-algebra videos index

Back to all videos index

© 2006-2024 MathMammoth.com