CBSE Expert


CBSE Case Study Questions Class 9 Maths Chapter 12 Heron’s Formula PDF Download
CBSE Case Study Questions Class 9 Maths Chapter 12 are very important to solve for your exam. Class 9 Maths Chapter 12 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 9 Maths Chapter 12 Heron’s Formula

Case Study Questions Class 9 Maths Chapter 12
Case Study 1: A group of students is learning about Heron’s Formula for finding the area of a triangle. They encountered the following scenario:
Rohan and Kavya came across a triangular field in their village. They made the following observations:
- The lengths of the three sides of the triangular field are 8 meters, 12 meters, and 15 meters.
- The perimeter of the triangular field is 35 meters.
Based on this information, the students were asked to apply Heron’s Formula to find the area of the triangular field. Let’s see if you can answer the questions correctly:
MCQ Questions:
Q1. The semiperimeter of the triangular field is: (a) 8 meters (b) 12 meters (c) 15 meters (d) 17.5 meters
Answer: (d) 17.5 meters
Q2. Using Heron’s Formula, the area of the triangular field is: (a) 24 square meters (b) 30 square meters (c) 36 square meters (d) 40 square meters
Answer: (b) 30 square meters
Q3. The type of triangle formed by the sides of the field is: (a) Equilateral (b) Isosceles (c) Scalene (d) Right-angled
Answer: (c) Scalene
Q4. The length of the altitude corresponding to the side of 15 meters is: (a) 2 meters (b) 4 meters (c) 6 meters (d) 8 meters
Answer: (c) 6 meters
Q5. The lengths of the altitudes corresponding to the sides of 8 meters and 12 meters are: (a) 4 meters and 6 meters (b) 6 meters and 8 meters (c) 8 meters and 10 meters (d) 10 meters and 12 meters
Answer: (a) 4 meters and 6 meters
Case Study 2: A group of students is studying Heron’s Formula for finding the area of a triangle. They encountered the following scenario:
Neha and Mohan went on a field trip to a riverbank. They noticed a triangular piece of land that they wanted to measure and calculate its area. They made the following observations:
- Neha measured the lengths of the three sides of the triangular piece of land as 7 meters, 9 meters, and 11 meters.
- Mohan measured the lengths of the three sides of the same triangular piece of land as 10 meters, 12 meters, and 15 meters.
Based on this information, the students were asked to apply Heron’s Formula to find the area of the triangular piece of land. Let’s see if you can answer the questions correctly:
Q1. Using Neha’s measurements, the semiperimeter of the triangular piece of land is: (a) 13 meters (b) 16 meters (c) 19 meters (d) 23 meters
Answer: (c) 19 meters
Q2. Using Neha’s measurements, the area of the triangular piece of land is: (a) 24 square meters (b) 26 square meters (c) 28 square meters (d) 30 square meters
Answer: (a) 24 square meters
Q3. Using Mohan’s measurements, the semiperimeter of the triangular piece of land is: (a) 16 meters (b) 18 meters (c) 21 meters (d) 25 meters
Answer: (c) 21 meters
Q4. Using Mohan’s measurements, the area of the triangular piece of land is: (a) 40 square meters (b) 42 square meters (c) 45 square meters (d) 48 square meters
Answer: (b) 42 square meters
Q5. The measurements taken by Neha represent a triangle that is: (a) Equilateral (b) Isosceles (c) Scalene (d) Right-angled
Hope the information shed above regarding Case Study and Passage Based Questions for Case Study Questions Class 9 Maths Chapter 12 Heron’s Formula with Answers Pdf free download has been useful to an extent. If you have any other queries about Case Study Questions Class 9 Maths Chapter 12 Heron’s Formula and Passage-Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible.
Leave a Comment Cancel reply
Save my name, email, and website in this browser for the next time I comment.
Download India's best Exam Preparation App Now.
Key Features
- Revision Notes
- Important Questions
- Previous Years Questions
- Case-Based Questions
- Assertion and Reason Questions
No thanks, I’m not interested!
Test: Heron`s Formula- Case Based Type Questions - Class 9 MCQ
10 questions mcq test - test: heron`s formula- case based type questions, direction: isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm. q. what is the length of equal sides.
So, x + x + 4 = 20
2x + 4 = 20
2x = 20 – 4
x = 16/2 = 8 cm.

Direction: Isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm. Q. If the sides of a triangle are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find its area.
100√2 m 2
500√2 m 2
1500√3 m 2
200√3 m 2
Let the sides of a triangle are a = 3x, b = 5x, c = 7x
Then a + b + c = 300
3x + 5x + 7x = 300
So, a = 60, b = 100, c = 140
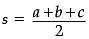
= 300/2 = 150
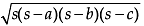
Direction: Isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm. Q. What is the Heron's formula for the area of?
{Area} = area
s = semi-perimeter
a = length of side a
b = length of side b
c = length of side c
Isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm. What is the semi perimeter of the Isosceles triangle?
Required semi perimeter = Perimeter/2 = 20/2 = 10 m.
Direction: Isosceles triangles were used to construct a bridge in which the base (unequal side) of an isosceles triangle is 4 cm and its perimeter is 20 cm.

Q. What is the area of highlighted triangle ?
Thus, area of the triangle
Direction: Shakshi prepared a Rangoli in triangular shape on Diwali. She makes a small triangle under a big triangle as shown in figure.
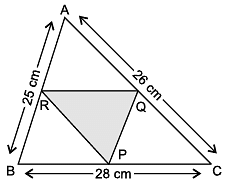
Sides of big triangle are 25 cm, 26 cm and 28 cm. Also, ΔPQR is formed by joining mid points of sides of ΔABC.
Use the above data to help her in resolving below doubts.
Q. What is the semi-perimeter of ΔABC?
= (25 + 26 + 28) cm = 79 cm
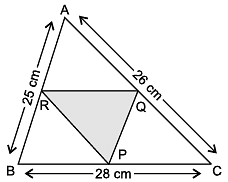
Q. Area of ΔPQR =
where s is the semi-perimeter of ΔPQR.
Q. ½ of AB =
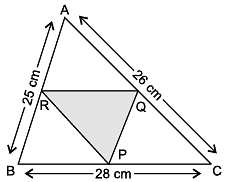
Q. What is the length of RQ?
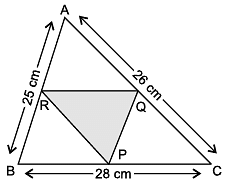
Q. If colourful rope is to be placed along the sides of small ΔPQR. What is the length of the rope?
= (12.5 + 13 + 14) cm
Top Courses for Class 9
Important Questions for Heron`s Formula- Case Based Type Questions
Heron`s formula- case based type questions mcqs with answers, online tests for heron`s formula- case based type questions, welcome back, create your account for free.

Forgot Password

Gurukul of Excellence
Classes for Physics, Chemistry and Mathematics by IITians
Join our Telegram Channel for Free PDF Download
Case Study Questions for Class 9 Maths Chapter 12 Herons Formula
- Last modified on: 2 months ago
- Reading Time: 1 Minute

Here we are providing case study questions for Class 9 Maths Chapter 12 Herons Formula. Students are suggested to solve the questions by themselves first and then check the answers. This will help students to check their grasp on this particular chapter Triangles.
Case Study Questions:
Related Posts
Category lists (all posts).
All categories of this website are listed below with number of posts in each category for better navigation. Visitors can click on a particular category to see all posts related to that category.
- Full Form (1)
- Biography of Scientists (1)
- Assertion Reason Questions in Biology (37)
- Case Study Questions for Class 12 Biology (14)
- DPP Biology for NEET (12)
- Blog Posts (35)
- Career Guidance (1)
- Assertion Reason Questions for Class 10 Maths (14)
- Case Study Questions for Class 10 Maths (15)
- Extra Questions for Class 10 Maths (12)
- Maths Formulas for Class 10 (1)
- MCQ Questions for Class 10 Maths (15)
- NCERT Solutions for Class 10 Maths (4)
- Quick Revision Notes for Class 10 Maths (14)
- Assertion Reason Questions for Class 10 Science (16)
- Case Study Questions for Class 10 Science (14)
- Evergreen Science Book Solutions for Class 10 (17)
- Extra Questions for Class 10 Science (23)
- HOTS for Class 10 Science (17)
- Important Questions for Class 10 Science (10)
- Lakhmir Singh Class 10 Biology Solutions (4)
- Lakhmir Singh Class 10 Chemistry Solutions (5)
- Lakhmir Singh Class 10 Physics Solutions (5)
- MCQ Questions for Class 10 Science (20)
- NCERT Exemplar Solutions for Class 10 Science (16)
- NCERT Solutions for Class 10 Science (15)
- Quick Revision Notes for Class 10 Science (4)
- Study Notes for Class 10 Science (17)
- Assertion Reason Questions for Class 10 Social Science (14)
- Case Study Questions for Class 10 Social Science (24)
- MCQ Questions for Class 10 Social Science (3)
- Topicwise Notes for Class 10 Social Science (4)
- CBSE CLASS 11 (1)
- Assertion Reason Questions for Class 11 Chemistry (14)
- Case Study Questions for Class 11 Chemistry (11)
- Free Assignments for Class 11 Chemistry (1)
- MCQ Questions for Class 11 Chemistry (8)
- Very Short Answer Questions for Class 11 Chemistry (7)
- Assertion Reason Questions for Class 11 Entrepreneurship (8)
- Important Questions for CBSE Class 11 Entrepreneurship (1)
- Assertion Reason Questions for Class 11 Geography (24)
- Case Study Questions for Class 11 Geography (24)
- Assertion Reason Questions for Class 11 History (12)
- Case Study Questions for Class 11 History (12)
- Assertion and Reason Questions for Class 11 Maths (16)
- Case Study Questions for Class 11 Maths (16)
- Formulas for Class 11 Maths (6)
- MCQ Questions for Class 11 Maths (17)
- NCERT Solutions for Class 11 Maths (8)
- Case Study Questions for Class 11 Physical Education (11)
- Assertion Reason Questions for Class 11 Physics (15)
- Case Study Questions for Class 11 Physics (12)
- Class 11 Physics Study Notes (5)
- Concept Based Notes for Class 11 Physics (2)
- Conceptual Questions for Class 11 Physics (10)
- Derivations for Class 11 Physics (3)
- Extra Questions for Class 11 Physics (13)
- MCQ Questions for Class 11 Physics (16)
- NCERT Solutions for Class 11 Physics (16)
- Numerical Problems for Class 11 Physics (4)
- Physics Formulas for Class 11 (7)
- Revision Notes for Class 11 Physics (11)
- Very Short Answer Questions for Class 11 Physics (11)
- Assertion Reason Questions for Class 11 Political Science (20)
- Case Study Questions for Class 11 Political Science (20)
- CBSE CLASS 12 (8)
- Extra Questions for Class 12 Biology (14)
- MCQ Questions for Class 12 Biology (13)
- Case Studies for CBSE Class 12 Business Studies (13)
- MCQ Questions for Class 12 Business Studies (1)
- Revision Notes for Class 12 Business Studies (10)
- Assertion Reason Questions for Class 12 Chemistry (15)
- Case Study Based Questions for Class 12 Chemistry (14)
- Extra Questions for Class 12 Chemistry (5)
- Important Questions for Class 12 Chemistry (15)
- MCQ Questions for Class 12 Chemistry (8)
- NCERT Solutions for Class 12 Chemistry (16)
- Revision Notes for Class 12 Chemistry (7)
- Assertion Reason Questions for Class 12 Economics (9)
- Case Study Questions for Class 12 Economics (9)
- MCQ Questions for Class 12 Economics (1)
- MCQ Questions for Class 12 English (2)
- Assertion Reason Questions for Class 12 Entrepreneurship (7)
- Case Study Questions for Class 12 Entrepreneurship (7)
- Case Study Questions for Class 12 Geography (18)
- Assertion Reason Questions for Class 12 History (8)
- Case Study Questions for Class 12 History (13)
- Assertion Reason Questions for Class 12 Informatics Practices (13)
- Case Study Questions for Class 12 Informatics Practices (11)
- MCQ Questions for Class 12 Informatics Practices (5)
- Assertion and Reason Questions for Class 12 Maths (14)
- Case Study Questions for Class 12 Maths (13)
- Maths Formulas for Class 12 (5)
- MCQ Questions for Class 12 Maths (14)
- Problems Based on Class 12 Maths (1)
- RD Sharma Solutions for Class 12 Maths (1)
- Assertion Reason Questions for Class 12 Physical Education (11)
- Case Study Questions for Class 12 Physical Education (11)
- MCQ Questions for Class 12 Physical Education (10)
- Assertion Reason Questions for Class 12 Physics (16)
- Case Study Based Questions for Class 12 Physics (14)
- Class 12 Physics Conceptual Questions (16)
- Class 12 Physics Discussion Questions (1)
- Class 12 Physics Latest Updates (2)
- Derivations for Class 12 Physics (8)
- Extra Questions for Class 12 Physics (4)
- Important Questions for Class 12 Physics (8)
- MCQ Questions for Class 12 Physics (14)
- NCERT Solutions for Class 12 Physics (18)
- Numerical Problems Based on Class 12 Physics (16)
- Physics Class 12 Viva Questions (1)
- Revision Notes for Class 12 Physics (7)
- Assertion Reason Questions for Class 12 Political Science (16)
- Case Study Questions for Class 12 Political Science (16)
- Notes for Class 12 Political Science (1)
- Assertion Reason Questions for Class 6 Maths (13)
- Case Study Questions for Class 6 Maths (13)
- Extra Questions for Class 6 Maths (1)
- Worksheets for Class 6 Maths (1)
- Assertion Reason Questions for Class 6 Science (16)
- Case Study Questions for Class 6 Science (16)
- Extra Questions for Class 6 Science (1)
- MCQ Questions for Class 6 Science (9)
- Assertion Reason Questions for Class 6 Social Science (1)
- Case Study Questions for Class 6 Social Science (26)
- NCERT Exemplar for Class 7 Maths (13)
- NCERT Exemplar for Class 7 Science (19)
- NCERT Exemplar Solutions for Class 7 Maths (12)
- NCERT Exemplar Solutions for Class 7 Science (18)
- NCERT Notes for Class 7 Science (18)
- Assertion Reason Questions for Class 7 Maths (14)
- Case Study Questions for Class 7 Maths (14)
- Extra Questions for Class 7 Maths (5)
- Assertion Reason Questions for Class 7 Science (18)
- Case Study Questions for Class 7 Science (17)
- Extra Questions for Class 7 Science (19)
- Assertion Reason Questions for Class 7 Social Science (1)
- Case Study Questions for Class 7 Social Science (30)
- Assertion Reason Questions for Class 8 Maths (7)
- Case Study Questions for Class 8 Maths (17)
- Extra Questions for Class 8 Maths (1)
- MCQ Questions for Class 8 Maths (6)
- Assertion Reason Questions for Class 8 Science (16)
- Case Study Questions for Class 8 Science (11)
- Extra Questions for Class 8 Science (2)
- MCQ Questions for Class 8 Science (4)
- Numerical Problems for Class 8 Science (1)
- Revision Notes for Class 8 Science (11)
- Assertion Reason Questions for Class 8 Social Science (27)
- Case Study Questions for Class 8 Social Science (23)
- CBSE Class 9 English Beehive Notes and Summary (2)
- Assertion Reason Questions for Class 9 Maths (14)
- Case Study Questions for Class 9 Maths (14)
- MCQ Questions for Class 9 Maths (11)
- NCERT Notes for Class 9 Maths (6)
- NCERT Solutions for Class 9 Maths (12)
- Revision Notes for Class 9 Maths (3)
- Study Notes for Class 9 Maths (10)
- Assertion Reason Questions for Class 9 Science (16)
- Case Study Questions for Class 9 Science (15)
- Evergreen Science Book Solutions for Class 9 (15)
- Extra Questions for Class 9 Science (22)
- MCQ Questions for Class 9 Science (11)
- NCERT Solutions for Class 9 Science (15)
- Revision Notes for Class 9 Science (1)
- Study Notes for Class 9 Science (15)
- Topic wise MCQ Questions for Class 9 Science (2)
- Topicwise Questions and Answers for Class 9 Science (15)
- Assertion Reason Questions for Class 9 Social Science (15)
- Case Study Questions for Class 9 Social Science (19)
- CHEMISTRY (8)
- Chemistry Articles (2)
- Daily Practice Problems (DPP) (3)
- Books for CBSE Class 9 (1)
- Books for ICSE Class 10 (3)
- Editable Study Materials (8)
- Exam Special for CBSE Class 10 (3)
- H. C. Verma (Concepts of Physics) (13)
- Study Materials for ICSE Class 10 Biology (14)
- Extra Questions for ICSE Class 10 Chemistry (1)
- Study Materials for ICSE Class 10 Chemistry (5)
- Study Materials for ICSE Class 10 Maths (16)
- Important Questions for ICSE Class 10 Physics (13)
- MCQ Questions for ICSE Class 10 Physics (4)
- Study Materials for ICSE Class 10 Physics (8)
- Study Materials for ICSE Class 9 Maths (7)
- Study Materials for ICSE Class 9 Physics (10)
- Topicwise Problems for IIT Foundation Mathematics (4)
- Challenging Physics Problems for JEE Advanced (2)
- Topicwise Problems for JEE Physics (1)
- DPP for JEE Main (1)
- Integer Type Questions for JEE Main (1)
- Integer Type Questions for JEE Chemistry (6)
- Chapterwise Questions for JEE Main Physics (1)
- Integer Type Questions for JEE Main Physics (8)
- Physics Revision Notes for JEE Main (4)
- JEE Mock Test Physics (1)
- JEE Study Material (1)
- JEE/NEET Physics (6)
- CBSE Syllabus (1)
- Maths Articles (2)
- NCERT Books for Class 12 Physics (1)
- NEET Chemistry (13)
- Important Questions for NEET Physics (17)
- Topicwise DPP for NEET Physics (5)
- Topicwise MCQs for NEET Physics (32)
- NTSE MAT Questions (1)
- Physics (1)
- Alternating Current (1)
- Electrostatics (6)
- Fluid Mechanics (2)
- PowerPoint Presentations (13)
- Previous Years Question Paper (3)
- Products for CBSE Class 10 (15)
- Products for CBSE Class 11 (10)
- Products for CBSE Class 12 (6)
- Products for CBSE Class 6 (2)
- Products for CBSE Class 7 (5)
- Products for CBSE Class 8 (1)
- Products for CBSE Class 9 (3)
- Products for Commerce (3)
- Products for Foundation Courses (2)
- Products for JEE Main & Advanced (10)
- Products for NEET (6)
- Products for ICSE Class 6 (1)
- Electrostatic Potential and Capacitance (1)
- Topic Wise Study Notes (Physics) (2)
- Topicwise MCQs for Physics (2)
- Uncategorized (138)
Test series for students preparing for Engineering & Medical Entrance Exams are available. We also provide test series for School Level Exams. Tests for students studying in CBSE, ICSE or any state board are available here. Just click on the link and start test.
Download CBSE Books
Exam Special Series:
- Sample Question Paper for CBSE Class 10 Science (for 2024)
- Sample Question Paper for CBSE Class 10 Maths (for 2024)
- CBSE Most Repeated Questions for Class 10 Science Board Exams
- CBSE Important Diagram Based Questions Class 10 Physics Board Exams
- CBSE Important Numericals Class 10 Physics Board Exams
- CBSE Practical Based Questions for Class 10 Science Board Exams
- CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
- Sample Question Papers for CBSE Class 12 Physics (for 2024)
- Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
- Sample Question Papers for CBSE Class 12 Maths (for 2024)
- Sample Question Papers for CBSE Class 12 Biology (for 2024)
- CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
- Master Organic Conversions CBSE Class 12 Chemistry Board Exams
- CBSE Important Numericals Class 12 Physics Board Exams
- CBSE Important Definitions Class 12 Physics Board Exams
- CBSE Important Laws & Principles Class 12 Physics Board Exams
- 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
- ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
- ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
- ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
- ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
- ICSE Important Functions and Locations Based Questions Class 10 Biology
- ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)
✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year
✨ Join our Online NEET Test Series for 499/- Only for 1 Year
Leave a Reply Cancel reply
Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs
Discover more from Gurukul of Excellence
Subscribe now to keep reading and get access to the full archive.
Type your email…
Continue reading
- Class 6 Maths
- Class 6 Science
- Class 6 Social Science
- Class 6 English
- Class 7 Maths
- Class 7 Science
- Class 7 Social Science
- Class 7 English
- Class 8 Maths
- Class 8 Science
- Class 8 Social Science
- Class 8 English
- Class 9 Maths
- Class 9 Science
- Class 9 Social Science
- Class 9 English
- Class 10 Maths
- Class 10 Science
- Class 10 Social Science
- Class 10 English
- Class 11 Maths
- Class 11 Computer Science (Python)
- Class 11 English
- Class 12 Maths
- Class 12 English
- Class 12 Economics
- Class 12 Accountancy
- Class 12 Physics
- Class 12 Chemistry
- Class 12 Biology
- Class 12 Computer Science (Python)
- Class 12 Physical Education
- GST and Accounting Course
- Excel Course
- Tally Course
- Finance and CMA Data Course
- Payroll Course
Interesting
- Learn English
- Learn Excel
- Learn Tally
- Learn GST (Goods and Services Tax)
- Learn Accounting and Finance
- GST Tax Invoice Format
- Accounts Tax Practical
- Tally Ledger List
- GSTR 2A - JSON to Excel
Are you in school ? Do you love Teachoo?
We would love to talk to you! Please fill this form so that we can contact you
You are learning...
Chapter 10 Class 9 Herons Formula
Click on any of the links below to start learning from Teachoo ...
Updated for new NCERT - 2023-24 Curriculmn
Get NCERT Solutions of all exercise questions and examples of Chapter 10 Class 9 Herons Formula. Answers to all question have been solved in a step-by-step manner, with videos of all questions available.
We have studied that
Area of triangle = 1/2 × Base × Height
In questions where Height and Base is given, we can find the area of triangle easily.
But, in cases where all 3 sides are given, how will we find the area?
If all 3 sides are given, we find Area of Triangle using Herons (or Hero's) Formula
By Hero's Formula
Area of triangle = Square root (s (s-a) (s-b) (s-c))
where a,b, c are sides of the triangle
and s = Semi-Perimeter of Triangle
i.e. s = (a+b+c)/2
In this chapter, we will find Area of Triangle using Herons formula
We will also find Area of Quadrilateral by dividing it into two triangles, and then finding Area of triangle using Hero's Formula
Click on an exercise link or a topic link below to start doing the chapter.
Serial order wise
Concept wise.
What's in it?
Hi, it looks like you're using AdBlock :(
Please login to view more pages. it's free :), solve all your doubts with teachoo black.
NCERT Solutions Class 9 Maths Chapter 12 Heron's Formula
NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula is a fundamental math concept applied in many fields. Therefore, it is necessary to learn this topic along with understanding its applications. One of the reliable resources to gain this knowledge is by referring to the NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula. The solutions are designed in an efficient way to cover these concepts in detail. By practicing questions and sample problems composed in these solutions, students will quickly gain the key skills required for advanced math studies.
There are some ways and formulas to calculate the area of triangles . Heron’s formula is a useful technique to calculate the area of a triangle when the length of all three sides is given. These Class 9 maths NCERT solutions Chapter 12 Heron’s Formula will help students to understand this concept in detail. For more such facts and formulas , read the detailed solution given below and also find some of these in the exercises given below.
- NCERT Solutions Class 9 Maths Chapter 12 Ex 12.1
- NCERT Solutions Class 9 Maths Chapter 12 Ex 12.2
NCERT Solutions for Class 9 Maths Chapter 12 PDF
Triangles are a foundational shape used in various fields of mathematics and other subjects like physics and geography. Learning to find the area of a triangle using Heron’s formula will enable students to gain a better understanding of the related topics and their applications. More details of this topic can be found in the NCERT solutions Class 9 maths chapter 12 Heron's Formula given below:
☛ Download Class 9 Maths NCERT Solutions Chapter 12 Heron’s Formula
NCERT Class 9 Maths Chapter 12 Download PDF


NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula
The area of a triangle refers to the space closed within the boundary of a triangle. These solutions will enable students to derive Heron’s formula step-by-step. The concepts explained in these solutions are noteworthy and hold great importance in various spheres of life. The exercise-wise detailed analysis of the NCERT Solutions Class 9 Maths Chapter 12 Heron's Formula is shown below:
- Class 9 Maths Chapter 12 Ex 12.1 - 6 Questions
- Class 9 Maths Chapter 12 Ex 12.2 - 19 Questions
☛ Download Class 9 Maths Chapter 12 NCERT Book
Topics Covered: The topics covered in the Class 9 maths NCERT solutions chapter 12 are as follows: Introduction to Heron’s Formula , Area of a triangle based on its height and base, Area of a triangle using Heron’s Formula, and applications of Heron’s Formula in finding the area of quadrilaterals.
Total Questions: The Class 9 maths chapter 12 Heron's Formula Chapter 12 consists of a total of 15 questions. The students will find some to be easy (3 sums), while others will fall in the moderate (7 sums) and tougher categories (2 sums).
List of Formulas in NCERT Solutions Class 9 Maths Chapter 12
The NCERT solutions Class 9 maths Chapter 12 involves studying the area of triangles and quadrilaterals , which requires applying different formulas explained in this chapter. Some of the important concepts and formulas listed in this chapter are given below:
- Area of a triangle using Heron’s Formula = A = √{s(s-a)(s-b)(s-c)} , where a, b and c are the length of the three sides of a triangle and s is the semi-perimeter of the triangle given by (a + b + c)/2.
- The area of a quadrilateral whose sides and one diagonal are given can be calculated by
dividing the quadrilateral into two triangles and using Heron’s formula.
Important Questions for Class 9 Maths NCERT Solutions Chapter 12
Video solutions for class 9 maths ncert chapter 12, faqs on ncert solutions class 9 maths chapter 12, why are ncert solutions class 9 maths chapter 12 important.
NCERT Solutions for Class 9 Maths Chapter 12 explains all the concepts and formulas in detail to quickly gain deep knowledge of this chapter. These solutions provide examples, sample problems, and illustrations that are highly beneficial for students to understand the concepts clearly. The solutions are well-organized guides prepared by a team of experts to deliver precise and accurate knowledge of this lesson.
Do I Need to Practice all Questions Provided in NCERT Solutions Class 9 Maths Heron's Formula?
Learning maths requires practice and perseverance. With the practice of a wide range of questions included in the NCERT solutions class 9 maths chapter 12, students will gain knowledge of the core concepts and learn some creative ways to memorize formulas and data. It will enable them to employ their knowledge of particular formulas in various situations, which is highly useful for facing competitive exams.
What are the Important Topics Covered in Class 9 Maths NCERT Solutions Chapter 12?
The important topics covered in the Class 9 maths NCERT solutions chapter 12 are an introduction to triangles, finding the area of a triangle based on its height and base, and calculating the area of a triangle using Heron’s Formula. Additionally, it also covers the topic of applications of Heron’s Formula in finding the area of quadrilaterals.
How Many Questions are there in NCERT Solutions Class 9 Maths Chapter 12 Heron's Formula?
The Class 9 maths chapter 12 Heron's Formula Chapter 12 consists of a total of 15 questions. All of them are based on this formula and its applications. Therefore, the students should practice and memorize it carefully.
How CBSE Students can utilize NCERT Solutions Class 9 Maths Chapter 12 effectively?
NCERT Solutions Class 9 Maths Chapter 12 comprises interactive illustrations and exercises that will assist students in gaining a better understanding of Heron's Formula in practical situations. The students should read the entire chapter carefully as each concept included in these solutions is vital for understanding facts and formulas applied in this lesson.
Why Should I Practice Class 9 Maths NCERT Solutions Heron's Formula chapter 12?
The NCERT Solutions Class 9 Maths Heron's Formula chapter 12 has been prepared by experts in their respective fields to deliver comprehensive knowledge of each and every concept. The facts and data incorporated in these solutions are compiled to promote accurate knowledge in an easy-to-understand manner. Thus, it is very necessary to practice all questions in the NCERT textbook.

NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula
Ncert solutions for class 9 maths chapter 12 heron's formula| pdf download.

- Exercise 12.1 Chapter 12 Class 9 Maths NCERT Solutions
- Exercise 12.2 Chapter 12 Class 9 Maths NCERT Solutions
NCERT Solutions for Class 9 Maths Chapters:
What are the benefits of ncert solutions for chapter 12 heron's formula class 9 ncert solutions, how many exercises in chapter 12 heron's formula, find the length of a diagonal of a square whose side is 2 cm., find the height of an equilateral triangle whose side is 2 cm., contact form.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 10: Heron's Formula
Area of triangle - by heron's formula.
- Heron's formula (Opens a modal)
- Heron's Formula 10.1 4 questions Practice
- Finding area of triangle using Heron's formula 4 questions Practice
NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula
NCERT Solutions for Class 9 Maths Chapter 12 Heron’s Formula are provided here. Our NCERT Maths solutions contain all the questions of the NCERT textbook that are solved and explained beautifully. Here you will get complete NCERT Solutions for Class 9 Maths Chapter 12 all exercises Exercise in one place. These solutions are prepared by the subject experts and as per the latest NCERT syllabus and guidelines. CBSE Class 9 Students who wish to score good marks in the maths exam must practice these questions regularly.
Class 9 Maths Chapter 12 Heron’s Formula NCERT Solutions
Below we have provided the solutions of each exercise of the chapter. Go through the links to access the solutions of exercises you want. You should also check out our NCERT Class 9 Solutions for other subjects to score good marks in the exams.
NCERT Solutions for Class 9 Maths Chapter 12 Exercise 12.1

NCERT Solutions for Class 9 Maths Chapter 12 Exercise 12.2

NCERT Solutions for Class 9 Maths Chapter 12 – Topic Discussion
Below we have listed the topics that have been discussed in this chapter.
- Heron’s Formula
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Heron's Formula Questions
Heron’s formula questions with answers are provided here. Class 9 students can practise the questions based on Heron’s formula to prepare for the exams. These extra questions are prepared by our subject experts, as per the NCERT curriculum and latest CBSE syllabus (2022-2023). Learn Heron’s formula in detail at BYJU’S.
Definition: Heron’s formula is a formula used to find the area of a triangle. According to this formula;
Area of triangle = √(s(s-a)(s-b)(s-c))
Where a, b and c are the sides of a triangle and s is the semiperimeter of triangle.
s = (a+b+c)/2
Heron’s Formula Questions and Solutions
Q.1: Find the area of a triangle whose sides are 12 cm, 6 cm and 15 cm.
Solution: Given the sides of a triangle are:
According to Heron’s formula;
s = (12 + 6 + 15)/2 = 33/2 = 16.5
Area = √(16.5(16.5-12)(16.5-6)(16.5-15))
= √(16.5 x 4.5 x 0.5 x 1.5)
= 34.2 cm 2
Q.2: Find the Area of a Triangle whose two sides are 18 cm and 10 cm, respectively and the perimeter is 42 cm.
Solution: Given two sides of a triangle are 18 cm and 10 cm, respectively.
a = 18cm, b = 10 cm
Perimeter of triangle = 42 cm
18+10+c = 42
c = 42 – 28 = 14 cm
Using Heron’s formula, we have;
Semiperimeter, s = 42/2 = 21
Area = √(21(21-18)(21-10)(21-14))
= √(21 x 3 x 11 x 7)
= 69.7 cm 2
Q.3: A triangular park has sides 120 m, 80 m and 50 m. A gardener has to put a fence all around it and also plant grass inside. How much area does he need to plant?
Solution: Given,
Sides of triangular park are 120m, 80m and 50m.
Semiperimeter, s = (120 + 80 + 50)/2 = 125 m
Area = √(125 (125-120) (125 – 80) (125 – 50)
= √(125 x 75 x 45 x 5)
= 375√15 m 2
Q.4: The sides of a triangle are in the ratio of 12: 17: 25 and its perimeter is 540 cm. Find its area.
Ratio of the sides of the triangle is 12: 17: 25
Let the sides of triangle be 12x, 17x and 25x
Given, perimeter of the triangle = 540 cm
12x + 17x + 25x = 540 cm
⇒ 54x = 540cm
Thus, the sides of the triangle are:
12 x 10 = 120 cm
17 x 10 = 170 cm
25 x 10 = 250 cm
Semiperimeter, s = 540/2 = 270 cm
Using Heron’s formula,
= √(270 x 150 x 100 x 20)
= 9000 cm 2
Q.5: Find the area of a triangle whose sides are 4.5 cm and 10 cm and perimeter 20.5 cm.
Side a = 4.5 cm
Side b = 10 cm
Perimeter of triangle = 20.5 cm
a+b+c = 20.5
4.5+10+c = 20.5
14.5+c = 20.5
c = 20.5 – 14.5
Semiperimeter, s = (4.5+10+6)/2 = 20.5/2 = 10.25 cm
Area = 7.91 cm 2
Q.6: What is the area of a triangle whose sides are 9 cm, 12 cm and 15 cm?
Solution: Given, the sides of a triangle are:
Semiperimeter, s = (9 + 12 + 15)/2 = 36/2 = 18 cm
Area = 54 cm 2
Q.7: The perimeter of a right triangle is 300m. If its sides are in the ratio 3 : 5 : 7. Find the area of the triangle.
Perimeter of right triangle = 300 m
Ratio of sides of triangle is 3 : 5 : 7
Let the sides of triangle be:
3x + 5x + 7x = 300
x = 300/15 = 20
Thus, the sides of triangle are:
a = 3x = 3 (20) = 60 m
b = 5x = 5 (20) = 100 m
c = 7x = 7 (20) = 140 m
Semiperimeter, s = 300/2 = 150 m
Area = √(150 (150 – 60) (150 – 100) (150 – 140))
Area = 1500√3 m 2
Q.8: The sides of a triangle are 7 cm, 9 cm, and 14 cm. What is the area of the triangle?
a = 7cm, b = 9 cm and c = 14 cm
Semiperimeter, s = (7 + 9 + 14)/2 = 15 cm
Area of triangle = = √[s (s-a) (s-b) (s-c)] By Heron’s formula.
= 12√5 cm 2
Q.9: The sides of a triangle are 11 m, 60 m and 61 m. What is the altitude to the smallest side?
Solution: Given, sides of the triangle are 11 m, 60 m and 61 m.
The smallest side is 11 m.
Area of triangle = ½ (base) (height)
A = ½ (11) h ….(i)
We can find the area of the triangle using Heron’s formula here.
s = (11+60+61)/2 = 66 m
Area = √(66 x 55 x 6 x 5) = 330 m 2
Now putting the value of area in equation (i), we get;
330 = ½ (11) h
h = (2 x 330)/11 = 60m
Therefore, the altitude to the smallest side is 60m.
Q.10: If every side of a triangle is doubled, by what percentage is the area of the triangle increased?
Solution: Let a, b and c be the sides of a triangle.
Semiperimeter, s = (a+b+c)/2
Now, if each of the side is doubled, then the new sides of a triangle are:
A = 2a, B = 2b, C = 2c
Semiperimeter, S = (A+B+C)/2 = (2a + 2b + 2c)/2 = 2s
By Heron’s formula,
= 4√s(s-a)(s-b)(s-c)
Increase in Area = (4A – A)/A x 100% = 300%
Hence, the area is increased by 300%, if the sides of the triangle are doubled.
Related Articles
- Class 9 Maths MCQs Chapter 12 Heron’s Formula
- Heron’s Formula Class 9 Notes: Chapter 12
- Important Questions Class 9 Maths Chapter 12-Heron’s Formula
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
- Share Share
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.


IMAGES
VIDEO
COMMENTS
Answer: (a) 4 meters and 6 meters. Case Study 2: A group of students is studying Heron's Formula for finding the area of a triangle. They encountered the following scenario: Neha and Mohan went on a field trip to a riverbank. They noticed a triangular piece of land that they wanted to measure and calculate its area.
Solutions of Test: Heron`s Formula- Case Based Type Questions questions in English are available as part of our course for Class 9 & Test: Heron`s Formula- Case Based Type Questions solutions in Hindi for Class 9 course. Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Here we are providing case study questions for Class 9 Maths Chapter 12 Herons Formula. Students are suggested to solve the questions by themselves first and then check the answers. This will help students to check their grasp on this particular chapter Triangles. Case Study Questions:
The semi perimeter of the each triangular shape = (28+9+35)/2 cm = 36 cm. By using Heron's formula, The area of each triangular shape will be. = 36√6 cm 2 = 88.2 cm 2. Now, the total area of 16 tiles = 16×88.2 cm 2 = 1411.2 cm 2. It is given that the polishing cost of tiles = 50 paise/cm 2.
Important Questions & Answers For Class 9 Maths Chapter 12. Q.1: Find the area of a triangle whose two sides are 18 cm and 10 cm and the perimeter is 42cm. Assume that the third side of the triangle to be "x". Q.2: The sides of a triangle are in the ratio of 12: 17: 25 and its perimeter is 540cm. Find its area.
Worried about how to learn the Heron's Formula - Case-Based MCQ Questions? from CBSE Class 9 Maths Chapter 12 (Board Exam 2021 - 2022) Term 1 Exam. Let's wat...
Heron's Formula Class 9. Heron's formula class 9 is used to determine the area of a triangle when the length of all three sides is given. This formula does not involve the use of the angles of a triangle.Heron's Formula class 9 is a fundamental math concept applied in many fields to calculate various dimensions of a triangle.
By Hero's Formula. Area of triangle = Square root (s (s-a) (s-b) (s-c)) where a,b, c are sides of the triangle. and s = Semi-Perimeter of Triangle. i.e. s = (a+b+c)/2. In this chapter, we will find Area of Triangle using Herons formula. We will also find Area of Quadrilateral by dividing it into two triangles, and then finding Area of triangle ...
Ex 12.1 Class 9 Maths Question 6. An isosceles triangle has perimeter 30 cm and each of the equal sides is 12 cm. Find the area of the triangle. Solution: Let the sides of an isosceles triangle be. a = 12cm, b = 12cm,c = x cm. Since, perimeter of the triangle = 30 cm. ∴ 12cm + 12cm + x cm = 30 cm. ⇒ x = (30 - 24) = 6.
The NCERT solutions Class 9 maths Chapter 12 involves studying the area of triangles and quadrilaterals, which requires applying different formulas explained in this chapter. Some of the important concepts and formulas listed in this chapter are given below: Area of a triangle using Heron's Formula = A = √ {s (s-a) (s-b) (s-c)}, where a, b ...
NCERT Solutions for Class 9 Maths Chapter 12, Heron's Formula, covers the following two exercises: Exercise 12.1: This exercise consists of six questions that are based on the concept of Heron's Formula. The questions cover topics such as finding the area of a triangle when the sides are given, finding the missing side when the area and two sides are given, and finding the height of a triangle ...
#CaseStudyonMaths #Class9Maths #Class9MathsCaseStudy #casestudy #cbse #mathscasestudy #SmartLearningWithRituMamClass 9 Maths Ch12 Heron's Formula: https://ww...
If you want to study offline then you can also Download PDF of NCERT Solutions for Class 9 Maths Chapter 12 Heron's Formula. You can also complete your homework on time through the help of these Chapter 12 NCERT Solutions and able to solve the difficult problems given in a exercise.
Class 9; Unit 10: Heron's Formula. Area of Triangle - by Heron's formula. Learn. Heron's formula (Opens a modal) Practice. Heron's Formula 10.1. 4 questions. Practice. Finding area of triangle using Heron's formula. 4 questions. Practice. Our mission is to provide a free, world-class education to anyone, anywhere. Khan Academy is a 501(c)(3 ...
Here you will get complete NCERT Solutions for Class 9 Maths Chapter 12 all exercises Exercise in one place. These solutions are prepared by the subject experts and as per the latest NCERT syllabus and guidelines. CBSE Class 9 Students who wish to score good marks in the maths exam must practice these questions regularly.
Heron's formula is an important mark in this subject. By this formula, we can calculate the area of the triangle if the length of all three sides is known. This can be calculated using the following two steps: Step 1: Calculate the "s" (half of the triangle's perimeter): S= a+ b = c2. Step 2: Then calculate the Area.
CBSE Class 9 Maths Heron's Formula Notes - Download PDF Here. In geometry, a triangle is a closed three-dimensional figure. In this article, you are going to learn Heron's formula for class 9, which is used to find the area of triangles. You will also learn how Heron's formula is used to find the area of other polygons in detail. Triangle
Heron's Formula is given in Chapter 12 of Class 9 Maths which is a part of Mensuration. Heron's formula helps students to find the area of a triangle in which the measure of all three sides is given. Students will understand the concept of Heron's formula by solving important questions given online.
Hello students, today we are going to solve Heron's formula based case study.#casestudy #maths #mathematicsStay safe and subscribe for more videos
This article provides you with detailed NCERT Solutions for Class 9 Maths Chapter 12-Heron's Formula. They have been solved by a team of experienced professionals at GFG, to make sure that every student can learn how to solve these questions with the easiest approach. This article provides solutions to all the problems asked in Class 9 Maths Chapter 12-Heron's Formula of the NCERT textbook ...
Class 9 students can practise the questions based on Heron's formula to prepare for the exams. These extra questions are prepared by our subject experts, as per the NCERT curriculum and latest CBSE syllabus (2022-2023). Learn Heron's formula in detail at BYJU'S. Definition: Heron's formula is a formula used to find the area of a ...
Given below are the Class 9 Maths Important Questions and Extra Questions for Heron's Formula (a) Concepts questions (b) Calculation problems (c) Multiple choice questions (d) Long answer questions (e) Fill in the blank's 1 Mark Questions Question 1 Calculate the area in each case. Triangle have sides as a=5 cm ,b=4 cm,c=3 cm; Equilateral triangle having side a=2 cm