geometry basics homework 3 distance and midpoint formulas answer key

Provide details on what you need help with along with a budget and time limit. Questions are posted anonymously and can be made 100% private.

Studypool matches you to the best tutor to help you with your question. Our tutors are highly qualified and vetted.

Your matched tutor provides personalized help according to your question details. Payment is made only after you have completed your 1-on-1 session and are satisfied with your session.

• Homework Q&A
• Become a Tutor

All Subjects

Mathematics

Programming

Health & Medical

Engineering

Computer Science

Foreign Languages

Access over 20 million homework & study documents

Unit 1 distance and midpoint formulas geometry basics worksheet.

Sign up to view the full document!

24/7 Homework Help

Stuck on a homework question? Our verified tutors can answer all questions, from basic  math  to advanced rocket science !

Similar Documents

working on a homework question?

Studypool is powered by Microtutoring TM

Copyright © 2024. Studypool Inc.

Studypool is not sponsored or endorsed by any college or university.

Ongoing Conversations

Access over 20 million homework documents through the notebank

Get on-demand Q&A homework help from verified tutors

Read 1000s of rich book guides covering popular titles

Sign up with Google

Sign up with Facebook

Already have an account? Login

Login with Google

Login with Facebook

Don't have an account? Sign Up

11.1 Distance and Midpoint Formulas; Circles

Learning objectives.

By the end of this section, you will be able to:

Use the Distance Formula

Use the Midpoint Formula

• Write the equation of a circle in standard form
• Graph a circle

Be Prepared 11.1

Before you get started, take this readiness quiz.

Find the length of the hypotenuse of a right triangle whose legs are 12 and 16 inches. If you missed this problem, review Example 2.34 .

Be Prepared 11.2

Factor: x 2 − 18 x + 81 . x 2 − 18 x + 81 . If you missed this problem, review Example 6.24 .

Be Prepared 11.3

Solve by completing the square: x 2 − 12 x − 12 = 0 . x 2 − 12 x − 12 = 0 . If you missed this problem, review Example 9.22 .

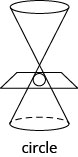
In this chapter we will be looking at the conic sections, usually called the conics, and their properties. The conics are curves that result from a plane intersecting a double cone—two cones placed point-to-point. Each half of a double cone is called a nappe.

There are four conics—the circle , parabola , ellipse , and hyperbola . The next figure shows how the plane intersecting the double cone results in each curve.

Each of the curves has many applications that affect your daily life, from your cell phone to acoustics and navigation systems. In this section we will look at the properties of a circle.

We have used the Pythagorean Theorem to find the lengths of the sides of a right triangle. Here we will use this theorem again to find distances on the rectangular coordinate system. By finding distance on the rectangular coordinate system, we can make a connection between the geometry of a conic and algebra—which opens up a world of opportunities for application.

Our first step is to develop a formula to find distances between points on the rectangular coordinate system. We will plot the points and create a right triangle much as we did when we found slope in Graphs and Functions . We then take it one step further and use the Pythagorean Theorem to find the length of the hypotenuse of the triangle—which is the distance between the points.

Example 11.1

Use the rectangular coordinate system to find the distance between the points ( 6 , 4 ) ( 6 , 4 ) and ( 2 , 1 ) . ( 2 , 1 ) .

Try It 11.1

Use the rectangular coordinate system to find the distance between the points ( 6 , 1 ) ( 6 , 1 ) and ( 2 , −2 ) . ( 2 , −2 ) .

Try It 11.2

Use the rectangular coordinate system to find the distance between the points ( 5 , 3 ) ( 5 , 3 ) and ( −3 , −3 ) . ( −3 , −3 ) .

The method we used in the last example leads us to the formula to find the distance between the two points ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) . ( x 2 , y 2 ) .

When we found the length of the horizontal leg we subtracted 6 − 2 6 − 2 which is x 2 − x 1 . x 2 − x 1 .

When we found the length of the vertical leg we subtracted 4 − 1 4 − 1 which is y 2 − y 1 . y 2 − y 1 .

If the triangle had been in a different position, we may have subtracted x 1 − x 2 x 1 − x 2 or y 1 − y 2 . y 1 − y 2 . The expressions x 2 − x 1 x 2 − x 1 and x 1 − x 2 x 1 − x 2 vary only in the sign of the resulting number. To get the positive value-since distance is positive- we can use absolute value. So to generalize we will say | x 2 − x 1 | | x 2 − x 1 | and | y 2 − y 1 | . | y 2 − y 1 | .

In the Pythagorean Theorem, we substitute the general expressions | x 2 − x 1 | | x 2 − x 1 | and | y 2 − y 1 | | y 2 − y 1 | rather than the numbers.

This is the Distance Formula we use to find the distance d between the two points ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) . ( x 2 , y 2 ) .

Distance Formula

The distance d between the two points ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) ( x 2 , y 2 ) is

Example 11.2

Use the Distance Formula to find the distance between the points ( −5 , −3 ) ( −5 , −3 ) and ( 7 , 2 ) . ( 7 , 2 ) .

Try It 11.3

Use the Distance Formula to find the distance between the points ( −4 , −5 ) ( −4 , −5 ) and ( 5 , 7 ) . ( 5 , 7 ) .

Try It 11.4

Use the Distance Formula to find the distance between the points ( −2 , −5 ) ( −2 , −5 ) and ( −14 , −10 ) . ( −14 , −10 ) .

Example 11.3

Use the Distance Formula to find the distance between the points ( 10 , −4 ) ( 10 , −4 ) and ( −1 , 5 ) . ( −1 , 5 ) . Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

Try It 11.5

Use the Distance Formula to find the distance between the points ( −4 , −5 ) ( −4 , −5 ) and ( 3 , 4 ) . ( 3 , 4 ) . Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

Try It 11.6

Use the Distance Formula to find the distance between the points ( −2 , −5 ) ( −2 , −5 ) and ( −3 , −4 ) . ( −3 , −4 ) . Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

It is often useful to be able to find the midpoint of a segment. For example, if you have the endpoints of the diameter of a circle, you may want to find the center of the circle which is the midpoint of the diameter. To find the midpoint of a line segment, we find the average of the x -coordinates and the average of the y -coordinates of the endpoints.

Midpoint Formula

The midpoint of the line segment whose endpoints are the two points ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) ( x 2 , y 2 ) is

To find the midpoint of a line segment, we find the average of the x -coordinates and the average of the y -coordinates of the endpoints.

Example 11.4

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are ( −5 , −4 ) ( −5 , −4 ) and ( 7 , 2 ) . ( 7 , 2 ) . Plot the endpoints and the midpoint on a rectangular coordinate system.

Try It 11.7

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are ( −3 , −5 ) ( −3 , −5 ) and ( 5 , 7 ) . ( 5 , 7 ) . Plot the endpoints and the midpoint on a rectangular coordinate system.

Try It 11.8

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are ( −2 , −5 ) ( −2 , −5 ) and ( 6 , −1 ) . ( 6 , −1 ) . Plot the endpoints and the midpoint on a rectangular coordinate system.

Both the Distance Formula and the Midpoint Formula depend on two points, ( x 1 , y 1 ) ( x 1 , y 1 ) and ( x 2 , y 2 ) . ( x 2 , y 2 ) . It is easy to confuse which formula requires addition and which subtraction of the coordinates. If we remember where the formulas come from, it may be easier to remember the formulas.

Write the Equation of a Circle in Standard Form

As we mentioned, our goal is to connect the geometry of a conic with algebra. By using the coordinate plane, we are able to do this easily.

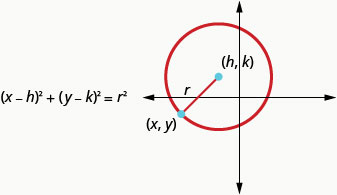
We define a circle as all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, ( h , k ) , ( h , k ) , and the fixed distance is called the radius , r , of the circle.

A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center , ( h , k ) , ( h , k ) , and the fixed distance is called the radius , r , of the circle.

This is the standard form of the equation of a circle with center, ( h , k ) , ( h , k ) , and radius, r .

Standard Form of the Equation a Circle

The standard form of the equation of a circle with center, ( h , k ) , ( h , k ) , and radius, r , is

Example 11.5

Write the standard form of the equation of the circle with radius 3 and center ( 0 , 0 ) . ( 0 , 0 ) .

Try It 11.9

Write the standard form of the equation of the circle with a radius of 6 and center ( 0 , 0 ) . ( 0 , 0 ) .

Try It 11.10

Write the standard form of the equation of the circle with a radius of 8 and center ( 0 , 0 ) . ( 0 , 0 ) .

In the last example, the center was ( 0 , 0 ) . ( 0 , 0 ) . Notice what happened to the equation. Whenever the center is ( 0 , 0 ) , ( 0 , 0 ) , the standard form becomes x 2 + y 2 = r 2 . x 2 + y 2 = r 2 .

Example 11.6

Write the standard form of the equation of the circle with radius 2 and center ( −1 , 3 ) . ( −1 , 3 ) .

Try It 11.11

Write the standard form of the equation of the circle with a radius of 7 and center ( 2 , −4 ) . ( 2 , −4 ) .

Try It 11.12

Write the standard form of the equation of the circle with a radius of 9 and center ( −3 , −5 ) . ( −3 , −5 ) .

In the next example, the radius is not given. To calculate the radius, we use the Distance Formula with the two given points.

Example 11.7

Write the standard form of the equation of the circle with center ( 2 , 4 ) ( 2 , 4 ) that also contains the point ( −2 , 1 ) . ( −2 , 1 ) .

The radius is the distance from the center to any point on the circle so we can use the distance formula to calculate it. We will use the center ( 2 , 4 ) ( 2 , 4 ) and point ( −2 , 1 ) ( −2 , 1 )

Now that we know the radius, r = 5 , r = 5 , and the center, ( 2 , 4 ) , ( 2 , 4 ) , we can use the standard form of the equation of a circle to find the equation.

Try It 11.13

Write the standard form of the equation of the circle with center ( 2 , 1 ) ( 2 , 1 ) that also contains the point ( −2 , −2 ) . ( −2 , −2 ) .

Try It 11.14

Write the standard form of the equation of the circle with center ( 7 , 1 ) ( 7 , 1 ) that also contains the point ( −1 , −5 ) . ( −1 , −5 ) .

Graph a Circle

Any equation of the form ( x − h ) 2 + ( y − k ) 2 = r 2 ( x − h ) 2 + ( y − k ) 2 = r 2 is the standard form of the equation of a circle with center, ( h , k ) , ( h , k ) , and radius, r. We can then graph the circle on a rectangular coordinate system.

Note that the standard form calls for subtraction from x and y . In the next example, the equation has x + 2 , x + 2 , so we need to rewrite the addition as subtraction of a negative.

Example 11.8

Find the center and radius, then graph the circle: ( x + 2 ) 2 + ( y − 1 ) 2 = 9 . ( x + 2 ) 2 + ( y − 1 ) 2 = 9 .

Try It 11.15

ⓐ Find the center and radius, then ⓑ graph the circle: ( x − 3 ) 2 + ( y + 4 ) 2 = 4 . ( x − 3 ) 2 + ( y + 4 ) 2 = 4 .

Try It 11.16

ⓐ Find the center and radius, then ⓑ graph the circle: ( x − 3 ) 2 + ( y − 1 ) 2 = 16 . ( x − 3 ) 2 + ( y − 1 ) 2 = 16 .

To find the center and radius, we must write the equation in standard form. In the next example, we must first get the coefficient of x 2 , y 2 x 2 , y 2 to be one.

Example 11.9

Find the center and radius and then graph the circle, 4 x 2 + 4 y 2 = 64 . 4 x 2 + 4 y 2 = 64 .

Try It 11.17

ⓐ Find the center and radius, then ⓑ graph the circle: 3 x 2 + 3 y 2 = 27 3 x 2 + 3 y 2 = 27

Try It 11.18

ⓐ Find the center and radius, then ⓑ graph the circle: 5 x 2 + 5 y 2 = 125 5 x 2 + 5 y 2 = 125

If we expand the equation from Example 11.8 , ( x + 2 ) 2 + ( y − 1 ) 2 = 9 , ( x + 2 ) 2 + ( y − 1 ) 2 = 9 , the equation of the circle looks very different.

This form of the equation is called the general form of the equation of the circle .

General Form of the Equation of a Circle

The general form of the equation of a circle is

If we are given an equation in general form, we can change it to standard form by completing the squares in both x and y . Then we can graph the circle using its center and radius.

Example 11.10

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 − 4 x − 6 y + 4 = 0 . x 2 + y 2 − 4 x − 6 y + 4 = 0 .

We need to rewrite this general form into standard form in order to find the center and radius.

Try It 11.19

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 − 6 x − 8 y + 9 = 0 . x 2 + y 2 − 6 x − 8 y + 9 = 0 .

Try It 11.20

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 + 6 x − 2 y + 1 = 0 . x 2 + y 2 + 6 x − 2 y + 1 = 0 .

In the next example, there is a y -term and a y 2 y 2 -term. But notice that there is no x -term, only an x 2 x 2 -term. We have seen this before and know that it means h is 0. We will need to complete the square for the y terms, but not for the x terms.

Example 11.11

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 + 8 y = 0 . x 2 + y 2 + 8 y = 0 .

Try It 11.21

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 − 2 x − 3 = 0 . x 2 + y 2 − 2 x − 3 = 0 .

Try It 11.22

ⓐ Find the center and radius, then ⓑ graph the circle: x 2 + y 2 − 12 y + 11 = 0 . x 2 + y 2 − 12 y + 11 = 0 .

Access these online resources for additional instructions and practice with using the distance and midpoint formulas, and graphing circles.

• Distance-Midpoint Formulas and Circles
• Finding the Distance and Midpoint Between Two Points
• Completing the Square to Write Equation in Standard Form of a Circle

Section 11.1 Exercises

Practice makes perfect.

In the following exercises, find the distance between the points. Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

( 2 , 0 ) ( 2 , 0 ) and ( 5 , 4 ) ( 5 , 4 )

( −4 , −3 ) ( −4 , −3 ) and ( 2 , 5 ) ( 2 , 5 )

( −4 , −3 ) ( −4 , −3 ) and ( 8 , 2 ) ( 8 , 2 )

( −7 , −3 ) ( −7 , −3 ) and ( 8 , 5 ) ( 8 , 5 )

( −1 , 4 ) ( −1 , 4 ) and ( 2 , 0 ) ( 2 , 0 )

( −1 , 3 ) ( −1 , 3 ) and ( 5 , −5 ) ( 5 , −5 )

( 1 , −4 ) ( 1 , −4 ) and ( 6 , 8 ) ( 6 , 8 )

( −8 , −2 ) ( −8 , −2 ) and ( 7 , 6 ) ( 7 , 6 )

( −3 , −5 ) ( −3 , −5 ) and ( 0 , 1 ) ( 0 , 1 )

( −1 , −2 ) ( −1 , −2 ) and ( −3 , 4 ) ( −3 , 4 )

( 3 , −1 ) ( 3 , −1 ) and ( 1 , 7 ) ( 1 , 7 )

( −4 , −5 ) ( −4 , −5 ) and ( 7 , 4 ) ( 7 , 4 )

In the following exercises, ⓐ find the midpoint of the line segments whose endpoints are given and ⓑ plot the endpoints and the midpoint on a rectangular coordinate system.

( 0 , −5 ) ( 0 , −5 ) and ( 4 , −3 ) ( 4 , −3 )

( −2 , −6 ) ( −2 , −6 ) and ( 6 , −2 ) ( 6 , −2 )

( 3 , −1 ) ( 3 , −1 ) and ( 4 , −2 ) ( 4 , −2 )

( −3 , −3 ) ( −3 , −3 ) and ( 6 , −1 ) ( 6 , −1 )

In the following exercises, write the standard form of the equation of the circle with the given radius and center ( 0 , 0 ) . ( 0 , 0 ) .

Radius: 2 2

Radius: 5 5

In the following exercises, write the standard form of the equation of the circle with the given radius and center

Radius: 1, center: ( 3 , 5 ) ( 3 , 5 )

Radius: 10, center: ( −2 , 6 ) ( −2 , 6 )

Radius: 2.5 , 2.5 , center: ( 1.5 , −3.5 ) ( 1.5 , −3.5 )

Radius: 1.5 , 1.5 , center: ( −5.5 , −6.5 ) ( −5.5 , −6.5 )

For the following exercises, write the standard form of the equation of the circle with the given center with point on the circle.

Center ( 3 , −2 ) ( 3 , −2 ) with point ( 3 , 6 ) ( 3 , 6 )

Center ( 6 , −6 ) ( 6 , −6 ) with point ( 2 , −3 ) ( 2 , −3 )

Center ( 4 , 4 ) ( 4 , 4 ) with point ( 2 , 2 ) ( 2 , 2 )

Center ( −5 , 6 ) ( −5 , 6 ) with point ( −2 , 3 ) ( −2 , 3 )

In the following exercises, ⓐ find the center and radius, then ⓑ graph each circle.

( x + 5 ) 2 + ( y + 3 ) 2 = 1 ( x + 5 ) 2 + ( y + 3 ) 2 = 1

( x − 2 ) 2 + ( y − 3 ) 2 = 9 ( x − 2 ) 2 + ( y − 3 ) 2 = 9

( x − 4 ) 2 + ( y + 2 ) 2 = 16 ( x − 4 ) 2 + ( y + 2 ) 2 = 16

( x + 2 ) 2 + ( y − 5 ) 2 = 4 ( x + 2 ) 2 + ( y − 5 ) 2 = 4

x 2 + ( y + 2 ) 2 = 25 x 2 + ( y + 2 ) 2 = 25

( x − 1 ) 2 + y 2 = 36 ( x − 1 ) 2 + y 2 = 36

( x − 1.5 ) 2 + ( y + 2.5 ) 2 = 0.25 ( x − 1.5 ) 2 + ( y + 2.5 ) 2 = 0.25

( x − 1 ) 2 + ( y − 3 ) 2 = 9 4 ( x − 1 ) 2 + ( y − 3 ) 2 = 9 4

x 2 + y 2 = 64 x 2 + y 2 = 64

x 2 + y 2 = 49 x 2 + y 2 = 49

2 x 2 + 2 y 2 = 8 2 x 2 + 2 y 2 = 8

6 x 2 + 6 y 2 = 216 6 x 2 + 6 y 2 = 216

In the following exercises, ⓐ identify the center and radius and ⓑ graph.

x 2 + y 2 + 2 x + 6 y + 9 = 0 x 2 + y 2 + 2 x + 6 y + 9 = 0

x 2 + y 2 − 6 x − 8 y = 0 x 2 + y 2 − 6 x − 8 y = 0

x 2 + y 2 − 4 x + 10 y − 7 = 0 x 2 + y 2 − 4 x + 10 y − 7 = 0

x 2 + y 2 + 12 x − 14 y + 21 = 0 x 2 + y 2 + 12 x − 14 y + 21 = 0

x 2 + y 2 + 6 y + 5 = 0 x 2 + y 2 + 6 y + 5 = 0

x 2 + y 2 − 10 y = 0 x 2 + y 2 − 10 y = 0

x 2 + y 2 + 4 x = 0 x 2 + y 2 + 4 x = 0

x 2 + y 2 − 14 x + 13 = 0 x 2 + y 2 − 14 x + 13 = 0

Writing Exercises

Explain the relationship between the distance formula and the equation of a circle.

Is a circle a function? Explain why or why not.

In your own words, state the definition of a circle.

In your own words, explain the steps you would take to change the general form of the equation of a circle to the standard form.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Whom can you ask for help?Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no - I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction

• Authors: Lynn Marecek, Andrea Honeycutt Mathis
• Publisher/website: OpenStax
• Book title: Intermediate Algebra 2e
• Publication date: May 6, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/intermediate-algebra-2e/pages/1-introduction
• Section URL: https://openstax.org/books/intermediate-algebra-2e/pages/11-1-distance-and-midpoint-formulas-circles

© Jan 23, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

11.2: Distance and Midpoint Formulas and Circles

• Last updated
• Save as PDF
• Page ID 5188

Learning Objectives

By the end of this section, you will be able to:

Use the Distance Formula

Use the midpoint formula.

• Write the equation of a circle in standard form
• Graph a circle

Before you get started, take this readiness quiz.

• Find the length of the hypotenuse of a right triangle whose legs are \(12\) and \(16\) inches. If you missed this problem, review Example 2.34.
• Factor: \(x^{2}-18 x+81\). If you missed this problem, review Example 6.24.
• Solve by completing the square: \(x^{2}-12 x-12=0\). If you missed this problem, review Example 9.22.

In this chapter we will be looking at the conic sections, usually called the conics, and their properties. The conics are curves that result from a plane intersecting a double cone—two cones placed point-to-point. Each half of a double cone is called a nappe.

There are four conics—the circle , parabola , ellipse , and hyperbola . The next figure shows how the plane intersecting the double cone results in each curve.

Each of the curves has many applications that affect your daily life, from your cell phone to acoustics and navigation systems. In this section we will look at the properties of a circle.

We have used the Pythagorean Theorem to find the lengths of the sides of a right triangle. Here we will use this theorem again to find distances on the rectangular coordinate system. By finding distance on the rectangular coordinate system, we can make a connection between the geometry of a conic and algebra—which opens up a world of opportunities for application.

Our first step is to develop a formula to find distances between points on the rectangular coordinate system. We will plot the points and create a right triangle much as we did when we found slope in Graphs and Functions. We then take it one step further and use the Pythagorean Theorem to find the length of the hypotenuse of the triangle—which is the distance between the points.

Example \(\PageIndex{1}\)

Use the rectangular coordinate system to find the distance between the points \((6,4)\) and \((2,1)\).

Exercise \(\PageIndex{1}\)

Use the rectangular coordinate system to find the distance between the points \((6,1)\) and \((2,-2)\).

Exercise \(\PageIndex{2}\)

Use the rectangular coordinate system to find the distance between the points \((5,3)\) and \((-3,-3)\).

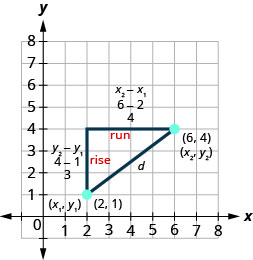
The method we used in the last example leads us to the formula to find the distance between the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\).

When we found the length of the horizontal leg we subtracted \(6−2\) which is \(x_{2}-x_{1}\).

When we found the length of the vertical leg we subtracted \(4−1\) which is \(y_{2}-y_{1}\).

If the triangle had been in a different position, we may have subtracted \(x_{1}-x_{2}\) or \(y_{1}-y_{2}\). The expressions \(x_{2}-x_{1}\) and \(x_{1}-x_{2}\) vary only in the sign of the resulting number. To get the positive value-since distance is positive- we can use absolute value. So to generalize we will say \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\).

In the Pythagorean Theorem, we substitute the general expressions \(\left|x_{2}-x_{1}\right|\) and \(\left|y_{2}-y_{1}\right|\) rather than the numbers.

\(\begin{array}{l c}{} & {a^{2}+b^{2}=c^{2}} \\ {\text {Substitute in the values. }}&{(|x_{2}-x_{1}|)^{2}+(|y_{2}-y_{1}|)^{2}=d^{2}} \\ {\text{Squaring the expressions makes}}&{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}} \\ \text{them positive, so we eliminate} \\\text{the absolute value bars.}\\ {\text{Use the Square Root Property.}}&{d=\pm\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\ {\text{Distance is positive, so eliminate}}&{d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\\\text{the negative value.}\end{array}\)

This is the Distance Formula we use to find the distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\).

Definition \(\PageIndex{1}\)

Distance Formula

The distance \(d\) between the two points \((x_{1},y_{1})\) and \((x_{2}, y_{2})\) is

\(d=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Example \(\PageIndex{2}\)

Use the Distance Formula to find the distance between the points \((-5,-3)\) and \((7,2)\).

Write the Distance Formula.

Label the points, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-5,-3}\end{array}\right)\), \(\left( \begin{array}{l}{x_{2}, y_{2}} \\ {7,2}\end{array}\right)\) and substitute.

\(d=\sqrt{(7-(-5))^{2}+(2-(-3))^{2}}\)

\(d=\sqrt{12^{2}+5^{2}}\) \(d=\sqrt{144+25}\) \(d=\sqrt{169}\) \(d=13\)

Exercise \(\PageIndex{3}\)

Use the Distance Formula to find the distance between the points \((-4,-5)\) and \((5,7)\).

Exercise \(\PageIndex{4}\)

Use the Distance Formula to find the distance between the points \((-2,-5)\) and \((-14,-10)\).

Example \(\PageIndex{3}\)

Use the Distance Formula to find the distance between the points \((10,−4)\) and \((−1,5)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

Label the points, \(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {10,-4}\end{array}\right)\), \(\left( \begin{array}{c}{x_{2}, y_{2}} \\ {-1,5}\end{array}\right)\) and substitute.

\(d=\sqrt{(-1-10)^{2}+(5-(-4))^{2}}\)

\(d=\sqrt{(-11)^{2}+9^{2}}\) \(d=\sqrt{121+81}\) \(d=\sqrt{202}\)

Since \(202\) is not a perfect square, we can leave the answer in exact form or find a decimal approximation.

\(d=\sqrt{202}\) or \(d \approx 14.2\)

Exercise \(\PageIndex{5}\)

Use the Distance Formula to find the distance between the points \((−4,−5)\) and \((3,4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

\(d=\sqrt{130}, d \approx 11.4\)

Exercise \(\PageIndex{6}\)

Use the Distance Formula to find the distance between the points \((−2,−5)\) and \((−3,−4)\). Write the answer in exact form and then find the decimal approximation, rounded to the nearest tenth if needed.

\(d=\sqrt{2}, d \approx 1.4\)

It is often useful to be able to find the midpoint of a segment. For example, if you have the endpoints of the diameter of a circle, you may want to find the center of the circle which is the midpoint of the diameter. To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.

Definition \(\PageIndex{2}\)

Midpoint Formula

The midpoint of the line segment whose endpoints are the two points \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\) is

\(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)

To find the midpoint of a line segment, we find the average of the \(x\)-coordinates and the average of the \(y\)-coordinates of the endpoints.

Example \(\PageIndex{4}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−5,−4)\) and \((7,2)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

Exercise \(\PageIndex{7}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−3,−5)\) and \((5,7)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

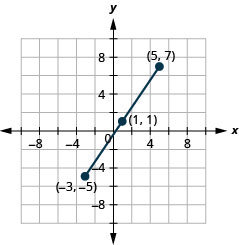
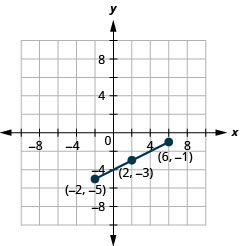
Exercise \(\PageIndex{8}\)

Use the Midpoint Formula to find the midpoint of the line segments whose endpoints are \((−2,−5)\) and \((6,−1)\). Plot the endpoints and the midpoint on a rectangular coordinate system.

Both the Distance Formula and the Midpoint Formula depend on two points, \(\left(x_{1}, y_{1}\right)\) and \(\left(x_{2}, y_{2}\right)\). It is easy to confuse which formula requires addition and which subtraction of the coordinates. If we remember where the formulas come from, is may be easier to remember the formulas.

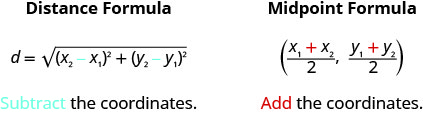
Write the Equation of a Circle in Standard Form

As we mentioned, our goal is to connect the geometry of a conic with algebra. By using the coordinate plane, we are able to do this easily.

We define a circle as all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius , \(r\), of the circle.

Definition \(\PageIndex{3}\)

A circle is all points in a plane that are a fixed distance from a given point in the plane. The given point is called the center , \((h,k)\), and the fixed distance is called the radius , \(r\), of the circle.

This is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\).

Definition \(\PageIndex{4}\)

The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\), is

Example \(\PageIndex{5}\)

Write the standard form of the equation of the circle with radius \(3\) and center \((0,0)\).

Exercise \(\PageIndex{9}\)

Write the standard form of the equation of the circle with a radius of \(6\) and center \((0,0)\).

\(x^{2}+y^{2}=36\)

Exercise \(\PageIndex{10}\)

Write the standard form of the equation of the circle with a radius of \(8\) and center \((0,0)\).

\(x^{2}+y^{2}=64\)

In the last example, the center was \((0,0)\). Notice what happened to the equation. Whenever the center is \((0,0)\), the standard form becomes \(x^{2}+y^{2}=r^{2}\).

Example \(\PageIndex{6}\)

Write the standard form of the equation of the circle with radius \(2\) and center \((−1,3)\).

Exercise \(\PageIndex{11}\)

Write the standard form of the equation of the circle with a radius of \(7\) and center \((2,−4)\).

\((x-2)^{2}+(y+4)^{2}=49\)

Exercise \(\PageIndex{12}\)

Write the standard form of the equation of the circle with a radius of \(9\) and center \((−3,−5)\).

\((x+3)^{2}+(y+5)^{2}=81\)

In the next example, the radius is not given. To calculate the radius, we use the Distance Formula with the two given points.

Example \(\PageIndex{7}\)

Write the standard form of the equation of the circle with center \((2,4)\) that also contains the point \((−2,1)\).

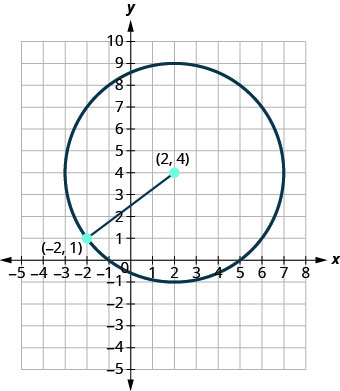
The radius is the distance from the center to any point on the circle so we can use the distance formula to calculate it. We will use the center \((2,4)\) and point \((−2,1)\)

Use the Distance Formula to find the radius.

\(r=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)

Substitute the values. \(\left( \begin{array}{l}{x_{1}, y_{1}} \\ {2,4}\end{array}\right), \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-2,1}\end{array}\right)\)

\(r=\sqrt{(-2-2)^{2}+(1-4)^{2}}\)

\(r=\sqrt{(-4)^{2}+(-3)^{2}}\) \(r=\sqrt{16+9}\) \(r=\sqrt{25}\) \(r=5\)

Now that we know the radius, \(r=5\), and the center, \((2,4)\), we can use the standard form of the equation of a circle to find the equation.

Use the standard form of the equation of a circle.

\((x-h)^{2}+(y-k)^{2}=r^{2}\)

Substitute in the values.

\((x-2)^{2}+(y-4)^{2}=5^{2}\)

\((x-2)^{2}+(y-4)^{2}=25\)

Exercise \(\PageIndex{13}\)

Write the standard form of the equation of the circle with center \((2,1)\) that also contains the point \((−2,−2)\).

\((x-2)^{2}+(y-1)^{2}=25\)

Exercise \(\PageIndex{14}\)

Write the standard form of the equation of the circle with center \((7,1)\) that also contains the point \((−1,−5)\).

\((x-7)^{2}+(y-1)^{2}=100\)

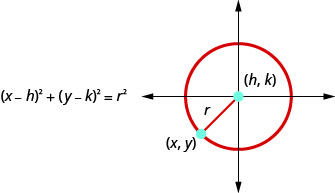
Graph a Circle

Any equation of the form \((x-h)^{2}+(y-k)^{2}=r^{2}\) is the standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\) . We can then graph the circle on a rectangular coordinate system.

Note that the standard form calls for subtraction from \(x\) and \(y\). In the next example, the equation has \(x+2\), so we need to rewrite the addition as subtraction of a negative.

Example \(\PageIndex{8}\)

Find the center and radius, then graph the circle: \((x+2)^{2}+(y-1)^{2}=9\).

Exercise \(\PageIndex{15}\)

• Find the center and radius, then
• Graph the circle: \((x-3)^{2}+(y+4)^{2}=4\).
• The circle is centered at \((3,-4)\) with a radius of \(2\).

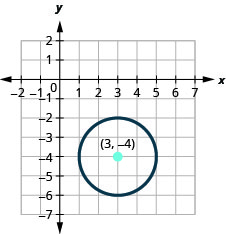
Exercise \(\PageIndex{16}\)

• Graph the circle: \((x-3)^{2}+(y-1)^{2}=16\).
• The circle is centered at \((3,1)\) with a radius of \(4\).

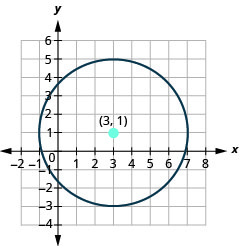
To find the center and radius, we must write the equation in standard form. In the next example, we must first get the coefficient of \(x^{2}, y^{2}\) to be one.

Example \(\PageIndex{9}\)

Find the center and radius and then graph the circle, \(4 x^{2}+4 y^{2}=64\).

Exercise \(\PageIndex{17}\)

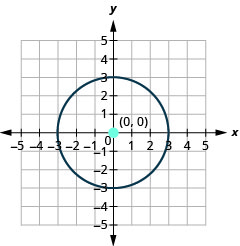
• Graph the circle: \(3 x^{2}+3 y^{2}=27\)
• The circle is centered at \((0,0)\) with a radius of \(3\).

Exercise \(\PageIndex{18}\)

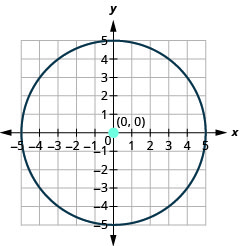
• Graph the circle: \(5 x^{2}+5 y^{2}=125\)
• The circle is centered at \((0,0)\) with a radius of \(5\).

If we expand the equation from Example 11.1.8, \((x+2)^{2}+(y-1)^{2}=9\), the equation of the circle looks very different.

\((x+2)^{2}+(y-1)^{2}=9\)

Square the binomials.

\(x^{2}+4 x+4+y^{2}-2 y+1=9\)

Arrange the terms in descending degree order, and get zero on the right

\(x^{2}+y^{2}+4 x-2 y-4=0\)

This form of the equation is called the general form of the equation of the circle .

Definition \(\PageIndex{5}\)

The general form of the equation of a circle is

\(x^{2}+y^{2}+a x+b y+c=0\)

If we are given an equation in general form, we can change it to standard form by completing the squares in both \(x\) and \(y\). Then we can graph the circle using its center and radius.

Example \(\PageIndex{10}\)

• Graph the circle: \(x^{2}+y^{2}-4 x-6 y+4=0\)

We need to rewrite this general form into standard form in order to find the center and radius.

Exercise \(\PageIndex{19}\)

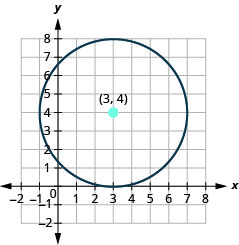
• Graph the circle: \(x^{2}+y^{2}-6 x-8 y+9=0\).
• The circle is centered at \((3,4)\) with a radius of \(4\).

Exercise \(\PageIndex{20}\)

• Graph the circle: \(x^{2}+y^{2}+6 x-2 y+1=0\)
• The circle is centered at \((-3,1)\) with a radius of \(3\).

In the next example, there is a \(y\)-term and a \(y^{2}\)-term. But notice that there is no \(x\)-term, only an \(x^{2}\)-term. We have seen this before and know that it means \(h\) is \(0\). We will need to complete the square for the \(y\) terms, but not for the \(x\) terms.

Example \(\PageIndex{11}\)

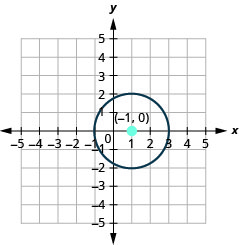
• Graph the circle: \(x^{2}+y^{2}+8 y=0\)

Exercise \(\PageIndex{21}\)

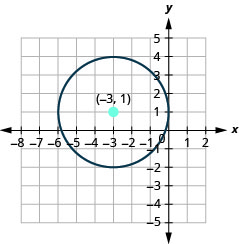
• Graph the circle: \(x^{2}+y^{2}-2 x-3=0\).
• The circle is centered at \((-1,0)\) with a radius of \(2\).

Exercise \(\PageIndex{22}\)

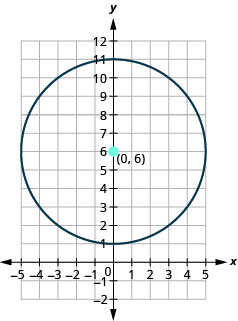
• Graph the circle: \(x^{2}+y^{2}-12 y+11=0\).
• The circle is centered at \((0,6)\) with a radius of \(5\).

Access these online resources for additional instructions and practice with using the distance and midpoint formulas, and graphing circles.

• Distance-Midpoint Formulas and Circles
• Finding the Distance and Midpoint Between Two Points
• Completing the Square to Write Equation in Standard Form of a Circle

Key Concepts

• Circle: A circle is all points in a plane that are a fixed distance from a fixed point in the plane. The given point is called the center, \((h,k)\), and the fixed distance is called the radius, \(r\), of the circle.
• Standard Form of the Equation a Circle: The standard form of the equation of a circle with center, \((h,k)\), and radius, \(r\) , is

Geometry Basics (Geometry Curriculum - Unit 1) | All Things Algebra®

• Google Apps™

What educators are saying

Also included in.

Description

This Geometry Basics Unit Bundle contains guided notes, homework assignments, three quizzes, dictionary, study guide and a unit test that cover the following topics:

• Points, Lines, and Planes

• Segment Addition Postulate

• The Distance Formula

• The Midpoint Formula

• Partitioning a Segment

• Naming and Classifying Angles

• Angle Addition Postulate

• Angle Relationships (Adjacent, Vertical, Complementary, Supplementary, Linear Pair)

• Solving for Missing Measures using Algebra

• Special Relationships: Perpendicular and Angle Bisectors

• Constructions (Perpendicular bisectors, perpendicular line through a point on the line, perpendicular line through a point not on the line, line parallel to a given line through a given point, angle bisector, congruent angles)

Note: This unit was updated on 8/25/19 to include partitioning a segment. If you do not teach this topic, I included the old unit without this topic in the download as well.

ADDITIONAL COMPONENTS INCLUDED:

(1) Links to Instructional Videos: Links to videos of each lesson in the unit are included. Videos were created by fellow teachers for their students using the guided notes and shared in March 2020 when schools closed with no notice.  Please watch through first before sharing with your students. Many teachers still use these in emergency substitute situations. (2) Editable Assessments: Editable versions of each quiz and the unit test are included. PowerPoint is required to edit these files. Individual problems can be changed to create multiple versions of the assessment. The layout of the assessment itself is not editable. If your Equation Editor is incompatible with mine (I use MathType), simply delete my equation and insert your own.

(3) Google Slides Version of the PDF: The second page of the Video links document contains a link to a Google Slides version of the PDF. Each page is set to the background in Google Slides. There are no text boxes;  this is the PDF in Google Slides.  I am unable to do text boxes at this time but hope this saves you a step if you wish to use it in Slides instead! 

This resource is included in the following bundle(s):

Geometry First Semester Notes Bundle

Geometry Curriculum

Geometry Curriculum (with Activities)

More Geometry Units:

Unit 2 – Logic and Proof

Unit 3 – Parallel and Perpendicular Lines

Unit 4 – Congruent Triangles

Unit 5 – Relationships in Triangles

Unit 6 – Similar Triangles

Unit 7 – Right Triangles and Trigonometry Unit 8 – Polygons and Quadrilaterals

Unit 9 – Transformations

Unit 10 – Circles

Unit 11 – Volume and Surface Area Unit 12 – Probability

LICENSING TERMS: This purchase includes a license for one teacher only for personal use in their classroom. Licenses are non-transferable , meaning they can not be passed from one teacher to another. No part of this resource is to be shared with colleagues or used by an entire grade level, school, or district without purchasing the proper number of licenses. If you are a coach, principal, or district interested in transferable licenses to accommodate yearly staff changes, please contact me for a quote at [email protected].

COPYRIGHT TERMS: This resource may not be uploaded to the internet in any form, including classroom/personal websites or network drives, unless the site is password protected and can only be accessed by students.

© All Things Algebra (Gina Wilson), 2012-present

Questions & Answers

All things algebra.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think

• Kindergarten
• Greater Than Less Than
• Measurement
• Multiplication
• Place Value
• Subtraction
• Punctuation
• 1st Grade Reading
• 2nd Grade Reading
• 3rd Grade Reading
• Cursive Writing

Distance And Midpoint Formulas Homework 3

Distance And Midpoint Formulas Homework 3 - Displaying top 8 worksheets found for this concept.

Some of the worksheets for this concept are 3 the midpoint formula, Geometry notes sol midpoint and distance formulas name, Infinite geometry, Gina wilson all things algebra distance and midpoint formulas, Find the distance between each pair of round your, Performance based learning and assessment task distance, Name teacher date distance and midpoint formulas, Unit 1 geometry basics homework 3 answer key.

Found worksheet you are looking for? To download/print, click on pop-out icon or print icon to worksheet to print or download. Worksheet will open in a new window. You can & download or print using the browser document reader options.

1. 3-The Midpoint Formula

2. geometry notes sol g.3 midpoint and distance formulas name ..., 3. infinite geometry, 4. gina wilson all things algebra distance and midpoint formulas, 5. find the distance between each pair of points. round your ..., 6. performance based learning and assessment task distance ..., 7. name: teacher: date: distance and midpoint formulas, 8. unit 1 geometry basics homework 3 answer key.