problem solving olympiad

Evan Chen《陳誼廷》

• CV

Teaching (otis), • otis excerpts, • mock aime, • for beginners, • for coaches, • problems, • mop, • elmo, • usemo, personal/hobbies, • puzzle hunts, • games, • photos, youtube/twitch, • discord, plz learn code, • filesys concepts, • learning path, • latex style, • asy guide, publications, • egmo book, • napkin (v1.5), • course notes, recommendations, • mentors, • quotes, • faqs, • rec letters.

Olympiad Problems and Solutions

This page contains problems and solutions to several USA contests, and a few others.

Check the AoPS contest index for even more problems and solutions, including most of the ones below.

Hardness scale #

Here is an index of many problems by my opinions on their difficulty and subject. The difficulties are rated from 0 to 50 in increments of 5, using a scale I devised called MOHS . 1

In 2020, Rustam Turdibaev and Olimjon Olimov, compiled a 336-problem index of recent problems by subject and MOHS rating . In addition, the linked file also contains a hyperlink to each of the corresponding solution threads on Art of Problem-Solving.

This document will probably see a lot of updates. Anyway, I cannot repeat enough the disclaimer that the ratings (and even philosophy) are my own personal opinion, rather than some sort of indisputable truth.

USA Math Olympiad (USAMO) #

Despite being part of the USA team selection process, these are not the “official” solution files, rather my own personal notes. In particular, I tend to be more terse than other sources.

My understanding is that the internal problems and solutions, from the actual USA(J)MO committee, are copyrighted by MAA. To my knowledge they are not published anywhere. The Math Magazine has recently resumed publishing yet another version of the problems and solutions of the olympiad.

Recent statistics for USAMO

Download statistics for 2015-present (PDF) .

Problems and solutions to USAMO

USAMO 1996 (PDF) (TeX)
USAMO 1997 (PDF) (TeX)
USAMO 1998 (PDF) (TeX)
USAMO 1999 (PDF) (TeX)
USAMO 2000 (PDF) (TeX)
USAMO 2001 (PDF) (TeX)
USAMO 2002 (PDF) (TeX)
USAMO 2003 (PDF) (TeX)
USAMO 2004 (PDF) (TeX)
USAMO 2005 (PDF) (TeX)
USAMO 2006 (PDF) (TeX)
USAMO 2007 (PDF) (TeX)
USAMO 2008 (PDF) (TeX)
USAMO 2009 (PDF) (TeX)
USAMO 2010 (PDF) (TeX)
USAMO 2011 (PDF) (TeX)
USAMO 2012 (PDF) (TeX)
USAMO 2013 (PDF) (TeX)
USAMO 2014 (PDF) (TeX)
USAMO 2015 (PDF) (TeX)
USAMO 2016 (PDF) (TeX)
USAMO 2017 (PDF) (TeX)
USAMO 2018 (PDF) (TeX)
USAMO 2019 (PDF) (TeX) (Math Jam)
USAMOO 2020 (PDF) (TeX) (video)
USAMO 2021 (PDF) (TeX) (video)
USAMO 2022 (PDF) (TeX)
USAMO 2023 (PDF) (TeX)
USAMO 2024 (PDF) (TeX)
JMO 2010 (PDF) (TeX)
JMO 2011 (PDF) (TeX)
JMO 2012 (PDF) (TeX)
JMO 2013 (PDF) (TeX)
JMO 2014 (PDF) (TeX)
JMO 2015 (PDF) (TeX) , featuring Steve !
JMO 2016 (PDF) (TeX)
JMO 2017 (PDF) (TeX)
JMO 2018 (PDF) (TeX)
JMO 2019 (PDF) (TeX) (Math Jam)
JMOO 2020 (PDF) (TeX) (video)
JMO 2021 (PDF) (TeX) (video)
JMO 2022 (PDF) (TeX)
JMO 2023 (PDF) (TeX)
JMO 2024 (PDF) (TeX)

USA TST Selection Test (TSTST) #

For an explanation of the name, see the FAQ on the USA IMO team selection .

TSTST 2011 (probs) (sols) (TeX)
TSTST 2012 (probs) (sols) (TeX)
TSTST 2013 (probs) (sols) (TeX)
TSTST 2014 (probs) (sols) (TeX)
TSTST 2015 (probs) (sols) (TeX)
TSTST 2016 (probs) (sols) (TeX)
TSTST 2017 (probs) (sols) (TeX)
TSTST 2018 (probs) (sols) (TeX) (stats)
TSTST 2019 (probs) (sols) (TeX) (stats)
(video 1) (video 2) (video 3)
TSTST 2021 (probs) (sols) (TeX) (stats)
TSTST 2022 (probs) (sols) (TeX) (stats)
TSTST 2023 (probs) (sols) (TeX) (stats)

USA Team Selection Test (TST) #

These exams are used in the final part of the selection process for the USA IMO team.

USA Team Selection Test 2000 (probs)
USA Team Selection Test 2001 (probs)
USA Team Selection Test 2002 (probs)
USA Winter TST 2012 (probs)
USA Winter TST 2013 (probs)
USA Winter TST 2014 (probs) (sols) (TeX)
USA Winter TST 2015 (probs) (sols) (TeX)
USA Winter TST 2016 (probs) (sols) (TeX)
USA Winter TST 2017 (probs) (sols) (TeX)
USA Winter TST 2018 (probs) (sols) (TeX) (stats)
USA Winter TST 2019 (probs) (sols) (TeX) (stats)
USA Winter TST 2020 (probs) (sols) (TeX) (stats)
USA Winter TST 2021 (probs) (sols) (TeX) (stats) (video)
Because of the pandemic, there was no USA Winter TST for IMO 2022.
USA Winter TST 2023 (probs) (sols) (TeX) (stats)

International Math Olympiad #

IMO 1997 (PDF) (TeX)
IMO 1998 (PDF) (TeX)
IMO 1999 (PDF) (TeX)
IMO 2000 (PDF) (TeX)
IMO 2001 (PDF) (TeX)
IMO 2002 (PDF) (TeX)
IMO 2003 (PDF) (TeX)
IMO 2004 (PDF) (TeX)
IMO 2005 (PDF) (TeX)
IMO 2006 (PDF) (TeX)
IMO 2007 (PDF) (TeX)
IMO 2008 (PDF) (TeX)
IMO 2009 (PDF) (TeX)
IMO 2010 (PDF) (TeX)
IMO 2011 (PDF) (TeX)
IMO 2012 (PDF) (TeX)
IMO 2013 (PDF) (TeX)
IMO 2014 (PDF) (TeX)
IMO 2015 (PDF) (TeX)
IMO 2016 (PDF) (TeX)
IMO 2017 (PDF) (TeX)
IMO 2018 (PDF) (TeX)
IMO 2019 (PDF) (TeX)
IMO 2020 (PDF) (TeX) (video)
IMO 2021 (PDF) (TeX)
IMO 2022 (PDF) (TeX)
IMO 2023 (PDF) (TeX)

Also listed on the USEMO page .

(video 1) (video 2)
USEMO 2022 (problems) (solutions+results)

Taiwan Team Selection Test #

These are the problems I worked on in high school when competing for a spot on the Taiwanese IMO team. These problems are in Chinese; English versions here .

Taiwan TST 2014 Round 1 (problems)
Taiwan TST 2014 Round 2 (problems)
Taiwan TST 2014 Round 3 (problems)

NIMO / OMO #

In high school, I and some others ran two online contests called NIMO (National Internet Math Olympiad) and OMO (Online Math Open). Neither contest is active at the time of writing (April 2021) but I collected all the materials and put them in a Google Drive link since the websites for those contests is not currently online. Most of the problems are short-answer problems.

The acronym stands from “math olympiad hardness scale”, pun fully intended . ↩

Choose Your Test

Sat / act prep online guides and tips, how to study for the math olympiad: amc 10/amc 12.

Other High School

Have you ever wondered what it would take to represent America at the International Math Olympiad? Or maybe you're a strong math student who is wondering what opportunities are available to you outside the classroom?

In this article, we'll answer all your Math Olympiad questions! We'll explain what it takes to qualify for the International Math Olympiad and how to ace the qualifying tests—the AMC 10 and AMC 12.

How Do You Qualify for Math Olympiad?

In this section we discuss the three key steps to qualifying for Math Olympiad.

Step 1: Take the AMC 10 or AMC 12

The AMC 10 and AMC 12 are nationwide tests administered by the Mathematical Association of America that qualify you for the American Invitational Mathematics Exam (AIME). Only those with top scores will be invited to take the AIME. The MAA recommends 9th and 10th graders take the AMC 10, and 11th and 12th graders take the AMC 12. You can take the AMC 10 and/or 12 multiple times.

The AMC 10 and AMC 12 each have 25 questions. You have 75 minutes for the entire exam. Each correct answer is worth 6 points (for a maximum score of 150) and each unanswered question is worth 1.5 points. There is no deduction for wrong answers.

Note that you don't need to get all of the questions right to get a qualifying score. You just have to do better than most of the other students taking the exam! Keep that in mind as you come up with a strategy for the test.

You need to be in the top 5% of scorers on the AMC 12 or the top 2.5% of scorers on the AMC 10 to qualify, so the vast majority of people who take the AMC exams don't qualify. But, if you do qualify, you can take the American Invitation Mathematics Examination, or AIME.

Step 2: Take the AIME

The AIME is a 15-question, three-hour exam, and each answer is an integer between 0 and 999, inclusive. Regardless of whether you took the AMC 10 or AMC 12, everyone takes the same AIME. It's offered once a year (with an alternate test date available for those who can't make the official exam date) in the spring.

Unlike the AMC 10 and the AMC 12, you can only take the AIME once per qualification. So while you can take the AMC 10 or AMC 12 multiple times to qualify, once you qualify, you've only got one shot at the AIME. That means you want to make sure you do your best on it.

After you take the AIME, your AIME score is multiplied by ten and added to your AMC score to determine if you qualify for Math Olympiad. The cutoff score for qualifying changes yearly, but it's set so about 260-270 students qualify for Math Olympiad each year.

Step 3: Qualify for and Compete in Math Olympiad

If you do well on the AIME, you can qualify for the US Mathematical Olympiad. The top scorers from that competition then have the opportunity to train to be on the US team that competes at the International Math Olympiad. (You can find more info on this process over at the Mathematical Association of American website .)

If you took the AMC 10, you'll compete in the USA Junior Mathematical Olympiad (USAJMO). Students who took the AMC 12 will compete in the USA Mathematical Olympiad (USAMO).

It's a long process to get to the IMO, and very few students make it that far. But even just taking the AIME can set you apart in the college admissions process, especially if you are interested in engineering programs. Along with a high GPA and strong SAT/ACT scores, taking the AIME is a way to signal to colleges you have superior math and problem-solving skills.

How Can You Learn Math Olympiad Content?

Math through pre-calculus covers most topics tested on the AMC 10 and 12 and the AIME, but math competition problems will be trickier than what you see on your usual math homework assignments.

If you're not up to pre-calculus in school yet, your first task will be learning the content before focusing on how to solve problems that the AMC 10 and 12 tend to ask.

See if there is a teacher or peer who is willing to tutor you if you haven't taken pre-calculus. You could also see if it's possible to take the course over the summer to get caught up quickly. There may also be private tutoring available in your area that can help get your precalculus skills up to speed!

In the meantime, you can explore parts of your own math textbook you haven't gotten to yet, or ask to borrow textbooks from teachers at your school if you want to brush up on a topic not covered in the math class you're taking this year.

Also check out these online content resources from the MAA to help you study (you'll need to create an online account).

How Can You Learn Problem-Solving Skills?

The key to doing well on AMC is not just knowing math and being able to do rote problems, but to know concepts inside and out and be able to use them to solve tricky problems.

Think outside the textbook.

The website Art of Problem Solving is a hub for math competition resources and problems, and has been mentioned by many former AMC-takers as a top resource. They have pages on learning to solve certain types of problems, advice on the best prep books, and forums where you can talk to other AIME hopefuls about studying and strategy.

This page provides links to practice problems and prep books and is a great place to get started.

Our advice to study for the AMC is to do lots of practice problems, and then correct them. Carefully analyze your weaknesses. Don't just notice what you did wrong, get inside your head and figure out why you got a problem wrong and how you will work to get it correct the next time.

To improve your problem-solving ability, you can also consider borrowing or purchasing books specifically about solving math problems. Try How To Solve It by George Polya, Problem-Solving Strategies by Arthur Engel, or Challenging Problems in Algebra by Alfred Posamentier and Charles Salkind. These books will give you skills not typically taught in your math classes.

How to Prepare for Math Olympiad

Studying is more than just putting the time in. You want to make sure you are using the best practice problems and really analyzing your weak points to get your math skills to where they need to be.

Read on to learn the six tips you need to follow to study like a pro.

#1: Use Quality Practice Problems

Use practice problems from past AMCs when possible. You want to prepare for the format and type of questions on the AMC. Any problem-solving practice you get will be helpful, but if you're set on qualifying the AIME, you should spend the majority of your time prepping for AMC-type questions.

If you're unclear on how to solve a problem, ask your math teacher, a math team friend, or an online forum like the one at Art of Problem Solving . The better you understand each AMC problem you encounter, the more likely you are to be prepared for the real thing.

#2: Don't Lounge Around

Quality practice time is key! Make sure to time yourself and simulate real test-taking conditions when doing practice problems— find a quiet room, don't use outside resources while you test, and sit at a proper table or desk (don't lounge in bed!). As you review problems, bring in your outside resources, from websites to problem-solving books, but remember to stay alert and focused.

Don't let study time turn into naptime!

#3: Focus on Your Weak Areas

When studying, spend the most time focusing on your weak areas. As you work through practice problems, keep track of problems you didn't know how to solve or concepts you're shaky on. You can log your mistakes into a journal or notebook to help focus your studying.

And don't just log your mistakes and move on, figure out why you made those mistakes —what didn't you know, what you assumed—and make a plan to get similar problems right in the future.

#4: Beware of Tiny Mistakes

Be very, very careful about small mistakes—like forgetting a negative sign, accidentally moving a decimal point, or making a basic arithmetic error. You could get the meat of a problem correct but still answer a problem wrong if you make a tiny mistake . Get in the habit of being hyper-vigilant and careful when you practice, so you don't make these mistakes when you take the exam for real. Never assume you're too smart for a silly mistake!

#5: Schedule Regular Study Time

Finally, set aside dedicated time each week for studying. By practicing at least once a week, you will retain all of the skills you learn and continue to build on your knowledge. Build studying into your schedule like it's another class or extracurricular . If you don't, your studying could fall by the wayside and you'll lose out on getting the amount of practice you need.

#6: Attend Other Math Competitions

If there is a math team or club at your school, join for the practice! Doing smaller competitions can help you learn to deal with nerves and will give you more opportunities to practice. It will also help you find a community of students with similar interests who you can study with.

Also, the earlier you can start, the better. Some middle schools and even elementary schools have math clubs that expose you to tricky problem-solving questions in a way your standard math classes will not.

What Should You Do the Night Before a Competition?

After all your preparation, you don't want to trip at the finish line and ruin all your hard work right before the competition. Don't do tons of studying the night before you take the AMC. By that point, you will have done all of the work you can. Focus on relaxing and getting in the right mindset for the exam.

Also, make sure you get enough sleep the night before, and follow our other tips for the night before a test . Don't waste all of your hard work studying by staying up late the night before!

Finally, make sure you are set to go in the morning with transportation and directions to where you are taking the test. You don't want to deal with a morning-of crisis! Plan to get to the exam center early in case you hit traffic or any other last-minute snags.

What's Next?

Curious about the math scores it takes to get into top tech schools like MIT and CalTech? Read more about admission to engineering schools .

Going for a perfect math SAT or ACT score? Get tips from our full-scorer on how to get to a perfect 800 on SAT math or a perfect 36 on ACT math .

Wondering about paying for college? Check out automatic scholarships available for high ACT and SAT scores.

Want to improve your SAT score by 160 points or your ACT score by 4 points? We've written a guide for each test about the top 5 strategies you must be using to have a shot at improving your score. Download it for free now:

These recommendations are based solely on our knowledge and experience. If you purchase an item through one of our links, PrepScholar may receive a commission.

Halle Edwards graduated from Stanford University with honors. In high school, she earned 99th percentile ACT scores as well as 99th percentile scores on SAT subject tests. She also took nine AP classes, earning a perfect score of 5 on seven AP tests. As a graduate of a large public high school who tackled the college admission process largely on her own, she is passionate about helping high school students from different backgrounds get the knowledge they need to be successful in the college admissions process.

Student and Parent Forum

Our new student and parent forum, at ExpertHub.PrepScholar.com , allow you to interact with your peers and the PrepScholar staff. See how other students and parents are navigating high school, college, and the college admissions process. Ask questions; get answers.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

Math Olympiads for Elementary and Middle Schools

Welcome to MOEMS ®

MOEMS® is one of the most influential and fun-filled math competition programs in the United States and throughout the world. More than 120,000 students from every state and 39 additional countries participate each year. The objectives of MOEMS® are to teach multiple strategies for out-of-the-box problem solving, develop mathematical flexibility in solving those problems, and foster mathematical creativity and ingenuity. MOEMS® was established in 1979 and is a 501(C)(3) nonprofit organization.

Local news... Click to read about some amazing students!

Click here to download the scoring bands

All awards packages will be sent out late April through mid May and will be received by all PICOS by the end of May. Packages will include awards and certificates. If you want the certificates earlier you may use the links below.

Click here to download participation certificate.

Click here to download template for student merge to participation certificate.

Available for Elementary and Middle School

(Grades 4-6) Division E

(Grades 6-8) Division M

Teams of up to 35 students.

Two Test Administration Formats

Paper tests for traditional settings

Online tests for remote settings

2024-2025 Fees & Deadlines

Early Bird Fee: Register and PAY IN FULL by July 31, 2024

United States/Canada/Mexico: $175.00

International Teams: $215.00

Standard Fee: Register by October 15, 2024

United States/Canada/Mexico: $200.00

International Teams: $240.00

Late Fee: Register by October 31, 2024

United States/Canada/Mexico: $250.00

International Teams: $290.00

Last Chance: Register after November 1, 2024

United States/Canada/Mexico: $300.00

International Teams: $340.00

2024- 2025 Season

Dates are the same for Divisons E and M.

MOEMS ® Affiliates

$problem solving olympiad$

Australian Problem Solving Mathematical Olympiads (APSMO)

MOEMS ® Mainland China

International Mathematical Olympiad

Hall of fame
Links and Resources

Language versions of problems are not complete. Please send relevant PDF files to the webmaster: [email protected] .

Mathematical Olympiad Challenges

© 2000
Titu Andreescu 0 ,
Răzvan Gelca 1

American Mathematics Competitions, University of Nebraska, Lincoln, USA

You can also search for this author in PubMed Google Scholar

Department of Mathematics, University of Michigan, Ann Arbor, USA

3740 Accesses

16 Citations

5 Altmetric

This is a preview of subscription content, log in via an institution to check access.

Access this book

Available as PDF
Read on any device
Instant download
Own it forever

Tax calculation will be finalised at checkout

Other ways to access

Licence this eBook for your library

Institutional subscriptions

Table of contents (6 chapters)

Front matter, geometry and trigonometry.

Titu Andreescu, Răzvan Gelca

Algebra and Analysis

Number theory and combinatorics, back matter.

number theory
combinatorics
Mathematica
prime number
transformation
trigonometry

About this book

Authors and affiliations.

Titu Andreescu

Răzvan Gelca

Bibliographic Information

Book Title : Mathematical Olympiad Challenges

Authors : Titu Andreescu, Răzvan Gelca

DOI : https://doi.org/10.1007/978-1-4612-2138-8

Publisher : Birkhäuser Boston, MA

eBook Packages : Springer Book Archive

eBook ISBN : 978-1-4612-2138-8 Published: 01 December 2013

Edition Number : 1

Number of Pages : XVI, 260

Topics : Mathematics, general , Algebra , Geometry , Number Theory

Publish with us

Policies and ethics

Find a journal
Track your research

We will keep fighting for all libraries - stand with us!

Internet Archive Audio

This Just In
Grateful Dead
Old Time Radio
78 RPMs and Cylinder Recordings
Audio Books & Poetry
Computers, Technology and Science
Music, Arts & Culture
News & Public Affairs
Spirituality & Religion
Radio News Archive

Flickr Commons
Occupy Wall Street Flickr
NASA Images
Solar System Collection
Ames Research Center

All Software
Old School Emulation
MS-DOS Games
Historical Software
Classic PC Games
Software Library
Kodi Archive and Support File
Vintage Software
CD-ROM Software
CD-ROM Software Library
Software Sites
Tucows Software Library
Shareware CD-ROMs
Software Capsules Compilation
CD-ROM Images
ZX Spectrum
DOOM Level CD

Smithsonian Libraries
FEDLINK (US)
Lincoln Collection
American Libraries
Canadian Libraries
Universal Library
Project Gutenberg
Children's Library
Biodiversity Heritage Library
Books by Language
Additional Collections

Prelinger Archives
Democracy Now!
Occupy Wall Street
TV NSA Clip Library
Animation & Cartoons
Arts & Music
Computers & Technology
Cultural & Academic Films
Ephemeral Films
Sports Videos
Videogame Videos
Youth Media

Search the history of over 866 billion web pages on the Internet.

Mobile Apps

Wayback Machine (iOS)
Wayback Machine (Android)

Browser Extensions

Archive-it subscription.

Explore the Collections
Build Collections

Save Page Now

Capture a web page as it appears now for use as a trusted citation in the future.

Please enter a valid web address

Donate Donate icon An illustration of a heart shape

The Mathematical Olympiad handbook : an introduction to problem solving based on the first 32 British mathematical olympiads 1965-1996

Bookreader item preview, share or embed this item, flag this item for.

Graphic Violence
Explicit Sexual Content
Hate Speech
Misinformation/Disinformation
Marketing/Phishing/Advertising
Misleading/Inaccurate/Missing Metadata

plus-circle Add Review comment Reviews

2,686 Previews

41 Favorites

Better World Books

DOWNLOAD OPTIONS

No suitable files to display here.

EPUB and PDF access not available for this item.

IN COLLECTIONS

Uploaded by station19.cebu on August 8, 2019

Effective problem-solving techniques for Olympiad questions

For students, participating in the olympiads is a matter of great pride and helps them identify their capability and real potential..

The Maths and Science Olympiads held across the world are distinguished competitions that allow brilliant young maths and science enthusiasts to come together and showcase their problem-solving skills.

To excel in these stimulating competitions, students must remember that practice plays a crucial role.(HT Photo)

For students, participating in the Olympiads is a matter of great pride and helps them identify their capability and real potential. Several national and international level Olympiads are run in India by different organisations.

The national level competitions are generally based on class-specific syllabus along with mental ability and logical reasoning sections, but the international level Olympiads where students represent India in different stages also require in-depth knowledge and application-oriented advanced-level preparation. To excel in these stimulating competitions, students must remember that practice plays a crucial role.

Let’s explore the benefits of practice and learn some effective problem-solving strategies that will allow students to efficiently prepare for these Maths and Science Olympiads keeping stress at bay.

Understand the Format

Students often find Olympiad questions challenging because they do not thoroughly understand the format of these questions. It is of prime importance that students familiarise themselves with the different formats and the nature of the difficulty level of Olympiad questions.

This knowledge will help them focus their practice efforts on specific areas and develop a well-rounded skill set. While targeting objective questions, they should carefully consider all options and while answering subjective questions they should focus on writing stepwise solutions.

Review Concepts

Building a strong grip on advanced-level concepts is not an overnight task. It takes persistent efforts and regular practice. In Maths, a strong foundation in the fundamentals of algebra, geometry, and number theory is essential for solving complex equations.

Students should review the fundamental concepts and familiarise themselves with advanced techniques related to equations, inequalities, functions and combinatorics.

In Science, they must review the basics of application-based problems on the syllabus of Physics, Chemistry and Biology ranging from Class 9 to 12 focusing on theoretical, observational and experimental tasks. This will help them confidently deal with advanced-level problems.

Solve Previous Years’ Olympiad Questions

There is nothing more beneficial for Olympiad preparation than Previous Years’ Papers. It opens for students the doors to strategic and effective preparation as per the desired level of Olympiads.

Practicing with previous years’ questions gives students a sense of the types of questions asked and the level of difficulty of these exams. They should solve a variety of questions from different years to expose themselves to various problem-solving techniques and strategies. Moreover, learning from their errors after analysing the solutions will improve their reasoning skills.

Use Logical Reasoning

One thing that Olympiads boost in all students is the power of Logical Reasoning . Mental Ability & Logical Reasoning questions and complex advanced-level questions in Maths and Science often require logical reasoning to visualise patterns and draw conclusions.

Students should pay attention to similar and recurring patterns among questions so that they can make logical deductions based on the given information, thereby applying relevant concepts to eliminate incorrect options. Elimination techniques will help them answer objective questions with more accuracy.

Also Read: Logical Reasoning series: Solving questions on Data Sufficiency

Develop Time Management

Effective time management is crucial for Olympiad preparation. Students should always practice solving problems within a stipulated time to develop speed and accuracy.

They can use a stopwatch or timer to create a simulated exam environment so that they learn how to perform under a restricted timespan. This way they can gradually work on reducing the time it takes to solve each question without compromising accuracy.

Remember, every second is crucial so students should devote time to their strengths first. This will boost their confidence, helping them perform better in the exam.

Practice on Advanced Problem-Solving Techniques

Solving Olympiad questions in the higher stages often requires creative thinking and advanced problem-solving techniques. Students can gradually build their ability to confidently tackle such complex questions with both objective and subjective practice.

Students should remember that objective questions that are asked in Olympiads require a clear understanding of fundamental concepts with utmost accuracy. While, for subjective problems, steps for solving the question are crucial. ‘How you think’ is important to answer subjective mathematical problems and numericals in science.

Seek Guidance from Teachers

When in doubt, reaching out to teachers and mentors keeps the motivation levels running high. Students should always reach out to experienced mentors or teachers who can provide specific guidance and overall mentorship.

They can offer valuable insights, clarify concepts, and help students navigate challenging questions and topics. Rather than ignoring their errors, working on their weaknesses will help students convert those into their strengths. Ultimately, with regular classes and doubt clearance students will be able to achieve the desired results.

Embrace Challenges and Learn from Setbacks

Students should always remember that the journey to the Olympiads will be filled with several challenges. Instead of getting demotivated, they should embrace these challenges as opportunities for growth, learn from the hurdles and use the setbacks as stepping stones towards improvement. It will help them cultivate resilience and push their boundaries to achieve excellence.

Practice, Practice and Practice

Like every other competitive exam , the path to success in Olympiads is also laid down with bricks of recurrent practice. Solving complex problems requires persistent practice and exposure to a variety of problem types.

Students must engage in regular problem-solving sessions, participate in mock Olympiads, and solve Olympiad questions repeatedly. The more they practice, the better they become at identifying problem-solving strategies and applying them effectively.

By following the above discussed strategies, students can enhance their problem-solving skills and excel in the Olympiads. With the three Ps - practice, perseverance, and passion - students can easily conquer the challenges and achieve remarkable success in the Olympiads.

(Authored by Vivek Bhatt, National Academic Director, Foundations, Aakash BYJU’S. Views are personal)

Terms of use
Privacy policy
Weather Today
HT Newsletters
Subscription
Print Ad Rates
Code of Ethics

Elections 2024
DC vs SRH Live Score
India vs England
T20 World Cup 2024 Schedule
IPL 2024 Auctions
T20 World Cup 2024
Cricket Teams
Cricket Players
ICC Rankings
Cricket Schedule
Other Cities
Income Tax Calculator
Budget 2024
Petrol Prices
Diesel Prices
Silver Rate
Relationships
Art and Culture
Taylor Swift: A Primer
Telugu Cinema
Tamil Cinema
Exam Results
Competitive Exams
Board Exams
BBA Colleges
Engineering Colleges
Medical Colleges
BCA Colleges
Medical Exams
Engineering Exams
Horoscope 2024
Festive Calendar 2024
Compatibility Calculator
The Economist Articles
Explainer Video
On The Record
Vikram Chandra Daily Wrap
PBKS vs DC Live Score
KKR vs SRH Live Score
EPL 2023-24
ISL 2023-24
Asian Games 2023
Public Health
Economic Policy
International Affairs
Climate Change
Gender Equality
future tech
Daily Sudoku
Daily Crossword
Daily Word Jumble
HT Friday Finance
Explore Hindustan Times
Privacy Policy
Terms of Use
Subscription - Terms of Use

+91-8368118421
+91-9810336335

Breaking Down 2024 Math Olympiad Problems: Tips for Solving Complex Equations

Introduction: Mathematics Olympiads are renowned for challenging students with complex equations that require deep problem-solving skills. In the 2024 Math Olympiad, participants will encounter a wide range of problems that demand creativity, logical thinking, and a solid understanding of mathematical concepts. In this blog, we will delve into the art of solving complex equations and provide valuable tips to help aspiring Olympians tackle these challenging problems with confidence. Read Also : Unleashing the Power of Vocabulary: How to Excel in English Olympiad

Understand the Problem : Before diving into solving an equation, it is crucial to carefully read and understand the problem statement. Break it down into smaller parts and identify the key information, variables, and constraints. Visualize the problem and formulate a clear objective.
Review Mathematical Concepts : A strong foundation in algebra, calculus, and number theory is essential for solving complex equations. Review the fundamental concepts related to equations, inequalities, functions, and logarithms. Familiarize yourself with advanced techniques such as factoring, completing the square, and manipulating expressions.
Use Logical Reasoning : Complex equations often require logical reasoning to find patterns and make deductions. Look for symmetries, recurring patterns, or relationships between variables. Make logical deductions based on the given information and apply mathematical principles to narrow down the possibilities.
Trial and Error : Experiment with different values and techniques to explore the equation's behavior. Test various approaches and observe the outcomes. While trial and error may not always lead to a direct solution, it can provide valuable insights and guide you towards the right path.
Break Down the Equation : Break down the complex equation into simpler components. Isolate variables, simplify expressions, and identify any hidden relationships. Use algebraic techniques to transform the equation into a more manageable form. Divide the problem into smaller steps and solve each part individually.
Seek Patterns and Symmetries : Patterns and symmetries often emerge in complex equations. Look for repetitions, cycles, or symmetrical structures that can be exploited to simplify the problem. Analyze the behavior of the equation for specific values or scenarios to gain insights into its properties.
Practice, Practice, Practice : Solving complex equations requires practice and exposure to a variety of problem types. Engage in regular problem-solving sessions, participate in mock Olympiads, and solve past Math Olympiad problems. The more you practice, the better you become at identifying problem-solving strategies and applying them effectively.

Conclusion: Mastering the art of solving complex equations is a valuable skill for Math Olympiad participants. By understanding the problem, reviewing mathematical concepts, employing logical reasoning, and breaking down equations into manageable parts, students can enhance their problem-solving abilities. With perseverance, practice, and a strategic approach, tackling the intricate equations of the 2024 Math Olympiad will become a rewarding experience. Embrace the challenge, unleash your mathematical prowess, and excel in the world of Olympiad mathematics! Remember, solving complex equations is not only about finding the correct answer but also about developing a deep understanding of mathematical concepts and honing critical thinking skills that will benefit you beyond the Olympiad journey.

DeepMind AI solves hard geometry problems from mathematics olympiad

AlphaGeometry scores almost as well as the best students on geometry questions from the International Mathematical Olympiad

By Alex Wilkins

17 January 2024

Geometrical problems involve proving facts about angles or lines in complicated shapes

Google DeepMind

An AI from Google DeepMind can solve some International Mathematical Olympiad (IMO) questions on geometry almost as well as the best human contestants.

How does ChatGPT work and do AI-powered chatbots “think” like us?

“The results of AlphaGeometry are stunning and breathtaking,” says Gregor Dolinar, the IMO president. “It seems that AI will win the IMO gold medal much sooner than was thought even a few months ago.”

The IMO, aimed at secondary school students, is one of the most difficult maths competitions in the world. Answering questions correctly requires mathematical creativity that AI systems have long struggled with. GPT-4, for instance, which has shown remarkable reasoning ability in other domains, scores 0 per cent on IMO geometry questions, while even specialised AIs struggle to answer as well as average contestants.

This is partly down to the difficulty of the problems, but it is also because of a lack of training data. The competition has been run annually since 1959, and each edition consists of just six questions. Some of the most successful AI systems, however, require millions or billions of data points. Geometrical problems in particular, which make up one or two of the six questions and involve proving facts about angles or lines in complicated shapes, are particularly difficult to translate to a computer-friendly format.

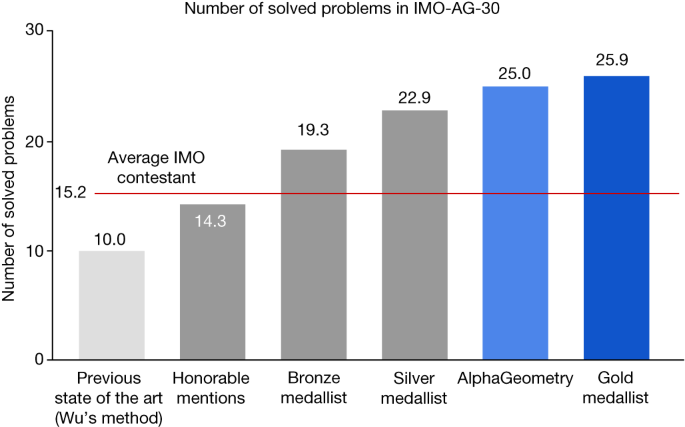
Thang Luong at Google DeepMind and his colleagues have bypassed this problem by creating a tool that can generate hundreds of millions of machine-readable geometrical proofs. When they trained an AI called AlphaGeometry using this data and tested it on 30 IMO geometry questions, it answered 25 of them correctly, compared with an estimated score of 25.9 for an IMO gold medallist based on their scores in the contest.

Sign up to our The Daily newsletter

The latest science news delivered to your inbox, every day.

“Our [current] AI systems are still struggling with the ability to do things like deep reasoning, where we need to plan ahead for many, many steps and also see the big picture, which is why mathematics is such an important benchmark and test set for us on our quest to artificial general intelligence,” Luong told a press conference.

AlphaGeometry consists of two parts, which Luong compares to different thinking systems in the brain: a fast, intuitive system and a slower, more analytical one. The first, intuitive part is a language model, similar to the technology behind ChatGPT, called GPT-f. It has been trained on the millions of generated proofs and suggests which theorems and arguments to try next for a problem. Once it suggests a next step, a slower but more careful “symbolic reasoning” engine uses logical and mathematical rules to fully construct the argument that GPT-f has suggested. The two systems then work in tandem, switching between one another until a problem has been solved.

While this method is remarkably successful at solving IMO geometry problems, the answers it constructs tend to be longer and less “beautiful” than human proofs, says Luong. However, it can also spot things that humans miss. For example, it discovered a better and more general solution to a question from the 2004 IMO than was listed in the official answers.

The future of AI: The 5 possible scenarios, from utopia to extinction

Solving IMO geometry problems in this way is impressive, says Yang-Hui He at the London Institute for Mathematical Sciences, but the system is inherently limited in the mathematics it can use because IMO problems should be solvable using theorems taught below undergraduate level. Expanding the amount of mathematical knowledge AlphaGeometry has access to might improve the system or even help it make new mathematical discoveries, he says.

It would also be interesting to see how AlphaGeometry copes with not knowing what it needs to prove, as mathematical insight can often come from exploring theorems with no set proof, says He. “If you don’t know what your endpoint is, can you find within the set of all [mathematical] paths whether there is a theorem that is actually interesting and new?”

Last year, algorithmic trading company XTX Markets announced a $10 million prize fund for AI maths models, with a $5 million grand prize for the first publicly shared AI model that can win an IMO gold medal, as well as smaller progress prizes for key milestones.

“Solving an IMO geometry problem is one of the planned progress prizes supported by the $10 million AIMO challenge fund,” says Alex Gerko at XTX Markets. “It’s exciting to see progress towards this goal, even before we have announced all the details of this progress prize, which would include making the model and data openly available, as well as solving an actual geometry problem during a live IMO contest.”

DeepMind declined to say whether it plans to enter AlphaGeometry in a live IMO contest or whether it is expanding the system to solve other IMO problems not based on geometry. However, DeepMind has previously entered public competitions for protein folding prediction to test its AlphaFold system .

Journal reference:

Nature DOI: 10.1038/s41586-023-06747-5

mathematics /

Sign up to our weekly newsletter

Receive a weekly dose of discovery in your inbox! We'll also keep you up to date with New Scientist events and special offers.

More from New Scientist

Explore the latest news, articles and features

DeepMind AI with built-in fact-checker makes mathematical discoveries

Crystal-hunting deepmind ai could help discover new wonder materials, game-playing deepmind ai can beat top humans at chess, go and poker, deepmind ai can beat the best weather forecasts - but there is a catch, popular articles.

Solving olympiad geometry without human demonstrations

Trieu H. Trinh ORCID: orcid.org/0000-0003-3597-6073 1 , 2 ,
Yuhuai Wu 1 ,
Quoc V. Le 1 ,
He He 2 &
Thang Luong 1

Nature volume 625 , pages 476–482 ( 2024 ) Cite this article

219k Accesses

8 Citations

966 Altmetric

Metrics details

Computational science
Computer science

An Author Correction to this article was published on 23 February 2024

This article has been updated

Proving mathematical theorems at the olympiad level represents a notable milestone in human-level automated reasoning 1 , 2 , 3 , 4 , owing to their reputed difficulty among the world’s best talents in pre-university mathematics. Current machine-learning approaches, however, are not applicable to most mathematical domains owing to the high cost of translating human proofs into machine-verifiable format. The problem is even worse for geometry because of its unique translation challenges 1 , 5 , resulting in severe scarcity of training data. We propose AlphaGeometry, a theorem prover for Euclidean plane geometry that sidesteps the need for human demonstrations by synthesizing millions of theorems and proofs across different levels of complexity. AlphaGeometry is a neuro-symbolic system that uses a neural language model, trained from scratch on our large-scale synthetic data, to guide a symbolic deduction engine through infinite branching points in challenging problems. On a test set of 30 latest olympiad-level problems, AlphaGeometry solves 25, outperforming the previous best method that only solves ten problems and approaching the performance of an average International Mathematical Olympiad (IMO) gold medallist. Notably, AlphaGeometry produces human-readable proofs, solves all geometry problems in the IMO 2000 and 2015 under human expert evaluation and discovers a generalized version of a translated IMO theorem in 2004.

Advancing mathematics by guiding human intuition with AI

Alex Davies, Petar Veličković, … Pushmeet Kohli

Solving the Rubik’s cube with deep reinforcement learning and search

Forest Agostinelli, Stephen McAleer, … Pierre Baldi

Rigor with machine learning from field theory to the Poincaré conjecture

Sergei Gukov, James Halverson & Fabian Ruehle

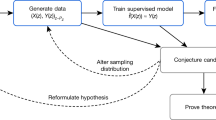
Proving theorems showcases the mastery of logical reasoning and the ability to search through an infinitely large space of actions towards a target, signifying a remarkable problem-solving skill. Since the 1950s (refs. 6 , 7 ), the pursuit of better theorem-proving capabilities has been a constant focus of artificial intelligence (AI) research 8 . Mathematical olympiads are the most reputed theorem-proving competitions in the world, with a similarly long history dating back to 1959, playing an instrumental role in identifying exceptional talents in problem solving. Matching top human performances at the olympiad level has become a notable milestone of AI research 2 , 3 , 4 .

Theorem proving is difficult for learning-based methods because training data of human proofs translated into machine-verifiable languages are scarce in most mathematical domains. Geometry stands out among other olympiad domains because it has very few proof examples in general-purpose mathematical languages such as Lean 9 owing to translation difficulties unique to geometry 1 , 5 . Geometry-specific languages, on the other hand, are narrowly defined and thus unable to express many human proofs that use tools beyond the scope of geometry, such as complex numbers (Extended Data Figs. 3 and 4 ). Overall, this creates a data bottleneck, causing geometry to lag behind in recent progress that uses human demonstrations 2 , 3 , 4 . Current approaches to geometry, therefore, still primarily rely on symbolic methods and human-designed, hard-coded search heuristics 10 , 11 , 12 , 13 , 14 .

We present an alternative method for theorem proving using synthetic data, thus sidestepping the need for translating human-provided proof examples. We focus on Euclidean plane geometry and exclude topics such as geometric inequalities and combinatorial geometry. By using existing symbolic engines on a diverse set of random theorem premises, we extracted 100 million synthetic theorems and their proofs, many with more than 200 proof steps, four times longer than the average proof length of olympiad theorems. We further define and use the concept of dependency difference in synthetic proof generation, allowing our method to produce nearly 10 million synthetic proof steps that construct auxiliary points, reaching beyond the scope of pure symbolic deduction. Auxiliary construction is geometry’s instance of exogenous term generation, representing the infinite branching factor of theorem proving, and widely recognized in other mathematical domains as the key challenge to proving many hard theorems 1 , 2 . Our work therefore demonstrates a successful case of generating synthetic data and learning to solve this key challenge. With this solution, we present a general guiding framework and discuss its applicability to other domains in Methods section ‘AlphaGeometry framework and applicability to other domains’.

We pretrain a language model on all generated synthetic data and fine-tune it to focus on auxiliary construction during proof search, delegating all deduction proof steps to specialized symbolic engines. This follows standard settings in the literature, in which language models such as GPT-f (ref. 15 ), after being trained on human proof examples, can generate exogenous proof terms as inputs to fast and accurate symbolic engines such as nlinarith or ring 2 , 3 , 16 , using the best of both worlds. Our geometry theorem prover AlphaGeometry, illustrated in Fig. 1 , produces human-readable proofs, substantially outperforms the previous state-of-the-art geometry-theorem-proving computer program and approaches the performance of an average IMO gold medallist on a test set of 30 classical geometry problems translated from the IMO as shown in Fig. 2 .

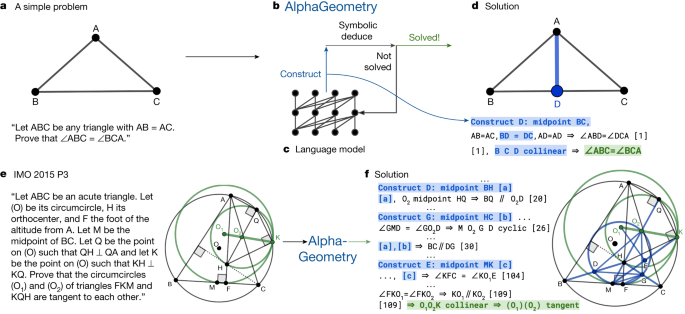
The top row shows how AlphaGeometry solves a simple problem. a , The simple example and its diagram. b , AlphaGeometry initiates the proof search by running the symbolic deduction engine. The engine exhaustively deduces new statements from the theorem premises until the theorem is proven or new statements are exhausted. c , Because the symbolic engine fails to find a proof, the language model constructs one auxiliary point, growing the proof state before the symbolic engine retries. The loop continues until a solution is found. d , For the simple example, the loop terminates after the first auxiliary construction “D as the midpoint of BC”. The proof consists of two other steps, both of which make use of the midpoint properties: “BD = DC” and “B, D, C are collinear”, highlighted in blue. The bottom row shows how AlphaGeometry solves the IMO 2015 Problem 3 (IMO 2015 P3). e , The IMO 2015 P3 problem statement and diagram. f , The solution of IMO 2015 P3 has three auxiliary points. In both solutions, we arrange language model outputs (blue) interleaved with symbolic engine outputs to reflect their execution order. Note that the proof for IMO 2015 P3 in f is greatly shortened and edited for illustration purposes. Its full version is in the Supplementary Information .

The test benchmark includes official IMO problems from 2000 to the present that can be represented in the geometry environment used in our work. Human performance is estimated by rescaling their IMO contest scores between 0 and 7 to between 0 and 1, to match the binary outcome of failure/success of the machines. For example, a contestant’s score of 4 out of 7 will be scaled to 0.57 problems in this comparison. On the other hand, the score for AlphaGeometry and other machine solvers on any problem is either 0 (not solved) or 1 (solved). Note that this is only an approximate comparison with humans on classical geometry, who operate on natural-language statements rather than narrow, domain-specific translations. Further, the general IMO contest also includes other types of problem, such as geometric inequality or combinatorial geometry, and other domains of mathematics, such as algebra, number theory and combinatorics.

Source Data

Synthetic theorems and proofs generation

Our method for generating synthetic data is shown in Fig. 3 . We first sample a random set of theorem premises, serving as the input to the symbolic deduction engine to generate its derivations. A full list of actions used for this sampling can be found in Extended Data Table 1 . In our work, we sampled nearly 1 billion of such premises in a highly parallelized setting, described in Methods . Note that we do not make use of any existing theorem premises from human-designed problem sets and sampled the eligible constructions uniformly randomly.

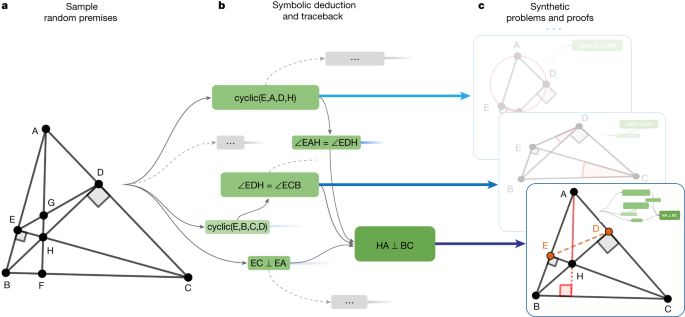
a , We first sample a large set of random theorem premises. b , We use the symbolic deduction engine to obtain a deduction closure. This returns a directed acyclic graph of statements. For each node in the graph, we perform traceback to find its minimal set of necessary premise and dependency deductions. For example, for the rightmost node ‘HA ⊥ BC’, traceback returns the green subgraph. c , The minimal premise and the corresponding subgraph constitute a synthetic problem and its solution. In the bottom example, points E and D took part in the proof despite being irrelevant to the construction of HA and BC; therefore, they are learned by the language model as auxiliary constructions.

Next we use a symbolic deduction engine on the sampled premises. The engine quickly deduces new true statements by following forward inference rules as shown in Fig. 3b . This returns a directed acyclic graph of all reachable conclusions. Each node in the directed acyclic graph is a reachable conclusion, with edges connecting to its parent nodes thanks to the traceback algorithm described in Methods . This allows a traceback process to run recursively starting from any node N , at the end returning its dependency subgraph G ( N ), with its root being N and its leaves being a subset of the sampled premises. Denoting this subset as P , we obtained a synthetic training example (premises, conclusion, proof) = ( P , N , G ( N )).

In geometry, the symbolic deduction engine is deductive database (refs. 10 , 17 ), with the ability to efficiently deduce new statements from the premises by means of geometric rules. DD follows deduction rules in the form of definite Horn clauses, that is, Q ( x ) ← P 1 ( x ),…, P k ( x ), in which x are points objects, whereas P 1 ,…, P k and Q are predicates such as ‘equal segments’ or ‘collinear’. A full list of deduction rules can be found in ref. 10 . To widen the scope of the generated synthetic theorems and proofs, we also introduce another component to the symbolic engine that can deduce new statements through algebraic rules (AR), as described in Methods . AR is necessary to perform angle, ratio and distance chasing, as often required in many olympiad-level proofs. We included concrete examples of AR in Extended Data Table 2 . The combination DD + AR, which includes both their forward deduction and traceback algorithms, is a new contribution in our work and represents a new state of the art in symbolic reasoning in geometry.

Generating proofs beyond symbolic deduction

So far, the generated proofs consist purely of deduction steps that are already reachable by the highly efficient symbolic deduction engine DD + AR. To solve olympiad-level problems, however, the key missing piece is generating new proof terms. In the above algorithm, it can be seen that such terms form the subset of P that N is independent of. In other words, these terms are the dependency difference between the conclusion statement and the conclusion objects. We move this difference from P to the proof so that a generative model that learns to generate the proof can learn to construct them, as illustrated in Fig. 3c . Such proof steps perform auxiliary constructions that symbolic deduction engines are not designed to do. In the general theorem-proving context, auxiliary construction is an instance of exogenous term generation, a notable challenge to all proof-search algorithms because it introduces infinite branching points to the search tree. In geometry theorem proving, auxiliary constructions are the longest-standing subject of study since inception of the field in 1959 (refs. 6 , 7 ). Previous methods to generate them are based on hand-crafted templates and domain-specific heuristics 8 , 9 , 10 , 11 , 12 , and are, therefore, limited by a subset of human experiences expressible in hard-coded rules. Any neural solver trained on our synthetic data, on the other hand, learns to perform auxiliary constructions from scratch without human demonstrations.

Training a language model on synthetic data

The transformer 18 language model is a powerful deep neural network that learns to generate text sequences through next-token prediction, powering substantial advances in generative AI technology. We serialize ( P , N , G ( N )) into a text string with the structure ‘<premises><conclusion><proof>’. By training on such sequences of symbols, a language model effectively learns to generate the proof, conditioning on theorem premises and conclusion.

Combining language modelling and symbolic engines

On a high level, proof search is a loop in which the language model and the symbolic deduction engine take turns to run, as shown in Fig. 1b,c . Proof search terminates whenever the theorem conclusion is found or when the loop reaches a maximum number of iterations. The language model is seeded with the problem statement string and generates one extra sentence at each turn, conditioning on the problem statement and past constructions, describing one new auxiliary construction such as “construct point X so that ABCX is a parallelogram”. Each time the language model generates one such construction, the symbolic engine is provided with new inputs to work with and, therefore, its deduction closure expands, potentially reaching the conclusion. We use beam search to explore the top k constructions generated by the language model and describe the parallelization of this proof-search algorithm in Methods .

Empirical evaluation

An olympiad-level benchmark for geometry.

Existing benchmarks of olympiad mathematics do not cover geometry because of a focus on formal mathematics in general-purpose languages 1 , 9 , whose formulation poses great challenges to representing geometry. Solving these challenges requires deep expertise and large research investment that are outside the scope of our work, which focuses on a methodology for theorem proving. For this reason, we adapted geometry problems from the IMO competitions since 2000 to a narrower, specialized environment for classical geometry used in interactive graphical proof assistants 13 , 17 , 19 , as discussed in Methods . Among all non-combinatorial geometry-related problems, 75% can be represented, resulting in a test set of 30 classical geometry problems. Geometric inequality and combinatorial geometry, for example, cannot be translated, as their formulation is markedly different to classical geometry. We include the full list of statements and translations for all 30 problems in the Supplementary Information . The final test set is named IMO-AG-30, highlighting its source, method of translation and its current size.

Geometry theorem prover baselines

Geometry theorem provers in the literature fall into two categories. The first category is computer algebra methods, which treats geometry statements as polynomial equations of its point coordinates. Proving is accomplished with specialized transformations of large polynomials. Gröbner bases 20 and Wu’s method 21 are representative approaches in this category, with theoretical guarantees to successfully decide the truth value of all geometry theorems in IMO-AG-30, albeit without a human-readable proof. Because these methods often have large time and memory complexity, especially when processing IMO-sized problems, we report their result by assigning success to any problem that can be decided within 48 h using one of their existing implementations 17 .

AlphaGeometry belongs to the second category of solvers, often described as search/axiomatic or sometime s ‘synthetic’ methods. These methods treat the problem of theorem proving as a step-by-step search problem using a set of geometry axioms. Thanks to this, they typically return highly interpretable proofs accessible to human readers. Baselines in this category generally include symbolic engines equipped with human-designed heuristics. For example, Chou et al. provided 18 heuristics such as “If OA ⊥ OB and OA = OB, construct C on the opposite ray of OA such that OC = OA ” , besides 75 deduction rules for the symbolic engine. Large language models 22 , 23 , 24 such as GPT-4 (ref. 25 ) can be considered to be in this category. Large language models have demonstrated remarkable reasoning ability on a variety of reasoning tasks 26 , 27 , 28 , 29 . When producing full natural-language proofs on IMO-AG-30, however, GPT-4 has a success rate of 0%, often making syntactic and semantic errors throughout its outputs, showing little understanding of geometry knowledge and of the problem statements itself. Note that the performance of GPT-4 performance on IMO problems can also be contaminated by public solutions in its training data. A better GPT-4 performance is therefore still not comparable with other solvers. In general, search methods have no theoretical guarantee in their proving performance and are known to be weaker than computer algebra methods 13 .

Synthetic data generation rediscovers known theorems and beyond

We find that our synthetic data generation can rediscover some fairly complex theorems and lemmas known to the geometry literature, as shown in Fig. 4 , despite starting from randomly sampled theorem premises. This can be attributed to the use of composite actions described in Extended Data Table 1 , such as ‘taking centroid’ or ‘taking excentre’, which—by chance—sampled a superset of well-known theorem premises, under our large-scale exploration setting described in Methods . To study the complexity of synthetic proofs, Fig. 4 shows a histogram of synthetic proof lengths juxtaposed with proof lengths found on the test set of olympiad problems. Although the synthetic proof lengths are skewed towards shorter proofs, a small number of them still have lengths up to 30% longer than the hardest problem in the IMO test set. We find that synthetic theorems found by this process are not constrained by human aesthetic biases such as being symmetrical, therefore covering a wider set of scenarios known to Euclidean geometry. We performed deduplication as described in Methods , resulting in more than 100 millions unique theorems and proofs, and did not find any IMO-AG-30 theorems, showing that the space of possible geometry theorems is still much larger than our discovered set.

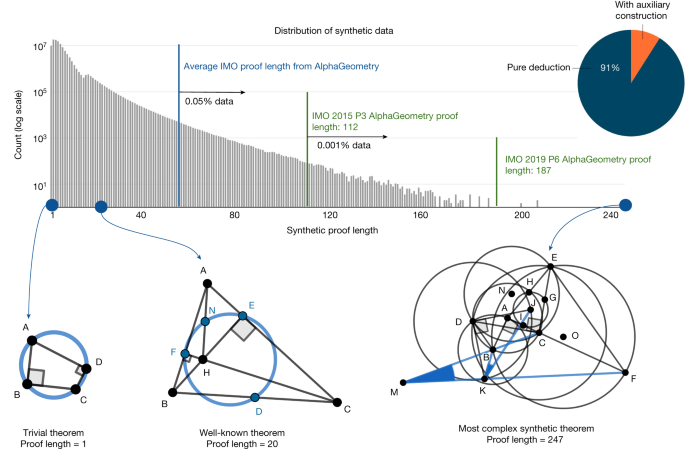
Of the generated synthetic proofs, 9% are with auxiliary constructions. Only roughly 0.05% of the synthetic training proofs are longer than the average AlphaGeometry proof for the test-set problems. The most complex synthetic proof has an impressive length of 247 with two auxiliary constructions. Most synthetic theorem premises tend not to be symmetrical like human-discovered theorems, as they are not biased towards any aesthetic standard.

Language model pretraining and fine-tuning

We first pretrained the language model on all 100 million synthetically generated proofs, including ones of pure symbolic deduction. We then fine-tuned the language model on the subset of proofs that requires auxiliary constructions, accounting for roughly 9% of the total pretraining data, that is, 9 million proofs, to better focus on its assigned task during proof search.

Proving results on IMO-AG-30

The performance of ten different solvers on the IMO-AG-30 benchmark is reported in Table 1 , of which eight, including AlphaGeometry, are search-based methods. Besides prompting GPT-4 to produce full proofs in natural language with several rounds of reflections and revisions, we also combine GPT-4 with DD + AR as another baseline to enhance its deduction accuracy. To achieve this, we use detailed instructions and few-shot examples in the prompt to help GPT-4 successfully interface with DD + AR, providing auxiliary constructions in the correct grammar. Prompting details of baselines involving GPT-4 is included in the Supplementary Information .

AlphaGeometry achieves the best result, with 25 problems solved in total. The previous state of the art (Wu’s method) solved ten problems, whereas the strongest baseline (DD + AR + human-designed heuristics) solved 18 problems, making use of the algebraic reasoning engine developed in this work and the human heuristics designed by Chou et al. 17 . To match the test time compute of AlphaGeometry, this strongest baseline makes use of 250 parallel workers running for 1.5 h, each attempting different sets of auxiliary constructions suggested by human-designed heuristics in parallel, until success or timeout. Other baselines such as Wu’s method or the full-angle method are not affected by parallel compute resources as they carry out fixed, step-by-step algorithms until termination.

Measuring the improvements made on top of the base symbolic deduction engine (DD), we found that incorporating algebraic deduction added seven solved problems to a total of 14 (DD + AR), whereas the language model’s auxiliary construction remarkably added another 11 solved problems, resulting in a total of 25. As reported in Extended Data Fig. 6 , we find that, using only 20% of the training data, AlphaGeometry still achieves state-of-the-art results with 21 problems solved. Similarly, using less than 2% of the search budget (beam size of 8 versus 512) during test time, AlphaGeometry can still solve 21 problems. On a larger and more diverse test set of 231 geometry problems, which covers textbook exercises, regional olympiads and famous theorems, we find that baselines in Table 1 remain at the same performance rankings, with AlphaGeometry solving almost all problems (98.7%), whereas Wu’s method solved 75% and DD + AR + human-designed heuristics solved 92.2%, as reported in Extended Data Fig. 6b .

Notably, AlphaGeometry solved both geometry problems of the same year in 2000 and 2015, a threshold widely considered difficult to the average human contestant at the IMO. Further, the traceback process of AlphaGeometry found an unused premise in the translated IMO 2004 P1, as shown in Fig. 5 , therefore discovering a more general version of the translated IMO theorem itself. We included AlphaGeometry solutions to all problems in IMO-AG-30 in the Supplementary Information and manually analysed some notable AlphaGeometry solutions and failures in Extended Data Figs. 2 – 5 . Overall, we find that AlphaGeometry operates with a much lower-level toolkit for proving than humans do, limiting the coverage of the synthetic data, test-time performance and proof readability.

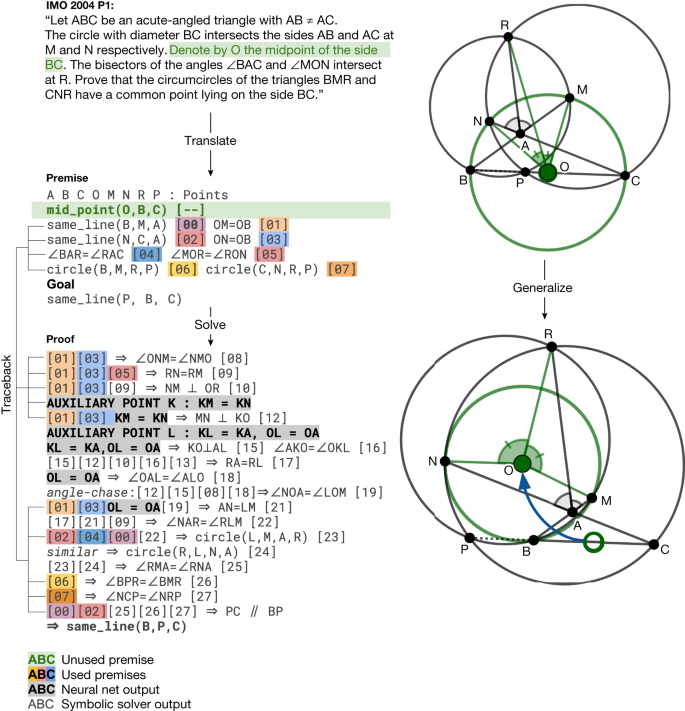
Left, top to bottom, the IMO 2004 P1 stated in natural language, its translated statement and AlphaGeometry solution. Thanks to the traceback algorithm necessary to extract the minimal premises, AlphaGeometry identifies a premise unnecessary for the proof to work: O does not have to be the midpoint of BC for P, B, C to be collinear. Right, top, the original theorem diagram; bottom, the generalized theorem diagram, in which O is freed from its midpoint position and P still stays on line BC. Note that the original problem requires P to be between B and C, a condition where the generalized theorem and solution does not guarantee.

Human expert evaluation of AlphaGeometry outputs

Because AlphaGeometry outputs highly interpretable proofs, we used a simple template to automatically translate its solutions to natural language. To obtain an expert evaluation in 2000 and 2015, during which AlphaGeometry solves all geometry problems and potentially passes the medal threshold, we submit these solutions to the USA IMO team coach, who is experienced in grading mathematical olympiads and has authored books for olympiad geometry training. AlphaGeometry solutions are recommended to receive full scores, thus passing the medal threshold of 14/42 in the corresponding years. We note that IMO tests also evaluate humans under three other mathematical domains besides geometry and under human-centric constraints, such as no calculator use or 4.5-h time limits. We study time-constrained settings with 4.5-h and 1.5-h limits for AlphaGeometry in Methods and report the results in Extended Data Fig. 1 .

Learning to predict the symbolic engine’s output improves the language model’s auxiliary construction

In principle, auxiliary construction strategies must depend on the details of the specific deduction engine they work with during proof search. We find that a language model without pretraining only solves 21 problems. This suggests that pretraining on pure deduction proofs generated by the symbolic engine DD + AR improves the success rate of auxiliary constructions. On the other hand, a language model without fine-tuning also degrades the performance but not as severely, with 23 problems solved compared with AlphaGeometry’s full setting at 25.

Hard problems are reflected in AlphaGeometry proof length

Figure 6 measures the difficulty of solved problems using public scores of human contestants at the IMO and plots them against the corresponding AlphaGeometry proof lengths. The result shows that, for the three problems with the lowest human score, AlphaGeometry also requires exceptionally long proofs and the help of language-model constructions to reach its solution. For easier problems (average human score > 3.5), however, we observe no correlation ( p = −0.06) between the average human score and AlphaGeometry proof length.

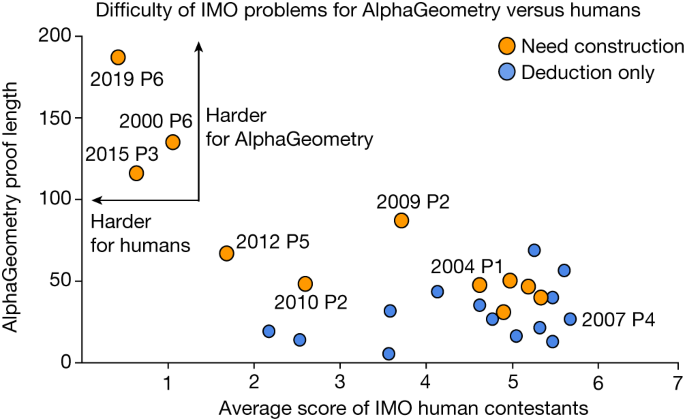
Among the solved problems, 2000 P6, 2015 P3 and 2019 P6 are the hardest for IMO participants. They also require the longest proofs from AlphaGeometry. For easier problems, however, there is little correlation between AlphaGeometry proof length and human score.

AlphaGeometry is the first computer program to surpass the performance of the average IMO contestant in proving Euclidean plane geometry theorems, outperforming strong computer algebra and search baselines. Notably, we demonstrated through AlphaGeometry a neuro-symbolic approach for theorem proving by means of large-scale exploration from scratch, sidestepping the need for human-annotated proof examples and human-curated problem statements. Our method to generate and train language models on purely synthetic data provides a general guiding framework for mathematical domains that are facing the same data-scarcity problem.

Geometry representation

General-purpose formal languages such as Lean 31 still require a large amount of groundwork to describe most IMO geometry problems at present. We do not directly address this challenge as it requires deep expertise and substantial research outside the scope of theorem-proving methodologies. To sidestep this barrier, we instead adopted a more specialized language used in GEX 10 , JGEX 17 , MMP/Geometer 13 and GeoLogic 19 , a line of work that aims to provide a logical and graphical environment for synthetic geometry theorems with human-like non-degeneracy and topological assumptions. Examples of this language are shown in Fig. 1d,f . Owing to its narrow formulation, 75% of all IMO geometry problems can be adapted to this representation. In this type of geometry environment, each proof step is logically and numerically verified and can also be evaluated by a human reader as if it is written by IMO contestants, thanks to the highly natural grammar of the language. To cover more expressive algebraic and arithmetic reasoning, we also add integers, fractions and geometric constants to the vocabulary of this language. We do not push further for a complete solution to geometry representation as it is a separate and extremely challenging research topic that demands substantial investment from the mathematical formalization community.

Sampling consistent theorem premises

We developed a constructive diagram builder language similar to that used by JGEX 17 to construct one object in the premise at a time, instead of freely sampling many premises that involve several objects, therefore avoiding the generation of a self-contradicting set of premises. An exhaustive list of construction actions is shown in Extended Data Table 1 . These actions include constructions to create new points that are related to others in a certain way, that is, collinear, incentre/excentre etc., as well as constructions that take a number as its parameter, for example, “construct point X such that given a number α , ∠ ABX = α ”. One can extend this list with more sophisticated actions to describe a more expressive set of geometric scenarios, improving both the synthetic data diversity and the test-set coverage. A more general and expressive diagram builder language can be found in ref. 32 . We make use of a simpler language that is sufficient to describe problems in IMO-AG-30 and can work well with the symbolic engine DD.

The symbolic deduction engine

The core functionality of the engine is deducing new true statements given the theorem premises. Deduction can be performed by means of geometric rules such as ‘If X then Y’, in which X and Y are sets of geometric statements such as ‘A, B, C are collinear’. We use the method of structured DD 10 , 17 for this purpose as it can find the deduction closure in just seconds on standard non-accelerator hardware. To further enhance deduction, we also built into AlphaGeometry the ability to perform deduction through AR. AR enable proof steps that perform angle/ratio/distance chasing. Detailed examples of AR are shown in Extended Data Table 2 . Such proof steps are ubiquitous in geometry proofs, yet not covered by geometric rules. We expand the Gaussian elimination process implemented in GeoLogic 19 to find the deduction closure for all possible linear operators in just seconds. Our symbolic deduction engine is an intricate integration of DD and AR, which we apply alternately to expand the joint closure of known true statements until expansion halts. This process typically finishes within a few seconds to at most a few minutes on standard non-accelerator hardware.

Algebraic reasoning

There has not been a complete treatment for algebraic deduction in the literature of geometry theorem proving. For example, in iGeoTutor 12 , Z3 (ref. 33 ) is used to handle arithmetic inferences but algebraic manipulations are not covered. DD (ref. 17 ) handles algebraic deductions by expressing them under a few limited deduction rules, therefore, it is unable to express more complex manipulations, leaving arithmetic inferences not covered. The most general treatment so far is a process similar that in ref. 34 for angle-only theorem discovery and implemented in GeoLogic 19 for both angle and ratios. We expanded this formulation to cover all reasoning about angles, ratios and distances between points and also arithmetic reasoning with geometric constants such as ‘pi’ or ‘1:2’. Concrete examples of algebraic reasoning are given in Extended Data Table 2 .

On a high level, we first convert the input linear equations to a matrix of their coefficients. In particular, we create a coefficient matrix A ∈ R M × N in which N is the number of variables and M is the number of input equations. In geometry, any equality is of the form a − b = c − d ⇔ a − b − c + d = 0. For example, the angle equality ∠ ABC = ∠ XYZ is represented as s (AB) − s (BC) = s (XY) − s (YZ), in which s (AB) is the angle between AB and the x-direction, modulo pi. Similarly, ratios AB:CD = EF:GH are represented as log(AB) − log(CD) = log(EF) − log(GH), in which log(AB) is the log of the length of segment AB. For distances, each variable is a (point, line) pair, representing a specific point on a specific line.

Because all equalities are of the form ‘ a − b − c + d = 0’, we populate the row for each equality with values +1, −1, −1, +1 at columns corresponding to variables a , b , c and d . Running Gaussian elimination on A returns a new matrix with leading 1s at each of the columns, essentially representing each variable as a unique linear combination of all remaining variables. As an example, suppose we have ‘ a − b = b − c ’, ‘ d − c = a − d ’ and ‘ b − c = c − e ’ as input equalities, running the Gaussian elimination process (denoted GE in the following equation) returns the following result:

From this result, we can deterministically and exhaustively deduce all new equalities by checking if x 1 = x 2 or x 1 − x 2 = x 2 − x 3 or x 1 − x 2 = x 3 − x 4 , in which { x 1 , x 2 , x 3 , x 4 } is any 4-permutation of all variables. In the above Gaussian Elimination, for example, AR deduced that b = d from the three input equalities. To handle geometric constants such as ‘0.5 pi’ or ‘5:12’, we included ‘pi’ and ‘1’ as default variables to all coefficient matrices.

Deductive database implementation

Unlike the original implementation of DD, we use a graph data structure to capture the symmetries of geometry, rather than using strings of canonical forms. With a graph data structure, we captured not only the symmetrical permutations of function arguments but also the transitivity of equality, collinearity and concyclicity. This graph data structure bakes into itself some deduction rules explicitly stated in the geometric rule list used in DD. These deduction rules from the original list are therefore not used anywhere in exploration but implicitly used and explicitly spelled out on-demand when the final proof is serialized into text.

Traceback to find minimal proofs

Each deduction step needs to be coupled with a traceback algorithm, which returns the minimal set of immediate ancestor statements that is necessary to deduce the conclusion statement of the step. This is the core building block for extracting proof graphs and minimal premises described in the main text. A minimal-premise-extraction algorithm is necessary to avoid superfluous auxiliary constructions that contribute to the proof through unnecessary transitivity. For example, ‘ a = b ’ and ‘ b = c ’ might not be necessary if ‘ a = c ’ can be obtained directly through other reasoning chains.

Traceback for geometric-rule deduction

To do this, we record the equality transitivity graph. For example, if ‘ a = b ’, ‘ b = c ’, ‘ c = d ’ and ‘ a = d ’ are deduced, which results in nodes a , b , c and d being connected to the same ‘equality node’ e , we maintain a graph within e that has edges [( a , b ), ( b , c ), ( c , d ), ( a , d )]. This allows the traceback algorithm to perform a breadth-first search to find the shortest path of transitivity of equality between any pair of variables among a , b , c and d . For collinearity and concyclicity, however, the representation is more complex. In these cases, hypergraphs G ( V , E ) with 3-edges or 4-edges are used as the equality transitivity graph. The traceback is now equivalent to finding a minimum spanning tree (denoted MST in the following equation) for the target set S of nodes (three collinear nodes or four concyclic nodes) whose weight is the cardinality of the union of its hyperedges e ′:

Such optimization is NP-hard, as it is a reduction from the decision version of vertex cover. We simply use a greedy algorithm in this case to find a best-effort minimum spanning tree.

Traceback for algebraic deduction

Traceback through Gaussian elimination can be done by recognizing that it is equivalent to a mixed integer linear programming problem. Given the coefficient matrix of input equations A constructed as described in the previous sections and a target equation with coefficients vector b ∈ R N , we determine the minimal set of premises for b by defining non-negative integer decision vectors x , y ∈ Z M and solve the following mixed-integer linear programming problem:

The minimum set of immediate parent nodes for the equality represented by b will be the i th equations ( i th rows in A ) whose corresponding decision value ( x i − y i ) is non-zero.

Integrating DD and AR

DD and AR are applied alternately to expand their joint deduction closure. The output of DD, which consists of new statements deduced with deductive rules, is fed into AR and vice versa. For example, if DD deduced ‘AB is parallel to CD’, the slopes of lines AB and CD will be updated to be equal variables in AR’s coefficient matrix A , defined in the ‘Algebraic reasoning’ section. Namely, a new row will be added to A with ‘1’ at the column corresponding to the variable slope(AB) and ‘−1’ at the column of slope(CD). Gaussian elimination and mixed-integer linear programming is run again as AR executes, producing new equalities as inputs to the next iteration of DD. This loop repeats until the joint deduction closure stops expanding. Both DD and AR are deterministic processes that only depend on the theorem premises, therefore they do not require any design choices in their implementation.

Proof pruning

Although the set of immediate ancestors to any node is minimal, this does not guarantee that the fully traced back dependency subgraph G ( N ) and the necessary premise P are minimal. Here we define minimality to be the property that G ( N ) and P cannot be further pruned without losing conclusion reachability. Without minimality, we obtained many synthetic proofs with vacuous auxiliary constructions, having shallow relation to the actual proof and can be entirely discarded. To solve this, we perform exhaustive trial and error, discarding each subset of the auxiliary points and rerunning DD + AR on the smaller subset of premises to verify goal reachability. At the end, we return the minimum proof obtainable across all trials. This proof-pruning procedure is done both during synthetic data generation and after each successful proof search during test time.

Parallelized data generation and deduplication

We run our synthetic-data-generation process on a large number of parallel CPU workers, each seeded with a different random seed to reduce duplications. After running this process on 100,000 CPU workers for 72 h, we obtained roughly 500 million synthetic proof examples. We reformat the proof statements to their canonical form (for example, sorting arguments of individual terms and sorting terms within the same proof step, etc.) to avoid shallow deduplication against itself and against the test set. At the end, we obtain 100 million unique theorem–proof examples. A total of 9 million examples involves at least one auxiliary construction. We find no IMO-AG-30 problems in the synthetic data. On the set of geometry problems collected in JGEX 17 , which consists mainly of problems with moderate difficulty and well-known theorems, we find nearly 20 problems in the synthetic data. This suggests that the training data covered a fair amount of common knowledge in geometry, but the space of more sophisticated theorems is still much larger.

Language model architecture and training

We use the Meliad library 35 for transformer training with its base settings. The transformer has 12 layers, embedding dimension of 1,024, eight heads of attention and an inter-attention dense layer of dimension 4,096 with ReLU activation. Overall, the transformer has 151 million parameters, excluding embedding layers at its input and output heads. Our customized tokenizer is trained with ‘word’ mode using SentencePiece 36 and has a vocabulary size of 757. We limit the maximum context length to 1,024 tokens and use T5-style relative position embedding 37 . Sequence packing 38 , 39 is also used because more than 90% of our sequences are under 200 in length. During training, a dropout 40 rate of 5% is applied pre-attention and post-dense. A 4 × 4 slice of TPUv3 (ref. 41 ) is used as its hardware accelerator. For pretraining, we train the transformer with a batch size of 16 per core and a cosine learning-rate schedule that decays from 0.01 to 0.001 in 10,000,000 steps. For fine-tuning, we maintain the final learning rate of 0.001 for another 1,000,000 steps. For the set-up with no pretraining, we decay the learning rate from 0.01 to 0.001 in 1,000,000 steps. We do not perform any hyperparameter tuning. These hyperparameter values are either selected to be a large round number (training steps) or are provided by default in the Meliad codebase.

Parallelized proof search

Because the language model decoding process returns k different sequences describing k alternative auxiliary constructions, we perform a beam search over these k options, using the score of each beam as its value function. This set-up is highly parallelizable across beams, allowing substantial speed-up when there are parallel computational resources. In our experiments, we use a beam size of k = 512, the maximum number of iterations is 16 and the branching factor for each node, that is, the decoding batch size, is 32. This is the maximum inference-time batch size that can fit in the memory of a GPU V100 for our transformer size. Scaling up these factors to examine a larger fraction of the search space might improve AlphaGeometry results even further.

For each problem, we used a pool of four GPU workers, each hosting a copy of the transformer language model to divide the work between alternative beams, and a pool of 10,000 CPU workers to host the symbolic solvers, shared across all beams across all 30 problems. This way, a problem that terminates early can contribute its share of computing power to longer-running problems. We record the running time of the symbolic solver on each individual problem, which—by design—stays roughly constant across all beams. We use this and the language model decoding speed to infer the necessary parallelism needed for each problem, in isolation, to stay under different time limits at the IMO in Extended Data Fig. 1 .

The effect of data and search

We trained AlphaGeometry on smaller fractions of the original training data (20%, 40%, 60% and 80%) and found that, even at 20% of training data, AlphaGeometry still solves 21 problems, more than the strongest baseline (DD + AR + human-designed heuristics) with 18 problems solved, as shown in Extended Data Fig. 6a . To study the effect of beam search on top of the language model, we reduced the beam size and search depth separately during proof search and reported the results in Extended Data Fig. 6c,d . We find that, with a beam size of 8, that is, a 64 times reduction from the original beam size of 512, AlphaGeometry still solves 21 problems. A similar result of 21 problems can be obtained by reducing the search depth from 16 to only two, while keeping the beam size constant at 512.

Evaluation on a larger test set

We evaluated AlphaGeometry and other baselines on a larger test set of 231 geometry problems, curated in ref. 17 . This set covers a wider range of sources outside IMO competitions: textbook examples and exercises, regional olympiads and famous geometry theorems; some are even more complex than typical IMO problems, such as the five circles theorem, Morley’s theorem or Sawayama and Thébault’s theorem. The results are reported in Extended Data Fig. 6b . The overall rankings of different approaches remained the same as in Table 1 , with AlphaGeometry solving almost all problems (98.7%). The strongest baseline DD + AR + human-designed heuristics solves 92.2%, whereas the previous state of the art solves 75%.

AlphaGeometry framework and applicability to other domains

The strength of AlphaGeometry’s neuro-symbolic set-up lies in its ability to generate auxiliary constructions, which is an important ingredient across many mathematical domains. In Extended Data Table 3 , we give examples in four other mathematical domains in which coming up with auxiliary constructions is key to the solution. In Extended Data Table 4 , we give a line-by-line comparison of a geometry proof and an inequality proof for the IMO 1964 Problem 2, highlighting how they both fit into the same framework.

Our paper shows that language models can learn to come up with auxiliary constructions from synthetic data, in which problem statements and auxiliary constructions are randomly generated together and then separated using the traceback algorithm to identify the dependency difference. Concretely, the AlphaGeometry framework requires the following ingredients:

An implementation of the domain’s objects and definitions.

A random premise sampler.

The symbolic engine(s) that operate within the implementation (1).

A traceback procedure for the symbolic engine.

Using these four ingredients and the algorithm described in the main text, one can generate synthetic data for any target domain. As shown in our paper, there are non-trivial engineering challenges in building each ingredient. For example, current formalizations of combinatorics are very nascent, posing challenges to (1) and (2). Also, building powerful symbolic engines for different domains requires deep domain expertise, posing challenges to (3) and (4). We consider applying this framework to a wider scope as future work and look forward to further innovations that tackle these challenges.

Transformer in theorem proving

Research in automated theorem proving has a long history dating back to the 1950s (refs. 6 , 42 , 43 ), resulting in highly optimized first-order logic solvers such as E (ref. 44 ) or Vampire 45 . In the 2010s, deep learning matured as a new powerful tool for automated theorem proving, demonstrating great successes in premise selection and proof guidance 46 , 47 , 48 , 49 , as well as SAT solving 50 . On the other hand, transformer 18 exhibits outstanding reasoning capabilities across a variety of tasks 51 , 52 , 53 . The first success in applying transformer language models to theorem proving is GPT-f (ref. 15 ). Its follow up extensions 2 , 16 further developed this direction, allowing machines to solve some olympiad-level problems for the first time. Innovation in the proof-search algorithm and online training 3 also improves transformer-based methods, solving a total of ten (adapted) IMO problems in algebra and number theory. These advances, however, are predicated on a substantial amount of human proof examples and standalone problem statements designed and curated by humans.

Geometry theorem proving

Geometry theorem proving evolves in an entirely separate space. Its literature is divided into two branches, one of computer algebra methods and one of search methods. The former is largely considered solved since the introduction of Wu’s method 21 , which can theoretically decide the truth value of any geometrical statement of equality type, building on specialized algebraic tools introduced in earlier works 54 , 55 . Even though computer algebra has strong theoretical guarantees, its performance can be limited in practice owing to their large time and space complexity 56 . Further, the methodology of computer algebra is not of interest to AI research, which instead seeks to prove theorems using search methods, a more human-like and general-purpose process.

Search methods also started as early as the 1950s (refs. 6 , 7 ) and continued to develop throughout the twentieth century 57 , 58 , 59 , 60 . With the introduction of DD 10 , 17 , area methods 61 and full-angle methods 30 , geometry solvers use higher-level deduction rules than Tarski’s or Hilbert’s axioms and are able to prove a larger number of more complex theorems than those operating in formal languages. Geometry theorem proving of today, however, is still relying on human-designed heuristics for auxiliary constructions 10 , 11 , 12 , 13 , 14 . Geometry theorem proving falls behind the recent advances made by machine learning because its presence in formal mathematical libraries such as Lean 31 or Isabelle 62 is extremely limited.

Synthetic data in theorem proving

Synthetic data has long been recognized and used as an important ingredient in theorem proving 63 , 64 , 65 , 66 . State-of-the-art machine learning methods make use of expert iteration to generate a curriculum of synthetic proofs 2 , 3 , 15 . Their methods, however, only generate synthetic proofs for a fixed set of predefined problems, designed and selected by humans. Our method, on the other hand, generates both synthetic problems and proofs entirely from scratch. Aygun et al. 67 similarly generated synthetic proofs with hindsight experience replay 68 , providing a smooth range of theorem difficulty to aid learning similar to our work. AlphaGeometry, however, is not trained on existing conjectures curated by humans and does not learn from proof attempts on the target theorems. Their approach is thus orthogonal and can be used to further improve AlphaGeometry. Most similar to our work is Firoiu et al. 69 , whose method uses a forward proposer to generate synthetic data by depth-first exploration and trains a neural network purely on these synthetic data. Our work, on the other hand, uses breadth-first exploration, necessary to obtain the minimal proofs and premises, and uses a traceback algorithm to identify auxiliary constructions, thus introducing new symbols and hypotheses that the forward proposer cannot propose.

Data availability

The data supporting the findings of this work are available in the Extended Data and the Supplementary Information . Source data are provided with this paper.

Code availability

Our code and model checkpoint is available at https://github.com/google-deepmind/alphageometry .

Change history

23 february 2024.

A Correction to this paper has been published: https://doi.org/10.1038/s41586-024-07115-7

Zheng, K., Han, J. M. & Polu, S. MiniF2F: a cross-system benchmark for formal olympiad-level mathematics. Preprint at https://doi.org/10.48550/arXiv.2109.00110 (2022).

Polu, S. et al. Formal mathematics statement curriculum learning. Preprint at https://doi.org/10.48550/arXiv.2202.01344 (2023).

Lample, G. et al. Hypertree proof search for neural theorem proving. Adv. Neural Inf. Process. Syst. 35 , 26337–26349 (2022).

Google Scholar

Potapov, A. et al. in Proc. 13th International Conference on Artificial General Intelligence, AGI 2020 (eds Goertzel, B., Panov, A., Potapov, A. & Yampolskiy, R.) 279–289 (Springer, 2020).

Marić, F. Formalizing IMO problems and solutions in Isabelle/HOL. Preprint at https://arxiv.org/abs/2010.16015 (2020).

Gelernter, H. L. in Proc. First International Conference on Information Processing (IFIP) 273–281 (UNESCO, 1959).

Gelernter, H., Hansen, J. R. & Loveland, D. W. in Papers presented at the May 3–5, 1960, western joint IRE-AIEE-ACM computer conference 143–149 (ACM, 1960).

Harrison, J., Urban, J. & Wiedijk, F. in Handbook of the History of Logic Vol. 9 (ed. Siekmann, J. H.) 135–214 (North Holland, 2014).

van Doorn, F., Ebner, G. & Lewis, R. Y. in Proc. 13th International Conference on Intelligent Computer Mathematics, CICM 2020 (eds Benzmüller, C. & Miller, B.) 251–267 (Springer, 2020).

Chou, S. C., Gao, X. S. & Zhang, J. Z. A deductive database approach to automated geometry theorem proving and discovering. J. Autom. Reason. 25 , 219–246 (2000).

Article MathSciNet Google Scholar

Matsuda, N. & Vanlehn, K. GRAMY: a geometry theorem prover capable of construction. J. Autom. Reason. 32 , 3–33 (2004).

Wang, K. & Su, Z. in Proc. Twenty-Fourth International Joint Conference on Artificial Intelligence (IJCAI 2015) (ACM, 2015).

Gao, X. S. & Lin, Q. in Proc. Automated Deduction in Geometry: 4th International Workshop, ADG 2002 (ed. Winkler, F.) 44–66 (Springer, 2004).

Zhou, M. & Yu, X. in Proc. 2nd International Conference on Artificial Intelligence in Education: Emerging Technologies, Models and Applications, AIET 2021 (eds Cheng, E. C. K., Koul, R. B., Wang, T. & Yu, X.) 151–161 (Springer, 2022).

Polu, S. & Sutskever, I. Generative language modeling for automated theorem proving. Preprint at https://arxiv.org/abs/2009.03393 (2020).

Han, J. M., Rute, J., Wu, Y., Ayers, E. W., & Polu, S. Proof artifact co-training for theorem proving with language models. Preprint at https://doi.org/10.48550/arXiv.2102.06203 (2022).

Ye, Z., Chou, S. C. & Gao, X. S. in Proc. Automated Deduction in Geometry: 7th International Workshop, ADG 2008 (eds Sturm, T. & Zengler, C.) 189–195 (Springer, 2011).

Vaswani, A. et al. Attention is all you need. Adv. Neural Inf. Process. Syst. 30 (2017).

Olšák, M. in Proc. 7th International Conference on Mathematical Software – ICMS 2020 (eds Bigatti, A., Carette, J., Davenport, J., Joswig, M. & de Wolff, T.) 263–271 (Springer, 2020).

Bose, N. K. in Multidimensional Systems Theory and Applications 89–127 (Springer, 1995).

Wu, W.-T. On the decision problem and the mechanization of theorem-proving in elementary geometry. Sci. Sin. 21 , 159–172 (1978).

MathSciNet Google Scholar

Radford, A., Narasimhan, K., Salimans, T. & Sutskever, I. Improving language understanding by generative pre-training. Preprint at https://paperswithcode.com/paper/improving-language-understanding-by (2018).

Radford, A. et al. Better language models and their implications. OpenAI Blog https://openai.com/blog/better-language-models (2019).

Brown, T. et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 33 , 1877–1901 (2020).

Bubeck, S. et al. Sparks of artificial general intelligence: early experiments with GPT-4. Preprint at https://arxiv.org/abs/2303.12712 (2023).

Lewkowycz, A. et al. Solving quantitative reasoning problems with language models. Adv. Neural Inf. Process. Syst. 35 , 3843–3857 (2022).

Liang, P. et al. Holistic evaluation of language models. Transact. Mach. Learn. Res. https://doi.org/10.48550/arXiv.2211.09110 (2023).

Srivastava, A. et al. Beyond the imitation game: quantifying and extrapolating the capabilities of language models. Transact. Mach. Learn. Res. https://doi.org/10.48550/arXiv.2206.04615 (2023).

Wei, J. et al. Emergent abilities of large language models. Transact. Mach. Learn. Res. https://doi.org/10.48550/arXiv.2206.07682 (2022).

Chou, S. C., Gao, X. S. & Zhang, J. Z. Automated generation of readable proofs with geometric invariants: II. Theorem proving with full-angles. J. Autom. Reason. 17 , 349–370 (1996).

de Moura, L. & Ullrich, S. in Proc. 28th International Conference on Automated Deduction, CADE 28 (eds Platzer, A. & Sutcliffe, G.) 625–635 (Springer, 2021).

Krueger, R., Han, J. M. & Selsam, D. in Proc. 28th International Conference on Automated Deduction, CADE 28 (eds Platzer, A. & Sutcliffe, G.) 577–588 (Springer, 2021).

de Moura, L. & Bjørner, N. in Proc. 14th International Conference on Tools and Algorithms for the Construction and Analysis of Systems, TACAS 2008 (eds Ramakrishnan, C. R. & Rehof, J.) 337–340 (Springer, 2008).

Todd, P. A method for the automated discovery of angle theorems. EPTCS 352 , 148–155 (2021).

Hutchins, D., Rabe, M., Wu, Y., Schlag, I. & Staats, C. Meliad. Github https://github.com/google-research/meliad (2022).

Kudo, T. & Richardson, J. SentencePiece: a simple and language independent subword tokenizer and detokenizer for neural text processing. Preprint at https://arxiv.org/abs/1808.06226 (2018).

Raffel, C. et al. Exploring the limits of transfer learning with a unified text-to-text transformer. J. Mach. Learn. Res. 21 , 5485–5551 (2020).

Kosec, M., Fu, S. & Krell, M. M. Packing: towards 2x NLP BERT acceleration. Preprint at https://openreview.net/forum?id=3_MUAtqR0aA (2021).

Krell, M. M., Kosec, M., Perez, S. P. & Iyer, M., Fitzgibbon A. W. Efficient sequence packing without cross-contamination: accelerating large language models without impacting performance. Preprint at https://arxiv.org/abs/2107.02027 (2022).

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I. & Salakhutdinov, R. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15 , 1929–1958 (2014).

Norrie, T. et al. The design process for Google’s training chips: TPUv2 and TPUv3. IEEE Micro. 41 , 56–63 (2021) Feb 9.

Article Google Scholar

Gilmore, P. C. A proof method for quantification theory: its justification and realization. IBM J. Res. Dev. 4 , 28–35 (1960).

Davis, M. & Putnam, H. A computing procedure for quantification theory. J. ACM. 7 , 201–215 (1960).

Schulz, S. E – a brainiac theorem prover. AI Commun. 15 , 111–126 (2002).

Riazanov, A. & Voronkov, A. in Proc. First International Joint Conference on Automated Reasoning, IJCAR 2001 (eds Goré, R., Leitsch, A. & Nipkow, T.) 376–380 (Springer, 2001).

Irving, G. et al. DeepMath - deep sequence models for premise selection. Adv. Neural Inf. Process. Syst. https://doi.org/10.48550/arXiv.1606.04442 (2016).

Wang, M., Tang, Y., Wang, J. & Deng, J. Premise selection for theorem proving by deep graph embedding. Adv. Neural Inf. Process. Syst. https://doi.org/10.48550/arXiv.1709.09994 (2017).

Loos, S., Irving, G., Szegedy, C. & Kaliszyk, C. Deep network guided proof search. Preprint at https://arxiv.org/abs/1701.06972 (2017).

Bansal, K., Loos, S., Rabe, M., Szegedy, C. & Wilcox S. in Proc. 36th International Conference on Machine Learning 454–463 (PMLR, 2019).

Selsam, D. et al. Learning a SAT solver from single-bit supervision. Preprint at https://doi.org/10.48550/arXiv.1802.03685 (2019).

Saxton, D., Grefenstette, E., Hill, F. & Kohli, P. Analysing mathematical reasoning abilities of neural models. Preprint at https://doi.org/10.48550/arXiv.1904.01557 (2019).

Lample, G. & Charton F. Deep learning for symbolic mathematics. Preprint at https://doi.org/10.48550/arXiv.1912.01412 (2019).

Charton, F., Hayat, A. & Lample, G. Learning advanced mathematical computations from examples. Preprint at https://doi.org/10.48550/arXiv.2006.06462 (2021).

Collins, G. E. in Proc. 2nd GI Conference on Automata Theory and Formal Languages (ed. Barkhage, H.) 134–183 (Springer, 1975).

Ritt, J. F. Differential Algebra (Colloquium Publications, 1950).

Chou, S. C. Proving Elementary Geometry Theorems Using Wu’s Algorithm . Doctoral dissertation, Univ. Texas at Austin (1985).

Nevins, A. J. Plane geometry theorem proving using forward chaining. Artif. Intell. 6 , 1–23 (1975).

Coelho, H. & Pereira, L. M. Automated reasoning in geometry theorem proving with Prolog. J. Autom. Reason. 2 , 329–390 (1986).

Quaife, A. Automated development of Tarski’s geometry. J. Autom. Reason. 5 , 97–118 (1989).

McCharen, J. D., Overbeek, R. A. & Lawrence, T. in The Collected Works of Larry Wos 166–196 (2000).

Chou, S. C., Gao, X. S. & Zhang, J. Machine Proofs in Geometry: Automated Production of Readable Proofs for Geometry Theorems (World Scientific, 1994).

Paulson, L. C. (ed.) Isabelle: A Generic Theorem Prover (Springer, 1994).

Wu, Y., Jiang, A. Q., Ba, J. & Grosse, R. INT: an inequality benchmark for evaluating generalization in theorem proving. Preprint at https://doi.org/10.48550/arXiv.2007.02924 (2021).

Zombori, Z., Csiszárik, A., Michalewski, H., Kaliszyk, C. & Urban, J. in Proc. 30th International Conference on Automated Reasoning with Analytic Tableaux and Related Methods (eds Das, A. & Negri, S.) 167–186 (Springer, 2021).

Fawzi, A., Malinowski, M., Fawzi, H., Fawzi, O. Learning dynamic polynomial proofs. Adv. Neural Inf. Process. Syst. https://doi.org/10.48550/arXiv.1906.01681 (2019).

Wang, M. & Deng, J. Learning to prove theorems by learning to generate theorems. Adv. Neural Inf. Process. Syst. 33 , 18146–18157 (2020).

Aygün, E. et al. in Proc. 39th International Conference on Machine Learning 1198–1210 (PMLR, 2022).

Andrychowicz, M. et al. Hindsight experience replay. Adv. Neural Inf. Process. Syst. https://doi.org/10.48550/arXiv.1707.01495 (2017).

Firoiu, V. et al. Training a first-order theorem prover from synthetic data. Preprint at https://doi.org/10.48550/arXiv.2103.03798 (2021).

Download references

Acknowledgements

This project is a collaboration between the Google Brain team and the Computer Science Department of New York University. We thank R. A. Saurous, D. Zhou, C. Szegedy, D. Hutchins, T. Kipf, H. Pham, P. Veličković, E. Lockhart, D. Dwibedi, K. Cho, L. Pinto, A. Canziani, T. Wies, H. He’s research group, E. Chen (the USA’s IMO team coach), M. Olsak and P. Bak.

Author information

Authors and affiliations.

Google Deepmind, Mountain View, CA, USA

Trieu H. Trinh, Yuhuai Wu, Quoc V. Le & Thang Luong

Computer Science Department, New York University, New York, NY, USA

Trieu H. Trinh & He He

You can also search for this author in PubMed Google Scholar

Contributions

T.H.T. conceived the project, built the codebase, carried out experiments, requested manual evaluation from experts and drafted the manuscript. Y.W. advocated for the neuro-symbolic setting and advised on data/training/codebase choices. Q.V.L. advised on scientific methodology and revised the manuscript. H.H. advised on scientific methodology, experimental set-ups and the manuscript. T.L. is the PI of the project, advised on model designs/implementations/experiments and helped with manuscript structure and writing.

Corresponding authors

Correspondence to Trieu H. Trinh or Thang Luong .

Ethics declarations

Competing interests.

The following US patent is related to this work: “Training language model neural networks using synthetic reasoning data”, filed in the United States Patent and Trademark Office (USPTO) on 1 May 2023 as application no. 63/499,469.

Peer review

Peer review information.

Nature thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

Extended data fig. 1 the minimum number of parallel cpu workers to solve all 25 problems and stay under the time limit, given four parallel copies of the gpu v100-accelerated language model..

Each problem has a different running time resulting from their unique size of the deduction closure. We observed that running time does not correlate with the difficulty of the problem. For example, IMO 2019 P6 is much harder than IMO 2008 P1a, yet it requires far less parallelization to reach a solution within IMO time limits.

Extended Data Fig. 2 Side-by-side comparison of AlphaGeometry proof versus human proof on the translated IMO 2004 P1.

Both the AlphaGeometry and human solutions recognize the axis of symmetry between M and N through O. AlphaGeometry constructs point K to materialize this axis, whereas humans simply use the existing point R for the same purpose. This is a case in which proof pruning itself cannot remove K and a sign of similar redundancy in our synthetic data. To prove five-point concyclicity, AlphaGeometry outputs very lengthy, low-level steps, whereas humans use a high-level insight (OR is the symmetrical axis of both LN and AM) to obtain a broad set of conclusions all at once. For algebraic deductions, AlphaGeometry cannot flesh out its intermediate derivations, which is implicitly carried out by Gaussian elimination, therefore leading to low readability. Overall, this comparison points to the use of higher-level tools to improve the synthetic data, proof search and readability of AlphaGeometry. Note that in the original IMO 2004 P1, the point P is proven to be between B and C. The generalized version needs further contraints on the position of O to satisfy this betweenness requirement.

Extended Data Fig. 3 Side-by-side comparison of human proof and AlphaGeometry proof for the IMO 2000 P6.

This is a harder problem (average human score = 1.05/7), with a large number of objects in the problem statements, resulting in a very crowded diagram. Left, the human solution uses complex numbers. With a well-chosen coordinate system, the problem is greatly simplified and a solution follows naturally through algebraic manipulation. Right, AlphaGeometry solution involves two auxiliary constructions and more than 100 deduction steps, with many low-level steps that are extremely tedious to a human reader. This is a case in which the search-based solution is much less readable and much less intuitive than coordinate bashing. A more structural organization, that is, a high-level proof outline, can improve readability of the AlphaGeometry solution substantially. Again, this suggests building into AlphaGeometry many higher-level deduction rules to encapsulate large groups of low-level deductions into fewer proof steps.

Extended Data Fig. 4 Side-by-side comparison of human proof and AlphaGeometry proof for the IMO 2019 P2.

This is one out of five unsolved problems by AlphaGeometry. Left, the human solution uses both auxiliary constructions and barycentric coordinates. With a well-chosen coordinate system, a solution becomes available through advanced algebraic manipulation. Right, AlphaGeometry solution when provided with the ground-truth auxiliary construction for a synthetic proof. This auxiliary construction can be found quickly with the knowledge of Reim’s theorem, which is not included in the deduction rule list used by the symbolic engine during synthetic data generation. Including such high-level theorems into the synthetic data generation can greatly improve the coverage of synthetic data and thus improve auxiliary construction capability. Further, higher-level steps using Reim’s theorem also cut down the current proof length by a factor of 3.

Extended Data Fig. 5 Human proof for the IMO 2008 P6.

This is an unsolved problem by AlphaGeometry and also the hardest one among all 30 problems, with an average human score of only 0.28/7. This human proof uses four auxiliary constructions (diameters of circles W1 and W2) and high-level theorems such as the Pitot theorem and the notion of homothety. These high-level concepts are not available to our current version of the symbolic deduction engine both during synthetic data generation and proof search. Supplying AlphaGeometry with the auxiliary constructions used in this human proof also does not yield any solution. There is also no guarantee that a synthetic solution exists for AlphaGeometry, across all possible auxiliary constructions, without enhancing its symbolic deduction with more powerful rules. Again, this suggests that enhancing the symbolic engine with more powerful tools that IMO contestants are trained to use can improve both the synthetic data and the test-time performance of AlphaGeometry.

Extended Data Fig. 6 Analysis of AlphaGeometry performance under changes made to its training and testing.

a , The effect of reducing training data on AlphaGeometry performance. At 20% of training data, AlphaGeometry still solves 21 problems, outperforming all other baselines. b , Evaluation on a larger set of 231 geometry problems, covering a diverse range of sources outside IMO competitions. The rankings of different machine solvers stays the same as in Table 1 , with AlphaGeometry solving almost all problems. c , The effect of reducing beam size during test time on AlphaGeometry performance. At beam size 8, that is, a 64 times reduction from its full setting, AlphaGeometry still solves 21 problems, outperforming all other baselines. d , The effect of reducing search depth on AlphaGeometry performance. At depth 2, AlphaGeometry still solves 21 problems, outperforming all other baselines.

Supplementary information

Supplementary information.

Supplementary Sections 1 and 2. Section 1 contains GPT-4 prompting details and includes prompting for two scenarios: (1) GPT-4 producing full proofs in natural language and (2) GPT-4 interfaces with DD + AR. Section 2 contains AlphaGeometry solutions for problems in IMO-AG-30. It lists the 30 problem statements, their diagrams to aid understanding and AlphaGeometry solution (if any) sequentially.

Source data

Source data fig. 2, source data fig. 4, source data fig. 6, source data extended data fig. 1, rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Trinh, T.H., Wu, Y., Le, Q.V. et al. Solving olympiad geometry without human demonstrations. Nature 625 , 476–482 (2024). https://doi.org/10.1038/s41586-023-06747-5

Download citation

Received : 30 April 2023

Accepted : 13 October 2023

Published : 17 January 2024

Issue Date : 18 January 2024

DOI : https://doi.org/10.1038/s41586-023-06747-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

Explore articles by subject
Guide to authors
Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Mobile Navigation

Solving (some) formal math olympiad problems.

$Solving Some Formal Math Olympiad Problems$

More resources

We built a neural theorem prover for Lean that learned to solve a variety of challenging high-school olympiad problems, including problems from the AMC12 and AIME competitions, as well as two problems adapted from the IMO . [^footnote-1] The prover uses a language model to find proofs of formal statements. Each time we find a new proof, we use it as new training data, which improves the neural network and enables it to iteratively find solutions to harder and harder statements.

We achieved a new state-of-the-art (41.2% vs 29.3%) on the miniF2F benchmark, a challenging collection of high-school olympiad problems. Our approach, which we call statement curriculum learning , consists of manually collecting a set of statements of varying difficulty levels (without proof) where the hardest statements are similar to the benchmark we target. Initially our neural prover is weak and can only prove a few of them. We iteratively search for new proofs and re-train our neural network on the newly discovered proofs, and after 8 iterations, our prover ends up being vastly superior when tested on miniF2F.

Formal mathematics is an exciting domain to study because of (i) its richness, letting you prove arbitrary theorems which require reasoning, creativity and insight and (ii) its similarity to games—where AI has been spectacularly successful—in that it has an automated way of determining whether a proof is successful (i.e., verified by the formal system). As demonstrated in the trivial example below, proving a formal statement requires generating a sequence of proof steps, each proof step consisting in a call to a tactic. [^footnote-2]

These tactics take mathematical terms as arguments and each tactic call will transform the current statement to prove, into statements that are easier to prove, until nothing is left to prove.

Prove that if ∣ x − 2 ∣ = p |x - 2| = p ∣ x − 2∣ = p , where x < 2 x < 2 x < 2 , then x − p = 2 − 2 p x - p = 2 - 2p x − p = 2 − 2 p .

We observe that the capability to generate original mathematical terms required as arguments of tactics, which cannot be done without a neural language model, emerges from our training procedure. The proof below is an example of it: the proof step use n + 1 (entirely generated by our models) proposes to use n + 1 as a solution, the rest of the formal proof relying on the ring_exp tactic to verify that it is indeed valid.

For all integers n ≥ 9 n ≥ 9 n ≥ 9 , prove that ( ( n + 2 ) ! − ( n + 1 ) ! ) / n ! ((n + 2)! −(n + 1)!) / n! (( n + 2 )! − ( n + 1 )!) / n ! is a perfect square.

We also observe that our models and search procedure are capable of producing proofs that chain multiple non-trivial reasoning steps. In the proof below, the model starts by using contraposition leading to the existential statement ( ∃ (x : ℝ), f x ≠ a * x + b ). It then generates a witness for it with use (0 : ℝ) and finishes the proof by leveraging the norm_num tactic.

Let f ( x ) = A x + B f(x) = Ax + B f ( x ) = A x + B and g ( x ) = B x + A g(x) = Bx + A g ( x ) = B x + A , where A < b r / > e B A <br />e B A < b r / > e B . If f ( g ( x ) ) − g ( f ( x ) ) = B − A f(g(x)) - g(f(x)) = B - A f ( g ( x )) − g ( f ( x )) = B − A , prove that A + B = 0 A + B = 0 A + B = 0 .

Our models, trained with statement curriculum learning , were able to close a variety of problems from training textbooks as well as AMC12 and AIME competitions, and 2 problems adapted from the IMO . We present below three examples of such generated proofs.

Suppose a a a , b b b , c c c are the sides of a triangle. Prove that a 2 ( b + c − a ) + b 2 ( c + a − b ) + c 2 ( a + b − c ) ≤ 3 a b c a^2(b + c − a) + b^2(c + a − b) + c^2(a + b − c) \leq 3abc a 2 ( b + c − a ) + b 2 ( c + a − b ) + c 2 ( a + b − c ) ≤ 3 ab c .

Prove that a 2 + a 4 + a 6 + a 8 + . . . + a 98 = 93 a2 + a4 + a6 + a8 + ...+ a98 = 93 a 2 + a 4 + a 6 + a 8 + ... + a 98 = 93 if a 1 a1 a 1 , a 2 a2 a 2 , a 3... a3... a 3... is an arithmetic progression with common difference 1 1 1 , and a 1 + a 2 + a 3 + . . . + a 98 = 137 a1 + a2 + a3 + ... + a98 = 137 a 1 + a 2 + a 3 + ... + a 98 = 137 ., for a , b , c a, b, c a , b , c reals, prove that ( a 2 + a b + b 2 ) ( b 2 + b c + c 2 ) ( c 2 + c a + a 2 ) ≥ ( a b + b c + c a ) 3 (a^2 + ab + b^2)(b^2 + bc + c^2)(c^2 + ca + a^2) \geq (ab + bc + ca)^3 ( a 2 + ab + b 2 ) ( b 2 + b c + c 2 ) ( c 2 + c a + a 2 ) ≥ ( ab + b c + c a ) 3 ..

Formal mathematics involves two main challenges that make a naive application of reinforcement learning unlikely to succeed.

(i) Infinite action space : not only does formal mathematics have an extremely large search space (like Go for example), it also has an infinite action space. At each step of a proof search, the model must choose not from a well-behaved finite set of actions, but a complex and infinite set of tactics, involving exogenous mathematical terms that have to be generated (e.g., generating a mathematical statement to be used as a witness, an object used in steps such as “there exists an x s.t. …”, or a cut, the introduction and the chaining of a lemma in the middle of a proof).
(ii) Lack of self-play : conversely to 2-player games, a prover is not playing against an opponent but against a set of statements to prove. When faced with a statement that is just too hard, there is no obvious reframing that will let the prover generate intermediary easier statements to tackle first. This asymmetry prevents naive application of the self-play algorithms that were successful with 2-player games.

In our work, we address the infinite action space problem by sampling actions from a language model as we search for a proof. Language models have the capability to generate the tactic calls as well as the original mathematical terms often required as arguments. Our basis for addressing the lack of self-play is the observation that the key role of self-play in 2-player games is to provide an unsupervised curriculum. Our methodology proposes to replace this unsupervised curriculum with an auxiliary set of problem statements (without requiring proofs) of varying difficulty. We empirically show that, when the difficulty of these auxiliary problems is varied enough, our training procedure is able to solve a curriculum of increasingly difficult problems, eventually generalizing to the set of problems we care about.

While these results are extremely exciting, as they demonstrate that deep learning models are capable of non-trivial mathematical reasoning when interacting with a formal system, we are still very far from best-student performance on these competitions, only occasionally, rather than consistently, closing challenging olympiad problems. We hope nonetheless that our work will motivate research in this domain, in particular towards the IMO Grand Challenge and that the statement curriculum learning methodology we propose will help accelerate progress in automated reasoning in general.

Stanislas Polu
Jesse Michael Han
Ilya Sutskever

Acknowledgments

Thanks to our paper co-authors: Igor Babuschkin, Kunhao Zheng and Mantas Baksys.

Thanks to the students of the Xena Project Discord who helped us formalize proofs and statements (in particular: Antoine Labelle, Hanting Zhang, Shing Tak Lam, Paul Lezeau, Sara Diaz, Nikita Golikov, Yael Dillies, Artem Vasilyev, Ollie Perree, and Yourong Zang).

Thanks in particular to Kevin Buzzard and Daniel Selsam for their support and thoughtful feedback since the very beginning of this project.

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

We're Hiring!
Help Center

Problemsolvingmethods in combinatorics an approach to olympiad

Problem Solving in Combinatorics

Related Papers

Nitsa Movshovitz-Hadar

Anthony Savitt

An international book series on Mathematical Combinatorics, Vol.2, 2019

Ahmed Abdelfattah

First lecture in course CS301: "Algorithmic Combinatorics I" for 3rd year students with a computer science major, Faculty of Science, Ain Shams University, Academic Year WS2014/2015.

Dina Ghinelli

Lecture #2 for course CS301: "Algorithmic Combinatorics I" for 3rd year students with a computer science major, Faculty of Science, Ain Shams University, Academic Year WS2014/2015.

arda nyoman

Janka Medova (Melusova)

Combinatorics is considered as one of the more difficult mathematical topics to teach and to learn. In past decade it worldwide appeared in curricula for primary and lower secondary schools. In 2008 it became part of lower-secondary curriculum in Slovakia. Students solve problems using different structuring for set of outcomes in grades 5 to 9. Formalization and names for combinatorial configurations is introduced in grade 10. It is generally agreed that more different structuring the student knows the more successful in solving combinatorial problems he is. The main aim of this study was to find out what strategies are used by upper-secondary students for solving combinatorial problem and how successful these strategies are. The set of 4 combinatorial problems with real-life context was designed. There were 55 students' solutions of the problems in set collected, analyzed and compared. We identified several strategies used by students. These strategies were not equally successful for higher dimensional problems. Students were able to use the multiplication rule. Ratio of correct answers to problems requiring more formal approach (e.g. combinations with repetitions) was lower. Students from grade 12 used different strategies comparing to students from grade 10. Combinations with repetition are in Slovakia taught only in grade 10. Students are neither introduced to appropriate structuring for the set of outcomes, nor pushed to find the strategies by themselves, but the formulas are usually straightforward presented. The period of listing all the elements of the set of outcomes seems to be irreplaceable.

Lecture #3 for course CS301: "Algorithmic Combinatorics I" for 3rd year students with a computer science major, Faculty of Science, Ain Shams University, Academic Year WS2014/2015.

Solving olympiad geometry without human demonstrations

Trieu h. trinh.

1 Google Deepmind, Mountain View, CA USA

2 Computer Science Department, New York University, New York, NY USA

Thang Luong

Associated data.

The data supporting the findings of this work are available in the Extended Data and the Supplementary Information . Source data are provided with this paper.

Our code and model checkpoint is available at https://github.com/google-deepmind/alphageometry .

Proving mathematical theorems at the olympiad level represents a notable milestone in human-level automated reasoning 1 – 4 , owing to their reputed difficulty among the world’s best talents in pre-university mathematics. Current machine-learning approaches, however, are not applicable to most mathematical domains owing to the high cost of translating human proofs into machine-verifiable format. The problem is even worse for geometry because of its unique translation challenges 1 , 5 , resulting in severe scarcity of training data. We propose AlphaGeometry, a theorem prover for Euclidean plane geometry that sidesteps the need for human demonstrations by synthesizing millions of theorems and proofs across different levels of complexity. AlphaGeometry is a neuro-symbolic system that uses a neural language model, trained from scratch on our large-scale synthetic data, to guide a symbolic deduction engine through infinite branching points in challenging problems. On a test set of 30 latest olympiad-level problems, AlphaGeometry solves 25, outperforming the previous best method that only solves ten problems and approaching the performance of an average International Mathematical Olympiad (IMO) gold medallist. Notably, AlphaGeometry produces human-readable proofs, solves all geometry problems in the IMO 2000 and 2015 under human expert evaluation and discovers a generalized version of a translated IMO theorem in 2004.

A new neuro-symbolic theorem prover for Euclidean plane geometry trained from scratch on millions of synthesized theorems and proofs outperforms the previous best method and reaches the performance of an olympiad gold medallist.

Theorem proving is difficult for learning-based methods because training data of human proofs translated into machine-verifiable languages are scarce in most mathematical domains. Geometry stands out among other olympiad domains because it has very few proof examples in general-purpose mathematical languages such as Lean 9 owing to translation difficulties unique to geometry 1 , 5 . Geometry-specific languages, on the other hand, are narrowly defined and thus unable to express many human proofs that use tools beyond the scope of geometry, such as complex numbers (Extended Data Figs. Figs.3 3 and and4). 4 ). Overall, this creates a data bottleneck, causing geometry to lag behind in recent progress that uses human demonstrations 2 – 4 . Current approaches to geometry, therefore, still primarily rely on symbolic methods and human-designed, hard-coded search heuristics 10 – 14 .

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig9_ESM.jpg

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig10_ESM.jpg

We pretrain a language model on all generated synthetic data and fine-tune it to focus on auxiliary construction during proof search, delegating all deduction proof steps to specialized symbolic engines. This follows standard settings in the literature, in which language models such as GPT-f (ref. 15 ), after being trained on human proof examples, can generate exogenous proof terms as inputs to fast and accurate symbolic engines such as nlinarith or ring 2 , 3 , 16 , using the best of both worlds. Our geometry theorem prover AlphaGeometry, illustrated in Fig. Fig.1, 1 , produces human-readable proofs, substantially outperforms the previous state-of-the-art geometry-theorem-proving computer program and approaches the performance of an average IMO gold medallist on a test set of 30 classical geometry problems translated from the IMO as shown in Fig. Fig.2 2 .

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig1_HTML.jpg

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig2_HTML.jpg

Source Data

Synthetic theorems and proofs generation

Our method for generating synthetic data is shown in Fig. Fig.3. 3 . We first sample a random set of theorem premises, serving as the input to the symbolic deduction engine to generate its derivations. A full list of actions used for this sampling can be found in Extended Data Table Table1. 1 . In our work, we sampled nearly 1 billion of such premises in a highly parallelized setting, described in Methods . Note that we do not make use of any existing theorem premises from human-designed problem sets and sampled the eligible constructions uniformly randomly.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig3_HTML.jpg

Extended Data Table 1

List of actions to construct the random premises

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Tab1_ESM.jpg

These actions include constructions to create new points that are related to others in a certain way, for example, collinear, incentre/excentre etc., and constructions that take a number as its parameter.

Next we use a symbolic deduction engine on the sampled premises. The engine quickly deduces new true statements by following forward inference rules as shown in Fig. Fig.3b. 3b . This returns a directed acyclic graph of all reachable conclusions. Each node in the directed acyclic graph is a reachable conclusion, with edges connecting to its parent nodes thanks to the traceback algorithm described in Methods . This allows a traceback process to run recursively starting from any node N , at the end returning its dependency subgraph G ( N ), with its root being N and its leaves being a subset of the sampled premises. Denoting this subset as P , we obtained a synthetic training example (premises, conclusion, proof) = ( P , N , G ( N )).

In geometry, the symbolic deduction engine is deductive database (refs. 10 , 17 ), with the ability to efficiently deduce new statements from the premises by means of geometric rules. DD follows deduction rules in the form of definite Horn clauses, that is, Q ( x ) ← P 1 ( x ),…, P k ( x ), in which x are points objects, whereas P 1 ,…, P k and Q are predicates such as ‘equal segments’ or ‘collinear’. A full list of deduction rules can be found in ref. 10 . To widen the scope of the generated synthetic theorems and proofs, we also introduce another component to the symbolic engine that can deduce new statements through algebraic rules (AR), as described in Methods . AR is necessary to perform angle, ratio and distance chasing, as often required in many olympiad-level proofs. We included concrete examples of AR in Extended Data Table Table2. 2 . The combination DD + AR, which includes both their forward deduction and traceback algorithms, is a new contribution in our work and represents a new state of the art in symbolic reasoning in geometry.

Extended Data Table 2

Three examples of algebraic reasoning (AR) in geometry theorem proving, with AR proof steps between the two tags <AR></AR>

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Tab2_ESM.jpg

In AlphaGeometry, the engine AR can execute all three examples efficiently, under a unified procedure of Gaussian elimination.

Generating proofs beyond symbolic deduction

So far, the generated proofs consist purely of deduction steps that are already reachable by the highly efficient symbolic deduction engine DD + AR. To solve olympiad-level problems, however, the key missing piece is generating new proof terms. In the above algorithm, it can be seen that such terms form the subset of P that N is independent of. In other words, these terms are the dependency difference between the conclusion statement and the conclusion objects. We move this difference from P to the proof so that a generative model that learns to generate the proof can learn to construct them, as illustrated in Fig. Fig.3c. 3c . Such proof steps perform auxiliary constructions that symbolic deduction engines are not designed to do. In the general theorem-proving context, auxiliary construction is an instance of exogenous term generation, a notable challenge to all proof-search algorithms because it introduces infinite branching points to the search tree. In geometry theorem proving, auxiliary constructions are the longest-standing subject of study since inception of the field in 1959 (refs. 6 , 7 ). Previous methods to generate them are based on hand-crafted templates and domain-specific heuristics 8 – 12 , and are, therefore, limited by a subset of human experiences expressible in hard-coded rules. Any neural solver trained on our synthetic data, on the other hand, learns to perform auxiliary constructions from scratch without human demonstrations.

Training a language model on synthetic data

Combining language modelling and symbolic engines

Empirical evaluation

An olympiad-level benchmark for geometry.

Geometry theorem prover baselines

AlphaGeometry belongs to the second category of solvers, often described as search/axiomatic or sometime s ‘synthetic’ methods. These methods treat the problem of theorem proving as a step-by-step search problem using a set of geometry axioms. Thanks to this, they typically return highly interpretable proofs accessible to human readers. Baselines in this category generally include symbolic engines equipped with human-designed heuristics. For example, Chou et al. provided 18 heuristics such as “If OA ⊥ OB and OA = OB, construct C on the opposite ray of OA such that OC = OA ” , besides 75 deduction rules for the symbolic engine. Large language models 22 – 24 such as GPT-4 (ref. 25 ) can be considered to be in this category. Large language models have demonstrated remarkable reasoning ability on a variety of reasoning tasks 26 – 29 . When producing full natural-language proofs on IMO-AG-30, however, GPT-4 has a success rate of 0%, often making syntactic and semantic errors throughout its outputs, showing little understanding of geometry knowledge and of the problem statements itself. Note that the performance of GPT-4 performance on IMO problems can also be contaminated by public solutions in its training data. A better GPT-4 performance is therefore still not comparable with other solvers. In general, search methods have no theoretical guarantee in their proving performance and are known to be weaker than computer algebra methods 13 .

Synthetic data generation rediscovers known theorems and beyond

We find that our synthetic data generation can rediscover some fairly complex theorems and lemmas known to the geometry literature, as shown in Fig. Fig.4, 4 , despite starting from randomly sampled theorem premises. This can be attributed to the use of composite actions described in Extended Data Table Table1, 1 , such as ‘taking centroid’ or ‘taking excentre’, which—by chance—sampled a superset of well-known theorem premises, under our large-scale exploration setting described in Methods . To study the complexity of synthetic proofs, Fig. Fig.4 4 shows a histogram of synthetic proof lengths juxtaposed with proof lengths found on the test set of olympiad problems. Although the synthetic proof lengths are skewed towards shorter proofs, a small number of them still have lengths up to 30% longer than the hardest problem in the IMO test set. We find that synthetic theorems found by this process are not constrained by human aesthetic biases such as being symmetrical, therefore covering a wider set of scenarios known to Euclidean geometry. We performed deduplication as described in Methods , resulting in more than 100 millions unique theorems and proofs, and did not find any IMO-AG-30 theorems, showing that the space of possible geometry theorems is still much larger than our discovered set.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig4_HTML.jpg

Language model pretraining and fine-tuning

Proving results on IMO-AG-30

The performance of ten different solvers on the IMO-AG-30 benchmark is reported in Table Table1, 1 , of which eight, including AlphaGeometry, are search-based methods. Besides prompting GPT-4 to produce full proofs in natural language with several rounds of reflections and revisions, we also combine GPT-4 with DD + AR as another baseline to enhance its deduction accuracy. To achieve this, we use detailed instructions and few-shot examples in the prompt to help GPT-4 successfully interface with DD + AR, providing auxiliary constructions in the correct grammar. Prompting details of baselines involving GPT-4 is included in the Supplementary Information .

Main results on our IMO-AG-30 test benchmark

We compare AlphaGeometry to other state-of-the-art methods (computer algebra and search approaches), most notably Wu’s method. We also show the results of DD + AR (our contribution) and its variants, resulting in the strongest baseline DD + AR + human-designed heuristics. Finally, we include ablation settings for AlphaGeometry without pretraining and fine-tuning.

Measuring the improvements made on top of the base symbolic deduction engine (DD), we found that incorporating algebraic deduction added seven solved problems to a total of 14 (DD + AR), whereas the language model’s auxiliary construction remarkably added another 11 solved problems, resulting in a total of 25. As reported in Extended Data Fig. Fig.6, 6 , we find that, using only 20% of the training data, AlphaGeometry still achieves state-of-the-art results with 21 problems solved. Similarly, using less than 2% of the search budget (beam size of 8 versus 512) during test time, AlphaGeometry can still solve 21 problems. On a larger and more diverse test set of 231 geometry problems, which covers textbook exercises, regional olympiads and famous theorems, we find that baselines in Table Table1 1 remain at the same performance rankings, with AlphaGeometry solving almost all problems (98.7%), whereas Wu’s method solved 75% and DD + AR + human-designed heuristics solved 92.2%, as reported in Extended Data Fig. Fig.6b 6b .

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig12_ESM.jpg

a , The effect of reducing training data on AlphaGeometry performance. At 20% of training data, AlphaGeometry still solves 21 problems, outperforming all other baselines. b , Evaluation on a larger set of 231 geometry problems, covering a diverse range of sources outside IMO competitions. The rankings of different machine solvers stays the same as in Table Table1, 1 , with AlphaGeometry solving almost all problems. c , The effect of reducing beam size during test time on AlphaGeometry performance. At beam size 8, that is, a 64 times reduction from its full setting, AlphaGeometry still solves 21 problems, outperforming all other baselines. d , The effect of reducing search depth on AlphaGeometry performance. At depth 2, AlphaGeometry still solves 21 problems, outperforming all other baselines.

Notably, AlphaGeometry solved both geometry problems of the same year in 2000 and 2015, a threshold widely considered difficult to the average human contestant at the IMO. Further, the traceback process of AlphaGeometry found an unused premise in the translated IMO 2004 P1, as shown in Fig. Fig.5, 5 , therefore discovering a more general version of the translated IMO theorem itself. We included AlphaGeometry solutions to all problems in IMO-AG-30 in the Supplementary Information and manually analysed some notable AlphaGeometry solutions and failures in Extended Data Figs. Figs.2 2 – 5 . Overall, we find that AlphaGeometry operates with a much lower-level toolkit for proving than humans do, limiting the coverage of the synthetic data, test-time performance and proof readability.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig5_HTML.jpg

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig8_ESM.jpg

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig11_ESM.jpg

Human expert evaluation of AlphaGeometry outputs

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig7_ESM.jpg

Learning to predict the symbolic engine’s output improves the language model’s auxiliary construction

Hard problems are reflected in AlphaGeometry proof length

Figure Figure6 6 measures the difficulty of solved problems using public scores of human contestants at the IMO and plots them against the corresponding AlphaGeometry proof lengths. The result shows that, for the three problems with the lowest human score, AlphaGeometry also requires exceptionally long proofs and the help of language-model constructions to reach its solution. For easier problems (average human score > 3.5), however, we observe no correlation ( p = −0.06) between the average human score and AlphaGeometry proof length.

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Fig6_HTML.jpg

Geometry representation

Sampling consistent theorem premises

We developed a constructive diagram builder language similar to that used by JGEX 17 to construct one object in the premise at a time, instead of freely sampling many premises that involve several objects, therefore avoiding the generation of a self-contradicting set of premises. An exhaustive list of construction actions is shown in Extended Data Table Table1. 1 . These actions include constructions to create new points that are related to others in a certain way, that is, collinear, incentre/excentre etc., as well as constructions that take a number as its parameter, for example, “construct point X such that given a number α , ∠ABX = α ”. One can extend this list with more sophisticated actions to describe a more expressive set of geometric scenarios, improving both the synthetic data diversity and the test-set coverage. A more general and expressive diagram builder language can be found in ref. 32 . We make use of a simpler language that is sufficient to describe problems in IMO-AG-30 and can work well with the symbolic engine DD.

The symbolic deduction engine

The core functionality of the engine is deducing new true statements given the theorem premises. Deduction can be performed by means of geometric rules such as ‘If X then Y’, in which X and Y are sets of geometric statements such as ‘A, B, C are collinear’. We use the method of structured DD 10 , 17 for this purpose as it can find the deduction closure in just seconds on standard non-accelerator hardware. To further enhance deduction, we also built into AlphaGeometry the ability to perform deduction through AR. AR enable proof steps that perform angle/ratio/distance chasing. Detailed examples of AR are shown in Extended Data Table Table2. 2 . Such proof steps are ubiquitous in geometry proofs, yet not covered by geometric rules. We expand the Gaussian elimination process implemented in GeoLogic 19 to find the deduction closure for all possible linear operators in just seconds. Our symbolic deduction engine is an intricate integration of DD and AR, which we apply alternately to expand the joint closure of known true statements until expansion halts. This process typically finishes within a few seconds to at most a few minutes on standard non-accelerator hardware.

Algebraic reasoning

On a high level, we first convert the input linear equations to a matrix of their coefficients. In particular, we create a coefficient matrix A ∈ R M × N in which N is the number of variables and M is the number of input equations. In geometry, any equality is of the form a − b = c − d ⇔ a − b − c + d = 0. For example, the angle equality ∠ABC = ∠XYZ is represented as s (AB) − s (BC) = s (XY) − s (YZ), in which s (AB) is the angle between AB and the x-direction, modulo pi. Similarly, ratios AB:CD = EF:GH are represented as log(AB) − log(CD) = log(EF) − log(GH), in which log(AB) is the log of the length of segment AB. For distances, each variable is a (point, line) pair, representing a specific point on a specific line.

Deductive database implementation

Traceback to find minimal proofs

Traceback for geometric-rule deduction

Such optimization is NP-hard, as it is a reduction from the decision version of vertex cover. We simply use a greedy algorithm in this case to find a best-effort minimum spanning tree.

Traceback for algebraic deduction

The minimum set of immediate parent nodes for the equality represented by b will be the i th equations ( i th rows in A ) whose corresponding decision value ( x i − y i ) is non-zero.

Integrating DD and AR

Proof pruning

Parallelized data generation and deduplication

Language model architecture and training

Parallelized proof search

The effect of data and search

We trained AlphaGeometry on smaller fractions of the original training data (20%, 40%, 60% and 80%) and found that, even at 20% of training data, AlphaGeometry still solves 21 problems, more than the strongest baseline (DD + AR + human-designed heuristics) with 18 problems solved, as shown in Extended Data Fig. Fig.6a. 6a . To study the effect of beam search on top of the language model, we reduced the beam size and search depth separately during proof search and reported the results in Extended Data Fig. 6c,d . We find that, with a beam size of 8, that is, a 64 times reduction from the original beam size of 512, AlphaGeometry still solves 21 problems. A similar result of 21 problems can be obtained by reducing the search depth from 16 to only two, while keeping the beam size constant at 512.

Evaluation on a larger test set

We evaluated AlphaGeometry and other baselines on a larger test set of 231 geometry problems, curated in ref. 17 . This set covers a wider range of sources outside IMO competitions: textbook examples and exercises, regional olympiads and famous geometry theorems; some are even more complex than typical IMO problems, such as the five circles theorem, Morley’s theorem or Sawayama and Thébault’s theorem. The results are reported in Extended Data Fig. Fig.6b. 6b . The overall rankings of different approaches remained the same as in Table Table1, 1 , with AlphaGeometry solving almost all problems (98.7%). The strongest baseline DD + AR + human-designed heuristics solves 92.2%, whereas the previous state of the art solves 75%.

AlphaGeometry framework and applicability to other domains

The strength of AlphaGeometry’s neuro-symbolic set-up lies in its ability to generate auxiliary constructions, which is an important ingredient across many mathematical domains. In Extended Data Table Table3, 3 , we give examples in four other mathematical domains in which coming up with auxiliary constructions is key to the solution. In Extended Data Table Table4, 4 , we give a line-by-line comparison of a geometry proof and an inequality proof for the IMO 1964 Problem 2, highlighting how they both fit into the same framework.

Extended Data Table 3

Examples of auxiliary constructions in four different domains

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Tab3_ESM.jpg

In these examples, the construction is key to the proof, whereas the remaining proof is relatively more mechanical. In AlphaGeometry, the mechanical portion is efficiently handled by the symbolic engine DD + AR.

Extended Data Table 4

A comparison between a geometry proof and an IMO inequality proof through the lens of the AlphaGeometry framework

An external file that holds a picture, illustration, etc.
Object name is 41586_2023_6747_Tab4_ESM.jpg

We assume AM-GM to be a symbolic engine capable of (1) algebraic rewrites and simplification and (2) applying the inequality rule of arithmetic means–geometric means. With the original premises, directly applying AM-GM fails to deliver a solution, which is similar to the geometry example, for which DD + AR fails to solve the simple problem. Some correct auxiliary constructions are necessary for both symbolic engines (DD + AR in the case of geometry and AM-GM in the case of inequality) to succeed, as shown in the last two rows of the table. Note that there are ten more common inequalities typically used at mathematical olympiads besides AM-GM, just as DD + AR itself encapsulates more than 50 different deduction rules for geometry commonly used at the olympiads.

An implementation of the domain’s objects and definitions.
A random premise sampler.
The symbolic engine(s) that operate within the implementation (1).
A traceback procedure for the symbolic engine.

Transformer in theorem proving

Research in automated theorem proving has a long history dating back to the 1950s (refs. 6 , 42 , 43 ), resulting in highly optimized first-order logic solvers such as E (ref. 44 ) or Vampire 45 . In the 2010s, deep learning matured as a new powerful tool for automated theorem proving, demonstrating great successes in premise selection and proof guidance 46 – 49 , as well as SAT solving 50 . On the other hand, transformer 18 exhibits outstanding reasoning capabilities across a variety of tasks 51 – 53 . The first success in applying transformer language models to theorem proving is GPT-f (ref. 15 ). Its follow up extensions 2 , 16 further developed this direction, allowing machines to solve some olympiad-level problems for the first time. Innovation in the proof-search algorithm and online training 3 also improves transformer-based methods, solving a total of ten (adapted) IMO problems in algebra and number theory. These advances, however, are predicated on a substantial amount of human proof examples and standalone problem statements designed and curated by humans.

Geometry theorem proving

Search methods also started as early as the 1950s (refs. 6 , 7 ) and continued to develop throughout the twentieth century 57 – 60 . With the introduction of DD 10 , 17 , area methods 61 and full-angle methods 30 , geometry solvers use higher-level deduction rules than Tarski’s or Hilbert’s axioms and are able to prove a larger number of more complex theorems than those operating in formal languages. Geometry theorem proving of today, however, is still relying on human-designed heuristics for auxiliary constructions 10 – 14 . Geometry theorem proving falls behind the recent advances made by machine learning because its presence in formal mathematical libraries such as Lean 31 or Isabelle 62 is extremely limited.

Synthetic data in theorem proving

Synthetic data has long been recognized and used as an important ingredient in theorem proving 63 – 66 . State-of-the-art machine learning methods make use of expert iteration to generate a curriculum of synthetic proofs 2 , 3 , 15 . Their methods, however, only generate synthetic proofs for a fixed set of predefined problems, designed and selected by humans. Our method, on the other hand, generates both synthetic problems and proofs entirely from scratch. Aygun et al. 67 similarly generated synthetic proofs with hindsight experience replay 68 , providing a smooth range of theorem difficulty to aid learning similar to our work. AlphaGeometry, however, is not trained on existing conjectures curated by humans and does not learn from proof attempts on the target theorems. Their approach is thus orthogonal and can be used to further improve AlphaGeometry. Most similar to our work is Firoiu et al. 69 , whose method uses a forward proposer to generate synthetic data by depth-first exploration and trains a neural network purely on these synthetic data. Our work, on the other hand, uses breadth-first exploration, necessary to obtain the minimal proofs and premises, and uses a traceback algorithm to identify auxiliary constructions, thus introducing new symbols and hypotheses that the forward proposer cannot propose.

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41586-023-06747-5.

Supplementary information

Source data

Acknowledgements.

Extended data figures and tables

Author contributions.

Peer review

Peer review information.

Nature thanks the anonymous reviewers for their contribution to the peer review of this work.

Data availability

Code availability, competing interests.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Change history

A Correction to this paper has been published: 10.1038/s41586-024-07115-7

Contributor Information

Trieu H. Trinh, Email: moc.elgoog@ueirtht .

Thang Luong, Email: moc.elgoog@gnoulgnaht .

Extended data

is available for this paper at 10.1038/s41586-023-06747-5.

The online version contains supplementary material available at 10.1038/s41586-023-06747-5.

Exploring maths through problem solving

Sample Questions

These sample Maths Olympiad papers contain actual past contest questions. A range of previous questions can also be found in our resource books, 'Maths Olympiad Contest Problems' Volume 1 to 4.

Maths Olympiad

Junior Division Suitable for Years 5 & 6

Senior Division Suitable for Years 7 & 8

These sample Maths Games papers contain actual past contest questions. A range of previous questions can also be found in our new resource book ‘Building Confidence in Maths Problem Solving’.

Maths Games

Junior Suitable for Years 5 & 6

Senior Suitable for Years 7 & 8

This sample Maths Explorer paper contains actual past contest questions. It will provide teachers with an understanding of the type of questions in the Maths Explorer program, together with sample solutions.

Maths Explorer

Sample Questions Suitable for Years 3 & 4

Contact Details

Phone: +61 2 9114 9255
Fax: +61 2 9114 9233
Email: [email protected]
Post: PO Box 629 WAHROONGA NSW 2076

Competitions & Programs

Maths Quest Years 1-2
Maths Explorer Years 3-4
Maths Games Years 5-6
Maths Games Years 7-8
Maths Olympiad Years 5-6
Maths Olympiad Years 7-8

Teacher & Parent Resources

Resource Books
Problem of the Week
Latest News

Professional Learning

Member sign in.

IMAGES

Problem-Solving Methods in Combinatorics : An Approach to Olympiad
Learn Ways of Solving Olympiad Questions: Laws of Motion L-26
Olympiad Mathematics m^7+64m^2=?, A Nice Algebra Problem
Math Olympiad Question
Solving Olympiad-Level Function Problems: Strategies and Techniques
Math olympiad problem you can solve

VIDEO

Math Olympiad Problem In Few Steps
A nice mathematics algebra problem
👍👍A Nice Math Olympiad Exponential Problem, Solving 7^x–11^x=sqrt(77^x–121^x) Differently
Math Olympiad Challenge: You should be able to solve this!
A Nice algebra math problem
Maths Olympiad :

COMMENTS

Art of Problem Solving
In the last 9 years, 53 USA International Math Olympiad team members have medaled and have taken over 300 AoPS Online courses. 41. 11. 1. ... Art of Problem Solving offers two other multifaceted programs. Beast Academy is our comic-based online math curriculum for students ages 6-13. And AoPS Academy brings our methodology to students grades ...
International Mathematical Olympiad
International Mathematical Olympiad. The International Mathematical Olympiad is the pinnacle of all high school mathematics competitions and the oldest of all international scientific competitions. Each year, countries from around the world send a team of 6 students to compete in a grueling competition. IMO. Region: International.
Art of Problem Solving
Similarly, problem 2020/3 was proposed by Hungary with one Hungarian and one non-Hungarian problem author. To the current moment, there is only a single IMO problem that has two distinct proposing countries: The if-part of problem 1994/2 was proposed by Australia and its only-if part by Armenia. See also. IMO problems statistics (eternal)
MathWOOT Online Math Course
A 7-month high school math Olympiad preparation and testing program that brings together many of the best students from around the world to learn advanced problem solving skills. ... This course helps students apply their knowledge to practical Olympiad problem solving. Tuition: original price. $895.00 sale price. $860 $860 Early bird pricing ...
Evan Chen • Problems
In 2020, Rustam Turdibaev and Olimjon Olimov, compiled a 336-problem index of recent problems by subject and MOHS rating. In addition, the linked file also contains a hyperlink to each of the corresponding solution threads on Art of Problem-Solving. ... The acronym stands from "math olympiad hardness scale", ...
How to Study for the Math Olympiad: AMC 10/AMC 12
You can take the AMC 10 and/or 12 multiple times. The AMC 10 and AMC 12 each have 25 questions. You have 75 minutes for the entire exam. Each correct answer is worth 6 points (for a maximum score of 150) and each unanswered question is worth 1.5 points. There is no deduction for wrong answers.
Math Olympiads for Elementary and Middle Schools
Welcome to MOEMS. MOEMS® is one of the most influential and fun-filled math competition programs in the United States and throughout the world. More than 120,000 students from every state and 39 additional countries participate each year. The objectives of MOEMS® are to teach multiple strategies for out-of-the-box problem solving, develop ...
Category:Olympiad Algebra Problems
1959 IMO Problems/Problem 2. 1959 IMO Problems/Problem 3. 1960 IMO Problems/Problem 2. 1961 IMO Problems/Problem 1. 1966 IMO Problems/Problem 5. 1968 IMO Problems/Problem 3. 1968 IMO Problems/Problem 5. 1970 Canadian MO Problems/Problem 1. 1970 IMO Problems/Problem 2.
Category:Olympiad Geometry Problems
1972 USAMO Problems/Problem 5. 1973 IMO Problems/Problem 1. 1973 IMO Problems/Problem 2. 1973 IMO Problems/Problem 6. 1973 IMO Shortlist Problems/Bulgaria 1. 1973 USAMO Problems/Problem 1. 1974 IMO Problems/Problem 3. 1974 IMO Problems/Problem 4. 1974 IMO Problems/Problem 6.
Problems
1979. Bulgarian Czech English Finnish French German Greek Hebrew Hungarian Polish Portuguese Romanian Serbian Slovak Swedish Vietnamese. 1978. English. 1977. English.
Mathematical Olympiad Challenges
Mathematical Olympiad Challenges is a rich collection of problems put together by two experienced and well-known professors and coaches of the U.S. International Mathematical Olympiad Team. Hundreds of beautiful, challenging, and instructive problems from algebra, geometry, trigonometry, combinatorics, and number theory were selected from numerous mathematical competitions and journals.
The Mathematical Olympiad handbook : an introduction to problem solving
The Mathematical Olympiad handbook : an introduction to problem solving based on the first 32 British mathematical olympiads 1965-1996 by Gardiner, A. (Anthony), 1947-Publication date 1997 Topics British Mathematical Olympiad, Mathematics -- Problems, exercises, etc Publisher
Effective problem-solving techniques for Olympiad questions
Effective problem-solving techniques for Olympiad questions. By Vivek C Bhatt, New Delhi. Mar 26, 2024 01:52 PM IST. For students, participating in the Olympiads is a matter of great pride and ...
Breaking Down 2024 Math Olympiad Problems: Tips for Solving Complex
Engage in regular problem-solving sessions, participate in mock Olympiads, and solve past Math Olympiad problems. The more you practice, the better you become at identifying problem-solving strategies and applying them effectively. Conclusion: Mastering the art of solving complex equations is a valuable skill for Math Olympiad participants. By ...
DeepMind AI solves hard geometry problems from mathematics olympiad
Solving IMO geometry problems in this way is impressive, says Yang-Hui He at the London Institute for Mathematical Sciences, but the system is inherently limited in the mathematics it can use ...
Solving olympiad geometry without human demonstrations
As reported in Extended Data Fig. 6, we find that, using only 20% of the training data, AlphaGeometry still achieves state-of-the-art results with 21 problems solved. Similarly, using less than 2% ...
Solving (some) formal math olympiad problems
We built a neural theorem prover for Lean that learned to solve a variety of challenging high-school olympiad problems, including problems from the AMC12 and AIME competitions, as well as two problems adapted from the IMO. [^footnote-1] The prover uses a language model to find proofs of formal statements. Each time we find a new proof, we use it as new training data, which improves the neural ...
Problemsolvingmethods in combinatorics an approach to olympiad
Problemsolvingmethods in combinatorics an approach to olympiad. Problemsolvingmethods in combinatorics an approach to olympiad. Iqbal Kharisudin. Problem Solving in Combinatorics. ... The main aim of this study was to find out what strategies are used by upper-secondary students for solving combinatorial problem and how successful these ...
Home
Professional Learning. APSMO offers a series of professional learning workshops for teachers looking to develop their skills in teaching problem solving in mathematics. Presented by experienced educators and maths specialists, the programs cover multiple strategies and techniques used in problem solving and provide examples and suggestions on ...
PDF Problem-Solving Methods in Combinatorics. An Approach to Olympiad Problems
solution, that does not mean the problem one has to solve is not hard. Many times the difﬁculty of a problem in combinatorics lies in the fact that the idea that works is very well "hidden". Due to this the only way to really learn combinatorics is solving many problems, rather than reading a lot of theory. This practice is precisely what
Solving olympiad geometry without human demonstrations
Mathematical olympiads are the most reputed theorem-proving competitions in the world, with a similarly long history dating back to 1959, playing an instrumental role in identifying exceptional talents in problem solving. Matching top human performances at the olympiad level has become a notable milestone of AI research 2-4.
PDF Can Language Models Solve Olympiad Programming?
Olympiad, along with high-quality unit tests, reference code, and official analyses for each problem. These resources enable us to construct and test ... Solving this problem requires a combination of grounded reasoning about the concept of leaders, creative thinking to precisely count different cases of leader pairs, and algorithmic reasoning ...
Sample Questions
Maths Olympiad. Senior Division. Suitable for Years 7 & 8. Download PDF. These sample Maths Games papers contain actual past contest questions. A range of previous questions can also be found in our new resource book 'Building Confidence in Maths Problem Solving'.

Evan Chen《陳誼廷》

• CV

Olympiad Problems and Solutions

Hardness scale #

USA Math Olympiad (USAMO) #

Recent statistics for USAMO

Problems and solutions to USAMO

USA TST Selection Test (TSTST) #

USA Team Selection Test (TST) #

International Math Olympiad #

Taiwan Team Selection Test #

NIMO / OMO #

Choose Your Test

How Do You Qualify for Math Olympiad?

Step 1: Take the AMC 10 or AMC 12

Step 2: Take the AIME

Step 3: Qualify for and Compete in Math Olympiad

How Can You Learn Math Olympiad Content?

How Can You Learn Problem-Solving Skills?

How to Prepare for Math Olympiad

#1: Use Quality Practice Problems

#2: Don't Lounge Around

#3: Focus on Your Weak Areas

#4: Beware of Tiny Mistakes

#5: Schedule Regular Study Time

#6: Attend Other Math Competitions

What Should You Do the Night Before a Competition?

What's Next?

Ask a Question Below

Improve With Our Famous Guides

Series: How to Get 800 on Each SAT Section:

Series: How to Get to 600 on Each SAT Section:

Series: How to Get 36 on Each ACT Section:

Series: How to Get to 24 on Each ACT Section:

Stay Informed

Looking for Graduate School Test Prep?

Welcome to MOEMS ®

Local news... Click to read about some amazing students!

Available for Elementary and Middle School

Two Test Administration Formats

2024-2025 Fees & Deadlines

2024- 2025 Season

MOEMS ® Affiliates

Australian Problem Solving Mathematical Olympiads (APSMO)

MOEMS ® Mainland China

International Mathematical Olympiad

Mathematical Olympiad Challenges

American Mathematics Competitions, University of Nebraska, Lincoln, USA

Department of Mathematics, University of Michigan, Ann Arbor, USA

Access this book

Other ways to access

Table of contents (6 chapters)

Algebra and Analysis

About this book

Bibliographic Information

Internet Archive Audio

Mobile Apps

Browser Extensions

Save Page Now

The Mathematical Olympiad handbook : an introduction to problem solving based on the first 32 British mathematical olympiads 1965-1996

plus-circle Add Review comment Reviews

DOWNLOAD OPTIONS

IN COLLECTIONS

SIMILAR ITEMS (based on metadata)

Effective problem-solving techniques for Olympiad questions

Understand the Format

Review Concepts

Solve Previous Years’ Olympiad Questions

Use Logical Reasoning

Develop Time Management

Practice on Advanced Problem-Solving Techniques

Seek Guidance from Teachers

Embrace Challenges and Learn from Setbacks

Practice, Practice and Practice

Breaking Down 2024 Math Olympiad Problems: Tips for Solving Complex Equations

DeepMind AI solves hard geometry problems from mathematics olympiad

Sign up to our The Daily newsletter

Sign up to our weekly newsletter

More from New Scientist

DeepMind AI with built-in fact-checker makes mathematical discoveries