SOLVING PROBLEMS WITH RATIONAL NUMBERS
In this section, we will learn how to solve problems with rational numbers.
A number that is expressed in the form a/b is called as rational number.
Here, both "a" and "b" are integers and also b ≠ 0.
Problem 1 :
The area of a rectangular sandbox is 56 2/3 square feet. The length of the sandbox is 8 1/2 feet. What is the width ?
We know the formula to find area of the rectangle.
That is,
Area of the rectangle = length x width
Plug the known values area and length and solve for the unknown value width.
56 2/3 = 8 1/2 x width
170/3 = 17/2 x width
(170/3) x (2/17) = width
20/3 = width
6 2/3 = width
Therefore, the width of the rectangle is 6 2/3 feet.
Problem 2 :
Mr. Webster is buying carpet for an exercise room where the basement of the room is in the shape of rectangle. The length and width of the room are 18 2/5 feet and 12 1/2 feet respectively. Find the total cost of the carpet, if the price of the carpet is $3 per square feet ?
To know the total cost of the carpet, first we have to know the area of the basement.
Area of the basement = length x width
= 18 2/5 x 12 1/2
= (92/5) x (25/2)
= 46 x 5
= 230 square feet
So, we need 230 square feet of carpet.
The cost each square feet of carpet = $3
Then, the cost of 230 square ft of carpet is
= 3 x 230
= $690
Therefore, the total cost of the carpet is $690.
Problem 3 :
Problem 4 :
David is cooking enough lentils for lentil barley soup and lentil salad. The lentil barley soup recipe calls for 3/ 4 cup of dried lentils. The lentil salad recipe calls for 1 1/ 2 cups of dried lentils. David has a 1/ 8 -cup scoop. How many scoops of dried lentils will David need to have enough for the soup and the salad?
David needs 3/ 4 cup of dried lentils for soup and 1 1/ 2 cups for salad.
Total amount dried lentils that David need is
= (3/4) + (1 1/2)
= 3/4 + 3/2
= 3/4 + 6/4
= (3+6) / 4
= 9/4
David needs 9/4 cups of dried lentils for both the soup and the salad.
To find how many 1/8 -cup scoops he needs, divide the total amount of dried lentils into groups of 1/8.
Then, we have
= 9/4 ÷ 1/8
= 9/4 x 8/1
= 9 x 2
Hence, David will need 18 scoops of dried lentils to have enough for both the lentil barley soup and the lentil salad.
Problem 5 :
If the numerator of a fraction is increased by 2 and the denominator by 1, it becomes 1. In case, the numerator is decreased by 4 and the denominator by 2, it becomes 1/2. Find the fraction.
Let "x/y" be the required fraction.
"If the numerator is increased by 2 and the denominator by 1, the fraction becomes 1"
From the above information, we have (x+2) / (y+1) = 1
(x + 2) / (y + 1) = 1
x + 2 = y + 1
x - y = -1 ----(1)
"In case the numerator is decreased by 4 and the denominator by 2, the fraction becomes 1/2"
From the above information, we have
(x - 4) / (y - 2) = 1 / 2
2(x - 4) = y - 2
2x - y = 6 ----(1)
Solving (1) and (2), we get
x = 7 and y = 8
x / y = 7 / 8
So, the required fraction is 7/8.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents

Recent Articles
Real Analysis
Apr 14, 24 02:50 AM
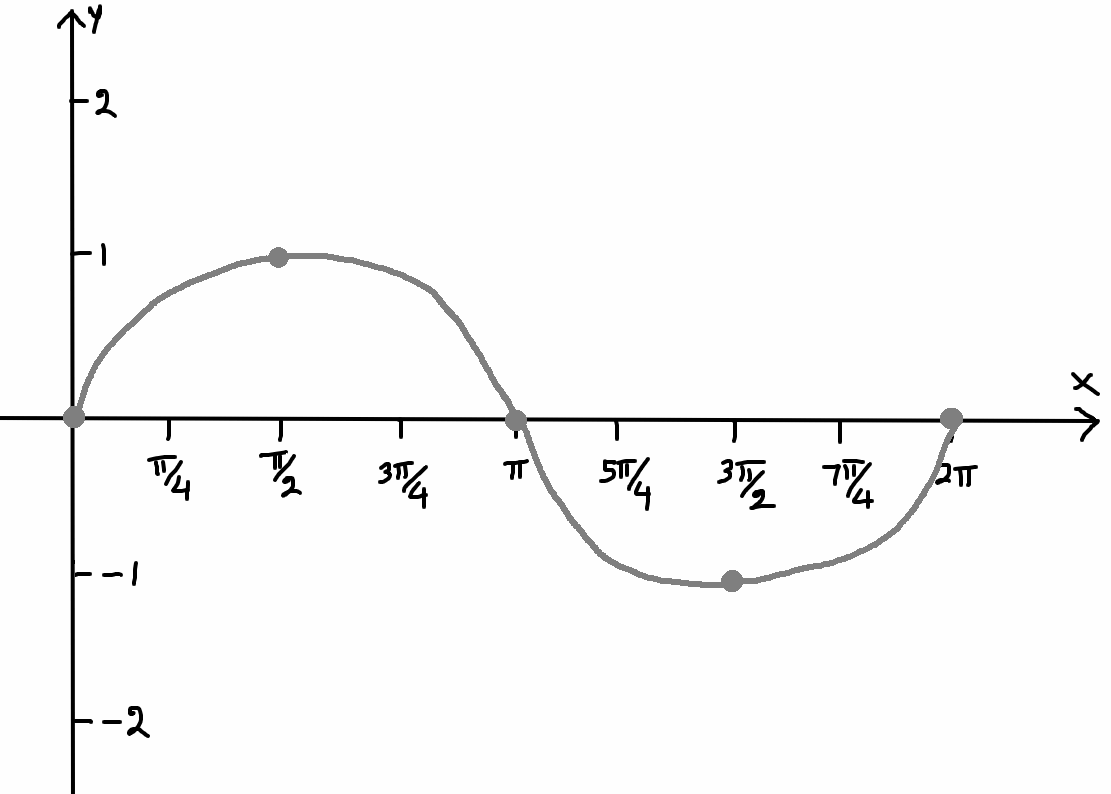
How to Sketch the Graph of Sinusoidal Function
Apr 13, 24 12:02 PM
Solve Exponential Equations Using Exponent Properties Worksheet
Apr 13, 24 10:20 AM

If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 2: Module 2: Rational numbers
About this unit.
"Students continue to build an understanding of the number line in Module 2 from their work in Grade 6. They learn to add, subtract, multiply, and divide rational numbers. Module 2 includes rational numbers as they appear in expressions and equations—work that is continued in Module 3." Eureka Math/EngageNY (c) 2015 GreatMinds.org
Topic A: Addition and subtraction of integers and rational numbers
- Zero pairs worked example (Opens a modal)
- Adding with integer chips (Opens a modal)
- Adding negative numbers on the number line (Opens a modal)
- Adding negative numbers example (Opens a modal)
- Signs of sums on a number line (Opens a modal)
- Subtracting with integer chips (Opens a modal)
- Adding the opposite with integer chips (Opens a modal)
- Adding the opposite with number lines (Opens a modal)
- Adding & subtracting negative numbers (Opens a modal)
- Subtracting a negative = adding a positive (Opens a modal)
- Adding negative numbers review (Opens a modal)
- Equivalent expressions with negative numbers (Opens a modal)
- Subtracting negative numbers review (Opens a modal)
- Number equations & number lines (Opens a modal)
- Graphing negative number addition and subtraction expressions (Opens a modal)
- Interpreting numeric expressions example (Opens a modal)
- Absolute value as distance between numbers (Opens a modal)
- Interpreting absolute value as distance (Opens a modal)
- Associative and commutative properties of addition with negatives (Opens a modal)
- Adding fractions with different signs (Opens a modal)
- Adding and subtracting fractions with negatives (Opens a modal)
- Comparing rational numbers (Opens a modal)
- Adding & subtracting rational numbers: 79% - 79.1 - 58 1/10 (Opens a modal)
- Adding & subtracting rational numbers: 0.79 - 4/3 - 1/2 + 150% (Opens a modal)
- Zero pairs Get 3 of 4 questions to level up!
- Add with integer chips Get 3 of 4 questions to level up!
- Adding negative numbers on the number line Get 5 of 7 questions to level up!
- Signs of sums Get 5 of 7 questions to level up!
- Adding negative numbers Get 5 of 7 questions to level up!
- Subtract with integer chips Get 3 of 4 questions to level up!
- Understand subtraction as adding the opposite Get 3 of 4 questions to level up!
- Subtracting negative numbers Get 5 of 7 questions to level up!
- Adding & subtracting negative numbers Get 5 of 7 questions to level up!
- Number equations & number lines Get 3 of 4 questions to level up!
- Interpret negative number addition and subtraction expressions Get 3 of 4 questions to level up!
- Absolute value to find distance Get 5 of 7 questions to level up!
- Absolute value to find distance challenge Get 3 of 4 questions to level up!
- Commutative and associative properties of addition with integers Get 3 of 4 questions to level up!
- Equivalent expressions with negative numbers Get 3 of 4 questions to level up!
- Adding & subtracting negative fractions Get 5 of 7 questions to level up!
- Order rational numbers Get 3 of 4 questions to level up!
- Adding & subtracting rational numbers Get 3 of 4 questions to level up!
- One-step equations with negatives (add & subtract) Get 5 of 7 questions to level up!
Topic B: Multiplication and division of integers and rational numbers
- Multiplying a positive and a negative number (Opens a modal)
- Multiplying two negative numbers (Opens a modal)
- Why a negative times a negative is a positive (Opens a modal)
- Why a negative times a negative makes sense (Opens a modal)
- Multiplying positive & negative numbers (Opens a modal)
- Dividing positive and negative numbers (Opens a modal)
- Multiplying negative numbers review (Opens a modal)
- Dividing negative numbers review (Opens a modal)
- Rewriting decimals as fractions: 2.75 (Opens a modal)
- Fraction to decimal: 11/25 (Opens a modal)
- Worked example: Converting a fraction (7/8) to a decimal (Opens a modal)
- Fraction to decimal with rounding (Opens a modal)
- Multiplying positive and negative fractions (Opens a modal)
- Dividing negative fractions (Opens a modal)
- Negative signs in fractions (Opens a modal)
- Dividing mixed numbers (Opens a modal)
- Simplifying complex fractions (Opens a modal)
- Expressions with rational numbers (Opens a modal)
- Equivalent expressions with negative numbers (multiplication and division) (Opens a modal)
- Why dividing by zero is undefined (Opens a modal)
- Signs of expressions Get 5 of 7 questions to level up!
- Multiplying negative numbers Get 3 of 4 questions to level up!
- Dividing negative numbers Get 3 of 4 questions to level up!
- One-step equations with negatives (multiply & divide) Get 5 of 7 questions to level up!
- Write decimals as fractions Get 5 of 7 questions to level up!
- Rewriting decimals as fractions challenge Get 5 of 7 questions to level up!
- Converting fractions to decimals Get 3 of 4 questions to level up!
- Multiplying positive and negative fractions Get 3 of 4 questions to level up!
- Dividing positive and negative fractions Get 3 of 4 questions to level up!
- Negative signs in fractions Get 3 of 4 questions to level up!
- Negative signs in fractions (with variables) Get 3 of 4 questions to level up!
- Dividing mixed numbers with negatives Get 3 of 4 questions to level up!
- Simplify complex fractions Get 5 of 7 questions to level up!
- Equivalent expressions with negative numbers (multiplication and division) Get 3 of 4 questions to level up!
- Dividing by zero Get 3 of 4 questions to level up!
Topic C: Applying operations with rational numbers to expressions and equations
- Order of operations example (Opens a modal)
- Order of operations with rational numbers (Opens a modal)
- Negative number word problem: temperatures (Opens a modal)
- Negative number word problem: Alaska (Opens a modal)
- Interpreting negative number statements (Opens a modal)
- Interpreting multiplication & division of negative numbers (Opens a modal)
- Adding integers: find the missing value (Opens a modal)
- Subtracting integers: find the missing value (Opens a modal)
- Substitution with negative numbers (Opens a modal)
- Ordering expressions (Opens a modal)
- Order of operations with negative numbers Get 5 of 7 questions to level up!
- Negative number addition and subtraction: word problems Get 3 of 4 questions to level up!
- Interpreting negative number statements Get 3 of 4 questions to level up!
- Multiplying & dividing negative numbers word problems Get 3 of 4 questions to level up!
- Addition & subtraction: find the missing value Get 3 of 4 questions to level up!
- Substitution with negative numbers Get 5 of 7 questions to level up!
- Ordering negative number expressions Get 3 of 4 questions to level up!

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

3.11: Problem Bank
- Last updated
- Save as PDF
- Page ID 10386

- Michelle Manes
- University of Hawaii
Compute the following using dots and boxes:
99916131 : 31
637824 : 302
2125122 : 1011
- Fill in the squares using the digits 4, 5, 6, 7, 8, and 9 exactly one time each to make the largest possible sum: $$\begin{split} \Box\; \Box\; \Box \\ +\; \Box\; \Box\; \Box \\ \hline \end{split}$$
- Fill in the squares using the digits 4, 5, 6, 7, 8, and 9 exactly one time each to make the smallest possible (positive) difference: $$\begin{split} \Box\; \Box\; \Box \\ -\; \Box\; \Box\; \Box \\ \hline \end{split}$$
- Make a base six addition table.
- Use the table to solve these subtraction problems. $$13_{six} - 5_{six} \qquad 12_{six} - 3_{six} \qquad 10_{six} - 4_{six} \ldotp$$
Do these calculations in base four. Don’t translate to base 10 and then calculate there — try to work in base four.
- $$33_{four} + 11_{four}$$
- $$123_{four} + 22_{four}$$
- $$223_{four} - 131_{four}$$
- $$112_{four} - 33_{four}$$
- Make a base five multiplication table.
- Use the table to solve these subtraction problems. $$11_{five} \div 2_{five} \qquad 22_{five} \div 3_{five} \qquad 13_{five} \div 4_{five} \ldotp$$
- Here is a true fact in base five: $$2_{five} \cdot 3_{five} = 11_{five}$$Write the rest of this four fact family.
- Here is a true fact in base five: $$13_{five} \div 2_{five} = 4_{five}$$Write the rest of this four fact family.
Directions for AlphaMath Problems (Problems 38 – 41):
- Letters stand for digits 0–9.
- In a given problem, the same letter always represents the same digit, and different letters always represent different digits.
- There is no relation between problems (so “A” in part 1 and “A” in part 3 might be different).
- Two, three, and four digit numbers never start with a zero.
- Your job: Figure out what digit each letter stands for, so that the calculation shown is correct.
Notes: In part 2, “O” represents the letter “oh,” not the digit zero.
- $$\begin{split} A & \\ A & \\ +\; A & \\ \hline H\; A & \end{split}$$
- $$\begin{split} O\; N\; E & \\ +\; O\; N\; E & \\ \hline T\; W\; O & \end{split}$$
- $$\begin{split} A\; B\; C & \\ +\; A\; C\; B & \\ \hline C\; B\; A & \end{split}$$
Here’s another AlphaMath problem. \[\begin{split} T\; E\; N & \\ +\; N\; O\; T & \\ \hline N\; I\; N\; E & \end{split} \nonumber \]
- Solve this AlphaMath problem in base 10.
- Now solve it in base 6.
Find all solutions to this AlphaMath problem in base 9 .
Notes: Even though this is two calculations, it is a single problem . All T’s in both calculations represent the same digit, all B’s represent the same digit, and so on.
Remember that “O” represents the letter “oh” and not the digit zero, and that two and three digit numbers never start with the digit zero
\[ \begin{split} T\; O & \\ -\; B\; E & \\ \hline O\; R & \end{split} \qquad \begin{split} N\; O\; T & \\ -\; T\; O & \\ \hline B\; E & \end{split} \nonumber \]
This is a single AlphaMath problem. (So all G’s represent the same digit. All A’s represent the same digit. And so on.)
Solve the problem in base 6 . \[GALON = (GOO)^{2} \qquad \qquad ALONG = (OOG)^{2} \nonumber \]
- Which of the following base seven numbers are perfect squares? For each number, answer yes (it is a perfect square) or no (it is not a perfect square) and give a justification of your answer. $$4_{seven} \qquad 25_{seven} \qquad 51_{seven}$$
Geoff spilled coffee on his homework. The answers were correct. Can you determine the missing digits and the bases?
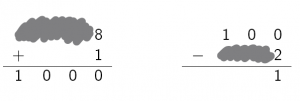
- Rewrite each subtraction problem as an addition problem: $$x - 156 = 279 \qquad 279 - 156 = x \qquad a - x = b \ldotp$$
- Rewrite each division problem as a multiplication problem: $$24 \div x = 12 \qquad x \div 3 = 27 \qquad a \div b = x \ldotp$$
Which of the following models represent the same multiplication problem? Explain your answer.
Show an area model for each of these multiplication problems. Write down the standard computation next to the area model and see how it compares. \[20 \times 33 \qquad 24 \times 13 \qquad 17 \times 11 \nonumber \]
Suppose the 2 key on your calculator is broken. How could you still use the calculator compute these products? Think about what properties of multiplication might be helpful. (Write out the calculation you would do on the calculator, not just the answer.) \[1592 \times 3344 \qquad 2008 \times 999 \qquad 655 \times 525 \nonumber \]
Today is Jennifer’s birthday, and she’s twice as old as her brother. When will she be twice as old as him again? Choose the best answer and justify your choice.
- Jennifer will always be twice as old as her brother.
- It will happen every two years.
- It depends on Jennifer’s age.
- It will happen when Jennifer is twice as old as she is now.
- It will never happen again.
- Find the quotient and remainder for each problem. $$7 \div 3 \qquad 3 \div 7 \qquad 7 \div 1 \qquad 1 \div 7$$
- How many possible remainders are there when dividing by these numbers? Justify what you say. $$2 \qquad 12 \qquad 62 \qquad 23$$
Identify each problem as either partitive or quotative division and say why you made that choice. Then solve the problem.
- Adriana bought 12 gallons of paint. If each room requires three gallons of paint, how many rooms can she paint?
- Chris baked 15 muffins for his family of five. How many muffins does each person get?
- Prof. Davidson gave three straws to each student for an activity. She used 51 straws. How many students are in her class?
Use the digits 1 through 9. Use each digit exactly once. Fill in the squares to make all of the equations true. \[\begin{split} \Box - \Box = \Box & \\ \times & \\ \Box \div \Box = \Box & \\ = & \\ \Box + \Box = \Box & \end{split} \nonumber \]
Illustrative Mathematics Grade 7, Unit 5, Lesson 14: Solving Problems with Rational Numbers
Learning Targets:
- I can represent situations with expressions that include rational numbers.
- I can solve problems using the four operations with rational numbers.
Related Pages Illustrative Math Grade 7
Lesson 14: Solving Problems with Rational Numbers
Let’s use all four operations with signed numbers to solve problems.
Illustrative Math Unit 7.5, Lesson 14 (printable worksheets)
Lesson 14 Summary

Lesson 14.1 Which One Doesn’t Belong: Equations
Which equation doesn’t belong? 1/2 x = -50 -60t = 30 x + 90 = -100 -0.01 = -0.001x
Lesson 14.2 Draining and Filling a Tank
A tank of water is being drained. Due to a problem, the sensor does not start working until some time into the draining process. The sensor starts its recording at time zero when there are 770 liters in the tank.
- Given that the drain empties the tank at a constant rate of 14 liters per minute, complete the table:
- Later, someone wants to use the data to find out how long the tank had been draining before the sensor started. Complete this table:
- If the sensor started working 15 minutes into the tank draining, how much was in the tank to begin with?
Lesson 14.3 Buying and Selling Power
A utility company charges $0.12 per kilowatt-hour for energy a customer uses. They give a credit of $0.025 for every kilowatt-hour of electricity a customer with a solar panel generates that they don’t use themselves. A customer has a charge of $82.04 and a credit of -$4.10 on this month’s bill.
- What is the amount due this month?
- How many kilowatt-hours did they use?
- How many kilowatt-hours did they generate that they didn’t use themselves?
Are you ready for more?
- Write an expression that uses addition, subtraction, multiplication, and division and only negative numbers that has the same value.
Lesson 14 Practice Problems
- A furniture store pays a wholesale price for a mattress. Then, the store marks up the retail price to 150% of the wholesale price. Later, they put the mattress on sale for 50% off of the retail price. A customer just bought the mattress on sale and paid $1,200. a. What was the retail price of the mattress, before the discount? b. What was the wholesale price, before the markup?
- The table shows transactions in a checking account. a. Find the total of the transactions for each month. b. Find the mean total for the four months.
- A bank charges a service fee of $7.50 per month for a checking account. A bank account has $85.00. If no money is deposited or withdrawn except the service charge, how many months until the account balance is negative?
- A large aquarium of water is being filled with a hose. Due to a problem, the sensor does not start working until some time into the filling process. The sensor starts its recording at the time zero minutes. The sensor initially detects the tank has 225 liters of water in it. a. The hose fills the aquarium at a constant rate of 15 liters per minute. What will the sensor read at the time 5 minutes? b. Later, someone wants to use the data to find the amount of water at times before the sensor started. What should the sensor have read at the time -7 minutes?
- a. A restaurant bill is $21. You leave a 15% tip. How much do you pay including the tip? b. Which of the following represents the amount a customer pays including the tip of 15% if the bill was dollars? Select all that apply.
The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics .

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

7.1.2B Problem Solving with Rational Numbers
Standard 7.1.2.
Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest.
Use proportional reasoning to solve problems involving ratios in various contexts.
For example : A recipe calls for milk, flour and sugar in a ratio of 4:6:3 (this is how recipes are often given in large institutions, such as hospitals). How much flour and milk would be needed with 1 cup of sugar?
Standard 7.1.2 Essential Understandings
In this standard, students will develop a unified understanding of number, recognizing fractions, decimals (that have a finite or a repeating decimal representation), and percents as different representations of rational numbers. Students extend addition, subtraction, multiplication and division to all rational numbers, maintaining the properties of operations and the relationships between addition and subtraction, and multiplication and division. By applying these properties, and by viewing negative numbers in terms of everyday contexts (e.g., amounts owed or temperatures below zero), students explain and interpret the rules for adding, subtracting, multiplying and dividing with negative numbers.
The focus of instruction at the 7th grade level is on being able to comfortably translate between decimal and fractional forms of a number for both positive and negative values. Students should be able to compare numbers and manipulate the values to derive other forms of the numbers to make comparing less inhibiting and more accessible. Students will also use ratios and proportional reasoning to solve problems in various contexts. Students will be able to use information given to help find missing values. Their knowledge of equivalent fractions and scaling will enable them to use ratios and solve proportions.
All Standard Benchmarks
7.1.2.1 Add, subtract, multiply and divide positive and negative rational numbers that are integers, fractions and terminating decimals; use efficient and generalizable procedures, including standard algorithms; raise positive rational numbers to whole-number exponents. 7.1.2.2 Use real-world contexts and the inverse relationship between addition and subtraction to explain why the procedures of arithmetic with negative rational numbers make sense. 7.1.2.3 Understand that calculators and other computing technologies often truncate or round numbers. 7.1.2.4 Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest. 7.1.2.5 Use proportional reasoning to solve problems involving ratios in various contexts. 7.1.2.6 Demonstrate an understanding of the relationship between the absolute value of a rational number and distance on a number line. Use the symbol for absolute value.
7.1.2 Group B - Problem Solving with Rational Numbers
7.1.2.4 Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest. 7.1.2.5 Use proportional reasoning to solve problems involving ratios in various contexts. For example, a recipe calls for milk, flour and sugar in a ratio of 4:6:3. (This is how recipes are often given in large institutions, such as hospitals.) How much flour and milk would be needed with 1 cup of sugar?
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Understand that simple interest does not use interest earned as new principal, but compound interest does;
- Model addition and subtraction of integers with physical materials and the number line;
- Perform calculations with and without the use of a calculator;
- Understand the rules for calculating with positive and negatives;
- Understand calculating with positive exponents;
- Scale values up and down;
- See the relationship as a proportional relationship;
- Use ratios accurately;
- Compare ratios;
- Be able to differentiate mathematical characteristics of proportional thinking from nonproportional contexts;
- Know the mathematical characteristics of proportional situations.
Work from previous grades that supports this new learning includes:
- Use and read output on a calculator;
- Know how to change percents to decimals and decimals to percents;
- Know how to calculate a percent of a number, such as 25% of 1000;
- Use and find percents;
- Use and find fractions and equivalent values;
- Multiply and divide;
- Input into a calculator, using correct keystrokes;
- Perform mental math;
- Understand equivalent fractions;
- Scale up and down;
- Use ratios;
- Know multiplication facts to 12's;
- Be proficient at problem solving ;
- Know how to work backwards;
- Understand and use the terms including numerator, denominator, greatest common factor and least common multiple;
- Know how to simplify fractions.
- Make use of estimation strategies.
NCTM Standards
Understand numbers, ways of representing numbers, relationships among numbers, and number systems:
- Work flexibly with fractions, decimals, and percents to solve problems;
- Understand and use ratios and proportions to represent quantitative relationships.
Understand meanings of operations and how they relate to one another:
- Understand the meaning and effects of arithmetic operations with fractions decimals, and integers;
- Understand and use the inverse relationships of addition and subtraction, multiplication and division, and squaring and finding square roots to simplify computations and solve problems.
Compute fluently and make reasonable estimates:
- Select appropriate methods and tools for computing for computing with fractions and decimals from among mental computation, estimation, calculators or computers, and paper and pencil, depending on the situations and apply the selected methods;
- Develop and use strategies to estimate the results of rational-number computations and judge the reasonableness of the results.
Common Core State Standards (CCSS)
7.NS ( The Number System ) Apply and extend previous understandings of operations with fractions to add, subtract, multiply, and divide rational numbers.
- 7.NS. 1. Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram;
- 7.NS.1.b. Understand p + q as the number located a distance |q| from p, in the positive or negative direction depending on whether q is positive or negative. Show that a number and its opposite have a sum of 0 (are additive inverses). Interpret sums of rational numbers by describing real-world contexts;
- 7.NS.1.c . Understand subtraction of rational numbers as adding the additive inverse, p - q = p + (-q). Show that the distance between two rational numbers on the number line is the absolute value of their difference, and apply this principle in real-world contexts;
- 7.NS.1.d. Apply properties of operations as strategies to add and subtract rational numbers;
- 7.NS.2. Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers;
- 7.NS.2a. Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (-1)(-1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts;
- 7.NS.2.c. Apply properties of operations as strategies to multiply and divide rational numbers;
- 7.NS.3. Solve real-world and mathematical problems involving the four operations with rational numbers.
6.NS (The Number System) Apply and extend previous understandings of numbers to the system of rational numbers.
- 6.NS.7c. Understand ordering and absolute value of rational numbers. Understand the absolute value of a rational number as its distance from 0 on the number line; interpret absolute value as magnitude for a positive or negative quantity in a real-world situation. For example, for an account balance of -30 dollars, write |-30| = 30 to describe the size of the debt in dollars.
- 6.EE (Expressions and Equations) Apply and extend previous understandings of arithmetic to algebraic expressions.
6.EE.1. Write and evaluate numerical expressions involving whole-number exponents.
7.EE (Expressions and Equations) Use properties of operations to generate equivalent expressions.
- 7.EE.3. Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations as strategies to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies.
- 7.RP (Ratios and Proportional Relationships) Analyze proportional relationships and use them to solve real-world and mathematical problems.
7.RP.3. Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.
Misconceptions
Student misconceptions and common errors.
- Students may not realize that finding the percent of a number always involves division.
- Students incorrectly enter the percent into the calculator instead of the decimal value, and thus get a value that does not make sense. Many students do not know how to use the % key on a calculator.
- Students get confused with the difference between simple and compound interest.
- Students may not realize that using a proportion is the only way to solve these problems.
- Students want to use addition to get equivalent values, not multiplication.
- Students forget how to multiply with fractional values.
- If using a fractional scale factor (cutting a recipe in $\frac{1}{2}$), students may just add $\frac{1}{2}$ to the values they have, instead of dividing all the values by 2.
In the Classroom
In this vignette, students will mix juice.
Mixing Juice
Teacher: How many of you have made orange juice from a can before?
Student 1: I make it all the time.
Student 2: My mom makes ours.
Others raise their hands to indicate they have either made it or helped make it.
Teacher: When you made juice or helped, what did you have to do?
Student 3: Make sure we didn't add too much water or it wouldn't taste very good.
Teacher: Anything else?
Student 2: Make sure we add enough water or it would be too sour and strong tasting.
Teacher: Today we are going to look at some different recipes for different juice mixes. Each recipe is different from the others, so we are going to use our math skills and see if we can decide which juice would be the most orangey, and which would be the least orangey.
Student 1: Won't it depend on the brand of juice we use, too?
Teacher: You are right; that could be a factor, and that could be something we explore at a different time, but for today, we are going to assume that all the juices are the same brand, so that won't be a factor.
Teacher: OK, here is your information. Cam and Scott are in charge of making juice for the 200 students at camp. They mix water and frozen concentrate to make the juice. They were given the following recipes from different campers:
Teacher: OK, your task is to figure out which one is the most orangey. Good luck!
As the teacher circulates around, she hears some of the following conversations.
Student 1 : I think Mix V will be the most orangey because it has 5 cups of concentrate, and no other juice has that much, so it has to be the most orangey.
Student 2 : I think Mix S and Mix T will be the same because they each have only one more cup of concentrate than juice, so they should taste the same, shouldn't they?
Teacher: Well, how about if we use some concepts we've talk about in class before. What could we do that might help us?
Student 3: Write them as fractions?
Student 2: Find out what percent of each is concentrate?
Student 1: We could write ratios for each recipe.
Teacher: OK. It sounds like we have many ideas. There are multiple ways to do this problem. Just make sure you understand what you are doing, and if you get an answer, make sure you know what it represents in terms of the problem.
Student 1: Well for Mix S, $\frac{2}{3}$ of the juice is concentrate.
Teacher: Let's look at that again. While fractions offer one way of working on this problem, what you said is not accurate. Remember what you know about fractions. If you say that $\frac{2}{3}$ of the juice is concentrate, then which number in the fraction tells you how many total cups are in the juice?
Student 2: Well, the denominator is the total, so the total would be 3 cups. In Mix S, though, there are 3 cups of concentrate AND 2 cups of water, so there's really 5 cups of ingredients in the juice.
Teacher: So is $\frac{2}{3}$ of Mix S concentrate?
Student 1: No, I guess it isn't. But shouldn't we be able to use the fraction $\frac{2}{3}$?
Teacher: Let's talk about that. If we use $\frac{2}{3}$, what does the 2 represent?
Student 3: The 2 cups of water.
Teacher: And what does the 3 represent?
Student 4: The 3 cups of concentrate.
Teacher: So if we wanted to know what fraction is concentrate, what fraction would we use?
Student 2: $\frac{2}{5}$, because 5 is the total amount of cups in the juice and 2 is the number of cups of concentrate.
Teacher: OK. Keep working and I'll come back to you. Again, we are trying to figure out which one is the most orangey.
The teacher continues to circulate around the room, listening to conversations that different groups are having.
Teacher: Who has an idea here? Which mix does your group think is the most orangey?
Student 2: We think it is Mix T. We set up ratios of concentrate to water, and compared the decimal values. So this is what we got:
Teacher: What do those decimal values represent?
Student 2: The ratio of concentrate to water.
Teacher: Did anyone do this another way?
Student 3: We found out what percent of the juice was concentrate. So here is what we got. We agree that Mix T is the most orangey.
Teacher: So, we can see from these two strategies that Mix T is the most orangey. Which one is the least orangey?
Student 1: Mix U. If you look at the percent that is concentrate, we can see that Mix U has the least percent of concentrate, so it is the least orangey.
Teacher: Let's move on to the next part of the problem. Assume each camper gets $\frac{1}{2}$ cup of juice. For each mix, you need to now figure out how many batches are needed to be made to serve all of the campers. Remember, there are 200 campers.
Student 4: I think we need to first figure out how many cups are in each batch of juice.
Teacher: Why would you need to know that?
Student 4: So we can scale the recipe up to make enough to feed the campers.
Teacher: Good thought process. Go ahead and give it a try and let me know how it goes.
Student 3: Can't we just multiply 200 by $\frac{1}{2}$ to get 100? We need 100 cups of juice made.
Teacher: OK. You are right that you need 100 cups, but that is 100 cups of juice. That doesn't say how many cups of each of the 2 ingredients you need.
Student 3: Oh. That's right. We need to do that. Hmm. Maybe putting the information into tables could help us.
Teacher: Nice. Any other way this could have been figured out?
Student 4: We used proportional reasoning to solve it. We knew that we needed 100 cups total. We also knew how many batches we needed. So, we knew we needed 100 cups total, and there were 5 total cups in the batch made. Since we needed two cups of concentrate, then we can scale that up. Here's the proportion we set up:
$\frac{2}{5}$ = $\frac{x}{100}$
Student 4: So, we can solve and get 40 for x, just like the other group did. So, we need 40 cups of concentrate and 60 cups of water. We did that same process for the rest of them, too, like our table shows. By doing it our way, we won't have as much left over, because they rounded the number of batches, and we set up proportions so we have a closer number of cups that would be needed. We still have Mix T using the most concentrate in proportion to the amount of water used.
Teacher: OK. Nice work! To finish the lesson, here is your final task: Which of the following will taste most orangey: 2 cups of concentrate and 3 cups of water; 4 cups of concentrate and 6 cups of water; or 10 cups of concentrate and 15 cups of water?
The students use various strategies that were discussed in class.
Teacher: Anyone have an answer?
Student 2 : I think they are all the same orangey-ness?
Teacher: How could that be if they all have different numbers of concentrate and water?
Student 1: Because when we compared all of the ratios, they were equivalent: 2 to 3 is equivalent to 4 to 6, is equivalent to 10 to 15. If we write them all as fractions we can see that even better.
Teacher: Can you come up to the board and show us what you are doing?
Student 1: Sure. Here is what I did:
$\frac{2}{3}$ = $\frac{4}{6}$ = $\frac{10}{15}$
They all simplify to being the same concentrate, $\frac{2}{3}$, so, they are all proportional to one another.
Teacher: Nice job today. We will review this tomorrow.
Teacher Notes
- To find percent increase or percent decrease, have the students subtract the two values being compared. Then, have them take that answer and divide it by the beginning value to get the ratio of change to starting value. Multiply this value by 100 to get the percent change. For example, the population changed from 1000 to 1150. What was the percent increase? The students would subtract 1150 - 1000 to get 150. They then need to divide 150 by 1000 to get 0.15. Multiply this value by 100 (change a decimal to a percent), and the percent increase is 0.15 × 100 which equals 15%. This website provides a calculator that will do this.
- The scale on a map suggests that 1 centimeter represents an actual distance of 5 kilometers. The map distance between two towns is 8 centimeters. What is the actual distance? In this situation, a table can help highlight this relationship.
Drawing pictures may help students see that the rate is a scalar concept.
- To help students learn the difference between compound and simple interest, work on simple interest first. In simple interest, the amount of interest earned is proportional to the number of months invested. For example, a deposit of $500 in an account earns 1% simple interest each month. After 1 month, $5 of interest would be earned, because $500×1% = $5. ($500x0.01 = $5). After two months, there will be $10 of interest earned. Interest is only earned on the original deposit with simple interest. With compound interest, interest is not only calculated on the original deposit, but also the interest that has previously been earned. So, one month, the interest earned would be $500x1% = $5. The balance after that first month is $505. After two months, the interest is earned on the total balance of $505. As shown in the table, the amount added each month is not constant, therefore, compound interest earned is not an example of a proportional relationship, whereas simple interest earned is showing a proportional relationship.
- Proportion problems This website will explain proportions, provide examples, and provides sample problems.
- Ratios and proportions This site includes ratios, comparing ratios, and proportions.
- Ratio and proportion factsheets
- Ratios and proportions in everyday life This site addresses ratios and proportions and how knowledge of these mathematical concepts is used in everyday life. It includes lesson plans, animation, online and printable worksheets, online exercises, games, quizzes, and a link to eThemes Resource on Math: Equivalent Ratios.
- Real-world proportions This site includes problems with solving proportions (algorithms) and real-world applications.
- Math in daily life: Cooking by numbers This webpage that helps make a connection between proportions and the real-life situation of cooking.
- Burns, M., and Sheffield, S. (2004). Jim and the Beanstalk. In Math and Literature (p. 60) . Sausalito, CA: Math Solutions Publications.
- Burns, M., and Sheffield, S. (2004). How Big is a Foot. In Math and Literature (p. 47). Sausalito, CA: Math Solutions Publications.

- interest: fee paid on loans or earned on invested money, based on the principal amount and the interest rate.
- simple interest: interest paid only on the original principal, not on the interest accrued.
- compound interest: interest computed on accumulated interest as well as on the principal.
- proportion: an equation which states that two ratios are equal; a relationship between two ratios. Example: $\frac{\text{hours spent on homework}}{\text{hours spent in school}}=\frac{2}{7}$
Note that this does not necessarily imply that "hours spent on homework" = 2 or that "hours spent in school" = 7. During a week, 10 hours may have been spent on homework while 35 hours were spent in school. The proportion is still true because $\frac{10}{35}=\frac{2}{7}$.
- proportional reasoning: a mathematical way of thinking in which students recognize proportional versus non-proportional situations and can use multiple approaches, not just the cross-products approach, for solving problems about proportional situations.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- What conclusions can be drawn about the student's understanding of applying relationships to solve problems in various contexts?
- Can students scale values up or down and understand why they are doing it?
- Can students tell if a relationship is proportional by looking at the verbal description of it, or do they need to mathematically figure it out?
- Are students able to transfer prior knowledge about equivalent fractions to the concept of proportionality?
- Do students understand why their procedures work?
- What connections have been made as students explored the mathematical characteristics of proportional situations?
- What models would help students in understanding the concepts addressed in the lesson?
- What aspects of proportional relationships are students still struggling with?
Cramer, K. & Post, T. (1993, February). Making connections: A case for proportionality. In Arithmetic Teacher, 60(6), 342-346.
- Massachusetts Comprehensive Assessment System Spring 2010 Test Items http://www.doe.mass.edu/mcas/2010/release/g7math.pdf
- Absolute value http :// www . purplemath . com / modules / absolute . htm
- Adding and subtracting negative numbers http :// www . purplemath . com / modules / negative 2. htm
- Lappan, G., Fey, J., Fitzgerald, W., Friel, S., Philips, E. (2009). Accentuate the Negative, CMP2. Pearson Prentice Hall.
- Lappan, G., Fey, J., Fitzgerald, W., Friel, S., Philips, E. (2009). Comparing and Scaling, CMP2. Pearson Prentice Hall.
- Rational Number Project: Proportional reasoning: the effect of two context variables, rate type, and problem setting http :// www . cehd . umn . edu / rationalnumberproject /89_6. html
- Dacey, L.S., and Gartland, K. (2009). Math for All: Differentiating Instruction. Sausalito, CA: Math Solutions.

Answer: a DOK: Level 3 Source: Minnesota Grade 7 Mathematics MCA - III Item Sampler Item, 2011, Benchmark 7.1.2.4
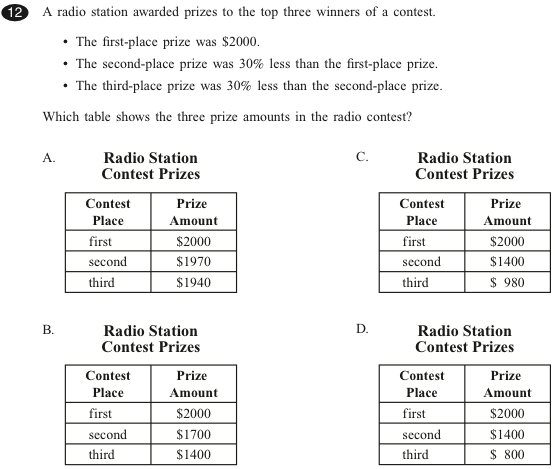
Answer: c DOK: Level 3 Source: Massachusetts Comprehensive Assessment System Release of Spring 2009 Test Items
Assume you borrow $900 at 7% annual compound interest for four years.
- How much money do you owe at the end of the four years? Show or explain your work.
- What is the total interest you will have to pay? Show or explain your work.
Answers: Part A: $900 + $252 = $1179.72; Part B: $279.72 DOK: Level 2 Source: Test Prep: Modified from MCA III Test Preparation Grade 7, Houghton Mifflin Harcourt Publishing Company, Attn: Contracts, Copyrights, and Licensing, 9400 South Park Center Loop, Orlando, FL 32819.
Tim is mixing 1 L of juice concentrate with 5L of water to make juice for his 10 guests. After he pours the mix into 10 different cups, he realizes that the juice is not sweet enough, so he adds 0.1 L of syrup into each of the cups. What is the final amount of juice in each cup? A. 0.5 L B. 0.7 L C. 1.7 L D. 2.0 L Answer: b DOK: Level 2 Source: Test Prep: MCA III Test Preparation Grade 7, Houghton Mifflin Harcourt Publishing Company, Attn: Contracts, Copyrights, and Licensing, 9400 South Park Center Loop, Orlando, FL 32819.

Answer: b DOK: Level 2 Source: Minnesota Grade 7 Mathematics MCA - III Item Sampler Item, 2011, Benchmark 7.1.2.5

Answer: b DOK: Level 2 Source: Minnesota Grade 7 Mathematics Modified MCA - III Item Sampler Item, 2011, Benchmark 7.1.2.5
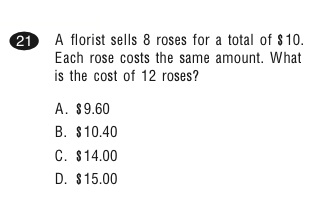
Answer: d DOK: Level 2 Source: Massachusetts Comprehensive Assessment System Release of Spring 2010 Test Items

Answer: b DOK: Level 2 Source: Massachusetts Comprehensive Assessment System Release of Spring 2010 Test Items
Differentiation
- Provide students with multiplication tables.
- Students may need to be given a place value chart to help them in rounding to the correct place (hundreds vs. hundredths).
- Use pictures and or tables to help the students see the pattern; always label the values they are trying to scale, such as 10 in = 3 ft, 3 in = ________ft. By keeping the labels with the numbers, fewer errors in relationships will be made.
- Students may see the word "ratio" as "radios." Assist them by clarifying the meaning and pronunciation of both words.
- Use a graphic organizer displaying operations with integer rules .
- Introduce √ of a number to plot on a number line.
- Do multi-step conversion-type problems to show proportional relationship.
- Explain the concept of compound interest using exponential growth and exponential equations.
- Create a gameboard activity. Have students work in groups of four to create gameboards marked with mathematical questions they must answer to be able to move ahead on the boards. They should use at least three addition, three subtraction, three multiplication and three division operations. They should also use positive numbers, negative numbers, decimals, and fractions. Students will fill in operation symbols and numbers on the boards. When they are done, the class can play the different games.
Parents/Admin
Administrative/peer classroom observation, parent resources.
- Math games, problems and puzzles
Related Frameworks
7.1.2a applying & making sense of rational numbers.
- 7.1.2.1 Arithmetic Procedures
- 7.1.2.2 Explain Arithmetic Procedures
- 7.1.2.3 Calculators & Rational Numbers
- 7.1.2.6 Absolute Value
- 7.1.2.4 Solve Problems with Rational Numbers Including Positive Integer Exponents
- 7.1.2.5 Proportional Reasoning
3.11 unit test problem solving with rational numbers part 1
Solving problems with rational numbers.
In this section, we will learn how to solve problems with rational numbers.
A number that is expressed in the form a/b is called as rational number.
Here, both "a" and "b" are integers and also b ≠ 0.
Problem 1 :
The area of a rectangular sandbox is 56 2/3 square feet. The length of the sandbox is 8 1/2 feet. What is the width ?
We know the formula to find area of the rectangle.
That is,
Area of the rectangle = length x width
Plug the known values area and length and solve for the unknown value width.
56 2/3 = 8 1/2 x width
170/3 = 17/2 x width
(170/3) x (2/17) = width
20/3 = width
6 2/3 = width
Therefore, the width of the rectangle is 6 2/3 feet.
Problem 2 :
Mr. Webster is buying carpet for an exercise room where the basement of the room is in the shape of rectangle. The length and width of the room are 18 2/5 feet and 12 1/2 feet respectively. Find the total cost of the carpet, if the price of the carpet is $3 per square feet ?
To know the total cost of the carpet, first we have to know the area of the basement.
Area of the basement = length x width
= 18 2/5 x 12 1/2
= (92/5) x (25/2)
= 46 x 5
= 230 square feet
So, we need 230 square feet of carpet.
The cost each square feet of carpet = $3
Then, the cost of 230 square ft of carpet is
= 3 x 230
= $690
Therefore, the total cost of the carpet is $690.
Problem 3 :
Problem 4 :
David is cooking enough lentils for lentil barley soup and lentil salad. The lentil barley soup recipe calls for 3/ 4 cup of dried lentils. The lentil salad recipe calls for 1 1/ 2 cups of dried lentils. David has a 1/ 8 -cup scoop. How many scoops of dried lentils will David need to have enough for the soup and the salad?
David needs 3/ 4 cup of dried lentils for soup and 1 1/ 2 cups for salad.
Total amount dried lentils that David need is
= (3/4) + (1 1/2)
= 3/4 + 3/2
= 3/4 + 6/4
= (3+6) / 4
= 9/4
David needs 9/4 cups of dried lentils for both the soup and the salad.
To find how many 1/8 -cup scoops he needs, divide the total amount of dried lentils into groups of 1/8.
Then, we have
= 9/4 ÷ 1/8
= 9/4 x 8/1
= 9 x 2
Hence, David will need 18 scoops of dried lentils to have enough for both the lentil barley soup and the lentil salad.
Problem 5 :
If the numerator of a fraction is increased by 2 and the denominator by 1, it becomes 1. In case, the numerator is decreased by 4 and the denominator by 2, it becomes 1/2. Find the fraction.
Let "x/y" be the required fraction.
"If the numerator is increased by 2 and the denominator by 1, the fraction becomes 1"
From the above information, we have (x+2) / (y+1) = 1
(x + 2) / (y + 1) = 1
x + 2 = y + 1
x - y = -1 ----(1)
"In case the numerator is decreased by 4 and the denominator by 2, the fraction becomes 1/2"
From the above information, we have
(x - 4) / (y - 2) = 1 / 2
2(x - 4) = y - 2
2x - y = 6 ----(1)
Solving (1) and (2), we get
x = 7 and y = 8
x / y = 7 / 8
So, the required fraction is 7/8.
Kindly mail your feedback to [email protected]
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
- Sat Math Practice
- SAT Math Worksheets
- PEMDAS Rule
- BODMAS rule
- GEMDAS Order of Operations
- Math Calculators
- Transformations of Functions
- Order of rotational symmetry
- Lines of symmetry
- Compound Angles
- Quantitative Aptitude Tricks
- Trigonometric ratio table
- Word Problems
- Times Table Shortcuts
- 10th CBSE solution
- PSAT Math Preparation
- Privacy Policy
- Laws of Exponents
Recent Articles
Honors Algebra 2 Problems on Solving Logarithmic Equations
Apr 01, 24 07:22 PM
Honors Algebra 2 Problems on Solving Exponential Equations
Mar 30, 24 11:45 PM
Properties of Parallelograms Worksheet
Mar 30, 24 09:11 PM

7.1.2B Problem Solving with Rational Numbers
Standard 7.1.2.
Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest.
Use proportional reasoning to solve problems involving ratios in various contexts.
For example : A recipe calls for milk, flour and sugar in a ratio of 4:6:3 (this is how recipes are often given in large institutions, such as hospitals). How much flour and milk would be needed with 1 cup of sugar?
Standard 7.1.2 Essential Understandings
In this standard, students will develop a unified understanding of number, recognizing fractions, decimals (that have a finite or a repeating decimal representation), and percents as different representations of rational numbers. Students extend addition, subtraction, multiplication and division to all rational numbers, maintaining the properties of operations and the relationships between addition and subtraction, and multiplication and division. By applying these properties, and by viewing negative numbers in terms of everyday contexts (e.g., amounts owed or temperatures below zero), students explain and interpret the rules for adding, subtracting, multiplying and dividing with negative numbers.
The focus of instruction at the 7th grade level is on being able to comfortably translate between decimal and fractional forms of a number for both positive and negative values. Students should be able to compare numbers and manipulate the values to derive other forms of the numbers to make comparing less inhibiting and more accessible. Students will also use ratios and proportional reasoning to solve problems in various contexts. Students will be able to use information given to help find missing values. Their knowledge of equivalent fractions and scaling will enable them to use ratios and solve proportions.
All Standard Benchmarks
7.1.2.1 Add, subtract, multiply and divide positive and negative rational numbers that are integers, fractions and terminating decimals; use efficient and generalizable procedures, including standard algorithms; raise positive rational numbers to whole-number exponents. 7.1.2.2 Use real-world contexts and the inverse relationship between addition and subtraction to explain why the procedures of arithmetic with negative rational numbers make sense. 7.1.2.3 Understand that calculators and other computing technologies often truncate or round numbers. 7.1.2.4 Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest. 7.1.2.5 Use proportional reasoning to solve problems involving ratios in various contexts. 7.1.2.6 Demonstrate an understanding of the relationship between the absolute value of a rational number and distance on a number line. Use the symbol for absolute value.
7.1.2 Group B - Problem Solving with Rational Numbers
7.1.2.4 Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest. 7.1.2.5 Use proportional reasoning to solve problems involving ratios in various contexts. For example, a recipe calls for milk, flour and sugar in a ratio of 4:6:3. (This is how recipes are often given in large institutions, such as hospitals.) How much flour and milk would be needed with 1 cup of sugar?
What students should know and be able to do [at a mastery level] related to these benchmarks:
- Understand that simple interest does not use interest earned as new principal, but compound interest does;
- Model addition and subtraction of integers with physical materials and the number line;
- Perform calculations with and without the use of a calculator;
- Understand the rules for calculating with positive and negatives;
- Understand calculating with positive exponents;
- Scale values up and down;
- See the relationship as a proportional relationship;
- Use ratios accurately;
- Compare ratios;
- Be able to differentiate mathematical characteristics of proportional thinking from nonproportional contexts;
- Know the mathematical characteristics of proportional situations.
Work from previous grades that supports this new learning includes:
- Use and read output on a calculator;
- Know how to change percents to decimals and decimals to percents;
- Know how to calculate a percent of a number, such as 25% of 1000;
- Use and find percents;
- Use and find fractions and equivalent values;
- Multiply and divide;
- Input into a calculator, using correct keystrokes;
- Perform mental math;
- Understand equivalent fractions;
- Scale up and down;
- Use ratios;
- Know multiplication facts to 12's;
- Be proficient at problem solving ;
- Know how to work backwards;
- Understand and use the terms including numerator, denominator, greatest common factor and least common multiple;
- Know how to simplify fractions.
- Make use of estimation strategies.
NCTM Standards
Understand numbers, ways of representing numbers, relationships among numbers, and number systems:
- Work flexibly with fractions, decimals, and percents to solve problems;
- Understand and use ratios and proportions to represent quantitative relationships.
Understand meanings of operations and how they relate to one another:
- Understand the meaning and effects of arithmetic operations with fractions decimals, and integers;
- Understand and use the inverse relationships of addition and subtraction, multiplication and division, and squaring and finding square roots to simplify computations and solve problems.
Compute fluently and make reasonable estimates:
- Select appropriate methods and tools for computing for computing with fractions and decimals from among mental computation, estimation, calculators or computers, and paper and pencil, depending on the situations and apply the selected methods;
- Develop and use strategies to estimate the results of rational-number computations and judge the reasonableness of the results.
Common Core State Standards (CCSS)
7.NS ( The Number System ) Apply and extend previous understandings of operations with fractions to add, subtract, multiply, and divide rational numbers.
- 7.NS. 1. Apply and extend previous understandings of addition and subtraction to add and subtract rational numbers; represent addition and subtraction on a horizontal or vertical number line diagram;
- 7.NS.1.b. Understand p + q as the number located a distance |q| from p, in the positive or negative direction depending on whether q is positive or negative. Show that a number and its opposite have a sum of 0 (are additive inverses). Interpret sums of rational numbers by describing real-world contexts;
- 7.NS.1.c . Understand subtraction of rational numbers as adding the additive inverse, p - q = p + (-q). Show that the distance between two rational numbers on the number line is the absolute value of their difference, and apply this principle in real-world contexts;
- 7.NS.1.d. Apply properties of operations as strategies to add and subtract rational numbers;
- 7.NS.2. Apply and extend previous understandings of multiplication and division and of fractions to multiply and divide rational numbers;
- 7.NS.2a. Understand that multiplication is extended from fractions to rational numbers by requiring that operations continue to satisfy the properties of operations, particularly the distributive property, leading to products such as (-1)(-1) = 1 and the rules for multiplying signed numbers. Interpret products of rational numbers by describing real-world contexts;
- 7.NS.2.c. Apply properties of operations as strategies to multiply and divide rational numbers;
- 7.NS.3. Solve real-world and mathematical problems involving the four operations with rational numbers.
6.NS (The Number System) Apply and extend previous understandings of numbers to the system of rational numbers.
- 6.NS.7c. Understand ordering and absolute value of rational numbers. Understand the absolute value of a rational number as its distance from 0 on the number line; interpret absolute value as magnitude for a positive or negative quantity in a real-world situation. For example, for an account balance of -30 dollars, write |-30| = 30 to describe the size of the debt in dollars.
- 6.EE (Expressions and Equations) Apply and extend previous understandings of arithmetic to algebraic expressions.
6.EE.1. Write and evaluate numerical expressions involving whole-number exponents.
7.EE (Expressions and Equations) Use properties of operations to generate equivalent expressions.
- 7.EE.3. Solve multi-step real-life and mathematical problems posed with positive and negative rational numbers in any form (whole numbers, fractions, and decimals), using tools strategically. Apply properties of operations as strategies to calculate with numbers in any form; convert between forms as appropriate; and assess the reasonableness of answers using mental computation and estimation strategies.
- 7.RP (Ratios and Proportional Relationships) Analyze proportional relationships and use them to solve real-world and mathematical problems.
7.RP.3. Use proportional relationships to solve multistep ratio and percent problems. Examples: simple interest, tax, markups and markdowns, gratuities and commissions, fees, percent increase and decrease, percent error.
Misconceptions
Student misconceptions and common errors.
- Students may not realize that finding the percent of a number always involves division.
- Students incorrectly enter the percent into the calculator instead of the decimal value, and thus get a value that does not make sense. Many students do not know how to use the % key on a calculator.
- Students get confused with the difference between simple and compound interest.
- Students may not realize that using a proportion is the only way to solve these problems.
- Students want to use addition to get equivalent values, not multiplication.
- Students forget how to multiply with fractional values.
- If using a fractional scale factor (cutting a recipe in $\frac{1}{2}$), students may just add $\frac{1}{2}$ to the values they have, instead of dividing all the values by 2.
In the Classroom
In this vignette, students will mix juice.
Mixing Juice
Teacher: How many of you have made orange juice from a can before?
Student 1: I make it all the time.
Student 2: My mom makes ours.
Others raise their hands to indicate they have either made it or helped make it.
Teacher: When you made juice or helped, what did you have to do?
Student 3: Make sure we didn't add too much water or it wouldn't taste very good.
Teacher: Anything else?
Student 2: Make sure we add enough water or it would be too sour and strong tasting.
Teacher: Today we are going to look at some different recipes for different juice mixes. Each recipe is different from the others, so we are going to use our math skills and see if we can decide which juice would be the most orangey, and which would be the least orangey.
Student 1: Won't it depend on the brand of juice we use, too?
Teacher: You are right; that could be a factor, and that could be something we explore at a different time, but for today, we are going to assume that all the juices are the same brand, so that won't be a factor.
Teacher: OK, here is your information. Cam and Scott are in charge of making juice for the 200 students at camp. They mix water and frozen concentrate to make the juice. They were given the following recipes from different campers:
Teacher: OK, your task is to figure out which one is the most orangey. Good luck!
As the teacher circulates around, she hears some of the following conversations.
Student 1 : I think Mix V will be the most orangey because it has 5 cups of concentrate, and no other juice has that much, so it has to be the most orangey.
Student 2 : I think Mix S and Mix T will be the same because they each have only one more cup of concentrate than juice, so they should taste the same, shouldn't they?
Teacher: Well, how about if we use some concepts we've talk about in class before. What could we do that might help us?
Student 3: Write them as fractions?
Student 2: Find out what percent of each is concentrate?
Student 1: We could write ratios for each recipe.
Teacher: OK. It sounds like we have many ideas. There are multiple ways to do this problem. Just make sure you understand what you are doing, and if you get an answer, make sure you know what it represents in terms of the problem.
Student 1: Well for Mix S, $\frac{2}{3}$ of the juice is concentrate.
Teacher: Let's look at that again. While fractions offer one way of working on this problem, what you said is not accurate. Remember what you know about fractions. If you say that $\frac{2}{3}$ of the juice is concentrate, then which number in the fraction tells you how many total cups are in the juice?
Student 2: Well, the denominator is the total, so the total would be 3 cups. In Mix S, though, there are 3 cups of concentrate AND 2 cups of water, so there's really 5 cups of ingredients in the juice.
Teacher: So is $\frac{2}{3}$ of Mix S concentrate?
Student 1: No, I guess it isn't. But shouldn't we be able to use the fraction $\frac{2}{3}$?
Teacher: Let's talk about that. If we use $\frac{2}{3}$, what does the 2 represent?
Student 3: The 2 cups of water.
Teacher: And what does the 3 represent?
Student 4: The 3 cups of concentrate.
Teacher: So if we wanted to know what fraction is concentrate, what fraction would we use?
Student 2: $\frac{2}{5}$, because 5 is the total amount of cups in the juice and 2 is the number of cups of concentrate.
Teacher: OK. Keep working and I'll come back to you. Again, we are trying to figure out which one is the most orangey.
The teacher continues to circulate around the room, listening to conversations that different groups are having.
Teacher: Who has an idea here? Which mix does your group think is the most orangey?
Student 2: We think it is Mix T. We set up ratios of concentrate to water, and compared the decimal values. So this is what we got:
Teacher: What do those decimal values represent?
Student 2: The ratio of concentrate to water.
Teacher: Did anyone do this another way?
Student 3: We found out what percent of the juice was concentrate. So here is what we got. We agree that Mix T is the most orangey.
Teacher: So, we can see from these two strategies that Mix T is the most orangey. Which one is the least orangey?
Student 1: Mix U. If you look at the percent that is concentrate, we can see that Mix U has the least percent of concentrate, so it is the least orangey.
Teacher: Let's move on to the next part of the problem. Assume each camper gets $\frac{1}{2}$ cup of juice. For each mix, you need to now figure out how many batches are needed to be made to serve all of the campers. Remember, there are 200 campers.
Student 4: I think we need to first figure out how many cups are in each batch of juice.
Teacher: Why would you need to know that?
Student 4: So we can scale the recipe up to make enough to feed the campers.
Teacher: Good thought process. Go ahead and give it a try and let me know how it goes.
Student 3: Can't we just multiply 200 by $\frac{1}{2}$ to get 100? We need 100 cups of juice made.
Teacher: OK. You are right that you need 100 cups, but that is 100 cups of juice. That doesn't say how many cups of each of the 2 ingredients you need.
Student 3: Oh. That's right. We need to do that. Hmm. Maybe putting the information into tables could help us.
Teacher: Nice. Any other way this could have been figured out?
Student 4: We used proportional reasoning to solve it. We knew that we needed 100 cups total. We also knew how many batches we needed. So, we knew we needed 100 cups total, and there were 5 total cups in the batch made. Since we needed two cups of concentrate, then we can scale that up. Here's the proportion we set up:
$\frac{2}{5}$ = $\frac{x}{100}$
Student 4: So, we can solve and get 40 for x, just like the other group did. So, we need 40 cups of concentrate and 60 cups of water. We did that same process for the rest of them, too, like our table shows. By doing it our way, we won't have as much left over, because they rounded the number of batches, and we set up proportions so we have a closer number of cups that would be needed. We still have Mix T using the most concentrate in proportion to the amount of water used.
Teacher: OK. Nice work! To finish the lesson, here is your final task: Which of the following will taste most orangey: 2 cups of concentrate and 3 cups of water; 4 cups of concentrate and 6 cups of water; or 10 cups of concentrate and 15 cups of water?
The students use various strategies that were discussed in class.
Teacher: Anyone have an answer?
Student 2 : I think they are all the same orangey-ness?
Teacher: How could that be if they all have different numbers of concentrate and water?
Student 1: Because when we compared all of the ratios, they were equivalent: 2 to 3 is equivalent to 4 to 6, is equivalent to 10 to 15. If we write them all as fractions we can see that even better.
Teacher: Can you come up to the board and show us what you are doing?
Student 1: Sure. Here is what I did:
$\frac{2}{3}$ = $\frac{4}{6}$ = $\frac{10}{15}$
They all simplify to being the same concentrate, $\frac{2}{3}$, so, they are all proportional to one another.
Teacher: Nice job today. We will review this tomorrow.
Teacher Notes
- To find percent increase or percent decrease, have the students subtract the two values being compared. Then, have them take that answer and divide it by the beginning value to get the ratio of change to starting value. Multiply this value by 100 to get the percent change. For example, the population changed from 1000 to 1150. What was the percent increase? The students would subtract 1150 - 1000 to get 150. They then need to divide 150 by 1000 to get 0.15. Multiply this value by 100 (change a decimal to a percent), and the percent increase is 0.15 × 100 which equals 15%. This website provides a calculator that will do this.
- The scale on a map suggests that 1 centimeter represents an actual distance of 5 kilometers. The map distance between two towns is 8 centimeters. What is the actual distance? In this situation, a table can help highlight this relationship.
Drawing pictures may help students see that the rate is a scalar concept.
- To help students learn the difference between compound and simple interest, work on simple interest first. In simple interest, the amount of interest earned is proportional to the number of months invested. For example, a deposit of $500 in an account earns 1% simple interest each month. After 1 month, $5 of interest would be earned, because $500×1% = $5. ($500x0.01 = $5). After two months, there will be $10 of interest earned. Interest is only earned on the original deposit with simple interest. With compound interest, interest is not only calculated on the original deposit, but also the interest that has previously been earned. So, one month, the interest earned would be $500x1% = $5. The balance after that first month is $505. After two months, the interest is earned on the total balance of $505. As shown in the table, the amount added each month is not constant, therefore, compound interest earned is not an example of a proportional relationship, whereas simple interest earned is showing a proportional relationship.
- Proportion problems This website will explain proportions, provide examples, and provides sample problems.
- Ratios and proportions This site includes ratios, comparing ratios, and proportions.
- Ratio and proportion factsheets
- Ratios and proportions in everyday life This site addresses ratios and proportions and how knowledge of these mathematical concepts is used in everyday life. It includes lesson plans, animation, online and printable worksheets, online exercises, games, quizzes, and a link to eThemes Resource on Math: Equivalent Ratios.
- Real-world proportions This site includes problems with solving proportions (algorithms) and real-world applications.
- Math in daily life: Cooking by numbers This webpage that helps make a connection between proportions and the real-life situation of cooking.
- Burns, M., and Sheffield, S. (2004). Jim and the Beanstalk. In Math and Literature (p. 60) . Sausalito, CA: Math Solutions Publications.
- Burns, M., and Sheffield, S. (2004). How Big is a Foot. In Math and Literature (p. 47). Sausalito, CA: Math Solutions Publications.

- interest: fee paid on loans or earned on invested money, based on the principal amount and the interest rate.
- simple interest: interest paid only on the original principal, not on the interest accrued.
- compound interest: interest computed on accumulated interest as well as on the principal.
- proportion: an equation which states that two ratios are equal; a relationship between two ratios. Example: $\frac{\text{hours spent on homework}}{\text{hours spent in school}}=\frac{2}{7}$
Note that this does not necessarily imply that "hours spent on homework" = 2 or that "hours spent in school" = 7. During a week, 10 hours may have been spent on homework while 35 hours were spent in school. The proportion is still true because $\frac{10}{35}=\frac{2}{7}$.
- proportional reasoning: a mathematical way of thinking in which students recognize proportional versus non-proportional situations and can use multiple approaches, not just the cross-products approach, for solving problems about proportional situations.
Reflection - Critical Questions regarding the teaching and learning of these benchmarks
- What conclusions can be drawn about the student's understanding of applying relationships to solve problems in various contexts?
- Can students scale values up or down and understand why they are doing it?
- Can students tell if a relationship is proportional by looking at the verbal description of it, or do they need to mathematically figure it out?
- Are students able to transfer prior knowledge about equivalent fractions to the concept of proportionality?
- Do students understand why their procedures work?
- What connections have been made as students explored the mathematical characteristics of proportional situations?
- What models would help students in understanding the concepts addressed in the lesson?
- What aspects of proportional relationships are students still struggling with?
Cramer, K. & Post, T. (1993, February). Making connections: A case for proportionality. In Arithmetic Teacher, 60(6), 342-346.
- Massachusetts Comprehensive Assessment System Spring 2010 Test Items http://www.doe.mass.edu/mcas/2010/release/g7math.pdf
- Absolute value http :// www . purplemath . com / modules / absolute . htm
- Adding and subtracting negative numbers http :// www . purplemath . com / modules / negative 2. htm
- Lappan, G., Fey, J., Fitzgerald, W., Friel, S., Philips, E. (2009). Accentuate the Negative, CMP2. Pearson Prentice Hall.
- Lappan, G., Fey, J., Fitzgerald, W., Friel, S., Philips, E. (2009). Comparing and Scaling, CMP2. Pearson Prentice Hall.
- Rational Number Project: Proportional reasoning: the effect of two context variables, rate type, and problem setting http :// www . cehd . umn . edu / rationalnumberproject /89_6. html
- Dacey, L.S., and Gartland, K. (2009). Math for All: Differentiating Instruction. Sausalito, CA: Math Solutions.

Answer: a DOK: Level 3 Source: Minnesota Grade 7 Mathematics MCA - III Item Sampler Item, 2011, Benchmark 7.1.2.4

Answer: c DOK: Level 3 Source: Massachusetts Comprehensive Assessment System Release of Spring 2009 Test Items
Assume you borrow $900 at 7% annual compound interest for four years.
- How much money do you owe at the end of the four years? Show or explain your work.
- What is the total interest you will have to pay? Show or explain your work.
Answers: Part A: $900 + $252 = $1179.72; Part B: $279.72 DOK: Level 2 Source: Test Prep: Modified from MCA III Test Preparation Grade 7, Houghton Mifflin Harcourt Publishing Company, Attn: Contracts, Copyrights, and Licensing, 9400 South Park Center Loop, Orlando, FL 32819.
Tim is mixing 1 L of juice concentrate with 5L of water to make juice for his 10 guests. After he pours the mix into 10 different cups, he realizes that the juice is not sweet enough, so he adds 0.1 L of syrup into each of the cups. What is the final amount of juice in each cup? A. 0.5 L B. 0.7 L C. 1.7 L D. 2.0 L Answer: b DOK: Level 2 Source: Test Prep: MCA III Test Preparation Grade 7, Houghton Mifflin Harcourt Publishing Company, Attn: Contracts, Copyrights, and Licensing, 9400 South Park Center Loop, Orlando, FL 32819.

Answer: b DOK: Level 2 Source: Minnesota Grade 7 Mathematics MCA - III Item Sampler Item, 2011, Benchmark 7.1.2.5

Answer: b DOK: Level 2 Source: Minnesota Grade 7 Mathematics Modified MCA - III Item Sampler Item, 2011, Benchmark 7.1.2.5
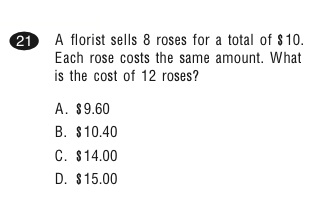
Answer: d DOK: Level 2 Source: Massachusetts Comprehensive Assessment System Release of Spring 2010 Test Items

Answer: b DOK: Level 2 Source: Massachusetts Comprehensive Assessment System Release of Spring 2010 Test Items
Differentiation
- Provide students with multiplication tables.
- Students may need to be given a place value chart to help them in rounding to the correct place (hundreds vs. hundredths).
- Use pictures and or tables to help the students see the pattern; always label the values they are trying to scale, such as 10 in = 3 ft, 3 in = ________ft. By keeping the labels with the numbers, fewer errors in relationships will be made.
- Students may see the word "ratio" as "radios." Assist them by clarifying the meaning and pronunciation of both words.
- Use a graphic organizer displaying operations with integer rules .
- Introduce √ of a number to plot on a number line.
- Do multi-step conversion-type problems to show proportional relationship.
- Explain the concept of compound interest using exponential growth and exponential equations.
- Create a gameboard activity. Have students work in groups of four to create gameboards marked with mathematical questions they must answer to be able to move ahead on the boards. They should use at least three addition, three subtraction, three multiplication and three division operations. They should also use positive numbers, negative numbers, decimals, and fractions. Students will fill in operation symbols and numbers on the boards. When they are done, the class can play the different games.
Parents/Admin
Administrative/peer classroom observation, parent resources.
- Math games, problems and puzzles
Related Frameworks
7.1.2a applying & making sense of rational numbers.
- 7.1.2.1 Arithmetic Procedures
- 7.1.2.2 Explain Arithmetic Procedures
- 7.1.2.3 Calculators & Rational Numbers
- 7.1.2.6 Absolute Value
- 7.1.2.4 Solve Problems with Rational Numbers Including Positive Integer Exponents
- 7.1.2.5 Proportional Reasoning

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

3.5: Rational Numbers
- Last updated
- Save as PDF
- Page ID 129525

Learning Objectives
After completing this section, you should be able to:
- Define and identify numbers that are rational.
- Simplify rational numbers and express in lowest terms.
- Add and subtract rational numbers.
- Convert between improper fractions and mixed numbers.
- Convert rational numbers between decimal and fraction form.
- Multiply and divide rational numbers.
- Apply the order of operations to rational numbers to simplify expressions.
- Apply density property of rational numbers.
- Solve problems involving rational numbers.
- Use fractions to convert between units.
- Define and apply percent.
Solve problems using percent.
We are often presented with percentages or fractions to explain how much of a population has a certain feature. For example, the 6-year graduation rate of college students at public institutions is 57.6%, or 72/125. That fraction may be unsettling. But without the context, the percentage is hard to judge. So how does that compare to private institutions? There, the 6-year graduation rate is 65.4%, or 327/500. Comparing the percentages is straightforward, but the fractions are harder to interpret due to different denominators. For more context, historical data could be found. One study reported that the 6-year graduation rate in 1995 was 56.4%. Comparing that historical number to the recent 6-year graduation rate at public institutions of 57.6% shows that there hasn't been much change in that rate.
Defining and Identifying Numbers That Are Rational
A rational number (called rational since it is a ratio) is just a fraction where the numerator is an integer and the denominator is a non-zero integer. As simple as that is, they can be represented in many ways. It should be noted here that any integer is a rational number. An integer, n n , written as a fraction of two integers is n 1 n 1 .
In its most basic representation, a rational number is an integer divided by a non-zero integer, such as 3 12 Figure 3.21). Similarly, if in a group of 20 people, 5 are wearing hats, then 5 20 Figure 3.22).
Another representation of rational numbers is as a mixed number, such as 2 5 8 Figure 3.23). This represents a whole number (2 in this case), plus a fraction (the 5 8 5 8 ).
Rational numbers may also be expressed in decimal form; for instance, as 1.34. When 1.34 is written, the decimal part, 0.34, represents the fraction 34 100 34 100 , and the number 1.34 is equal to 1 34 100 1 34 100 . However, not all decimal representations are rational numbers.
A number written in decimal form where there is a last decimal digit (after a given decimal digit, all following decimal digits are 0) is a terminating decimal , as in 1.34 above. Alternately, any decimal numeral that, after a finite number of decimal digits, has digits equal to 0 for all digits following the last non-zero digit.
All numbers that can be expressed as a terminating decimal are rational. This comes from what the decimal represents. The decimal part is the fraction of the decimal part divided by the appropriate power of 10. That power of 10 is the number of decimal digits present, as for 0.34, with two decimal digits, being equal to 34 100 34 100 .
Another form that is a rational number is a decimal that repeats a pattern, such as 67.1313… When a rational number is expressed in decimal form and the decimal is a repeated pattern, we use special notation to designate the part that repeats. For example, if we have the repeating decimal 4.3636…, we write this as 4. 36 ¯ 4. 36 ¯ . The bar over the 36 indicates that the 36 repeats forever.
If the decimal representation of a number does not terminate or form a repeating decimal, that number is not a rational number.
One class of numbers that is not rational is the square roots of integers or rational numbers that are not perfect squares , such as 10 10 and 25 6 25 6 . More generally, the number b b is the square root of the number a a if a = b 2 a = b 2 . The notation for this is b = a b = a , where the symbol is the square root sign. An integer perfect square is any integer that can be written as the square of another integer. A rational perfect square is any rational number that can be written as a fraction of two integers that are perfect squares.
Sometimes you may be able to identify a perfect square from memory. Another process that may be used is to factor the number into the product of an integer with itself. Or a calculator (such as Desmos) may be used to find the square root of the number. If the calculator yields an integer, the original number was a perfect square.
Using Desmos to Find the Square Root of a Number
When Desmos is used, there is a tab at the bottom of the screen that opens the keyboard for Desmos. The keyboard is shown below. On the keyboard (Figure 3.24) is the square root symbol ( ) ( ) . To find the square root of a number, click the square root key, and then type the number. Desmos will automatically display the value of the square root as you enter the number.
Example 3.51
Identifying perfect squares.
Which of the following are perfect squares?
- We could attempt to find the perfect square by factoring. Writing all the factor pairs of 45 results in 1 × 45 , 3 × 15 1 × 45 , 3 × 15 , and 5 × 9 5 × 9 . None of the pairs is a square, so 45 is not a perfect square. Using a calculator to find the square root of 45, we obtain 6.708 (rounded to three decimal places). Since this was not an integer, the original number was not a perfect square.
- We could attempt to find the perfect square by factoring. Writing all the factor pairs of 144 results in 1 × 144 , 2 × 72 , 3 × 48 , 6 × 24 , 8 × 18 1 × 144 , 2 × 72 , 3 × 48 , 6 × 24 , 8 × 18 , and 12 × 12 12 × 12 . Since the last pair is an integer multiplied by itself, 144 is a perfect square. Alternately, using Desmos to find the square root of 144, we obtain 12. Since the square root of 144 is an integer, 144 is a perfect square.
Your Turn 3.51
Introduction to Fractions
Example 3.52
Identifying rational numbers.
Determine which of the following are rational numbers:
- 4.556 4.556
- 3 1 5 3 1 5
- 41 17 41 17
- 5 . 64 ¯ 5 . 64 ¯
- Since 73 is not a perfect square, its square root is not a rational number. This can also be seen when a calculator is used. Entering 73 73 into a calculator results in 8.544003745317 (and then more decimal values after that). There is no repeated pattern, so this is not a rational number.
- Since 4.556 is a decimal that terminates, this is a rational number.
- 3 1 5 3 1 5 is a mixed number, so it is a rational number.
- 41 17 41 17 is an integer divided by an integer, so it is a rational number.
- 5.646464... 5.646464... is a decimal that repeats a pattern, so it is a rational number.
Your Turn 3.52
Simplifying rational numbers and expressing in lowest terms.
A rational number is one way to express the division of two integers. As such, there may be multiple ways to express the same value with different rational numbers. For instance, 4 5 4 5 and 12 15 12 15 are the same value. If we enter them into a calculator, they both equal 0.8. Another way to understand this is to consider what it looks like in a figure when two fractions are equal.
In Figure 3.25, we see that 3 5 3 5 of the rectangle and 9 15 9 15 of the rectangle are equal areas.
They are the same proportion of the area of the rectangle. The left rectangle has 5 pieces, three of which are shaded. The right rectangle has 15 pieces, 9 of which are shaded. Each of the pieces of the left rectangle was divided equally into three pieces. This was a multiplication. The numerator describing the left rectangle was 3 but it becomes 3 × 3 3 × 3 , or 9, as each piece was divided into three. Similarly, the denominator describing the left rectangle was 5, but became 5 × 3 5 × 3 , or 15, as each piece was divided into 3. The fractions 3 5 3 5 and 9 15 9 15 are equivalent because they represent the same portion (often loosely referred to as equal).
This understanding of equivalent fractions is very useful for conceptualization, but it isn’t practical, in general, for determining when two fractions are equivalent. Generally, to determine if the two fractions a b a b and c d c d are equivalent, we check to see that a × d = b × c a × d = b × c . If those two products are equal, then the fractions are equal also.
Example 3.53
Determining if two fractions are equivalent.
Determine if 12 30 12 30 and 14 35 14 35 are equivalent fractions.
Applying the definition, a = 12 , b = 30 , c = 14 a = 12 , b = 30 , c = 14 and d = 35 d = 35 . So a × d = 12 × 35 = 420 a × d = 12 × 35 = 420 . Also, b × c = 30 × 14 = 420 b × c = 30 × 14 = 420 . Since these values are equal, the fractions are equivalent.
Your Turn 3.53
That a × d = b × c a × d = b × c indicates the fractions a b a b and c d c d are equivalent is due to some algebra. One property of natural numbers, integers, and rational numbers (also irrational numbers) is that for any three numbers a , b , a , b , and c c with c ≠ 0 c ≠ 0 , if a = b a = b , then a / c = b / c a / c = b / c . In other words, when two numbers are equal, then dividing both numbers by the same non-zero number, the two newly obtained numbers are also equal. We can apply that to a × d a × d and b × c b × c , to show that a b a b and c d c d are equivalent if a × d = b × c a × d = b × c .
If a × d = b × c a × d = b × c , and c ≠ 0 , d ≠ 0 c ≠ 0 , d ≠ 0 , we can divide both sides by and obtain the following: a × d c = b × c c a × d c = b × c c . We can divide out the c c on the right-hand side of the equation, resulting in a × d c = b a × d c = b . Similarly, we can divide both sides of the equation by d d and obtain the following: a × d c × d = b d a × d c × d = b d . We can divide out d d the on the left-hand side of the equation, resulting in a c = b d a c = b d . So, the rational numbers a c a c and b d b d are equivalent when a × d = b × c a × d = b × c .
Equivalent Fractions
Recall that a common divisor or common factor of a set of integers is one that divides all the numbers of the set of numbers being considered. In a fraction, when the numerator and denominator have a common divisor, that common divisor can be divided out . This is often called canceling the common factors or, more colloquially, as canceling .
To show this, consider the fraction 36 63 36 63 . The numerator and denominator have the common factor 3. We can rewrite the fraction as 36 63 = 12 × 3 21 × 3 36 63 = 12 × 3 21 × 3 . The common divisor 3 is then divided out, or canceled, and we can write the fraction as 12 × 3 21 × 3 = 12 21 12 × 3 21 × 3 = 12 21 . The 3s have been crossed out to indicate they have been divided out. The process of dividing out two factors is also referred to as reducing the fraction .
If the numerator and denominator have no common positive divisors other than 1, then the rational number is in lowest terms .
The process of dividing out common divisors of the numerator and denominator of a fraction is called reducing the fraction .
One way to reduce a fraction to lowest terms is to determine the GCD of the numerator and denominator and divide out the GCD. Another way is to divide out common divisors until the numerator and denominator have no more common factors.
Example 3.54
Reducing Fractions to Lowest Terms
Express the following rational numbers in lowest terms:
- 36 48 36 48
- 100 250 100 250
- 51 136 51 136
Step 1: We can then rewrite the numerator and denominator by factoring 12 from both.
36 48 = 12 × 3 12 × 4 36 48 = 12 × 3 12 × 4
Step 2: We can now divide out the 12s from the numerator and denominator.
36 48 = 12 × 3 12 × 4 = 3 4 36 48 = 12 × 3 12 × 4 = 3 4
So, when 36 48 36 48 is reduced to lowest terms, the result is 3 4 3 4 .
Alternately, you could identify a common factor, divide out that common factor, and repeat the process until the remaining fraction is in lowest terms.
Step 1: You may notice that 4 is a common factor of 36 and 48.
Step 2: Divide out the 4, as in 36 48 = 4 × 9 4 × 12 = 4 × 9 4 × 12 = 9 12 36 48 = 4 × 9 4 × 12 = 4 × 9 4 × 12 = 9 12 .
Step 3: Examining the 9 and 12, you identify 3 as a common factor and divide out the 3, as in 9 12 = 3 × 3 3 × 4 = 3 4 9 12 = 3 × 3 3 × 4 = 3 4 . The 3 and 4 have no common positive factors other than 1, so it is in lowest terms.
Step 2: We can then rewrite the numerator and denominator by factoring 50 from both.
100 250 = 50 × 2 50 × 5 100 250 = 50 × 2 50 × 5 .
Step 3: We can now divide out the 50s from the numerator and denominator.
100 250 = 50 × 2 50 × 5 = 2 5 100 250 = 50 × 2 50 × 5 = 2 5
So, when 100 250 100 250 is reduced to lowest terms, the result is 2 5 2 5 .
Step 2: We can then rewrite the numerator and denominator by factoring 17 from both.
51 136 = 17 × 3 17 × 8 51 136 = 17 × 3 17 × 8
Step 3: We can now divide out the 17s from the numerator and denominator.
51 136 = 17 × 3 17 × 8 = 3 8 51 136 = 17 × 3 17 × 8 = 3 8
So, when 51 136 51 136 is reduced to lowest terms, the result is 3 8 3 8 .
Your Turn 3.54
Using desmos to find lowest terms.
Desmos is a free online calculator . Desmos supports reducing fractions to lowest terms. When a fraction is entered, Desmos immediately calculates the decimal representation of the fraction. However, to the left of the fraction, there is a button that, when clicked, shows the fraction in reduced form.
Using Desmos to Reduce a Fraction
Adding and Subtracting Rational Numbers
Adding or subtracting rational numbers can be done with a calculator, which often returns a decimal representation, or by finding a common denominator for the rational numbers being added or subtracted.
Using Desmos to Add Rational Numbers in Fractional Form
To create a fraction in Desmos, enter the numerator, then use the division key (/) on your keyboard, and then enter the denominator. The fraction is then entered. Then click the right arrow key to exit the denominator of the fraction. Next, enter the arithmetic operation (+ or –). Then enter the next fraction. The answer is displayed dynamically (calculates as you enter). To change the Desmos result from decimal form to fractional form, use the fraction button (Figure 3.26) on the left of the line that contains the calculation:
Example 3.55
Adding rational numbers using desmos.
Calculate 23 42 + 9 56 23 42 + 9 56 using Desmos.
Enter 23 42 + 9 56 23 42 + 9 56 in Desmos. The result is displayed as 0.70833333333 0.70833333333 (which is 0.708 3 ¯ 0.708 3 ¯ ). Clicking the fraction button to the left on the calculation line yields 17 24 17 24 .
Your Turn 3.55
Performing addition and subtraction without a calculator may be more involved. When the two rational numbers have a common denominator, then adding or subtracting the two numbers is straightforward. Add or subtract the numerators, and then place that value in the numerator and the common denominator in the denominator. Symbolically, we write this as a c ± b c = a ± b c Figure 3.27, which shows 3 20 + 4 20 = 7 20 3 20 + 4 20 = 7 20 .
It is customary to then write the result in lowest terms.
If c c is a non-zero integer, then a c ± b c = a ± b c a c ± b c = a ± b c .
Example 3.56
Adding rational numbers with the same denominator.
Calculate 13 28 + 7 28 13 28 + 7 28 .
Since the rational numbers have the same denominator, we perform the addition of the numerators, 13 + 7 13 + 7 , and then place the result in the numerator and the common denominator, 28, in the denominator. 13 28 + 7 28 = 13 + 7 28 = 20 28 13 28 + 7 28 = 13 + 7 28 = 20 28
Once we have that result, reduce to lowest terms, which gives 20 28 = 4 × 5 4 × 7 = 4 × 5 4 × 7 = 5 7 20 28 = 4 × 5 4 × 7 = 4 × 5 4 × 7 = 5 7 .
Your Turn 3.56
Example 3.57, subtracting rational numbers with the same denominator.
Calculate 45 136 − 17 136 45 136 − 17 136 .
Since the rational numbers have the same denominator, we perform the subtraction of the numerators, 45 − 17 45 − 17 , and then place the result in the numerator and the common denominator, 136, in the denominator. 45 136 − 17 136 − 45 − 17 136 = 28 136 45 136 − 17 136 − 45 − 17 136 = 28 136
Once we have that result, reduce to lowest terms, this gives 28 136 = 4 × 7 4 × 34 = 4 × 7 4 × 34 = 7 34 28 136 = 4 × 7 4 × 34 = 4 × 7 4 × 34 = 7 34 .
Your Turn 3.57
When the rational numbers do not have common denominators, then we have to transform the rational numbers so that they do have common denominators. The common denominator that reduces work later in the problem is the LCM of the numerator and denominator. When adding or subtracting the rational numbers a b a b and c d c d , we perform the following steps.
Step 1: Find LCM ( b , d ) LCM ( b , d ) .
Step 2: Calculate n = LCM ( b , d ) b n = LCM ( b , d ) b and m = L C M ( b , d ) d m = L C M ( b , d ) d .
Step 3: Multiply the numerator and denominator of a b a b by n n , yielding a × n b × n a × n b × n .
Step 4: Multiply the numerator and denominator of c d c d by m m , yielding c × m d × m c × m d × m .
Step 5: Add or subtract the rational numbers from Steps 3 and 4, since they now have the common denominators.
You should be aware that the common denominator is LCM ( b , d ) LCM ( b , d ) . For the first denominator, we have b × n = b × L C M ( b , d ) b = L C M ( b , d ) b × n = b × L C M ( b , d ) b = L C M ( b , d ) , since we multiply and divide LCM ( b , d ) LCM ( b , d ) by the same number. For the same reason, d × m = d × L C M ( b , d ) b = L C M ( b , d ) d × m = d × L C M ( b , d ) b = L C M ( b , d ) .
Example 3.58
Adding rational numbers with unequal denominators.
Calculate 11 18 + 2 15 11 18 + 2 15 .
The denominators of the fractions are 18 and 15, so we label b = 18 b = 18 and d = 15 d = 15 .
Step 1: Find LCM(18,15). This is 90.
Step 2 : Calculate n n and m m . n = 90 18 = 5 n = 90 18 = 5 and m = 90 15 = 6 m = 90 15 = 6 .
Step 3: Multiplying the numerator and denominator of 11 18 11 18 by n = 5 n = 5 yields 11 × 5 18 × 5 = 55 90 11 × 5 18 × 5 = 55 90 .
Step 4: Multiply the numerator and denominator of 2 15 2 15 by m = 6 m = 6 yields 2 × 6 15 × 6 = 12 90 2 × 6 15 × 6 = 12 90 .
Step 5: Now we add the values from Steps 3 and 4: 55 90 + 12 90 = 67 90 55 90 + 12 90 = 67 90 .
This is in lowest terms, so we have found that 11 18 + 2 15 = 67 90 11 18 + 2 15 = 67 90 .
Your Turn 3.58
Example 3.59, subtracting rational numbers with unequal denominators.
Calculate 14 25 − 9 70 14 25 − 9 70 .
The denominators of the fractions are 25 and 70, so we label b = 25 b = 25 and d = 70 d = 70 .
Step 1: Find LCM(25,70). This is 350.
Step 2: Calculate n n and m m : n = 350 25 = 14 n = 350 25 = 14 and m = 350 70 = 5 m = 350 70 = 5 .
Step 3: Multiplying the numerator and denominator of 14 25 14 25 by n = 14 n = 14 yields 14 × 14 25 × 14 = 196 350 14 × 14 25 × 14 = 196 350 .
Step 4: Multiplying the numerator and denominator of 9 70 9 70 by m = 5 m = 5 yields 9 × 5 70 × 5 = 45 350 9 × 5 70 × 5 = 45 350 .
Step 5: Now we subtract the value from Step 4 from the value in Step 3: 196 350 − 45 350 = 151 350 196 350 − 45 350 = 151 350 .
This is in lowest terms, so we have found that 14 25 − 9 70 = 151 350 14 25 − 9 70 = 151 350 .
Your Turn 3.59
Adding and Subtracting Fractions with Different Denominators
Converting Between Improper Fractions and Mixed Numbers
One way to visualize a fraction is as parts of a whole, as in 5 12 5 12 of a pizza. But when the numerator is larger than the denominator, as in 23 12 23 12 , then the idea of parts of a whole seems not to make sense. Such a fraction is an improper fraction. That kind of fraction could be written as an integer plus a fraction, which is a mixed number . The fraction 23 12 23 12 rewritten as a mixed number would be 1 11 12 1 11 12 . Arithmetically, 1 11 12 1 11 12 is equivalent to 1 + 11 12 1 + 11 12 , which is read as “one and 11 twelfths.”
Improper fractions can be rewritten as mixed numbers using division and remainders. To find the mixed number representation of an improper fraction, divide the numerator by the denominator. The quotient is the integer part, and the remainder becomes the numerator of the remaining fraction.
Example 3.60
Rewriting an improper fraction as a mixed number.
Rewrite 48 13 48 13 as a mixed number.
When 48 is divided by 13, the result is 3 with a remainder of 9. So, we can rewrite 48 13 48 13 as 3 9 13 3 9 13 .
Your Turn 3.60
Converting an Improper Fraction to a Mixed Number Using Desmos
Similarly, we can convert a mixed number into an improper fraction. To do so, first convert the whole number part to a fraction by writing the whole number as itself divided by 1, and then add the two fractions.
Alternately, we can multiply the whole number part and the denominator of the fractional part. Next, add that product to the numerator. Finally, express the number as that product divided by the denominator.
Example 3.61
Rewriting a mixed number as an improper fraction.
Rewrite 5 4 9 5 4 9 as an improper fraction.
Step 1: Multiply the integer part, 5, by the denominator, 9, which gives 5 × 9 = 45 5 × 9 = 45 .
Step 2: Add that product to the numerator, which gives 45 + 4 = 49 45 + 4 = 49 .
Step 3: Write the number as the sum, 49, divided by the denominator, 9, which gives 49 9 49 9 .
Your Turn 3.61
Using desmos to rewrite a mixed number as an improper fraction.
Desmos can be used to convert from a mixed number to an improper fraction. To do so, we use the idea that a mixed number, such as 5 6 11 5 6 11 , is another way to represent 5 + 6 11 5 + 6 11 . If 5 + 6 11 5 + 6 11 is entered in Desmos, the result is the decimal form of the number. However, clicking the fraction button to the left will convert the decimal to an improper fraction, 61 11 61 11 . As an added bonus, Desmos will automatically reduce the fraction to lowest terms.
Converting Rational Numbers Between Decimal and Fraction Forms
Understanding what decimals represent is needed before addressing conversions between the fractional form of a number and its decimal form , or writing a number in decimal notation . The decimal number 4.557 is equal to 4 557 1,000 4 557 1,000 . The decimal portion, .557, is 557 divided by 1,000. To write any decimal portion of a number expressed as a terminating decimal, divide the decimal number by 10 raised to the power equal to the number of decimal digits. Since there were three decimal digits in 4.557, we divided 557 by 10 3 = 1000 10 3 = 1000 .
Decimal representations may be very long. It is convenient to round off the decimal form of the number to a certain number of decimal digits. To round off the decimal form of a number to n n (decimal) digits, examine the ( n + 1 n + 1 )st decimal digit. If that digit is 0, 1, 2, 3, or 4, the number is rounded off by writing the number to the n n th decimal digit and no further. If the ( n + 1 n + 1 )st decimal digit is 5, 6, 7, 8, or 9, the number is rounded off by writing the number to the n n th digit, then replacing the n n th digit by one more than the n n th digit.
Example 3.62
Rounding off a number in decimal form to three digits.
Round 5.67849 to three decimal digits.
The third decimal digit is 8. The digit following the 8 is 4. When the digit is 4, we write the number only to the third digit. So, 5.67849 rounded off to three decimal places is 5.678.
Your Turn 3.62
Example 3.63, rounding off a number in decimal form to four digits.
Round 45.11475 to four decimal digits.
The fourth decimal digit is 7. The digit following the 7 is 5. When the digit is 5, we write the number only to the fourth decimal digit, 45.1147. We then replace the fourth decimal digit by one more than the fourth digit, which yields 45.1148. So, 45.11475 rounded off to four decimal places is 45.1148.
Your Turn 3.63
To convert a rational number in fraction form to decimal form, use your calculator to perform the division.
Example 3.64
Converting a rational number in fraction form into decimal form.
Convert 47 25 47 25 into decimal form.
Using a calculator to divide 47 by 25, the result is 1.88.
Your Turn 3.64
Converting a terminating decimal to the fractional form may be done in the following way:
Step 1: Count the number of digits in the decimal part of the number, labeled n n .
Step 2: Raise 10 to the n n th power.
Step 3: Rewrite the number without the decimal.
Step 4: The fractional form is the number from Step 3 divided by the result from Step 2.
This process works due to what decimals represent and how we work with mixed numbers. For example, we could convert the number 7.4536 to fractional from. The decimal part of the number, the .4536 part of 7.4536, has four digits. By the definition of decimal notation, the decimal portion represents 4,536 10 4 = 4,536 10,000 4,536 10 4 = 4,536 10,000 . The decimal number 7.4536 is equal to the improper fraction 7 4,536 10,000 7 4,536 10,000 . Adding those to fractions yields 74,536 10,000 74,536 10,000 .
Example 3.65
Converting from decimal form to fraction form with terminating decimals.
Convert 3.2117 to fraction form.
Step 1: There are four digits after the decimal point, so n = 4 n = 4 .
Step 2: Raise 10 to the fourth power, 10 4 = 10,000 10 4 = 10,000 .
Step 3: When we remove the decimal point, we have 32,117.
Step 4: The fraction has as its numerator the result from Step 3 and as its denominator the result of Step 2, which is the fraction 32,117 10,000 32,117 10,000 .
Your Turn 3.65
The process is different when converting from the decimal form of a rational number into fraction form when the decimal form is a repeating decimal. This process is not covered in this text.
Multiplying and Dividing Rational Numbers
Multiplying rational numbers is less complicated than adding or subtracting rational numbers, as there is no need to find common denominators. To multiply rational numbers, multiply the numerators, then multiply the denominators, and write the numerator product divided by the denominator product. Symbolically, a b × c d = a × c b × d a b × c d = a × c b × d . As always, rational numbers should be reduced to lowest terms.
If b b and d d are non-zero integers, then a b × c d = a × c b × d a b × c d = a × c b × d .
Example 3.66
Multiplying rational numbers.
Calculate 12 25 × 10 21 12 25 × 10 21 .
Multiply the numerators and place that in the numerator, and then multiply the denominators and place that in the denominator.
12 25 × 10 21 = 12 × 10 25 × 21 = 120 525 12 25 × 10 21 = 12 × 10 25 × 21 = 120 525
This is not in lowest terms, so this needs to be reduced. The GCD of 120 and 525 is 15.
120 525 = 15 × 8 15 × 35 = 8 35 120 525 = 15 × 8 15 × 35 = 8 35
Your Turn 3.66
Multiplying Fractions
As with multiplication, division of rational numbers can be done using a calculator.
Example 3.67
Dividing decimals with a calculator.
Calculate 3.45 ÷ 2.341 using a calculator. Round to three decimal places if necessary.
Using a calculator, we obtain 1.473729175565997. Rounding to three decimal places we have 1.474.
Your Turn 3.67
Before discussing division of fractions without a calculator, we should look at the reciprocal of a number. The reciprocal of a number is 1 divided by the number. For a fraction, the reciprocal is the fraction formed by switching the numerator and denominator. For the fraction a b a b , the reciprocal is b a b a . An important feature for a number and its reciprocal is that their product is 1.
When dividing two fractions by hand, find the reciprocal of the divisor (the number that is being divided into the other number). Next, replace the divisor by its reciprocal and change the division into multiplication. Then, perform the multiplication. Symbolically, b a ÷ c d = a b × d c = a × d b × c b a ÷ c d = a b × d c = a × d b × c . As before, reduce to lowest terms.
If b , c b , c and d d are non-zero integers, then b a ÷ c d = a b × d c = a × d b × c b a ÷ c d = a b × d c = a × d b × c .
Example 3.68
Dividing rational numbers.
- Calculate 4 21 ÷ 6 35 4 21 ÷ 6 35 .
- Calculate 1 8 ÷ 5 28 1 8 ÷ 5 28 .
Step 2: Multiply the first fraction by that reciprocal.
4 21 ÷ 6 35 = 4 21 × 35 6 = 140 126 4 21 ÷ 6 35 = 4 21 × 35 6 = 140 126
The answer, 140 126 140 126 is not in lowest terms. The GCD of 140 and 126 is 14. Factoring and canceling gives 140 126 = 14 × 10 14 × 9 = 10 9 140 126 = 14 × 10 14 × 9 = 10 9 .
Step 2: Multiply the first fraction by that reciprocal: 1 8 ÷ 5 28 = 1 8 × 28 5 = 28 40 1 8 ÷ 5 28 = 1 8 × 28 5 = 28 40
The answer, 28 40 28 40 , is not in lowest reduced form. The GCD of 28 and 40 is 4. Factoring and canceling gives 28 40 = 4 × 7 4 × 10 = 7 10 28 40 = 4 × 7 4 × 10 = 7 10 .
Your Turn 3.68
Dividing Fractions
Applying the Order of Operations to Simplify Expressions
The order of operations for rational numbers is the same as for integers, as discussed in Order of Operations. The order of operations makes it easier for anyone to correctly calculate and represent. The order follows the well-known acronym PEMDAS:
The first step in calculating using the order of operations is to perform operations inside the parentheses. Moving down the list, next perform all exponent operations moving from left to right. Next (left to right once more), perform all multiplications and divisions. Finally, perform the additions and subtractions.
Example 3.69
Applying the order of operations with rational numbers.
Correctly apply the rules for the order of operations to accurately compute ( 5 7 − 2 7 ) × 2 3 ( 5 7 − 2 7 ) × 2 3 .
Step 1: To calculate this, perform all calculations within the parentheses before other operations.
( 5 7 − 2 7 ) × 2 3 = ( 3 7 ) × 2 3 ( 5 7 − 2 7 ) × 2 3 = ( 3 7 ) × 2 3
Step 2: Since all parentheses have been cleared, we move left to right, and compute all the exponents next.
( 3 7 ) × 2 3 = ( 3 7 ) × 8 ( 3 7 ) × 2 3 = ( 3 7 ) × 8
Step 3: Now, perform all multiplications and divisions, moving left to right.
( 3 7 ) × 8 = 24 7 ( 3 7 ) × 8 = 24 7
Your Turn 3.69
Example 3.70.
Correctly apply the rules for the order of operations to accurately compute 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 .
To calculate this, perform all calculations within the parentheses before other operations. Evaluate the innermost parentheses first. We can work separate parentheses expressions at the same time.
Step 1: The innermost parentheses contain 2 3 + 5 2 3 + 5 . Calculate that first, dividing after finding the common denominator.
4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 1 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 15 3 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 1 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 15 3 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2
Step 2: Calculate the exponent in the parentheses, ( 5 9 ) 2 ( 5 9 ) 2 .
4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 = 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 = 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2
Step 3: Subtract inside the parentheses is done, using a common denominator.
4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 × 27 3 × 27 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 459 81 ) ) 2 4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 × 27 3 × 27 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 459 81 ) ) 2 4 + 2 3 ÷ ( ( − 434 81 ) ) 2
Step 4: At this point, evaluate the exponent and divide.
4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( 188,356 6,561 ) = 4 + 2 3 × ( 6,561 188,356 ) = 4 + 2,187 94,178 4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( 188,356 6,561 ) = 4 + 2 3 × ( 6,561 188,356 ) = 4 + 2,187 94,178
Step 5: Add.
4 + 2,187 94,178 = 378,899 94,178 4 + 2,187 94,178 = 378,899 94,178
Had this been done on a calculator, the decimal form of the answer would be 4.0232 (rounded to four decimal places).
Your Turn 3.70
Order of Operations Using Fractions
Applying the Density Property of Rational Numbers
Between any two rational numbers, there is another rational number. This is called the density property of the rational numbers.
Finding a rational number between any two rational numbers is very straightforward.
Step 1: Add the two rational numbers.
Step 2: Divide that result by 2.
The result is always a rational number. This follows what we know about rational numbers. If two fractions are added, then the result is a fraction. Also, when a fraction is divided by a fraction (and 2 is a fraction), then we get another fraction. This two-step process will give a rational number, provided the first two numbers were rational.
Example 3.71
Demonstrate the density property of rational numbers by finding a rational number between 4 11 4 11 and 7 12 7 12 .
To find a rational number between 4 11 4 11 and 7 12 7 12 :
Step 1: Add the fractions.
4 11 + 7 12 = 4 × 12 11 × 12 + 7 × 11 12 × 11 = 48 132 + 77 132 = 125 132 4 11 + 7 12 = 4 × 12 11 × 12 + 7 × 11 12 × 11 = 48 132 + 77 132 = 125 132
Step 2: Divide the result by 2. Recall that to divide by 2, you multiply by the reciprocal of 2. The reciprocal of 2 is 1 2 1 2 , as seen below.
125 132 ÷ 2 = 125 132 × 1 2 = 125 264 125 132 ÷ 2 = 125 132 × 1 2 = 125 264
So, one rational number between 4 11 4 11 and 7 12 7 12 is 125 264 125 264 .
We could check that the number we found is between the other two by finding the decimal representation of the numbers. Using a calculator, the decimal representations of the rational numbers are 0.363636…, 0.473484848…, and 0.5833333…. Here it is clear that 125 264 125 264 is between 4 11 4 11 and 7 12 7 12 .
Your Turn 3.71
Solving problems involving rational numbers.
Rational numbers are used in many situations, sometimes to express a portion of a whole, other times as an expression of a ratio between two quantities. For the sciences, converting between units is done using rational numbers, as when converting between gallons and cubic inches. In chemistry, mixing a solution with a given concentration of a chemical per unit volume can be solved with rational numbers. In demographics, rational numbers are used to describe the distribution of the population. In dietetics, rational numbers are used to express the appropriate amount of a given ingredient to include in a recipe. As discussed, the application of rational numbers crosses many disciplines.
Example 3.72
Mixing soil for vegetables.
James is mixing soil for a raised garden, in which he plans to grow a variety of vegetables. For the soil to be suitable, he determines that 2 5 2 5 of the soil can be topsoil, but 2 5 2 5 needs to be peat moss and 1 5 1 5 has to be compost. To fill the raised garden bed with 60 cubic feet of soil, how much of each component does James need to use?
In this example, we know the proportion of each component to mix, and we know the total amount of the mix we need. In this kind of situation, we need to determine the appropriate amount of each component to include in the mixture. For each component of the mixture, multiply 60 cubic feet, which is the total volume of the mixture we want, by the fraction required of the component.
Step 1: The required fraction of topsoil is 2 5 2 5 , so James needs 60 × 2 5 60 × 2 5 cubic feet of topsoil. Performing the multiplication, James needs 60 × 2 5 = 120 5 = 24 60 × 2 5 = 120 5 = 24 (found by treating the fraction as division, and 120 divided by 5 is 24) cubic feet of topsoil.
Step 2: The required fraction of peat moss is also 2 5 2 5 , so he also needs 60 × 2 5 60 × 2 5 cubic feet, or 60 × 2 5 = 120 5 = 24 60 × 2 5 = 120 5 = 24 cubic feet of peat moss.
Step 3: The required fraction of compost is 1 5 1 5 . For the compost, he needs 60 × 1 5 = 60 5 = 12 60 × 1 5 = 60 5 = 12 cubic feet.
Your Turn 3.72
Example 3.73, determining the number of specialty pizzas.
At Bella’s Pizza, one-third of the pizzas that are ordered are one of their specialty varieties. If there are 273 pizzas ordered, how many were specialty pizzas?
One-third of the whole are specialty pizzas, so we need one-third of 273, which gives 1 3 × 273 = 273 3 = 91 1 3 × 273 = 273 3 = 91 , found by dividing 273 by 3. So, 91 of the pizzas that were ordered were specialty pizzas.
Your Turn 3.73
Finding a Fraction of a Total
Using Fractions to Convert Between Units
A common application of fractions is called unit conversion , or converting units , which is the process of changing from the units used in making a measurement to different units of measurement.
For instance, 1 inch is (approximately) equal to 2.54 cm. To convert between units, the two equivalent values are made into a fraction. To convert from the first type of unit to the second type, the fraction has the second unit as the numerator, and the first unit as the denominator.
From the inches and centimeters example, to change from inches to centimeters, we use the fraction 2.54 cm 1 in 2.54 cm 1 in . If, on the other hand, we wanted to convert from centimeters to inches, we’d use the fraction 1 in 2.54 cm 1 in 2.54 cm . This fraction is multiplied by the number of units of the type you are converting from , which means the units of the denominator are the same as the units being multiplied.

Example 3.74
Converting liters to gallons.
It is known that 1 liter (L) is 0.264172 gallons (gal). Use this to convert 14 liters into gallons.
We know that 1 liter = 0.264172 gal. Since we are converting from liters, when we create the fraction we use, make sure the liter part of the equivalence is in the denominator. So, to convert the 14 liters to gallons, we multiply 14 by 1 gal 0.264172 gal / 1 liter 1 gal 0.264172 gal / 1 liter . Notice the gallon part is in the numerator since we’re converting to gallons, and the liter part is in the denominator since we are converting from liters. Performing this and rounding to three decimal places, we find that 14 liters is 14 liter × 0.264172 gal 1 liter = 3.69841 gal 14 liter × 0.264172 gal 1 liter = 3.69841 gal .
Your Turn 3.74
Example 3.75, converting centimeters to inches.
It is known that 1 inch is 2.54 centimeters. Use this to convert 100 centimeters into inches.
We know that 1 inch = 2.54 cm. Since we are converting from centimeters, when we create the fraction we use, make sure the centimeter part of the equivalence is in the denominator, 1 in 2.54 cm 1 in 2.54 cm . To convert the 100 cm to inches, multiply 100 by 1 in 2.54 cm 1 in 2.54 cm . Notice the inch part is in the numerator since we’re converting to inches, and the centimeter part is in the denominator since we are converting from centimeters. Performing this and rounding to three decimal places, we obtain 100 cm × 1 in 2.54 cm = 39.370 in 100 cm × 1 in 2.54 cm = 39.370 in . This means 100 cm equals 39.370 in.
Your Turn 3.75
Converting Units
Defining and Applying Percent
A percent is a specific rational number and is literally per 100. n n percent, denoted n n %, is the fraction n 100 n 100 .
Example 3.76
Rewriting a percentage as a fraction.
Rewrite the following as fractions:
- Using the definition and n = 31 n = 31 , 31% in fraction form is 31 100 31 100 .
- Using the definition and n = 93 n = 93 , 93% in fraction form is 93 100 93 100 .
Your Turn 3.76
Example 3.77, rewriting a percentage as a decimal.
Rewrite the following percentages in decimal form:
- Using the definition and n = 54 n = 54 , 54% in fraction form is 54 100 54 100 . Dividing a number by 100 moves the decimal two places to the left; 54% in decimal form is then 0.54.
- Using the definition and n = 83 n = 83 , 83% in fraction form is 83 100 83 100 . Dividing a number by 100 moves the decimal two places to the left; 83% in decimal form is then 0.83.
Your Turn 3.77
You should notice that you can simply move the decimal two places to the left without using the fractional definition of percent.
Percent is used to indicate a fraction of a total. If we want to find 30% of 90, we would perform a multiplication, with 30% written in either decimal form or fractional form. The 90 is the total , 30 is the percentage , and 27 (which is 0.30 × 90 0.30 × 90 ) is the percentage of the total .
n % n % of x x items is n 100 × x n 100 × x . The x x is referred to as the total , the n n is referred to as the percent or percentage , and the value obtained from n 100 × x n 100 × x is the part of the total and is also referred to as the percentage of the total .
Example 3.78
Finding a percentage of a total.
- Determine 40% of 300.
- Determine 64% of 190.
- The total is 300, and the percentage is 40. Using the decimal form of 40% and multiplying we obtain 0.40 × 300 = 120 0.40 × 300 = 120 .
- The total is 190, and the percentage is 64. Using the decimal form of 64% and multiplying we obtain 0.64 × 190 = 121.6 0.64 × 190 = 121.6 .
Your Turn 3.78
In the previous situation, we knew the total and we found the percentage of the total. It may be that we know the percentage of the total, and we know the percent, but we don't know the total. To find the total if we know the percentage the percentage of the total, use the following formula.
If we know that n n % of the total is x x , then the total is 100 × x n 100 × x n .
Example 3.79
Finding the total when the percentage and percentage of the total are known.
- What is the total if 28% of the total is 140?
- What is the total if 6% of the total is 91?
- 28 is the percentage, so n = 28 n = 28 . 28% of the total is 140, so x = 140 x = 140 . Using those we find that the total was 100 × 140 28 = 500 100 × 140 28 = 500 .
- 6 is the percentage, so n = 6 n = 6 . 6% of the total is 91, so x = 91 x = 91 . Using those we find that the total was 100 × 91 6 = 1,516.6 100 × 91 6 = 1,516.6 .
Your Turn 3.79
The percentage can be found if the total and the percentage of the total is known. If you know the total, and the percentage of the total, first divide the part by the total. Move the decimal two places to the right and append the symbol %. The percentage may be found using the following formula.
The percentage, n n , of b b that is a a is a b × 100 % a b × 100 % .
Example 3.80
Finding the percentage when the total and percentage of the total are known.
Find the percentage in the following:
- Total is 300, percentage of the total is 60.
- Total is 440, percentage of the total is 176.
- The total is 300; the percentage of the total is 60. Calculating yields 0.2. Moving the decimal two places to the right gives 20. Appending the percentage to this number results in 20%. So, 60 is 20% of 300.
- The total is 440; the percentage of the total is 176. Calculating yields 0.4. Moving the decimal two places to the right gives 40. Appending the percentage to this number results in 40%. So, 176 is 40% of 440.
Your Turn 3.80
In the media, in research, and in casual conversation percentages are used frequently to express proportions. Understanding how to use percent is vital to consuming media and understanding numbers. Solving problems using percentages comes down to identifying which of the three components of a percentage you are given, the total, the percentage, or the percentage of the total. If you have two of those components, you can find the third using the methods outlined previously.
Example 3.81
Percentage of students who are sleep deprived.
A study revealed that 70% of students suffer from sleep deprivation, defined to be sleeping less than 8 hours per night. If the survey had 400 participants, how many of those participants had less than 8 hours of sleep per night?
The percentage of interest is 70%. The total number of students is 400. With that, we can find how many were in the percentage of the total, or, how many were sleep deprived. Applying the formula from above, the number who were sleep deprived was 0.70 × 400 = 280 0.70 × 400 = 280 ; 280 students on the study were sleep deprived.
Your Turn 3.81
Example 3.82, amazon prime subscribers.
There are 126 million users who are U.S. Amazon Prime subscribers. If there are 328.2 million residents in the United States, what percentage of U.S. residents are Amazon Prime subscribers?
We are asked to find the percentage. To do so, we divide the percentage of the total, which is 126 million, by the total, which is 328.2 million. Performing this division and rounding to three decimal places yields 126 328.2 = 0.384 126 328.2 = 0.384 . The decimal is moved to the right by two places, and a % sign is appended to the end. Doing this shows us that 38.4% of U.S. residents are Amazon Prime subscribers.
Your Turn 3.82
Example 3.83.
Evander plays on the basketball team at their university and 73% of the athletes at their university receive some sort of scholarship for attending. If they know 219 of the student-athletes receive some sort of scholarship, how many student-athletes are at the university?
We need to find the total number of student-athletes at Evander’s university.
Step 1: Identify what we know. We know the percentage of students who receive some sort of scholarship, 73%. We also know the number of athletes that form the part of the whole, or 219 student-athletes.
Step 2: To find the total number of student-athletes, use 100 × x n 100 × x n , with x = 219 x = 219 and n = 73 n = 73 . Calculating with those values yields 100 × 219 73 = 300 100 × 219 73 = 300 .
So, there are 300 total student-athletes at Evander’s university
Your Turn 3.83
Check your understanding, section 3.4 exercises.
- Studying and going to class?
- Not sleeping?
- Determine the markup in dollars.
- The markup is what percent of the original cost? Round the percentage to one decimal place.
- Calculate the markup on the item, in dollars.
- What is the price for which Wegmans sells the item? This is the price Wegmans paid, plus the markup.
- Suppose Wegmans then offers a 25% discount on the sale price of the item (found in part b). In dollars, how much is the discount?
- Determine the price of the item after the discount (this is the sales price of the item minus the discount). Round to two decimal places.
- Is the new price after the markup and discount equal to the price Wegmans paid for the item? Explain.
- The original price was $150. After the 50% discount, what is the price of the item?
- The coupon is applied to the discount price. The coupon is for 25%. Find 25% of the sale price (found in part a).
- Find the price after applying the coupon (this is the value from part a minus the value from part b).
- The total amount saved on the item is the original price after all the discounts. Determine the total amount saved by subtracting the final price paid (part c) from the original price of the item.
- Determine the effective discount percentage, which is the total amount saved divided by the original price of the item.
- Was the effective discount percentage equal to 75%, which would be the 50% plus the 25%? Explain.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 2: Module 2: Rational numbers
About this unit, topic a: addition and subtraction of integers and rational numbers.
- Zero pairs worked example (Opens a modal)
- Adding with integer chips (Opens a modal)
- Adding negative numbers on the number line (Opens a modal)
- Adding negative numbers example (Opens a modal)
- Signs of sums on a number line (Opens a modal)
- Subtracting with integer chips (Opens a modal)
- Adding the opposite with integer chips (Opens a modal)
- Adding the opposite with number lines (Opens a modal)
- Adding & subtracting negative numbers (Opens a modal)
- Subtracting a negative = adding a positive (Opens a modal)
- Adding negative numbers review (Opens a modal)
- Equivalent expressions with negative numbers (Opens a modal)
- Subtracting negative numbers review (Opens a modal)
- Number equations & number lines (Opens a modal)
- Graphing negative number addition and subtraction expressions (Opens a modal)
- Interpreting numeric expressions example (Opens a modal)
- Absolute value as distance between numbers (Opens a modal)
- Interpreting absolute value as distance (Opens a modal)
- Associative and commutative properties of addition with negatives (Opens a modal)
- Adding fractions with different signs (Opens a modal)
- Adding and subtracting fractions with negatives (Opens a modal)
- Comparing rational numbers (Opens a modal)
- Adding & subtracting rational numbers: 79% - 79.1 - 58 1/10 (Opens a modal)
- Adding & subtracting rational numbers: 0.79 - 4/3 - 1/2 + 150% (Opens a modal)
- Zero pairs Get 3 of 4 questions to level up!
- Add with integer chips Get 3 of 4 questions to level up!
- Adding negative numbers on the number line Get 5 of 7 questions to level up!
- Signs of sums Get 5 of 7 questions to level up!
- Adding negative numbers Get 5 of 7 questions to level up!
- Subtract with integer chips Get 3 of 4 questions to level up!
- Understand subtraction as adding the opposite Get 3 of 4 questions to level up!
- Subtracting negative numbers Get 5 of 7 questions to level up!
- Adding & subtracting negative numbers Get 5 of 7 questions to level up!
- Number equations & number lines Get 3 of 4 questions to level up!
- Interpret negative number addition and subtraction expressions Get 3 of 4 questions to level up!
- Absolute value to find distance Get 5 of 7 questions to level up!
- Absolute value to find distance challenge Get 3 of 4 questions to level up!
- Commutative and associative properties of addition with integers Get 3 of 4 questions to level up!
- Equivalent expressions with negative numbers Get 3 of 4 questions to level up!
- Adding & subtracting negative fractions Get 5 of 7 questions to level up!
- Order rational numbers Get 3 of 4 questions to level up!
- Adding & subtracting rational numbers Get 3 of 4 questions to level up!
- One-step equations with negatives (add & subtract) Get 5 of 7 questions to level up!
Topic B: Multiplication and division of integers and rational numbers
- Multiplying a positive and a negative number (Opens a modal)
- Multiplying two negative numbers (Opens a modal)
- Why a negative times a negative is a positive (Opens a modal)
- Why a negative times a negative makes sense (Opens a modal)
- Multiplying positive & negative numbers (Opens a modal)
- Dividing positive and negative numbers (Opens a modal)
- Multiplying negative numbers review (Opens a modal)
- Dividing negative numbers review (Opens a modal)
- Rewriting decimals as fractions: 2.75 (Opens a modal)
- Fraction to decimal: 11/25 (Opens a modal)
- Worked example: Converting a fraction (7/8) to a decimal (Opens a modal)
- Fraction to decimal with rounding (Opens a modal)
- Multiplying positive and negative fractions (Opens a modal)
- Dividing negative fractions (Opens a modal)
- Negative signs in fractions (Opens a modal)
- Dividing mixed numbers (Opens a modal)
- Simplifying complex fractions (Opens a modal)
- Expressions with rational numbers (Opens a modal)
- Equivalent expressions with negative numbers (multiplication and division) (Opens a modal)
- Why dividing by zero is undefined (Opens a modal)
- Signs of expressions Get 5 of 7 questions to level up!
- Multiplying negative numbers Get 3 of 4 questions to level up!
- Dividing negative numbers Get 3 of 4 questions to level up!
- One-step equations with negatives (multiply & divide) Get 5 of 7 questions to level up!
- Write decimals as fractions Get 5 of 7 questions to level up!
- Rewriting decimals as fractions challenge Get 5 of 7 questions to level up!
- Converting fractions to decimals Get 3 of 4 questions to level up!
- Multiplying positive and negative fractions Get 3 of 4 questions to level up!
- Dividing positive and negative fractions Get 3 of 4 questions to level up!
- Negative signs in fractions Get 3 of 4 questions to level up!
- Negative signs in fractions (with variables) Get 3 of 4 questions to level up!
- Dividing mixed numbers with negatives Get 3 of 4 questions to level up!
- Simplify complex fractions Get 5 of 7 questions to level up!
- Equivalent expressions with negative numbers (multiplication and division) Get 3 of 4 questions to level up!
- Dividing by zero Get 3 of 4 questions to level up!
Topic C: Applying operations with rational numbers to expressions and equations
- Order of operations example (Opens a modal)
- Order of operations with rational numbers (Opens a modal)
- Negative number word problem: temperatures (Opens a modal)
- Negative number word problem: Alaska (Opens a modal)
- Interpreting negative number statements (Opens a modal)
- Interpreting multiplication & division of negative numbers (Opens a modal)
- Adding integers: find the missing value (Opens a modal)
- Subtracting integers: find the missing value (Opens a modal)
- Substitution with negative numbers (Opens a modal)
- Ordering expressions (Opens a modal)
- Order of operations with negative numbers Get 5 of 7 questions to level up!
- Negative number addition and subtraction: word problems Get 3 of 4 questions to level up!
- Interpreting negative number statements Get 3 of 4 questions to level up!
- Multiplying & dividing negative numbers word problems Get 3 of 4 questions to level up!
- Addition & subtraction: find the missing value Get 3 of 4 questions to level up!
- Substitution with negative numbers Get 5 of 7 questions to level up!
- Ordering negative number expressions Get 3 of 4 questions to level up!
3.4 Rational Numbers
Learning objectives.
In its most basic representation, a rational number is an integer divided by a non-zero integer, such as 3 12 3 12 . Fractions may be used to represent parts of a whole. The denominator is the total number of parts to the object, and the numerator is how many of those parts are being used or selected. So, if a pizza is cut into 8 equal pieces, each piece is 1 8 1 8 of the pizza. If you take three slices, you have 3 8 3 8 of the pizza ( Figure 3.21 ). Similarly, if in a group of 20 people, 5 are wearing hats, then 5 20 5 20 of the people are wearing hats ( Figure 3.22 ).
Another representation of rational numbers is as a mixed number, such as 2 5 8 2 5 8 ( Figure 3.23 ). This represents a whole number (2 in this case), plus a fraction (the 5 8 5 8 ).
Another form that is a rational number is a decimal that repeats a pattern, such as 67.1313… When a rational number is expressed in decimal form and the decimal is a repeated pattern, we use special notation to designate the part that repeats. For example, if we have the repeating decimal 4.3636…, we write this as 4. 36 ¯ 4. 36 ¯ . The bar over the 36 indicates that the 36 repeats forever.
When Desmos is used, there is a tab at the bottom of the screen that opens the keyboard for Desmos. The keyboard is shown below. On the keyboard ( Figure 3.24 ) is the square root symbol ( ) ( ) . To find the square root of a number, click the square root key, and then type the number. Desmos will automatically display the value of the square root as you enter the number.
- We could attempt to find the perfect square by factoring. Writing all the factor pairs of 45 results in 1 × 45 , 3 × 15 1 × 45 , 3 × 15 , and 5 × 9 5 × 9 . None of the pairs is a square, so 45 is not a perfect square. Using a calculator to find the square root of 45, we obtain 6.708 (rounded to three decimal places). Since this was not an integer, the original number was not a perfect square.
- We could attempt to find the perfect square by factoring. Writing all the factor pairs of 144 results in 1 × 144 , 2 × 72 , 3 × 48 , 6 × 24 , 8 × 18 1 × 144 , 2 × 72 , 3 × 48 , 6 × 24 , 8 × 18 , and 12 × 12 12 × 12 . Since the last pair is an integer multiplied by itself, 144 is a perfect square. Alternately, using Desmos to find the square root of 144, we obtain 12. Since the square root of 144 is an integer, 144 is a perfect square.
- 5 . 64 ¯ 5 . 64 ¯
In Figure 3.25 , we see that 3 5 3 5 of the rectangle and 9 15 9 15 of the rectangle are equal areas.
They are the same proportion of the area of the rectangle. The left rectangle has 5 pieces, three of which are shaded. The right rectangle has 15 pieces, 9 of which are shaded. Each of the pieces of the left rectangle was divided equally into three pieces. This was a multiplication. The numerator describing the left rectangle was 3 but it becomes 3 × 3 3 × 3 , or 9, as each piece was divided into three. Similarly, the denominator describing the left rectangle was 5, but became 5 × 3 5 × 3 , or 15, as each piece was divided into 3. The fractions 3 5 3 5 and 9 15 9 15 are equivalent because they represent the same portion (often loosely referred to as equal).
This understanding of equivalent fractions is very useful for conceptualization, but it isn’t practical, in general, for determining when two fractions are equivalent. Generally, to determine if the two fractions a b a b and c d c d are equivalent, we check to see that a × d = b × c a × d = b × c . If those two products are equal, then the fractions are equal also.
Applying the definition, a = 12 , b = 30 , c = 14 a = 12 , b = 30 , c = 14 and d = 35 d = 35 . So a × d = 12 × 35 = 420 a × d = 12 × 35 = 420 . Also, b × c = 30 × 14 = 420 b × c = 30 × 14 = 420 . Since these values are equal, the fractions are equivalent.
That a × d = b × c a × d = b × c indicates the fractions a b a b and c d c d are equivalent is due to some algebra. One property of natural numbers, integers, and rational numbers (also irrational numbers) is that for any three numbers a , b , a , b , and c c with c ≠ 0 c ≠ 0 , if a = b a = b , then a / c = b / c a / c = b / c . In other words, when two numbers are equal, then dividing both numbers by the same non-zero number, the two newly obtained numbers are also equal. We can apply that to a × d a × d and b × c b × c , to show that a b a b and c d c d are equivalent if a × d = b × c a × d = b × c .
If a × d = b × c a × d = b × c , and c ≠ 0 , d ≠ 0 c ≠ 0 , d ≠ 0 , we can divide both sides by and obtain the following: a × d c = b × c c a × d c = b × c c . We can divide out the c c on the right-hand side of the equation, resulting in a × d c = b a × d c = b . Similarly, we can divide both sides of the equation by d d and obtain the following: a × d c × d = b d a × d c × d = b d . We can divide out d d the on the left-hand side of the equation, resulting in a c = b d a c = b d . So, the rational numbers a c a c and b d b d are equivalent when a × d = b × c a × d = b × c .
To show this, consider the fraction 36 63 36 63 . The numerator and denominator have the common factor 3. We can rewrite the fraction as 36 63 = 12 × 3 21 × 3 36 63 = 12 × 3 21 × 3 . The common divisor 3 is then divided out, or canceled, and we can write the fraction as 12 × 3 21 × 3 = 12 21 12 × 3 21 × 3 = 12 21 . The 3s have been crossed out to indicate they have been divided out. The process of dividing out two factors is also referred to as reducing the fraction .
36 48 = 12 × 3 12 × 4 36 48 = 12 × 3 12 × 4
36 48 = 12 × 3 12 × 4 = 3 4 36 48 = 12 × 3 12 × 4 = 3 4
Step 2: Divide out the 4, as in 36 48 = 4 × 9 4 × 12 = 4 × 9 4 × 12 = 9 12 36 48 = 4 × 9 4 × 12 = 4 × 9 4 × 12 = 9 12 .
Step 3: Examining the 9 and 12, you identify 3 as a common factor and divide out the 3, as in 9 12 = 3 × 3 3 × 4 = 3 4 9 12 = 3 × 3 3 × 4 = 3 4 . The 3 and 4 have no common positive factors other than 1, so it is in lowest terms.
100 250 = 50 × 2 50 × 5 100 250 = 50 × 2 50 × 5 .
100 250 = 50 × 2 50 × 5 = 2 5 100 250 = 50 × 2 50 × 5 = 2 5
51 136 = 17 × 3 17 × 8 51 136 = 17 × 3 17 × 8
51 136 = 17 × 3 17 × 8 = 3 8 51 136 = 17 × 3 17 × 8 = 3 8
To create a fraction in Desmos, enter the numerator, then use the division key (/) on your keyboard, and then enter the denominator. The fraction is then entered. Then click the right arrow key to exit the denominator of the fraction. Next, enter the arithmetic operation (+ or –). Then enter the next fraction. The answer is displayed dynamically (calculates as you enter). To change the Desmos result from decimal form to fractional form, use the fraction button ( Figure 3.26 ) on the left of the line that contains the calculation:
Enter 23 42 + 9 56 23 42 + 9 56 in Desmos. The result is displayed as 0.70833333333 0.70833333333 (which is 0.708 3 ¯ 0.708 3 ¯ ). Clicking the fraction button to the left on the calculation line yields 17 24 17 24 .
Performing addition and subtraction without a calculator may be more involved. When the two rational numbers have a common denominator, then adding or subtracting the two numbers is straightforward. Add or subtract the numerators, and then place that value in the numerator and the common denominator in the denominator. Symbolically, we write this as a c ± b c = a ± b c a c ± b c = a ± b c . This can be seen in the Figure 3.27 , which shows 3 20 + 4 20 = 7 20 3 20 + 4 20 = 7 20 .
If c c is a non-zero integer, then a c ± b c = a ± b c a c ± b c = a ± b c .
Once we have that result, reduce to lowest terms, which gives 20 28 = 4 × 5 4 × 7 = 4 × 5 4 × 7 = 5 7 20 28 = 4 × 5 4 × 7 = 4 × 5 4 × 7 = 5 7 .
Calculate 45 136 − 17 136 45 136 − 17 136 .
Since the rational numbers have the same denominator, we perform the subtraction of the numerators, 45 − 17 45 − 17 , and then place the result in the numerator and the common denominator, 136, in the denominator. 45 136 − 17 136 − 45 − 17 136 = 28 136 45 136 − 17 136 − 45 − 17 136 = 28 136
Once we have that result, reduce to lowest terms, this gives 28 136 = 4 × 7 4 × 34 = 4 × 7 4 × 34 = 7 34 28 136 = 4 × 7 4 × 34 = 4 × 7 4 × 34 = 7 34 .
Step 3: Multiply the numerator and denominator of a b a b by n n , yielding a × n b × n a × n b × n .
Step 4: Multiply the numerator and denominator of c d c d by m m , yielding c × m d × m c × m d × m .
You should be aware that the common denominator is LCM ( b , d ) LCM ( b , d ) . For the first denominator, we have b × n = b × L C M ( b , d ) b = L C M ( b , d ) b × n = b × L C M ( b , d ) b = L C M ( b , d ) , since we multiply and divide LCM ( b , d ) LCM ( b , d ) by the same number. For the same reason, d × m = d × L C M ( b , d ) b = L C M ( b , d ) d × m = d × L C M ( b , d ) b = L C M ( b , d ) .
Step 3: Multiplying the numerator and denominator of 11 18 11 18 by n = 5 n = 5 yields 11 × 5 18 × 5 = 55 90 11 × 5 18 × 5 = 55 90 .
Step 4: Multiply the numerator and denominator of 2 15 2 15 by m = 6 m = 6 yields 2 × 6 15 × 6 = 12 90 2 × 6 15 × 6 = 12 90 .
Calculate 14 25 − 9 70 14 25 − 9 70 .
Step 3: Multiplying the numerator and denominator of 14 25 14 25 by n = 14 n = 14 yields 14 × 14 25 × 14 = 196 350 14 × 14 25 × 14 = 196 350 .
Step 4: Multiplying the numerator and denominator of 9 70 9 70 by m = 5 m = 5 yields 9 × 5 70 × 5 = 45 350 9 × 5 70 × 5 = 45 350 .
Step 5: Now we subtract the value from Step 4 from the value in Step 3: 196 350 − 45 350 = 151 350 196 350 − 45 350 = 151 350 .
This is in lowest terms, so we have found that 14 25 − 9 70 = 151 350 14 25 − 9 70 = 151 350 .
One way to visualize a fraction is as parts of a whole, as in 5 12 5 12 of a pizza. But when the numerator is larger than the denominator, as in 23 12 23 12 , then the idea of parts of a whole seems not to make sense. Such a fraction is an improper fraction. That kind of fraction could be written as an integer plus a fraction, which is a mixed number . The fraction 23 12 23 12 rewritten as a mixed number would be 1 11 12 1 11 12 . Arithmetically, 1 11 12 1 11 12 is equivalent to 1 + 11 12 1 + 11 12 , which is read as “one and 11 twelfths.”
Step 1: Multiply the integer part, 5, by the denominator, 9, which gives 5 × 9 = 45 5 × 9 = 45 .
Multiplying rational numbers is less complicated than adding or subtracting rational numbers, as there is no need to find common denominators. To multiply rational numbers, multiply the numerators, then multiply the denominators, and write the numerator product divided by the denominator product. Symbolically, a b × c d = a × c b × d a b × c d = a × c b × d . As always, rational numbers should be reduced to lowest terms.
If b b and d d are non-zero integers, then a b × c d = a × c b × d a b × c d = a × c b × d .
Calculate 12 25 × 10 21 12 25 × 10 21 .
12 25 × 10 21 = 12 × 10 25 × 21 = 120 525 12 25 × 10 21 = 12 × 10 25 × 21 = 120 525
120 525 = 15 × 8 15 × 35 = 8 35 120 525 = 15 × 8 15 × 35 = 8 35
Calculate 3.45 ÷ 2.341 using a calculator. Round to three decimal places if necessary.
When dividing two fractions by hand, find the reciprocal of the divisor (the number that is being divided into the other number). Next, replace the divisor by its reciprocal and change the division into multiplication. Then, perform the multiplication. Symbolically, b a ÷ c d = a b × d c = a × d b × c b a ÷ c d = a b × d c = a × d b × c . As before, reduce to lowest terms.
If b , c b , c and d d are non-zero integers, then b a ÷ c d = a b × d c = a × d b × c b a ÷ c d = a b × d c = a × d b × c .
- Calculate 4 21 ÷ 6 35 4 21 ÷ 6 35 .
- Calculate 1 8 ÷ 5 28 1 8 ÷ 5 28 .
Step 1: Find the reciprocal of the number being divided by 6 35 6 35 . The reciprocal of that is 35 6 35 6 .
4 21 ÷ 6 35 = 4 21 × 35 6 = 140 126 4 21 ÷ 6 35 = 4 21 × 35 6 = 140 126
The answer, 140 126 140 126 is not in lowest terms. The GCD of 140 and 126 is 14. Factoring and canceling gives 140 126 = 14 × 10 14 × 9 = 10 9 140 126 = 14 × 10 14 × 9 = 10 9 .
Step 1: Find the reciprocal of the number being divided by, which is 5 28 5 28 . The reciprocal of that is 28 5 28 5 .
Step 2: Multiply the first fraction by that reciprocal: 1 8 ÷ 5 28 = 1 8 × 28 5 = 28 40 1 8 ÷ 5 28 = 1 8 × 28 5 = 28 40
The answer, 28 40 28 40 , is not in lowest reduced form. The GCD of 28 and 40 is 4. Factoring and canceling gives 28 40 = 4 × 7 4 × 10 = 7 10 28 40 = 4 × 7 4 × 10 = 7 10 .
The order of operations for rational numbers is the same as for integers, as discussed in Order of Operations . The order of operations makes it easier for anyone to correctly calculate and represent. The order follows the well-known acronym PEMDAS:
Correctly apply the rules for the order of operations to accurately compute ( 5 7 − 2 7 ) × 2 3 ( 5 7 − 2 7 ) × 2 3 .
( 5 7 − 2 7 ) × 2 3 = ( 3 7 ) × 2 3 ( 5 7 − 2 7 ) × 2 3 = ( 3 7 ) × 2 3
( 3 7 ) × 2 3 = ( 3 7 ) × 8 ( 3 7 ) × 2 3 = ( 3 7 ) × 8
( 3 7 ) × 8 = 24 7 ( 3 7 ) × 8 = 24 7
Correctly apply the rules for the order of operations to accurately compute 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 .
4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 1 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 15 3 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 1 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 15 3 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2
4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 = 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 = 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2
4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 × 27 3 × 27 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 459 81 ) ) 2 4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 × 27 3 × 27 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 459 81 ) ) 2 4 + 2 3 ÷ ( ( − 434 81 ) ) 2
4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( 188,356 6,561 ) = 4 + 2 3 × ( 6,561 188,356 ) = 4 + 2,187 94,178 4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( 188,356 6,561 ) = 4 + 2 3 × ( 6,561 188,356 ) = 4 + 2,187 94,178
4 11 + 7 12 = 4 × 12 11 × 12 + 7 × 11 12 × 11 = 48 132 + 77 132 = 125 132 4 11 + 7 12 = 4 × 12 11 × 12 + 7 × 11 12 × 11 = 48 132 + 77 132 = 125 132
125 132 ÷ 2 = 125 132 × 1 2 = 125 264 125 132 ÷ 2 = 125 132 × 1 2 = 125 264
We could check that the number we found is between the other two by finding the decimal representation of the numbers. Using a calculator, the decimal representations of the rational numbers are 0.363636…, 0.473484848…, and 0.5833333…. Here it is clear that 125 264 125 264 is between 4 11 4 11 and 7 12 7 12 .
Step 1: The required fraction of topsoil is 2 5 2 5 , so James needs 60 × 2 5 60 × 2 5 cubic feet of topsoil. Performing the multiplication, James needs 60 × 2 5 = 120 5 = 24 60 × 2 5 = 120 5 = 24 (found by treating the fraction as division, and 120 divided by 5 is 24) cubic feet of topsoil.
Step 2: The required fraction of peat moss is also 2 5 2 5 , so he also needs 60 × 2 5 60 × 2 5 cubic feet, or 60 × 2 5 = 120 5 = 24 60 × 2 5 = 120 5 = 24 cubic feet of peat moss.
Step 3: The required fraction of compost is 1 5 1 5 . For the compost, he needs 60 × 1 5 = 60 5 = 12 60 × 1 5 = 60 5 = 12 cubic feet.
At Bella’s Pizza, one-third of the pizzas that are ordered are one of their specialty varieties. If there are 273 pizzas ordered, how many were specialty pizzas?
One-third of the whole are specialty pizzas, so we need one-third of 273, which gives 1 3 × 273 = 273 3 = 91 1 3 × 273 = 273 3 = 91 , found by dividing 273 by 3. So, 91 of the pizzas that were ordered were specialty pizzas.
From the inches and centimeters example, to change from inches to centimeters, we use the fraction 2.54 cm 1 in 2.54 cm 1 in . If, on the other hand, we wanted to convert from centimeters to inches, we’d use the fraction 1 in 2.54 cm 1 in 2.54 cm . This fraction is multiplied by the number of units of the type you are converting from , which means the units of the denominator are the same as the units being multiplied.
We know that 1 liter = 0.264172 gal. Since we are converting from liters, when we create the fraction we use, make sure the liter part of the equivalence is in the denominator. So, to convert the 14 liters to gallons, we multiply 14 by 1 gal 0.264172 gal / 1 liter 1 gal 0.264172 gal / 1 liter . Notice the gallon part is in the numerator since we’re converting to gallons, and the liter part is in the denominator since we are converting from liters. Performing this and rounding to three decimal places, we find that 14 liters is 14 liter × 0.264172 gal 1 liter = 3.69841 gal 14 liter × 0.264172 gal 1 liter = 3.69841 gal .
We know that 1 inch = 2.54 cm. Since we are converting from centimeters, when we create the fraction we use, make sure the centimeter part of the equivalence is in the denominator, 1 in 2.54 cm 1 in 2.54 cm . To convert the 100 cm to inches, multiply 100 by 1 in 2.54 cm 1 in 2.54 cm . Notice the inch part is in the numerator since we’re converting to inches, and the centimeter part is in the denominator since we are converting from centimeters. Performing this and rounding to three decimal places, we obtain 100 cm × 1 in 2.54 cm = 39.370 in 100 cm × 1 in 2.54 cm = 39.370 in . This means 100 cm equals 39.370 in.
Percent is used to indicate a fraction of a total. If we want to find 30% of 90, we would perform a multiplication, with 30% written in either decimal form or fractional form. The 90 is the total , 30 is the percentage , and 27 (which is 0.30 × 90 0.30 × 90 ) is the percentage of the total .
n % n % of x x items is n 100 × x n 100 × x . The x x is referred to as the total , the n n is referred to as the percent or percentage , and the value obtained from n 100 × x n 100 × x is the part of the total and is also referred to as the percentage of the total .
- The total is 300, and the percentage is 40. Using the decimal form of 40% and multiplying we obtain 0.40 × 300 = 120 0.40 × 300 = 120 .
- The total is 190, and the percentage is 64. Using the decimal form of 64% and multiplying we obtain 0.64 × 190 = 121.6 0.64 × 190 = 121.6 .
If we know that n n % of the total is x x , then the total is 100 × x n 100 × x n .
- 28 is the percentage, so n = 28 n = 28 . 28% of the total is 140, so x = 140 x = 140 . Using those we find that the total was 100 × 140 28 = 500 100 × 140 28 = 500 .
- 6 is the percentage, so n = 6 n = 6 . 6% of the total is 91, so x = 91 x = 91 . Using those we find that the total was 100 × 91 6 = 1,516.6 100 × 91 6 = 1,516.6 .
The percentage, n n , of b b that is a a is a b × 100 % a b × 100 % .
The percentage of interest is 70%. The total number of students is 400. With that, we can find how many were in the percentage of the total, or, how many were sleep deprived. Applying the formula from above, the number who were sleep deprived was 0.70 × 400 = 280 0.70 × 400 = 280 ; 280 students on the study were sleep deprived.
We need to find the total number of student-athletes at Evander’s university.
Step 2: To find the total number of student-athletes, use 100 × x n 100 × x n , with x = 219 x = 219 and n = 73 n = 73 . Calculating with those values yields 100 × 219 73 = 300 100 × 219 73 = 300 .
So, there are 300 total student-athletes at Evander’s university
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Authors: Donna Kirk
- Publisher/website: OpenStax
- Book title: Contemporary Mathematics
- Publication date: Mar 22, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Section URL: https://openstax.org/books/contemporary-mathematics/pages/3-4-rational-numbers
© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.
Illustrative Mathematics Grade 7, Unit 5, Lesson 14: Solving Problems with Rational Numbers
Learning Targets:
- I can represent situations with expressions that include rational numbers.
- I can solve problems using the four operations with rational numbers.
Related Pages Illustrative Math Grade 7
Lesson 14: Solving Problems with Rational Numbers
Let’s use all four operations with signed numbers to solve problems.
Illustrative Math Unit 7.5, Lesson 14 (printable worksheets)
Lesson 14 Summary

Lesson 14.1 Which One Doesn’t Belong: Equations
Which equation doesn’t belong? 1/2 x = -50 -60t = 30 x + 90 = -100 -0.01 = -0.001x
Lesson 14.2 Draining and Filling a Tank
A tank of water is being drained. Due to a problem, the sensor does not start working until some time into the draining process. The sensor starts its recording at time zero when there are 770 liters in the tank.
- Given that the drain empties the tank at a constant rate of 14 liters per minute, complete the table:
- Later, someone wants to use the data to find out how long the tank had been draining before the sensor started. Complete this table:
- If the sensor started working 15 minutes into the tank draining, how much was in the tank to begin with?
Lesson 14.3 Buying and Selling Power
A utility company charges $0.12 per kilowatt-hour for energy a customer uses. They give a credit of $0.025 for every kilowatt-hour of electricity a customer with a solar panel generates that they don’t use themselves. A customer has a charge of $82.04 and a credit of -$4.10 on this month’s bill.
- What is the amount due this month?
- How many kilowatt-hours did they use?
- How many kilowatt-hours did they generate that they didn’t use themselves?
Are you ready for more?
- Write an expression that uses addition, subtraction, multiplication, and division and only negative numbers that has the same value.
Lesson 14 Practice Problems
- A furniture store pays a wholesale price for a mattress. Then, the store marks up the retail price to 150% of the wholesale price. Later, they put the mattress on sale for 50% off of the retail price. A customer just bought the mattress on sale and paid $1,200. a. What was the retail price of the mattress, before the discount? b. What was the wholesale price, before the markup?
- The table shows transactions in a checking account. a. Find the total of the transactions for each month. b. Find the mean total for the four months.
- A bank charges a service fee of $7.50 per month for a checking account. A bank account has $85.00. If no money is deposited or withdrawn except the service charge, how many months until the account balance is negative?
- A large aquarium of water is being filled with a hose. Due to a problem, the sensor does not start working until some time into the filling process. The sensor starts its recording at the time zero minutes. The sensor initially detects the tank has 225 liters of water in it. a. The hose fills the aquarium at a constant rate of 15 liters per minute. What will the sensor read at the time 5 minutes? b. Later, someone wants to use the data to find the amount of water at times before the sensor started. What should the sensor have read at the time -7 minutes?
- a. A restaurant bill is $21. You leave a 15% tip. How much do you pay including the tip? b. Which of the following represents the amount a customer pays including the tip of 15% if the bill was dollars? Select all that apply.
The Open Up Resources math curriculum is free to download from the Open Up Resources website and is also available from Illustrative Mathematics .

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Have an account?
Suggestions for you See more

Rational and Irrational Numbers
Real number system, 7th - 9th , multiplying and dividing rational expres..., 11th - 12th , rational numbers.

Unit 1 Rational Numbers Test Review
Mathematics.

10 questions

Introducing new Paper mode
No student devices needed. Know more
- 6. Multiple Choice Edit 2 minutes 1 pt A Gatorade cooler has 36 cups of water. If a serving is ¾ of a cup how many servings are in the cooler? 48 servings 27 servings 36 ¾ servings 60 servings
- 8. Multiple Choice Edit 30 seconds 1 pt natural, or counting numbers, include zero true false
- 9. Multiple Choice Edit 30 seconds 1 pt -1 is a whole number, integer, and rational number True False
Explore all questions with a free account

Continue with email
Continue with phone
i need help with my Rational Numbers unit test part 1
Rational functions unit test part 1 all correct 100%.
1: Suppose that y varies jointly with w and x and inversely with z and y = 540 when w = 15, x = 30, and z = 5. Write the equation that models the relationship. ANSWER: (6wx)/z 2: A drama club is planning a bus trip to New York City to see a Broadway play. The cost per person for the bus rental varies inversely to the number of people going on the trip. It will cost $30 per person if 44 people go on the trip. How much will it cost per person if 60 people go on the trip? Round your answer to the nearest cent, if necessary. ANSWER: $22.00 3:Graph the function. xy + 9 = 0 ANSWER: letter C, the one with the curvy line in the top left and bottom right 4:Sketch the asymptotes and graph the function y=5/(x-2) + 3 ANSWER: letter A, the graph with a vertical asymptote of 2 and a horizontal asymptote of 3 5:What is the equation of the function y=2/x translated 3 units to the left and 4 units up? ANSWER: y=2/(x+3) + 4 6:Find any points of discontinuity for the rational function. y=(x-8)/(x^2+5x-6) ANSWER: x=1, x=-6 7:Describe the vertical asymptote(s) and hole(s) for the graph of y=(x-6)/(x^2+5x+6) ANSWER: asymptotes:x=-2, -3 and no holes 8: Find the horizontal asymptote of the graph of y=(2x^6+5x+8)/8x^6+6x+5) ANSWER: y=-1/4 9: Which of the following is the graph of the rational function? (x^2+2x-8)/(x^2-9) ANSWER: letter A, the one with a line in the top right quadrant and a line down the middle 10: Simplify the rational expression. State any restrictions on the variable. (t^2+4t-12)/(t^2-4) ANSWER: (t+6)/(t+2), t does not equal 2 or -2 11: What is the product in simplest form? State any restrictions on the variable. (x^2+5x+6)/(x+4) • (x^2+x-12)/(x^2+x-2) ANSWER: (x+3)(x-3)/(x-1) 12: Which is equivalent to (3x)/(x-7) - (x+7)/x ? ANSWER: (2x^2+49)/x(x-7) 13: What is the difference in simplest form? (n^2+3n+2)/(n^2+6n+8) - (2n)/(n+4) ANSWER: (1-n)/(n+4) 14: Simplify the sum. (d^2-9d+20)/(d^2-3d-10) + (d^2-2d-8)/(d^2+4d-32) ANSWER: (2d^2+8d-28)/(d+2)(d+8) 15: Simplify the complex fraction. (n-6)/(n^2+11n+24) / (n+1)/(n+3) ANSWER: (n-6)/(n+1)(n+8) 16: Solve the equation. Check the solution. (a)/(a^2-16) + (2)/(a-4) = (2)/(a+4) ANSWER: -16 17: A group of college students is volunteering for Help the Homeless during their spring break. They are putting the finishing touches on a house they built. Working alone, Irina can paint a certain room in 9 hours. Paulo can paint the same room in 8 hours. Write an equation that can be used to find how long it will take them working together to paint the room. How many hours will it take them to paint the room? If necessary, round your answer to the nearest hundredth. ANSWER: (x)/(9) + (x)/(8) = 1; 4.24 hours 18:Does the relation in the table represent direct variation, inverse variation, or neither? If it is direct or inverse variation, write an equation to represent the relation. Explain your answer. x 5 10 15 20 y 2 1 2/3 1/2 ANSWER: inverse variation, the equation is y=(10)/(x)
Am I the only one with 25 questions??
I do too, can someone please tell the answers, i think i'm going to be better off guessing. the teachers really tricking us up on this question., oi oi oi pp, oi oi oi erwin pp pee pee, is . correct, i’m so confused, ok so what are the steps to solve this problem 0.000027 divided by 0.000009 guys all were doing here is divideing im pretty sure tha the answer is 3 or negative 3 ok moveing on to question 3 o.54 written as a simplified fraction well since the 54 is in the hundreths place i would say 54 over 100 but the answer has to be simplfied so the answer is 27/50 question 4 idk that one its to long and confuseing ok so i was only able to help with question 1 and 3 sorry but once i get the answers cuz imma do it quik i will tell you, mine has 18, oui oui baugette.

260%. Write 2.6 as a percent. 2 3/5. Write 260% as a fraction. 0.32. Mrs. Allred surveyed her class of 25 students. 8 of the students chose math as their favorite class. What decimal represents the fraction of students who chose math as their favorite class? 19/50. Nathalie has a stuffed animal collection.
Which of the following statements is true? The product of a positive and negative fraction is negative. Express -5 2/5 as an improper fraction. - 27/5. Add - 3/x + 7y/x . not - 4y/2x. Subtract 8/x - 11/3x . not 24m - 11/3m. Study with Quizlet and memorize flashcards containing terms like 125.7 - (-1.82) = 1.439, (0.05) (-0.25) = -1.25, (1.2)^2 ...
the repeating ones: 7.777777 , 6.213¯, 4.04. the non-repeating ones: 5.152535
SOLVING PROBLEMS WITH RATIONAL NUMBERS. In this section, we will learn how to solve problems with rational numbers. A number that is expressed in the form a/b is called as rational number. Here, both "a" and "b" are integers and also b ≠ 0. Problem 1 : The area of a rectangular sandbox is 56 2/3 square feet. The length of the sandbox is 8 1/2 ...
Directions for AlphaMath Problems (Problems 38 - 41): Letters stand for digits 0-9. In a given problem, the same letter always represents the same digit, and different letters always represent different digits. There is no relation between problems (so "A" in part 1 and "A" in part 3 might be different).
7.1.2B Problem Solving with Rational Numbers. Standard 7.1.2. Solve problems in various contexts involving calculations with positive and negative rational numbers and positive in
7.1.2 Group B - Problem Solving with Rational Numbers. 7.1.2.4 Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest. 7.1.2.5 Use proportional reasoning to solve problems involving ratios in various contexts.
Rational numbers may also be expressed in decimal form; for instance, as 1.34. When 1.34 is written, the decimal part, 0.34, represents the fraction 34 100 34 100, and the number 1.34 is equal to 1 34 100 1 34 100.However, not all decimal representations are rational numbers.
Unit test. Level up on all the skills in this unit and collect up to 4100 Mastery points! "Students continue to build an understanding of the number line in Module 2 from their work in Grade 6. They learn to add, subtract, multiply, and divide rational numbers. Module 2 includes rational numbers as they appear in expressions and equations ...
Rational numbers may also be expressed in decimal form; for instance, as 1.34. When 1.34 is written, the decimal part, 0.34, represents the fraction 34 100, and the number 1.34 is equal to 1 34 100. However, not all decimal representations are rational numbers. A number written in decimal form where there is a last decimal digit (after a given ...
Lesson 14.3 Buying and Selling Power. A utility company charges $0.12 per kilowatt-hour for energy a customer uses. They give a credit of $0.025 for every kilowatt-hour of electricity a customer with a solar panel generates that they don't use themselves. A customer has a charge of $82.04 and a credit of -$4.10 on this month's bill.
19 Qs. Real Number System. 3.2K plays. 7th - 9th. 12 Qs. Multiplying and Dividing Rational Expres... 1.7K plays. 11th - 12th. Unit 1 Rational Numbers Test Review quiz for 7th grade students.
Irrational Numbers. is a real number that cannot be expressed as a ratio of integers. Repeating Decimals to Fraction. 1.) Let "x" equal the repeating decimal you are trying to convert to a fraction. 2.) Examine the repeating decimal to find the repeating digit (s) 3.) Place the repeating digit (s) to the left of the decimal point.
RATIONAL FUNCTIONS UNIT TEST PART 1 ALL CORRECT 100%. 1: Suppose that y varies jointly with w and x and inversely with z and y = 540 when w = 15, x = 30, and z = 5. Write the equation that models the relationship. ANSWER: (6wx)/z. 2: A drama club is planning a bus trip to New York City to see a Broadway play.
Problem Solving with Rational Numbers. Finding percentages can be done using mental math. Percent means 'per hundred' so finding a percentage of a number involves turning the percentage into a fraction with a denominator of 100 and multiplying it by the number. Here are the calculations: 1a) 10% of 40 is (10/100)*40 = 4; 1b) 20% of 40 is (20/ ...
Graded Assignment 3.11 part 2 math graded assignment interim test, part interim name: date: graded assignment interim test, part interim answer the questions ... 3.12 Unit Test Part 2 - 3.12 Unit Test Part 2. Math. Assignments. 100% (2) 3. Math 4 - Math 4 ... Use x to represent the number of juice cartons Quan can purchase and write an ...
Section 2.5 : Quadratic Equations - Part I. Back to Problem List. 11. Use factoring to solve the following equation. 4z z+1 + 5 z = 6z+5 z2+z 4 z z + 1 + 5 z = 6 z + 5 z 2 + z. Show All Steps Hide All Steps. Start Solution.
Section 2.13 : Rational Inequalities. Back to Problem List. 1. Solve the following inequality. 4 −x x +3 >0 4 − x x + 3 > 0. Show All Steps Hide All Steps.
The to be subtracted from another number. Sum. The total from adding two numbers. Zero Property of Multiplication. Multiplying a number by zero equals ZERO. Example: 2 * 0 = 0. Study with Quizlet and memorize flashcards containing terms like addend, Associative Property of Addition, Associative Property of Multiplication and more.
2.7A Composition of Functions. Next Lesson. If you find errors in our work, please let us know at [email protected] so we can fix it. AP Precalculus - 2.7A Composition of Functions.
Section 1.2 : Rational Exponents. For problems 1 - 6 evaluate the given expression and write the answer as a single number with no exponents. For problems 7 - 10 simplify the given expression and write the answer with only positive exponents. Here is a set of practice problems to accompany the Rational Exponents section of the Preliminaries ...
So, we are now going to solve quadratic equations. First, the standard form of a quadratic equation is. ax2 +bx +c = 0 a ≠ 0 a x 2 + b x + c = 0 a ≠ 0. The only requirement here is that we have an x2 x 2 in the equation. We guarantee that this term will be present in the equation by requiring a ≠ 0 a ≠ 0. Note however, that it is okay ...
Section 2.6 : Quadratic Equations - Part II. For problems 1 - 6 complete the square. w2 +3w w 2 + 3 w. x2 −10x x 2 − 10 x. y2 +14y y 2 + 14 y. 3u2 −36u 3 u 2 − 36 u. 2t2 −9t 2 t 2 − 9 t. 18x −x2 18 x − x 2. For problems 7 - 16 solve the quadratic equation by completing the square.
- business plan
- course work
- research paper
Adding and Subtracting Rational Numbers
This lesson is about adding and subtracting rational numbers. The topic is a bit complex. Here we need to use the entire previously gained knowledge.
The rules of addition and subtraction of integers are also valid for rational numbers .
In this lesson we will increasingly refer to fractions and mixed numbers by one common phrase: rational numbers.
Adding rational numbers with different signs
This is an addition of rational numbers with different signs.
To add rational numbers with different signs, you need to subtract the smaller modulus from the larger modulus, and put the sign of the rational number whose modulus is larger before the result you get.
And to understand which modulus is greater and which is less, you should be able to compare both modulus of these fractions before calculating them:
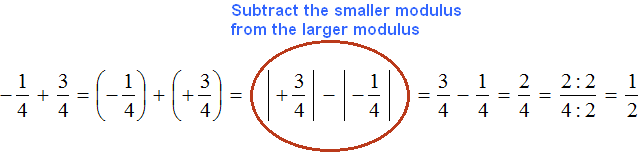
Some primitive operations, such as putting numbers in parentheses and modulus calculations can be skipped. This example may well be written in a shorter form:
Replace subtraction with addition. Recall that to do this you must add to the subtractor the number opposite to the subtractor:
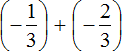
We have obtained the addition of negative rational numbers.
To add negative rational numbers, add their both modulus and put minus sign in front of the result:
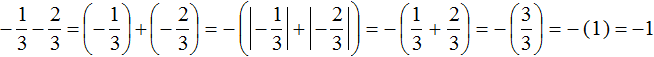
Let's write down the solution to this example in shorter form:
Note. It is not necessary to bracket each rational number. This is done for convenience, to see clearly what signs rational numbers have.
In this expression, the fractions have different denominators. To make the exercise easier, let's reduce these fractions to a common denominator . We won't go into detail about how to do this. If you have trouble with it, be sure to revise lesson actions with fractions .
After reducing the fractions to a common denominator, the expression will take the following form:
Put each rational number in parentheses together with its signs:
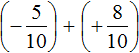
This is an addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and precede the answer with the sign of the rational number whose modulus is greater:
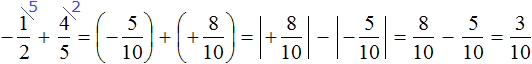
Put each rational number in parentheses along with its signs:
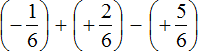
Second act:
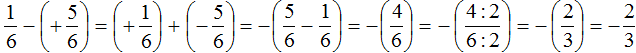
Let's reduce these fractions to a common denominator. After reducing them to a common denominator, they will take the following form:
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the rational number whose modulus is greater in front of the answer:
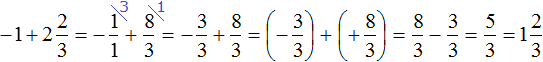
There is a second way to solve this problem. It consists in adding the whole parts separately.
So, let's go back to the original expression:
Let's put each number in parentheses.
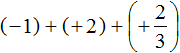
Let's calculate the whole parts:
(−1) + (+2) = 1
In the main expression instead of (-1) + (+2) write the resulting unit:
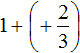
Replace subtraction with addition:
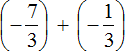
We obtained the addition of negative rational numbers. Add the modules of these numbers and put minus in front of the result:
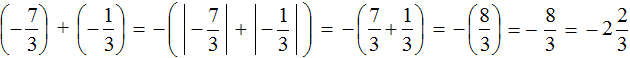
Let's reduce these fractions to a common denominator. After reducing them to a common denominator , they will take the following form:
We obtained the addition of negative rational numbers. Add the modules of these numbers and put minus sign in front of the result:
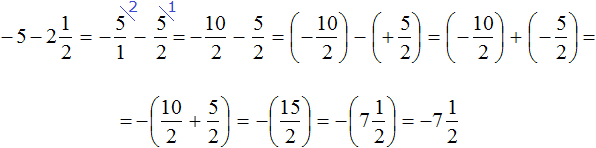
Let us solve this example in the second way. Let us return to the original expression:
Replace subtraction with addition where possible:
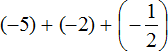
Let's convert the mixed numbers into improper fraction:
We obtained the addition of negative rational numbers. Add the modules of these numbers and put minus in front of the obtained answer:
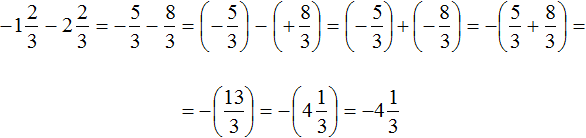
This example can also be solved in the second way. It consists of adding the whole and fractional parts separately. Let's return to the original expression:
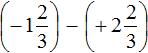
Now let's try to solve the same example in the second way, namely by adding the whole and fractional parts separately.
This time, in order to get a short solution, we will try to skip some steps, such as: writing the mixed number in expanded form and replacing subtraction with addition:
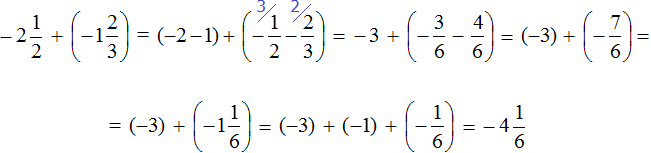
Note that the fractional parts have been reduced to a common denominator.
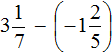
The resulting expression has no negative numbers, which are the main cause of errors. And since there are no negative numbers, we can remove the plus before the subtractor and also remove the parentheses:
We have obtained a simple expression, which is easy to calculate. Let's calculate it any way we want:
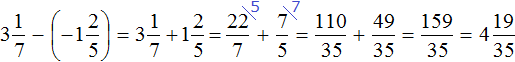
This is an addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the rational number whose modulus is greater in front of the answer:
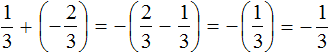
The expression consists of several rational numbers. According to the order of operations , you must perform what is inside the brackets first .
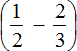
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the rational number whose modulus is greater in front of the obtained result:
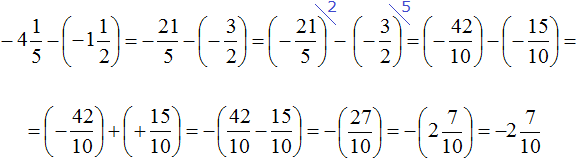
Consider addition and subtraction of decimals, which are also rational numbers and can be both positive and negative.
Example 14. Find the value of the expression -3.2 + 4.3
Put each rational number in parentheses together with its signs. Note that the plus sign given in the expression is a sign of the operation and does not apply to the decimal 4.3. This decimal has its own plus sign, which is invisible because it is not written down. But we will write it down for clarity:
(−3.2) + (+4.3)
To add rational numbers with different signs, you need to subtract the smaller modulus from the larger modulus, and put the sign of the rational number whose modulus is larger in front of the answer you get.
And to understand which modulus is greater and which is less, you need to be able to compare both modulus of these decimals before calculating them:
(−3.2) + (+4.3) = |+4.3| − |−3.2| = 1.1
The modulus of 4.3 is greater than the modulus of -3.2, so we subtracted 3.2 from 4.3. The answer is 1.1. The answer is positive because the answer must be preceded by the sign of the rational number whose modulus is greater. And the modulus of 4.3 is greater than the modulus of -3.2
Therefore, the value of -3.2 + (+4.3) is 1.1
This example can be written in a shorter form:
−3.2 + (+4.3) = 1.1
Example 15. Find the value of the expression 3.5 + (-8.3)
This is an addition of rational numbers with different signs. As in the previous example, subtract the smaller one from the larger modulus and put the sign of the rational number whose modulus is larger in front of the answer:
3.5 + (−8.3) = −(|−8.3| − |3.5|) = −(8.3 − 3.5) = −(4.8) = −4.8
Thus, the value of the expression 3.5 + (-8.3) is -4.8
This example can be written in shorter form:
3.5 + (−8.3) = −4.8
Example 16. Find the value of the expression -7.2 + (-3.11)
This is an addition of negative rational numbers. To add negative rational numbers, add their both modulus and put minus in front of the result.
Calcualtions with modules can be skipped:
−7.2 + (−3.11) = −7.20 + (−3.11) = −(7.20 + 3.11) = −(10.31) = −10.31
Thus, the value of the expression -7.2 + (-3.11) is -10.31
−7.2 + (−3.11) = −10.31
Example 17. Find the value of the expression -0.48 + (-2.7)
This is an addition of negative rational numbers. Add their modules and put a minus in front of the answer. You may omit both modulus, so as not to overload the expression:
−0.48 + (−2.7) = (−0.48) + (−2.70) = −(0.48 + 2.70) = −(3.18) = −3.18
Example 18. Find the value of the expression -4.9 - 5.9
Put each rational number in parentheses together with its signs. Note that the minus sign between the rational numbers -4.9 and 5.9 is an operation sign and does not apply to the number 5.9. This rational number has its own plus sign, which is invisible because it is not written down. But we will write it down for clarity:
(−4.9) − (+5.9)
(−4,9) + (−5,9)
We obtained the addition of negative rational numbers. Add their modules and put minus in front of the obtained answer:
(−4.9) + (−5.9) = −(4.9 + 5.9) = −(10.8) = −10.8
Thus, the value of the expression -4.9 - 5.9 is -10.8
−4.9 − 5.9 = −10.8
Example 19. Find the value of the expression 7 - 9.3
Bracket each number together with its signs
(+7) − (+9.3)
Replacing subtraction with addition
(+7) + (−9.3)
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the number whose modulus is greater in front of the result:
(+7) + (−9.3) = −(9.3 − 7) = −(2.3) = −2.3
Thus, the value of the expression 7 - 9.3 is -2.3
7 − 9.3 = −2.3
Example 20. Find the value of the expression -0.25 - (-1.2)
−0.25 + (+1.2)
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the number whose modulus is greater in front of the answer:
−0.25 + (+1.2) = 1.2 − 0.25 = 0.95
−0.25 − (−1.2) = 0.95
Example 21. Find the value of the expression -3.5 + (4.1 - 7.1)
Follow the steps in parentheses, then add the answer to the number -3.5
4.1 − 7.1 = (+4.1) − (+7.1) = (+4.1) + (−7.1) = −(7.1 − 4.1) = −(3.0) = −3.0
−3.5 + (−3.0) = −(3.5 + 3.0) = −(6.5) = −6.5
Answer: The value of the expression -3.5 + (4.1 - 7.1) is -6.5
Example 22. Find the value of the expression (3.5 - 2.9) - (3.7 - 9.1)
Perform the actions in parentheses. Then subtract the number resulting from the first parentheses from the number resulting from the second parentheses:
3.5 − 2.9 = (+3.5) − (+2.9) = (+3.5) + (−2.9) = 3.5 − 2.9 = 0.6
3.7 − 9.1 = (+3.7) − (+9.1) = (+3.7) + (−9.1) = −(9.1 − 3.7) = −(5.4) = −5.4
0.6 − (−5.4) = (+0.6) + (+5.4) = 0.6 + 5.4 = 6.0 = 6
Answer: The value of the expression (3.5 - 2.9) - (3.7 - 9.1) is 6.
Example 23. Find the value of the expression -3.8 + 17.15 - 6.2 - 6.15
Bracket each rational number together with its signs
(−3.8) + (+17.15) − (+6.2) − (+6.15)
(−3.8) + (+17.15) + (−6.2) + (−6.15)
An expression consists of several summands. According to the commutative law of addition , if an expression consists of several summands, the sum will not depend on the order of operations. This means that the summands can be added in any order .
So let's add up all the summands from left to right in the order of their order:
(−3.8) + (+17.15) = 17.15 − 3.80 = 13.35
13.35 + (−6.2) = 13.35 − −6.20 = 7.15
7.15 + (−6.15) = 7.15 − 6.15 = 1.00 = 1
Answer: The value of the expression -3.8 + 17.15 - 6.2 - 6.15 is 1.
Let's convert the decimal -1.8 to a mixed number. Let's rewrite the rest without changing:
Then we calculate this expression by applying the previously learned rules:
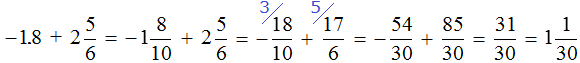
Replace subtraction with addition. At the same time, convert the decimal fraction (-4.4) into an improper fraction
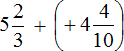
There are no negative numbers in the resulting expression. And since there are no negative numbers, we can remove the plus before the second number and remove the parentheses. Then we get a simple addition expression, which is easy to solve
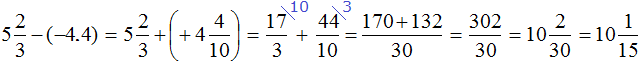
Convert decimal and fraction into improper fractions.
To convert the decimal 2.05 to an improper fraction, you can first convert it to a mixed number and then to an improper fraction:
After converting them into improper fraction, we obtain the following expression:
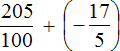
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus and precede the answer with the sign of the number whose modulus is greater:
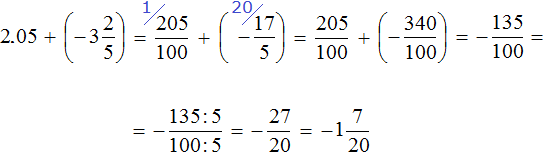
Replace subtraction with addition. Next, convert the decimal to fraction. Then calculate the resulting expression by applying the previously learned rules:
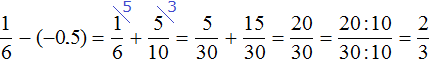
Convert the decimals -0.25 and -1.25 into fractions, and rewrite the rest unchanged. We obtain the following expression:
You can first replace subtraction with addition where possible and add rational numbers one by one.
Example 30. Find the value of the expression
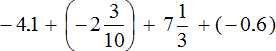
Convert the decimals into fractions. Let's rewrite the rest without changing:
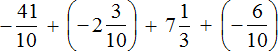
You have obtained the sum of several summands. If the sum is consist of several summands, the expression can be calculated in any order. This follows from the combinatorial law of addition.
Video lesson
- Comparing Rational Numbers
- Multiplying and dividing rational numbers
Add comment
Name (required)
E-mail (required, but will not display)
Notify me of follow-up comments
- You are here:
- Home >>
- 36. Adding and subtracting rational numbers
- 2. Basic operations
- 3. Expressions
- 4. Substitutions in expressions
- 5. Place value for beginners
- 6. Multiplication
- 7. Division
- 8. Order of operations
- Basic Laws of Math
- 9. Basic Laws of Math
- 10. Divisors and multiples
- 11. GCD and LCM
- 12. Fractions
- 13. Actions with fractions
- 14. Mixed numbers
- 15. Comparing Fractions
- 16. Units of Measurement
- 17. Ways to use fractions
- 18. Decimals
- 19. Operations with decimals
- 20. Using decimals
- 21. Rounding numbers
- 22. Repeating Decimals
- 23. Unit conversion
- Ratios & Proportion
- 25. Proportion
- 26. Distance, speed, time
- 27. Direct and inverse proportions
- 28. What are percentages?
- Additional topic & Number line
- 29. Negative numbers
- 30. Absolute value or modulus
- 31. What is a set?
- 32. Adding and subtracting integers
- 33. Multiplication and division of integers
- Rational numbers
- 34. Rational numbers
- 35. Comparing rational numbers
- 37. Multiplying and dividing rational numbers
- 38. More information about fractions
- 39. Algebraic expressions
- 40. Taking out a common factor
- 41. Expanding brackets
- 42. Simple math problems
- 43. Tasks on fractions
- 44. Percent worksheets for practice
- 45. Speed, distance, time tasks
- 46. Productivity problem
- 47. Statistics in Math
- 48. Basic theory of equation
- 49. Problem solving with equations
- 50. Proportions: exercises
- 51. Systems of linear equations
- 52. Introduction to Inequalities
- 53. Systems of linear inequalities with one variable
- 54. Set Operations | Union | Intersection
- 55. Power with a natural exponent
- 56. Power with integer exponent
- 57. Perimeter, area and volume
- 58. Monomials
- 59. Polynomials
- 60. Reduced multiplication formulas
- 61. Polynomial decomposition
- 62. Dividing polynomials
- 63. Identical transformations of polynomials
- 64. Square root
- 65. Algorithm for extracting the square root
- 66. Quadratic equation
- 67. A quadratic equation with an even second coefficient
- 68. Viette's Theorem
- 69. Factoring a trinomial using decomposition
- 70. More about modules
- 71. Absolute value equations
- 72. Solving equations with module by method of intervals
- 73. Inequalities with module
- 74. Solving inequalities with module by method intervals
- 75. Square root from both parts of an equation
- Functions and graphs
- 76. What is a function?
- 77. Linear function and its graph
- 78. Power function
- 79. Direct Proportion and its Graph
- 80. Function y=x² and its graph
- 81. Function y = √x its properties and graph
- 82. Function y=k*x² its properties and graph
- 83. Function y=k/x its properties and graph
- 84. Graphical solution of equations and inequalities
- coming soon... (new lessons every month)
3.4 Rational Numbers
Learning objectives.
After completing this section, you should be able to:
- Define and identify numbers that are rational.
- Simplify rational numbers and express in lowest terms.
- Add and subtract rational numbers.
- Convert between improper fractions and mixed numbers.
- Convert rational numbers between decimal and fraction form.
- Multiply and divide rational numbers.
- Apply the order of operations to rational numbers to simplify expressions.
- Apply density property of rational numbers.
- Solve problems involving rational numbers.
- Use fractions to convert between units.
- Define and apply percent.
- Solve problems using percent.
We are often presented with percentages or fractions to explain how much of a population has a certain feature. For example, the 6-year graduation rate of college students at public institutions is 57.6%, or 72/125. That fraction may be unsettling. But without the context, the percentage is hard to judge. So how does that compare to private institutions? There, the 6-year graduation rate is 65.4%, or 327/500. Comparing the percentages is straightforward, but the fractions are harder to interpret due to different denominators. For more context, historical data could be found. One study reported that the 6-year graduation rate in 1995 was 56.4%. Comparing that historical number to the recent 6-year graduation rate at public institutions of 57.6% shows that there hasn't been much change in that rate.
Defining and Identifying Numbers That Are Rational
A rational number (called rational since it is a ratio) is just a fraction where the numerator is an integer and the denominator is a non-zero integer. As simple as that is, they can be represented in many ways. It should be noted here that any integer is a rational number. An integer, n n , written as a fraction of two integers is n 1 n 1 .
In its most basic representation, a rational number is an integer divided by a non-zero integer, such as 3 12 3 12 . Fractions may be used to represent parts of a whole. The denominator is the total number of parts to the object, and the numerator is how many of those parts are being used or selected. So, if a pizza is cut into 8 equal pieces, each piece is 1 8 1 8 of the pizza. If you take three slices, you have 3 8 3 8 of the pizza ( Figure 3.21 ). Similarly, if in a group of 20 people, 5 are wearing hats, then 5 20 5 20 of the people are wearing hats ( Figure 3.22 ).
Another representation of rational numbers is as a mixed number, such as 2 5 8 2 5 8 ( Figure 3.23 ). This represents a whole number (2 in this case), plus a fraction (the 5 8 5 8 ).
Rational numbers may also be expressed in decimal form; for instance, as 1.34. When 1.34 is written, the decimal part, 0.34, represents the fraction 34 100 34 100 , and the number 1.34 is equal to 1 34 100 1 34 100 . However, not all decimal representations are rational numbers.
A number written in decimal form where there is a last decimal digit (after a given decimal digit, all following decimal digits are 0) is a terminating decimal , as in 1.34 above. Alternately, any decimal numeral that, after a finite number of decimal digits, has digits equal to 0 for all digits following the last non-zero digit.
All numbers that can be expressed as a terminating decimal are rational. This comes from what the decimal represents. The decimal part is the fraction of the decimal part divided by the appropriate power of 10. That power of 10 is the number of decimal digits present, as for 0.34, with two decimal digits, being equal to 34 100 34 100 .
Another form that is a rational number is a decimal that repeats a pattern, such as 67.1313… When a rational number is expressed in decimal form and the decimal is a repeated pattern, we use special notation to designate the part that repeats. For example, if we have the repeating decimal 4.3636…, we write this as 4. 36 ¯ 4. 36 ¯ . The bar over the 36 indicates that the 36 repeats forever.
If the decimal representation of a number does not terminate or form a repeating decimal, that number is not a rational number.
One class of numbers that is not rational is the square roots of integers or rational numbers that are not perfect squares , such as 10 10 and 25 6 25 6 . More generally, the number b b is the square root of the number a a if a = b 2 a = b 2 . The notation for this is b = a b = a , where the symbol is the square root sign. An integer perfect square is any integer that can be written as the square of another integer. A rational perfect square is any rational number that can be written as a fraction of two integers that are perfect squares.
Sometimes you may be able to identify a perfect square from memory. Another process that may be used is to factor the number into the product of an integer with itself. Or a calculator (such as Desmos) may be used to find the square root of the number. If the calculator yields an integer, the original number was a perfect square.
Using Desmos to Find the Square Root of a Number
When Desmos is used, there is a tab at the bottom of the screen that opens the keyboard for Desmos. The keyboard is shown below. On the keyboard ( Figure 3.24 ) is the square root symbol ( ) ( ) . To find the square root of a number, click the square root key, and then type the number. Desmos will automatically display the value of the square root as you enter the number.
Example 3.51
Identifying perfect squares.
Which of the following are perfect squares?
- We could attempt to find the perfect square by factoring. Writing all the factor pairs of 45 results in 1 × 45 , 3 × 15 1 × 45 , 3 × 15 , and 5 × 9 5 × 9 . None of the pairs is a square, so 45 is not a perfect square. Using a calculator to find the square root of 45, we obtain 6.708 (rounded to three decimal places). Since this was not an integer, the original number was not a perfect square.
- We could attempt to find the perfect square by factoring. Writing all the factor pairs of 144 results in 1 × 144 , 2 × 72 , 3 × 48 , 6 × 24 , 8 × 18 1 × 144 , 2 × 72 , 3 × 48 , 6 × 24 , 8 × 18 , and 12 × 12 12 × 12 . Since the last pair is an integer multiplied by itself, 144 is a perfect square. Alternately, using Desmos to find the square root of 144, we obtain 12. Since the square root of 144 is an integer, 144 is a perfect square.
Your Turn 3.51
Introduction to Fractions
Example 3.52
Identifying rational numbers.
Determine which of the following are rational numbers:
- 4.556 4.556
- 3 1 5 3 1 5
- 41 17 41 17
- 5 . 64 ¯ 5 . 64 ¯
- Since 73 is not a perfect square, its square root is not a rational number. This can also be seen when a calculator is used. Entering 73 73 into a calculator results in 8.544003745317 (and then more decimal values after that). There is no repeated pattern, so this is not a rational number.
- Since 4.556 is a decimal that terminates, this is a rational number.
- 3 1 5 3 1 5 is a mixed number, so it is a rational number.
- 41 17 41 17 is an integer divided by an integer, so it is a rational number.
- 5.646464... 5.646464... is a decimal that repeats a pattern, so it is a rational number.
Your Turn 3.52
Simplifying rational numbers and expressing in lowest terms.
A rational number is one way to express the division of two integers. As such, there may be multiple ways to express the same value with different rational numbers. For instance, 4 5 4 5 and 12 15 12 15 are the same value. If we enter them into a calculator, they both equal 0.8. Another way to understand this is to consider what it looks like in a figure when two fractions are equal.
In Figure 3.25 , we see that 3 5 3 5 of the rectangle and 9 15 9 15 of the rectangle are equal areas.
They are the same proportion of the area of the rectangle. The left rectangle has 5 pieces, three of which are shaded. The right rectangle has 15 pieces, 9 of which are shaded. Each of the pieces of the left rectangle was divided equally into three pieces. This was a multiplication. The numerator describing the left rectangle was 3 but it becomes 3 × 3 3 × 3 , or 9, as each piece was divided into three. Similarly, the denominator describing the left rectangle was 5, but became 5 × 3 5 × 3 , or 15, as each piece was divided into 3. The fractions 3 5 3 5 and 9 15 9 15 are equivalent because they represent the same portion (often loosely referred to as equal).
This understanding of equivalent fractions is very useful for conceptualization, but it isn’t practical, in general, for determining when two fractions are equivalent. Generally, to determine if the two fractions a b a b and c d c d are equivalent, we check to see that a × d = b × c a × d = b × c . If those two products are equal, then the fractions are equal also.
Example 3.53
Determining if two fractions are equivalent.
Determine if 12 30 12 30 and 14 35 14 35 are equivalent fractions.
Applying the definition, a = 12 , b = 30 , c = 14 a = 12 , b = 30 , c = 14 and d = 35 d = 35 . So a × d = 12 × 35 = 420 a × d = 12 × 35 = 420 . Also, b × c = 30 × 14 = 420 b × c = 30 × 14 = 420 . Since these values are equal, the fractions are equivalent.
Your Turn 3.53
That a × d = b × c a × d = b × c indicates the fractions a b a b and c d c d are equivalent is due to some algebra. One property of natural numbers, integers, and rational numbers (also irrational numbers) is that for any three numbers a , b , a , b , and c c with c ≠ 0 c ≠ 0 , if a = b a = b , then a / c = b / c a / c = b / c . In other words, when two numbers are equal, then dividing both numbers by the same non-zero number, the two newly obtained numbers are also equal. We can apply that to a × d a × d and b × c b × c , to show that a b a b and c d c d are equivalent if a × d = b × c a × d = b × c .
If a × d = b × c a × d = b × c , and c ≠ 0 , d ≠ 0 c ≠ 0 , d ≠ 0 , we can divide both sides by and obtain the following: a × d c = b × c c a × d c = b × c c . We can divide out the c c on the right-hand side of the equation, resulting in a × d c = b a × d c = b . Similarly, we can divide both sides of the equation by d d and obtain the following: a × d c × d = b d a × d c × d = b d . We can divide out d d the on the left-hand side of the equation, resulting in a c = b d a c = b d . So, the rational numbers a c a c and b d b d are equivalent when a × d = b × c a × d = b × c .
Equivalent Fractions
Recall that a common divisor or common factor of a set of integers is one that divides all the numbers of the set of numbers being considered. In a fraction, when the numerator and denominator have a common divisor, that common divisor can be divided out . This is often called canceling the common factors or, more colloquially, as canceling .
To show this, consider the fraction 36 63 36 63 . The numerator and denominator have the common factor 3. We can rewrite the fraction as 36 63 = 12 × 3 21 × 3 36 63 = 12 × 3 21 × 3 . The common divisor 3 is then divided out, or canceled, and we can write the fraction as 12 × 3 21 × 3 = 12 21 12 × 3 21 × 3 = 12 21 . The 3s have been crossed out to indicate they have been divided out. The process of dividing out two factors is also referred to as reducing the fraction .
If the numerator and denominator have no common positive divisors other than 1, then the rational number is in lowest terms .
The process of dividing out common divisors of the numerator and denominator of a fraction is called reducing the fraction .
One way to reduce a fraction to lowest terms is to determine the GCD of the numerator and denominator and divide out the GCD. Another way is to divide out common divisors until the numerator and denominator have no more common factors.
Example 3.54
Reducing Fractions to Lowest Terms
Express the following rational numbers in lowest terms:
- 36 48 36 48
- 100 250 100 250
- 51 136 51 136
Step 1: We can then rewrite the numerator and denominator by factoring 12 from both.
36 48 = 12 × 3 12 × 4 36 48 = 12 × 3 12 × 4
Step 2: We can now divide out the 12s from the numerator and denominator.
36 48 = 12 × 3 12 × 4 = 3 4 36 48 = 12 × 3 12 × 4 = 3 4
So, when 36 48 36 48 is reduced to lowest terms, the result is 3 4 3 4 .
Alternately, you could identify a common factor, divide out that common factor, and repeat the process until the remaining fraction is in lowest terms.
Step 1: You may notice that 4 is a common factor of 36 and 48.
Step 2: Divide out the 4, as in 36 48 = 4 × 9 4 × 12 = 4 × 9 4 × 12 = 9 12 36 48 = 4 × 9 4 × 12 = 4 × 9 4 × 12 = 9 12 .
Step 3: Examining the 9 and 12, you identify 3 as a common factor and divide out the 3, as in 9 12 = 3 × 3 3 × 4 = 3 4 9 12 = 3 × 3 3 × 4 = 3 4 . The 3 and 4 have no common positive factors other than 1, so it is in lowest terms.
Step 2: We can then rewrite the numerator and denominator by factoring 50 from both.
100 250 = 50 × 2 50 × 5 100 250 = 50 × 2 50 × 5 .
Step 3: We can now divide out the 50s from the numerator and denominator.
100 250 = 50 × 2 50 × 5 = 2 5 100 250 = 50 × 2 50 × 5 = 2 5
So, when 100 250 100 250 is reduced to lowest terms, the result is 2 5 2 5 .
Step 2: We can then rewrite the numerator and denominator by factoring 17 from both.
51 136 = 17 × 3 17 × 8 51 136 = 17 × 3 17 × 8
Step 3: We can now divide out the 17s from the numerator and denominator.
51 136 = 17 × 3 17 × 8 = 3 8 51 136 = 17 × 3 17 × 8 = 3 8
So, when 51 136 51 136 is reduced to lowest terms, the result is 3 8 3 8 .
Your Turn 3.54
Using desmos to find lowest terms.
Desmos is a free online calculator . Desmos supports reducing fractions to lowest terms. When a fraction is entered, Desmos immediately calculates the decimal representation of the fraction. However, to the left of the fraction, there is a button that, when clicked, shows the fraction in reduced form.
Using Desmos to Reduce a Fraction
Adding and Subtracting Rational Numbers
Adding or subtracting rational numbers can be done with a calculator, which often returns a decimal representation, or by finding a common denominator for the rational numbers being added or subtracted.
Using Desmos to Add Rational Numbers in Fractional Form
To create a fraction in Desmos, enter the numerator, then use the division key (/) on your keyboard, and then enter the denominator. The fraction is then entered. Then click the right arrow key to exit the denominator of the fraction. Next, enter the arithmetic operation (+ or –). Then enter the next fraction. The answer is displayed dynamically (calculates as you enter). To change the Desmos result from decimal form to fractional form, use the fraction button ( Figure 3.26 ) on the left of the line that contains the calculation:
Example 3.55
Adding rational numbers using desmos.
Calculate 23 42 + 9 56 23 42 + 9 56 using Desmos.
Enter 23 42 + 9 56 23 42 + 9 56 in Desmos. The result is displayed as 0.70833333333 0.70833333333 (which is 0.708 3 ¯ 0.708 3 ¯ ). Clicking the fraction button to the left on the calculation line yields 17 24 17 24 .
Your Turn 3.55
Performing addition and subtraction without a calculator may be more involved. When the two rational numbers have a common denominator, then adding or subtracting the two numbers is straightforward. Add or subtract the numerators, and then place that value in the numerator and the common denominator in the denominator. Symbolically, we write this as a c ± b c = a ± b c a c ± b c = a ± b c . This can be seen in the Figure 3.27 , which shows 3 20 + 4 20 = 7 20 3 20 + 4 20 = 7 20 .
It is customary to then write the result in lowest terms.
If c c is a non-zero integer, then a c ± b c = a ± b c a c ± b c = a ± b c .
Example 3.56
Adding rational numbers with the same denominator.
Calculate 13 28 + 7 28 13 28 + 7 28 .
Since the rational numbers have the same denominator, we perform the addition of the numerators, 13 + 7 13 + 7 , and then place the result in the numerator and the common denominator, 28, in the denominator. 13 28 + 7 28 = 13 + 7 28 = 20 28 13 28 + 7 28 = 13 + 7 28 = 20 28
Once we have that result, reduce to lowest terms, which gives 20 28 = 4 × 5 4 × 7 = 4 × 5 4 × 7 = 5 7 20 28 = 4 × 5 4 × 7 = 4 × 5 4 × 7 = 5 7 .
Your Turn 3.56
Example 3.57, subtracting rational numbers with the same denominator.
Calculate 45 136 − 17 136 45 136 − 17 136 .
Since the rational numbers have the same denominator, we perform the subtraction of the numerators, 45 − 17 45 − 17 , and then place the result in the numerator and the common denominator, 136, in the denominator. 45 136 − 17 136 − 45 − 17 136 = 28 136 45 136 − 17 136 − 45 − 17 136 = 28 136
Once we have that result, reduce to lowest terms, this gives 28 136 = 4 × 7 4 × 34 = 4 × 7 4 × 34 = 7 34 28 136 = 4 × 7 4 × 34 = 4 × 7 4 × 34 = 7 34 .
Your Turn 3.57
When the rational numbers do not have common denominators, then we have to transform the rational numbers so that they do have common denominators. The common denominator that reduces work later in the problem is the LCM of the numerator and denominator. When adding or subtracting the rational numbers a b a b and c d c d , we perform the following steps.
Step 1: Find LCM ( b , d ) LCM ( b , d ) .
Step 2: Calculate n = LCM ( b , d ) b n = LCM ( b , d ) b and m = L C M ( b , d ) d m = L C M ( b , d ) d .
Step 3: Multiply the numerator and denominator of a b a b by n n , yielding a × n b × n a × n b × n .
Step 4: Multiply the numerator and denominator of c d c d by m m , yielding c × m d × m c × m d × m .
Step 5: Add or subtract the rational numbers from Steps 3 and 4, since they now have the common denominators.
You should be aware that the common denominator is LCM ( b , d ) LCM ( b , d ) . For the first denominator, we have b × n = b × L C M ( b , d ) b = L C M ( b , d ) b × n = b × L C M ( b , d ) b = L C M ( b , d ) , since we multiply and divide LCM ( b , d ) LCM ( b , d ) by the same number. For the same reason, d × m = d × L C M ( b , d ) b = L C M ( b , d ) d × m = d × L C M ( b , d ) b = L C M ( b , d ) .
Example 3.58
Adding rational numbers with unequal denominators.
Calculate 11 18 + 2 15 11 18 + 2 15 .
The denominators of the fractions are 18 and 15, so we label b = 18 b = 18 and d = 15 d = 15 .
Step 1: Find LCM(18,15). This is 90.
Step 2 : Calculate n n and m m . n = 90 18 = 5 n = 90 18 = 5 and m = 90 15 = 6 m = 90 15 = 6 .
Step 3: Multiplying the numerator and denominator of 11 18 11 18 by n = 5 n = 5 yields 11 × 5 18 × 5 = 55 90 11 × 5 18 × 5 = 55 90 .
Step 4: Multiply the numerator and denominator of 2 15 2 15 by m = 6 m = 6 yields 2 × 6 15 × 6 = 12 90 2 × 6 15 × 6 = 12 90 .
Step 5: Now we add the values from Steps 3 and 4: 55 90 + 12 90 = 67 90 55 90 + 12 90 = 67 90 .
This is in lowest terms, so we have found that 11 18 + 2 15 = 67 90 11 18 + 2 15 = 67 90 .
Your Turn 3.58
Example 3.59, subtracting rational numbers with unequal denominators.
Calculate 14 25 − 9 70 14 25 − 9 70 .
The denominators of the fractions are 25 and 70, so we label b = 25 b = 25 and d = 70 d = 70 .
Step 1: Find LCM(25,70). This is 350.
Step 2: Calculate n n and m m : n = 350 25 = 14 n = 350 25 = 14 and m = 350 70 = 5 m = 350 70 = 5 .
Step 3: Multiplying the numerator and denominator of 14 25 14 25 by n = 14 n = 14 yields 14 × 14 25 × 14 = 196 350 14 × 14 25 × 14 = 196 350 .
Step 4: Multiplying the numerator and denominator of 9 70 9 70 by m = 5 m = 5 yields 9 × 5 70 × 5 = 45 350 9 × 5 70 × 5 = 45 350 .
Step 5: Now we subtract the value from Step 4 from the value in Step 3: 196 350 − 45 350 = 151 350 196 350 − 45 350 = 151 350 .
This is in lowest terms, so we have found that 14 25 − 9 70 = 151 350 14 25 − 9 70 = 151 350 .
Your Turn 3.59
Adding and Subtracting Fractions with Different Denominators
Converting Between Improper Fractions and Mixed Numbers
One way to visualize a fraction is as parts of a whole, as in 5 12 5 12 of a pizza. But when the numerator is larger than the denominator, as in 23 12 23 12 , then the idea of parts of a whole seems not to make sense. Such a fraction is an improper fraction. That kind of fraction could be written as an integer plus a fraction, which is a mixed number . The fraction 23 12 23 12 rewritten as a mixed number would be 1 11 12 1 11 12 . Arithmetically, 1 11 12 1 11 12 is equivalent to 1 + 11 12 1 + 11 12 , which is read as “one and 11 twelfths.”
Improper fractions can be rewritten as mixed numbers using division and remainders. To find the mixed number representation of an improper fraction, divide the numerator by the denominator. The quotient is the integer part, and the remainder becomes the numerator of the remaining fraction.
Example 3.60
Rewriting an improper fraction as a mixed number.
Rewrite 48 13 48 13 as a mixed number.
When 48 is divided by 13, the result is 3 with a remainder of 9. So, we can rewrite 48 13 48 13 as 3 9 13 3 9 13 .
Your Turn 3.60
Converting an Improper Fraction to a Mixed Number Using Desmos
Similarly, we can convert a mixed number into an improper fraction. To do so, first convert the whole number part to a fraction by writing the whole number as itself divided by 1, and then add the two fractions.
Alternately, we can multiply the whole number part and the denominator of the fractional part. Next, add that product to the numerator. Finally, express the number as that product divided by the denominator.
Example 3.61
Rewriting a mixed number as an improper fraction.
Rewrite 5 4 9 5 4 9 as an improper fraction.
Step 1: Multiply the integer part, 5, by the denominator, 9, which gives 5 × 9 = 45 5 × 9 = 45 .
Step 2: Add that product to the numerator, which gives 45 + 4 = 49 45 + 4 = 49 .
Step 3: Write the number as the sum, 49, divided by the denominator, 9, which gives 49 9 49 9 .
Your Turn 3.61
Using desmos to rewrite a mixed number as an improper fraction.
Desmos can be used to convert from a mixed number to an improper fraction. To do so, we use the idea that a mixed number, such as 5 6 11 5 6 11 , is another way to represent 5 + 6 11 5 + 6 11 . If 5 + 6 11 5 + 6 11 is entered in Desmos, the result is the decimal form of the number. However, clicking the fraction button to the left will convert the decimal to an improper fraction, 61 11 61 11 . As an added bonus, Desmos will automatically reduce the fraction to lowest terms.
Converting Rational Numbers Between Decimal and Fraction Forms
Understanding what decimals represent is needed before addressing conversions between the fractional form of a number and its decimal form , or writing a number in decimal notation . The decimal number 4.557 is equal to 4 557 1,000 4 557 1,000 . The decimal portion, .557, is 557 divided by 1,000. To write any decimal portion of a number expressed as a terminating decimal, divide the decimal number by 10 raised to the power equal to the number of decimal digits. Since there were three decimal digits in 4.557, we divided 557 by 10 3 = 1000 10 3 = 1000 .
Decimal representations may be very long. It is convenient to round off the decimal form of the number to a certain number of decimal digits. To round off the decimal form of a number to n n (decimal) digits, examine the ( n + 1 n + 1 )st decimal digit. If that digit is 0, 1, 2, 3, or 4, the number is rounded off by writing the number to the n n th decimal digit and no further. If the ( n + 1 n + 1 )st decimal digit is 5, 6, 7, 8, or 9, the number is rounded off by writing the number to the n n th digit, then replacing the n n th digit by one more than the n n th digit.
Example 3.62
Rounding off a number in decimal form to three digits.
Round 5.67849 to three decimal digits.
The third decimal digit is 8. The digit following the 8 is 4. When the digit is 4, we write the number only to the third digit. So, 5.67849 rounded off to three decimal places is 5.678.
Your Turn 3.62
Example 3.63, rounding off a number in decimal form to four digits.
Round 45.11475 to four decimal digits.
The fourth decimal digit is 7. The digit following the 7 is 5. When the digit is 5, we write the number only to the fourth decimal digit, 45.1147. We then replace the fourth decimal digit by one more than the fourth digit, which yields 45.1148. So, 45.11475 rounded off to four decimal places is 45.1148.
Your Turn 3.63
To convert a rational number in fraction form to decimal form, use your calculator to perform the division.
Example 3.64
Converting a rational number in fraction form into decimal form.
Convert 47 25 47 25 into decimal form.
Using a calculator to divide 47 by 25, the result is 1.88.
Your Turn 3.64
Converting a terminating decimal to the fractional form may be done in the following way:
Step 1: Count the number of digits in the decimal part of the number, labeled n n .
Step 2: Raise 10 to the n n th power.
Step 3: Rewrite the number without the decimal.
Step 4: The fractional form is the number from Step 3 divided by the result from Step 2.
This process works due to what decimals represent and how we work with mixed numbers. For example, we could convert the number 7.4536 to fractional from. The decimal part of the number, the .4536 part of 7.4536, has four digits. By the definition of decimal notation, the decimal portion represents 4,536 10 4 = 4,536 10,000 4,536 10 4 = 4,536 10,000 . The decimal number 7.4536 is equal to the improper fraction 7 4,536 10,000 7 4,536 10,000 . Adding those to fractions yields 74,536 10,000 74,536 10,000 .
Example 3.65
Converting from decimal form to fraction form with terminating decimals.
Convert 3.2117 to fraction form.
Step 1: There are four digits after the decimal point, so n = 4 n = 4 .
Step 2: Raise 10 to the fourth power, 10 4 = 10,000 10 4 = 10,000 .
Step 3: When we remove the decimal point, we have 32,117.
Step 4: The fraction has as its numerator the result from Step 3 and as its denominator the result of Step 2, which is the fraction 32,117 10,000 32,117 10,000 .
Your Turn 3.65
The process is different when converting from the decimal form of a rational number into fraction form when the decimal form is a repeating decimal. This process is not covered in this text.
Multiplying and Dividing Rational Numbers
Multiplying rational numbers is less complicated than adding or subtracting rational numbers, as there is no need to find common denominators. To multiply rational numbers, multiply the numerators, then multiply the denominators, and write the numerator product divided by the denominator product. Symbolically, a b × c d = a × c b × d a b × c d = a × c b × d . As always, rational numbers should be reduced to lowest terms.
If b b and d d are non-zero integers, then a b × c d = a × c b × d a b × c d = a × c b × d .
Example 3.66
Multiplying rational numbers.
Calculate 12 25 × 10 21 12 25 × 10 21 .
Multiply the numerators and place that in the numerator, and then multiply the denominators and place that in the denominator.
12 25 × 10 21 = 12 × 10 25 × 21 = 120 525 12 25 × 10 21 = 12 × 10 25 × 21 = 120 525
This is not in lowest terms, so this needs to be reduced. The GCD of 120 and 525 is 15.
120 525 = 15 × 8 15 × 35 = 8 35 120 525 = 15 × 8 15 × 35 = 8 35
Your Turn 3.66
Multiplying Fractions
As with multiplication, division of rational numbers can be done using a calculator.
Example 3.67
Dividing decimals with a calculator.
Calculate 3.45 ÷ 2.341 using a calculator. Round to three decimal places if necessary.
Using a calculator, we obtain 1.473729175565997. Rounding to three decimal places we have 1.474.
Your Turn 3.67
Before discussing division of fractions without a calculator, we should look at the reciprocal of a number. The reciprocal of a number is 1 divided by the number. For a fraction, the reciprocal is the fraction formed by switching the numerator and denominator. For the fraction a b a b , the reciprocal is b a b a . An important feature for a number and its reciprocal is that their product is 1.
When dividing two fractions by hand, find the reciprocal of the divisor (the number that is being divided into the other number). Next, replace the divisor by its reciprocal and change the division into multiplication. Then, perform the multiplication. Symbolically, b a ÷ c d = a b × d c = a × d b × c b a ÷ c d = a b × d c = a × d b × c . As before, reduce to lowest terms.
If b , c b , c and d d are non-zero integers, then b a ÷ c d = a b × d c = a × d b × c b a ÷ c d = a b × d c = a × d b × c .
Example 3.68
Dividing rational numbers.
- Calculate 4 21 ÷ 6 35 4 21 ÷ 6 35 .
- Calculate 1 8 ÷ 5 28 1 8 ÷ 5 28 .
Step 1: Find the reciprocal of the number being divided by 6 35 6 35 . The reciprocal of that is 35 6 35 6 .
Step 2: Multiply the first fraction by that reciprocal.
4 21 ÷ 6 35 = 4 21 × 35 6 = 140 126 4 21 ÷ 6 35 = 4 21 × 35 6 = 140 126
The answer, 140 126 140 126 is not in lowest terms. The GCD of 140 and 126 is 14. Factoring and canceling gives 140 126 = 14 × 10 14 × 9 = 10 9 140 126 = 14 × 10 14 × 9 = 10 9 .
Step 1: Find the reciprocal of the number being divided by, which is 5 28 5 28 . The reciprocal of that is 28 5 28 5 .
Step 2: Multiply the first fraction by that reciprocal: 1 8 ÷ 5 28 = 1 8 × 28 5 = 28 40 1 8 ÷ 5 28 = 1 8 × 28 5 = 28 40
The answer, 28 40 28 40 , is not in lowest reduced form. The GCD of 28 and 40 is 4. Factoring and canceling gives 28 40 = 4 × 7 4 × 10 = 7 10 28 40 = 4 × 7 4 × 10 = 7 10 .
Your Turn 3.68
Dividing Fractions
Applying the Order of Operations to Simplify Expressions
The order of operations for rational numbers is the same as for integers, as discussed in Order of Operations . The order of operations makes it easier for anyone to correctly calculate and represent. The order follows the well-known acronym PEMDAS:
The first step in calculating using the order of operations is to perform operations inside the parentheses. Moving down the list, next perform all exponent operations moving from left to right. Next (left to right once more), perform all multiplications and divisions. Finally, perform the additions and subtractions.
Example 3.69
Applying the order of operations with rational numbers.
Correctly apply the rules for the order of operations to accurately compute ( 5 7 − 2 7 ) × 2 3 ( 5 7 − 2 7 ) × 2 3 .
Step 1: To calculate this, perform all calculations within the parentheses before other operations.
( 5 7 − 2 7 ) × 2 3 = ( 3 7 ) × 2 3 ( 5 7 − 2 7 ) × 2 3 = ( 3 7 ) × 2 3
Step 2: Since all parentheses have been cleared, we move left to right, and compute all the exponents next.
( 3 7 ) × 2 3 = ( 3 7 ) × 8 ( 3 7 ) × 2 3 = ( 3 7 ) × 8
Step 3: Now, perform all multiplications and divisions, moving left to right.
( 3 7 ) × 8 = 24 7 ( 3 7 ) × 8 = 24 7
Your Turn 3.69
Example 3.70.
Correctly apply the rules for the order of operations to accurately compute 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 .
To calculate this, perform all calculations within the parentheses before other operations. Evaluate the innermost parentheses first. We can work separate parentheses expressions at the same time.
Step 1: The innermost parentheses contain 2 3 + 5 2 3 + 5 . Calculate that first, dividing after finding the common denominator.
4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 1 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 15 3 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 5 1 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 2 3 + 15 3 ) ) 2 = 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2
Step 2: Calculate the exponent in the parentheses, ( 5 9 ) 2 ( 5 9 ) 2 .
4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 = 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 5 9 ) 2 − ( 17 3 ) ) 2 = 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2
Step 3: Subtract inside the parentheses is done, using a common denominator.
4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 × 27 3 × 27 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 459 81 ) ) 2 4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 3 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 17 × 27 3 × 27 ) ) 2 4 + 2 3 ÷ ( ( 25 81 ) − ( 459 81 ) ) 2 4 + 2 3 ÷ ( ( − 434 81 ) ) 2
Step 4: At this point, evaluate the exponent and divide.
4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( 188,356 6,561 ) = 4 + 2 3 × ( 6,561 188,356 ) = 4 + 2,187 94,178 4 + 2 3 ÷ ( ( − 434 81 ) ) 2 4 + 2 3 ÷ ( 188,356 6,561 ) = 4 + 2 3 × ( 6,561 188,356 ) = 4 + 2,187 94,178
Step 5: Add.
4 + 2,187 94,178 = 378,899 94,178 4 + 2,187 94,178 = 378,899 94,178
Had this been done on a calculator, the decimal form of the answer would be 4.0232 (rounded to four decimal places).
Your Turn 3.70
Order of Operations Using Fractions
Applying the Density Property of Rational Numbers
Between any two rational numbers, there is another rational number. This is called the density property of the rational numbers.
Finding a rational number between any two rational numbers is very straightforward.
Step 1: Add the two rational numbers.
Step 2: Divide that result by 2.
The result is always a rational number. This follows what we know about rational numbers. If two fractions are added, then the result is a fraction. Also, when a fraction is divided by a fraction (and 2 is a fraction), then we get another fraction. This two-step process will give a rational number, provided the first two numbers were rational.
Example 3.71
Demonstrate the density property of rational numbers by finding a rational number between 4 11 4 11 and 7 12 7 12 .
To find a rational number between 4 11 4 11 and 7 12 7 12 :
Step 1: Add the fractions.
4 11 + 7 12 = 4 × 12 11 × 12 + 7 × 11 12 × 11 = 48 132 + 77 132 = 125 132 4 11 + 7 12 = 4 × 12 11 × 12 + 7 × 11 12 × 11 = 48 132 + 77 132 = 125 132
Step 2: Divide the result by 2. Recall that to divide by 2, you multiply by the reciprocal of 2. The reciprocal of 2 is 1 2 1 2 , as seen below.
125 132 ÷ 2 = 125 132 × 1 2 = 125 264 125 132 ÷ 2 = 125 132 × 1 2 = 125 264
So, one rational number between 4 11 4 11 and 7 12 7 12 is 125 264 125 264 .
We could check that the number we found is between the other two by finding the decimal representation of the numbers. Using a calculator, the decimal representations of the rational numbers are 0.363636…, 0.473484848…, and 0.5833333…. Here it is clear that 125 264 125 264 is between 4 11 4 11 and 7 12 7 12 .
Your Turn 3.71
Solving problems involving rational numbers.
Rational numbers are used in many situations, sometimes to express a portion of a whole, other times as an expression of a ratio between two quantities. For the sciences, converting between units is done using rational numbers, as when converting between gallons and cubic inches. In chemistry, mixing a solution with a given concentration of a chemical per unit volume can be solved with rational numbers. In demographics, rational numbers are used to describe the distribution of the population. In dietetics, rational numbers are used to express the appropriate amount of a given ingredient to include in a recipe. As discussed, the application of rational numbers crosses many disciplines.
Example 3.72
Mixing soil for vegetables.
James is mixing soil for a raised garden, in which he plans to grow a variety of vegetables. For the soil to be suitable, he determines that 2 5 2 5 of the soil can be topsoil, but 2 5 2 5 needs to be peat moss and 1 5 1 5 has to be compost. To fill the raised garden bed with 60 cubic feet of soil, how much of each component does James need to use?
In this example, we know the proportion of each component to mix, and we know the total amount of the mix we need. In this kind of situation, we need to determine the appropriate amount of each component to include in the mixture. For each component of the mixture, multiply 60 cubic feet, which is the total volume of the mixture we want, by the fraction required of the component.
Step 1: The required fraction of topsoil is 2 5 2 5 , so James needs 60 × 2 5 60 × 2 5 cubic feet of topsoil. Performing the multiplication, James needs 60 × 2 5 = 120 5 = 24 60 × 2 5 = 120 5 = 24 (found by treating the fraction as division, and 120 divided by 5 is 24) cubic feet of topsoil.
Step 2: The required fraction of peat moss is also 2 5 2 5 , so he also needs 60 × 2 5 60 × 2 5 cubic feet, or 60 × 2 5 = 120 5 = 24 60 × 2 5 = 120 5 = 24 cubic feet of peat moss.
Step 3: The required fraction of compost is 1 5 1 5 . For the compost, he needs 60 × 1 5 = 60 5 = 12 60 × 1 5 = 60 5 = 12 cubic feet.
Your Turn 3.72
Example 3.73, determining the number of specialty pizzas.
At Bella’s Pizza, one-third of the pizzas that are ordered are one of their specialty varieties. If there are 273 pizzas ordered, how many were specialty pizzas?
One-third of the whole are specialty pizzas, so we need one-third of 273, which gives 1 3 × 273 = 273 3 = 91 1 3 × 273 = 273 3 = 91 , found by dividing 273 by 3. So, 91 of the pizzas that were ordered were specialty pizzas.
Your Turn 3.73
Finding a Fraction of a Total
Using Fractions to Convert Between Units
A common application of fractions is called unit conversion , or converting units , which is the process of changing from the units used in making a measurement to different units of measurement.
For instance, 1 inch is (approximately) equal to 2.54 cm. To convert between units, the two equivalent values are made into a fraction. To convert from the first type of unit to the second type, the fraction has the second unit as the numerator, and the first unit as the denominator.
From the inches and centimeters example, to change from inches to centimeters, we use the fraction 2.54 cm 1 in 2.54 cm 1 in . If, on the other hand, we wanted to convert from centimeters to inches, we’d use the fraction 1 in 2.54 cm 1 in 2.54 cm . This fraction is multiplied by the number of units of the type you are converting from , which means the units of the denominator are the same as the units being multiplied.
Example 3.74
Converting liters to gallons.
It is known that 1 liter (L) is 0.264172 gallons (gal). Use this to convert 14 liters into gallons.
We know that 1 liter = 0.264172 gal. Since we are converting from liters, when we create the fraction we use, make sure the liter part of the equivalence is in the denominator. So, to convert the 14 liters to gallons, we multiply 14 by 1 gal 0.264172 gal / 1 liter 1 gal 0.264172 gal / 1 liter . Notice the gallon part is in the numerator since we’re converting to gallons, and the liter part is in the denominator since we are converting from liters. Performing this and rounding to three decimal places, we find that 14 liters is 14 liter × 0.264172 gal 1 liter = 3.69841 gal 14 liter × 0.264172 gal 1 liter = 3.69841 gal .
Your Turn 3.74
Example 3.75, converting centimeters to inches.
It is known that 1 inch is 2.54 centimeters. Use this to convert 100 centimeters into inches.
We know that 1 inch = 2.54 cm. Since we are converting from centimeters, when we create the fraction we use, make sure the centimeter part of the equivalence is in the denominator, 1 in 2.54 cm 1 in 2.54 cm . To convert the 100 cm to inches, multiply 100 by 1 in 2.54 cm 1 in 2.54 cm . Notice the inch part is in the numerator since we’re converting to inches, and the centimeter part is in the denominator since we are converting from centimeters. Performing this and rounding to three decimal places, we obtain 100 cm × 1 in 2.54 cm = 39.370 in 100 cm × 1 in 2.54 cm = 39.370 in . This means 100 cm equals 39.370 in.
Your Turn 3.75
Converting Units
Defining and Applying Percent
A percent is a specific rational number and is literally per 100. n n percent, denoted n n %, is the fraction n 100 n 100 .
Example 3.76
Rewriting a percentage as a fraction.
Rewrite the following as fractions:
- Using the definition and n = 31 n = 31 , 31% in fraction form is 31 100 31 100 .
- Using the definition and n = 93 n = 93 , 93% in fraction form is 93 100 93 100 .
Your Turn 3.76
Example 3.77, rewriting a percentage as a decimal.
Rewrite the following percentages in decimal form:
- Using the definition and n = 54 n = 54 , 54% in fraction form is 54 100 54 100 . Dividing a number by 100 moves the decimal two places to the left; 54% in decimal form is then 0.54.
- Using the definition and n = 83 n = 83 , 83% in fraction form is 83 100 83 100 . Dividing a number by 100 moves the decimal two places to the left; 83% in decimal form is then 0.83.
Your Turn 3.77
You should notice that you can simply move the decimal two places to the left without using the fractional definition of percent.
Percent is used to indicate a fraction of a total. If we want to find 30% of 90, we would perform a multiplication, with 30% written in either decimal form or fractional form. The 90 is the total , 30 is the percentage , and 27 (which is 0.30 × 90 0.30 × 90 ) is the percentage of the total .
n % n % of x x items is n 100 × x n 100 × x . The x x is referred to as the total , the n n is referred to as the percent or percentage , and the value obtained from n 100 × x n 100 × x is the part of the total and is also referred to as the percentage of the total .
Example 3.78
Finding a percentage of a total.
- Determine 40% of 300.
- Determine 64% of 190.
- The total is 300, and the percentage is 40. Using the decimal form of 40% and multiplying we obtain 0.40 × 300 = 120 0.40 × 300 = 120 .
- The total is 190, and the percentage is 64. Using the decimal form of 64% and multiplying we obtain 0.64 × 190 = 121.6 0.64 × 190 = 121.6 .
Your Turn 3.78
In the previous situation, we knew the total and we found the percentage of the total. It may be that we know the percentage of the total, and we know the percent, but we don't know the total. To find the total if we know the percentage the percentage of the total, use the following formula.
If we know that n n % of the total is x x , then the total is 100 × x n 100 × x n .
Example 3.79
Finding the total when the percentage and percentage of the total are known.
- What is the total if 28% of the total is 140?
- What is the total if 6% of the total is 91?
- 28 is the percentage, so n = 28 n = 28 . 28% of the total is 140, so x = 140 x = 140 . Using those we find that the total was 100 × 140 28 = 500 100 × 140 28 = 500 .
- 6 is the percentage, so n = 6 n = 6 . 6% of the total is 91, so x = 91 x = 91 . Using those we find that the total was 100 × 91 6 = 1,516.6 100 × 91 6 = 1,516.6 .
Your Turn 3.79
The percentage can be found if the total and the percentage of the total is known. If you know the total, and the percentage of the total, first divide the part by the total. Move the decimal two places to the right and append the symbol %. The percentage may be found using the following formula.
The percentage, n n , of b b that is a a is a b × 100 % a b × 100 % .
Example 3.80
Finding the percentage when the total and percentage of the total are known.
Find the percentage in the following:
- Total is 300, percentage of the total is 60.
- Total is 440, percentage of the total is 176.
- The total is 300; the percentage of the total is 60. Calculating yields 0.2. Moving the decimal two places to the right gives 20. Appending the percentage to this number results in 20%. So, 60 is 20% of 300.
- The total is 440; the percentage of the total is 176. Calculating yields 0.4. Moving the decimal two places to the right gives 40. Appending the percentage to this number results in 40%. So, 176 is 40% of 440.
Your Turn 3.80
Solve problems using percent.
In the media, in research, and in casual conversation percentages are used frequently to express proportions. Understanding how to use percent is vital to consuming media and understanding numbers. Solving problems using percentages comes down to identifying which of the three components of a percentage you are given, the total, the percentage, or the percentage of the total. If you have two of those components, you can find the third using the methods outlined previously.
Example 3.81
Percentage of students who are sleep deprived.
A study revealed that 70% of students suffer from sleep deprivation, defined to be sleeping less than 8 hours per night. If the survey had 400 participants, how many of those participants had less than 8 hours of sleep per night?
The percentage of interest is 70%. The total number of students is 400. With that, we can find how many were in the percentage of the total, or, how many were sleep deprived. Applying the formula from above, the number who were sleep deprived was 0.70 × 400 = 280 0.70 × 400 = 280 ; 280 students on the study were sleep deprived.
Your Turn 3.81
Example 3.82, amazon prime subscribers.
There are 126 million users who are U.S. Amazon Prime subscribers. If there are 328.2 million residents in the United States, what percentage of U.S. residents are Amazon Prime subscribers?
We are asked to find the percentage. To do so, we divide the percentage of the total, which is 126 million, by the total, which is 328.2 million. Performing this division and rounding to three decimal places yields 126 328.2 = 0.384 126 328.2 = 0.384 . The decimal is moved to the right by two places, and a % sign is appended to the end. Doing this shows us that 38.4% of U.S. residents are Amazon Prime subscribers.
Your Turn 3.82
Example 3.83.
Evander plays on the basketball team at their university and 73% of the athletes at their university receive some sort of scholarship for attending. If they know 219 of the student-athletes receive some sort of scholarship, how many student-athletes are at the university?
We need to find the total number of student-athletes at Evander’s university.
Step 1: Identify what we know. We know the percentage of students who receive some sort of scholarship, 73%. We also know the number of athletes that form the part of the whole, or 219 student-athletes.
Step 2: To find the total number of student-athletes, use 100 × x n 100 × x n , with x = 219 x = 219 and n = 73 n = 73 . Calculating with those values yields 100 × 219 73 = 300 100 × 219 73 = 300 .
So, there are 300 total student-athletes at Evander’s university
Your Turn 3.83
Check your understanding, section 3.4 exercises.
- Studying and going to class?
- Not sleeping?
- Determine the markup in dollars.
- The markup is what percent of the original cost? Round the percentage to one decimal place.
- Calculate the markup on the item, in dollars.
- What is the price for which Wegmans sells the item? This is the price Wegmans paid, plus the markup.
- Suppose Wegmans then offers a 25% discount on the sale price of the item (found in part b). In dollars, how much is the discount?
- Determine the price of the item after the discount (this is the sales price of the item minus the discount). Round to two decimal places.
- Is the new price after the markup and discount equal to the price Wegmans paid for the item? Explain.
- The original price was $150. After the 50% discount, what is the price of the item?
- The coupon is applied to the discount price. The coupon is for 25%. Find 25% of the sale price (found in part a).
- Find the price after applying the coupon (this is the value from part a minus the value from part b).
- The total amount saved on the item is the original price after all the discounts. Determine the total amount saved by subtracting the final price paid (part c) from the original price of the item.
- Determine the effective discount percentage, which is the total amount saved divided by the original price of the item.
- Was the effective discount percentage equal to 75%, which would be the 50% plus the 25%? Explain.
As an Amazon Associate we earn from qualifying purchases.
This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.
Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.
Access for free at https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Authors: Donna Kirk
- Publisher/website: OpenStax
- Book title: Contemporary Mathematics
- Publication date: Mar 22, 2023
- Location: Houston, Texas
- Book URL: https://openstax.org/books/contemporary-mathematics/pages/1-introduction
- Section URL: https://openstax.org/books/contemporary-mathematics/pages/3-4-rational-numbers
© Dec 21, 2023 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

IMAGES
VIDEO
COMMENTS
Quiz yourself with questions and answers for QUIZ 2: SOLVING PROBLEMS WITH RATIONAL NUMBERS, so you can be ready for test day. ... Expert Solutions. Log in. Sign up. Test: QUIZ 2: SOLVING PROBLEMS WITH RATIONAL NUMBERS. 3.3 (28 reviews) Name: Score: 20 Multiple choice questions. Term. 125.7 - (-1.82) = 1.439. True. False. 1 of 20. Term (0.05 ...
SOLVING PROBLEMS WITH RATIONAL NUMBERS. In this section, we will learn how to solve problems with rational numbers. A number that is expressed in the form a/b is called as rational number. Here, both "a" and "b" are integers and also b ≠ 0. Problem 1 : The area of a rectangular sandbox is 56 2/3 square feet. The length of the sandbox is 8 1/2 ...
In its most basic representation, a rational number is an integer divided by a non-zero integer, such as. Figure 3.21 Pizza cut in 8 slices, with 3 slices highlighted. Figure 3.22 Group of 20 people, with 5 people wearing hats. Another representation of rational numbers is as a mixed number, such as.
Unit test. Level up on all the skills in this unit and collect up to 4,100 Mastery points! "Students continue to build an understanding of the number line in Module 2 from their work in Grade 6. They learn to add, subtract, multiply, and divide rational numbers. Module 2 includes rational numbers as they appear in expressions and equations ...
Problem 51. Use the digits 1 through 9. Use each digit exactly once. Fill in the squares to make all of the equations true. − = × ÷ = = + = . This page titled 3.11: Problem Bank is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Michelle Manes via source content that was edited to the style and standards of ...
Lesson 14.3 Buying and Selling Power. A utility company charges $0.12 per kilowatt-hour for energy a customer uses. They give a credit of $0.025 for every kilowatt-hour of electricity a customer with a solar panel generates that they don't use themselves. A customer has a charge of $82.04 and a credit of -$4.10 on this month's bill.
7.1.2 Group B - Problem Solving with Rational Numbers. 7.1.2.4 Solve problems in various contexts involving calculations with positive and negative rational numbers and positive integer exponents, including computing simple and compound interest. 7.1.2.5 Use proportional reasoning to solve problems involving ratios in various contexts.
7.1.2B Problem Solving with Rational Numbers. Standard 7.1.2. Solve problems in various contexts involving calculations with positive and negative rational numbers and positive in
We obtained the addition of rational numbers with different signs. Subtract the lesser modulus from the greater modulus, and put the sign of the number whose modulus is greater in front of the answer: −0.25 + (+1.2) = 1.2 − 0.25 = 0.95. This example can be written in a shorter form: −0.25 − (−1.2) = 0.95. Example 21.
Problem Solving with Rational Numbers. Finding percentages can be done using mental math. Percent means 'per hundred' so finding a percentage of a number involves turning the percentage into a fraction with a denominator of 100 and multiplying it by the number. Here are the calculations: 1a) 10% of 40 is (10/100)*40 = 4; 1b) 20% of 40 is (20/ ...
4.6 Add and Subtract Mixed Numbers; 4.7 Solve Equations with Fractions; Chapter Review. Key Terms; Key Concepts; Exercises. ... Introduction to the Properties of Real Numbers; 7.1 Rational and Irrational Numbers; 7.2 Commutative and Associative Properties; ... 9.1 Use a Problem Solving Strategy; 9.2 Solve Money Applications; 9.3 Use Properties ...
Find a rational number between 3.1 and 3.11. Find an irrational number between 3.1 and 3.11. Here's the best way to solve it.
Rational numbers may also be expressed in decimal form; for instance, as 1.34. When 1.34 is written, the decimal part, 0.34, represents the fraction 34 100 34 100, and the number 1.34 is equal to 1 34 100 1 34 100.However, not all decimal representations are rational numbers.
1. Multiple Choice. 2. Multiple Choice. 3. Multiple Choice. Already have an account? Unit 1 Rational Numbers Test Review quiz for 7th grade students. Find other quizzes for Mathematics and more on Quizizz for free!
The to be subtracted from another number. Sum. The total from adding two numbers. Zero Property of Multiplication. Multiplying a number by zero equals ZERO. Example: 2 * 0 = 0. Study with Quizlet and memorize flashcards containing terms like addend, Associative Property of Addition, Associative Property of Multiplication and more.