probability tree homework

3.5 Tree and Venn Diagrams

Sometimes, when the probability problems are complex, it can be helpful to graph the situation. Tree diagrams and Venn diagrams are two tools that can be used to visualize and solve conditional probabilities.

Tree Diagrams

A tree diagram is a special type of graph used to determine the outcomes of an experiment. It consists of branches that are labeled with either frequencies or probabilities. Tree diagrams can make some probability problems easier to visualize and solve. The following example illustrates how to use a tree diagram:

Example 3.24

In an urn, there are 11 balls. Three balls are red ( R ) and eight balls are blue ( B ). Draw two balls, one at a time, with replacement . With replacement means that you put the first ball back in the urn before you select the second ball. Therefore, you are selecting from exactly the same group each time, so each draw is independent. The tree diagram shows all the possible outcomes.

The first set of branches represents the first draw. There are 8 ways to draw a blue marble and 3 ways to draw a red one. The second set of branches represents the second draw. Regardless of the choice on the first draw, there are again eight ways to draw a blue marble and 3 ways to draw a red one. Read down each branch to see the total number of possible outcomes. For example, there are 8 ways to get a blue marble on the first draw, and eight ways to get one on the second draw, so there are 8 × 8 = 64 different ways to draw two blue marbles in succession. Each of the outcomes is distinct. In fact, we can list each red ball as R 1, R 2, and R 3 and each blue ball as B 1, B 2, B 3, B 4, B 5, B 6, B 7, and B 8. Then the nine RR outcomes can be written as follows:

R 1 R 1, R 1 R 2, R 1 R 3, R 2 R 1, R 2 R 2, R 2 R 3, R 3 R 1, R 3 R 2, R 3 R 3.

The other outcomes are similar.

There are a total of 11 balls in the urn. Draw two balls, one at a time, with replacement. There are 11(11) = 121 outcomes, the size of the sample space .

a. List the 24 BR outcomes: B 1 R 1, B 1 R 2, B 1 R 3, . . .

a. We know that there will be 24 different possible outcomes because there are eight ways to draw blue and three ways to draw red. Make a systematic list of possible outcomes that consist of a blue marble on the first draw and a red marble on the second draw.

B 1 R 1, B 1 R 2, B 1 R 3 B 2 R 1, B 2 R 2, B 2 R 3 B 3 R 1, B 3 R 2, B 3 R 3 B 4 R 1, B 4 R 2, B 4 R 3 B 5 R 1, B 5 R 2, B 5 R 3 B 6 R 1, B 6 R 2, B 6 R 3 B 7 R 1, B 7 R 2, B 7 R 3 B 8 R 1, B 8 R 2, B 8 R 3

b. Calculate P ( RR ).

b. You can use the tree diagram. There are nine ways to draw two reds and 121 possible outcomes. So, P ( RR ) = 9 121 . 9 121 . .

Each draw is independent, so you can also use the formula: P ( RR ) = P ( R ) P ( R ) = ( 3 11 ) ( 3 11 ) ( 3 11 ) ( 3 11 ) = 9 121 . 9 121 .

c. Calculate P ( RB OR BR ).

c. The tree diagram shows that there are 24 ways to draw RB and 24 ways to draw BR . There are 121 possible outcomes, so P ( RB or BR ) = 24 + 24 121 = 48 121 24 + 24 121 = 48 121 .

The events RB and BR are mutually exclusive, so P ( RB OR BR ) = P ( RB ) + P ( BR ) = P ( R ) P ( B ) + P ( B ) P ( R ) = ( 3 11 ) ( 8 11 ) ( 3 11 ) ( 8 11 ) + ( 8 11 ) ( 3 11 ) ( 8 11 ) ( 3 11 ) = 48 121 . 48 121 .

d. Using the tree diagram, calculate P ( R on 1st draw AND B on 2nd draw).

d. Follow the path on the tree. There are three ways to get a red marble on the first draw and eight ways to get a blue on the second draw. There are 3 × 8 = 24 ways to draw red then blue, so P ( RB ) = 24 121 24 121 .

Can you think of another way to find this probability? P ( R on 1st draw AND B on 2nd draw) = P ( RB ) = ( 3 11 ) ( 8 11 ) ( 3 11 ) ( 8 11 ) = 24 121 24 121

e. Using the tree diagram, calculate P ( R on 2nd draw GIVEN B on 1st draw).

e. Given that a blue marble is selected first, we need only follow the left set of branches on the tree diagram. In this case, there are three ways to obtain red on the second draw and 11 possible outcomes.

P ( R on 2nd draw GIVEN B on 1st ) = P ( R on 2nd | B on 1st ) = 3 11 P ( R on 2nd draw GIVEN B on 1st ) = P ( R on 2nd | B on 1st ) = 3 11

You can also use the formula

f. Using the tree diagram, calculate P ( BB ).

f. P ( BB ) =  64 121 64 121

g. Using the tree diagram, calculate P ( B on the 2nd draw GIVEN R on the first draw).

g. P ( B  on 2nd draw| R  on 1st draw) =  8 11 8 11

There are 9 + 24 outcomes that have R on the first draw (9 RR and 24 RB ). The sample space is then 9 + 24 = 33. Twenty-four of the 33 outcomes have B on the second draw. The probability is then 24 33 24 33 .

Try It 3.24

In a standard deck, there are 52 cards. Twelve cards are face cards (event F ) and 40 cards are not face cards (event N ). Draw two cards, one at a time, with replacement. All possible outcomes are shown in the tree diagram as frequencies. Using the tree diagram, calculate P ( FF ).

Example 3.25

An urn has three red marbles and eight blue marbles in it. Draw two marbles, one at a time, this time without replacement, from the urn. Without replacement means that you do not put the first ball back before you select the second marble. Following is a tree diagram for this situation. The branches are labeled with probabilities instead of frequencies. The numbers at the ends of the branches are calculated by multiplying the numbers on the two corresponding branches, for example, P ( RR ) = ( 3 11 ) ( 2 10 ) = 6 110 ( 3 11 ) ( 2 10 ) = 6 110 .

If you draw a red on the first draw from the three red possibilities, there are two red marbles left to draw on the second draw. You do not put back or replace the first marble after you have drawn it. You draw without replacement , so that on the second draw there are 10 marbles left in the urn.

Calculate the following probabilities using the tree diagram:

a. P ( RR ) = ________

a. P ( RR ) = ( 3 11 ) ( 2 10 ) = 6 110 ( 3 11 ) ( 2 10 ) = 6 110

b. Fill in the blanks.

P ( RB OR BR ) = ( 3 11 ) ( 8 10 )   +  (________)(________)  =   48 110 ( 3 11 ) ( 8 10 )   +  (________)(________)  =   48 110

b. P ( RB OR BR ) = P ( RB ) + P ( BR ) = P ( R on 1st) P ( B on 2nd) + P ( B on 1st) P ( R on 2nd) = ( 3 11 ) ( 8 10 ) ( 3 11 ) ( 8 10 ) + ( 8 11 ) ( 3 10 ) ( 8 11 ) ( 3 10 ) = 48 110 48 110

c. Because this is a conditional probability, we restrict the sample space to consider only those outcomes that have a blue marble in the first draw. Look at the second level of the tree to see that P ( R on 2nd| B on 1st) = 3 10 3 10

c. P ( R on 2nd| B on 1st) = 3 10 3 10

d. Fill in the blanks.

P ( R on 1st AND B on 2nd) = P ( RB ) = (________)(________) = 24 100 24 100

d. P ( R on 1st AND B on 2nd) = P ( RB ) = ( 3 11 ) ( 8 10 ) ( 3 11 ) ( 8 10 ) = 24 100 24 100

e. Find P ( BB ).

e. P ( BB ) = ( 8 11 ) ( 7 10 ) ( 8 11 ) ( 7 10 )

f. Find P ( B on 2nd| R on 1st).

f. Using the tree diagram, P ( B on 2nd| R on 1st) = P ( R | B ) = 8 10 8 10 .

If we are using probabilities, we can label the tree in the following general way:

• P ( R | R ) here means P ( R on 2nd| R on 1st)
• P ( B | R ) here means P ( B on 2nd| R on 1st)
• P ( R | B ) here means P ( R on 2nd| B on 1st)
• P ( B | B ) here means P ( B on 2nd| B on 1st)

Try It 3.25

In a standard deck, there are 52 cards. Twelve cards are face cards ( F ) and 40 cards are not face cards ( N ). Draw two cards, one at a time, without replacement. The tree diagram is labeled with all possible probabilities.

• Find P ( FN OR NF ).
• Find P ( N | F ).
• Find P (at most one face card). Hint: At most one face card means zero or one face card.
• Find P (at least one face card). Hint: At least one face card means one or two face cards.

Example 3.26

A litter of kittens available for adoption at the Humane Society has four tabby kittens and five black kittens. A family comes in and randomly selects two kittens (without replacement) for adoption.

• Which shows the probability that both kittens are tabby? a. ( 1 2 ) ( 1 2 ) a. ( 1 2 ) ( 1 2 ) b. ( 4 9 ) ( 4 9 ) b. ( 4 9 ) ( 4 9 ) c. ( 4 9 ) ( 3 8 ) c. ( 4 9 ) ( 3 8 ) d. ( 4 9 ) ( 5 9 ) d. ( 4 9 ) ( 5 9 )
• What is the probability that one kitten of each coloring is selected? a. ( 4 9 ) ( 5 9 ) a. ( 4 9 ) ( 5 9 ) b. ( 4 9 ) ( 5 8 ) b. ( 4 9 ) ( 5 8 ) c. ( 4 9 ) ( 5 9 ) + ( 5 9 ) ( 4 9 ) c. ( 4 9 ) ( 5 9 ) + ( 5 9 ) ( 4 9 ) d. ( 4 9 ) ( 5 8 ) + ( 5 9 ) ( 4 8 ) d. ( 4 9 ) ( 5 8 ) + ( 5 9 ) ( 4 8 )
• What is the probability that a tabby is chosen as the second kitten when a black kitten was chosen as the first?
• What is the probability of choosing two kittens of the same color?

a. ( 4 9 ) ( 3 8 ) ( 4 9 ) ( 3 8 ) , b. ( 4 9 ) ( 5 8 ) + ( 5 9 ) ( 4 8 ) ( 4 9 ) ( 5 8 ) + ( 5 9 ) ( 4 8 ) , c. 4 8 4 8 , d. 32 72 32 72

Try It 3.26

Suppose there are four red balls and three yellow balls in a box. Three balls are drawn from the box without replacement. What is the probability that one ball of each coloring is selected?

Venn Diagram

A Venn diagram is a picture that represents the outcomes of an experiment. It generally consists of a box that represents the sample space S together with circles or ovals. The circles or ovals represent events.

Example 3.27

Suppose an experiment has the outcomes 1, 2, 3, . . . , 12 where each outcome has an equal chance of occurring. Let event A = {1, 2, 3, 4, 5, 6} and event B = {6, 7, 8, 9}. Then A AND B = {6} and A  OR  B = {1, 2, 3, 4, 5, 6, 7, 8, 9}. The Venn diagram is as follows:

Try It 3.27

Suppose an experiment has outcomes black, white, red, orange, yellow, green, blue, and purple, where each outcome has an equal chance of occurring. Let event C = {green, blue, purple} and event P = {red, yellow, blue}. Then C AND P = {blue} and C OR P = {green, blue, purple, red, yellow}. Draw a Venn diagram representing this situation.

Example 3.28

Flip two fair coins. Let A = tails on the first coin. Let B = tails on the second coin. Then A = { TT , TH } and B = { TT , HT }. Therefore, A AND B = { TT }. A OR B = { TH , TT , HT }.

The sample space when you flip two fair coins is X = { HH , HT , TH , TT }. The outcome HH is in NEITHER A NOR B . The Venn diagram is as follows:

Try It 3.28

Roll a fair, six-sided die. Let A = a prime number of dots is rolled. Let B = an odd number of dots is rolled. Then A = {2, 3, 5} and B = {1, 3, 5}. Therefore, A AND B = {3, 5}. A OR B = {1, 2, 3, 5}. The sample space for rolling a fair die is S = {1, 2, 3, 4, 5, 6}. Draw a Venn diagram representing this situation.

Example 3.29

Forty percent of the students at a local college belong to a club and 50 percent work part time. Five percent of the students work part time and belong to a club. Draw a Venn diagram showing the relationships. Let C = student belongs to a club and PT = student works part time.

Start by drawing a rectangle to represent the sample space. Then draw two circles or ovals inside the rectangle to represent the events of interest: belonging to a club ( C ) and working part time ( PT ). Always draw overlapping shapes to represent outcomes that are in both events.

Label each piece of the diagram clearly and note the probability or frequency of each part. Start by labeling the overlapping section first. Note that the probabilities in C total 0.40 and the sum of the probabilities in PT is 0.50. The total of all probabilities displayed must be 1, representing 100 percent of the sample space.

If a student is selected at random, find the following:

• the probability that the student belongs to a club.
• the probability that the student works part time.
• the probability that the student belongs to a club AND works part time.
• the probability that the student belongs to a club given that the student works part time.
• the probability that the student belongs to a club OR works part time.

P ( C ) = .40

P ( PT ) = .50

P ( C AND PT ) = .05

P ( C | P T )   =   P ( C  AND  P T ) P ( P T )   =   .05 .50   =   .1 P ( C | P T )   =   P ( C  AND  P T ) P ( P T )   =   .05 .50   =   .1

P ( C OR PT ) = P ( C ) + P ( PT ) − P ( C AND PT ) = .40 + .50 − .05 = .85

Try It 3.29

Fifty percent of the workers at a factory work a second job, 25 percent have a spouse who also works, and 5 percent work a second job and have a spouse who also works. Draw a Venn diagram showing the relationships. Let W = works a second job and S = spouse also works.

Example 3.30

A person with type O blood and a negative Rh factor (Rh–) can donate blood to any person with any blood type. Four percent of African Americans have type O blood and a negative Rh factor, 5−10 percent of African Americans have the Rh– factor, and 51 percent have type O blood.

The “O” circle represents the African Americans with type O blood. The “Rh––" oval represents the African Americans with the Rh– –factor.

We will use the average of 5 percent and 10 percent, 7.5 percent, as the percentage of African Americans who have the Rh–– factor. Let O = African American with Type O blood and R = African American with Rh– –factor.

• P ( O ) = ___________
• P ( R ) = ___________
• P ( O AND R ) = ___________
• P ( O OR R ) = ____________
• In the Venn Diagram, describe the overlapping area using a complete sentence.
• In the Venn Diagram, describe the area in the rectangle but outside both the circle and the oval using a complete sentence.

a. P ( O ) = .51

b. P ( R ) = .075 because an average of 7.5 percent of African Americans have the Rh– –factor.

c. P ( O AND R ) = 0.04 because 4 percent of African Americans have both Type O blood and the Rh– –factor.

d. P ( O OR R ) = P ( O ) + P ( R ) - P ( O AND R ) = .51 + .075 − .04 = .545

e. The area represents the African Americans that have type O blood and the Rh–– factor.

f. The area represents the African Americans that have neither type O blood nor the Rh–– factor.

Try It 3.30

In a bookstore, the probability that the customer buys a novel is .6, and the probability that the customer buys a nonfiction book is .4. Suppose that the probability that the customer buys both is .2.

• Draw a Venn diagram representing the situation.
• Find the probability that the customer buys either a novel or a nonfiction book.
• In the Venn diagram, describe the overlapping area using a complete sentence.
• Suppose that some customers buy only compact disks. Draw an oval in your Venn diagram representing this event.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/3-5-tree-and-venn-diagrams

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Probability Tree Diagram

A probability tree diagram is a diagram that is used to give a visual representation of the probabilities as well as the outcomes of an event. A probability tree diagram consists of two parts - nodes and branches. A node is used to represent an event. A branch is used to denote the connection between an event and its outcome.

A probability tree diagram can be used to depict conditional probabilities as well as independent events. In this article, we will learn more about a probability tree diagram, how to draw a probability tree, and see some examples.

What is a Probability Tree Diagram?

A probability tree diagram is used to represent the probability of occurrence of events without using complicated formulas. It displays all the possible outcomes of an event. The purpose of a probability tree is that it shows all the possible outcomes of an event and calculates the probability of these outcomes. A probability tree diagram can either represent a series of independent events or it can be used to denote conditional probabilities.

Parts of a Probability Tree Diagram

There are two main parts of a probability tree. These are the nodes and the branches. The nodes can further be classified into a parent node and a sibling node. The parent node represents a certain event and has a probability of 1. The sibling nodes denote other additional possible events or outcomes. The branches denote the probability of occurrence of these events. Suppose a fair coin is tossed once, then the probability tree can be constructed as follows:

This is a simple probability tree and has two branches only. Here, the first node represents the parent event of a coin being tossed. Head and tail are the two possible outcomes forming the sibling nodes. 0.5 is written on the branch and represents the probability of occurrence of each sibling event.

Probability Tree Diagram Example

Suppose a probability tree diagram needs to be constructed for flipping a fair coin twice. This is an example of an independent event as the outcome of each coin toss is independent of the previous flip. First, the probability tree diagram of a coin being flipped once is drawn as given in the previous section. The next step is to extend it to two coin tosses as follows:

The second set of probabilities represents the second coin toss. Thus, in total there are 4 sets of possible outcomes.

To calculate the probabilities of a series of events, multiply the probabilities along the branches of the probability tree diagram. The total probability can be computed by adding these probabilities and its value will always be equal to 1.

Some useful inferences can be made from the probability tree diagram as follows:

• The probability of getting the outcome (Head, Head) = 0.5 × 0.5 = 0.25. Similarly, the probability of the other outcomes can be calculated.
• 0.25 + 0.25 + 0.25 + 0.25 = 1. This implies that on adding the probabilities of each outcome, the total is equal to 1.
• By looking at the probability tree, the probability of getting exactly one head can be calculated as 0.25 + 0.25 = 0.5.

Conditional Probability Tree Diagram

A conditional probability tree diagram is very useful in depicting the outcome of dependent events . A dependent event is one whose outcome is affected by an event that has previously occurred. Suppose a student has to appear for two tests. The probability that he will pass the first test is 0.7. If he passes the first test, the probability that he passes the second test is 0.8. Furthermore, if he fails the first test, the probability that he passes the second test is 0.6. To determine the conditional probability that he fails in both tests, the probability tree diagram can be constructed using the following steps.

• Step 1: Construct the probability tree diagram for the first test. As the probability of passing the first test is 0.7 thus, the probability of failure is 1 - 0.7 = 0.3.
• Step 2: Construct branches for the second test given that the student passes the first test. It must be noted that the sum of probabilities of outcomes, 0.8 + 0.2, is 1.
• Step 3: Now, draw branches for the second test given that the student fails the first test.
• Step 4: Multiply the probabilities along each branch of the probability tree to get the conditional probability results.

From the probability tree diagram, it can be concluded that the conditional probability for a student who fails the second test given that he fails the first is 0.12.

How to Draw a Probability Tree?

To draw a probability tree diagram it is necessary to identify all the possible outcomes and the probabilities associated with them. The steps to construct a probability tree are as follows:

• Step 1: Identify whether the events are dependent or independent.
• Step 2: Draw branches to represent the first set of outcomes.
• Step 3: Write the probabilities associated with each outcome on the branch.
• Step 4: Draw the next set of branches taking into account whether the subsequent events are dependent or independent. Also, write the associated probabilities.
• Step 5: Repeat step 5 for as many branches as required.
• Step 6: To calculate the overall probability of the probability tree, the probabilities along the branches have to be multiplied. The sum of these probabilities should always be equal to 1.

Related Articles:

• Probability and Statistics
• Probability Rules
• Mutually Exclusive Events

Important Notes on Probability Tree Diagram

• A probability tree diagram is used to visually represent all the possible outcomes of an event along with the associated probabilities.
• Nodes and branches make up the parts of a probability tree diagram. The node represents an event and their occurence probabilities are written on the branches.
• Multiply the probabilities along the branches to calculate the probability of outcomes.
• Add the probabilities to get the probability of multiple outcomes.
• The sum of the probabilities of all possible outcomes of a probability tree diagram is always 1.

Examples on Probability Tree Diagram

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Probability Tree Diagram

What is a probability tree diagram in probability theory.

A probability tree diagram is used to give a visual representation of the probability of occurrences of all possible outcomes of an event. It can be used to demonstrate dependent and independent events .

What are the Parts of a Probability Tree Diagram?

There are two parts to a probability tree diagram. These are given as follows:

• Node - it is used to represent an event.
• Branch - it is used to connect two events. The probability of occurrence of an event is written on a branch.

How to Calculate the Probability Using a Probability Tree Diagram?

By multiplying the probabilities of connecting branches the probability of a series of events can be calculated. The sum of all these probabilities must be equal to 1.

What is a Conditonal Probability Tree Diagram?

A conditional probability tree diagram is used to represent conditional probabilities. In other words, this probability tree can be used to find the probabilities of outcomes of dependent events.

How To Draw a Probability Tree?

The steps to draw a probability tree are as follows:

• Draw branches of the first set of outcomes and write the individual probabilities along the branches.
• Repeat this process for the remaining outcomes.
• Multiply the values of probabilities of connecting branches to get the likelihood of occurrence of each outcome.

Can the Sum of Probabilities of Outcomes of a Probability Tree Diagram be Negative?

The value of a probability will always lie between 0 and 1. Thus, the probability of outcomes of a probability tree diagram will always be positive. Furthermore, the sum of all probabilities will always be equal to 1.

How to Calculate the Probability of Multiple Events Using a Probability Tree Diagram?

The first step is to find the probability of each outcome by multiplying the probability values of connecting branches in the probability tree diagram. Next, add the probabilities associated with the required events to determine the probability of multiple events.

Probability Tree Diagrams

Calculating probabilities can be hard, sometimes we add them, sometimes we multiply them, and often it is hard to figure out what to do ... tree diagrams to the rescue!

Here is a tree diagram for the toss of a coin:

We can extend the tree diagram to two tosses of a coin:

How do we calculate the overall probabilities?

• We multiply probabilities along the branches
• We add probabilities down columns

Now we can see such things as:

• The probability of "Head, Head" is 0.5×0.5 = 0.25
• All probabilities add to 1.0 (which is always a good check)
• The probability of getting at least one Head from two tosses is 0.25+0.25+0.25 = 0.75
• ... and more

That was a simple example using independent events (each toss of a coin is independent of the previous toss), but tree diagrams are really wonderful for figuring out dependent events (where an event depends on what happens in the previous event) like this example:

Example: Soccer Game

You are off to soccer, and love being the Goalkeeper, but that depends who is the Coach today:

• with Coach Sam the probability of being Goalkeeper is 0.5
• with Coach Alex the probability of being Goalkeeper is 0.3

Sam is Coach more often ... about 6 out of every 10 games (a probability of 0.6 ).

So, what is the probability you will be a Goalkeeper today?

Let's build the tree diagram. First we show the two possible coaches: Sam or Alex:

The probability of getting Sam is 0.6, so the probability of Alex must be 0.4 (together the probability is 1)

Now, if you get Sam, there is 0.5 probability of being Goalie (and 0.5 of not being Goalie):

If you get Alex, there is 0.3 probability of being Goalie (and 0.7 not):

The tree diagram is complete, now let's calculate the overall probabilities. This is done by multiplying each probability along the "branches" of the tree.

Here is how to do it for the "Sam, Yes" branch:

(When we take the 0.6 chance of Sam being coach and include the 0.5 chance that Sam will let you be Goalkeeper we end up with an 0.3 chance.)

But we are not done yet! We haven't included Alex as Coach:

An 0.4 chance of Alex as Coach, followed by an 0.3 chance gives 0.12.

Now we add the column:

0.3 + 0.12 = 0.42 probability of being a Goalkeeper today

(That is a 42% chance)

One final step: complete the calculations and make sure they add to 1:

0.3 + 0.3 + 0.12 + 0.28 = 1

Yes, it all adds up.

You can see more uses of tree diagrams on Conditional Probability .

So there you go, when in doubt draw a tree diagram, multiply along the branches and add the columns. Make sure all probabilities add to 1 and you are good to go.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.E: Probability Using Tree Diagrams and Combinations (Optional Exercises)

• Last updated
• Save as PDF
• Page ID 11512

• Rupinder Sekhon and Roberta Bloom
• De Anza College

SECTION 8.3 PROBLEM SET: PROBABILITIES USING TREE DIAGRAMS AND COMBINATIONS

Two apples are chosen from a basket containing five red and three yellow apples. Draw a tree diagram below, and find the following probabilities.

A basket contains six red and four blue marbles. Three marbles are drawn at random. Find the following probabilities using the method shown in Example 8.3.2. Do not use combinations.

Three marbles are drawn from a jar containing five red, four white, and three blue marbles. Find the following probabilities using combinations.

A committee of four is selected from a total of 4 freshmen, 5 sophomores, and 6 juniors. Find the probabilities for the following events.

Five cards are drawn from a deck. Find the probabilities for the following events.

Jorge has 6 rock songs, 7 rap songs and 4 country songs that he likes to listen to while he exercises. He randomly selects six (6) of these songs to create a playlist to listen to today while he exercises.

Find the following probabilities:

A project is staffed 12 people: 5 engineers, 4 salespeople, and 3 customer service representatives. A committee of 5 people is selected to make a presentation to senior management.

Find the probabilities of the following events.

Do the following birthday problems.

Probability Trees

Learn maths at home

A Complete Guide to Probability Tree Diagrams

Probability tree video lessons, independent probability trees: video lesson, conditional probability trees: video lesson, how to draw a probability tree.

• Draw a branch for each outcome of the first event.
• Write the outcome at the end of each branch.
• Write the probability of each outcome next to the corresponding branch.
• For further events, draw new branches coming out of the ends of each preceding outcome.

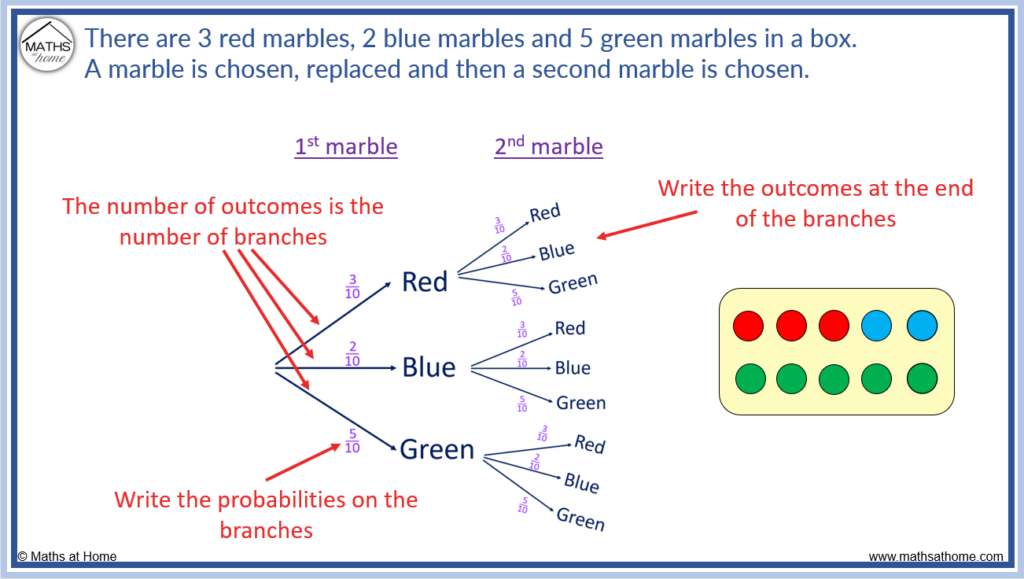
When drawing probability trees, use the following rules:

• Outcomes are written at the end of each branch
• Probabilities are drawn next to each branch
• Draw branches for each event above each other
• The probabilities on the branches for each event must add to 1
• Branches for new events are drawn on the right of the outcomes which come before them

How to Calculate Probabilities Using a Probability Tree

• Identify the paths through the tree that contain the desired outcomes.
• Multiply the probabilities on the branches of each of these individual paths.
• Add together all of the probabilities from the paths that give the desired outcomes.

Here is an example of how to do a probability tree. The probability of it raining is 0.2. If it rains, the probability I am late is 0.3 and if it doesn’t rain, the probability of me being late is 0.1.

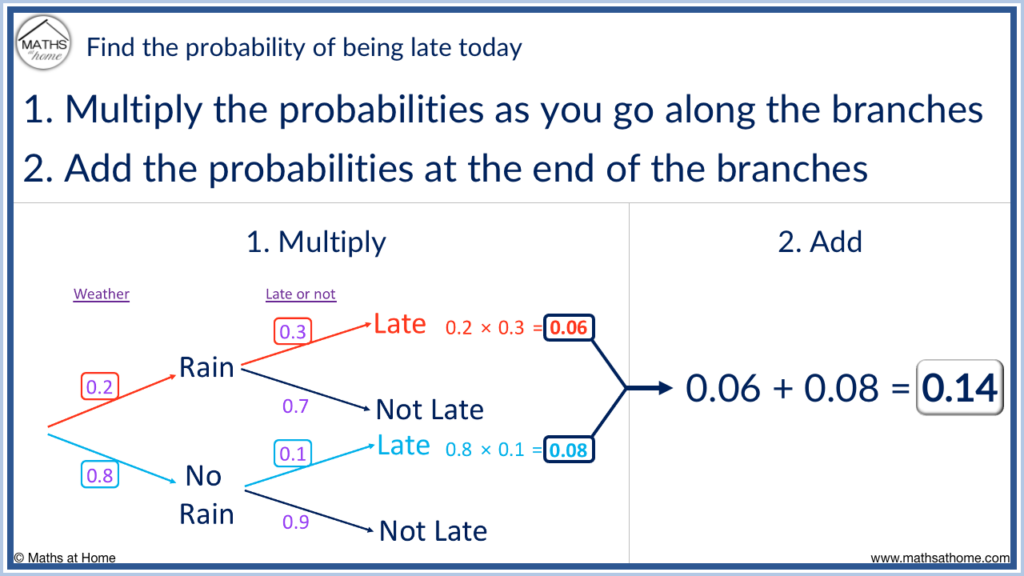
Step 1. Identify the desired outcomes

The desired outcomes are those that result in a late.

That is, if it rains and then we are late or if it does not rain and then we are late.

Step 2. Multiply the probabilities on the branches of the desired outcomes

The probability of rain is 0.2 and the probability of being late given it has rained is 0.3.

0.2 × 0.3 = 0.06 and so, the probability of it raining and then being late is 0.06.

The probability of no rain is 0.8 and the probability of being late given it has rained is 0.1.

0.8 × 0.1 = 0.08 and so, the probability of it not raining and then being late is 0.08.

Step 3. Add the probabilities of all desired outcomes

There are two pathways that produce the desired outcome of being late.

The probability of it raining and then being late is 0.06.

The probability of no rain and then being late is 0.08.

0.06 + 0.08 = 0.14 and so, the probability of being late is 0.14.

Probability Trees with Fractions

On a probability tree, fractions can be used to represent the probability of each outcome. The fractions are written on each branch. To find the probability of two or more outcomes occurring, multiply the fractions that are written on the branches of these outcomes.

When multiplying fractions, the answer is also a fraction.

• Multiply the numerators together to find the numerator of the answer.
• Multiply the denominators together to find the denominator of the answer.
• Simplify the fraction if possible.

Here is a probability tree showing a coin which is tossed twice.

To make a probability tree for tossing a coin:

• Draw two branches for the two outcomes of heads and tails
• The probability of both heads and tails is 1 / 2 since both outcomes are equally likely on a fair coin
• Label the two branches with the probability of 1 / 2
• Repeat these two branches coming out of each heads and tails outcome for however many times the coin is tossed

In this example, the coin is tossed twice, so heads and tails branches are drawn for the first coin toss and then another 2 sets of heads and tails branches are drawn coming out of the outcomes for the second toss.

If we get a heads on the first toss, we can then get a heads or a tails on the second toss.

If we get a tails on the first toss, we can then get a heads or a tails on the second toss.

The probability of tossing a heads or a tails does not change. It is always 1 / 2 .

To find the probability of getting two heads in a row, multiply the two fractions that are found next to heads on the first coin and heads on the second coin.

We have 1 / 2 × 1 / 2 .

For the numerator of our answer, 1 × 1 = 1.

For the denominator of our answer, 2 × 2 =4.

1 / 2 × 1 / 2 = 1 / 4 and so the probability of tossing two heads in a row is 1 / 4 .

Probability Trees with Decimals

Decimals can be used to represent probabilities on a probability tree diagram. Simply multiply the decimals found on the branches of the required outcome. When multiplying decimals, the answer will always have the same number of decimal places as the decimals being multiplied combined.

For example, a biased coin has a probability of heads = 0.9. It is tossed twice. Find the probability of obtaining a heads or a tails in any order.

In probability, biased means that the outcomes do not all have an equal chance of occurring. The probabilities of the outcomes will be different.

A fair coin would have a probability of heads equal to 0.5 and a probability of tails equal to 0.5. On this biased coin, the probability of heads is 0.9 and so, the probability of tails is 0.1. Remember that the probabilities on any set of branches must add up to 1.

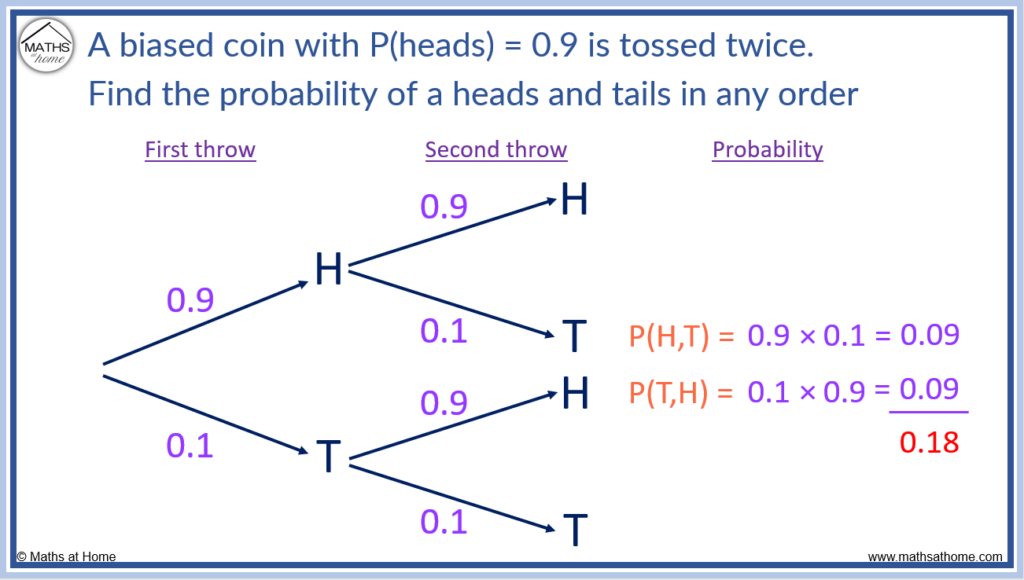
When tossing a coin twice, to obtain a heads and tails in any order, there are two outcomes. Either a heads first then a tails or a tails first then a heads.

The probabilities are found by multiplying the decimals on each path.

The probability of a heads then tails is 0.9 × 0.1 = 0.09.

The probability of a tails then heads is 0.1 × 0.9 = 0.09.

To multiply decimals, simply ignore the decimal point and any zeros in front of the non-zero digits.

We just multiply 1 × 9 to get 9.

Then the answer needs to have the same number of decimal places as the decimals in the question combined.

In the question of 0.1 × 0.9, the 0.1 has 1 decimal place and the 0.9 has 1 decimal place. In total there are 2 decimal places in the question and so the answer of 0.09 also has two decimal places.

Probability Trees For Independent Events

Events are independent if the outcome of the first event has no impact on the probabilities in the second event. When drawn on a probability tree, the probabilities of a particular outcome will always remain the same regardless of any other outcomes.

Rolling a dice is an example of an independent event. The number obtained on the first roll of the dice does not effect the probabilities on the following roll of a dice.

The probability of rolling a particular number on a dice is always 1 / 6 .

If the number 2 was obtained on the first roll, it is still a 1 / 6 chance of rolling a 2 on the next roll of the dice.

Find the probability of not rolling a 2 on 4 rolls of a dice.

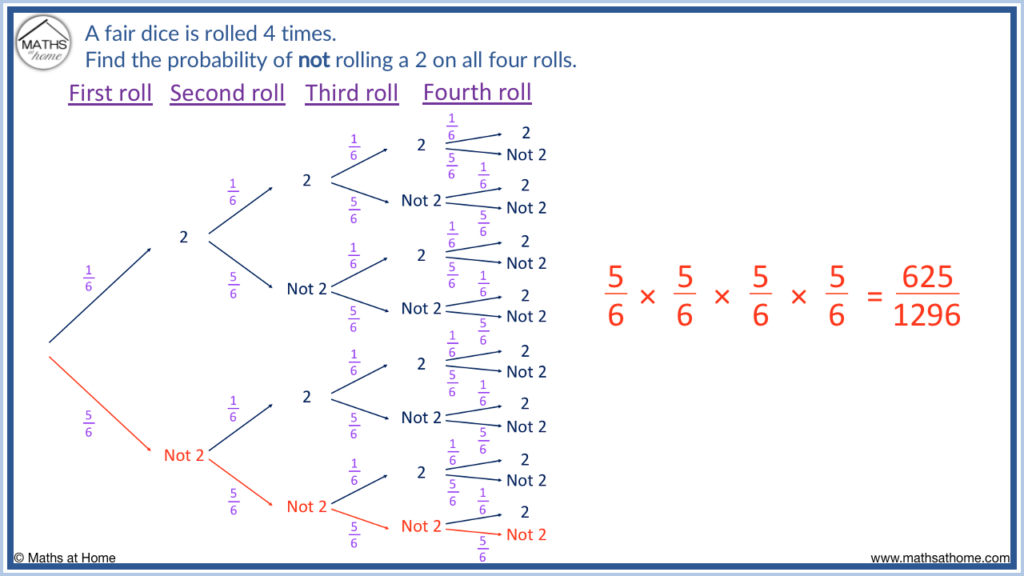
The probability of rolling a 2 is 1 / 6 and so, the probability of not rolling a 2 is 5 / 6 . This is because 5 out of the 6 numbers are not a 2.

We follow the bottom path on the independent probability tree, where we obtain ‘not 2’, ‘not 2’, ‘not 2’ and ‘not 2’.

This means we multiply 5 / 6 × 5 / 6 × 5 / 6 × 5 / 6 = 625 / 1296 .

Probability Trees For Dependent Events

Probability trees are particularly useful for representing dependent events. Dependent events are when the probability of an outcome depends on the outcome of the event before it. Simply draw the relevant branches coming out of the outcomes of the previous event.

For example, there are 3 red marbles and 7 blue marbles in a box. A marble is taken out and not replaced and then a second marble is taken out.

Because the first marble is not replaced, the probabilities when taking the second marble are now different to the probabilities for the first marble.

The probability of selecting a red or a blue for the second marble also depends on the colour of the first marble that was removed. Therefore we say these are dependent events.

On the tree below, the first pair of branches shows the outcomes of taking the first marble. We have red on the top and blue on the bottom.

Coming out of the first red outcome are another two branches. These show the probabilities for red and blue if a red was the first marble taken.

Coming out of the first blue outcome are another two branches. These show the probabilities for red and blue if a blue was the first marble taken.

It is helpful to draw a diagram of the objects when considering the probabilities of dependent events.

There were 3 reds and 7 blues to begin with.

If we take a red first, we now only have 2 reds left and 9 marbles in total. The probability of now selecting a second red marble is 2 / 9 . With there still being 7 blues, the probability of selecting a blue becomes 7 / 9 .

If a blue was taken first, we now only have 6 blue marbles out of a total of 9. The probability of now selecting a second blue marble is 6 / 9 . There are still 3 reds and so the probability of selecting a red becomes 3 / 9 .

Now further probabilities can be calculated. For example the probability of selecting two blue counters in a row would be 7 / 10 × 6 / 9 , which equals 42 / 90 or 7 / 15 .

Probability Trees With Replacement

Probability trees can be made for events where an object is selected and then replaced before it is selected again. The replacement means that the total number of objects remains the same throughout and therefore the probabilities on each pair of branches remain the same.

For example, there are 6 red marbles and 4 blue marbles in a box. A marble is selected and then replaced. A second marble is then selected.

Replacing the marble means that it is put back into the box. This means that the probabilities for selecting the second marble will be identical to the probabilities for selecting the first marble.

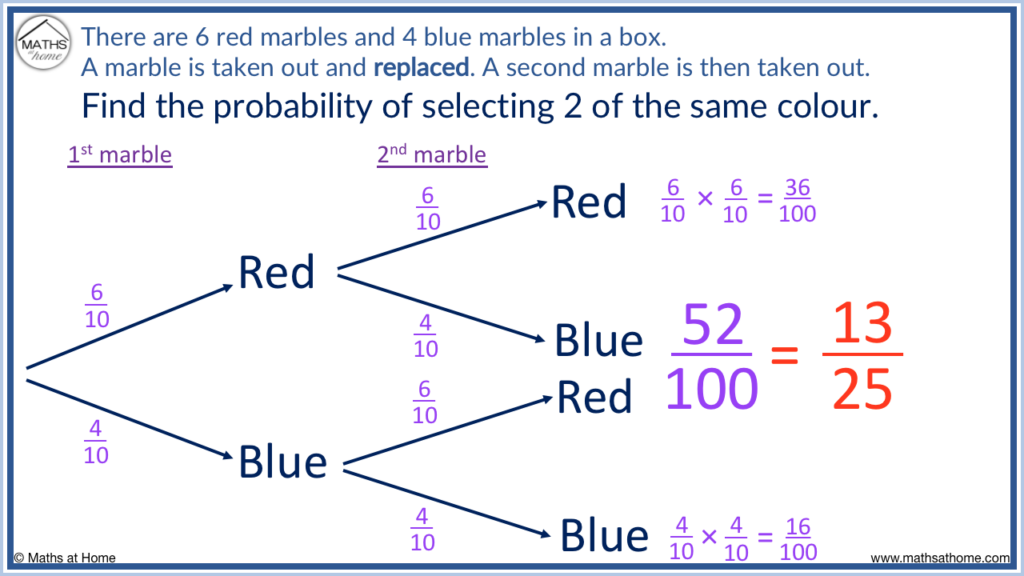
In this example we find the probability of selecting 2 marbles of the same colour.

That is, a red then a red or a blue then a blue.

We multiply the probabilities found on the branches for red and red or blue and blue.

The probability of a red then a red is 6 / 10 × 6 / 10 = 36 / 100 .

The probability of a blue then a blue is 4 / 10 × 4 / 10 = 16 / 100 .

The total probability of getting any 2 marbles the same colour is found by adding these probabilties together.

36 / 100 + 16 / 100 = 52 / 100 . This simplifies to 13 / 25 .

Probability Trees Without Replacement

Probability trees without replacement involve the selection of an object that is not returned after it is chosen. This means that the probabilities have now changed. If there is no replacement, the outcomes of an event are dependent on the outcome of the event before it.

For example, there are 3 red marbles and 7 blue marbles in a box. A marble is taken out and not replaced. A second marble is then taken out.

It helps to draw a diagram to show the outcomes when looking at probability trees without replacement.

This helps us to visualise how the probabilities change.

For example, on the tree diagram above, selecting a red first results in there now only being 2 red marbles left out of 9. Then 7 blue marbles remain out of 9.

However, selecting a blue marble first results in 6 blue marbles left out of 9. There will still be 3 red marbles left out of 9.

Probability Trees With 3 Events

Each event on a probability tree is shown with sets of branches which are aligned above each other. For a probability tree with 3 events, there are three columns of branches. The first event is shown on the left, the second event is in the middle and the third event is on the right.

For example, when a dice is rolled three times, the first roll will be shown on the left, the second roll will be shown in the middle and the third roll will be shown on the right.

Here we want to find the probability of rolling a 5 on all three rolls. Rather than making 6 branches to show all of the numbers from one to 6, it is easier to make a branch that is for rolling a 5 and another branch which is for not rolling a 5.

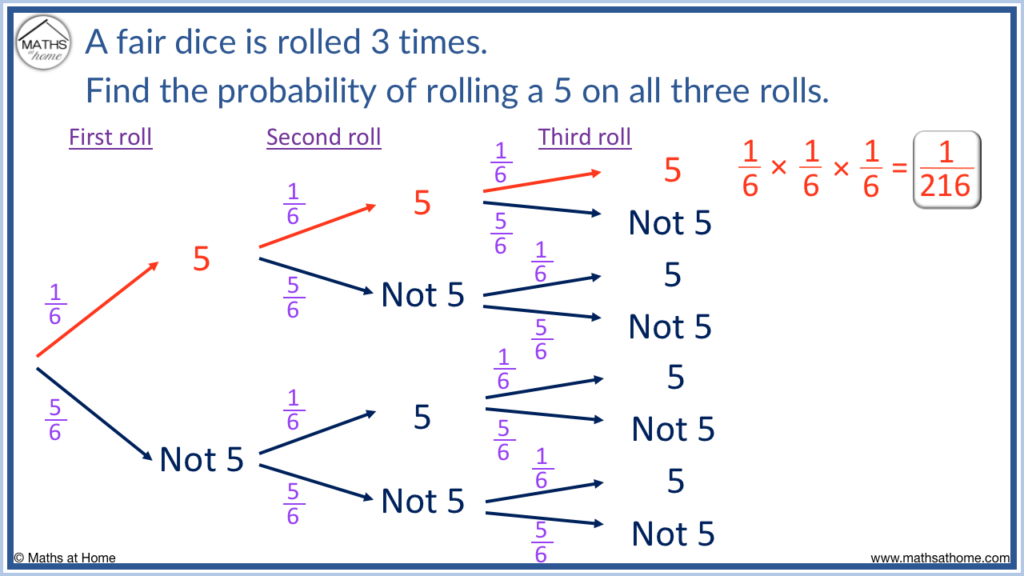
The probability of rolling a dice is 1 / 6 since there are 6 different outcomes, all with the same likelihood of occurring.

1 / 6 × 1 / 6 × 1 / 6 = 1 / 216 and so, the probability of rolling three sizes in a row is 1 / 216 .

Probability Trees With 3 Branches

On a probability tree, the number of branches needed is the same as the number of outcomes. If there are 3 possible outcomes, three branches are drawn. For example, if a box contains red, blue and green marbles, then 3 branches are drawn for the outcomes of red, blue and green.

In the example below there are 5 red marbles, 3 blue marbles and 2 green marbles in a box. Since three colours can be chosen, there are three branches on the tree.

When the first marble is taken, we can then take a red, blue or green marble as the second marble chosen. Therefore there are another three branches at the ends of the first marble outcome.

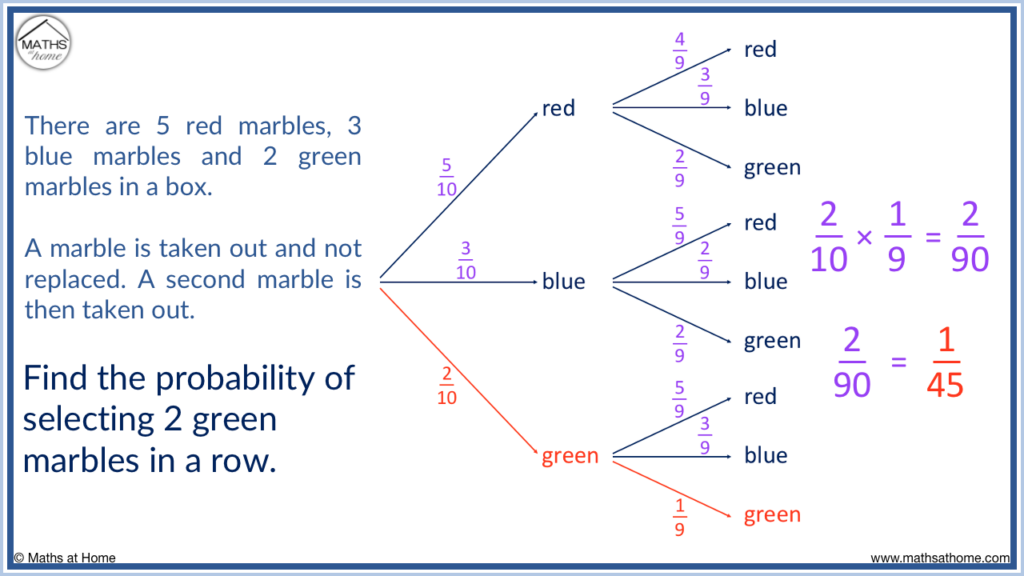
In the example above we find the probability of selecting 2 green marbles in a row.

There are 2 green marbles out of the 10 marbles in total and so, the probability of selecting a green marble the first time is 2 / 10 .

If a green marble is taken, there is now only 1 green marble left. There were 10 marbles but now that one has been taken, there are 9.

Therefore the probability of choosing a second green marble becomes 1 / 9 .

We multiply the two probabilities of getting a green marble together to find the probability of getting two green marbles in a row.

2 / 10 × 1 / 9 = 2 / 90 . This can be simplified to 1 / 45 .

Probability Trees with Algebra

Probability trees can also involve algebra. For example, there are n red marbles and n + 2 blue marbles in a box. Two marbles are taken out one after another. Find the probability of selecting 2 blue marbles.

In this example, there are n + n + 2 marbles in total. This means that there are 2n + 2 marbles in the box.

If there are n red marbles out of 2n + 2 marbles in total, the probability of selecting a red marble is n / (2n + 2) .

If there are n + 2 blue marbles out of 2n + 2 marbles in total, the probability of selecting a blue marble is (n+2) / (2n + 2) .

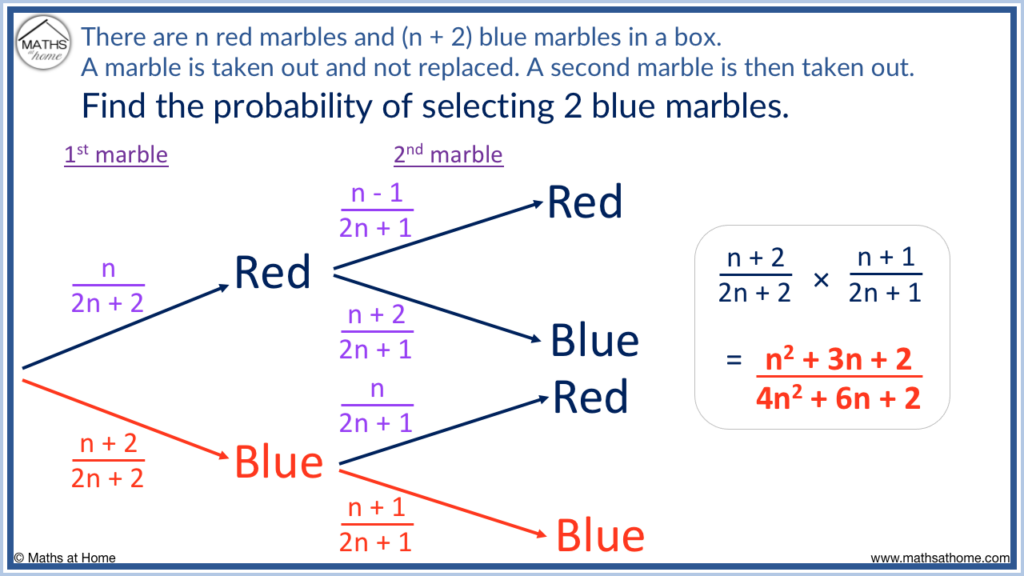
If a red marble is selected, then there is 1 less red marble. We originally had n red marbles and so, we now have n – 1 red marbles.

In total there were 2n + 2 marbles and if one has been selected then there are now 2n + 1 marbles in total because we have subtracted one.

If a red was selected first, the probability of a second red is now (n-1) / (2n + 1) and the probability of a blue is now (n+2) / (2n + 1) .

If a blue was selected first, there will be 1 less blue marble. We originally had n + 2 blue marbles and now we will have n + 1 blue marbles. We subtracted one from n + 2 to make n + 1.

The probability of obtaining a second blue is now (n+1) / (2n + 1) and the probability of obtaining a red after a blue is n / (2n + 1) .

We can see that on each pair of branches the probabilities always add up to one whole. With algebraic fractions, this means that if we add the numerators on each pair of branches, we obtain the denominator.

For example on the first pair of branches, n + n + 2 = 2n + 2.

On the pair of branches following a red being taken first, we have n – 1 + n + 2 = 2n + 1.

On the pair of branches following a blue being taken first, we have n + n + 1 = 2n + 1.

• International
• Schools directory
• Resources Jobs Schools directory News Search

Probability Trees (Workbook with Solutions)

Subject: Mathematics

Age range: 14-16

Resource type: Unit of work

Last updated

17 January 2019

• Share through email
• Share through twitter
• Share through linkedin
• Share through facebook
• Share through pinterest

Creative Commons "Sharealike"

Your rating is required to reflect your happiness.

It's good to leave some feedback.

Something went wrong, please try again later.

Empty reply does not make any sense for the end user

secondarymaths2017

Such a great resource. Really helpful. Thanks!

Super!<br />

Report this resource to let us know if it violates our terms and conditions. Our customer service team will review your report and will be in touch.

Not quite what you were looking for? Search by keyword to find the right resource:

Course blog for INFO 2040/CS 2850/Econ 2040/SOC 2090

Probability Tree Diagrams – A Zero-Equation Methodology to Understanding and Applying Bayes Rule

When it comes to probability, people generally do not have a good intuitive understanding as to how probability works. This is not a baseless claim. In a study conducted by researchers at the University of Toronto, it was found that upward and downward changes in probability cause a psychological momentum effect on people, leading people to make baseless decisions. As an example from the research study, the researchers were determining how people interpret probabilities associated with weather forecasting. What they found was that upward trends in a forecast’s probability, for example the chance of rain going from 20% to 30%, caused people to assume that the trend would continue and it would rain. Inversely, if the chance of rain went from 40% to 30%, people would assume that the trend would continue downwards, meaning that it would not rain. However, this conceptual model as to how probability works is inherently wrong. The probability that it rains given a chance of rain of 30% and an increase from 20% is no different from the probability that it rains given the same chance of rain (30%) and a decrease from 40%, yet people seem to believe that they are different.

So how do we remedy the incorrect conceptual models of probability that people have? A means by which I have been able to properly understand probability is via visualization methods. Enter the Probability Tree Diagram, a visual representation of probability using graphs as a means to model probability. Take for example an experiment where we flip a fair-sided coin twice (Probability of heads is ½ and probability of tails is ½). For this experiment we would have a probability tree of topology:

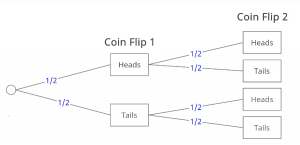
Each branch of the Probability tree diagram corresponds to an outcome of the experiment, in this case, whether the coin is heads or tails. Additionally, each outcome branch has its probability written on its respective edge. We can now use this probability tree diagram to model probabilities. For example, let’s say we are trying to determine the probability that two heads show up in a row, or P(Coin Flip 1 = Heads and Coin Flip 2 = Heads):

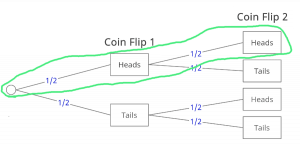
This outcome corresponds to the top branch in the probability tree where the outcomes are heads for each coin flip. We then calculate the probability by multiplying each of the probabilities on each outcome’s edge, which is equal to ½ x ½ = ¼. Thus, there is a probability of ¼ of getting two heads in a row. Now, lets model a different example, such as the probability of the second coin flip being heads:

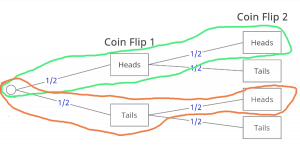
In this case, there are two possible outcomes that result in the second coin flip being heads, a heads after a tails and a heads after a heads. To calculate the probability of this outcome, we first need to calculate the probabilities for each outcome. P(Heads after Tails) = ½ x ½ = ¼ , P(Heads after Heads) = ½ x ½ = ¼. Then to get the total probability, we simply add these two probabilities together. P(Heads after Tails) + P(Heads after Heads) = ¼ + ¼ = ½.

So how can this methodology be applied to understanding Bayes’ Rule. Well, continuing with the coin flip example, let’s say we want to calculate the probability of coin flip 2 being heads given that coin flip 1 is heads, or P(Second Coin = Heads | First Coin = Heads). Thus, on the probability tree diagram, we would be looking at probability:

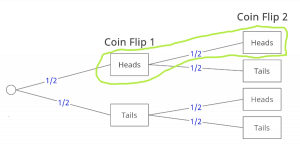
The probability is ½. In this case, we do not need to look at any of the other outcome branches in the tree besides this one. Inversely, let’s calculate the probability that the first coin is heads given that the second coin is heads, or P(First Coin = Heads | Second Coin = Heads). First, we need to calculate the probability of all possible outcomes where the second coin is heads. From one of the previous examples, we know that this probability is:

And calculating this probability, we get P(Heads after Tails) + P(Heads after Heads) = ¼ + ¼ = ½. Now we need to calculate the probability of both coin flips being heads, or P(Coin Flip 1 = Heads and P(Coin Flip 2 = Heads). From one of the previous examples, we know that this probability is:

To calculate the probability of Coin flip 1 being heads given coin flip 2 is heads, we divide the probability P(Coin Flip 1 = Heads and Coin Flip 2 = Heads) by the sum of the probabilities of all outcomes where the second coin is heads, or P(Heads after Tails) + P(Heads after Heads). So this probability is P(Coin Flip 1 = Heads and Coin Flip 2 = Heads) / P(Heads after Tails) + P(Heads after Heads), which is equal to ¼ / ½ = ½.

As is shown in all of these examples utilizing coin tosses as well as the tree diagram, coin toss probabilities are independent. This means the probability of getting heads on the second toss is not influenced by what the previous coin toss outcome was. It is equally likely to get heads after tails as it is after heads. Additionally, the outcome of the second toss also does not yield information as to what the previous coin toss was. It is equally as likely for the previous coin toss to be heads given the second coin toss was heads as it is to be heads given the second coin toss was tails. And this assertion holds for no matter how many coin tosses are done. It is equally as likely to get heads given the previous ten coins were heads as it is to get heads given the previous one coin toss was heads.

Now that we understand the fundamentals as to how Tree Diagrams can be utilized for probabilities, let’s move on to a more complex example. Taking a problem from one of the recent homework assignments, let’s say there’s a disease called BCF that afflicts a small portion of the population (1/1000 people). There exists a BCF detection test, although it is imperfect: it has false negatives (test is negative even though you have BCF) of 1/100, and it has false positives (test is positive even though you don’t have BCF) of 3/100. Modeling this experiment via probability tree diagram:

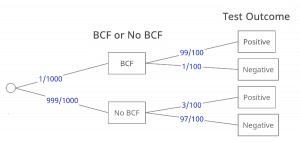
As in the homework problem, let’s calculate the probability of an erroneous diagnosis, meaning testing positive when you do not have BCF or testing negative when you do have BCF. On the probability tree diagram, these outcomes correspond to:

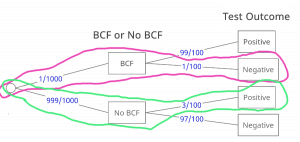
Calculating the probability for these outcomes, first we calculate the probability of testing negative when you do have BCF, which is equal to 1/1000 x 1/100 = 1/100000. Now calculating the probability of testing positive when you don’t have BCF, we get 999/1000 x 3/100 = 2997/100000. Adding these two probabilities gives us the probability of an erroneous diagnosis, which is 2998/100000 or 2.998%.

Now let’s calculate the probability that you have BCF if you test positive for it. On our probability tree diagram, the applicable outcomes are:

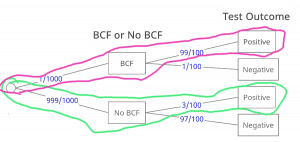
To calculate the probability of having BCF if you test positive, we are dividing P(Test Positive given BCF) by the sum of P(Test Positive given BCF) and P(Test Positive Given No BCF). Calculating for P(Test Positive given BCF), we get 1/1000 x 99/100 = 99/100000. Calculating for P(Test Positive Given No BCF), we get 999/1000 * 3/100 = 2997/100000. So calculating for the probability of having BCF if you test positive, we get (99/100000) / (99/100000 + 2997/100000) = 3.1%.

Ultimately, as I found and hope that you find, the probability tree diagram serves as a useful tool for modeling probability problems, as well as understanding the concepts of conditional probability and Bayes’ rule.

New research uncovers why an increase in probability feels riskier than a decrease

Probability Tree Diagrams: Step-by-Step

November 17, 2021 | category: Uncategorized

Leave a Comment

Leave a Reply

Name (required)

Mail (will not be published) (required)

XHTML: You can use these tags: <a href="" title=""> <abbr title=""> <acronym title=""> <b> <blockquote cite=""> <cite> <code> <del datetime=""> <em> <i> <q cite=""> <s> <strike> <strong>

Blogging Calendar

©2024 Cornell University Powered by Edublogs Campus and running on blogs.cornell.edu

First refuelling for Russia’s Akademik Lomonosov floating NPP

!{Model.Description}

The FNPP includes two KLT-40S reactor units. In such reactors, nuclear fuel is not replaced in the same way as in standard NPPs – partial replacement of fuel once every 12-18 months. Instead, once every few years the entire reactor core is replaced with and a full load of fresh fuel.

The KLT-40S reactor cores have a number of advantages compared with standard NPPs. For the first time, a cassette core was used, which made it possible to increase the fuel cycle to 3-3.5 years before refuelling, and also reduce by one and a half times the fuel component in the cost of the electricity produced. The operating experience of the FNPP provided the basis for the design of the new series of nuclear icebreaker reactors (series 22220). Currently, three such icebreakers have been launched.

The Akademik Lomonosov was connected to the power grid in December 2019, and put into commercial operation in May 2020.

Electricity generation from the FNPP at the end of 2023 amounted to 194 GWh. The population of Pevek is just over 4,000 people. However, the plant can potentially provide electricity to a city with a population of up to 100,000. The FNPP solved two problems. Firstly, it replaced the retiring capacities of the Bilibino Nuclear Power Plant, which has been operating since 1974, as well as the Chaunskaya Thermal Power Plant, which is more than 70 years old. It also supplies power to the main mining enterprises located in western Chukotka. In September, a 490 km 110 kilovolt power transmission line was put into operation connecting Pevek and Bilibino.

Image courtesy of TVEL

• Terms and conditions
• Privacy Policy
• Newsletter sign up
• Digital Edition
• Editorial Standards

Turn Your Curiosity Into Discovery

Latest facts.

How To Protect Children From Junk Food Marketing

12 Intriguing Facts About Balatro

40 facts about elektrostal.

Written by Lanette Mayes

Modified & Updated: 02 Mar 2024

Reviewed by Jessica Corbett

Elektrostal is a vibrant city located in the Moscow Oblast region of Russia. With a rich history, stunning architecture, and a thriving community, Elektrostal is a city that has much to offer. Whether you are a history buff, nature enthusiast, or simply curious about different cultures, Elektrostal is sure to captivate you.

This article will provide you with 40 fascinating facts about Elektrostal, giving you a better understanding of why this city is worth exploring. From its origins as an industrial hub to its modern-day charm, we will delve into the various aspects that make Elektrostal a unique and must-visit destination.

So, join us as we uncover the hidden treasures of Elektrostal and discover what makes this city a true gem in the heart of Russia.

Key Takeaways:

• Elektrostal, known as the “Motor City of Russia,” is a vibrant and growing city with a rich industrial history, offering diverse cultural experiences and a strong commitment to environmental sustainability.
• With its convenient location near Moscow, Elektrostal provides a picturesque landscape, vibrant nightlife, and a range of recreational activities, making it an ideal destination for residents and visitors alike.

Known as the “Motor City of Russia.”

Elektrostal, a city located in the Moscow Oblast region of Russia, earned the nickname “Motor City” due to its significant involvement in the automotive industry.

Home to the Elektrostal Metallurgical Plant.

Elektrostal is renowned for its metallurgical plant, which has been producing high-quality steel and alloys since its establishment in 1916.

Boasts a rich industrial heritage.

Elektrostal has a long history of industrial development, contributing to the growth and progress of the region.

Founded in 1916.

The city of Elektrostal was founded in 1916 as a result of the construction of the Elektrostal Metallurgical Plant.

Located approximately 50 kilometers east of Moscow.

Elektrostal is situated in close proximity to the Russian capital, making it easily accessible for both residents and visitors.

Known for its vibrant cultural scene.

Elektrostal is home to several cultural institutions, including museums, theaters, and art galleries that showcase the city’s rich artistic heritage.

A popular destination for nature lovers.

Surrounded by picturesque landscapes and forests, Elektrostal offers ample opportunities for outdoor activities such as hiking, camping, and birdwatching.

Hosts the annual Elektrostal City Day celebrations.

Every year, Elektrostal organizes festive events and activities to celebrate its founding, bringing together residents and visitors in a spirit of unity and joy.

Has a population of approximately 160,000 people.

Elektrostal is home to a diverse and vibrant community of around 160,000 residents, contributing to its dynamic atmosphere.

Boasts excellent education facilities.

The city is known for its well-established educational institutions, providing quality education to students of all ages.

A center for scientific research and innovation.

Elektrostal serves as an important hub for scientific research, particularly in the fields of metallurgy, materials science, and engineering.

Surrounded by picturesque lakes.

The city is blessed with numerous beautiful lakes, offering scenic views and recreational opportunities for locals and visitors alike.

Well-connected transportation system.

Elektrostal benefits from an efficient transportation network, including highways, railways, and public transportation options, ensuring convenient travel within and beyond the city.

Famous for its traditional Russian cuisine.

Food enthusiasts can indulge in authentic Russian dishes at numerous restaurants and cafes scattered throughout Elektrostal.

Home to notable architectural landmarks.

Elektrostal boasts impressive architecture, including the Church of the Transfiguration of the Lord and the Elektrostal Palace of Culture.

Offers a wide range of recreational facilities.

Residents and visitors can enjoy various recreational activities, such as sports complexes, swimming pools, and fitness centers, enhancing the overall quality of life.

Provides a high standard of healthcare.

Elektrostal is equipped with modern medical facilities, ensuring residents have access to quality healthcare services.

Home to the Elektrostal History Museum.

The Elektrostal History Museum showcases the city’s fascinating past through exhibitions and displays.

A hub for sports enthusiasts.

Elektrostal is passionate about sports, with numerous stadiums, arenas, and sports clubs offering opportunities for athletes and spectators.

Celebrates diverse cultural festivals.

Throughout the year, Elektrostal hosts a variety of cultural festivals, celebrating different ethnicities, traditions, and art forms.

Electric power played a significant role in its early development.

Elektrostal owes its name and initial growth to the establishment of electric power stations and the utilization of electricity in the industrial sector.

Boasts a thriving economy.

The city’s strong industrial base, coupled with its strategic location near Moscow, has contributed to Elektrostal’s prosperous economic status.

Houses the Elektrostal Drama Theater.

The Elektrostal Drama Theater is a cultural centerpiece, attracting theater enthusiasts from far and wide.

Popular destination for winter sports.

Elektrostal’s proximity to ski resorts and winter sport facilities makes it a favorite destination for skiing, snowboarding, and other winter activities.

Promotes environmental sustainability.

Elektrostal prioritizes environmental protection and sustainability, implementing initiatives to reduce pollution and preserve natural resources.

Home to renowned educational institutions.

Elektrostal is known for its prestigious schools and universities, offering a wide range of academic programs to students.

Committed to cultural preservation.

The city values its cultural heritage and takes active steps to preserve and promote traditional customs, crafts, and arts.

Hosts an annual International Film Festival.

The Elektrostal International Film Festival attracts filmmakers and cinema enthusiasts from around the world, showcasing a diverse range of films.

Encourages entrepreneurship and innovation.

Elektrostal supports aspiring entrepreneurs and fosters a culture of innovation, providing opportunities for startups and business development.

Offers a range of housing options.

Elektrostal provides diverse housing options, including apartments, houses, and residential complexes, catering to different lifestyles and budgets.

Home to notable sports teams.

Elektrostal is proud of its sports legacy, with several successful sports teams competing at regional and national levels.

Boasts a vibrant nightlife scene.

Residents and visitors can enjoy a lively nightlife in Elektrostal, with numerous bars, clubs, and entertainment venues.

Promotes cultural exchange and international relations.

Elektrostal actively engages in international partnerships, cultural exchanges, and diplomatic collaborations to foster global connections.

Surrounded by beautiful nature reserves.

Nearby nature reserves, such as the Barybino Forest and Luchinskoye Lake, offer opportunities for nature enthusiasts to explore and appreciate the region’s biodiversity.

Commemorates historical events.

The city pays tribute to significant historical events through memorials, monuments, and exhibitions, ensuring the preservation of collective memory.

Promotes sports and youth development.

Elektrostal invests in sports infrastructure and programs to encourage youth participation, health, and physical fitness.

Hosts annual cultural and artistic festivals.

Throughout the year, Elektrostal celebrates its cultural diversity through festivals dedicated to music, dance, art, and theater.

Provides a picturesque landscape for photography enthusiasts.

The city’s scenic beauty, architectural landmarks, and natural surroundings make it a paradise for photographers.

Connects to Moscow via a direct train line.

The convenient train connection between Elektrostal and Moscow makes commuting between the two cities effortless.

A city with a bright future.

Elektrostal continues to grow and develop, aiming to become a model city in terms of infrastructure, sustainability, and quality of life for its residents.

In conclusion, Elektrostal is a fascinating city with a rich history and a vibrant present. From its origins as a center of steel production to its modern-day status as a hub for education and industry, Elektrostal has plenty to offer both residents and visitors. With its beautiful parks, cultural attractions, and proximity to Moscow, there is no shortage of things to see and do in this dynamic city. Whether you’re interested in exploring its historical landmarks, enjoying outdoor activities, or immersing yourself in the local culture, Elektrostal has something for everyone. So, next time you find yourself in the Moscow region, don’t miss the opportunity to discover the hidden gems of Elektrostal.

Q: What is the population of Elektrostal?

A: As of the latest data, the population of Elektrostal is approximately XXXX.

Q: How far is Elektrostal from Moscow?

A: Elektrostal is located approximately XX kilometers away from Moscow.

Q: Are there any famous landmarks in Elektrostal?

A: Yes, Elektrostal is home to several notable landmarks, including XXXX and XXXX.

Q: What industries are prominent in Elektrostal?

A: Elektrostal is known for its steel production industry and is also a center for engineering and manufacturing.

Q: Are there any universities or educational institutions in Elektrostal?

A: Yes, Elektrostal is home to XXXX University and several other educational institutions.

Q: What are some popular outdoor activities in Elektrostal?

A: Elektrostal offers several outdoor activities, such as hiking, cycling, and picnicking in its beautiful parks.

Q: Is Elektrostal well-connected in terms of transportation?

A: Yes, Elektrostal has good transportation links, including trains and buses, making it easily accessible from nearby cities.

Q: Are there any annual events or festivals in Elektrostal?

A: Yes, Elektrostal hosts various events and festivals throughout the year, including XXXX and XXXX.

Was this page helpful?

Our commitment to delivering trustworthy and engaging content is at the heart of what we do. Each fact on our site is contributed by real users like you, bringing a wealth of diverse insights and information. To ensure the highest standards of accuracy and reliability, our dedicated editors meticulously review each submission. This process guarantees that the facts we share are not only fascinating but also credible. Trust in our commitment to quality and authenticity as you explore and learn with us.

Share this Fact:

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

8.3: Probability Using Tree Diagrams and Combinations

• Last updated
• Save as PDF
• Page ID 37908

• Rupinder Sekhon and Roberta Bloom
• De Anza College

Learning Objectives

In this section, you will learn to:

• Use probability tree diagrams to calculate probabilities
• Use combinations to calculate probabilities

In this section, we will apply previously learnt counting techniques in calculating probabilities, and use tree diagrams to help us gain a better understanding of what is involved.

USING TREE DIAGRAMS TO CALCULATE PROBABILITIES

We already used tree diagrams to list events in a sample space. Tree diagrams can be helpful in organizing information in probability problems; they help provide a structure for understanding probability. In this section we expand our previous use of tree diagrams to situations in which the events in the sample space are not all equally likely.

We assign the appropriate probabilities to the events shown on the branches of the tree. By multiplying probabilities along a path through the tree, we can find probabilities for “and” events, which are intersections of events.

We begin with an example.

Example \(\PageIndex{1}\)

Suppose a jar contains 3 red and 4 white marbles. If two marbles are drawn with replacement, what is the probability that both marbles are red?

Let \(\mathrm{E}\) be the event that the first marble drawn is red, and let \(\mathrm{F}\) be the event that the second marble drawn is red.

We need to find \(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\).

By the statement, "two marbles are drawn with replacement," we mean that the first marble is replaced before the second marble is drawn.

There are 7 choices for the first draw. And since the first marble is replaced before the second is drawn, there are, again, seven choices for the second draw. Using the multiplication axiom, we conclude that the sample space \(\mathrm{S}\) consists of 49 ordered pairs. Of the 49 ordered pairs, there are \(3 \times 3 = 9\) ordered pairs that show red on the first draw and, also, red on the second draw. Therefore,

\[P(E \cap F)=\frac{9}{49} \nonumber \]

Further note that in this particular case

\[P(E \cap F)=\frac{9}{49}=\frac{3}{7} \cdot \frac{3}{7} \nonumber \]

giving us the result that in this example: \(\mathbf{P}(\mathbf{E} \cap \mathbf{F})=\mathbf{P}(\mathbf{E}) \cdot \mathbf{P}(\mathbf{F})\)

Example \(\PageIndex{2}\)

If in Example \(\PageIndex{1}\), the two marbles are drawn without replacement, then what is the probability that both marbles are red?

By the statement, "two marbles are drawn without replacement," we mean that the first marble is not replaced before the second marble is drawn.

Again, we need to find \(\mathrm{P}(\mathrm{E} \cap \mathrm{F})\).

There are, again, 7 choices for the first draw. And since the first marble is not replaced before the second is drawn, there are only six choices for the second draw. Using the multiplication axiom, we conclude that the sample space S consists of 42 ordered pairs. Of the 42 ordered pairs, there are \(3 \times 2 = 6\) ordered pairs that show red on the first draw and red on the second draw. Therefore,

\[P(E \cap F)=\frac{6}{42} \nonumber \]

Note that we can break this calculation down as

\[P(E \cap F)=\frac{6}{42}=\frac{3}{7} \cdot \frac{2}{6} \nonumber \].

Here 3/7 represents \(\mathrm{P}(\mathrm{E})\), and 2/6 represents the probability of drawing a red on the second draw, given that the first draw resulted in a red.

We write the latter as \(\mathrm{P}\)(red on the second | red on first) or \(\mathrm{P}(\mathrm{F} | \mathrm{E})\). The "|" represents the word "given" or “if”. This leads to the result that:

\[\mathbf{P}(\mathbf{E} \cap \mathbf{F})=\mathbf{P}(\mathbf{E}) \cdot \mathbf{P}(\mathbf{F} | \mathbf{E}) \nonumber \]

The is an important result, called the Multiplication Rule, which will appear again in later sections.

We now demonstrate the above results with a tree diagram.

Example \(\PageIndex{3}\)

Suppose a jar contains 3 red and 4 white marbles. If two marbles are drawn without replacement, find the following probabilities using a tree diagram.

• The probability that both marbles are red.
• The probability that the first marble is red and the second white.
• The probability that one marble is red and the other white.

Let \(\mathrm{R}\) be the event that the marble drawn is red, and let W be the event that the marble drawn is white.

We draw the following tree diagram.

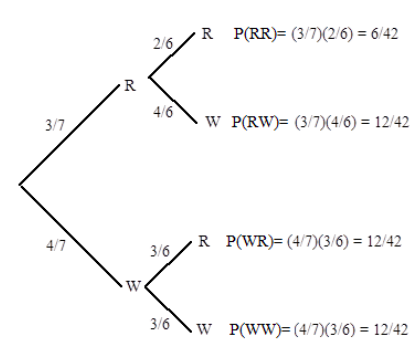
• The probability that both marbles are red is \(\mathrm{P}(\mathrm{RR})=6/42\)
• The probability that the first marble is red and the second is white is \(\mathrm{P}(\mathrm{RW})=12/42\)
• For the probability that one marble is red and the other is white, we observe that this can be satisfied if the first is red and the second is white, or if the first is white and the second is red. The “or” tells us we’ll be using the Addition Rule from Section 7.2.

Furthermore events \(\mathrm{RW}\) and \(\mathrm{WR}\) are mutually exclusive events, so we use the form of the Addition Rule that applies to mutually exclusive events.

\(\mathrm{P}\)(one marble is red and the other marble is white)

\[\begin{array}{l} =\mathrm{P}(\mathrm{RW} \text { or } \mathrm{WR}) \\ =\mathrm{P}(\mathrm{RW})+\mathrm{P}(\mathrm{WR}) \\ =12 / 42+12 / 42=24 / 42 \end{array} \nonumber \]

USING COMBINATIONS TO FIND PROBABILITIES

Although the tree diagrams give us better insight into a problem, they are not practical for problems where more than two or three things are chosen. In such cases, we use the concept of combinations that we learned in the last chapter. This method is best suited for problems where the order in which the objects are chosen is not important, and the objects are chosen without replacement.

Example \(\PageIndex{4}\)

Suppose a jar contains 3 red, 2 white, and 3 blue marbles. If three marbles are drawn without replacement, find the following probabilities.

• \(\mathrm{P}\)(Two red and one white)
• \(\mathrm{P}\)(One of each color)
• \(\mathrm{P}\)(None blue)
• \(\mathrm{P}\)(At least one blue)

Let us suppose the marbles are labeled as \(R_1,R_2,R_3,W_1,W_2,B_1,B_2,B_3\).

a. \(\mathrm{P}\)(Two red and one white)

Since we are choosing 3 marbles from a total of 8, there are 8\(\mathrm{C}\)3 = 56 possible combinations. Of these 56 combinations, there are \(3 \mathrm{C} 2 \times 2 \mathrm{C}1=6\) combinations consisting of 2 red and one white. Therefore,

\[P(\text { Two red and one white })=\frac{3 \mathrm{C} 2 \times 2 \mathrm{C} 1}{8 \mathrm{C} 3}=\frac{6}{56} \nonumber. \nonumber \]

b. \(\mathrm{P}\)(One of each color)

Again, there are 8\(\mathrm{C}\)3 = 56 possible combinations. Of these 56 combinations, there are \(3 \mathrm{Cl} \times 2 \mathrm{Cl} \times 3 \mathrm{Cl}=18\) combinations consisting of one red, one white, and one blue. Therefore,

\[P(\text { One of each color })=\frac{3 \mathrm{C} 1 \times 2 \mathrm{C} 1 \times 3 \mathrm{C} 1}{8 \mathrm{C} 3}=\frac{18}{56} \nonumber \]

c. \(\mathrm{P}\)(None blue)

There are 5 non-blue marbles, therefore

\[\mathrm{P}(\text { None blue })=\frac{5 \mathrm{C} 3}{8 \mathrm{C} 3}=\frac{10}{56}=\frac{5}{28} \nonumber \]

d. \(\mathrm{P}\)(At least one blue)

By "at least one blue marble," we mean the following: one blue marble and two non-blue marbles, OR two blue marbles and one non-blue marble, OR all three blue marbles. So we have to find the sum of the probabilities of all three cases.

\[\mathrm{P}(\mathrm{At} \text { least one blue })=\mathrm{P}(1 \text { blue, } 2 \text { non-blue) }+\mathrm{P}(2 \text { blue, l non-blue) }+\mathrm{P}(3\text { blue) } \nonumber \]

\[P( \text { At least one blue })=\frac{3 \mathrm{C} 1 \times 5 \mathrm{C} 2}{8 \mathrm{C} 3}+\frac{3 \mathrm{C} 2 \times 5 \mathrm{C} 1}{8 \mathrm{C} 3}+\frac{3 \mathrm{C} 3}{8 \mathrm{C} 3} \nonumber \]

\[ P(\text { At least one blue })=30 / 56+15 / 56+1 / 56=46 / 56=23 / 28 \nonumber \]

Alternately, we can use the fact that \(\mathrm{P}(\mathrm{E}) = 1 - \mathrm{P}(\mathrm{E}^c)\). If the event \(\mathrm{E}\) = At least one blue, then \(E^c\) = None blue.

But from part c of this example, we have \((\mathrm{E}^c) = 5/28\), so \(\mathrm{P}(\mathrm{E}) = 1 - 5/28 = 23/28\).

Example \(\PageIndex{5}\)

Five cards are drawn from a deck. Find the probability of obtaining two pairs, that is, two cards of one value, two of another value, and one other card.

Let us first do an easier problem-the probability of obtaining a pair of kings and queens.

Since there are four kings, and four queens in the deck, the probability of obtaining two kings, two queens and one other card is

\[\mathrm{P}(\mathrm{A} \text { pair of kings and queens })=\frac{4 \mathrm{C} 2 \times 4 \mathrm{C} 2 \times 44 \mathrm{C}1}{52 \mathrm{C} 5} \nonumber \]

To find the probability of obtaining two pairs, we have to consider all possible pairs.

Since there are altogether 13 values, that is, aces, deuces, and so on, there are 13\(\mathrm{C}\)2 different combinations of pairs.

\[P(\text { Two pairs })=13 \mathrm{C} 2 \cdot \frac{4 \mathrm{C} 2 \times 4 \mathrm{C} 2 \times 44 \mathrm{C}1}{52 \mathrm{C} 5}=.04754 \nonumber \]

Example \(\PageIndex{6}\)

A cell phone store receives a shipment of 15 cell phones that contains 8 iPhones and 7 Android phones. Suppose that 6 cell phones are randomly selected from this shipment. Find the probability that a randomly selected set of 6 cell phones consists of 2 iPhones and 4 Android phones.

There are 8\(\mathrm{C}\)2 ways of selecting 2 out of the 8 iPhones.

and 7\(\mathrm{C}\)4 ways of selecting 4 out of the 7 Android phones

But altogether there are 15\(\mathrm{C}\)6 ways of selecting 6 out of 15 cell phones.

Therefore we have

\[P(2 \text { iPhones and } 4 \text { Android phones })=\frac{8 \mathrm{C} 2 \times 7 \mathrm{C} 4}{15 \mathrm{C} 6}=\frac{(28)(35)}{5005}=\frac{980}{5005}=0.1958 \nonumber \]

Example \(\PageIndex{7}\)

One afternoon, a bagel store still has 53 bagels remaining: 20 plain, 15 poppyseed, and 18 sesame seed bagels. Suppose that the store owner packages up a bag of 9 bagels to bring home for tomorrow’s breakfast, and selects the bagels randomly. Find the probability that the bag contains 4 plain, 3 poppyseed, and 2 sesame seed.

There are 20\(\mathrm{C}\)4 ways of selecting 4 out of the 20 plain bagels,

and 15\(\mathrm{C}\)3 ways of selecting 3 out of the 15 poppyseed bagels,

and 18\(\mathrm{C}\)2 ways of selecting 2 out of the 18 sesame seed bagels.

But altogether there are 53\(\mathrm{C}\)9 ways of selecting 9 out of the 53 bagels.

\begin{array}{l} \mathrm{P} \text{(4 plain, 3 poppyseed, and 2 sesame seed)} &=\frac{20 \mathrm{C} 4 \times 15 \mathrm{C} 3 \times 18 \mathrm{C} 2}{53 \mathrm{C} 9} \\ &=\frac{(4845)(455)(153)}{4431613550} \\ &=0.761 \end{array}

We end the section by solving a famous problem called the Birthday Problem .

Example \(\PageIndex{8}\): Birthday Problem

If there are 25 people in a room, what is the probability that at least two people have the same birthday?

Let event \(\mathrm{E}\) represent that at least two people have the same birthday.

We first find the probability that no two people have the same birthday.

We analyze as follows.

Suppose there are 365 days to every year. According to the multiplication axiom, there are 365 25 possible birthdays for 25 people. Therefore, the sample space has 365 25 elements. We are interested in the probability that no two people have the same birthday. There are 365 possible choices for the first person and since the second person must have a different birthday, there are 364 choices for the second, 363 for the third, and so on. Therefore,

\[\mathrm{P}(\mathrm{No} \text { two have the same birthday })=\frac{365 \cdot 364 \cdot 363 \cdots 341}{365^{25}}=\frac{365 \mathrm{P} 25}{365^{25}} \nonumber \]

Since \(\mathrm{P}\)(at least two people have the same birthday) = 1 - \(\mathrm{P}\)(No two have the same birthday),

\[\mathrm{P} \text { at least two people have the same birthday ) }=1-\frac{365 \mathrm{P} 25}{365^{25}}=.5687\ \nonumber \]