assignment problems in or

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

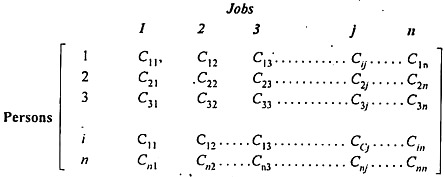
Check it out now on O’Reilly

Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.

• Data Structures
• Linked List
• Binary Tree
• Binary Search Tree
• Segment Tree
• Disjoint Set Union
• Fenwick Tree
• Red-Black Tree
• Advanced Data Structures
• Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
• Count of nodes with maximum connection in an undirected graph
• Erdos Renyl Model (for generating Random Graphs)
• Types of Graphs with Examples
• Clustering Coefficient in Graph Theory
• Maximum number of edges in Bipartite graph
• Find node having maximum number of common nodes with a given node K
• Convert the undirected graph into directed graph such that there is no path of length greater than 1
• Count of Disjoint Groups by grouping points that are at most K distance apart
• Maximize count of nodes disconnected from all other nodes in a Graph
• Program to find the number of region in Planar Graph
• Cost of painting n * m grid
• Ways to Remove Edges from a Complete Graph to make Odd Edges
• Number of Simple Graph with N Vertices and M Edges
• Balance pans using given weights that are powers of a number
• Chiliagon Number
• Sum of all the numbers in the Nth parenthesis
• Shortest path in a graph from a source S to destination D with exactly K edges for multiple Queries
• Find if two given Quadratic equations have common roots or not

Hungarian Algorithm for Assignment Problem | Set 1 (Introduction)

• For each row of the matrix, find the smallest element and subtract it from every element in its row.
• Do the same (as step 1) for all columns.
• Cover all zeros in the matrix using minimum number of horizontal and vertical lines.
• Test for Optimality: If the minimum number of covering lines is n, an optimal assignment is possible and we are finished. Else if lines are lesser than n, we haven’t found the optimal assignment, and must proceed to step 5.
• Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.

Try it before moving to see the solution

Explanation for above simple example:

  An example that doesn’t lead to optimal value in first attempt: In the above example, the first check for optimality did give us solution. What if we the number covering lines is less than n.

Time complexity : O(n^3), where n is the number of workers and jobs. This is because the algorithm implements the Hungarian algorithm, which is known to have a time complexity of O(n^3).

Space complexity :   O(n^2), where n is the number of workers and jobs. This is because the algorithm uses a 2D cost matrix of size n x n to store the costs of assigning each worker to a job, and additional arrays of size n to store the labels, matches, and auxiliary information needed for the algorithm.

In the next post, we will be discussing implementation of the above algorithm. The implementation requires more steps as we need to find minimum number of lines to cover all 0’s using a program. References: http://www.math.harvard.edu/archive/20_spring_05/handouts/assignment_overheads.pdf https://www.youtube.com/watch?v=dQDZNHwuuOY

Please Login to comment...

• Mathematical
• How to Delete Whatsapp Business Account?
• Discord vs Zoom: Select The Efficienct One for Virtual Meetings?
• Otter AI vs Dragon Speech Recognition: Which is the best AI Transcription Tool?
• Google Messages To Let You Send Multiple Photos
• 30 OOPs Interview Questions and Answers (2024)

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

www.springer.com The European Mathematical Society

• StatProb Collection
• Recent changes
• Current events
• Random page
• Project talk
• Request account
• What links here
• Related changes
• Special pages
• Printable version
• Permanent link
• Page information
• View source

Assignment problem

The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :

maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $

$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$

(origins or supply),

$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$

(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.

If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).

In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.

The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.

In turn, the transportation problem is a special case of the network optimization problem.

A totally different assignment problem is the pole assignment problem in control theory.

• This page was last edited on 5 April 2020, at 18:48.
• Privacy policy
• About Encyclopedia of Mathematics
• Disclaimers
• Impressum-Legal

OPERATIONS RESEARCH

Lesson 9. solution of assignment problem.

Current course

Unbalanced Assignment Problem: Definition, Formulation, and Solution Methods

Table of Contents

Are you familiar with the assignment problem in Operations Research (OR)? This problem deals with assigning tasks to workers in a way that minimizes the total cost or time needed to complete the tasks. But what if the number of tasks and workers is not equal? In this case, we face the Unbalanced Assignment Problem (UAP). This blog will help you understand what the UAP is, how to formulate it, and how to solve it.

What is the Unbalanced Assignment Problem?

The Unbalanced Assignment Problem is an extension of the Assignment Problem in OR, where the number of tasks and workers is not equal. In the UAP, some tasks may remain unassigned, while some workers may not be assigned any task. The objective is still to minimize the total cost or time required to complete the assigned tasks, but the UAP has additional constraints that make it more complex than the traditional assignment problem.

Formulation of the Unbalanced Assignment Problem

To formulate the UAP, we start with a matrix that represents the cost or time required to assign each task to each worker. If the matrix is square, we can use the Hungarian algorithm to solve the problem. But when the matrix is not square, we need to add dummy tasks or workers to balance the matrix. These dummy tasks or workers have zero costs and are used to make the matrix square.

Once we have a square matrix, we can apply the Hungarian algorithm to find the optimal assignment. However, we need to be careful in interpreting the results, as the assignment may include dummy tasks or workers that are not actually assigned to anything.

Solutions for the Unbalanced Assignment Problem

Besides the Hungarian algorithm, there are other methods to solve the UAP, such as the transportation algorithm and the auction algorithm. The transportation algorithm is based on transforming the UAP into a transportation problem, which can be solved with the transportation simplex method. The auction algorithm is an iterative method that simulates a bidding process between the tasks and workers to find the optimal assignment.

In summary, the Unbalanced Assignment Problem is a variant of the traditional Assignment Problem in OR that deals with assigning tasks to workers when the number of tasks and workers is not equal. To solve the UAP, we need to balance the matrix by adding dummy tasks or workers and then apply algorithms such as the Hungarian algorithm, the transportation algorithm, or the auction algorithm. Understanding the UAP can help businesses and organizations optimize their resource allocation and improve their operational efficiency.

How useful was this post?

Click on a star to rate it!

Average rating 1 / 5. Vote count: 1

No votes so far! Be the first to rate this post.

We are sorry that this post was not useful for you! 😔

Let us improve this post!

Tell us how we can improve this post?

Operations Research

1 Operations Research-An Overview

• History of O.R.
• Approach, Techniques and Tools
• Phases and Processes of O.R. Study
• Typical Applications of O.R
• Limitations of Operations Research
• Models in Operations Research
• O.R. in real world

2 Linear Programming: Formulation and Graphical Method

• General formulation of Linear Programming Problem
• Optimisation Models
• Basics of Graphic Method
• Important steps to draw graph
• Multiple, Unbounded Solution and Infeasible Problems
• Solving Linear Programming Graphically Using Computer
• Application of Linear Programming in Business and Industry

3 Linear Programming-Simplex Method

• Principle of Simplex Method
• Computational aspect of Simplex Method
• Simplex Method with several Decision Variables
• Two Phase and M-method
• Multiple Solution, Unbounded Solution and Infeasible Problem
• Sensitivity Analysis
• Dual Linear Programming Problem

4 Transportation Problem

• Basic Feasible Solution of a Transportation Problem
• Modified Distribution Method
• Stepping Stone Method
• Unbalanced Transportation Problem
• Degenerate Transportation Problem
• Transhipment Problem
• Maximisation in a Transportation Problem

5 Assignment Problem

• Solution of the Assignment Problem
• Unbalanced Assignment Problem
• Problem with some Infeasible Assignments
• Maximisation in an Assignment Problem
• Crew Assignment Problem

6 Application of Excel Solver to Solve LPP

• Building Excel model for solving LP: An Illustrative Example

7 Goal Programming

• Concepts of goal programming
• Goal programming model formulation
• Graphical method of goal programming
• The simplex method of goal programming
• Using Excel Solver to Solve Goal Programming Models
• Application areas of goal programming

8 Integer Programming

• Some Integer Programming Formulation Techniques
• Binary Representation of General Integer Variables
• Unimodularity
• Cutting Plane Method
• Branch and Bound Method
• Solver Solution

9 Dynamic Programming

• Dynamic Programming Methodology: An Example
• Definitions and Notations
• Dynamic Programming Applications

10 Non-Linear Programming

• Solution of a Non-linear Programming Problem
• Convex and Concave Functions
• Kuhn-Tucker Conditions for Constrained Optimisation
• Quadratic Programming
• Separable Programming
• NLP Models with Solver

11 Introduction to game theory and its Applications

• Important terms in Game Theory
• Saddle points
• Mixed strategies: Games without saddle points
• 2 x n games
• Exploiting an opponent’s mistakes

12 Monte Carlo Simulation

• Reasons for using simulation
• Monte Carlo simulation
• Limitations of simulation
• Steps in the simulation process
• Some practical applications of simulation
• Two typical examples of hand-computed simulation
• Computer simulation

13 Queueing Models

• Characteristics of a queueing model
• Notations and Symbols
• Statistical methods in queueing
• The M/M/I System
• The M/M/C System
• The M/Ek/I System
• Decision problems in queueing

Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research.

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

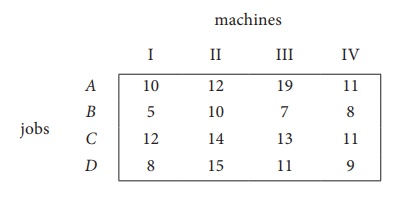
Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

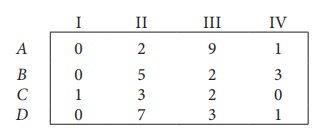
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

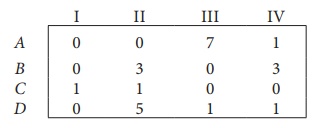
Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

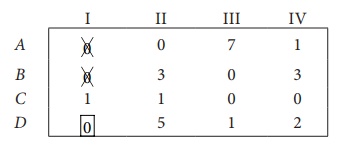
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

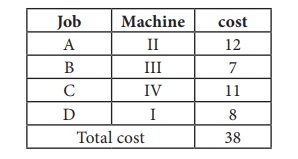
The optimal assignment (minimum) cost

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

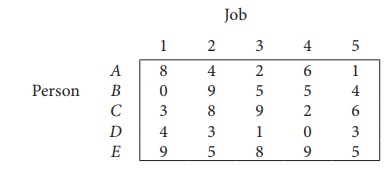
∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

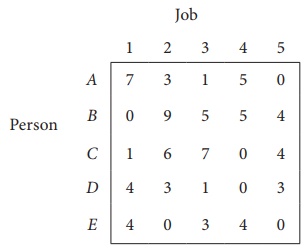
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

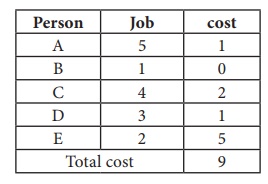
The optimal assignment (minimum) cost = ` 9

Example 10.9

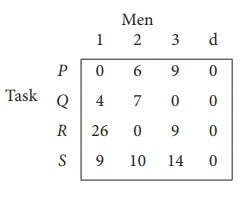
Solve the following assignment problem.

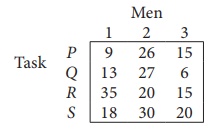
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

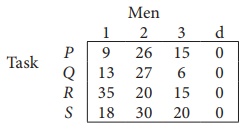
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

Step 3 (Assignment) :

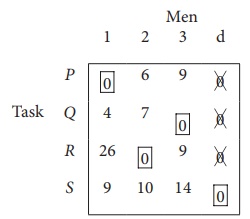
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

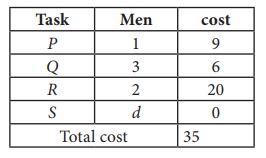
The optimal assignment (minimum) cost = ₹ 35

Related Topics

Privacy Policy , Terms and Conditions , DMCA Policy and Compliant

Copyright © 2018-2024 BrainKart.com; All Rights Reserved. Developed by Therithal info, Chennai.

A Study on the Weapon–Target Assignment Problem Considering Heading Error

• Original Paper
• Open access
• Published: 27 March 2024

Cite this article

You have full access to this open access article

• Ji-Eun Kim 1 ,
• Chang-Hun Lee 2 &
• Mun Yong Yi   ORCID: orcid.org/0000-0003-1784-8983 1  

61 Accesses

Explore all metrics

The focus of this study is to investigate the assignment of weapons to multiple targets in a scenario, specifically when an air defense system is confronted with numerous targets, such as low-altitude rockets or groups of drones. The accuracy of weapons in destroying these targets depends heavily on the correct alignment of the launchers with the targets, which can be affected by errors in launcher orientation. Therefore, in solving weapon–target assignment (WTA) problems, it is crucial to account for the heading errors caused by the launcher’s orientation angle. To address this issue, the use of a rotation strategy to align the orientation angle with the target’s approach direction can significantly improve the probability of kill (PK) against the target. However, its unitary implementation has limitations, which may result in missed engagements if there is insufficient time to rotate to the desired orientation angle. Thus, as a remedy, we propose a new WTA method that combines rotation and rotation fix strategy, improving the weakness of losing the opportunity of engagement due to rotation time and heading errors. The efficacy of this approach is evaluated through numerical simulations.

Similar content being viewed by others

Fast and Simple Method for Weapon Target Assignment in Air Defense Command and Control System

Bi-objective dynamic weapon-target assignment problem with stability measure

Ahmet Silav, Esra Karasakal & Orhan Karasakal

Weapon-Target Assignment and Firing Scheduling for Rapid Engagement with Heterogeneous Interceptors

Hyeon-Woo Park & Han-Lim Choi

Avoid common mistakes on your manuscript.

1 Introduction

Over the past few decades, weapon–target assignment (WTA) has been considered a crucial procedure for providing autonomous decision support in air defense systems [ 1 , 2 ]. The WTA involves determining which interceptors to use and when to launch them to counter identified threats. The WTA problem has been proven to be NP-complete, according to references [ 3 , 4 ]. Consequently, many previous research efforts have focused on tackling the computational complexity of the general WTA problem. Various search methods have been developed over the last few decades, including Lagrangian relaxation [ 5 ], exact and heuristic approaches [ 6 , 7 ], and meta-heuristic algorithms like ant colony optimization [ 8 ], particle swarm optimization [ 9 ], genetic algorithm [ 10 , 11 ], permutation and tabu search [ 12 , 13 ], variable neighborhood search [ 14 ], harmony search [ 15 ], hybrid discrete gray wolf optimization [ 16 ], and greedy maximization algorithm [ 17 , 18 , 19 , 20 ].

The primary objective of WTA, as highlighted in the references [ 21 , 22 , 23 ], is to minimize the potential damage to friendly assets and increase the survivability of identified threat targets. The optimization model for the WTA problem focuses on a single goal, which is to minimize the survival probability of the targets. Moreover, there are additional objectives that can be considered, including optimizing resource usage, minimizing target flight duration, and refining the fire doctrine in defense site zones [ 24 , 25 ]. To address the multi-objective WTA problem, various methods are employed, such as rule-based heuristics, goal programming, and evolutionary algorithms [ 24 , 26 , 27 , 28 ].

There are two main categories of the WTA problem: static WTA (SWTA) and dynamic WTA (DWTA) [ 29 ]. The former, SWTA, assumes that time is not a factor, and therefore subsequent engagements are not taken into consideration. Moreover, it is typically assumed that all weapons have an equal probability of success when targeting each type of enemy. The latter, DWTA, on the other hand, takes into account the available time windows during which targets can be engaged. This approach, proposed by Leboucher et al. [ 30 ], involves calculating the time to impact for each target and identifying the earliest moment at which each weapon can intercept the target. Xin et al. [ 31 ] have proposed a model that allows for variable probabilities of success for each weapon against each target and across different time periods. Khosla [ 32 ] has formulated a mixed integer program to address some of the key considerations in the WTA problem, including the inclusion of additional time constraints such as reload time.

Recent research has highlighted the need for more realistic WTA engagement scenarios [ 30 , 33 , 34 , 35 ], leading to the development of new models that reflect the characteristics of both the interceptors and targets in specific scenarios [ 36 , 37 , 38 , 39 , 40 ]. Cho and Choi [ 18 ] have proposed a time-based WTA problem that considers the interceptor’s firing time in relation to the target’s incoming direction and provides a time-dependent reward for determining the interceptor and its firing time. Leboucher and colleagues [ 30 ] have proposed a two-step approach for solving dynamic WTA problems, where the selection of weapon types and specific weapons occurs in the first step, followed by the determination of a sequence of firing times in the second step. Uhm and Lee [ 41 ] have also proposed a two-step algorithm that uses a time-based probability of success, which is a convex function of the firing time. Bogdanowicz and colleagues [ 37 , 38 ] have developed a novel method for the WTA problem based on the assumption of a fixed probability of success for a given time of engagement. Guo and colleagues [ 39 ] and Na and Lee [ 40 ] have considered factors that can affect the probability of success in a realistic engagement scenario, such as the time-to-go, line-of-sight, and miss distance between the target and interceptor. By incorporating these factors into the problem formulation, the engagement performance of the WTA problem can be improved in a real environment.

In recent years, area targets, such as drone swarms and low-altitude rockets, have emerged as significant threats, leading to an increased demand for air defense systems to counter them [ 42 , 43 , 44 , 45 , 46 ]. Such air defense systems require a large number of interceptors during the engagement, each of which is typically developed using low-cost and small-sized components. Thus, these interceptors have lower maneuverability than other types of interceptors, which can lead to the varying probability of kill (PK) depending on the relative engagement geometry between the target and launcher (i.e., the heading errors between the launcher’s orientation angle and the interceptor’s flight direction). Additionally, Guo et al. [ 39 ] have pointed out that initial heading errors can negatively affect the entire course of action. To overcome this limitation of interceptor countering area targets, WTA methods should consider the degradation of PK due to heading errors. Kim and colleagues [ 46 ] have addressed the aforementioned concerns by developing a model that considers the variation in PK as a function of changes in heading errors. They compared the performance of two strategies: the rotation-fixed (RF) strategy and the rotation (R) strategy, which differ in how they manage the launcher’s orientation angle relative to the target’s approach angle. The RF strategy fixes the orientation angle at a specific value for all engagements, while the R strategy rotates the launcher’s orientation angle to align with the target’s approach angle. The authors analyzed the trade-off between reaction time and PK degradation for each strategy. To achieve a more effective balance between PK degradation and reaction time, they extended the strategies to the clustering-based WTA (CWTA) method, where targets are clustered using a representative point that can potentially be intercepted for each target. The initial orientation angle of each launcher is then determined based on the centroid of each cluster relative to each launcher.

However, the previous study was limited because it used a single strategy, either R or RF, for all engagements without the flexibility to adjust to different engagement situations. More specifically, when the two strategies are properly mixed and used, more optimal results can be obtained by the trade-off between reaction time and PK degradation, depending on engagement situations. Based on this rationale, this study aims to propose a mixed version of R and RF strategies that allows for the selection of either R or RF strategies for each engagement based on the launcher’s orientation angle. This mixed strategy approach provides greater flexibility, allowing for the decision to maintain the current orientation angle or rotate it to some extent when using the R strategy for a particular engagement. Unlike the previous study, where the optimal orientation angle for each engagement was predetermined under the R strategy, the proposed method permits variations in the orientation angle for each engagement. Additionally, the clustering approach from the previous study can still be applied in the mixed version to further reduce the rotation angle. In this study, numerical simulations are performed to investigate the performance of the proposed method. The results will show that the proposed method (i.e., the mixed version of R and RF) is superior to using only R or RF strategies. The main contribution of this study is to establish a new WTA method for the rotation-mixed (M) strategy, which considers the launcher’s orientation angle as a decision variable for each engagement, unlike the prior R and RF strategies. The key feature of the proposed method lies in its simplicity and superiority, suitable for the interception of area targets.

The structure of the paper is as follows: In Sect.  2 , the formulation of the WTA problems is presented, taking into account the mixed version of R and RF strategies. Section  3 describes the proposed WTA algorithm. The effectiveness of the proposed method is demonstrated through numerical simulations in Sect.  4 . Finally, Sect.  6 summarizes the findings and draws conclusions.

2 PK Modeling

The main goal of WTA problems is to achieve the highest possible expected PK for all targets that have been identified. Therefore, when defining the objective function for WTA problems, the focus should be on maximizing the overall PK against targets that pose a threat and are being countered by interceptors. In this study, a three-dimensional (3D) engagement scenario is considered. However, the PK value is determined based on the \(X_I-Y_I\) planar engagement geometry between the launcher and the target, as illustrated in Fig.  1 . This rationale stems from the similarity in the impact of PK value fluctuations resulting from vertical engagement geometry on both R strategy and RF strategy. In contrast, the variations in PK attributed to horizontal engagement geometry significantly influence both R strategy and RF strategy.

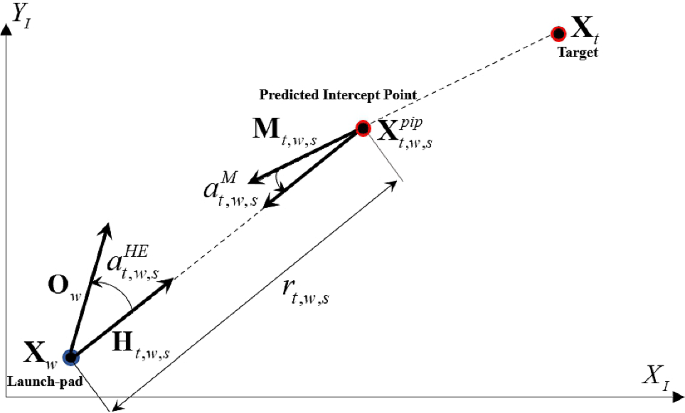
Planar engagement geometry

The PK value is calculated using the three geometric parameters. The first parameter, denoted as \(a^{\textrm{HE}}_{t,w,s}\) , refers to the heading errors between the predicted intercept point (PIP) \(X^{\textrm{pip}}_{t,w,s}\) of the target t at a specific time slot s and the launcher w located at \(X_{w}\) . The second parameter, denoted as \(a^{M}_{t,w,s}\) , represents the predicted intercept angle between the moving direction \(M_{t,w,s}\) of the target at the time of interception and the approaching direction \(H_{t,w,s}\) of the interceptor. Finally, the third parameter is the relative distance \(r_{t,w,s}\) calculated based on the positions of the target and launcher.

More specifically, the heading error is defined as the angle between \(O_{w}\) , which denotes the orientation angle of the launcher w , and \(H_{t,w,s}\) , which indicates the heading angle toward the PIP of the target t , given by:

The PK variation according to a relative distance and heading error, b expected target’s leading angle and heading error

In this context, the PIP refers to the expected location of the interception between the target t and the interceptor launched from the launcher w at a specific time s . In order to compute the PIP, it is essential to ensure that the flight time for the target to reach the PIP is equal to the flight time of the assigned interceptor to reach the PIP, starting from the moment of firing. The predicted intercept angle \(a^{M}_{t,w,s}\) can be determined by calculating the angle between the approaching angle of the target \(M_{t,w,s}\) and the opposite angle of the interceptor’s flight direction \(-H_{t,w,s}\) as follows:

The Euclidean distance between a launcher position \(X_{w}\) and a particular PIP \(X^{\textrm{pip}}_{t,w,s}\) is established as the relative distance between the two points. This relative distance is calculated as follows:

The computation of the expected PK \(P_{t,w,s}\) involves the multiplication of three separate Gaussian functions, denoted as G , which depend on the geometric parameters \(a^{\textrm{HE}}_{t,w,s}\) , \(a^{M}_{t,w,s}\) , and \(r_{t,w,s}\) as follows:

The Gaussian function used in this study is given by

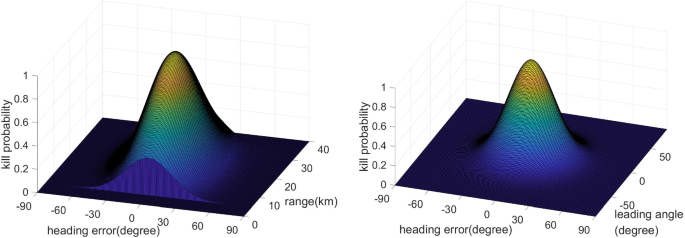
The first term on the right-hand side of Eq. ( 4 ) describes how the PK varies as a result of changes in heading errors. This variation is modeled using a Gaussian function, where \(\mu ^{a_{\textrm{HE}}}\) represents the mean and \(\sigma ^{a_{\textrm{HE}}}\) represents the standard deviation. An increase in heading errors can cause a degradation in the PK, as it requires more maneuverability to intercept the target. The second term in Eq. ( 4 ) represents the PK variation as a function of the expected angle difference between the approach direction of the interceptor and the velocity direction of the target. The mean is represented by \(\mu ^{a_{M}}\) , while the standard deviation is denoted by \(\sigma ^{a_{M}}\) . In Eq. ( 4 ), the third term expresses the PK variation due to changes in relative distance, where \(\mu ^{r}\) represents the mean and \(\sigma ^{r}\) represents the standard deviation. The Gaussian functions for each term have a value ranging from 0 to 1. Accordingly, the overall PK \(P_{t,w,s}\) also has a value ranging from 0 to 1.

Figure  2 illustrates the PK model used in the study, where the design parameters for heading errors, relative distance, and the expected target’s leading angle are specified. The values chosen for the parameters are \(\mu ^{a^{\textrm{HE}}}=0\;\deg \) , \(\sigma ^{a^{\textrm{HE}}}=20\;\deg \) , \(\mu ^{r}=20\;\textrm{km}\) , \(\sigma ^{r}=10\;\textrm{km}\) , \(r^{\max }=35\;\textrm{km}\) , \(r^{\min }=5\;\textrm{km}\) , \(\mu ^{a^{M}}=0\;\deg \) , and \(\sigma ^{a^{M}}=20\;\deg \) , respectively. The PK variation patterns shown in Fig.  2 are adjusted by manipulating a two-factor pair: the expected target’s leading angle versus heading error and relative distance versus heading error. This study presents two figures to illustrate this manipulation. In Fig.  2 a, the PK variation is based on changes in relative distance and heading error, while the PK induced by only an expected target’s leading angle is kept constant at 1. The engagement region is limited to \(r_{t,w,s} > r^{\min }\) and \(r_{t,w,s} < r^{\max }\) in Fig.  2 (a). The PK reaches its maximum at \(r_{t,w,s}=\mu ^{r}\) and \(a^{\textrm{HE}}_{t,w,s}=\mu ^{a^{\textrm{HE}}}\) , and decreases as the relative distance deviates from \(\mu ^{r}\) and heading error deviates from \(\mu ^{a^{\textrm{HE}}}\) . In Fig.  2 b, the PK induced by only a relative distance is fixed at 1, while the PK variation based on changes in the expected target’s leading angle and heading error is shown. The parameter \(\sigma \) (i.e., \(\sigma ^{r}\) , \(\sigma ^{a^{\textrm{HE}}}\) , and \(\sigma ^{a^{M}}\) ) governs the rate at which the PK decreases. As the value of \(\sigma ^{a^{\textrm{HE}}}\) increases, the decreasing rate of the PK due to heading error decreases. When \(\sigma ^{a^{\textrm{HE}}}\rightarrow \infty \) , the effect of PK variation due to heading errors is diminished in the model. The parameter \(\sigma \) is highly related to the interceptor’s maneuverability, and it is meaningful to examine how the PK variation changes with alterations to \(\sigma ^{a^{\textrm{HE}}}\) .

In the comprehensive design of a fire control system, the development of a weapon–target assignment algorithm operates under the premise that a PK model is available. This PK model can either stem from a distinct computation process or be a streamlined version that captures the core attributes of the complete PK model [ 18 , 47 ]. Subsequently, the accurate PK model is determined and integrated with the weapon–target assignment algorithm. In general, the discrepancy in the PK modeling would lead to a decline in the performance of the weapon–target assignment algorithm. Therefore, an exhaustive and quantitative analysis, including sensitivity assessments, becomes imperative. However, this study focuses on the development of the weapon–target assignment algorithm itself. Thus, it is assumed that the consideration of a streamlined PK model that encapsulates the fundamental features of the accurate PK model is sufficient for achieving this purpose in practice, as in the previous studies [ 18 , 47 ].

As shown in Eqs. ( 4 ) and ( 5 ), we employ scaled Gaussian functions with uniform weighting factors to establish the PK model. This choice stems from the fact that constant scale factors within the PK model have no impact on the optimization outcomes when the objective function aims to maximize the aggregate PK value.

3 Problem Formulation

This section describes the formulations of the WTA problem for three strategies: RF, R, and M strategies, using the mixed-integer linear programming (MILP) framework. The formulation proposed by Kim and colleagues focuses on RF strategy and R strategy separately (i.e., unitary strategy), and it cannot be applied by combining RF and R [ 46 ]. A new formulation for the mixed version of the R and RF strategy is proposed in this chapter. It is worth noting that the main difference between the M strategy and the unitary strategies (R and RF) is whether the decision of a launcher’s orientation angle for each engagement is considered as a decision variable.

3.1 Formulation of Unitary Strategy

The WTA problems can be expressed by defining decision variables and constraints, as well as an objective function that takes into account the degradation of PK resulting from changes in heading errors. The constraints in this problem involve the rotation of the orientation angle of a launcher, and the choice between using the R strategy or the RF strategy depends on whether these constraints are taken into account. Under the RF strategy, the orientation angle of each launcher is fixed during engagement to reduce the delay in firing an interceptor against a target. On the other hand, the R strategy involves aligning the orientation angle of each launcher with the heading angle towards the PIP of a target in order to eliminate the heading errors. Thus, the RF strategy has a short reaction time, so it can engage a large number of targets in a given time, but the PK for each engagement is reduced. The R strategy has a relatively large reaction time, so the number of targets that can be engaged in a given time is reduced, but the PK for each engagement is high.

3.1.1 Decision Variable

The primary determinant in the WTA problem is whether a particular launcher w ’s firing time slot s is designated for a specific target t , which serves as the key variable to be decided. This research defines a decision variable, denoted as \(\ominus _{t,w,s}\) , for unitary strategies. The variable \(\ominus _{t,w,s}\) represents the assignment of a launcher w against a target t at firing time slot s . The variable \(\ominus _{t,w,s}\) is 1 if the launcher w is assigned to the target t at time slot s , otherwise 0.

3.1.2 Objective Function

In this context, the objective function is chosen to reflect the PK function that takes into account the factors of heading errors, relative distance, and the expected target’s leading angle, as previously mentioned. The ultimate goal of the WTA problem considered in this study is to maximize the total PK value of all identified targets as follows:

where the function \(p\left( r_{t,w,s}, a^{\textrm{HE}}_{t,w,s}, a^{M}_{t,w,s}\right) \) indicates the probability of successful destruction of target t by the interceptor launched from launcher w .

3.1.3 Practical Constraints for General WTA Problems

Due to the limited availability of interceptors and a limited time window of opportunity to use them against targets, there are restrictions on assigning launchers to targets. In addition, the system has inherent limitations, including the time required for the launcher to prepare for firing an interceptor and the need to stabilize vibrations resulting from the launch. These conditions and limitations are considered as constraints. One of the primary constraints is that each launcher can only fire one interceptor at a time, which means that each designated time slot for a launcher should be assigned to a specific target. This limitation can be expressed as follows:

In this study, it is assumed that the number of interceptors assigned to each launcher is predetermined without considering the reloading process. Furthermore, as the firing process continues, the number of interceptors available for each launcher decreases, which means that the constraint related to the number of available interceptors should be considered in the WTA problem formulation. Accordingly, the limitation pertaining to the overall number of interceptors available for each launcher can be expressed as follows:

where the variable \(n^{st}_{w}\) represents the highest possible quantity of usable interceptors for a launcher denoted by w . “st” of \(n^{st}_{w}\) is an abbreviation for “stock”. Additionally, it is necessary to set a limit on the number of interceptors that can be assigned to a single target. This restriction is in place to avoid wastage of interceptors due to redundant allocations to a single target. This limitation on the total number of interceptors that can be assigned to a target is expressed as follows:

where the variable \(n^{\textrm{as}}_{t}\) represents the upper limit on the number of interceptors assigned to the target t . “as” of \(n^{\textrm{as}}_{t}\) is an abbreviation for “assign”.

In addition to these constraints, real-world engagement systems have additional practical constraints that should be considered. For example, there is a delay between receiving a firing command and the actual firing of the interceptor. A certain amount of time is also required for the launcher to stabilize after each firing. As a result, the constraints related to the time required for the firing process and the delay between subsequent firings can be formulated as follows:

where the parameter \(\tau ^{d}\) stands for the time required between successive firing processes of a launcher. If a weapon w is assigned to target \(t_{1}\) at time slot \(s_{1}\) , then the value of \(\ominus _{t_{1},w,s_{1}}\) is set to 1; otherwise, it is set to 0. Similarly, if a weapon w is assigned to target \(t_{2}\) at time slot \(s_{2}\) , then the value of \(\ominus _{t_{2},w,s_{2}}\) is set to 1; otherwise, it is set to 0. This constraint ensures that \(\ominus _{t_{1},w,s_{1}}\) and \(\ominus _{t_{2},w,s_{2}}\) cannot both be 1 at the same time, preventing any additional assignment from being made within the time required for the launch procedure.

Moreover, the available firing time slot for a launcher-target pair is determined by the flight time required to reach the PIP, which should be within the interceptor’s maneuverability range. Thus, the feasible firing time slot is defined as the time slot corresponding to the PIP within the engagement region, as given by the following constraint.

where the parameter \(L_{t,w}\) represents the collection of launch time slots associated with the region within which an interceptor fired from the launcher w can reach and intercept the target t . Therefore, any time slots of the launcher w , not included in \(L_{t,w}\) , are unavailable for deployment against the target t .

3.1.4 Additional Constraints for Rotation Strategy

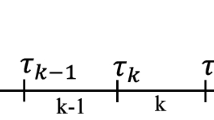
If a WTA problem for the R strategy is considered, it is essential to also take into account time limitations. These include the time needed to rotate an orientation angle of a launcher and the time required to align the launcher and interceptors after the rotation. To calculate the time needed to rotate the launcher’s orientation angle, the required rotation angle and the launcher’s rotational velocity should be considered. The necessary rotation angle for the launcher between two consecutive engagements can be determined using the following equation:

where the variable \(H_{t_{1},w,s_{1}}\) refers to the orientation angle that the launcher w needs to be directed towards the PIP of a specific target \(t_{1}\) at a particular time slot \(s_{1}\) . Similarly, the variable \(H_{t_{2},w,s_{2}}\) represents the orientation angle required for the same launcher w to point towards the PIP of another target \(t_{2}\) at a different time slot \(s_{2}\) . By assuming that the launcher’s rotation speed is constant, we can determine the time required to adjust the orientation angle of the launcher as follows:

where the parameter \(v^{\textrm{rot}}\) represents the angular velocity required to rotate the orientation angle of a launcher, and the variable \(a^{\textrm{rot}}_{w,t{1},s_{1},t_{2},s_{2}}\) represents the extent of the angle that needs to be rotated by the launcher. Additionally, after rotating the orientation angle of a launcher, time to realign internal devices of a launcher is required for the stable fire of the next interceptor. Based on this parameter, the constraint for the required time to rotate the launcher’s orientation angle and stabilize the launcher after rotating can be written as:

where the variable \(\tau ^{\textrm{rot}}_{w,t_{1},s_{1},t_{2},s_{2}}\) denotes the time that the launcher takes to rotate its orientation from the angle \(s_1\) at time \(t_1\) to the angle \(s_2\) at time \(t_2\) . The parameter \(\tau ^{\textrm{align}}\) is a fixed time period required for the launcher to stabilize its orientation following a rotation. In addition, there is a requirement to restrict the range of rotation. To enforce this limitation, the condition that the launcher’s rotation should not exceed the designated angle of rotation can be expressed as follows:

where the variable \(a^{\textrm{ini}}_{w}\) represents the initial orientation angle of launcher w , and the parameter \(a^{\max }\) denotes the maximum allowable range of rotation for the launcher relative to its initial orientation angle.

3.2 Formulation of Mixed Strategy

If a single strategy of either R strategy or RF strategy is applied consistently throughout all engagements, it can impose limitations on its effectiveness. The R strategy aims to eliminate heading errors but incurs a time penalty due to rotation. This approach can yield the maximum predicted PK for each engagement, but it also poses a risk of missing engagement opportunities due to the time lost during rotation. On the other hand, the RF strategy eliminates time loss caused by rotation, but it may result in lower PK due to heading errors. Although this approach may not achieve the maximum predicted PK for all engagements, it eliminates the risk of missed opportunities due to time loss. Moreover, using a single strategy does not resolve the two essential limitations present in both R and RF strategies: the inability to identify the appropriate strategy and select the orientation angle against a target for each engagement.

Consequently, this research paper investigates a new WTA strategy by combining R and RF strategies with orientation angle determination for each engagement. The R strategy determines a rotation angle that aligns with the PIP and only attempts engagement if there is enough time to rotate to the objective angle. However, if there is not enough time, the system may not attempt engagement. To address missed opportunities, incorporating flexibility into the system to engage while maintaining the current angle or rotating within a limited angle range, given the time constraints, could be beneficial. Conversely, the RF strategy maintains a constant orientation angle for all engagements. This implies that even if there is enough time to rotate, the system is unable to choose an alternative to rotate the angle to reduce potential PK loss. In such situations, having flexibility in the system to decide on rotating the angle within specified time constraints could potentially prevent PK loss in some engagements.

To decide whether and how much to rotate the launcher’s orientation angle for each engagement, the decision variable should be changed from \(\ominus _{t,w,s}\) to \(\ominus _{t,w,s,o}\) . However, this modification increases the search space from three to four dimensions, adding the orientation angle as a new variable alongside target, weapon, and time slots. This expansion in search space may result in longer search times and larger input data sizes, making it impractical for real-world air defense systems. To address this issue, we propose a two-level hierarchical formulation of the WTA problem that restricts the increase in search space for a decision variable. Previous studies, including those by Leboucher and colleagues [ 30 ] and Uhm and Lee [ 41 ], have also used a two-level hierarchical structure to solve the WTA problem, particularly when considering PKs that change over time. During the first level of the WTA model, pairs of targets and launchers are chosen while considering time constraints such as firing time windows. The reason why time constraints should be considered in the first level is to prevent the possibility of not being able to engage at the second level due to time constraints such as firing time window and successive launching delay. To account for these constraints, the decision variable \(\ominus _{t,w,s}\) is used. During the second level process, the firing time slot and orientation angle are established for the targets assigned to each launcher. A new decision variable, \(\zeta _{t,s,o}\) , is introduced in the second level to facilitate this process. The decision variable \(\zeta _{t,s,o}\) represents the assignment of time slot s of a certain launcher against a target t at an orientation angle o , and \(\zeta _{t,s,o}\) is 1 if time slot s of a certain launcher against a target t at an orientation angle o ; otherwise 0. The determination of firing time and orientation angle for targets is carried out on a per-launcher basis, meaning that it is performed independently for each launcher. The following formulation is established to address the problem of determining the appropriate firing time and orientation angle for targets assigned to a specific launcher.

The objective function in this context is to obtain the maximum overall PK against assigned targets, similar to that of the first level.

where the variable \(a^{\textrm{HE}}_{t,s,o}\) represents the difference between the orientation angle o of a launcher during the firing time slot s and the approach angle of target t . The variable \(a^{M}_{t,s,o}\) denotes the leading angle of the target. The function \(p\left( r_{t,s,o}, a^{\textrm{HE}}_{t,s,o}, a^{M}_{t,s,o}\right) \) denotes the expected probability of effectively destroying the target t by the interceptor launched during the time slot s with the orientation angle o . It is important to define and take into account limitations related to time, such as the time period for firing and the need to adjust the orientation angle of a launcher. These restrictions should be incorporated into the decision variable \(\zeta _{t,s,o}\) . The constraint specifying that each designated time slot of a launcher can only be assigned to a single target is written as:

where the notation \(\ominus _{t,s,o}\) indicates whether a particular time slot s and orientation angle o have been assigned to a target t . The feasible firing time window for each target is determined as the time slot that corresponds to the PIP within the engagement region, as specified by:

where the parameter \(L_{t}\) represents the set of firing time slots associated with the region in which an interceptor can reach and intercept target t . Thus, any time slots that are not included in \(L_{t}\) are not applicable for deploying against target t . The constraint for successive launches should consider the time required for firing, the time needed to rotate the orientation angle of a launcher, and the assignment of the launcher and interceptors. It can be expressed as:

where the set T represents the assigned targets for a launcher. If the orientation angles \(o_{1}\) and \(o_{2}\) are identical, the RF strategy is chosen. Conversely, if the orientation angles \(o_{1}\) and \(o_{2}\) are different, the R strategy is chosen. The limitation of the range of rotation can be expressed as follows:

Here, the variable \(a^{\textrm{ini}}\) represents the initial orientation angle of a launcher, and the parameter \(a^{\max }\) represents the maximum allowable range of rotation for the launcher relative to its initial orientation angle as described before.

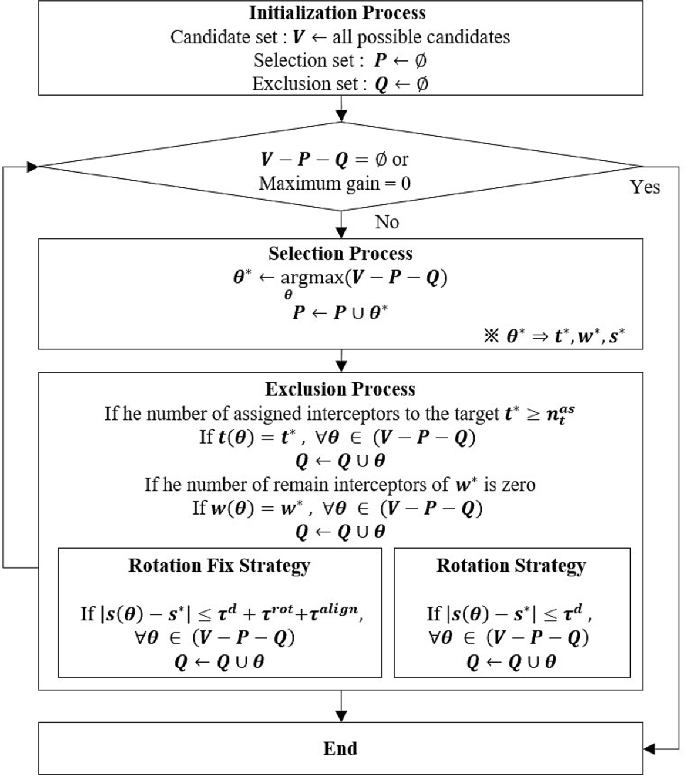
The flow of WTA under unitary strategies

This section delves into two WTA methods: the first one is the unitary strategies developed by Kim et al. (referred to as [ 46 ]), while the second one is a WTA method that combines the R and RF strategies proposed in this study.

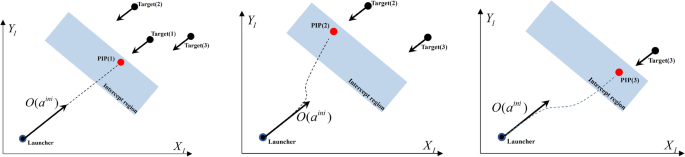
The WTA under RF strategy a first engagement, b second engagement, c third engagement

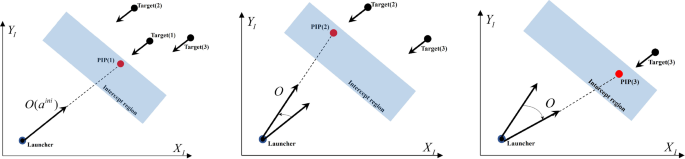
The WTA under R strategy a first engagement, b second engagement, c third engagement

4.1 WTA Under Unitary Strategy

Kim et al. (referenced as [ 46 ]) introduced the RF strategy and R strategy for WTA methods, which utilize the Greedy Maximization (GM) algorithm for efficiency in terms of computation time and performance [ 48 , 49 ]. In the case of WTAs utilizing unitary strategies, a selection and exclusion loop framework is employed, as illustrated in Fig.  3 . The set of candidates ( V ) comprises all possible combinations of targets, weapons, and time slots. During the selection process, a candidate ( \(\ominus ^{*}\) ) is chosen from the candidate set, which maximizes the gain in the candidate set excluding the selection set ( P ) and the exclusion set ( Q ). Once selected, this candidate is added to the selection set. Any candidate that violates constraints due to the inclusion of the new candidate is placed into the exclusion set. This process of selecting and excluding candidates continues until the candidate set (excluding the selection set and the exclusion set) is empty or no further gain can be achieved. In the exclusion phase, the constraints for the stock of selected launchers and the maximum number of interceptors ( \(n_{t}^{\textrm{as}}\) ) for a target within a specific time interval for successive launches are taken into account. Additionally, for the R strategy, the time interval between successive launches includes the time ( \(\tau ^{\textrm{rot}} + \tau ^{\textrm{align}}\) ) required for rotating the orientation angle of a launcher along with the time interval ( \(\tau ^{d}\) ).

Figures  4 and  5 depict sequential engagement strategies used by WTA. Figure  4 employs the RF strategy, which maintains the launcher’s orientation angle at an initial angle of \(a_{\textrm{ini}}\) . To achieve the desired probability of interception and avoid degradation of the PK caused by heading errors, the guided interceptor should have sufficient maneuverability to approach the PIP. The engagement region depicted in Fig.  4 represents the area where the probability of interception satisfies or exceeds a reference value, and the firing window is a constraint that ensures interception occurs within this region. In the case of the RF strategy, where the initial orientation angle is maintained, a significant loss of PK can occur when targets approach from a completely different orientation compared to the initial angle. To mitigate this PK loss, Kim et al. [ 46 ] adjust the initial orientation angle to align with the direction of the target. This adjustment aims to reduce the PK loss, but not necessarily eliminate it entirely.

4.2 WTA Under Mixed Strategy

The flow of CWTA under M strategy

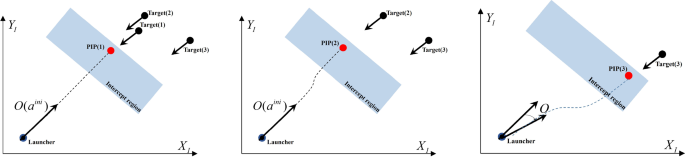
The WTA under the combination of R and RF strategy a first engagement, b second engagement, and c third engagement

The proposed WTA method has been extended to a mixed strategy of RF and R in order to improve upon the unitary strategies of the previous WTA methods. Figure  6 provides an illustration of the process flow for the WTA method under the mixed strategy. This method utilizes the target–launcher assignment results obtained from the WTA method under RF strategy while also implementing an additional procedure in step 1 to determine the initial orientation angle of the launcher based on the target distribution. This step helps to reduce the difference between the launcher’s orientation angle and the target’s approaching angle. In step 2, targets are assigned to each launcher, taking into account time constraints such as the restricted firing time window and delay for successive launches. In step 3, the time slot and orientation angle are determined for each assigned target on an individual launcher basis using the newly proposed Algorithm 1, which builds on the problem formulation presented in Sect.  3 . The constraints relating to the firing window and the time required to rotate the launcher’s orientation angle are inspected to select a feasible solution that satisfies the time limitation. The process of examining these constraints is described in Algorithm 2 in detail.

Sequential engagements from the WTA method under the mixed strategy are illustrated in Fig.  7 . The first engagement is carried out using the RF strategy, which maintains the launcher’s initial orientation angle (i.e., \(a^{\textrm{ini}}\) ). The second engagement is also accomplished using the RF strategy, but a slight loss in PK occurs due to heading errors. The proposed WTA method is capable of selecting R and RF strategies for each engagement. If the R strategy is selected, the extent of rotation is determined to align completely with the PIP or a certain proper angle. The third engagement is computed using the R strategy, but the orientation angle of the launcher rotates close to the completely aligned angle with the PIP. As a result, there is also a slight loss in PK, but the amount of PK loss is less than that of maintaining the initial orientation angle.

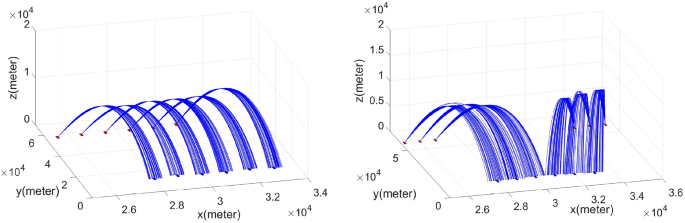
The trajectory demonstration of a scenario 1, b scenario 2

Algorithm 1 outlines the process of determining the appropriate pairs of target, orientation angle, and firing time slot using the greedy maximization assignment algorithm. The algorithm follows a selection and exclusion framework and selects a new solution candidate that achieves the maximum marginal gain \(\bigtriangleup f\left( \ominus | P_{w} \right) \) as shown in (lines 14–18). Feasible pairs within the time slot and target set are considered as long as they are not apart from the limit angle of \(a^{\max }\) (lines 2–13). The algorithm also takes into account constraints for the firing time window and rotation angle limit. The exclusion process described in Algorithm 2 ensures that there is no duplicated assignment of each time slot (lines 20–26) and considers the time delay \(\tau ^{d}\) of successive launch, based on the determined strategy of R and RF (lines 2–19). In the RF strategy, only the delay time for the firing process and stabilization of vibration after launch are considered (lines 7–9), while in the R strategy, the time delay for rotating the orientation angle \(\tau ^{\textrm{rot}}_{o,o^{*}}\) and time for alignment \(\tau ^{\textrm{align}}\) after rotation are also considered along with the delay time for firing (lines 11–13).

5 Simulations

This section examines the simulation results of some scenarios using four different methods, and their performance is evaluated based on the indicators recommended by Kim et al. [ 46 ]. These indicators include overall PK ( \(PK^{overall}\) ), PK loss ( \(PK^{loss}\) ), time loss due to rotation, and missed opportunities for engagement ( \(E^{loss}\) ). Table  1 presents a summary of the four distinct methods: WTA-RF, WTA-R, CWTA-RF, and the proposed CWTA-M. The WTA-RF is a conventional method that does not take heading error into account. The WTA-R method applies the R strategy to nullify heading error. The CWTA-RF method follows the RF strategy but initializes the orientation angle based on the target population. Lastly, the CWTA-M proposed in this paper applies both R and RF strategies depending on the situation.

During the simulation, we investigated defense scenarios against a considerable number of targets concentrated in a confined area, specifically low-altitude rocket threats in 3D space. These multiple targets, representing low-altitude rocket threats, were assumed to follow a ballistic trajectory with speeds ranging from 400 to 500 m/s during their descent phase. Additionally, we considered a situation where there are six enemy launchers, and each launcher sequentially fired 18–45 rocket threats. The minimum firing interval in this simulation was set to 0.5 s. To determine the ground target points for the low-altitude rocket threats, we employed Monte Carlo simulations to randomly select locations within a small region of approximately 9 to 12 km \(^2\) . The trajectories of the enemies are illustrated in Fig.  8 a, b. In Fig.  8 a, the enemy launchers are evenly distributed at regular intervals. In contrast, the scenario depicted in Fig.  8 b involves enemy launchers divided into two groups, attacking a specific region within the defense area. The experiment used parameters that reflect realistic weapon systems, with a defense system’s engagement region limited between \(4\;\textrm{km}\) and \(12\;\textrm{km}\) . The experiment assumed two scenarios, each with 6 launchers and up to 270 targets. The time delay between the launching of each interceptor was set to 0.5 seconds, with an average speed of \(400\;\mathrm{m/s}\) assumed for the interceptor. The launcher’s alignment time after launch, rotational speed, and maximum rotation limit were set to \(\tau ^{\textrm{align}} = 1.5\) seconds, \(v^{\textrm{rot}} = 15\) degrees per second, and \(a^{\max } = 60\) degree, respectively. The experiment evaluated the effectiveness of the engagement using a randomly selected chance factor from the PK model. It is presumed that the defensive system’s area of operation for which an interceptor can intercept a target is limited by a maximum radius of \(12\;\textrm{km}\) and a minimum radius of \(4\;\textrm{km}\) . The mean and standard deviation of the engagement range were set to \(\mu ^{r}=\left( r^{\max }+r^{\min }\right) /2\) and \(\sigma ^{r} = 4\;\textrm{km}\) , respectively.

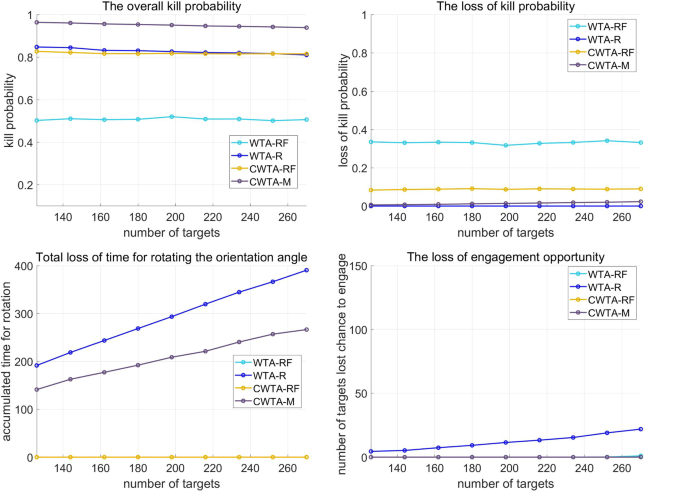
The result of simulation for scenario 1 according to the number of target increase a the overall PK, b the loss of PK, c the loss of time for rotation, and d the loss of engagement opportunity

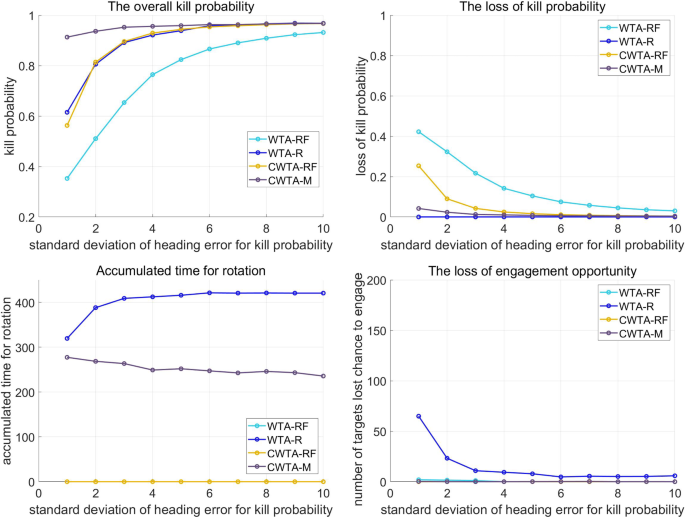
The result of simulation for scenario 1 according to the standard deviation \(\sigma ^{a_{\textrm{HE}}}\) of heading error increase a the overall PK, b the loss of PK, c the loss of time for rotation, and d the loss of engagement opportunity

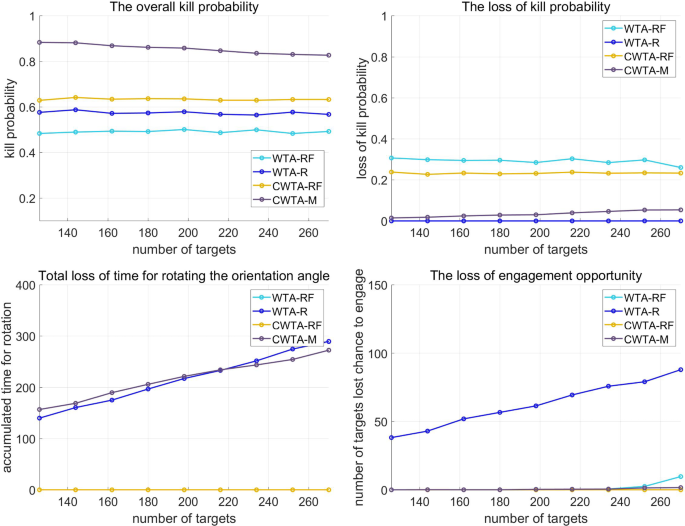
The result of simulation for scenario 2 according to the number of target increase, a the overall PK, b the loss of PK, c the loss of time for rotation, and d the loss of engagement opportunity

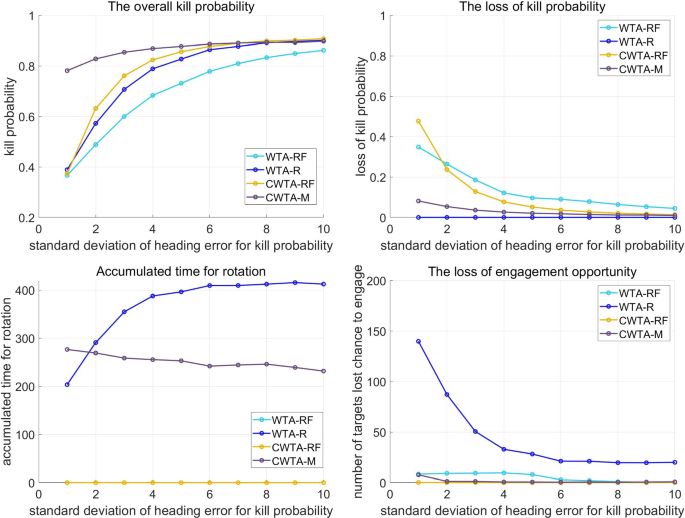
The result of simulation for scenario 2 according to the standard deviation \(\sigma ^{a_{\textrm{HE}}}\) of heading error increase a the overall PK, b the loss of PK, c the loss of time for rotation, and d the loss of engagement opportunity

The results of the simulation in Fig.  9 exhibit an increase in the number of targets in scenario 1. It is evident that WTA-R is inferior to WTA-RF since the latter nullifies the heading error by rotating the orientation angle of a launcher to the PIP direction. Additionally, CWTA-RF surpasses WTA-RF by reducing the heading error by adjusting the initial orientation angle to the region where PIP is formed. However, there are limitations to both WTA-R and CWTA-RF. While WTA-R improves the vulnerability of WTA-RF, it cannot engage certain targets due to the time required for rotating the orientation angles of launchers. Similarly, CWTA-RF cannot use the rotation strategy, even if there is time to apply it for some targets. To address these limitations, CWTA-M combines both R and RF strategies, resulting in the reduction of missed targets compared to WTA-R, as shown in Fig.  9 d. Additionally, CWTA-M further alleviates PK gradation by heading errors compared to CWTA-RF by applying the R strategy for some engagements, as shown in Fig.  9 b. Figure  9 c demonstrates that CWTA-M reduces the rotation time of launchers compared to WTA-R by applying the RF strategy together with the R strategy. Overall, the simulation results reveal that CWTA-M shows the most dominant performance by overcoming the limitations of both WTA-R and CWTA-RF. In Fig.  10 , the simulation results for scenario 1 display a comparison of the performance of the four methods according to the variable \(\sigma ^{{a_{\textrm{HE}}}}\) , which determines the ratio of PK degradation by heading errors in relation to the interceptor’s characteristics.

As shown in Fig.  11 a, CWTA-M outperforms WTA-R and CWTA-RF in scenario 2 simulations. Figure  11 b indicates that CWTA-M mitigates PK degradation due to heading errors compared to CWTA-RF. Additionally, Fig.  11 d shows that CWTA-M has fewer missed targets than CWTA-R. In Fig.  11 c, there is no significant difference in the time required for rotation. However, the results presented in Fig.  11 b, d suggest that the total amount of rotation is not a crucial factor. Instead, the reduction of missed targets and PK degradation due to heading errors can be achieved by selecting an appropriate rotation strategy for each target, determining when and at what angle to rotate. Figure  12 depicts the simulation results for the increasing values of \(\sigma ^{{a_{\textrm{HE}}}}\) in scenario 2. The trend of the results is similar to that observed in scenario 1. With an increase in \(\sigma ^{{a_{\textrm{HE}}}}\) , the PK degradation ratio decreases due to heading errors. Therefore, if \(\sigma ^{{a_{\textrm{HE}}}}\) increases, the results of the four methods become similar. In this study, our focus is on cases where the impact of heading error on PK degradation is significant. Accordingly, the performance of CWTA-M dominates in situations where \(\sigma ^{{a_{\textrm{HE}}}}\) is less than 10. Similarly, as illustrated in Fig.  12 b, d, it is evident that CWTA-M is superior in terms of the number of targets engaged in PK loss caused by heading errors.

To summarize, the R strategy is effective in mitigating PK loss caused by heading errors and improving engagement success rates. However, its unitary implementation has limitations, as it only determines the rotation angle towards the PIP direction, which may result in missed engagements if there is insufficient time to rotate to the objective orientation angle. In such cases, alternative strategies like the RF strategy or determining a rotation angle within the available time constraints could increase engagement success rates. By allowing for the selection of R and RF strategies and determining the rotation angle for each engagement, the limitation of the unitary R strategy was overcome, and the CWTA-M outperformed WTA under the unitary strategy, as demonstrated in the simulation results.

6 Conclusions

The proposed WTA algorithms aim to improve the defense against multiple targets in narrow areas, which is a challenging task due to the limited maneuverability of interceptors. The use of a rotation strategy to align the orientation angle with the target’s approach direction can significantly improve the PK against the target. However, the unitary implementation of the WTA algorithm with a rotation strategy only aligns the orientation angle toward the PIP direction, which may result in missed engagements if there is insufficient time to rotate to the objective orientation angle. To overcome this limitation, the study proposes a mixed version of the strategy that allows for the selection of R and RF strategies and the determination of the rotation angle for each engagement. This approach can reduce PK degradation and reaction time, leading to better performance against multiple targets. The proposed approach involves the inclusion of a step to determine the rotation angle to determine the R and RF strategy, alongside making modifications to the WTA formulation. Numerical simulations were then conducted to evaluate the effectiveness of these methods. Results from the simulations indicate that the proposed methods outperformed the unitary strategy when faced with multiple targets. One of the main advantages of the proposed algorithms is their ability to overcome PK degradation caused by heading errors while also achieving high performance and efficient use of resources through the flexible application of the R and RF strategy to manage the trade-off between PK degradation and reaction time.

In future research, it would be beneficial to identify additional factors and challenges that could be taken into account during a WTA process to aid decision-making for defending against area targets. Such considerations may include avoiding interference between interceptors, accounting for misidentification between debris and actual targets due to collisions, and expanding sensor–weapon–target assignment problems for cooperative engagements. Additionally, WTA simulations should be conducted using various types of area targets and interceptors, along with more realistic and diverse scenarios that incorporate target attack patterns.

Manne AS (1958) A target-assignment problem. Oper Res 6(3):346–351

Article   MathSciNet   Google Scholar  

Roux JN, Van Vuuren JH (2007) Threat evaluation and weapon assignment decision support: a review of the state of the art. ORiON 23(2):151–187

Article   Google Scholar  

Day RH (1966) Allocating weapons to target complexes by means of nonlinear programming. Oper Res 14(6):992–1013

Lloyd SP, Witsenhausen HS (1986) Weapon allocation is NP complete. In: Proc. IEEE Summer Comput. Simul. Conf., Reno, pp 1054–1058

Ni M, Yu Z, Ma F, Wu X (2011) A lagrange relaxation method for solving weapon-target assignment problem. Math Probl Eng 2011:873292. https://doi.org/10.1155/2011/873292

Denbroeder G, Ellison R, Emerling L (1959) On optimum target assignments. Oper Res 7(3):322–326

Ahuja RK, Kumar A, Jha KC, Orlin JB (2007) Exact and heuristic algorithms for the weapon-target assignment problem. Oper Res 55(6):1136–1146

Lee ZJ, Lee CY, Su SF (2002) An immunity-based ant colony optimization algorithm for solving weapon-target assignment problem. Appl Soft Comput 2(1):39–47

Zhou Y, Li X, Wang W (2016) A discrete particle swarm optimization algorithm applied in constrained static weapon-target assignment problem. In: Proc. IEEE 12th World Congr. Intell. Control Automat. (WCICA), pp 3118–3123

Li P, Wu L, Lu F (2009) A mutation-based GA for weapon-target allocation problem subject to spatial constraints. In: International workshop on intelligent systems and applications. IEEE, pp 1–4. https://doi.org/10.1109/IWISA.2009.5072642

Bisht S (2004) Hybrid genetic-simulated annealing algorithm for optimal weapon allocation in multilayer defence scenario. Defence Sci J 54(3):395–405

Blodgett DE, Gendreau M, Guertin F, Potvin J-Y, Seguin R (2003) A tabu search heuristic for resource management in naval warfare. J Heurist 9(2):145–169

Xin B, Chen J, Zhang J, Dou LH, Peng ZH (2010) Efficient decision makings for dynamic weapon-target assignment by virtual permutation and tabu search heuristics. IEEE Trans Syst Man Cybern C 40(6):649–662

Lee MZ (2010) Constrained weapon-target assignment: enhanced very large scale neighborhood search algorithm. IEEE Trans Syst Man Cybern A Syst Hum 40(1):198–204

Chang Y-Z, Li Z-W, Kou Y-X, Sun Q-P, Yang H-Y, Zhao Z-Y et al (2017) A new approach to weapon-target assignment in cooperative air combat. Math Probl Eng 2017

Wang J, Luo P, Hu X, Zhang X (2018) A hybrid discrete grey wolf optimizer to solve weapon target assignment problems. Discrete Dyn Nat Soc 2018:1–17

MathSciNet   Google Scholar  

Wang Z, Wang X, Liang Y, Pan Q (2013) Weapon target assignment leveraging strong submodularity. In: Proc. IEEE Int. Conf. Inf. Autom., Yinchuan, pp 74–79

Cho DH, Choi HL (2017) Greedy maximization for asset-based weapon-target assignment with time-dependent rewards. In: Wang Y (ed) Cooperative control of multi-agent systems: theory and applications. Wiley, New York, pp 115–139

Chapter   Google Scholar  

Jeong H (2020) Hierarchical lazy greedy algorithm for weapon target assignment. J KIMS Technol 23(4):381–388

Xin B, Wang Y, Chen J (2019) An efficient marginal-return-based constructive heuristic to solve the sensor-weapon-target assignment problem. IEEE Trans Syst Man Cybern Syst 49(2):2536–2547

Karasakal O (2008) Air defense missile-target allocation models for a naval task group. Comput Oper Res 35(2):1759–1770

Bogdanowicz ZR (2009) A new efficient algorithm for optimal assignment of smart weapons to targets. Comput Math Appl 58(4):1759–1770

Google Scholar  

Huaiping C, Jingxu L, Yingwu C, Hao W (2006) Survey of the research on dynamic weapon-target assignment problem. J Syst Eng Electron 17(3):559–565

Hocaoglu MF (2019) Weapon target assignment optimization for land based multi-air defense systems: a goal programming approach. Comput Ind Eng 128:681–689

Mekawey HI, El-Wahab MSA, Hashem M (2009) Novel goal-based weapon target assignment doctrine. J Aerosp Comput Inf Comput 6:2–29

Xin B, Chen J, Peng Z, Dou L, Zhang J (2011) An efficient rule-based constructive heuristic to solve dynamic weapon-target assignment problem. IEEE Trans Syst Man Cybern Syst 41:598–606

Zhang K, Zhou D, Yang Z, Pan Q, Kong W (2019) Constrained multi-objective weapon target assignment for area targets by efficient evolutionary algorithm. IEEE Access 7:176339–176360

Gao C, Kou Y, Li Y, Li Z, Xu A (2011) Multi-objective weapon target assignment based on D-NSGA-III-A. IEEE Trans Syst Man Cybern Syst 7:50240–50254

Kline A, Ahner D, Hill R (2019) The weapon-target assignment problem. Comput Oper Res 105:226–236

Leboucher C, Shin H-S, Siarry P, Chelouah R, Le Ménec S, Tsourdos A (2013) A two-step optimisation method for dynamic weapon target assignment problem. In: Recent advances on meta-heuristics and their application to real scenarios, pp 109–129

Xin B, Chen J, Peng ZH, Dou LH, Zhang J (2011) An efficient rule-based constructive heuristic to solve dynamic weapon-target assignment problem. IEEE Trans Syst Man Cybern A Syst Hum 41:598–606

Khosla D (2001) Hybrid genetic approach for the dynamic weapon-target allocation problem. In: Battlespace digitization and network-centric warfare, vol 4396. International Society for Optics and Photonics, pp 244–260 . https://doi.org/10.1117/12.438322

Xin B, Chen J (2012) An estimation of distribution algorithm with efficient constructive repair/improvement operator for the dynamic weapon-target assignment. In: Proc. 31st Chin. Control Conf., Hefei

Park HW, Choi HL (2011) Weapon-target assignment and firing scheduling for rapid engagement with heterogeneous interceptors. ScienceDirect

Bogdanowicz ZR (2012) Advanced input generating algorithm for effect-based weapon-target pairing optimization. IEEE Trans Syst Man Cybern A Syst Hum 42:276–280

Ash M (1959) Letter to the editor-flood’s assignment model for small kill levels. Oper Res 7:258–260

Bogdanowicz ZR, Patel K (2015) Quick collateral damage estimation based on weapons assigned to targets. IEEE Trans Syst Man Cybern Syst 45:762–769

Bogdanowicz ZR, Tolano A, Patel K, Coleman NP (2013) Optimization of weapon-target pairings based on kill probabilities. IEEE Trans Cybern 43:1835–1844

Guo D, Liang Z, Jiang P, Dong X, Li Q, Ren Z (2019) Weapon-target assignment for multi-to-multi interception with grouping constraint. IEEE Access 7:34838–34849

Na H, Lee J (2020) Optimal arrangement of missile defense systems considering kill probability. IEEE Trans Aerosp Electron Syst 56:972–983

Uhm HS, Lee YH (2019) A heuristic algorithm for weapon target assignment and scheduling. Mil Oper Res 24:53–62

Evans RC (2011) National air defense: Challenges, solution profiles, and technology needs. The MITRE Corporation [Online]. http://ww.mitre.org/work/tech-papers/tech-papers-04/04-1108/04-1108.pdf

Missile defense review (2019). Office of the Secretary of Defense, 2019. [Online]. https://www.defense.gov/Portals/1/Interactive/2018/11-2019-Missile-Defense-Review/The

Andrew MAJ, Sanders W, US Army: Drone Swarms (2017) School of Advanced Military Studies. United States Army Command and General Staff College, Fort Leavenworth

Zhang K, Zhou D, Yang Z, Pan Q, Kong W (2017) Constrained multi-objective weapon target assignment for area targets by efficient evolutionary algorithm. IEEE Access 7:173669–176360

Kim JE, Lee CH, Yi MY (2022) New weapon target assignment algorithms for multiple targets using a rotational strategy and clustering approach. IEEE Access 10:43738–43750

Jang J, Yoon HG, Kim JC, Kim CO (2019) Adaptive weapon-to-target assignment model based on the real-time prediction of hit probability. IEEE Access 7:72210–72220

Krause A, Golovin D (2014) Submodular function maximization. In: Bordeaux L (ed) Tractability practical approaches to hard problems. Cambridge University Press, Cambridge, pp 71–104

Feldman M, Harshaw C, Karbasi A (2017) Greed is good: near-optimal submodular maximization via greedy optimization . arXiv preprint arXiv:1704.01652

Download references

Open Access funding enabled and organized by KAIST.

Author information

Authors and affiliations.

Industrial and Systems Engineering, KAIST, Daejeon, 34141, Republic of Korea

Ji-Eun Kim & Mun Yong Yi

Aerospace Engineering, KAIST, Daejeon, 34141, Republic of Korea

Chang-Hun Lee

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Mun Yong Yi .

Ethics declarations

Conflict of interest.

The authors clarify that there is no competing financial or non-financial interests that could have appeared to influence the work reported in this paper.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Kim, JE., Lee, CH. & Yi, M.Y. A Study on the Weapon–Target Assignment Problem Considering Heading Error. Int. J. Aeronaut. Space Sci. (2024). https://doi.org/10.1007/s42405-024-00717-5

Download citation

Received : 29 March 2023

Revised : 22 August 2023

Accepted : 05 February 2024

Published : 27 March 2024

DOI : https://doi.org/10.1007/s42405-024-00717-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Weapon–target assignment
• Heading error
• Air defense system
• Probability of kill
• Find a journal
• Publish with us
• Track your research

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Assignment with Teams of Workers

There are many versions of the assignment problem, which have additional constraints on the workers or tasks. In the next example, six workers are divided into two teams, and each team can perform at most two tasks.

The following sections present a Python program that solves this problem using the CP-SAT or the MIP solver. For a solution using the min cost flow solver, see the section Assignment with teams .

CP-SAT solution

First, let's take a look at the CP-SAT solution to the problem.

Import the libraries

The following code imports the required library.

Define the data

The following code creates the data for the program.

Create the model

The following code creates the model.

Create the variables

The following code creates an array of variables for the problem.

There is one variable for each pair of a worker and task. Note that the workers are numbered 0 - 5 , while the tasks are numbered 0 - 3 , unlike in the original example , in which all nodes had to be numbered differently, as required by the min cost flow solver.

Add the constraints

The following code creates the constraints for the program.

Create the objective

The following code creates the objective function.

The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.

Invoke the solver

The following code invokes the solver and displays the results.

Display the results

Now, we can print the solution.

Here's the output of the program.

The entire program

Here is the entire program.

MIP solution

Next, we describe a solution to this assignment problem using the MIP solver.

Declare the solver

The following code creates the solver.

Here is the output of the program.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-02 UTC.

The Assignment with Audie Cornish

Each week on the assignment, host audie cornish pulls listeners out of their digital echo chambers to hear from the people whose lives intersect with the news cycle. from the sex work economy to the battle over what’s taught in classrooms, no topic is off the table. listen to the assignment every monday and thursday..

• Apple Podcasts

Back to episodes list

When James Carville criticized the “preachy females” at the forefront of Democratic politics, he kicked off a firestorm of outrage and perhaps a little introspection. Did “The Ragin’ Cajun” have a point, however impolitely made? Do Democrats have a problem with men? Especially Black men and other men of color? Jamil Smith is an award-winning writer and the new editor-in-chief of The Emancipator , a nonprofit newsroom run by the Center for Antiracist Research at Boston University, co-founded by Dr. Ibram X. Kendi.

Learn more about your ad choices. Visit podcastchoices.com/adchoices