case study questions on application of derivatives

Andhra Pradesh
Chhattisgarh
West Bengal
Madhya Pradesh
Maharashtra
Jammu & Kashmir
NCERT Books 2022-23
NCERT Solutions
NCERT Notes
NCERT Exemplar Books
NCERT Exemplar Solution
States UT Book
School Kits & Lab Manual
NCERT Books 2021-22
NCERT Books 2020-21
NCERT Book 2019-2020
NCERT Book 2015-2016
RD Sharma Solution
TS Grewal Solution
TR Jain Solution
Selina Solution
Frank Solution
ML Aggarwal Solution
Lakhmir Singh and Manjit Kaur Solution
I.E.Irodov solutions
ICSE - Goyal Brothers Park
ICSE - Dorothy M. Noronhe
Sandeep Garg Textbook Solution
Micheal Vaz Solution
S.S. Krotov Solution
Evergreen Science
KC Sinha Solution
ICSE - ISC Jayanti Sengupta, Oxford
ICSE Focus on History
ICSE GeoGraphy Voyage
ICSE Hindi Solution
ICSE Treasure Trove Solution
Thomas & Finney Solution
SL Loney Solution
SB Mathur Solution
P Bahadur Solution
Narendra Awasthi Solution
MS Chauhan Solution
LA Sena Solution
Integral Calculus Amit Agarwal Solution
IA Maron Solution
Hall & Knight Solution
Errorless Solution
Pradeep's KL Gogia Solution
OP Tandon Solutions
Sample Papers
Previous Year Question Paper
Value Based Questions
CBSE Syllabus
CBSE MCQs PDF
Assertion & Reason
New Revision Notes
Revision Notes
HOTS Question
Marks Wise Question
Toppers Answer Sheets
Exam Paper Aalysis
Concept Map
CBSE Text Book
Additional Practice Questions
Vocational Book
CBSE - Concept
KVS NCERT CBSE Worksheets
Formula Class Wise
Formula Chapter Wise
JEE Crash Course
JEE Previous Year Paper
Important Info
JEE Mock Test
JEE Sample Papers
SRM-JEEE Mock Test
VITEEE Mock Test
BITSAT Mock Test
Manipal Engineering Mock Test
AP EAMCET Previous Year Paper
COMEDK Previous Year Paper
GUJCET Previous Year Paper
KCET Previous Year Paper
KEAM Previous Year Paper
Manipal Previous Year Paper
MHT CET Previous Year Paper
WBJEE Previous Year Paper
AMU Previous Year Paper
TS EAMCET Previous Year Paper
SRM-JEEE Previous Year Paper
VITEEE Previous Year Paper
BITSAT Previous Year Paper
UPSEE Previous Year Paper
CGPET Previous Year Paper
CUSAT Previous Year Paper
AEEE Previous Year Paper
Crash Course
Previous Year Paper
NCERT Based Short Notes
NCERT Based Tests
NEET Sample Paper
Previous Year Papers
Quantitative Aptitude
Numerical Aptitude Data Interpretation
General Knowledge
Mathematics
Agriculture
Accountancy
Business Studies
Political science
Enviromental Studies
Mass Media Communication
Teaching Aptitude
NAVODAYA VIDYALAYA
SAINIK SCHOOL (AISSEE)
Mechanical Engineering
Electrical Engineering
Electronics & Communication Engineering
Civil Engineering
Computer Science Engineering
CBSE Board News
Scholarship Olympiad
School Admissions
Entrance Exams
All Board Updates
Miscellaneous
State Wise Books
Engineering Exam

Case Study on Application Of Derivatives Class 12 Maths PDF

The passage-based questions are commonly known as case study questions. Students looking for Case Study on Application Of Derivatives Class 12 Maths can use this page to download the PDF file.

The case study questions on Application Of Derivatives are based on the CBSE Class 12 Maths Syllabus, and therefore, referring to the Application Of Derivatives case study questions enable students to gain the appropriate knowledge and prepare better for the Class 12 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.

Case Study on Application Of Derivatives Class 12 Maths with Solutions in PDF

Our experts have also kept in mind the challenges students may face while solving the case study on Application Of Derivatives, therefore, they prepared a set of solutions along with the case study questions on Application Of Derivatives.

The case study on Application Of Derivatives Class 12 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Application Of Derivatives case study questions are very easy to grasp from the PDF - download links are given on this page.

Why Solve Application Of Derivatives Case Study Questions on Class 12 Maths?

There are three major reasons why one should solve Application Of Derivatives case study questions on Class 12 Maths - all those major reasons are discussed below:

To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 12 Maths students, therefore, it is important to solve Application Of Derivatives Case study questions as it will help better prepare for the Class 12 board exam preparation.
Develop Problem-Solving Skills: Class 12 Maths Application Of Derivatives case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 12 students develop their problem-solving skills, which are essential for success in any profession rather than Class 12 board exam preparation.
Understand Real-Life Applications: Several Application Of Derivatives Class 12 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Application Of Derivatives as well as real-life implications of those learnings too.

How to Answer Case Study Questions on Application Of Derivatives?

Students can choose their own way to answer Case Study on Application Of Derivatives Class 12 Maths, however, we believe following these three steps would help a lot in answering Class 12 Maths Application Of Derivatives Case Study questions.

Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Application Of Derivatives questions quickly.
Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Application Of Derivatives Class 12 Maths case study questions make sure you are approaching each question in a step-wise manner.

What to Know to Solve Case Study Questions on Class 12 Application Of Derivatives?

A few essential things to know to solve Case Study Questions on Class 12 Application Of Derivatives are -

Basic Formulas of Application Of Derivatives: One of the most important things to know to solve Case Study Questions on Class 12 Application Of Derivatives is to learn about the basic formulas or revise them before solving the case-based questions on Application Of Derivatives.
To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 12 Maths Application Of Derivatives case study questions.
Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.

Where to Find Case Study on Application Of Derivatives Class 12 Maths?

Use Selfstudys.com to find Case Study on Application Of Derivatives Class 12 Maths. For ease, here is a step-wise procedure to download the Application Of Derivatives Case Study for Class 12 Maths in PDF for free of cost.

Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Application Of Derivatives. To help others reach this page let them know these steps:

Open Selfstudys.com on your computer/laptop or Smartphone
Once the website gets loaded, click on the navigation button

Case Study on Application Of Derivatives Class 12 Maths, Maths Case Study on Application Of Derivatives Class 12, Class 12 Maths Case Study on Application Of Derivatives, Application Of Derivatives Case Study for Class 12 Maths, Case Study on Application Of Derivatives Class 12 Maths with Solutions, Application Of Derivatives Case Study Questions, Case Study Questions on Application Of Derivatives, Case Study Questions on Class 12 Application Of Derivatives

Find CBSE from the given menu

Click on Case Study

Choose Class 12
Search Maths and then navigate to the Application Of Derivatives Class 12 Maths Case Study

NCERT Solutions for Class 12 Maths
NCERT Solutions for Class 10 Maths
CBSE Syllabus 2023-24
Social Media Channels
Login Customize Your Notification Preferences

case study questions on application of derivatives

One Last Step...

Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

CBSE Case Study Questions for Class 12 Maths Applications of Derivatives Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions for Class 12 Maths Applications of Derivatives in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams! I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 12 Maths Applications of Derivatives PDF

Checkout our case study questions for other chapters.

Chapter 4 Determinants Case Study Questions
Chapter 5 Continuity and Differentiability Case Study Questions
Chapter 7 Integrals Case Study Questions
Chapter 8 Applications of Integrals Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Comments are closed.

Contact Form

Class 12 Maths: Case Study of Chapter 6 Applications of Derivatives PDF Download

Post author: studyrate
Post published:
Post category: 12 board / Class 12
Post comments: 0 Comments

In Class 12 Boards there will be Case studies and Passage Based Questions will be asked, So practice these types of questions. Study Rate is always there to help you. Free PDF Download of CBSE Class 12 Mathematics Chapter 6 Applications of Derivatives Case Study and Passage Based Questions with Answers were Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Applications of Derivatives to know their preparation level.

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 12 Maths Paper, There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Applications of Derivatives Case Study Questions With answers

Here, we have provided case-based/passage-based questions for Class 12 Mathematics Chapter 6 Applications of Derivatives

Case Study/Passage-Based Questions

(i) To construct a garden using 200 ft of fencing, we need to maximize its

Answer: (b) area

(ii) If x denote the length of side of garden perpendicular to brick wall and y denote the length, of side parallel to brick wall, then find the relation representing total amount of fencing wire.

Answer: (c) y+2x=200

(iii) Area of the garden as a function of x, say A(x), can be represented as

Answer: (c) 200x – 2×2

(iv) Maximum value of A(x) occurs at x equals

Answer: (a) 50 ft

(v) Maximum area of garden will be

Answer: (c) 5000sq.ft

Hope the information shed above regarding Case Study and Passage Based Questions for Class 12 Maths Chapter 6 Applications of Derivatives with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 12 Mathematics Applications of Derivatives Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible. By Team Study Rate

Class 12 physics case study questions chapter 8 electromagnetic waves, class 12 biology case study questions chapter 7 evolution, the tiger king summary class 12 english pdf, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

The Topper Combo Flashcards

Contains the Latest NCERT in just 350 flashcards.
Colourful and Interactive
Summarised Important reactions according to the latest PYQs of NEET(UG) and JEE

No thanks, I’m not interested!

Privacy Policy
Terms and Conditions

Web Stories

Saturday, April 3, 2021

Case study questions chapter 6 class 12 maths application of derivatives cbse board term 1.

Based on the above information answer the following questions:

CASE STUDY 2:

Based on the above information, answer the following questions:

CASE STUDY 3:

2 comments:

Helpful Post.

ThankYou very much. Connect with us on Instagram and YouTube for every minute update.

Please do not enter any spam link in the comment box.

Warning: Do Not Copy!

Blog Archives

Best Books for IIT JEE
Best Colleges Of India
class 10 Case Study Based questions
Class 10 Maths MCQ
Class 11 Maths Case Study Questions
Class 11 Maths MCQ
Class 12 Math Case Study questions
Class 12 Maths MCQ
JEE MAIN MCQ
Maths Strategy JEE
News for Students

Blog Archive

► April (3)
► March (2)
► February (1)
► January (5)
► December (9)
► November (5)
► October (6)
► September (5)
Case Study Questions Class 12 MATHS chapter 9 Dif...
Case Study Questions Class 12 MATHS Chapter 7 Inte...
Case Study Questions chapter 6 Class 12 MATHS Appl...
Case Study Questions Class 12 MATHS Chapter 5 Con...
► March (3)
► October (2)
► September (7)
► August (2)
► July (4)

New QB365-SLMS
NEET Materials
JEE Materials
Banking first yr Materials
TNPSC Materials
DIPLOMA COURSE Materials
5th Standard Materials
12th Standard Materials
11th Standard Materials
10th Standard Materials
9th Standard Materials
8th Standard Materials
7th Standard Materials
6th Standard Materials
12th Standard CBSE Materials
11th Standard CBSE Materials
10th Standard CBSE Materials
9th Standard CBSE Materials
8th Standard CBSE Materials
7th Standard CBSE Materials
6th Standard CBSE Materials
Tamilnadu Stateboard
Scholarship Exams
Scholarships

Class 12th Maths - Application of Derivatives Case Study Questions and Answers 2022 - 2023

By QB365 on 08 Sep, 2022

QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 12 Maths Subject - Application of Derivatives, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.

QB365 - Question Bank Software

Application of derivatives case study questions with answer key.

12th Standard CBSE

Final Semester - June 2015

(ii) Volume of the open box formed by folding up the cutting corner can be expressed as

(iii) The values of x for which \(\begin{equation} \frac{d V}{d x}=0 \end{equation}\) ,are

(iv) Megha is interested in maximising the volume of the box. So, what should be the side of the square to be cut off so that the volume of the box is maximum?

(v) The maximum value of the volume is

(ii) If x denote the length of side of garden perpendicular to brick wall and y denote the length, of side parallel to brick wall, then find the relation representing total amount of fencing wire.

(iii) Area of the garden as a function of x, say A(x), can be represented as

(iv) Maximum value of A(x) occurs at x equals

(v) Maximum area of garden will be

(ii) Revenue R as a function of x can be represented as

(iii) Find the number of days after 1stJuly, when Shyams father attain maximum revenue.

(iv) On which day should Shyam's father harvest the onions to maximise his revenue?

(v) Maximum revenue is equal to

An owner of an electric bi~e rental company have determined that if they charge customers Rs. x per day to rent a bike, where 50 Rs. x Rs. 200, then number of bikes (n), they rent per day can be shown by linear function n(x) = 2000 - 10x. If they charge Rs. 50 per day or less, they will rent all their bikes. If they charge Rs. 200 or more per day, they will not rent any bike. Based on the above information, answer the following questions.

(ii) If R(x) denote the revenue, then maximum value of R(x) occur when x equals

(iii) At x = 260, the revenue collected by the company is

(iv) The number of bikes rented per day, if x = 105 is

(v) Maximum revenue collected by company is

(ii) If x represent the number of apartments which are not rented, then the profit expressed as a function of x is

(iii) If P = 10500, then N =

(iv) If P = 11,000, then the profit is

(ii) The range of x is

(iii) The value of xfor which revenue is maximum, is

(iv) When the revenue is maximum, the price of the ticket is

(v) How any spectators should be present to maximize the revenue?

(ii) The radius that will minimize the cost of the material to manufacture the tin can is

(iii) The height thatt will minimize the cost of the material to manufacture the tin can is

(iv) If the cost of material used to manufacture the tin can is Rs.100/m 2 and \(\sqrt[3]{\frac{1500}{\pi}} \approx 7.8\) then minimum cost is approximately

(v) To minimize the cost of the material used to manufacture the tin can, we need to minimize the

(ii) The relation between a and b is given by

(iii) Area of poster in terms of b is given by

(iv) The value of b, so that area of the poster is minimized, is

(v) The value of a, so that area of the poster is minimized, is

(i) In order to make a least expensive water tank, Nitin need to minimize its

(ii) Total cost of tank as a function of h can' be' represented as

(iii) Range of h is

(iv) Value of h at which c(h) is minimum, is

(v) The cost ofleast expensive tank is

(ii) If sum of the surface areas of box and ball are given to be constant k 2 , then x is equal to

(iii) The radius of the ball, when S is minimum, is

(iv) Relation between length of the box and radius of the ball can be represented as

(v) Minimum value of S is

(ii) If C(x) denote the maintenance cost function, then maximum value of C(x) occur at x =

(iii) The maximum value of C(x) would be

(iv) The number of apartments, that the complex should have in order to minimize the maintenance cost, is

(v) If the minimum maintenance cost is attain, then the maintenance cost for each apartment would be

(ii) If x is the length of the outer rectangle, then area of inner rectangle in terms of x is

(iii) Find the range of x.

(iv) If area of inner rectangle is m~imum, then x is equal to

(v) If area of inner rectangle is maximum, then length and breadth of this rectangle are respectively

(ii) If magazine company increases Rs.500 as annual charges, then R is equal to

(iv) What amount of increase in annual charges will bring maximum revenue?

(ii) The maximum value of x can not be

(iii) The rainimum value of x can not be

(iv) If l(x) denote the combined light intensity, then lex) will be minimum when x =

(v) The darkest spot between the two lights is

(ii) The relation between x and y is

(iii) The outer surface area of tank will be minimum when depth of tank is equal to

(iv) The cost of material will be least when width of tank is equal to

(v) If cost of aluminium sheet is Rs.360/m 2 , then the minimum cost for the construction of tank will be

(ii) Distance (say D) between Arun and Manita will be

(iii) For which real value(s) of x, first derivative of D 2 w.r.t. 'x' will Vanish?

(iv) Find the position of Arun when Manita will hit the paper hall.

(v) The minimum value of D is

(ii) The area (A) of green grass, in terms of x, is given by

(iii) The maximum value of A is

(iv) The value oflength of rectangle, when A is maximum, is

(v) The area of gravelling path is

(ii) The length PQ is

(iii) Let there be a quantity S such that S = Rp 2 + RQ 2 , then S is given by

(iv) Find the value of x for which value of S is minimum.

(v) For minimum value of S, find the value of PR and RQ

(ii) The area (A) of the window can be given by

(iii) Rohan is interested in maximizing the area of the whole window, for this to happen, the value of x should be

(iv) Maximum area of the window is

(v) For maximum value of A, the breadth of rectangular part of the window is

(ii) The area (A) of the rectangular region, as a function of x, can be expressed as

(iii) School's manager is interested in maximising the area of floor 'A' for this to be happen, the value of x should be

(iv) The value of y, for which the area of floor is maximum is

(v) Maximum area of floor is

*****************************************

Application of derivatives case study questions with answer key answer keys.

(i) (b) : Since, side of square is of length 20 cm therefore \(\begin{equation} x \in(0,10) \end{equation}\) . ( ii) (a) : Clearly, height of open box = x cm Length of open box = 20 - 2x and width of open box = 20 - 2x \(\therefore\) Volume (V) of the open box = x x (20 - 2x) x (20 - 2x (iii) (d) : We have, V = x(20 - 2X) 2 \(\begin{equation} \therefore \frac{d V}{d x}=x \cdot 2(20-2 x)(-2)+(20-2 x)^{2} \end{equation}\) = (20 - 2x)( -4x + 20 - 2x) = (20 - 2x)(20 - 6x) Now, \(\begin{equation} \frac{d V}{d x}=0 \Rightarrow 20-2 x=0 \text { or } 20-6 x=0 \end{equation}\) \(\begin{equation} \Rightarrow x=10 \text { or } \frac{10}{3} \end{equation}\) (iv) (c) : We have, V = x(20 - 2X) 2 and \(\begin{equation} \frac{d V}{d x}=(20-2 x)(20-6 x) \end{equation}\) \(\begin{equation} \Rightarrow \frac{d^{2} V}{d x^{2}}=(20-2 x)(-6)+(20-6 x)(-2) \end{equation}\) = (-2)[60 - 6x + 20 - 6x] = (-2)[80 - 12x] = 24x - 160 For \(\begin{equation} x=\frac{10}{3}, \frac{d^{2} V}{d x^{2}}<0 \end{equation}\) and for \(\begin{equation} x=10, \frac{d^{2} V}{d x^{2}}>0 \end{equation}\) So, volume will be maximum when \(\begin{equation} x=\frac{10}{3} \end{equation}\) . (v) (d) : We have, V = x(20 - 2x) 2 ,which will be maximum when \(\begin{equation} x=\frac{10}{3} \end{equation}\) . \(\begin{equation} \therefore \ \text { Maximum volume }=\frac{10}{3}\left(20-2 \times \frac{10}{3}\right)^{2} \end{equation}\) \(\begin{equation} =\frac{10}{3} \times \frac{40}{3} \times \frac{40}{3}=\frac{16000}{27} \mathrm{~cm}^{3} \end{equation}\)

(i) (b) : To create a garden using 200 ft fencing, we need to maximise its area. (ii) (c) : Required relation is given by 2x + y = 200. (iii) (c) : Area of garden as a function of x can be represented as \(A(x)=x \cdot y=x(200-2 x)=200 x-2 x^{2}\) (iv) (a) : \(\begin{equation} A(x)=200 x-2 x^{2} \Rightarrow A^{\prime}(x)=200-4 x \end{equation}\) For the area to be maximum A'(x) = 0 \(\begin{equation} \Rightarrow 200-4 x=0 \Rightarrow x=50 \mathrm{ft} \end{equation}\) (v) (c) : Maximum-area of the garden = 200(50) - 2(50)2 = 10000 - 5000 = 5000 sq. ft

(i) (a) : Let x be the number of extra days after 1 st July. \(\therefore\) Price = Rs.(300 - 3Xx) = Rs.(300 - 3x) Quantity = 80 quintals + x(1 quintal per day) = (80 + x) quintals (ii) (b) : R(x) = Quantity x Price = (80 + x) (300 - 3x) = 24000 - 240x + 300x -3x 2 = 24000 + 60x - 3x 2 (iii) (a) : We have, R(x) = 24000 + 60x - 3x 2 \(\begin{equation} \Rightarrow R^{\prime}(x)=60-6 x \Rightarrow R^{\prime \prime}(x)=-6 \end{equation}\) For R(x) to be maximum, R'(x) = 0 and R"(x) < 0 \(\begin{equation} \Rightarrow 60-6 x=0 \Rightarrow x=10 \end{equation}\) (iv) (a) : Shyams father will attain maximum revenue after 10 days. So, he should harvest the onions after 10 days of 1 st July i.e., on 11 th July. (v) (c) : Maximum revenue is collected by Shyams father when x = 10 \(\therefore\) Maximum revenue = R(10) = 24000 + 60(10) - 3(10)2 = 24000 + 600 - 300 = 24300

(i) (a) : Let x be the charges per bike per day and n be the number of bikes rented per day. R(x) = n x x = (2000 - lOx) x = -10x 2 + 2000x (ii) (b) : We have, R(x) = 2000x - 10x 2 \(\Rightarrow R^{\prime}(x)=2000-20 x\) For R(x) to be maximum or minimum, R'(x) = 0 \(\Rightarrow 2000-20 x=0 \Rightarrow x=100\) Also, \(R^{\prime \prime}(x)=-20<0\) Thus, R(x) is maximum at x = 100 (iii) (c) : If company charge ~ 200 or more, they will not rent any bike. Therefore, revenue collected by him will be zero. (iv) (c) : If x = 105, number of bikes rented per day is given by n = 2000 - 10 x 105 = 950 (v) (d) : At x = 100, R(x) is maximum \(\therefore\) Maximum revenue = R(100) = -10(100) 2 + 2000(100) = Rs. 1,00,000

(i) (c) : If P is the rent price per apartment and N is the number of rented apartment, the profit is given by NP - 500 N = N(P- 500) [ \(\therefore\) Rs. 500/month is the maintenance charges for each occupied unit] (ii) (c) : Now, if x be the number of non-rented apartments, then N= 50 - x and P = 10000 + 250 x Thus, profit = N(P- 500) = (50 - x ) (10000 + 250x - 500 = (50 - x) (9500 + 250 x) = 250(50 - x) (38 + x) (iii) (b) : Clearly, if P = 10500, then \(10500=10000+250 x \Rightarrow x=2 \Rightarrow N=48\) (iv) (a) : Also, if P = 11000, then \(11000=10000+250 x \Rightarrow x=4\) and so profit (v) (b) : We have, P(x) = 250(50 - x) (38 + x) Now, P'(x) = 250[50 - x - (38 + x)] = 250[12 - 2x] For maxima/minima, put P'(x) = 0 \(\Rightarrow 12-2 x=0 \Rightarrow x=6\) Thus, price per apartment is, P = 10000 + 1500 = 11500 Hence, the rent that maximizes the profit is Rs. 11500.

(i) (a) : Let p be the price per ticket and x be the number of tickets sold. Then, revenue function \(R(x)=p \times x=\left(15-\frac{x}{3000}\right) x\) \(=15 x-\frac{x^{2}}{3000}\) (ii) (c) : Since, more than 36000 tickets cannot be sold. So, range of x is [0, 36000]. (iii) (c) : We have, \(R(x)=15 x-\frac{x^{2}}{3000}\) \(\Rightarrow R^{\prime}(x)=15-\frac{x}{1500}\) For maxima/minima, put R'(x) = 0 \(\Rightarrow \quad 15-\frac{x}{1500}=0 \Rightarrow x=22500\) Also, \(R^{\prime \prime}(x)=-\frac{1}{1500}<0\) (iv) (d) : Maximum revenue will be at x = 22500 \(\therefore \text { Price of a ticket }=15-\frac{22500}{3000}=15-7.5=Rs.7.5\) (v) (d) : Number of spectators will be equal to number of tickets sold. \(\therefore\) Required number of spectators = 22500

(i) (d) : Given, r cm is the radius and h cm is the height of required cylindrical can Given that, volume = 3 l= 3000 cm 3 \(\left(\because 1 l=1000 \mathrm{~cm}^{3}\right)\) \(\Rightarrow \pi r^{2} h=3000 \Rightarrow h=\frac{3000}{\pi r^{2}}\) Now, the surface area, as a function of r is given by \(S(r)=2 \pi r^{2}+2 \pi r h=2 \pi r^{2}+2 \pi r\left(\frac{3000}{\pi r^{2}}\right)\) \(=2 \pi r^{2}+\frac{6000}{r}\) (ii) (c) : Now, \(S(r)=2 \pi r^{2}+\frac{6000}{r}\) \(\Rightarrow S^{\prime}(r)=4 \pi r-\frac{6000}{r^{2}}\) To find criti£al points, put S'(r) = 0 \(\Rightarrow \frac{4 \pi r^{3}-6000}{r^{2}}=0\) \(\Rightarrow r^{3}=\frac{6000}{4 \pi} \Rightarrow r=\left(\frac{1500}{\pi}\right)^{1 / 3}\) Also, \(\left.S^{\prime \prime}(r)\right|_{r=} \sqrt[3]{\frac{1500}{\pi}}=4 \pi+\frac{12000 \times \pi}{1500}\) \(=4 \pi+8 \pi=12 \pi>0\) Thus, the critical point is the point of minima. (iii) (b) : The cost of material for the tin can is minimized when \(r=\sqrt[3]{\frac{1500}{\pi}} \mathrm{cm}\) and the height is \(\frac{3000}{\pi\left(\sqrt[3]{\frac{1500}{\pi}}\right)^{2}}=2 \sqrt[3]{\frac{1500}{\pi}} \mathrm{cm} .\) . (iv) (a) : We have,minimum surface area = \(\frac{2 \pi r^{3}+6000}{r}\) . \(=\frac{2 \pi \cdot \frac{1500}{\pi}+6000}{\sqrt[3]{\frac{1500}{\pi}}}=\frac{9000}{7.8}=1153.84 \mathrm{~cm}^{2}\) Cost of 1 m 2 material = Rs.100 \(\therefore \ \text { Cost of } 1 \mathrm{~cm}^{2} \text { material }=Rs. \frac{1}{100}\) \(\therefore \ \text { Minimum cost }=Rs. \frac{1153.84}{100}=Rs. 11.538\) (v) (c) : To minimize the cost we need to minimize the total surface area.

(i) (d) : In order to make least expensive water tank, Nitin need to minimize its cost. (ii) (d) : Let 1ft be the length and h ft be the height of the tank. Since breadth is equal to 5 ft. (Given) \(\therefore\) Two sides will be 5h sq. feet and two sides will be 1h sq. feet. So, the total area of the sides is (10 h + 2 1h)ft 2 Cost of the sides is Rs.10 per sq. foot. So, the cost to build the sides is (10h + 21h) x 10 = Rs.(100h + 20lh) Also, cost of base = (5l) x 20 = Rs. 100 l \(\therefore\) Total cost of the tank in Rs. is given by c = 100 h + 20 I h + 100 l Since, volume of tank = 80ft 3 \(\therefore \quad 5 l h=80 \mathrm{ft}^{3} \quad \therefore l=\frac{80}{5 h}=\frac{16}{h}\) \(\therefore \quad c(h)=100 h+20\left(\frac{16}{h}\right) h+100\left(\frac{16}{h}\right)\) \(=100 h+320+\frac{1600}{h}\) (iii) (b) : Since, all side lengths must be positive \(\therefore \quad h>0\) and \(\frac{16}{h}>0\) Since, \(\frac{16}{h}>0, \text { whenever } h>0\) \(\therefore \text { Range of } h \text { is }(0, \infty)\) (iv) (a) : To minimize cost, \(\frac{d c}{d h}=0\) \(\Rightarrow \quad 100-\frac{1600}{h^{2}}=0\) \(\Rightarrow 100 h^{2}=1600 \Rightarrow h^{2}=16 \Rightarrow h=\pm 4\) \(\Rightarrow h=4\) [ \(\therefore\) height can not be negative] (v) (c) : Cost of least expensive tank is given by \(c(4)=400+320+\frac{1600}{4}\) = 720 + 400 = Rs. 1120

(i) (c) : Let Sbe the sum of volume of parallelopiped and sphere, then \(S=x(2 x)\left(\frac{x}{3}\right)+\frac{4}{3} \pi r^{3}=\frac{2 x^{3}}{3}+\frac{4}{3} \pi r^{3}\) ...(i) (ii) (a) : Since, sum of surface area of box and sphere is given to be constant k 2 . \(\therefore \quad 2\left(x \times 2 x+2 x \times \frac{x}{3}+\frac{x}{3} \times x\right)+4 \pi r^{2}=k^{2}\) \(\Rightarrow 6 x^{2}+4 \pi r^{2}=k^{2}\) \(\Rightarrow x^{2}=\frac{k^{2}-4 \pi r^{2}}{6} \Rightarrow x=\sqrt{\frac{k^{2}-4 \pi r^{2}}{6}}\) ...(2) (iii) (b) : From (1) and (2), we get \(S=\frac{2}{3}\left(\frac{k^{2}-4 \pi r^{2}}{6}\right)^{3 / 2}+\frac{4}{3} \pi r^{3}\) \(=\frac{2}{3 \times 6 \sqrt{6}}\left(k^{2}-4 \pi r^{2}\right)^{3 / 2}+\frac{4}{3} \pi r^{3}\) \(\Rightarrow \quad \frac{d S}{d r}=\frac{1}{9 \sqrt{6}} \frac{3}{2}\left(k^{2}-4 \pi r^{2}\right)^{1 / 2}(-8 \pi r)+4 \pi r^{2}\) \(=4 \pi r\left[r-\frac{1}{3 \sqrt{6}} \sqrt{k^{2}-4 \pi r^{2}}\right]\) For maximum /minimum \(\frac{d S}{d r}=0\) \(\Rightarrow \frac{-4 \pi r}{3 \sqrt{6}} \sqrt{k^{2}-4 \pi r^{2}}=-4 \pi r^{2}\) \(\Rightarrow k^{2}-4 \pi r^{2}=54 r^{2}\) \(\Rightarrow r^{2}=\frac{k^{2}}{54+4 \pi} \Rightarrow r=\sqrt{\frac{k^{2}}{54+4 \pi}}\) ...(3) (iv) (d) : Since, \(x^{2}=\frac{k^{2}-4 \pi r^{2}}{6}=\frac{1}{6}\left[k^{2}-4 \pi\left(\frac{k^{2}}{54+4 \pi}\right)\right]\) [From (2) and (3)] \(=\frac{9 k^{2}}{54+4 \pi}=9\left(\frac{k^{2}}{54+4 \pi}\right)=9 r^{2}=(3 r)^{2}\) \(\Rightarrow x=3 r\) (v) (c) : Minimum value of S is given by \(\frac{2}{3}(3 r)^{3}+\frac{4}{3} \pi r^{3}\) \(=18 r^{3}+\frac{4}{3} \pi r^{3}=\left(18+\frac{4}{3} \pi\right) r^{3}\) \(=\left(18+\frac{4}{3} \pi\right)\left(\frac{k^{2}}{54+4 \pi}\right)^{3 / 2}\) [Using (3)] \(=\frac{1}{3} \frac{k^{3}}{(54+4 \pi)^{1 / 2}}\)

(i) (c) : Let C(x) be the maintenance cost function, then C(x) = 5000000 + 160x - 0.04x 2 (ii) (b) : We have, C(x) = 5000000 + 160x - 0.04x 2 Now, C(x) = 160 - 0.08x For maxima/minima, put C'(x) = 0 \(\Rightarrow\) 160 = 0.08x \(\Rightarrow\) x = 2000 (iii) (b) : Clearly, from the given condition we can see that we only want critical points that are in the interval [0,4500]. Now, we have C(0) = 5000000 C(2000) = 5160000 and C(4500) = 4910000 \(\therefore\) Maximum value of C(x)would be Rs.5160000 (iv) (a) : The complex must have 4500 apartments to minimise the maintenance cost. (v) (a) : The minimum maintenance cost for each apartment woud be Rs.1091.11

(i) (b) : In order to paint in the maximum area, Kyra needs to maximize the area of inner rectangle. (ii) (c) : Let x be the length and y be the breadth of outer rectangle. \(\therefore\) Length of inner rectangle = x - 1 and breadth of inner rectangle = y - 1.5 \(\therefore A(x)=(x-1)(y-1.5)\) \([\because x y=24 \text { (given) }]\) \(=(x-1)\left(\frac{24}{x}-1.5\right)\) (iii) (b) : Dimensions of rectangle (outer/inner) should be positive. \(\therefore \ x-1>0\) and \(\frac{24}{x}-1.5>0\) \(\Rightarrow x>1\) and \(x<16\) (iv) (c) : We have, \(A(x)=(x-1)\left(\frac{24}{x}-1.5\right)\) and \(A^{\prime \prime}(x)=\frac{-48}{x^{3}}\) For A(x) to be maximum or minimum, A'(x) = 0 \(\Rightarrow -1.5+\frac{24}{x^{2}}=0 \Rightarrow x^{2}=16 \Rightarrow x=\pm 4\) \(\therefore \ x=4\) [Since, length can't be negative] Also, \(A^{\prime \prime}(4)=\frac{-48}{4^{3}}<0\) Thus, at x = 4, area is maximum. (v) (a) : If area of inner rectangle is maximum, then Length of inner rectangle = x-1 = 4 - 1 = 3 ft And breadth of inner rectangle = \(y-1.5=\frac{24}{x}-1.5\) \(=\frac{24}{4}-1.5=6-1.5=4.5 \mathrm{ft}\)

(i) (d) : If x be the amount of increase in annual charges, then number of subscriber reduces to 5000 - x. \(\therefore\) Revenue, R(x) = (3000 + x) (5000 - x) \(=15000000+2000 x-x^{2}, 0 (ii) (a) : Clearly, at x = 500 R(500) = 15000000 + 2000(500) - (500) 2 = 15000000 + 1000000 - 250000 = Rs.15750000 (iii) (c) : Since, 15000000 + 2000x - x 2 = 15640000 (Given) \(\Rightarrow x^{2}-2000 x+640000=0\) \(\Rightarrow \quad x^{2}-1600 x-400 x+640000=0\) \(\Rightarrow x(x-1600)-400(x-1600)=0 \Rightarrow x=400,1600\) (iv) (a) : \(\frac{d R}{d x}=2000-2 x\) and \(\frac{d^{2} R}{d x^{2}}=-2<0\) For maximum revenue, \(\frac{d R}{d x}=0 \Rightarrow x=1000\) \(\therefore\) Required amount = Rs. 1000 (v) (b) : Maximum revenue = R(1000) = (3000 + 1000) (5000 - 1000) = 4000 x 4000 = ~ 16000000

(i) (c) : Since, the distance is x feet from the stronger light, therefore the distance from the weaker light will be 600 - x. So, the combined light intensity from both lamp posts is given by \(\frac{1000}{x^{2}}+\frac{125}{(600-x)^{2}}\) . (ii) (c) : Since, the person is in between the lamp posts, therefore x will lie in the interval (0, 600). So, maximum value of x can't be 600. (iii) (a) : Since, \(0 ,therefore minimum value of x can't be 0. (iv) (b) : We have , \(I(x)=\frac{1000}{x^{2}}+\frac{125}{(600-x)^{2}}\) \(\Rightarrow I^{\prime}(x)=\frac{-2000}{x^{3}}+\frac{250}{(600-x)^{3}}\) and \(\Rightarrow I^{\prime \prime}(x)=\frac{6000}{x^{4}}+\frac{750}{(600-x)^{4}}\) For maxima/minima, I'(x) = 0 \(\Rightarrow \frac{2000}{x^{3}}=\frac{250}{(600-x)^{3}} \Rightarrow 8(600-x)^{3}=x^{3}\) Taking cube root on both sides, we get \(2(600-x)=x \Rightarrow 1200=3 x \Rightarrow x=400\) Thus, I(x) is minimum when you are at 400 feet from the strong intensity lamp post. (v) (a) : Since, I(x) is minimum when x = 400 feet,therefore the darkest spot between the two light is at a distance of 400 feet from stronger lamp post, i.e., at a distance of 600 - 400 = 200 feet from the weaker lamp post.

(i) (c) : Length, AB = 2x Breadth, BC = 2y Also, radius, OA = 10 \(\therefore\) AC = 20 In \(\Delta A B C, A B+B C^{2}=A C^{2}\) \(\Rightarrow (2 x)^{2}+(2 y)^{2}=(20)^{2}\) \(\Rightarrow x^{2}+y^{2}=100\) (ii) (b) : Area of green grass = Area of rectangular part \(\therefore \ A=2 x \cdot 2 y\) [ \(\therefore\) Area of rectangle = length x breadth] \(=4 x y=4 x \sqrt{100-x^{2}}\) \(\left[\because x^{2}+y^{2}=100\right]\) (iii) (b) : We have, \(A=4 x \sqrt{100-x^{2}}\) \(\frac{d A}{d x}=\frac{4 x(-2 x)}{2 \sqrt{100-x^{2}}}+\sqrt{100-x^{2}} \cdot 4\) \(=\frac{-4 x^{2}+4\left(100-x^{2}\right)}{\sqrt{100-x^{2}}}\) For maximum value, \(\frac{d A}{d x}=0\) \(\Rightarrow-4 x^{2}+400-4 x^{2}=0\) \(\Rightarrow-8 x^{2}+400=0\) \(\Rightarrow x^{2}=50 \Rightarrow x=5 \sqrt{2}\) At \(x=5 \sqrt{2}\) \(A=4 x \sqrt{100-x^{2}}\) \(=4 \times 5 \sqrt{2} \cdot \sqrt{100-50}=4 \times 5 \sqrt{2} \times 5 \sqrt{2}=200 \mathrm{~m}^{2}\) (iv) (a) : Length of rectangle for which A is maximum \(=2 \times 5 \sqrt{2}=10 \sqrt{2}\) (v) (b) : Area of gravelling path = \(\pi(10)^{2}-200\) \(=100(\pi-2) \mathrm{m}^{2}\)

(i) (b) : Given, perimeter of window = 10 m \(\therefore\) x + y + y + perimeter of semicircle = 10 \(\Rightarrow x+2 y+\pi \frac{x}{2}=10\) (ii) (b) : \(A=x \cdot y+\frac{1}{2} \pi\left(\frac{x}{2}\right)^{2}\) \(=x\left(5-\frac{x}{2}-\frac{\pi x}{4}\right)+\frac{1}{2} \frac{\pi x^{2}}{4}\left[\because \text { From }(\mathrm{i}), y=5-\frac{x}{2}-\frac{\pi x}{4}\right]\) \(=5 x-\frac{x^{2}}{2}-\frac{\pi x^{2}}{4}+\frac{\pi x^{2}}{8}=5 x-\frac{x^{2}}{2}-\frac{\pi x^{2}}{8}\) (iii) (c) : We have, \(A=5 x-\frac{x^{2}}{2}-\frac{\pi x^{2}}{8}\) \(\Rightarrow \quad \frac{d A}{d x}=5-x-\frac{\pi x}{4}\) Now, \(\frac{d A}{d x}=0 \Rightarrow 5=x+\frac{\pi x}{4}\) \(\Rightarrow x(4+\pi)=20 \Rightarrow x=\frac{20}{4+\pi}\) \(\left[\text { Clearly, } \frac{d^{2} A}{d x^{2}}<0 \text { at } x=\frac{20}{4+\pi}\right]\) (iv) (d) : At \(x=\frac{20}{4+\pi}\) \(A=5\left(\frac{20}{4+\pi}\right)-\left(\frac{20}{4+\pi}\right)^{2} \frac{1}{2}-\frac{\pi}{8}\left(\frac{20}{4+\pi}\right)^{2}\) \(=\frac{100}{4+\pi}-\frac{200}{(4+\pi)^{2}}-\frac{50 \pi}{(4+\pi)^{2}}\) \(=\frac{(4+\pi)(100)-200-50 \pi}{(4+\pi)^{2}}=\frac{400+100 \pi-200-50 \pi}{(4+\pi)^{2}}\) \(=\frac{200+50 \pi}{(4+\pi)^{2}}=\frac{50(4+\pi)}{(4+\pi)^{2}}=\frac{50}{4+\pi}\) (v) (a) : We have, \(y=5-\frac{x}{2}-\frac{\pi x}{4}=5-x\left(\frac{1}{2}+\frac{\pi}{4}\right)\) \(=5-x\left(\frac{2+\pi}{4}\right)=5-\left(\frac{20}{4+\pi}\right)\left(\frac{2+\pi}{4}\right)\) \(=5-5 \frac{(2+\pi)}{4+\pi}=\frac{20+5 \pi-10-5 \pi}{4+\pi}=\frac{10}{4+\pi}\)

(i) (c) : Perimeter of floor = 2(length + breadth) \(\Rightarrow P=2(x+y)\) (ii) (c) : Area, A = length x breadth \(\Rightarrow A=x y\) Since, P = 2(x + y) \(\Rightarrow \frac{P-2 x}{2}=y\) \(\therefore \quad A=x\left(\frac{P-2 x}{2}\right) \Rightarrow A=\frac{P x-2 x^{2}}{2}\) (iii) (d) : We have, \(A=\frac{1}{2}\left(P x-2 x^{2}\right)\) \(\frac{d A}{d x}=\frac{1}{2}(P-4 x)=0\) \(\Rightarrow P-4 x=0 \Rightarrow x=\frac{P}{4}\) Clearly, at \(x=\frac{P}{4}, \frac{d^{2} A}{d x^{2}}=-2<0\) \(\therefore\) Area is maximum at \(x=\frac{P}{4}\) (iv) (c) : We have , \(y=\frac{P-2 x}{2}=\frac{P}{2}-\frac{P}{4}=\frac{P}{4}\) (v) (a) : We have, \(A=x y=\frac{P}{4} \cdot \frac{P}{4}=\frac{P^{2}}{16}\)

Related 12th Standard CBSE Maths Materials

12th standard cbse syllabus & materials, cbse 12th physics wave optics chapter case study question with answers, cbse 12th physics ray optics and optical instruments chapter case study question with answers, cbse 12th physics nuclei chapter case study question with answers, cbse 12th physics moving charges and magnetism chapter case study question with answers, cbse 12th physics electromagnetic induction chapter case study question with answers, cbse 12th physics atoms chapter case study question with answers, 12th physics alternating current chapter case study question with answers cbse, 12th chemistry the d and f block elements chapter case study question with answers cbse, 12th chemistry haloalkanes and haloarenes chapter case study question with answers cbse, 12th chemistry coordination compounds chapter case study question with answers cbse, 12th chemistry chemical kinetics chapter case study question with answers cbse, 12th chemistry biomolecules chapter case study question with answers cbse, 12th chemistry amines chapter case study question with answers cbse, 12th aldehydes ketones and carboxylic acids chapter case study question with answers cbse, 12th chemistry alcohols phenols and ethers chapter case study question with answers cbse.

Class VI to XII

Tn state board / cbse, 3000+ q&a's per subject, score high marks.

12th Standard CBSE Study Materials

12th Standard CBSE Subjects

Class 12 CBSE A.O.D ML AGGARWAL Case Study

Please select, case-study-1 a political party placed an order to a screen printer for the printing of party's slogan on a rectangular cloth sheets. a margin of 2.5 cm along length and 1 cm along width of cloth was left. the pictorial view of the slogan in shown below: if the total area of cloth is 640 cm2, based on the above information, answer the following questions: (i) the length and the breadth (in cm) of the rectangular part on which the slogan is printed respectively are (a)x-2.5, y-1 (b) x-5,y-2 (c) x-2,y-5 (d) x-5,y-1 (ii) the relation between x and y is (a) (x-2.5)(y-1)=640 (b) (x-5)(y-2)=640 (c) xy=640 (d) (x-2)(y-5)= (iii) area 'a' of cloth on which slogan matter was written is given by (a) 650-2x-3200/x (b) 650+2x+ 3200/x (c) 600-2x-3200/x (d) 600 +2x + 3200/x (iv) what is the value of x for which the printing area is maximum (a) 16 cm (b) 40 cm (c) 14 cm (d) 11 cm (v) what is the value of 'a' when printing of slogan is done on maximum area (a) 640 cm² (b) 418 cm² (c) 490 cm² (d) none of these.

Case-study-2 Saloni has a piece of tin rectangular in shape as shown in the diagram given below. She is going to cut squares from each corners and fold up the sides to form an open box. Based on the above information, answer the following questions: (i) If x is the side of square cut off from each corner of the sheet, then what is the length of open box? (a) 45-x (b) 45-2x (c) 45 +2x (d) none of these (ii) What is width of open box? (a) 24-x (b) 24+ x (c) 24-2x (d) none of these (iii) Volume 'V' of open box is given by (a) V = (45-x)(24-x) x (b) V=(45+x)(24+x) x (c) V=(45+2x) (24+2x) x (d) V=(45-2x)(24-2x) x (iv) What should be the side of square to be cut off so that the volume of box is maximum? (a) 18 cm (b) 5 cm (c) both (a) and (b) (d) none of these (v) The maximum value of V (in cm³) is (a) 5400 (b) 4200 (c) 3600 (d) 2450

Case-study-3 A company is planning to launch a new product and decides to pack the new product in closed right circular cylindrical cans of volume 432 πcm³. The cans are to be made from tin sheet. The company tried different options. Based on the above information, answer the following questions: (i) If 7 cm is the radius of the base of the cylinder and h cm is height, then (a) rh=216 (b) r(r+h)=216 (c) rh² = 432 (d) r 2 h=432 (ii) If S cm² is the surface area of the closed cylindrical can, then (a) S= 2π (r 2 +432/r) (b) S= π (r 2 +864/r) (c) S= π (r 2 +432/r) (d) S= 432π/r (iii) For S to be minimum r is equal to (a) 3 cm (b) 6 cm (c) 8 cm (d) 12 cm (iv) Minimum surface area of cylindrical can is (a) 54 πcm 2 (b) 108 πcm² (c) 216 πcm² (d) none of these (v) The relation between the radius and the height of cylindrical area is (a) height is equal to radius of base (b) height is equal to twice the radius of base (c) radius is equal to twice the height (d) radius is two-third of the height.

Case-study-4 A factory owner wants to construct a tank with rectangular base and rectangular sides, open at the top, so that its depth is 2 m and capacity is 8 m³. The building of the tank costs ₹250 per square metre for the base and ₹180 per square metre for the sides. Based on the above information, answer the following questions: (i) If the length and the breadth of the rectangular base of the tank are x metres and mimiy metres respectively, then the relation between x and y is (a)x+y=4 (b) xy=4 (c) xy=8 (d) xy+x+y=4 (ii) The cost of construction of the sides of the tank is (a) ₹180 (x+y) (b) ₹360 (x+y) (c) ₹720 (x + y) (d) ₹1120 (x+y) (iii) If C (in ₹) is the cost of construction of the tank, then C as a function of x is (d) C= 1120 + 720 (x+4/x) (b) C=720+1120 (x+4/x) (c) C=1120+360 (x+4/x) (d) C=1120+180 (x+4/x) (iv) The cost of construction of the tank is least when the value of x is (a) 1 (b) 3 /2 (c) 2 (d) 3 (v) The least cost of construction of the tank is (a) ₹2000 (b) ₹3000 (c)₹3600 (d) ₹4000

Case-study-5 A carpenter has a wire of length 28 m. He wants to cut into two pieces, one of the two pieces is to be made into a square and other into a circle. Based on the above information, answer the following questions: (i)If x metres wire is used in making a square, then what is the expression of combined area A? (ii) What is the length of radius for minimum combined area? (a) 28/π+4 (b) 112/π+4 (c) 14/π+4 (d) none of these (iii) What is the length of circular part? (a) 28/π+4 (b) 14/π+4 (c) 14π/π+4 (d) 28π/π+4 (iv) What is the length of square part? (a) 112/π+4 (b) 112π/π+4 (c) 14π/π+4 (d) 28/π+4 (v) The minimum combined area of square and circle is (a) 196/π+4 m 2 (b) 196/(π+4) 2 m 2 (c) 196/π-4 m 2 (d) none of these

Case-study-6 A firm has the cost function C(x)=x 3 /3-7x 2 + 111x +50 and demand function x = 100-p. Based on the above information, answer the following questions: (i) The total revenue function is (a) R(x) = x²-100x (b) R(x) = 100x-x 2 (c) R(x) = 100-x (d) none of these (ii) The total profit function is (a)-x 3 /3 +6x²-11x-50 (b)-x 3 /3-6x²-11x+50 (c)x 3 /3+6x²-11x+50 (d) -x 3 /3-6x²-11x+50 (iii) The value of x for which profit is maximum is (a) 8 (b) 9 (c) 10 (d) 11 (iv) The maximum profit is (a) ₹133.11 (b) ₹113.31 (c) ₹111.33 (d) ₹133.11 (b) The marginal revenue when x = 10 units is (a) 900 (b) 80 (c) 90 (d) 800

Case-study-7 The average cost function associated with producing and marketing x units of an item is given by 50 AC=2x-11 + 50/x Based on the above information, answer the following questions: (i) The total cost function is (a) C(x)=2x²-11x+50 (b) C(x)=2- 50/x 2 (c) C(x)=2x- 50/x (d) C(x)=2x²+11x-50 (ii) The marginal cost function is (a) MC=4x+ 11 (b) MC=4x-11 (c) MC = 2 + 50/x 2 (d) MC= 100/x 3 (iii) The marginal cost when x = 4 units is (a) ₹5 (b) ₹27 (c) ₹18 (d) ₹13 (iv) The range of values of x for which AC is increasing is (a) x (b) x>-5 (c) x (d) x>5 (v) The range of values of x for which total cost is decreasing is (a) x ≤ 11/4 (b) x ≥ 11/4 (c) x (d) x>-11/4

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 12 Maths Chapter 6 Application of Derivatives

Last modified on: 1 year ago
Reading Time: 6 Minutes

[PDF] Download Case Study Questions for Class 12 Maths Chapter 6 Application of Derivatives

Here we are providing case study questions for class 12 maths. In this article, we are sharing Class 12 Maths Chapter 6 Application of Derivatives case study questions. All case study questions of class 12 maths are solved so that students can check their solutions after attempting questions.

Case Study Questions for Class 12 Maths

Case study questions are a type of question that is commonly used in academic and professional settings to evaluate a person’s ability to analyze, interpret, and solve problems based on a given scenario or case study.

Typically, a case study question presents a real-world situation or problem that requires the individual to apply their knowledge and skills to identify the issues, consider various solutions, and recommend a course of action.

Case study questions are designed to test critical thinking skills, problem-solving abilities, and the capacity to work through complex and ambiguous situations.

Preparing for case study questions involves developing a deep understanding of the subject matter, being able to analyze and synthesize information quickly, and being able to communicate ideas clearly and effectively.

Importance of Solving Case Study Questions for Class 12 Maths

Solving case study questions for Class 12 Maths is extremely important as it provides students with an opportunity to apply the mathematical concepts they have learned to real-world scenarios. These questions present a situation or problem that requires students to use their problem-solving skills and critical thinking abilities to arrive at a solution.

The importance of solving case study questions for Class 12 Maths can be summarized as follows:

Enhances problem-solving skills: Case study questions challenge students to think beyond textbook examples and apply their knowledge to real-world situations. This enhances their problem-solving skills and helps them develop a deeper understanding of the mathematical concepts.
Improves critical thinking abilities: Case study questions require students to analyze and evaluate information, and draw conclusions based on their understanding of the situation. This helps them develop their critical thinking abilities, which are essential for success in many areas of life.
Helps in retaining concepts: Solving case study questions helps students retain the concepts they have learned for a longer period of time. This is because they are more likely to remember the concepts when they have applied them to a real-world situation.
Better preparation for exams: Many competitive exams, including the Class 12 Maths board exam, contain case study questions. Solving these questions helps students become familiar with the format of the questions and the skills required to solve them, which can improve their performance in exams.

In conclusion, solving case study questions for Class 12 Maths is important as it helps students develop problem-solving and critical thinking skills, retain concepts better, and prepare for exams.

Category lists (all posts).

All categories of this website are listed below with number of posts in each category for better navigation. Visitors can click on a particular category to see all posts related to that category.

Full Form (1)
Biography of Scientists (1)
Assertion Reason Questions in Biology (37)
Case Study Questions for Class 12 Biology (14)
DPP Biology for NEET (12)
Blog Posts (35)
Career Guidance (1)
Assertion Reason Questions for Class 10 Maths (14)
Case Study Questions for Class 10 Maths (15)
Extra Questions for Class 10 Maths (12)
Maths Formulas for Class 10 (1)
MCQ Questions for Class 10 Maths (15)
NCERT Solutions for Class 10 Maths (4)
Quick Revision Notes for Class 10 Maths (14)
Assertion Reason Questions for Class 10 Science (16)
Case Study Questions for Class 10 Science (14)
Evergreen Science Book Solutions for Class 10 (17)
Extra Questions for Class 10 Science (23)
HOTS for Class 10 Science (17)
Important Questions for Class 10 Science (10)
Lakhmir Singh Class 10 Biology Solutions (4)
Lakhmir Singh Class 10 Chemistry Solutions (5)
Lakhmir Singh Class 10 Physics Solutions (5)
MCQ Questions for Class 10 Science (20)
NCERT Exemplar Solutions for Class 10 Science (16)
NCERT Solutions for Class 10 Science (15)
Quick Revision Notes for Class 10 Science (4)
Study Notes for Class 10 Science (17)
Assertion Reason Questions for Class 10 Social Science (14)
Case Study Questions for Class 10 Social Science (24)
MCQ Questions for Class 10 Social Science (3)
Topicwise Notes for Class 10 Social Science (4)
CBSE CLASS 11 (1)
Assertion Reason Questions for Class 11 Chemistry (14)
Case Study Questions for Class 11 Chemistry (11)
Free Assignments for Class 11 Chemistry (1)
MCQ Questions for Class 11 Chemistry (8)
Very Short Answer Questions for Class 11 Chemistry (7)
Assertion Reason Questions for Class 11 Entrepreneurship (8)
Important Questions for CBSE Class 11 Entrepreneurship (1)
Assertion Reason Questions for Class 11 Geography (24)
Case Study Questions for Class 11 Geography (24)
Assertion Reason Questions for Class 11 History (12)
Case Study Questions for Class 11 History (12)
Assertion and Reason Questions for Class 11 Maths (16)
Case Study Questions for Class 11 Maths (16)
Formulas for Class 11 Maths (6)
MCQ Questions for Class 11 Maths (17)
NCERT Solutions for Class 11 Maths (8)
Case Study Questions for Class 11 Physical Education (11)
Assertion Reason Questions for Class 11 Physics (15)
Case Study Questions for Class 11 Physics (12)
Class 11 Physics Study Notes (5)
Concept Based Notes for Class 11 Physics (2)
Conceptual Questions for Class 11 Physics (10)
Derivations for Class 11 Physics (3)
Extra Questions for Class 11 Physics (13)
MCQ Questions for Class 11 Physics (16)
NCERT Solutions for Class 11 Physics (16)
Numerical Problems for Class 11 Physics (4)
Physics Formulas for Class 11 (7)
Revision Notes for Class 11 Physics (11)
Very Short Answer Questions for Class 11 Physics (11)
Assertion Reason Questions for Class 11 Political Science (20)
Case Study Questions for Class 11 Political Science (20)
CBSE CLASS 12 (8)
Extra Questions for Class 12 Biology (14)
MCQ Questions for Class 12 Biology (13)
Case Studies for CBSE Class 12 Business Studies (13)
MCQ Questions for Class 12 Business Studies (1)
Revision Notes for Class 12 Business Studies (10)
Assertion Reason Questions for Class 12 Chemistry (15)
Case Study Based Questions for Class 12 Chemistry (14)
Extra Questions for Class 12 Chemistry (5)
Important Questions for Class 12 Chemistry (15)
MCQ Questions for Class 12 Chemistry (8)
NCERT Solutions for Class 12 Chemistry (16)
Revision Notes for Class 12 Chemistry (7)
Assertion Reason Questions for Class 12 Economics (9)
Case Study Questions for Class 12 Economics (9)
MCQ Questions for Class 12 Economics (1)
MCQ Questions for Class 12 English (2)
Assertion Reason Questions for Class 12 Entrepreneurship (7)
Case Study Questions for Class 12 Entrepreneurship (7)
Case Study Questions for Class 12 Geography (18)
Assertion Reason Questions for Class 12 History (8)
Case Study Questions for Class 12 History (13)
Assertion Reason Questions for Class 12 Informatics Practices (13)
Case Study Questions for Class 12 Informatics Practices (11)
MCQ Questions for Class 12 Informatics Practices (5)
Assertion and Reason Questions for Class 12 Maths (14)
Case Study Questions for Class 12 Maths (13)
Maths Formulas for Class 12 (5)
MCQ Questions for Class 12 Maths (14)
Problems Based on Class 12 Maths (1)
RD Sharma Solutions for Class 12 Maths (1)
Assertion Reason Questions for Class 12 Physical Education (11)
Case Study Questions for Class 12 Physical Education (11)
MCQ Questions for Class 12 Physical Education (10)
Assertion Reason Questions for Class 12 Physics (16)
Case Study Based Questions for Class 12 Physics (14)
Class 12 Physics Conceptual Questions (16)
Class 12 Physics Discussion Questions (1)
Class 12 Physics Latest Updates (2)
Derivations for Class 12 Physics (8)
Extra Questions for Class 12 Physics (4)
Important Questions for Class 12 Physics (8)
MCQ Questions for Class 12 Physics (14)
NCERT Solutions for Class 12 Physics (18)
Numerical Problems Based on Class 12 Physics (16)
Physics Class 12 Viva Questions (1)
Revision Notes for Class 12 Physics (7)
Assertion Reason Questions for Class 12 Political Science (16)
Case Study Questions for Class 12 Political Science (16)
Notes for Class 12 Political Science (1)
Assertion Reason Questions for Class 6 Maths (13)
Case Study Questions for Class 6 Maths (13)
Extra Questions for Class 6 Maths (1)
Worksheets for Class 6 Maths (1)
Assertion Reason Questions for Class 6 Science (16)
Case Study Questions for Class 6 Science (16)
Extra Questions for Class 6 Science (1)
MCQ Questions for Class 6 Science (9)
Assertion Reason Questions for Class 6 Social Science (1)
Case Study Questions for Class 6 Social Science (26)
NCERT Exemplar for Class 7 Maths (13)
NCERT Exemplar for Class 7 Science (19)
NCERT Exemplar Solutions for Class 7 Maths (12)
NCERT Exemplar Solutions for Class 7 Science (18)
NCERT Notes for Class 7 Science (18)
Assertion Reason Questions for Class 7 Maths (14)
Case Study Questions for Class 7 Maths (14)
Extra Questions for Class 7 Maths (5)
Assertion Reason Questions for Class 7 Science (18)
Case Study Questions for Class 7 Science (17)
Extra Questions for Class 7 Science (19)
Assertion Reason Questions for Class 7 Social Science (1)
Case Study Questions for Class 7 Social Science (30)
Assertion Reason Questions for Class 8 Maths (7)
Case Study Questions for Class 8 Maths (17)
Extra Questions for Class 8 Maths (1)
MCQ Questions for Class 8 Maths (6)
Assertion Reason Questions for Class 8 Science (16)
Case Study Questions for Class 8 Science (11)
Extra Questions for Class 8 Science (2)
MCQ Questions for Class 8 Science (4)
Numerical Problems for Class 8 Science (1)
Revision Notes for Class 8 Science (11)
Assertion Reason Questions for Class 8 Social Science (27)
Case Study Questions for Class 8 Social Science (23)
CBSE Class 9 English Beehive Notes and Summary (2)
Assertion Reason Questions for Class 9 Maths (14)
Case Study Questions for Class 9 Maths (14)
MCQ Questions for Class 9 Maths (11)
NCERT Notes for Class 9 Maths (6)
NCERT Solutions for Class 9 Maths (12)
Revision Notes for Class 9 Maths (3)
Study Notes for Class 9 Maths (10)
Assertion Reason Questions for Class 9 Science (16)
Case Study Questions for Class 9 Science (15)
Evergreen Science Book Solutions for Class 9 (15)
Extra Questions for Class 9 Science (22)
MCQ Questions for Class 9 Science (11)
NCERT Solutions for Class 9 Science (15)
Revision Notes for Class 9 Science (1)
Study Notes for Class 9 Science (15)
Topic wise MCQ Questions for Class 9 Science (2)
Topicwise Questions and Answers for Class 9 Science (15)
Assertion Reason Questions for Class 9 Social Science (15)
Case Study Questions for Class 9 Social Science (19)
CHEMISTRY (8)
Chemistry Articles (2)
Daily Practice Problems (DPP) (3)
Books for CBSE Class 9 (1)
Books for ICSE Class 10 (3)
Editable Study Materials (8)
Exam Special for CBSE Class 10 (3)
H. C. Verma (Concepts of Physics) (13)
Study Materials for ICSE Class 10 Biology (14)
Extra Questions for ICSE Class 10 Chemistry (1)
Study Materials for ICSE Class 10 Chemistry (5)
Study Materials for ICSE Class 10 Maths (16)
Important Questions for ICSE Class 10 Physics (13)
MCQ Questions for ICSE Class 10 Physics (4)
Study Materials for ICSE Class 10 Physics (8)
Study Materials for ICSE Class 9 Maths (7)
Study Materials for ICSE Class 9 Physics (10)
Topicwise Problems for IIT Foundation Mathematics (4)
Challenging Physics Problems for JEE Advanced (2)
Topicwise Problems for JEE Physics (1)
DPP for JEE Main (1)
Integer Type Questions for JEE Main (1)
Integer Type Questions for JEE Chemistry (6)
Chapterwise Questions for JEE Main Physics (1)
Integer Type Questions for JEE Main Physics (8)
Physics Revision Notes for JEE Main (4)
JEE Mock Test Physics (1)
JEE Study Material (1)
JEE/NEET Physics (6)
CBSE Syllabus (1)
Maths Articles (2)
NCERT Books for Class 12 Physics (1)
NEET Chemistry (13)
Important Questions for NEET Physics (17)
Topicwise DPP for NEET Physics (5)
Topicwise MCQs for NEET Physics (32)
NTSE MAT Questions (1)
Physics (1)
Alternating Current (1)
Electrostatics (6)
Fluid Mechanics (2)
PowerPoint Presentations (13)
Previous Years Question Paper (3)
Products for CBSE Class 10 (15)
Products for CBSE Class 11 (10)
Products for CBSE Class 12 (6)
Products for CBSE Class 6 (2)
Products for CBSE Class 7 (5)
Products for CBSE Class 8 (1)
Products for CBSE Class 9 (3)
Products for Commerce (3)
Products for Foundation Courses (2)
Products for JEE Main & Advanced (10)
Products for NEET (6)
Products for ICSE Class 6 (1)
Electrostatic Potential and Capacitance (1)
Topic Wise Study Notes (Physics) (2)
Topicwise MCQs for Physics (2)
Uncategorized (138)

Test series for students preparing for Engineering & Medical Entrance Exams are available. We also provide test series for School Level Exams. Tests for students studying in CBSE, ICSE or any state board are available here. Just click on the link and start test.

Download CBSE Books

Exam Special Series:

Sample Question Paper for CBSE Class 10 Science (for 2024)
Sample Question Paper for CBSE Class 10 Maths (for 2024)
CBSE Most Repeated Questions for Class 10 Science Board Exams
CBSE Important Diagram Based Questions Class 10 Physics Board Exams
CBSE Important Numericals Class 10 Physics Board Exams
CBSE Practical Based Questions for Class 10 Science Board Exams
CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
Sample Question Papers for CBSE Class 12 Physics (for 2024)
Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
Sample Question Papers for CBSE Class 12 Maths (for 2024)
Sample Question Papers for CBSE Class 12 Biology (for 2024)
CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
Master Organic Conversions CBSE Class 12 Chemistry Board Exams
CBSE Important Numericals Class 12 Physics Board Exams
CBSE Important Definitions Class 12 Physics Board Exams
CBSE Important Laws & Principles Class 12 Physics Board Exams
10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
ICSE Important Functions and Locations Based Questions Class 10 Biology
ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Discover more from Gurukul of Excellence

Subscribe now to keep reading and get access to the full archive.

Type your email…

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 7: Applications of derivatives

About this unit.

Differential calculus is all about instantaneous rate of change. Let's see how the tools we've developed are applied in order to solve real-world word problems.

Rates of change in applied contexts

Applied rate of change: forgetfulness (Opens a modal)
Analyzing problems involving rates of change in applied contexts (Opens a modal)
Marginal cost & differential calculus (Opens a modal)
Rates of change in other applied contexts (non-motion problems) Get 3 of 4 questions to level up!

Related rates intro

Related rates intro (Opens a modal)
Analyzing problems involving related rates (Opens a modal)
Analyzing related rates problems: expressions (Opens a modal)
Analyzing related rates problems: equations (Pythagoras) (Opens a modal)
Analyzing related rates problems: equations (trig) (Opens a modal)
Analyzing related rates problems: expressions Get 3 of 4 questions to level up!
Analyzing related rates problems: equations Get 3 of 4 questions to level up!

Optimization

Optimization: sum of squares (Opens a modal)
Optimization: box volume (Part 1) (Opens a modal)
Optimization: box volume (Part 2) (Opens a modal)
Optimization: profit (Opens a modal)
Optimization: cost of materials (Opens a modal)
Optimization: area of triangle & square (Part 1) (Opens a modal)
Optimization: area of triangle & square (Part 2) (Opens a modal)
Optimization problem: extreme normaline to y=x² (Opens a modal)
Optimization Get 3 of 4 questions to level up!

Motion problems

Motion problems: when a particle is speeding up (Opens a modal)
Motion problems: finding the maximum acceleration (Opens a modal)
Motion problems (differential calc) Get 3 of 4 questions to level up!

Class 6 Maths
Class 6 Science
Class 6 Social Science
Class 6 English
Class 7 Maths
Class 7 Science
Class 7 Social Science
Class 7 English
Class 8 Maths
Class 8 Science
Class 8 Social Science
Class 8 English
Class 9 Maths
Class 9 Science
Class 9 Social Science
Class 9 English
Class 10 Maths
Class 10 Science
Class 10 Social Science
Class 10 English
Class 11 Maths
Class 11 Computer Science (Python)
Class 11 English
Class 12 Maths
Class 12 English
Class 12 Economics
Class 12 Accountancy
Class 12 Physics
Class 12 Chemistry
Class 12 Biology
Class 12 Computer Science (Python)
Class 12 Physical Education
GST and Accounting Course
Excel Course
Tally Course
Finance and CMA Data Course
Payroll Course

Interesting

Learn English
Learn Excel
Learn Tally
Learn GST (Goods and Services Tax)
Learn Accounting and Finance
GST Tax Invoice Format
Accounts Tax Practical
Tally Ledger List
GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

You are learning...

Chapter 6 Class 12 Application of Derivatives

Click on any of the links below to start learning from Teachoo ...

Learn Chapter 6 Application of Derivatives (AOD) of Class 12 free with solutions of all NCERT Questions for Maths Boards

We learned Derivatives in the last chapter, in Chapter 5 Class 12. In this Chapter we will learn the applications of those derivatives.

The topics in the chapter include

Finding rate of change
Checking if a function is increasing or decreasing in an interval
Checking if a function is increasing or decreasing in whole domain
Finding if function is strictly increasing or decreasing in an interval
Finding equation (and slope) of tangent and normal using derivatives
Finding approximate value of numbers and functions
Finding minimum and maximum values from graph of a function
Definition of - Maxima, Minima, Absolute Maxima, Absolute Minima, Point of Inflexion
Finding local maxima, local minima using first derivative test
Finding local maxima, local minima using second derivative test
Finding maximum and minimum values in closed interval ( Finding Absolute Maxima and Absolute Minima )
Statement questions of maxima and minima where we form equations and solve

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.

myCBSEguide

Mathematics
Class 12 Maths Case...

Class 12 Maths Case Study Questions

Table of Contents

myCBSEguide App

Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.

Class 12 Maths question paper will have 1-2 Case Study Questions. These questions will carry 5 MCQs and students will attempt any four of them. As all of these are only MCQs, it is easy to score good marks with a little practice. Class 12 Maths Case Study Questions are available on the myCBSEguide App and Student Dashboard .

Why Case Studies in CBSE Syllabus?

CBSE has introduced case study questions in the CBSE curriculum recently. The purpose was to make students ready to face real-life challenges with the knowledge acquired in their classrooms. It means, there was a need to connect theories with practicals. Whatsoever the students are learning, they must know how to apply it in their day-to-day life. That’s why CBSE is emphasizing case studies and competency-based education .

Case Study Questions in Maths

Let’s have a look over the class 12 Mathematics sample question paper issued by CBSE, New Delhi. Question numbers 17 and 18 are case study questions.

Focus on concepts

If you go through each MCQ there, you will find that the theme/case study is common but the questions are based on different concepts related to the theme. It means, that if you have done ample practice on the various concepts, you can solve all these MCQs in minutes.

Easy Questions with a Practical Approach

The difficulty level of the questions is average or say easy in some cases. On the other hand, you get four options to choose from. So, you get two levels of support to get full marks with very little effort.

Practice Questions Regularly

Most of the time we feel that it’s easy and neglect it. But in the end, we have to pay for this negligence. This may happen here too. Although it’s easy to score good marks on the case study questions if you don’t practice such questions, you may lose your marks. So, we suggest students should practice at least 30-40 such questions before writing the board exam.

12 Maths Case-Based Questions

We are giving you some examples of case study questions here. We have arranged hundreds of such questions chapter-wise on the myCBSEguide App. It is the complete guide for CBSE students. You can download the myCBSEguide App and get more case study questions there.

Case Study Question – 1

A is a diagonal matrix
A is a scalar matrix
A is a zero matrix
A is a square matrix
If A and B are two matrices such that AB = B and BA = A, then B 2 is equal to

Case Study Question – 2

4(x 3 – 24x 2 + 144x)
4(x 3 – 34x 2 + 244x)
x 3 – 24x 2 + 144x
4x 3 – 24x 2 + 144x
Local maxima at x = c 1
Local minima at x = c 1
Neither maxima nor minima at x = c 1
None of these

Case Study Questions Matrices -1

Answer Key:

Case Study Questions Matrices – 2

Read the case study carefully and answer any four out of the following questions: Once a mathematics teacher drew a triangle ABC on the blackboard. Now he asked Jose,” If I increase AB by 11 cm and decrease the side BC by 11 cm, then what type of triangle it would be?” Jose said, “It will become an equilateral triangle.”

Again teacher asked Suraj,” If I multiply the side AB by 4 then what will be the relation of this with side AC?” Suraj said it will be 10 cm more than the three times AC.

Find the sides of the triangle using the matrix method and answer the following questions:

(a) 3 × 3

Case Study Questions Determinants – 01

DETERMINANTS: A determinant is a square array of numbers (written within a pair of vertical lines) that represents a certain sum of products. We can solve a system of equations using determinants, but it becomes very tedious for large systems. We will only do 2 × 2 and 3 × 3 systems using determinants. Using the properties of determinants solve the problem given below and answer the questions that follow:

Three shopkeepers Ram Lal, Shyam Lal, and Ghansham are using polythene bags, handmade bags (prepared by prisoners), and newspaper envelopes as carrying bags. It is found that the shopkeepers Ram Lal, Shyam Lal, and Ghansham are using (20,30,40), (30,40,20), and (40,20,30) polythene bags, handmade bags, and newspapers envelopes respectively. The shopkeeper’s Ram Lal, Shyam Lal, and Ghansham spent ₹250, ₹270, and ₹200 on these carry bags respectively.

(b) Shyam Lal
(a) Ram Lal

Case Study Questions Determinants – 02

Case study questions application of derivatives.

R(x) = -x 2 + 200x + 150000
R(x) = x 2 – 200x – 140000
R(x) = 200x 2 + x + 150000
R(x) = -x 2 + 100 x + 100000
R'(x) > 0
R'(x) < 0
R”(x) = 0
(a) -x 2 + 200x + 150000
(a) R'(x) = 0
(c) 257, -63

Case Study Questions Vector Algebra

tan−1⁡(5/12)
tan−1⁡(12/3)
(b) 130 m/s
(a) tan−1⁡(5/12)
(b) 170 m/s

12 Maths Exam pattern

Question Paper Design of CBSE class 12 maths is as below. It clearly shows that 20% weightage will be given to HOTS questions. Whereas 55% of questions will be easy to solve.

No. chapter-wise weightage. Care to be taken to cover all the chapters
Suitable internal variations may be made for generating various templates keeping the overall weightage to different forms of questions and typology of questions the same.

Choice(s): There will be no overall choice in the question paper. However, 33% of internal choices will be given in all the sections

12 Maths Prescribed Books

Mathematics Part I – Textbook for Class XII, NCERT Publication
Mathematics Part II – Textbook for Class XII, NCERT Publication
Mathematics Exemplar Problem for Class XII, Published by NCERT
Mathematics Lab Manual class XII, published by NCERT

Test Generator

Create question paper PDF and online tests with your own name & logo in minutes.

Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes

CBSE Reduced Syllabus Class 10 (2020-21)
CBSE Class 10 Maths Sample Paper 2020-21
Case Study Class 10 Maths Questions
Competency Based Learning in CBSE Schools
Class 11 Physical Education Case Study Questions
Class 11 Sociology Case Study Questions
Class 12 Applied Mathematics Case Study Questions
Class 11 Applied Mathematics Case Study Questions

1 thought on “Class 12 Maths Case Study Questions”

plz provide solutions too

Save my name, email, and website in this browser for the next time I comment.

The Site is down as we are performing important server maintenance, during which time the server will be unavailable for approximately 24 hours. Please hold off on any critical actions until we are finished. As always your feedback is appreciated.

Study Packages
NCERT Solutions
Sample Papers
Online Test

Questions Bank
Mathematics
Applications of Derivatives
Test Series
Ncert Solutions
Solved Papers
Current Affairs
JEE Main & Advanced
Pre-Primary
MP State Exams
UP State Exams
Rajasthan State Exams
Jharkhand State Exams
Chhattisgarh State Exams
Bihar State Exams
Haryana State Exams
Gujarat State Exams
MH State Exams
Himachal State Exams
Delhi State Exams
Uttarakhand State Exams
Punjab State Exams
J&K State Exams

12th Class Mathematics Applications of Derivatives Question Bank

Done case based (mcqs) - derivatives total questions - 40.

A) 1 done clear

B) -1 done clear

C) 0 done clear

D) 2 done clear

question_answer 2) L.H.D. of \[f\left( x \right)\] at \[x=1\] is

question_answer 3) \[f\left( x \right)\] is non-differentiable at

A) x = 1 done clear

B) x = 2 done clear

C) x = 3 done clear

D) x = 4 done clear

question_answer 4) Find the value of\[f'\left( 2 \right)\]

B) 2 done clear

C) 3 done clear

D) -1 done clear

question_answer 5) The value of f''(-1) is

A) 2 done clear

B) 1 done clear

C) -2 done clear

A) \[\frac{1}{\sqrt{2}}\] done clear

B) \[\sqrt{2}\] done clear

C) 1 done clear

D) 0 done clear

question_answer 7) The derivative of \[{{\sin }^{-1}}\left( \frac{2x}{1+{{x}^{2}}} \right)\]with respect to \[{{\cos }^{-1}}\left( \frac{1-{{x}^{2}}}{1+{{x}^{2}}} \right)\] is

A) - 1 done clear

C) 2 done clear

D) 4 done clear

question_answer 8) The derivative of \[{{e}^{{{x}^{3}}}}\]with respect to log x is

A) \[{{e}^{{{x}^{3}}}}\] done clear

B) \[3{{x}^{2}}\,2{{e}^{{{x}^{3}}}}\] done clear

C) \[3{{x}^{3}}{{e}^{{{x}^{3}}}}\] done clear

D) \[3{{x}^{2}}{{e}^{{{x}^{3}}}}+3x\] done clear

question_answer 9) The derivative of \[{{\cos }^{-1}}\left( 2x-1 \right)\]w.r.t. \[{{\cos }^{-1}}x\]is

B) \[\frac{-1}{2\sqrt{1-{{x}^{2}}}}\] done clear

C) \[\frac{2}{x}\] done clear

D) \[1-{{x}^{2}}\] done clear

question_answer 10) If \[y=\frac{1}{4}\,{{u}^{4}}\] and \[u=\frac{2}{3}\,{{x}^{3}}+5\], then \[\frac{dy}{dx}=\]

A) \[\frac{2}{27}{{x}^{2}}{{\left( 2{{x}^{3}}+15 \right)}^{3}}\] done clear

B) \[\frac{2}{27}{{x}^{2}}{{\left( 2{{x}^{3}}+15 \right)}^{3}}\] done clear

C) \[\frac{2}{27}x{{\left( 2{{x}^{3}}+5 \right)}^{3}}\] done clear

D) \[\frac{2}{27}{{\left( 2{{x}^{3}}+15 \right)}^{3}}\] done clear

question_answer 12) \[\frac{d}{dx}\left\{ gof\left( x \right) \right\}=\]

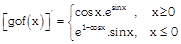
question_answer 13) R.H.D. of \[gof\left( x \right)\]at x = 0 is

A) 0 done clear

C) -1 done clear

question_answer 14) L.H.D. of \[gof\left( x \right)\]at x = 0 is

C) - 1 done clear

question_answer 15) The value of \[f'\left( x \right)\]at \[x=\frac{\pi }{4}\] is

A) 1/9 done clear

B) \[1/\sqrt{2}\] done clear

C) 1/2 done clear

D) not defined done clear

A) \[f\left( x \right)\] is differentiable and continuous done clear

B) \[f\left( x \right)\] is neither continuous nor differentiable done clear

C) \[f\left( x \right)\] is continuous but not differentiable done clear

D) none of these done clear

question_answer 17) If \[f\left( x \right)=\left| x-1 \right|,\,\,x\in R\], then at x=1

A) \[f\left( x \right)\]is not continuous done clear

B) \[f\left( x \right)\] is continuous but not differentiable done clear

C) \[f\left( x \right)\] is continuous and differentiable done clear

question_answer 18) \[f\left( x \right)={{x}^{3}}\] is

A) continuous but not differentiable at x = 3 done clear

B) continuous and differentiable at x = 3 done clear

C) neither continuous nor differentiable at x = 3 done clear

question_answer 19) If \[f\left( x \right)=\left[ sin\text{ }x \right]\], then which of the following is true?

A) \[f\left( x \right)\]is continuous and differentiable at x = 0. done clear

B) \[f\left( x \right)\]is discontinuous at x = 0 done clear

C) \[f\left( x \right)\]is discontinuous at x = 0 but not differentiable. done clear

D) \[f\left( x \right)\] is differentiable but not continuous at \[x=\pi /2\]. done clear

question_answer 20) If\[f\left( x \right)={{\sin }^{-1}}x,\,-1\,\le \,x\,\le \,\,1\], then

A) \[f\left( x \right)\] is both continuous and differentiable done clear

B) \[f\left( x \right)\] is neither continuous nor differentiable. done clear

C) \[f\left( x \right)\] is continuous but not differentiable. done clear

D) None of these. done clear

question_answer 22) If \[u={{x}^{2}}+{{y}^{2}}\] and \[x=s+3t\], \[y=2s-t\], then \[\frac{{{d}^{2}}u}{d{{s}^{2}}}\] is equal to

A) 12 done clear

B) 32 done clear

C) 36 done clear

D) 10 done clear

question_answer 23) \[f\left( x \right)=2\,\,\log \,\,\sin \,x\], then \[f''\left( x \right)\] is equal to

A) \[2\,\,\cos e{{c}^{3}}\,x\] done clear

B) \[2\,{{\cot }^{2}}x-4{{x}^{2}}\,\cos e{{c}^{2}}\,{{x}^{2}}\] done clear

C) \[2x\,\cot \,{{x}^{2}}\] done clear

D) \[-2\,\cos e{{c}^{2}}\,x\] done clear

question_answer 24) If \[f\left( x \right)={{e}^{x}}\,\sin \,x\], then \[f'''\left( x \right)=\]

A) \[2{{e}^{x}}\left( \sin \,x+\cos \,x \right)\] done clear

B) \[2{{e}^{x}}\left( \cos x-\sin x \right)\] done clear

C) \[2{{e}^{x}}\left( \sin \,x-\cos \,x \right)\] done clear

D) \[2{{e}^{x}}\,\cos x\] done clear

question_answer 25) If \[{{y}^{2}}=a{{x}^{2}}+bx+c\], then \[\frac{d}{dx}\left( {{y}^{3}}{{y}_{2}} \right)=\]

C) \[\frac{4ac-{{b}^{2}}}{{{a}^{2}}}\] done clear

A) \[{{x}^{x}}\left( 1+\log \,x \right)\] done clear

B) \[{{x}^{x}}\left( 1-\log \,x \right)\] done clear

C) \[-{{x}^{x}}\left( 1+\log \,x \right)\] done clear

D) \[{{x}^{x}}\,\log \,x\] done clear

question_answer 27) Differentiate \[{{x}^{x}}+{{a}^{x}}+{{x}^{a}}+{{a}^{a}}\] w.r.t. x

A) \[\left( 1+\log \,x \right)+\left( {{a}^{x}}\,\log \,a+a{{x}^{a-1}} \right)\] done clear

B) \[{{x}^{x}}\left( 1+\log \,x \right)+\log \,a+a{{x}^{a-1}}\] done clear

C) \[{{x}^{x}}\left( 1+\log \,x \right)+{{x}^{a}}\,\operatorname{logx}+a{{x}^{a-1}}\] done clear

D) \[{{x}^{x}}\left( 1+\log \,x \right)+{{a}^{x}}\,\log \,a\,+\,a{{x}^{a-1}}\] done clear

question_answer 28) If \[x={{e}^{x/y}}\], then find \[\frac{dy}{dx}\].

A) \[-\frac{\left( x+y \right)}{x\,\log \,x}\] done clear

B) \[-\frac{\left( x-y \right)}{x\,\log \,x}\] done clear

C) \[\frac{\left( x+y \right)}{x\,\log \,x}\] done clear

D) \[\frac{\left( x-y \right)}{x\,\log \,x}\] done clear

question_answer 29) If \[y={{\left( 2-x \right)}^{3}}\,{{\left( 3+2x \right)}^{5}}\], then find \[\frac{dy}{dx}\].

A) \[{{\left( 2-x \right)}^{3}}{{\left( 3+2x \right)}^{5}}\left[ \frac{15}{3+2x}-\frac{8}{2-x} \right]\] done clear

B) \[{{\left( 2-x \right)}^{3}}{{\left( 3+2x \right)}^{5}}\left[ \frac{15}{3+2x}+\frac{3}{2-x} \right]\] done clear

C) \[{{\left( 2-x \right)}^{3}}{{\left( 3+2x \right)}^{5}}\left[ \frac{10}{3+2x}-\frac{3}{2-x} \right]\] done clear

D) \[{{\left( 2-x \right)}^{3}}{{\left( 3+2x \right)}^{5}}\left[ \frac{10}{3+2x}+\frac{3}{2-x} \right]\] done clear

question_answer 30) If \[y={{x}^{x}}\,\,{{e}^{\left( 2x+5 \right)}}\] , then \[\frac{dy}{dx}\]is

A) \[{{x}^{x}}{{e}^{\left( 2x+5 \right)}}\,\left( 2+\log \,\,x \right)\] done clear

B) \[{{x}^{x}}{{e}^{\left( 2x+5 \right)}}\,\left( 3+2\,\log \,x \right)\] done clear

C) \[{{x}^{x}}\,{{e}^{\left( 2x+5 \right)}}\,\,\left( 2+3\,\log \,x \right)\] done clear

D) \[{{x}^{x}}\,{{e}^{\left( 2x+5 \right)}}\,\left( 3+\log \,x \right)\] done clear

A) \[\frac{-\sin \sqrt{x}}{2\sqrt{x}}\] done clear

B) \[\frac{\sin \sqrt{x}}{-\sin \sqrt{x}}\] done clear

C) \[sin\sqrt{x}\] done clear

D) \[-\sin \sqrt{x}\] done clear

question_answer 32) \[{{7}^{x+\frac{1}{x}}}\]

A) \[\left( \frac{{{x}^{2}}-1}{{{x}^{2}}} \right)\centerdot {{7}^{x+\frac{1}{x}}}\centerdot \log 7\] done clear

B) \[\left( \frac{{{x}^{2}}+1}{{{x}^{2}}} \right)\centerdot {{7}^{x+\frac{1}{x}}}\centerdot \log 7\] done clear

C) \[\left( \frac{{{x}^{2}}-1}{{{x}^{2}}} \right)\centerdot {{7}^{x-\frac{1}{x}}}\centerdot \log 7\] done clear

D) \[\left( \frac{{{x}^{2}}+1}{{{x}^{2}}} \right)\centerdot {{7}^{x+\frac{1}{x}}}\centerdot \log 7\] done clear

question_answer 33) \[\sqrt{\frac{1-\cos x}{1+\cos \,x}}\]

A) \[\frac{1}{2}{{\sec }^{2}}\frac{x}{2}\] done clear

B) \[-\frac{1}{2}{{\sec }^{2}}\frac{x}{2}\] done clear

C) \[{{\sec }^{2}}\frac{x}{2}\] done clear

D) \[-{{\sec }^{2}}\frac{x}{2}\] done clear

question_answer 34) \[\frac{1}{b}{{\tan }^{-1}}\left( \frac{x}{b} \right)+\frac{1}{a}{{\tan }^{-1}}\left( \frac{x}{a} \right)\]

A) \[\frac{-1}{{{x}^{2}}+{{b}^{2}}}+\frac{1}{{{x}^{2}}+{{a}^{2}}}\] done clear

B) \[\frac{1}{{{x}^{2}}+{{b}^{2}}}+\frac{1}{{{x}^{2}}+{{a}^{2}}}\] done clear

C) \[\frac{1}{{{x}^{2}}+{{b}^{2}}}-\frac{1}{{{x}^{2}}+{{a}^{2}}}\] done clear

question_answer 35) \[{{\sec }^{-1}}x+\cos e{{c}^{-1}}\frac{x}{\sqrt{{{x}^{2}}-1}}\]

A) \[\frac{2}{\sqrt{{{x}^{2}}-1}}\] done clear

B) \[\frac{-2}{\sqrt{{{x}^{2}}-1}}\] done clear

C) \[\frac{1}{\left| x \right|\,\sqrt{{{x}^{2}}-1}}\] done clear

D) \[\frac{2}{\left| x \right|\,\sqrt{{{x}^{2}}-1}}\] done clear

A) \[\frac{\left( 3{{x}^{2}}+2xy+{{y}^{2}} \right)}{{{x}^{2}}+2xy+3{{y}^{2}}}\] done clear

B) \[\frac{-\left( 3{{x}^{2}}+2xy+{{y}^{2}} \right)}{{{x}^{2}}+2xy+3{{y}^{2}}}\] done clear

C) \[\frac{\left( 3{{x}^{2}}+2xy-{{y}^{2}} \right)}{{{x}^{2}}-2xy+3{{y}^{2}}}\] done clear

D) \[\frac{3{{x}^{2}}+xy+{{y}^{2}}}{{{x}^{2}}+xy+3{{y}^{2}}}\] done clear

question_answer 37) \[{{x}^{y}}={{e}^{x-y}}\]

A) \[\frac{x-y}{\left( 1+\log \,x \right)}\] done clear

B) \[\frac{x+y}{\left( 1+\log \,x \right)}\] done clear

C) \[\frac{x-y}{x\left( 1+\log x \right)}\] done clear

D) \[\frac{x+y}{x\left( 1+\log \,x \right)}\] done clear

question_answer 38) \[{{e}^{\sin \,y}}=xy\]

A) \[\frac{-y}{x\,\left( y\,\cos y-1 \right)}\] done clear

B) \[\frac{y}{v\,\cos \,y-1}\] done clear

C) \[\frac{y}{y\,cos\,y+1}\] done clear

D) \[\frac{y}{x\left( y\,\cos y-1 \right)}\] done clear

question_answer 39) \[{{\sin }^{2}}x+{{\cos }^{2}}y=1\]

A) \[\frac{\sin \,2y}{\sin \,2x}\] done clear

B) \[-\frac{\sin \,2x}{\sin \,2y}\] done clear

C) \[-\frac{\sin \,2y}{\sin \,2x}\] done clear

D) \[\frac{\sin \,2y}{\sin \,2x}\] done clear

question_answer 40) \[y={{\left( \sqrt{x} \right)}^{{{\sqrt{x}}^{\sqrt{x}....\infty }}}}\]

A) \[\frac{-{{y}^{2}}}{x\left( 2-y\,\log \,x \right)}\] done clear

B) \[\frac{{{y}^{2}}}{2+y\,\log \,x}\] done clear

C) \[\frac{{{y}^{2}}}{x\left( 2+y\,\log \,x \right)}\] done clear

D) \[\frac{{{y}^{2}}}{x\left( 2-y\,\log \,x \right)}\] done clear

Study Package

Case Based (MCQs) - Derivatives

Reset Password.

OTP has been sent to your mobile number and is valid for one hour

Mobile Number Verified

Your mobile number is verified.

IIT JEE Study Material

JEE Main Maths Applications of Derivatives Previous Year Questions With Solutions

JEE main previous year solved questions on Applications of Derivatives give students the opportunity to learn and solve questions in a more effective manner. In calculus, we use derivative to determine the maximum and minimum values of particular functions and many more. There are many important applications of derivatives. In this section, we will solve the problems based on the concepts such as maxima and minima of a function, approximation, Rolle’s theorem and intermediate value theorem, monotonicity, tangent and normal, subtangent and the subnormal, shortest distance between two curves etc. Collection of chapter wise JEE previous year questions with solutions is very useful study material for the JEE aspirants to check their preparation level. Students can expect about 1-2 questions from this chapter in the JEE examination. Click on the below link to get your PDF.

JEE Main Applications of Derivatives Past Year Questions With Solutions

A) Increasing

B) Decreasing

D) None of these

f(x) is an odd function.

f(x) is an increasing function.

Question 2: If f(x) = 2x 3 – 3x 2 – 12x + 5 and x belongs to [-2, 4], then the maximum value of function is at the following value of x

Therefore, the maximum value of function is 37 at x = 4.

Hence option D is the answer.

Question 3: The ratio of the height of cone of maximum volume inscribed in a sphere to its radius is

Diameter of the sphere = 2r

The radius of the cone is x and height is y.

Volume of cone is given by

Put \(\begin{array}{l}y=\frac{4}{3}r\end{array} \) \(\begin{array}{l}\frac{{{d}^{2}}V}{d{{y}^{2}}}=\frac{1}{3}\pi \,\left( 4r-6\times \frac{4}{3}r \right)\end{array} \) = negative value

Question 4: If ab = 2a + 3b, a > 0, b > 0 then the minimum value of ab is

When a = 6, b = 4;

(ab)min. = 6 × 4 = 24.

Question 5: If y = cot -1 (cos 2x) 1/2, then find the value of dy/dx at x = π/6.

Question 6: If f(x + y) = f(x).f(y) for all x and y and f(5) = 2, f'(0) = 3, then find f'(5).

Let x = 5, y = 0,

⇒ f(5+0) = f(5) f(0)

⇒ f(5) = f(5) f(0)

⇒ f(0) = 1

Question 7: If xe xy = y + sin 2 x, then at x = 0, dy/dx =

When x = 0, we get y = 0

Differentiating both sides with respect to x, we get;

Putting x = 0, y = 0, we get;

Question 8: If y = f(2x – 1)/(x 2 + 1) and f ‘(x) = sin x 2 then find dy/dx.

Let t = (2x – 1)/(x 2 + 1) then

Question 9: If x = sec θ – cos θ and y = sec n θ – cos n θ, then which of the following option is correct?

Option (A) is correct.

Question 10: If y 2 = p(x) is a polynomial of degree three, then 2(d/dx)(y 3 . d 2 y/dx 2 ) is

Question 11: At what points of the curve y = (2/3)x 3 + (1/2)x 2 , tangent makes the equal angle with axis?

Now tangent makes equal angle with axis

y = 45 0 and y = -45 0

and when x = -1,

Therefore, the required points are (1/2, 5/24) and (-1, -1/6).

Question 12: The function \(\begin{array}{l}f(x)=\int\limits_{-1}^{x}{t({{e}^{t}}-1)(t-1){{(t-2)}^{3}}{{(t-3)}^{5}}}dt\end{array} \) has a local minimum at x =

For local minima, slope, i.e. f′ (x) should change the sign from −ve to +ve.

If x = 0 + h; f′ (x) = (+) (+) (−) (−1) (−1) = −ve

Hence at x = 0, neither maxima or minima.

If x = 1 − h; f′ (x) = (+) (+) (−) (−1) (−1) = −ve

If x = 1 + h; f′ (x) = (+) (+) (+) (−1) (−1) = +ve

Hence at x = 1, there is a local minima.

If x = 2 − h; f′ (x) = (+) (+1) (+) (−) (−) = +ve

If x = 2 + h; f′ (x) = (+) (+) (+) (+) (−1) = −ve

Hence at x = 2, there is a local maxima.

If x = 3 − h; f′ (x) = (+) (+) (+) (+) (−) = −ve

If x = 3 + h; f′ (x) = (+) (+) (+) (+) (+) = +ve

Hence at x = 3, there is a local minima.

Question 13: Check whether the function \(\begin{array}{l}f(x)=\frac{\text{ln}(\pi +x)}{\text{ln}(e+x)}\end{array} \) is increasing or decreasing.

Hence, f (x) is decreasing in [0, ∞).

Question 14: Let \(\begin{array}{l}f(x)=\left\{\begin{Bmatrix} {x}^{\alpha}lnx, &x>0 \\ 0,& x=0 \end{Bmatrix}\right.\end{array} \) Rolle’s theorem is applicable to f for x ∈ [0, 1], if α =

For Rolle’s theorem to be applicable to f, for x ∈ [0, 1] we should have

(i) f (1) = f (0),

From (i), f (1) = 0, which is true.

From (ii), \(\begin{array}{l}0=f(0)=f({{0}_{+}})=\underset{x\to {{0}_{+}}}{\mathop{\lim }}\,{{x}^{\alpha }}\ln x\end{array} \) which is true only for positive values of α > 0, thus option (4) is correct.

Question 15: The distance travelled s (in metre) by a particle in t seconds is given by, s = t 3 + 2t 2 + t. What is the speed of the particle after 1 second?

Speed of the particle after 1 second is given by

Application of Derivatives Important JEE Main Questions 1

Application of Derivatives Important JEE Main Questions 2

JEE Advanced Maths Method of Differentiation Previous Year Questions with Solutions

Applications of Derivatives – Top 10 Most Important and Expected JEE Questions

Register with Aakash BYJU'S & Download Free PDFs

Man or bear? Hypothetical question sparks conversation about women's safety

Women explain why they would feel safer encountering a bear in the forest than a man they didn't know. the hypothetical has sparked a broader discussion about why women fear men..

If you were alone in the woods, would you rather encounter a bear or a man? Answers to that hypothetical question have sparked a debate about why the vast majority say they would feel more comfortable choosing a bear.

The topic has been hotly discussed for weeks as men and women chimed in with their thoughts all over social media.

Screenshot HQ , a TikTok account, started the conversation, asking a group of women whether they would rather run into a man they didn't know or a bear in the forest. Out of the seven women interviewed for the piece, only one picked a man.

"Bear. Man is scary," one of the women responds.

A number of women echoed the responses given in the original video, writing in the comments that they, too, would pick a bear over a man. The hypothetical has people split, with some expressing their sadness over the state of the world and others cracking jokes. Some men were flabbergasted.

Here's what we know.

A bear is the safer choice, no doubt about it, many say

There were a lot of responses, more than 65,000, under the original post. Many wrote that they understood why the women would choose a bear.

"No one’s gonna ask me if I led the bear on or give me a pamphlet on bear attack prevention tips," @celestiallystunning wrote.

@Brennduhh wrote: "When I die leave my body in the woods, the wolves will be gentler than any man."

"I know a bear's intentions," another woman wrote. "I don't know a man's intentions. no matter how nice they are."

Other TikTok users took it one step further, posing the hypothetical question to loved ones. Meredith Steele, who goes by @babiesofsteele , asked her husband last week whether he would rather have their daughter encounter a bear or a man in the woods. Her husband said he "didn't like either option" but said he was leaning toward the bear.

"Maybe it's a friendly bear," he says.

Diana, another TikTok user , asked her sister-in-law what she would choose and was left speechless.

"I asked her the question, you know, just for giggles. She was like, 'You know, I would rather it be a bear because if the bear attacks me, and I make it out of the woods, everybody’s gonna believe me and have sympathy for me," she said. "But if a man attacks me and I make it out, I’m gonna spend my whole life trying to get people to believe me and have sympathy for me.'"

Bear vs. man debate stirs the pot, woman and some men at odds

The hypothetical has caused some tension, with some women arguing that men will never truly understand what it's like to be a woman or the inherent dangers at play.

Social media users answered this question for themselves, producing memes, spoken word poetry and skits in the days and weeks since.

So, what would you choose?

Noncovalent interactions between quinoxalines and protoporphyrinogen oxidase (PPO): a computational case study for herbicidal applications

Original Paper
Published: 08 May 2024

Cite this article

Melek Hajji ORCID: orcid.org/0000-0002-6145-2858 2 nAff1 ,
Nadeem Abad 3 , 4 ,
Meriem Dallel 5 ,
Hanan Al-Ghulikah 6 ,
Mohamed El Hafi 4 ,
Taha Guerfel 2 ,
Joel T. Mague 7 ,
El Mokhtar Essassi 4 &
Youssef Ramli 3 , 8

18 Accesses

Explore all metrics

Quinoxaline-based compounds show promising inhibition of protoporphyrinogen oxidase (PPO), a key enzyme in chlorophyll production and a prime target for herbicide development. However, their precise molecular interactions remain largely unexplored. This study investigates 1-propyl-3-phenylquinoxalin-2(1H)-one (Qnz), a novel quinoxaline derivative designed and synthesized as a representative system. We examined its interaction, at the atomic level, with the active site of Nicotiana tabacum PPO (NtPPO) using an integrated molecular docking and DFT-based quantum mechanics cluster approach. The nature and strength of observed noncovalent interactions were theoretically evaluated using quantum theory of atoms-in-molecules (QTAIM), independent gradient model (IGM), and natural bond orbital (NBO) methods. Our analysis revealed a fascinating set of unconventional interactions that contribute to the stability of the Qnz–NtPPO complex, namely weak hydrogen bonding, homopolar dihydrogen interactions, π –stacking, and carbonyl–carbonyl interactions. Interestingly, the study uncovered the unexpected role of several less common amino acids—including Gly178, Ser235, and nonpolar aliphatic leucines—in facilitating molecular recognition. Moreover, the employed computational approaches have proven to be a powerful tool for analyzing interactions within the binding pocket.

Graphical abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

In vitro antioxidant activities and in silico molecular docking studies of N-substituted oxime derivatives

A DFT study on the structure activity relationship of the natural xanthotoxin-based pharmaceutical cocrystals

In silico docking and molecular dynamics simulation of 3-dehydroquinate synthase (dhqs) from mycobacterium tuberculosis.

Abad N, Guelmami L, Haouas A, Hajji M, El Hafi M, Sebhaoui J, Guerfel T, Mague JT, Essassi EM, Ramli Y (2023) Synthesis, non-covalent interactions and chemical reactivity of 1-pentyl-3-phenylquinoxalin-2(1H)-one—Structural and computational studies. J Mol Struct 1286:135622. https://doi.org/10.1016/J.MOLSTRUC.2023.135622

Article CAS Google Scholar

Adasme MF, Linnemann KL, Bolz SN, Kaiser F, Salentin S, Haupt VJ, Schroeder M (2021) PLIP 2021: expanding the scope of the protein–ligand interaction profiler to DNA and RNA. Nucleic Acids Res 49:W530–W534. https://doi.org/10.1093/nar/gkab294

Article CAS PubMed PubMed Central Google Scholar

Alanazi MA, Arafa WAA, Althobaiti IO, Altaleb HA, Bakr RB, Elkanzi NAA (2022) Green design, synthesis, and molecular docking study of novel quinoxaline derivatives with insecticidal potential against Aphis craccivora . ACS Omega 7:27674–27689. https://doi.org/10.1021/acsomega.2c03332

Avram S, Funar-Timofei S, Borota A, Chennamaneni SR, Manchala AK, Muresan S (2014) Quantitative estimation of pesticide-likeness for agrochemical discovery. J Cheminform 6:42. https://doi.org/10.1186/s13321-014-0042-6

Bauzá A, Frontera A (2022) Noncovalent interactions involving Group 6 in biological systems: the case of molybdopterin and tungstopterin cofactors. Chem Eur J 28:e202201660. https://doi.org/10.1002/chem.202201660

Article CAS PubMed Google Scholar

Blomberg MRA, Borowski T, Himo F, Liao R-Z, Siegbahn PEM (2014) Quantum chemical studies of mechanisms for metalloenzymes. Chem Rev 114:3601–3658. https://doi.org/10.1021/cr400388t

Boys SF, Bernardi F (1970) The calculation of small molecular interactions by the differences of separate total energies. some procedures with reduced errors. Mol Phys 19:553–566. https://doi.org/10.1080/00268977000101561

Briceño-Vargas FM, Quesadas-Rojas M, Mirón-López G, Cáceres-Castillo D, Carballo RM, Mena-Rejón GJ, Quijano-Quiñones RF (2023) Molecular orbital and topological electron density study of n → π* interactions: amides and thioamides cases. RSC Adv 13:31321–31329. https://doi.org/10.1039/D3RA06038A

Article PubMed PubMed Central Google Scholar

Dayan FE, Duke SO (2002) Herbicides, protoporphyrinogen oxidase inhibitors. encyclopedia of agrochemicals. Wiley, New York. https://doi.org/10.1002/047126363X.agr204

Dennington R, Keith TA, Millam JM (2016) GaussView Version 6. Semichem Inc., Shawnee Mission KS

Google Scholar

Eberhardt J, Santos-Martins D, Tillack AF, Forli S (2021) AutoDock Vina 1.2.0: new docking methods, expanded force field, and python bindings. J Chem Inf Model 61:3891–3898. https://doi.org/10.1021/acs.jcim.1c00203

Fernández Riveras JA, Frontera A, Bauzá A (2021) Selenium chalcogen bonds are involved in protein–carbohydrate recognition: a combined PDB and theoretical study. Phys Chem Chem Phys 23:17656–17662. https://doi.org/10.1039/D1CP01929E

Article PubMed Google Scholar

Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Scalmani G, Barone V, Mennucci B, Petersson GA, Nakatsuji H, Caricato M, Li X, Hratchian HP, Izmaylov AF, Bloino J, Zheng G, Sonnenberg JL, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Vreven T, Montgomery J, Peralta JE, Ogliaro F, Bearpark M, Heyd JJ, Brothers E, Kudin KN, Staroverov VN, Kobayashi R, Normand J, Raghavachari K, Rendell A, Burant JC, Iyengar SS, Tomasi J, Cossi M, Rega N, Millam JM, Klene M, Knox JE, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Martin RL, Morokuma K, Zakrzewski VG, Voth GA, Salvador P, Dannenberg JJ, Dapprich S, Daniels AD, Farkas O, Foresman JB, Ortiz JV, Cioslowski J, Fox DJ (2009) Gaussian 09, Revision D01. Gaussian Inc., Wallingford

García-Gutiérrez P, Zubillaga RA, Ibarra IA, Martínez A, Vargas R, Garza J (2021) Non-conventional interactions of N3 inhibitor with the main protease of SARS-CoV and SARS-CoV-2. Comput Struct Biotechnol J 19:4669–4675. https://doi.org/10.1016/j.csbj.2021.08.015

Grabowski SJ (2019) A−H…σ hydrogen bonds: dihydrogen and cycloalkanes as proton acceptors. ChemPhysChem 20:565–574. https://doi.org/10.1002/cphc.201900045

Grimme S, Antony J, Ehrlich S, Krieg H (2010) A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys 132:154104. https://doi.org/10.1063/1.3382344

Hajji M, Abad N, Habib MA, Elmgirhi SMH, Guerfel T (2021a) Computational chemistry methods for modelling non-covalent interactions and chemical reactivity—an overview. J Indian Chem Soc 98:100208. https://doi.org/10.1016/J.JICS.2021.100208

Hajji M, Al-Otaibi JS, Belkhiria M, Dhifaoui S, Habib MA, Elmgirhi SMH, Mtiraoui H, Bel-Hadj-Tahar R, Msaddek M, Guerfel T (2021b) Structural and computational analyses of a 2-propanolammonium-chlorocadmate(II) assembly: pivotal role of hydrogen bonding and H–H interactions. J Mol Struct 1223:128998. https://doi.org/10.1016/j.molstruc.2020.128998

Hajji M, Haouas A, Abad N, Guerfel T (2023) The unconventional noncovalent interactions control: crystallographic and theoretical analyses of the crystalline structure of 1,1′-(1-Chloro-4-methoxyphenyl)dibenzene as a Case Study. ChemistrySelect 8:e202302624. https://doi.org/10.1002/slct.202302624

Hao G-F, Zuo Y, Yang S-G, Yang G-F (2011) Protoporphyrinogen oxidase inhibitor: an ideal target for herbicide discovery. Chimia (Aarau) 65:961. https://doi.org/10.2533/chimia.2011.961

Hao G-F, Tan Y, Yang S-G, Wang Z-F, Zhan C-G, Xi Z, Yang G-F (2013) Computational and experimental insights into the mechanism of substrate recognition and feedback inhibition of protoporphyrinogen oxidase. PLoS ONE 8:e69198. https://doi.org/10.1371/journal.pone.0069198

Hou Y, Bai Y, Lu C, Wang Q, Wang Z, Gao J, Xu H (2023) Applying molecular docking to pesticides. Pest Manag Sci. https://doi.org/10.1002/ps.7700

Humphrey W, Dalke A, Schulten K (1996) VMD: Visual molecular dynamics. J Mol Graph 14:33–38. https://doi.org/10.1016/0263-7855(96)00018-5

Jacobs JM, Jacobs NJ (1984) Protoporphyrinogen oxidation, an enzymatic step in heme and chlorophyll synthesis: partial characterization of the reaction in plant organelles and comparison with mammalian and bacterial systems. Arch Biochem Biophys 229:312–319. https://doi.org/10.1016/0003-9861(84)90157-7

Jena S, Dutta J, Tulsiyan KD, Sahu AK, Choudhury SS, Biswal HS (2022) Noncovalent interactions in proteins and nucleic acids: beyond hydrogen bonding and π-stacking. Chem Soc Rev 51:4261–4286. https://doi.org/10.1039/D2CS00133K

Koch M, Breithaupt C, Kiefersauer R, Freigang J, Huber R, Messerschmidt A (2004) Crystal structure of protoporphyrinogen IX oxidase: a key enzyme in haem and chlorophyll biosynthesis. EMBO J 23:1720–1728. https://doi.org/10.1038/sj.emboj.7600189

Laskowski RA, Swindells MB (2011) LigPlot+: multiple ligand-protein interaction diagrams for drug discovery. J Chem Inf Model 51:2778–2786. https://doi.org/10.1021/ci200227u

Lefebvre C, Khartabil H, Boisson J, Contreras-García J, Piquemal J, Hénon E (2018) The independent gradient model: a new approach for probing strong and weak interactions in molecules from wave function calculations. ChemPhysChem 19:724–735. https://doi.org/10.1002/cphc.201701325

Liu X-H, Yu W, Min L-J, Wedge DE, Tan C-X, Weng J-Q, Wu H-K, Cantrell CL, Bajsa-Hirschel J, Hua X-W, Duke SO (2020) Synthesis and pesticidal activities of new quinoxalines. J Agric Food Chem 68:7324–7332. https://doi.org/10.1021/acs.jafc.0c01042

Liu H-Y, Yu L-K, Qin S-N, Yang H-Z, Wang D-W, Xi Z (2023) Design, synthesis, and metabolism studies of N-1,4-diketophenyltriazinones as protoporphyrinogen IX oxidase inhibitors. J Agric Food Chem 71(7):3225–3238. https://doi.org/10.1021/acs.jafc.2c09082

Losev TV, Gerasimov IS, Panova MV, Lisov AA, Abdyusheva YR, Rusina PV, Zaletskaya E, Stroganov OV, Medvedev MG, Novikov FN (2023) Quantum mechanical-cluster approach to solve the bioisosteric replacement problem in drug design. J Chem Inf Model 63:1239–1248. https://doi.org/10.1021/acs.jcim.2c01212

Lu T, Chen F (2012) Multiwfn: a multifunctional wavefunction analyzer. J Comput Chem 33:580–592. https://doi.org/10.1002/jcc.22885

Mandal N, Pratik SM, Datta A (2017) Exploring ultrashort hydrogen-hydrogen nonbonded contacts in constrained molecular cavities. J Phys Chem B 121:825–834. https://doi.org/10.1021/acs.jpcb.6b12391

Martínez A, García-Gutiérrez P, Zubillaga RA, Garza J, Vargas R (2021) Main interactions of dopamine and risperidone with the dopamine D2 receptor. Phys Chem Chem Phys 23:14224–14230. https://doi.org/10.1039/D1CP01637G

Mei L-C, Chen H-M, Dong A-Y, Huang G-Y, Liu Y-W, Zhang X, Wang W, Hao G-F, Yang G-F (2022) Pesticide informatics platform (PIP): an international platform for pesticide discovery, residue, and risk evaluation. J Agric Food Chem 70:6617–6623. https://doi.org/10.1021/acs.jafc.2c02141

Morris GM, Huey R, Lindstrom W, Sanner MF, Belew RK, Goodsell DS, Olson AJ (2009) AutoDock4 and AutoDockTools4: automated docking with selective receptor flexibility. J Comput Chem 30:2785–2791. https://doi.org/10.1002/jcc.21256

Muchowska KB, Pascoe DJ, Borsley S, Smolyar IV, Mati IK, Adam C, Ling NGS, Cockroft SL (2020) Reconciling electrostatic and n→π* orbital contributions in carbonyl interactions. Angew Chem 132:14710–14716. https://doi.org/10.1002/ange.202005739

Article Google Scholar

Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE (2004) UCSF Chimera—a visualization system for exploratory research and analysis. J Comput Chem 25:1605–1612. https://doi.org/10.1002/jcc.20084

Qin X, Sun L, Wen X, Yang X, Tan Y, Jin H, Cao Q, Zhou W, Xi Z, Shen Y (2010) Structural insight into unique properties of protoporphyrinogen oxidase from Bacillus subtilis. J Struct Biol 170:76–82. https://doi.org/10.1016/j.jsb.2009.11.012

Rahim A, Saha P, Jha KK, Sukumar N, Sarma BK (2017) Reciprocal carbonyl–carbonyl interactions in small molecules and proteins. Nat Commun 8:78. https://doi.org/10.1038/s41467-017-00081-x

Rocha-Santos A, Chaves EJF, Grillo IB, de Freitas AS, Araújo DAM, Rocha GB (2021) Thermochemical and quantum descriptor calculations for gaining insight into ricin toxin A (RTA) Inhibitors. ACS Omega 6:8764–8777. https://doi.org/10.1021/acsomega.0c02588

Schrödinger LLC (2021) The PyMOL molecular graphics system. Version 2:5

Shi J, Zhao L, Wang J, Cao H, Gao S, Ye F, Fu Y (2023) Identification of 4-hydroxyphenylpyruvate dioxygenase inhibitors by virtual screening, molecular docking, molecular dynamic simulation. J Sci Food Agric 103:5547–5559. https://doi.org/10.1002/jsfa.12629

Steiner T (1996) C-H-O hydrogen bonding in crystals. Crystallogr Rev 6:1–51. https://doi.org/10.1080/08893119608035394

Sukhoverkov KV, Corral MG, Leroux J, Haywood J, Johnen P, Newton T, Stubbs KA, Mylne JS (2021) Improved herbicide discovery using physico-chemical rules refined by antimalarial library screening. RSC Adv 11:8459–8467. https://doi.org/10.1039/D1RA00914A

Sun Z, Wei C, Wu S, Zhang W, Song R, Hu D (2022) Synthesis, Anti-potato virus Y activities, and interaction mechanisms of novel quinoxaline derivatives bearing dithioacetal moiety. J Agric Food Chem 70:7029–7038. https://doi.org/10.1021/acs.jafc.2c01898

Sun J (2023) PyMOL ChatGPT Plugin. GitHub repository. https://github.com/JinyuanSun/ChatMol.git

Tang X, Zhou Q, Zhan W, Hu D, Zhou R, Sun N, Chen S, Wu W, Xue W (2022) Synthesis of novel antibacterial and antifungal quinoxaline derivatives. RSC Adv 12:2399–2407. https://doi.org/10.1039/D1RA07559D

Tian W, Chen C, Lei X, Zhao J, Liang J (2018) CASTp 3.0: computed atlas of surface topography of proteins. Nucleic Acids Res 46:W363–W367. https://doi.org/10.1093/nar/gky473

Wang Z-W, Zhao L-X, Gao S, Leng X-Y, Yu Y, Fu Y, Ye F (2021b) Quinoxaline derivatives as herbicide safeners by improving Zea mays tolerance. Pestic Biochem Physiol 179:104958. https://doi.org/10.1016/j.pestbp.2021.104958

Wang D, Wang B, Xi Z (2021) Development of Protoporphyrinogen IX oxidase inhibitors for sustainable agriculture. pp. 11–41 in: Crop Protection Products for Sustainable Agriculture. https://doi.org/10.1021/bk-2021-1390.ch002

Wojtkowiak K, Michalczyk M, Zierkiewicz W, Jezierska A, Panek JJ (2022) Chalcogen bond as a factor stabilizing ligand conformation in the binding pocket of carbonic anhydrase IX receptor Mimic. Int J Mol Sci 23:13701. https://doi.org/10.3390/ijms232213701

Zagar C, Liebl R, Theodoridis G, Witschel M (2019) Protoporphyrinogen IX Oxidase Inhibitors. In: Modern crop protection compounds. Weinheim, Germany, pp. 173–211. https://doi.org/10.1002/9783527699261.ch3

Zhao H, Tang S, Zhang Q, Du L (2017) Weak hydrogen bonding competition between O-H⋯π and O–H⋯Cl. RSC Adv 7:22485–22491. https://doi.org/10.1039/C7RA00901A

Zhao L, Peng J, Liu F, Zou Y, Gao S, Fu Y, Ye F (2022a) Discovery of novel phenoxypyridine as promising protoporphyrinogen IX oxidase inhibitors. Pestic Biochem Physiol 184:105102. https://doi.org/10.1016/j.pestbp.2022.105102

Zhao L-X, Peng J-F, Hu J-J, Zou Y-L, Yin M-L, Wang Z-X, Gao S, Fu Y, Ye F (2022b) Design, synthesis, herbicidal activity, and the molecular docking study of novel diphenyl ether derivatives as protoporphyrinogen IX oxidase inhibitors. J Mol Struct 1258:132670. https://doi.org/10.1016/j.molstruc.2022.132670

Zhao W, Huang Y, Hao G-F (2022c) Pesticide informatics expands the opportunity for structure-based molecular design and optimization. Adv Agrochem 1:139–147. https://doi.org/10.1016/j.aac.2022.11.006

Zheng B-F, Zuo Y, Huang G-Y, Wang Z-Z, Ma J-Y, Wu Q-Y, Yang G-F (2023a) Synthesis and biological activity evaluation of benzoxazinone-pyrimidinedione hybrids as potent protoporphyrinogen IX oxidase inhibitor. J Agric Food Chem 71(39):14221–14231. https://doi.org/10.1021/acs.jafc.3c03593

Zheng B-F, Wang Z-Z, Dong J, Ma J-Y, Zuo Y, Wu Q-Y, Yang G-F (2023b) Discovery of a subnanomolar inhibitor of protoporphyrinogen IX oxidase via fragment-based virtual screening. J Agric Food Chem 71(23):8746–8756. https://doi.org/10.1021/acs.jafc.3c00168

Download references

Acknowledgements

The authors extend their appreciation to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R95), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The author, Melek Hajji, acknowledges the invaluable support and resources provided by Assalam International University-Sirte, throughout this research.

Author information

Melek Hajji

Present address: Department of Chemistry, College of Pharmacy, Assalam International University-Sirte, Sirte, Libya

Authors and Affiliations

Research Unit: Electrochemistry, Materials and Environment, University of Kairouan, 3100, Kairouan, Tunisia

Melek Hajji & Taha Guerfel

Laboratory of Medicinal Chemistry, Drug Sciences Research Center, Faculty of Medicine and Pharmacy, Mohammed V University in Rabat, Rabat, Morocco

Nadeem Abad & Youssef Ramli

Laboratoire de Chimie Organique Heterocyclique, Faculté Des Sciences, Université Mohammed V Rabat, Rabat, Morocco

Nadeem Abad, Mohamed El Hafi & El Mokhtar Essassi

Laboratory of Human Genome and Multifactorial Diseases (LR12ES07), Faculty of Pharmacy of Monastir, University of Monastir, Monastir, Tunisia

Meriem Dallel

Department of Chemistry, College of Science, Princess Nourah Bint Abdulrahman University, P.O. Box 84428, 11671, Riyadh, Saudi Arabia

Hanan Al-Ghulikah

Department of Chemistry, Tulane University, New Orleans, LA, 70118, USA

Joel T. Mague

Mohammed VI Center for Research and Innovation (CM6), 10000, Rabat, Morocco

Youssef Ramli

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Melek Hajji .

Ethics declarations

Conflict of interest.

The authors have no relevant financial or non-financial interests to disclose.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (PDF 183 KB)

Rights and permissions.

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Hajji, M., Abad, N., Dallel, M. et al. Noncovalent interactions between quinoxalines and protoporphyrinogen oxidase (PPO): a computational case study for herbicidal applications. Chem. Pap. (2024). https://doi.org/10.1007/s11696-024-03485-4

Download citation

Received : 02 February 2024

Accepted : 25 April 2024

Published : 08 May 2024

DOI : https://doi.org/10.1007/s11696-024-03485-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quinoxalines
Noncovalent interactions
Protoporphyrinogen oxidase (PPO)
In silico docking
Density functional theory (DFT)
Find a journal
Publish with us
Track your research

IMAGES

Application of Derivative Case Study Questions
Mind Maps For Application of Derivative- Class 12, JEE (Main + Advanced)
Application of derivatives class 12 math
Application Of Derivatives
Case Study Based on Applications of Derivatives
Applications of derivatives in economics

VIDEO

Application of Derivatives NCERT Exemplar Q1 to 5
CASE STUDY QUESTION APPLICATIONS OF DERIVATIVES CLASS 12 MATHS || IMPORTANT CASE STUDY QUESTION
Application of Derivatives Class 12th Introductions
Application of Derivatives || BCS
Final Paper 2: SFM
INDEFINITE INTEGRATION LEC 1 MHT-CET

COMMENTS

Case Study on Application Of Derivatives Class 12 Maths PDF
The case study on Application Of Derivatives Class 12 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Application Of Derivatives case study questions are very easy to grasp from the PDF - download links are given on this page.
CBSE 12th Standard Maths Application of Derivatives Case Study Questions
QB365 Provides the updated CASE Study Questions for Class 12 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
CBSE Case Study Questions For Class 12 Maths Applications Of
Mere Bacchon, you must practice the CBSE Case Study Questions for Class 12 Maths Applications of Derivatives in order to fully complete your preparation.They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams! I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams.
Applications of Derivatives Case Study Questions With answers
Free PDF Download of CBSE Class 12 Mathematics Chapter 6 Applications of Derivatives Case Study and Passage Based Questions with Answers were Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Applications of Derivatives to know their preparation level. Download Books for Boards. Join our Telegram Channel, there you ...
Applications of derivatives
Learn. Introduction to one-dimensional motion with calculus. Interpreting direction of motion from position-time graph. Interpreting direction of motion from velocity-time graph. Interpreting change in speed from velocity-time graph. Worked example: Motion problems with derivatives. Analyzing straight-line motion graphically.
Case Study Questions chapter 6 Class 12 MATHS Application Of
In this post, you will get CASE Study Questions of Chapter 6 (Application Of Derivatives) of Class 12th. These Case study Questions are based on the Latest Syllabus for 2021- 22 of the CBSE Board.
Application of Derivative Case Study Questions
#casestudyquestions #casestudyquestionsforclass12mathIn this video you will learn how to solve case study questions of class 12 math's board exams as per lat...
Case Study
CASE STUDY | CASE BASED QUESTIONS | APPLICATION OF DERIVATIVES CLASS 12 MATS 2023-24OSWAL GURUKUL SAMPLE PAPERBuy Link Amazon - https://www.amazon.in/stores/...
Class 12th Maths
Class 12th Maths - Application of Derivatives Case Study Questions and Answers 2022 - 2023 - Complete list of 12th Standard CBSE question papers, syllabus, exam tips, study material, previous year exam question papers, centum tips, formula, answer keys, solutions etc..
12th Maths Application of Derivatives Case Study Questions & Answers
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 12 Maths Subject - Application of Derivatives, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
Application Of Derivatives Objective Questions
Application Of Derivatives Class 12 Objective Questions By Harsh Sir. Solve Class 12 Maths Application Of Derivatives Objective Questions With Vedantu Math. ...
Question 6
Question 6 - Case Based Questions (MCQ) - Chapter 6 Class 12 Application of Derivatives Last updated at April 16, 2024 by Teachoo. There is a bridge whose length of three sides of a trapezium other than base are equal to 10 cm. Based on the above information answer the following: This ...
Class 12 CBSE Applied Maths Application Of Derivatives Case Study
Case-study-4 A factory owner wants to construct a tank with rectangular base and rectangular sides, open at the top, so that its depth is 2 m and capacity is 8 m³. The building of the tank costs ₹250 per square metre for the base and ₹180 per square metre for the sides.
Case Study Questions for Class 12 Maths Chapter 6 Application of
The importance of solving case study questions for Class 12 Maths can be summarized as follows: Enhances problem-solving skills: Case study questions challenge students to think beyond textbook examples and apply their knowledge to real-world situations. This enhances their problem-solving skills and helps them develop a deeper understanding of ...
Applications of derivatives
Let's see how the tools we've developed are applied in order to solve real-world word problems. Up next for you: Rates of change in other applied contexts (non-motion problems) Differential calculus is all about instantaneous rate of change. Let's see how the tools we've developed are applied in order to solve real-world word problems.
Chapter 6 Class 12 Application of Derivatives
We learned Derivatives in the last chapter, in Chapter 5 Class 12. In this Chapter we will learn the applications of those derivatives. The topics in the chapter include. Finding rate of change. Checking if a function is increasing or decreasing in an interval. Checking if a function is increasing or decreasing in whole domain.
Class 12 Maths Case Study Questions
Case Study Questions Application of Derivatives. A telephone company in a town has 500 subscribers on its list and collects fixed charges of 300 per subscriber per year. The company proposes to increase the annual subscription and it is believed that for every increase of 1 one subscriber will discontinue the service.
Application of Derivatives Class 12 Maths Important Questions Chapter 6
Application of Derivatives Class 12 Important Questions with Solutions Previous Year Questions. Rate Measure, Increasing-Decreasing Functions and Approximation. Question 1. The total cost C (x) associated with the production of x units of an item is given by C (x) = 0.005x 3 - 0.02x 2 + 30x + 5000.
12th Class Mathematics Applications of Derivatives Question Bank
Free Question Bank for 12th Class Mathematics Applications of Derivatives Case Based (MCQs) - Derivatives. Customer Care : 6267349244. Toggle navigation 0 . 0 . Railways; UPSC; CET; Banking; CUET; SSC; ... Study Packages Question Bank Online Test Rajasthan State Exams ; Videos Sample Papers Study Packages Question Bank Online Test
CBSE 12th Standard Maths Subject Application of Derivatives Case Study
QB365 Provides the updated CASE Study Questions for Class 12 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams - Complete list of 12th Standard CBSE question papers, syllabus, exam tips, study material, previous year exam question papers, centum ...
Case Study Questions on Application of Derivatives
In this Session , Vishal Mahajan discuss the Application of Derivatives .This Session will be beneficial Of Class 12 & all aspirants preparing for Competitive Exams.This session will be Conducted in English & Hindi and notes will be provided in English. Understand the concept of Case Study Questions on Application of Derivatives with CBSE Class ...
JEE Main Previous Year Questions on Applications of Derivatives
JEE main previous year solved questions on Applications of Derivatives give students the opportunity to learn and solve questions in a more effective manner. In calculus, we use derivative to determine the maximum and minimum values of particular functions and many more. There are many important applications of derivatives.
CASE STUDY BASED QUESTION || Application of Derivative
CBSE Exam, class 12. About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features NFL Sunday Ticket
2024 AP Exam Dates
The 2024 AP Exams will be administered in schools over two weeks in May: May 6-10 and May 13-17. AP coordinators are responsible for notifying students when and where to report for the exams.
Man or bear explained: Online debate has women talking about safety
"Bear. Man is scary," one of the women responds. A number of women echoed the responses given in the original video, writing in the comments that they, too, would pick a bear over a man.
Noncovalent interactions between quinoxalines and protoporphyrinogen
Quinoxaline-based compounds show promising inhibition of protoporphyrinogen oxidase (PPO), a key enzyme in chlorophyll production and a prime target for herbicide development. However, their precise molecular interactions remain largely unexplored. This study investigates 1-propyl-3-phenylquinoxalin-2(1H)-one (Qnz), a novel quinoxaline derivative designed and synthesized as a representative ...