problem solving using fraction

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 4: Understand fractions

About this unit.

From cooking measurements to geometry, fractions are all around us. By understanding how the numerator and denominator work together, you'll be able to break down numbers into smaller parts, compare different fractions, and get a grasp on concepts like equivalent fractions.

Fractions intro

• Intro to fractions (Opens a modal)
• Cutting shapes into equal parts (Opens a modal)
• Cut shapes into equal parts Get 5 of 7 questions to level up!

What fractions mean

• Identifying numerators and denominators (Opens a modal)
• Recognize fractions (Opens a modal)
• Recognizing fractions greater than 1 (Opens a modal)
• Understand numerators and denominators Get 5 of 7 questions to level up!
• Recognize fractions Get 5 of 7 questions to level up!
• Recognize fractions greater than 1 Get 3 of 4 questions to level up!

Fractions on the number line

• Fractions on a number line (Opens a modal)
• Fractions on number line widget (Opens a modal)
• Finding 1 on the number line (Opens a modal)
• Fractions greater than 1 on the number line (Opens a modal)
• Fractions on the number line Get 5 of 7 questions to level up!
• Find 1 on the number line Get 5 of 7 questions to level up!
• Fractions greater than 1 on the number line Get 3 of 4 questions to level up!

Fractions and whole numbers

• Representing 1 as a fraction (Opens a modal)
• Whole numbers as fractions (Opens a modal)
• Writing whole numbers as fractions (Opens a modal)
• Write whole numbers as fractions Get 5 of 7 questions to level up!

Equivalent fractions

• Equivalent fractions with visuals (Opens a modal)
• Equivalent fraction models (Opens a modal)
• Equivalent fraction visually (Opens a modal)
• Creating equivalent fractions (Opens a modal)
• Equivalent fraction models Get 5 of 7 questions to level up!
• Equivalent fractions on the number line Get 3 of 4 questions to level up!
• Equivalent fractions Get 3 of 4 questions to level up!

Fraction Worksheets

Conversion :: Addition :: Subtraction :: Multiplication :: Division

Conversions

Fractions - addition, fractions - subtraction, fractions - multiplication, fractions - division.

Fractions Questions and Problems with Solutions

Questions and problems with solutions on fractions are presented. Detailed solutions to the examples are also included. In order to master the concepts and skills of fractions, you need a thorough understanding (NOT memorizing) of the rules and properties and lot of practice and patience. I hope the examples, questions, problems in the links below will help you.

• Fractions and Mixed Numbers , define fractions and mixed numbers, and introduce important vocabulary.
• Evaluate Fractions of Quantities .
• Fractions Rules including questions with Solutions
• Properties of Fractions
• Complex Fractions with Variables
• Equivalent Fractions examples and questions with solutions.
• Reduce Fractions examples and questions with solutions.
• Reduce Fractions Calculator
• Simplify Fractions , examples and questions including solutions.
• Factor Fractions , examples with questions including solutions.
• Adding Fractions. Add fractions with same denominator or different denominator. Several examples with detailed solutions and exercises.
• Multiply Fractions. Multiply a fraction by another fraction or a number by a fraction. Examples with solutions and exercises.
• Divide Fractions. Divide a fraction by a fraction, a fraction by a number of a number by a fraction. Several examples with solutions and exercises with answers.

Fractions Per Grade

• Fractions and Mixed Numbers , questions and problems with solutions for grade 7
• Fractions and Mixed Numbers , questions and problems with solutions for grade 6
• Fractions , questions for grade 5 and their solutions
• Fractions , questions for grade 4 their answers.

Fractions Calculators

• Fractions Calculator including reducing, adding and multiplying fractions.
• Add Mixed Numbers Calculator

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Pre-Algebra >
• Fractions >

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Two-step without parentheses
• Two-step with parentheses
• Three/four steps without parentheses
• Three/four steps with parentheses
• Multi-step without parentheses
• Multi-step with parentheses
• Prime Factorization
• Negative Factors
• Positive Factors
• Odd Factors
• Even Factors
• Biggest Factor
• Equivalent Fractions
• Add, Subtract
• Add, Subtract Like Denominators
• Add, Subtract Unlike Denominators
• Multiply with Whole Number
• Divide with Whole Number
• Mixed Numbers
• Complex Fractions
• Improper Fractions
• Long Addition
• Long Subtraction
• Long Multiplication
• Long Division
• Add/Subtract
• Multiplication
• Decimal to Fraction
• Fraction to Decimal
• Square Root
• Ratios & Proportions

Number Line

• Expanded Form
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

• reduce\:fraction\:\frac{4}{8}
• \frac{1}{2}+\frac{1}{4}+\frac{3}{4}
• \frac{1}{2}\cdot\frac{8}{7}
• \frac{-\frac{1}{5}}{\frac{7}{4}}
• descending\:order\:\frac{1}{2},\:\frac{3}{6},\:\frac{7}{2}
• decimal\:to\:fraction\:0.35
• What is a mixed number?
• A mixed number is a combination of a whole number and a fraction.
• How can I compare two fractions?
• To compare two fractions, first find a common denominator, then compare the numerators.Alternatively, compare the fractions by converting them to decimals.
• How do you add or subtract fractions with different denominators?
• To add or subtract fractions with different denominators, convert the fractions to have a common denominator. Then you can add or subtract the numerators of the fractions, leaving the denominator unchanged.

fractions-calculator

• My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

Mastery-Aligned Maths Tutoring

“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."

FREE daily maths challenges

A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

28 Fraction Word Problems for Year 2 to Year 6 With Tips On Supporting Pupils’ Progress

Emma Johnson

Fraction word problems are an important piece in teaching fractions. Fractions are a key component of the National Curriculum throughout primary, with children introduced to the concept in Year 1 and continuously building upon their knowledge and understanding, through to Year 6 and beyond.

The abstract nature of fractions makes them one of the more difficult areas of maths for children to understand. It is essential that they are taught through the use of concrete resources and visual images, but also through a link to the real world. Word problems are a great way to help children develop this understanding and should be used alongside any fluency work the children do.

To help you with this, we have put together a collection of 20 word problems which can be used with children from Year 2 to Year 6.

Fraction word problems in the national curriculum

• Why are word problems important for children’s understanding of fractions?

How to teach fraction word problem solving in primary school

Fraction word problems for primary , fraction word problems for year 2, fraction word problems for year 3, fraction word problems for year 4, fraction word problems for year 5, fraction word problems for year 6, more word problems resources.

Fraction Lessons Resource Pack

Download this free pack of fraction lessons to support your students and help them to practice fractions problems.

Fractions in KS1

Pupils are first introduced to fractions in Year 1, where they begin to recognise a half and quarter of a shape or quantity. As they progress through Key Stage 1, they are introduced to a wider range of fractions.

In Year 2 pupils need to be able to recognise, find, name and write fractions \frac{1}{3}, \ \frac{1}{4}, \ \frac{2}{4} and \frac{3}{4} of lengths, shape, a set of objects or quantity.

Fractions in lower KS2

Once pupils move into Key Stage 2, there is an increased focus on fractions, with a significant period of time dedicated to developing students’ knowledge and building on previous learning from Year 3 through to Year 6.

In Year 3, pupils are taught to count in tenths; recognise, find and write fractions of a discrete set of objects; understand the term ‘unit’ and ‘non-unit’ fractions; recognise equivalent fractions, compare and order fractions and add/subtract fractions with the same denominator. At this stage, pupils also begin to solve simple problems involving fractions.

As pupils progress into Year 4, they are also introduced to the concept of decimals alongside the work on fractions. They build upon their understanding of equivalent fractions and adding/ subtracting fractions (still with the same denominator.

They also learn to count up and down in hundredths, recognise and write decimals equivalent to \frac{1}{4}, \ \frac{1}{2} and \frac{3}{4} and begin to solve problems with increasingly harder fractions.

Fractions in upper KS2

As pupils continue through the school, into upper Key Stage 2, they continue to build on their learning. They are introduced to mixed numbers and improper fractions. They are also introduced to the concept of percentages alongside fractions and decimals.

In Year 5, children build on the knowledge gained in Year 4, comparing and ordering fractions; recognising equivalent fractions; addition and subtraction of fractions (with different denominators, but multiples of the same number). Fractions appear in addition and subtraction word problems .

They are also introduced to the multiplication of fractions; converting between improper fractions and mixed numbers and the link between fractions, decimals and percentages. By Year 5 pupils will be completing more complex problems, including multi-step word problems and multiplication word problems .

In Year 6, pupils consolidate and build upon the knowledge of fractions they have gained so far. Pupils continue to add and subtract fractions (with different denominators and mixed numbers). They also develop their understanding of how to multiply fractions and begin to divide fractions by whole numbers, combining fraction and division word problems .

Pupils also continue to build upon their understanding of the equivalences between fractions, decimals and percentages and solve increasingly complex one-step, two-step and multi-step percentage word problems .

Why are word problems important for children’s understanding of fractions?

Word problems, alongside the use of concrete resources and visual images, help children to make sense of the abstract nature of fractions. 

For example, if children were presented with the question \frac{6}{8} ÷ 3, some might find this difficult to access. If children are given it as a word problem, alongside a visual image, it becomes much more accessible.

The above calculation as a word problem :

 ‘3 children shared \ \it{\frac{6}{8}} of a pizza, how much did each child get?’

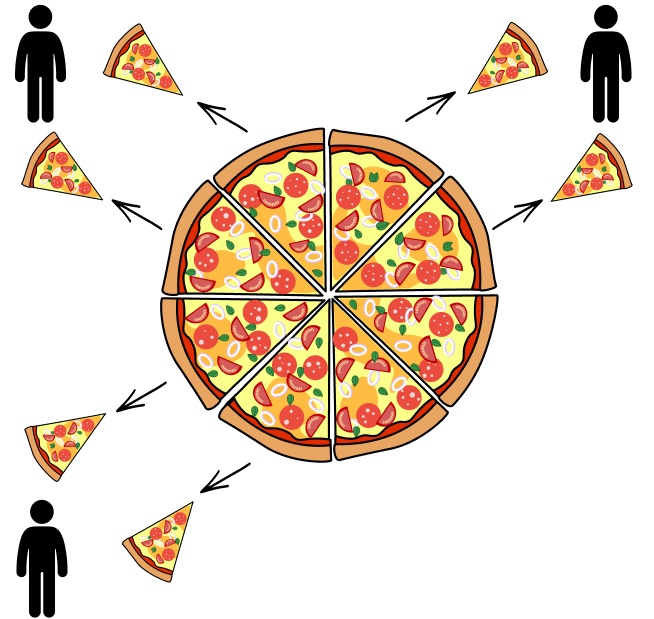
Children can see and understand the concept of 3 children sharing 6 slices of pizza, compared to just seeing the written calculation.

As with all word problems, the first thing children need to do is read the question carefully and make sure they understand what is being asked. They then have to decide what calculation is needed and whether they can represent it pictorially.

Here is an example:

Ben has a bag of 48 sweets.

He gives \frac{3}{8} of his bag to his brother

How many sweets does he have left?

How to solve:

What do you already know?

• There are 48 sweets altogether. 
• The denominator is 8, so we know we need to divide the 48 by 8. This will tell us how many sweets in \frac{1}{8} .
• The numerator is 3, therefore we need to multiply the answer by 3, to tell us how many sweets are \frac{3}{8} .
• The last step of the problem is to find out how many sweets Ben has left.
• We can either calculate \frac{5}{8} , as we know Ben must have \frac{5}{8} left, or we subtract the number of sweets in \frac{3}{8} from the total of 48.

How can this be drawn/represented pictorially?

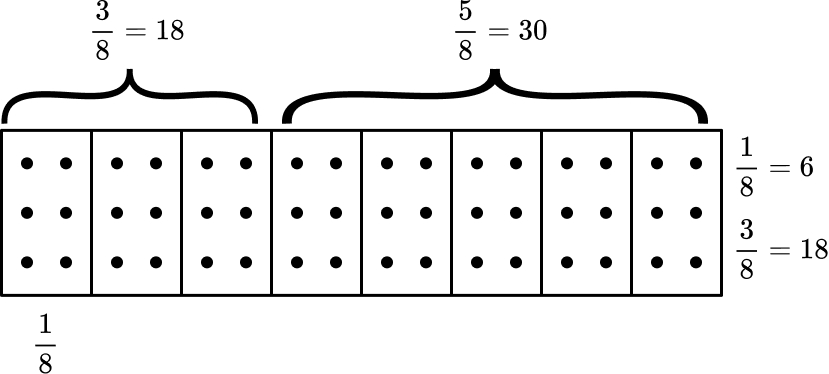
• We can draw a bar model, split into 8 sections. 
• The 48 sweets are then shared between the 8 sections (each worth \frac{1}{8} ). 
• We can see that \frac{3}{8} of the 48 sweets equals 18 sweets. 
• We can then either subtract 18 from 48, to work out how many sweets were left. 48 – 18 = 30
• Alternatively, we can calculate how many sweets are in \frac{5}{8} , which is 30.

Word problems are tied in throughout Third Space Learning’s online one-to-one tuition programmes. Tutors work with students to break down word problems and identify the operations needed to solve problems.

The following section lays out the types of fraction word problems that you can expect to see by year group in primary school. 

At Third Space Learning we incorporate word problems into our one-to-one online tutoring . With each lesson designed to suit the needs of each individual student, our tutoring programme aims to deepen mathematical understanding and confidence in maths. 

Fraction word problems are a great way to strengthen students’ conceptual understanding of fractions and grow their problem solving skills. Take a look at our article on fraction games to help with this.

• What Is A Unit Fraction: Explain For Primary School
• What Is An Improper Fraction: Explained For Primary School
• Fractions: A Comprehensive Guide
• How To Teach Fractions Key Stage 2: Maths Bootcamp
• How To Simplify Fractions: A Comprehensive Guide

Word problems in Year 2 involve recognising and naming simple fractions and beginning to understand the concept of equivalence.

Maisie was having a birthday party.

She invited 16 friends. Half of her friends were from her class and a half were from the other Year 2 class. 

How many friends did she invite from each class?

Answer: 8 friends

\frac{1}{2} of 16 = 8

Ahmed baked 12 cookies. 

He ate \frac{1}{4} of them.

How many cookies did Ahmed eat?

\frac{1}{4} of 12 = 3

Sara says ‘I ate \frac{1}{2} a pizza and my friend ate \frac{2}{4} . My friend had more than me, as she had 2 pieces’.

Is she correct? Explain why you have chosen your answer.

Answer: Sara is not correct

\frac{1}{2} is the same as \frac{2}{4}

Tom and Zeyn shared a chocolate bar.

They both had a quarter of the chocolate bar. 

How much was left?

Answer : \frac{1}{2} of the chocolate bar

\frac{2}{4} are equivalent to \frac{1}{2}

Word problems for Year 3 include proper fractions, fractions of amounts, simple equivalent fractions and adding and subtracting fractions with the same denominator. 

Sophie ate \frac{1}{4} of her chocolate bar. 

If the bar had 20 squares, how many squares did Sophie eat?

Answer : 5 squares

\frac{1}{4} of 20 = 20 ÷ 4 = 5

Hamza and Khalifa shared a pizza.

Hamza ate two fourths of the pizza and Khalifa ate one fourth.

How much pizza was left?

Answer : \frac{1}{4}

There are 24 hours in a day.

Maise worked out that she spends \frac{1}{8} of her day on Saturday, doing exercise.

How long does she spend exercising on a Saturday?

Answer: 3 hours

\frac{1}{8} of 24 hours = 24 ÷ 8 = 3

There are 30 children in the class.

\frac{2}{5} of the children are wearing jumpers.

How many children are wearing jumpers?

Answer: 12 children

\frac{1}{5} of 30 = 30 ÷ 5 = 6

\frac{2}{5} of 20 = 12

Word problems for year 4 include equivalent fractions, fractions of quantities (including non-unit fractions and adding/subtracting fractions with the same denominator. Money word problems often appear in Year 4.

Abdullah spent \frac{1}{3} of his pocket money for the month on a new game.

He receives £18 per month.

How much did he spend on the game?

Answer : £6

\frac{1}{3} of 18 = £6

Bethan had a bag of sweets.

She gave \frac{2}{7} of the bag to her mum and ate \frac{3}{7} of herself.

What fraction of the bag was left?

Answer : \frac{2}{7}

Jamal ate \frac{6}{18} of a chocolate bar.

Mason ate \frac{1}{3}

Mason said that Jamal ate more than him. Do you agree? Explain your answer.

Answer : No – they both ate the same.

\frac{1}{3} is equivalent to \frac{6}{18}

\frac{2}{7} of a piece of ribbon is 10cm.

How long is the whole piece of ribbon?

Answer: 35cm

\frac{2}{7} = 10

\frac{1}{7} = 5

\frac{7}{7} = 5 x 7 = 35

Word problems for Year 5 include more complex equivalent fractions, problems involving mixed numbers and improper fractions, adding and subtracting fractions (with different denominators) and multiplying fractions.

There are 60 pupils in Year 5.

Eden carried out a survey on favourite foods.

\frac{1}{5} of the children said pizza, \frac{2}{6} said burgers and \frac{3}{10} said hot dogs.

How many pupils did she survey altogether?

Answer: 50 pupils

\frac{1}{5} of 60 = 12

\frac{2}{6} 0f 60 = 20

\frac{3}{10} = 18

The Johnson family are driving to the zoo.

They have driven \frac{5}{9} of their journey, which is 45 miles.

How much further do they have to drive, to reach their holiday home?

Answer: 20 miles left to drive

\frac{5}{9} = 45, therefore \frac{1}{9} = 45 ÷ 9 = 5. 

\frac{5}{9} = 5 x 5 = 25 miles

\frac{9}{9} = 9 x 5 = 45 miles

45 – 25 = 20

Macy is taking part in the school maths challenge. 

She is given a word problems worksheet containing 36 questions.

Macy gets \frac{7}{9} of the questions correct.

How many does she get wrong?

Answer: 8 questions wrong

\frac{1}{9} of 36 = 4

\frac{7}{9} = 28

\frac{2}{9} = 8

Oliver and Zac are making smoothies.

They make 800 ml of smoothies.

\frac{2}{5} is made from apples, \frac{3}{7} from strawberries and the rest from orange juice.

How many ml of orange juice do they add to the apples and strawberries?

Answer: 180ml orange juice

\frac{2}{5} of 800: \frac{1}{5} = 160ml, \frac{2}{5} = 320 ml apple juice

\frac{3}{8} of 800: \frac{1}{8} = 100, \frac{3}{8} = 300 ml strawberry juice

800 – 620 = 180ml 

Word problems for year 6 include adding and subtracting fractions with different denominators and mixed numbers, multiplying fractions, dividing fractions by whole numbers and finding equivalent fractions, decimals and percentages.

Children in a Year 6 Class at Oak Tree Middle School are answering a set of ratio questions. 

There are 10 questions and 28 children completing the activity. 

If the children got \frac{6}{7} of the total number of questions correct between them. 

How many did they get wrong?

Answer: 40 questions wrong

28 x 10 = 280 questions

\frac{1}{7} of 280 = 40 

\frac{6}{7} = 40 x 6 = 240

Amber and her 5 friends are sharing 4 pizzas for her birthday party.

The pizzas are split into sixths. 

If they each eat the same amount of pizza, how many slices does each person at the party get?

Answer: 4 slices

This is a dividing fractions word problem

\frac{24}{6} ÷ 6 = \frac{4}{6}

A group of friends win a quarter of the total lottery prize for the week.

There are 4 friends and each friend shares an equal fraction of the quarter.

What fraction of the total lottery prize does each friend get?

Answer: \frac{1}{16} of the prize fund

Each friend gets \frac{1}{4} of the \frac{1}{4} prize fund

There are 30 children in the class

\frac{7}{10} of the pupils in the class are girls.

\frac{3}{7} of the girls have their ears pierced.

How many girls have their ears pierced?

Answer: 9 girls have their ears pierced

\frac{1}{10} = 3, \ \frac{7}{10} = 21 girls

\frac{1}{7} of 21 = 3. \ \frac{3}{7} = 3 x 3 = 9

Third Space Learning offers a wide range of practice word problems for all primary year groups and covering a large number of topics, including; time word problems , ratio word problems , fraction questions , addition word problems and subtraction word problems .

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist primary maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn how tutors develop pupils’ maths fluency or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils

What Is Numicon? Explained For Primary School Teachers, Parents And Pupils

FREE Guide to Maths Mastery

All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.

Ideal for running staff meetings on mastery or sense checking your own approach to mastery.

Privacy Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.26: Solving Fractional Equations

• Last updated
• Save as PDF
• Page ID 48329

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

A fractional equation is an equation involving fractions which has the unknown in the denominator of one or more of its terms.

Example 24.1

The following are examples of fractional equations:

a) \(\frac{3}{x}=\frac{9}{20}\)

b) \(\frac{x-2}{x+2}=\frac{3}{5}\)

c) \(\frac{3}{x-3}=\frac{4}{x-5}\)

d) \(\frac{3}{4}-\frac{1}{8 x}=0\)

e) \(\frac{x}{6}-\frac{2}{3 x}=\frac{2}{3}\)

The Cross-Product property can be used to solve fractional equations.

Cross-Product Property

If \(\frac{A}{B}=\frac{C}{D}\) then \(A \cdot D=B \cdot C\).

Using this property we can transform fractional equations into non-fractional ones. We must take care when applying this property and use it only when there is a single fraction on each side of the equation. So, fractional equations can be divided into two categories.

I. Single Fractions on Each Side of the Equation

Equations a), b) and c) in Example 24.1 fall into this category. We solve these equations here.

a) Solve \(\frac{3}{x}=\frac{9}{20}\)

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot 20=9 \cdot x \\ \text{Linear Equation} & 60=9 x \\ \text{Divide by 9 both sides} & \frac{60}{9}=x \end{array}\nonumber\]

The solution is \(x=\frac{60}{9}=\frac{20}{3}\).

\[\begin{array}{ll} \text{Cross-Product} & 5 \cdot(x-2)=3 \cdot(x+2) \\ \text{Remove parentheses} & 5 x-10=3 x+6 \\ \text{Linear Equation: isolate the variable} & 5 x-3 x=10+6 \\ & 2 x=16 \\ \text{Divide by 2 both sides} & \frac{2 x}{2}=\frac{16}{2}\end{array}\nonumber\]

the solution is \(x=8\).

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot(x-5)=4 \cdot(x-3) \\ \text{Remove parentheses} & 3 x-15=4 x-12 \\ \text{Linear Equation: isolate the variable} & 3 x-4 x=15-12 \\ & -x=3 \\ \text{Divide by 2 both sides} & \frac{-x}{-1}=\frac{3}{-1}\end{array}\nonumber\]

The solution is \(x=-3\)

Note: If you have a fractional equation and one of the terms is not a fraction, you can always account for that by putting 1 in the denominator. For example:

\[\frac{3}{x}=15\nonumber\]

We re-write the equation so that all terms are fractions.

\[\frac{3}{x}=\frac{15}{1}\nonumber\]

\[\begin{array}{ll} \text{Cross-Product} & 3 \cdot 1=15 \cdot x \\ \text{Linear Equation: isolate the variable} & 3=15 x \\ \text{Divide by 15 both sides} & \frac{3}{15}=\frac{15 x}{15} \end{array}\nonumber\]

The solution is \(x=\frac{3}{15}=\frac{3 \cdot 1}{3 \cdot 5}=\frac{1}{5}\).

II. Multiple Fractions on Either Side of the Equation

Equations d) and e) in Example 24.1 fall into this category. We solve these equations here.

We use the technique for combining rational expressions we learned in Chapter 23 to reduce our problem to a problem with a single fraction on each side of the equation.

d) Solve \(\frac{3}{4}-\frac{1}{8 x}=0\)

First we realize that there are two fractions on the LHS of the equation and thus we cannot use the Cross-Product property immediately. To combine the LHS into a single fraction we do the following:

\[\begin{array}{ll} \text{Find the LCM of the denominators} & 8 x \\ \text{Rewrite each fraction using the LCM} & \frac{3 \cdot 2 x}{8 x}-\frac{1}{8 x}=0 \\ \text{Combine into one fraction} & \frac{6 x-1}{8 x}=0 \\ \text{Re-write the equation so that all terms are fractions} & \frac{6 x-1}{8 x}=\frac{0}{1} \\ \text{Cross-Product} & (6 x-1) \cdot 1=8 x \cdot 0 \\ \text{Remove parentheses} & 6 x-1=0 \\\text{Linear Equation: isolate the variable} & 6 x=1 \\ \text{Divide by 6 both sides} & \frac{6 x}{6}=\frac{1}{6} \end{array}\nonumber\]

The solution is \(x=\frac{1}{6}\).

e) Solve \(\frac{x}{6}+\frac{2}{3 x}=\frac{2}{3}\)

\[\begin{array}{ll} \text{Find the LCM of the denominators of LHS} & 6x \\ \text{Rewrite each fraction on LHS using their LCM} & \frac{x \cdot x}{6 x}+\frac{2 \cdot 2}{6 x}=\frac{2}{3} \\ \frac{x^{2}+4}{6 x}=\frac{2}{3} \text{Combine into one fraction} & \left(x^{2}+4\right) \cdot 3=6 x \cdot 2 \\ \text{Cross-Product} & 3 x^{2}+12=12 x \\ \text{Remove parentheses} & 3 x^{2}-12 x+12=0 \\ \text{Quadratic Equation: Standard form} & 3 x^{2}-12 x+12=0 \\\text{Quadratic Equation: Factor} & 3 \cdot x^{2}-3 \cdot 4 x+3 \cdot 4=0 \\ & 3\left(x^{2}-4 x+4\right)=0 \\ & 3(x-2)(x-2)=0 \\ \text{Divide by 3 both sides} & \frac{3(x-2)(x-2)}{3}=\frac{0}{3} \\ & (x-2)(x-2)=0 \\ \text{Quadratic Equation: Zero-Product Property} & (x-2)=0 \text { or }(x-2)=0 \end{array}\nonumber\]

Since both factors are the same, then \(x-2=0\) gives \(x=2\). The solution is \(x=2\)

Note: There is another method to solve equations that have multiple fractions on either side. It uses the LCM of all denominators in the equation. We demonstrate it here to solve the following equation: \(\frac{3}{2}-\frac{9}{2 x}=\frac{3}{5}\)

\[\begin{array} \text{Find the LCM of all denominators in the equation} & 10x \\ \text{Multiply every fraction (both LHS and RHS) by the LCM} & 10 x \cdot \frac{3}{2}-10 x \cdot \frac{9}{2 x}=10 x \cdot \frac{3}{5} \\ & \frac{10 x \cdot 3}{2}-\frac{10 x \cdot 9}{2 x}=\frac{10 x \cdot 3}{5} \\ \text{Simplify every fraction} & \frac{5 x \cdot 3}{1}-\frac{5 \cdot 9}{1}=\frac{2 x \cdot 3}{1} \\ \text{See how all denominatiors are now 1, thus can be disregarded} & 5 x \cdot 3-5 \cdot 9=2 x \cdot 3 \\ \text{Solve like you would any other equation} & 15 x-45=6 x \\ \text{Linear equation: islolate the variable} & 15 x-6 x=45 \\ & 9 x=45 \\ & x=\frac{45}{9} \\ & x=5 \end{array} \nonumber\]

The solution is \(x=5\)

Exit Problem

Solve: \(\frac{2}{x}+\frac{1}{3}=\frac{1}{2}\)

Fraction Word Problems - Introductory

Related Pages Fraction Word Problems: Examples Harder Fraction Word Problems Singapore Math Lessons Fraction Problems Using Algebra More Math Word Problems

Lessons on solving fraction word problems using visual methods like bar models or tape diagrams.

Printable “Fraction Word Problems” Worksheets: Fraction Word Problems (Add, Subtract) 2-Step Fraction Word Problems (Add, Subtract) 1-Step Mixed Number Word Problems (Add, Subtract) 2-Step Mixed Number Word Problems (Add, Subtract) Fraction Word Problems (Add, Subtract, Multiply) Fraction Word Problems (Tape Diagrams)

Here are some examples of fraction word problems. We will illustrate how block diagrams can be used to help you to visualize the fraction word problems in terms of the information given and the answer that needs to be found. Block Diagrams, (also called Tape Diagrams) are used in Singapore Math and the Common Core.

1 unit = 21 3 units = 21 × 3 = 63

Answer: The sum of money is $63

3 units = 24 1 unit = 24 ÷ 3 = 8 5 units = 5 × 8 = 40

Answer: There were 40 children in the group.

2 units = 14 1 unit = 7 5 units = 7 × 5 = 35

Answer: Bill originally had 35 stamps.

5 units = 30 1 unit = 6 3 units = 3 × 6 = 18

Answer: He bought 18 burgers.

How to create bar models for fraction word problems?

Problem 1: Grace thought that a plane journey would take 7/10 h but the actual journey took 1/5 h longer. How long did the actual journey take?

Problem 2: Timothy took 2/3 h to paint a portrait. This was 1/3 h shorter than the time he took to paint scenery. How long did he take to paint scenery?

How to solve fraction word problems using bar models?

Problem: A craft store has a 9 yd spool of ribbon. In the morning, a customer buys 1/5 yd of ribbon from the spool. In the afternoon another customer buys 7/10 yd of ribbon from the spool. How much ribbon is left?

How to use bar models to solve a word problem that involves adding fractions with unlike denominators?

The first step is to find the same denominator. Then add and subtract because you have the same unit or denominator.

Problem: Kayla counted her Halloween treats. She counted 1/4 of a pound of lollipops and 2/7 of a pound of gobstoppers. She also counted 1/3 of a pound of mints.

How many pounds of candy did Kayla have altogether?

How to solve a problem involving fractions of fractions and fractions of remaining parts?

Problem: 1/4 of my trail mix recipe is raisins and the rest is nuts. 3/5 of the nuts are peanuts and the rest are almonds. What fraction of my trail mix are almonds?

How to solve word problems by multiplying a fraction by a whole number?

It uses the Singapore math modeling strategy of a bar model and the “unitary method”.

Problem: Sean has 63 classical song in his mp3 player. That is 7/8 of his entire collection. How many songs does Sean have altogether?

How to use bar models in a word problem that involves multiplying fractions?

Example: Philip purchased 1/4 pound of fruit. He ate half of the fruit after lunch. How much fruit did Philip eat?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Fractions Unpacked

Exploring Fractions   Age 5 to 11

Fractions Unpacked - Starting Points   Age 5 to 11

Fractions Unpacked - Progression in Fractions Through Problem Solving   Age 5 to 11

• More Fractions Lower Primary
• More Fractions Upper Primary
• History of Fractions
• Models in Mind

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Math Word Problems

Welcome to the math word problems worksheets page at Math-Drills.com! On this page, you will find Math word and story problems worksheets with single- and multi-step solutions on a variety of math topics including addition, multiplication, subtraction, division and other math topics. It is usually a good idea to ensure students already have a strategy or two in place to complete the math operations involved in a particular question. For example, students may need a way to figure out what 7 × 8 is or have previously memorized the answer before you give them a word problem that involves finding the answer to 7 × 8.

There are a number of strategies used in solving math word problems; if you don't have a favorite, try the Math-Drills.com problem-solving strategy:

• Question : Understand what the question is asking. What operation or operations do you need to use to solve this question? Ask for help to understand the question if you can't do it on your own.
• Estimate : Use an estimation strategy, so you can check your answer for reasonableness in the evaluate step. Try underestimating and overestimating, so you know what range the answer is supposed to be in. Be flexible in rounding numbers if it will make your estimate easier.
• Strategize : Choose a strategy to solve the problem. Will you use mental math, manipulatives, or pencil and paper? Use a strategy that works for you. Save the calculator until the evaluate stage.
• Calculate : Use your strategy to solve the problem.
• Evaluate : Compare your answer to your estimate. If you under and overestimated, is the answer in the correct range. If you rounded up or down, does the answer make sense (e.g. is it a little less or a little more than the estimate). Also check with a calculator.

Most Popular Math Word Problems this Week

Arithmetic Word Problems

• Addition Word Problems One-Step Addition Word Problems Using Single-Digit Numbers One-Step Addition Word Problems Using Two-Digit Numbers
• Subtraction Word Problems Subtraction Facts Word Problems With Differences from 5 to 12
• Multiplication Word Problems One-Step Multiplication Word Problems up to 10 × 10
• Division Word Problems Division Facts Word Problems with Quotients from 5 to 12
• Multi-Step Word Problems Easy Multi-Step Word Problems

Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.

Teens come up with answer to problem that stumped math world for centuries

A s the school year ends, many students will be only too happy to see math classes in their rearview mirrors. It may seem to some of us non-mathematicians that geometry and trigonometry were created by the Greeks as a form of torture, so imagine our amazement when we heard two high school seniors had proved a mathematical puzzle that was thought to be impossible for 2,000 years. 

We met Calcea Johnson and Ne'Kiya Jackson at their all-girls Catholic high school in New Orleans. We expected to find two mathematical prodigies.

Instead, we found at St. Mary's Academy , all students are told their possibilities are boundless.

Come Mardi Gras season, New Orleans is alive with colorful parades, replete with floats, and beads, and high school marching bands.

In a city where uniqueness is celebrated, St. Mary's stands out – with young African American women playing trombones and tubas, twirling batons and dancing - doing it all, which defines St. Mary's, students told us.

Junior Christina Blazio says the school instills in them they have the ability to accomplish anything. 

Christina Blazio: That is kinda a standard here. So we aim very high - like, our aim is excellence for all students. 

The private Catholic elementary and high school sits behind the Sisters of the Holy Family Convent in New Orleans East. The academy was started by an African American nun for young Black women just after the Civil War. The church still supports the school with the help of alumni.

In December 2022, seniors Ne'Kiya Jackson and Calcea Johnson were working on a school-wide math contest that came with a cash prize.

Ne'Kiya Jackson: I was motivated because there was a monetary incentive.

Calcea Johnson: 'Cause I was like, "$500 is a lot of money. So I-- I would like to at least try."

Both were staring down the thorny bonus question.

Bill Whitaker: So tell me, what was this bonus question?

Calcea Johnson: It was to create a new proof of the Pythagorean Theorem. And it kind of gave you a few guidelines on how would you start a proof.

The seniors were familiar with the Pythagorean Theorem, a fundamental principle of geometry. You may remember it from high school: a² + b² = c². In plain English, when you know the length of two sides of a right triangle, you can figure out the length of the third.

Both had studied geometry and some trigonometry, and both told us math was not easy. What no one told  them  was there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible, … and that was the bonus question facing them.

Bill Whitaker: When you looked at the question did you think, "Boy, this is hard"?

Ne'Kiya Jackson: Yeah. 

Bill Whitaker: What motivated you to say, "Well, I'm going to try this"?

Calcea Johnson: I think I was like, "I started something. I need to finish it." 

Bill Whitaker: So you just kept on going.

Calcea Johnson: Yeah.

For two months that winter, they spent almost all their free time working on the proof.

CeCe Johnson: She was like, "Mom, this is a little bit too much."

CeCe and Cal Johnson are Calcea's parents.

CeCe Johnson: So then I started looking at what she really was doing. And it was pages and pages and pages of, like, over 20 or 30 pages for this one problem.

Cal Johnson: Yeah, the garbage can was full of papers, which she would, you know, work out the problems and-- if that didn't work she would ball it up, throw it in the trash. 

Bill Whitaker: Did you look at the problem? 

Neliska Jackson is Ne'Kiya's mother.

Neliska Jackson: Personally I did not. 'Cause most of the time I don't understand what she's doing (laughter).

Michelle Blouin Williams: What if we did this, what if I write this? Does this help? ax² plus ….

Their math teacher, Michelle Blouin Williams, initiated the math contest.

Bill Whitaker: And did you think anyone would solve it?

Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't—

Bill Whitaker: What were you looking for?

Michelle Blouin Williams: I was just looking for some ingenuity, you know—

Calcea and Ne'Kiya delivered on that! They tried to explain their groundbreaking work to 60 Minutes. Calcea's proof is appropriately titled the Waffle Cone.

Calcea Johnson: So to start the proof, we start with just a regular right triangle where the angle in the corner is 90°. And the two angles are alpha and beta.

Bill Whitaker: Uh-huh

Calcea Johnson: So then what we do next is we draw a second congruent, which means they're equal in size. But then we start creating similar but smaller right triangles going in a pattern like this. And then it continues for infinity. And eventually it creates this larger waffle cone shape.

Calcea Johnson: Am I going a little too—

Bill Whitaker: You've been beyond me since the beginning. (laughter) 

Bill Whitaker: So how did you figure out the proof?

Ne'Kiya Jackson: Okay. So you have a right triangle, 90° angle, alpha and beta.

Bill Whitaker: Then what did you do?

Ne'Kiya Jackson: Okay, I have a right triangle inside of the circle. And I have a perpendicular bisector at OP to divide the triangle to make that small right triangle. And that's basically what I used for the proof. That's the proof.

Bill Whitaker: That's what I call amazing.

Ne'Kiya Jackson: Well, thank you.

There had been one other documented proof of the theorem using trigonometry by mathematician Jason Zimba in 2009 – one in 2,000 years. Now it seems Ne'Kiya and Calcea have joined perhaps the most exclusive club in mathematics. 

Bill Whitaker: So you both independently came up with proof that only used trigonometry.

Ne'Kiya Jackson: Yes.

Bill Whitaker: So are you math geniuses?

Calcea Johnson: I think that's a stretch. 

Bill Whitaker: If not genius, you're really smart at math.

Ne'Kiya Jackson: Not at all. (laugh) 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

Ne'Kiya Jackson: Well, our teacher approached us and was like, "Hey, you might be able to actually present this," I was like, "Are you joking?" But she wasn't. So we went. I got up there. We presented and it went well, and it blew up.

Bill Whitaker: It blew up.

Calcea Johnson: Yeah. 

Ne'Kiya Jackson: It blew up.

Bill Whitaker: Yeah. What was the blowup like?

Calcea Johnson: Insane, unexpected, crazy, honestly.

It took millenia to prove, but just a minute for word of their accomplishment to go around the world. They got a write-up in South Korea and a shout-out from former first lady Michelle Obama, a commendation from the governor and keys to the city of New Orleans. 

Bill Whitaker: Why do you think so many people found what you did to be so impressive?

Ne'Kiya Jackson: Probably because we're African American, one. And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part.

Bill Whitaker: So you think people were surprised that young African American women, could do such a thing?

Calcea Johnson: Yeah, definitely.

Ne'Kiya Jackson: I'd like to actually be celebrated for what it is. Like, it's a great mathematical achievement.

Achievement, that's a word you hear often around St. Mary's academy. Calcea and Ne'Kiya follow a long line of barrier-breaking graduates. 

The late queen of Creole cooking, Leah Chase , was an alum. so was the first African-American female New Orleans police chief, Michelle Woodfork …

And judge for the Fifth Circuit Court of Appeals, Dana Douglas. Math teacher Michelle Blouin Williams told us Calcea and Ne'Kiya are typical St. Mary's students.  

Bill Whitaker: They're not unicorns.

Michelle Blouin Williams: Oh, no no. If they are unicorns, then every single lady that has matriculated through this school is a beautiful, Black unicorn.

Pamela Rogers: You're good?

Pamela Rogers, St. Mary's president and interim principal, told us the students hear that message from the moment they walk in the door.

Pamela Rogers: We believe all students can succeed, all students can learn. It does not matter the environment that you live in. 

Bill Whitaker: So when word went out that two of your students had solved this almost impossible math problem, were they universally applauded?

Pamela Rogers: In this community, they were greatly applauded. Across the country, there were many naysayers.

Bill Whitaker: What were they saying?

Pamela Rogers: They were saying, "Oh, they could not have done it. African Americans don't have the brains to do it." Of course, we sheltered our girls from that. But we absolutely did not expect it to come in the volume that it came.  

Bill Whitaker: And after such a wonderful achievement.

Pamela Rogers: People-- have a vision of who can be successful. And-- to some people, it is not always an African American female. And to us, it's always an African American female.

Gloria Ladson-Billings: What we know is when teachers lay out some expectations that say, "You can do this," kids will work as hard as they can to do it.

Gloria Ladson-Billings, professor emeritus at the University of Wisconsin, has studied how best to teach African American students. She told us an encouraging teacher can change a life.

Bill Whitaker: And what's the difference, say, between having a teacher like that and a whole school dedicated to the excellence of these students?

Gloria Ladson-Billings: So a whole school is almost like being in Heaven. 

Bill Whitaker: What do you mean by that?

Gloria Ladson-Billings: Many of our young people have their ceilings lowered, that somewhere around fourth or fifth grade, their thoughts are, "I'm not going to be anything special." What I think is probably happening at St. Mary's is young women come in as, perhaps, ninth graders and are told, "Here's what we expect to happen. And here's how we're going to help you get there."

At St. Mary's, half the students get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. Here, there's no test to get in, but expectations are high and rules are strict: no cellphones, modest skirts, hair must be its natural color.

Students Rayah Siddiq, Summer Forde, Carissa Washington, Tatum Williams and Christina Blazio told us they appreciate the rules and rigor.

Rayah Siddiq: Especially the standards that they set for us. They're very high. And I don't think that's ever going to change.

Bill Whitaker: So is there a heart, a philosophy, an essence to St. Mary's?

Summer Forde: The sisterhood—

Carissa Washington: Sisterhood.

Tatum Williams: Sisterhood.

Bill Whitaker: The sisterhood?

Voices: Yes.

Bill Whitaker: And you don't mean the nuns. You mean-- (laughter)

Christina Blazio: I mean, yeah. The community—

Bill Whitaker: So when you're here, there's just no question that you're going to go on to college.

Rayah Siddiq: College is all they talk about. (laughter) 

Pamela Rogers: … and Arizona State University (Cheering)

Principal Rogers announces to her 615 students the colleges where every senior has been accepted.

Bill Whitaker: So for 17 years, you've had a 100% graduation rate—

Pamela Rogers: Yes.

Bill Whitaker: --and a 100% college acceptance rate?

Pamela Rogers: That's correct.

Last year when Ne'Kiya and Calcea graduated, all their classmates went to college and got scholarships. Ne'Kiya got a full ride to the pharmacy school at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University.

Bill Whitaker: So wait a minute. Neither one of you is going to pursue a career in math?

Both: No. (laugh)

Calcea Johnson: I may take up a minor in math. But I don't want that to be my job job.

Ne'Kiya Jackson: Yeah. People might expect too much out of me if (laugh) I become a mathematician. (laugh)

But math is not completely in their rear-view mirrors. This spring they submitted their high school proofs for final peer review and publication … and are still working on further proofs of the Pythagorean Theorem. Since their first two …

Calcea Johnson: We found five. And then we found a general format that could potentially produce at least five additional proofs.

Bill Whitaker: And you're not math geniuses?

Bill Whitaker: I'm not buying it. (laughs)

Produced by Sara Kuzmarov. Associate producer, Mariah B. Campbell. Edited by Daniel J. Glucksman.

Game Central

Similar problems from web search.

ChatGPT’s Next Magic Trick Is Singing and Solving Math Problems With Your Phone Camera

GPT-4o responds as fast as humans.

ChatGPT 4 may still be relatively new, but OpenAI is already iterating with an upgrade that can respond as quickly as humans do in normal conversation. The company showed off GPT-4o in a live demo , showing off its ability to use your phone’s camera to solve math equations and deliver a much more conversational voice assistant experience.

While we only have the event demo to go off of, GPT-4o looks impressive. It doesn’t even have to wait for you to finish your request and can roll with interruptions mid-prompt, bringing one step closer to living out Her in real life.

Even Faster Response Times

According to OpenAI, the GPT-4o model can respond as fast as 232 milliseconds to audio inputs. More realistically, it averages around 320 milliseconds to respond, which OpenAI said is similar to how fast humans respond in conversation.

On top of the speed, GPT-4o can handle interruptions and any adjustment requests. As seen in the bedtime story demo, GPT-4o immediately stopped talking when interrupted and quickly handled requests like adding more dramatic inflections, narrating in a robot voice, and even singing the entire prompt out loud. If that demo doesn’t convince you, two GPT-4o models improvising a song together should.

GPT-4o isn’t just more responsive to voice, it can also see better. The new vision features allow it to see through your device’s camera and understand things like handwritten math equations or messages . It’s eerie how genuinely touched GPT-4o sounds when it sees and understands a message that says “I Heart ChatGPT.” Even more impressive, GPT-4o can handle coding tasks and live translations between two people. This should feel way more natural than Google Translate when you’re trying to have a conversation in a foreign country.

Available for Free

OpenAI said the text and image capabilities for GPT-4o roll out today, but the voice feature will be coming to alpha within ChatGPT Plus in the coming weeks. Once it’s fully ready, the upgraded ChatGPT model will be available to all users, subscribers or otherwise. However, if you pay $20 per month for ChatGPT Plus , you’ll get five times the message limits of GPT-4o compared to the free version.

Anytime a large language model gets such an impressive update, we have to consider the potential for misuse . Considering how smoothly the live demo for solving the equation went, it looks like an even better way to help students get out of their math homework. However, OpenAI said that GPT-4o was built with new safety systems to offer guardrails on voice outputs. We’ll have to wait and see if these guardrails are enough.

How to use math.sin() to spin a wheel?

I’m trying to use math.sin() to spin a wheel, problem is that it doesn’t go back to 0 and I don’t know why. It’s even harder because I still haven’t learned cos, sin and tan at school yet and there aren’t any documentations nor forums helping me understand how to use cos and sin in studio. I’ve understand cos and sin now but I have a problem of making it work in roblox, any help?

the sin function is periodic, meaning after some time it repeats, this isn’t a bad thing on it’s own, but sin is wave:

sin stands for sine, so this is a sine wave. A sine wave might make your wheel go back and forth like it’s on a spring instead of spin like an actual wheel.

You don’t need sine at all the way you’re using it. You already have the angle you want the wheel to be rotated at.

Edit: Just realised this will result in half spins. You don’t need the sine wave at all.

If you want to use sinusoidals to spin a wheel, you can make use of the sinulsodal squared (range is 0 <= x <= 1 ). Each period is pi radians. You can divide this by 2 to get the range where it smoothly transitions from 0 to 1.

As a side note, you shouldn’t be using for loops with a yielding function to spin a wheel. You should be using a connection to the runservice heartbeat and using the elapsed time to calculate the new position of the wheel.

You don’t need math.sin() for this, just add a number to the rotation:

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Solve Max-Cut Problem Using QAOA

This example uses:

• MATLAB Support Package for Quantum Computing MATLAB Support Package for Quantum Computing
• Global Optimization Toolbox Global Optimization Toolbox
• Optimization Toolbox Optimization Toolbox

This example shows how to use the quantum approximate optimization algorithm (QAOA) to solve max-cut problems. The max-cut problem is a graph partitioning problem whose objective is to create two subsets of vertices that maximize the number of edges between the two groups. In this example, you first solve a max-cut problem classically by considering all graph partitions and then solve it using QAOA.

Set up Max-Cut Problem

Generally, the max-cut problem can be expressed as

max   ∑ i , j = 1 N w ij x i ( 1 - x j ) ,

where N is the number of nodes in the graph, x i denotes which node subset node i is in using 0 or 1, and w ij is the weight of the edge between nodes i and j .

Create and plot a four-node graph where all edges have unit weight 1.

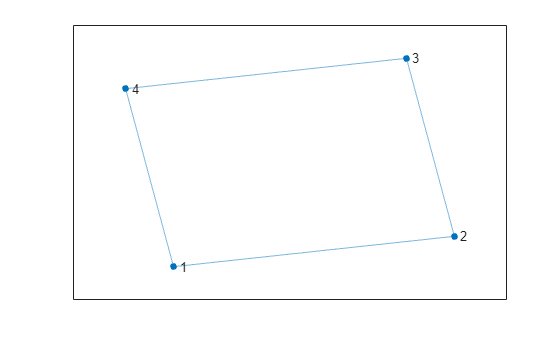
Using the max-cut expression, the objective function to maximize for this graph is:

f = ∑ i , j = 1 4 w ij x i ( 1 - x j )     = ( x 1 ( 1 - x 2 ) + x 2 ( 1 - x 1 ) ) + ( x 1 ( 1 - x 4 ) + x 4 ( 1 - x 1 ) )           + ( x 2 ( 1 - x 3 ) + x 3 ( 1 - x 2 ) ) + ( x 3 ( 1 - x 4 ) + x 4 ( 1 - x 3 ) )

Solve Using Classical Approach

A graph with N nodes has 2 N possible solutions, or ways to partition the nodes into two subsets. For the four-node example, there are 2 4 , or 16, possible solutions. Use the objective function to calculate the solution for each partition and list them in a table. Each row of the allSols table represents a possible partition, and the table variable f represents the objective value for the corresponding partition, or how many edges are between the subsets.

Two solutions maximize the number of edges between the two subsets of nodes. In both solutions, the graph is partitioned so that nodes x 1 and x 3 are in one subset and nodes x 2 and x 4 are in the other subset. These partitions result in four edges between the two groups.

Set Up QAOA Approach

QAOA is a quantum-classical hybrid approach to solving optimization problems. In this hybrid approach, you create a quantum circuit that represents potential solutions to the problem, and a classical optimizer iteratively adjusts the angles in the circuit to improve the quality of the solution. For the max-cut problem, the QAOA approach has steps for initialization, optimization, and termination.

Initialization

Create a QAOA circuit that encodes the max-cut problem. This circuit is composed of Hadamard and rotation gates that are parameterized by the set of angles θ .

Define a set of initial angles θ 0 .

Optimization

Measure the QAOA circuit.

Calculate the expected objective value from the measurements.

Update the angles that are used in the QAOA circuit if the termination criteria is not met.

Termination

Measure the QAOA circuit at the set of angles θ that satisfy the termination criteria.

Return the final values.

This expectedObjectiveValue function implements the algorithm steps for the four-node example.

QAOA Circuit

The QAOA circuit for the max-cut problem uses a set of Hadamard gates, which place all gates in an equal superposition, and layers of cost and mixer gates, as seen in the circuit from [2] . The cost gates encode a Hamiltonian for the objective function of the optimization problem. The mixer gates, which allow the quantum state to transition between energy states, encode a simple Hamiltonian whose maximal state is + + + + . This maximal state is the equal superposition state generated by the initial Hadamard gates and the initial QAOA state.

Create the QAOA circuit for one layer of the max-cut problem using the qaoaCircuit helper function. Here, gamma and beta define the angle of the cost gate and the angle of the mixer gate, respectively. To view the code for this helper function, see Helper Function .

This circuit has four qubits, one for each node in the graph. Four Hadamard gates place all the qubits in an equal superposition and are followed by cost gates, composed of RZZ gates, and mixer gates, composed of RX gates. Each RZZ gate encodes an edge relationship in the original graph.

In general, the alternating cost and mixer gates approximately solve the problem because QAOA is a discretized example of adiabatic quantum computation (AQC), as described in [1] and [2] .

AQC uses a quantum system that combines a mixer Hamiltonian H M , which represents an energy state that is easy to prepare, and a cost Hamiltonian H C , which represents the energy state of the problem of interest. The adiabatic theorem states that if a quantum system starts in the given energy state of H M , then it will remain in that state while H M is evolved to H C , given that the change occurs at a sufficiently slow rate.

The Hamiltonian combination for the max-cut problem is

H ( t ) = t T H C + ( 1 - t T ) H M ,

where T is the total run time of the system. The solution to the Schrödinger equation for this circuit can be written using the Trotter-Suzuki approximation as a series of multiplications of cost and mixer gates.

Simulate Iterations of Max-Cut

Use surrogateopt (Global Optimization Toolbox) with the objective function to maximize the expected objective value. In this example, use two layers of cost-mixer gates and sample the circuit 1000 times each time the optimizer calculates the expected objective value. surrogateopt calculates a global minimum, so the negation of the expected objective value is minimized. Set the maximum number of objective function evaluations to 100.

The best function value is approximately 4. In other words, the maximum number of edges between two subsets of nodes is 4.

Construct the quantum circuit using the optimized angles, and simulate the circuit to see the expected probability distribution over qubit states. The 0101 and 1010 states appear with the highest probabilities, which were the two solutions found when calculating the expected values classically.

Run Final Iteration on QPU

Connect to an IonQ device using quantum.backend.QuantumDeviceAWS . Specify the region of the device and path to a bucket to store results.

Create a task to run the circuit with optimized angles on the QPU. Specify the number of shots as 1000.

Fetch the results and plot a histogram of the states.

The states 0101 and 1010 appear again as the states with the highest probabilities, so the QPU results agree with the local simulation of the circuit.

Helper Function

This code defines the qaoaCircuit helper function.

[1] J., Abhijith, Adetokunbo Adedoyin, John Ambrosiano, Petr Anisimov, William Casper, Gopinath Chennupati, Carleton Coffrin, et al. “Quantum Algorithm Implementations for Beginners.” ACM Transactions on Quantum Computing 3, no. 4 (December 31, 2022): 1–92. https://doi.org/10.1145/3517340 .

[2] Zhou, Leo, Sheng-Tao Wang, Soonwon Choi, Hannes Pichler, and Mikhail D. Lukin. “Quantum Approximate Optimization Algorithm: Performance, Mechanism, and Implementation on Near-Term Devices.” Physical Review X 10, no. 2 (June 24, 2020): 021067. https://doi.org/10.1103/PhysRevX.10.021067 .

quantumCircuit

Related Topics

• Workflow for QUBO Problems

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

• Share full article

For more audio journalism and storytelling, download New York Times Audio , a new iOS app available for news subscribers.

• May 15, 2024   •   25:48 The Possible Collapse of the U.S. Home Insurance System
• May 14, 2024   •   35:20 Voters Want Change. In Our Poll, They See It in Trump.
• May 13, 2024   •   27:46 How Biden Adopted Trump’s Trade War With China
• May 10, 2024   •   27:42 Stormy Daniels Takes the Stand
• May 9, 2024   •   34:42 One Strongman, One Billion Voters, and the Future of India
• May 8, 2024   •   28:28 A Plan to Remake the Middle East
• May 7, 2024   •   27:43 How Changing Ocean Temperatures Could Upend Life on Earth
• May 6, 2024   •   29:23 R.F.K. Jr.’s Battle to Get on the Ballot
• May 3, 2024   •   25:33 The Protesters and the President
• May 2, 2024   •   29:13 Biden Loosens Up on Weed
• May 1, 2024   •   35:16 The New Abortion Fight Before the Supreme Court
• April 30, 2024   •   27:40 The Secret Push That Could Ban TikTok

The Possible Collapse of the U.S. Home Insurance System

A times investigation found climate change may now be a concern for every homeowner in the country..

Hosted by Sabrina Tavernise

Featuring Christopher Flavelle

Produced by Nina Feldman ,  Shannon M. Lin and Jessica Cheung

Edited by MJ Davis Lin

With Michael Benoist

Original music by Dan Powell ,  Marion Lozano and Rowan Niemisto

Engineered by Alyssa Moxley

Listen and follow The Daily Apple Podcasts | Spotify | Amazon Music | YouTube

Across the United States, more frequent extreme weather is starting to cause the home insurance market to buckle, even for those who have paid their premiums dutifully year after year.

Christopher Flavelle, a climate reporter, discusses a Times investigation into one of the most consequential effects of the changes.

On today’s episode

Christopher Flavelle , a climate change reporter for The New York Times.

Background reading

As American insurers bleed cash from climate shocks , homeowners lose.

See how the home insurance crunch affects the market in each state .

Here are four takeaways from The Times’s investigation.

There are a lot of ways to listen to The Daily. Here’s how.

We aim to make transcripts available the next workday after an episode’s publication. You can find them at the top of the page.

Christopher Flavelle contributed reporting.

The Daily is made by Rachel Quester, Lynsea Garrison, Clare Toeniskoetter, Paige Cowett, Michael Simon Johnson, Brad Fisher, Chris Wood, Jessica Cheung, Stella Tan, Alexandra Leigh Young, Lisa Chow, Eric Krupke, Marc Georges, Luke Vander Ploeg, M.J. Davis Lin, Dan Powell, Sydney Harper, Mike Benoist, Liz O. Baylen, Asthaa Chaturvedi, Rachelle Bonja, Diana Nguyen, Marion Lozano, Corey Schreppel, Rob Szypko, Elisheba Ittoop, Mooj Zadie, Patricia Willens, Rowan Niemisto, Jody Becker, Rikki Novetsky, John Ketchum, Nina Feldman, Will Reid, Carlos Prieto, Ben Calhoun, Susan Lee, Lexie Diao, Mary Wilson, Alex Stern, Dan Farrell, Sophia Lanman, Shannon Lin, Diane Wong, Devon Taylor, Alyssa Moxley, Summer Thomad, Olivia Natt, Daniel Ramirez and Brendan Klinkenberg.

Our theme music is by Jim Brunberg and Ben Landsverk of Wonderly. Special thanks to Sam Dolnick, Paula Szuchman, Lisa Tobin, Larissa Anderson, Julia Simon, Sofia Milan, Mahima Chablani, Elizabeth Davis-Moorer, Jeffrey Miranda, Renan Borelli, Maddy Masiello, Isabella Anderson and Nina Lassam.

Christopher Flavelle is a Times reporter who writes about how the United States is trying to adapt to the effects of climate change. More about Christopher Flavelle

Advertisement