problem solving and math

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.1: Introduction to Problem Solving

• Last updated
• Save as PDF
• Page ID 9821

• Michelle Manes
• University of Hawaii

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The Common Core State Standards for Mathematics ( http://www.corestandards.org/Math/Practice ) identify eight “Mathematical Practices” — the kinds of expertise that all teachers should try to foster in their students, but they go far beyond any particular piece of mathematics content. They describe what mathematics is really about, and why it is so valuable for students to master. The very first Mathematical Practice is:

Make sense of problems and persevere in solving them.

Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary.

This chapter will help you develop these very important mathematical skills, so that you will be better prepared to help your future students develop them. Let’s start with solving a problem!

Draw curves connecting A to A, B to B, and C to C. Your curves cannot cross or even touch each other,they cannot cross through any of the lettered boxes, and they cannot go outside the large box or even touch it’s sides.

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it).

• What did you try?
• What makes this problem difficult?
• Can you change the problem slightly so that it would be easier to solve?

Problem Solving Strategy 1 (Wishful Thinking).

Do you wish something in the problem was different? Would it then be easier to solve the problem?

For example, what if ABC problem had a picture like this:

Can you solve this case and use it to help you solve the original case? Think about moving the boxes around once the lines are already drawn.

Here is one possible solution.

• Our Mission

6 Tips for Teaching Math Problem-Solving Skills

Solving word problems is tougher than computing with numbers, but elementary teachers can guide students to do the deep thinking involved.

A growing concern with students is the ability to problem-solve, especially with complex, multistep problems. Data shows that students struggle more when solving word problems than they do with computation , and so problem-solving should be considered separately from computation. Why?

Consider this. When we’re on the way to a new destination and we plug in our location to a map on our phone, it tells us what lane to be in and takes us around any detours or collisions, sometimes even buzzing our watch to remind us to turn. When I experience this as a driver, I don’t have to do the thinking. I can think about what I’m going to cook for dinner, not paying much attention to my surroundings other than to follow those directions. If I were to be asked to go there again, I wouldn’t be able to remember, and I would again seek help.

If we can switch to giving students strategies that require them to think instead of giving them too much support throughout the journey to the answer, we may be able to give them the ability to learn the skills to read a map and have several ways to get there.

Here are six ways we can start letting students do this thinking so that they can go through rigorous problem-solving again and again, paving their own way to the solution. 

1. Link problem-solving to reading

When we can remind students that they already have many comprehension skills and strategies they can easily use in math problem-solving, it can ease the anxiety surrounding the math problem. For example, providing them with strategies to practice, such as visualizing, acting out the problem with math tools like counters or base 10 blocks, drawing a quick sketch of the problem, retelling the story in their own words, etc., can really help them to utilize the skills they already have to make the task less daunting.

We can break these skills into specific short lessons so students have a bank of strategies to try on their own. Here's an example of an anchor chart that they can use for visualizing . Breaking up comprehension into specific skills can increase student independence and help teachers to be much more targeted in their problem-solving instruction. This allows students to build confidence and break down the barriers between reading and math to see they already have so many strengths that are transferable to all problems.

2. Avoid boxing students into choosing a specific operation

It can be so tempting to tell students to look for certain words that might mean a certain operation. This might even be thoroughly successful in kindergarten and first grade, but just like when our map tells us where to go, that limits students from becoming deep thinkers. It also expires once they get into the upper grades, where those words could be in a problem multiple times, creating more confusion when students are trying to follow a rule that may not exist in every problem.

We can encourage a variety of ways to solve problems instead of choosing the operation first. In first grade, a problem might say, “Joceline has 13 stuffed animals and Jordan has 17. How many more does Jordan have?” Some students might choose to subtract, but a lot of students might just count to find the amount in between. If we tell them that “how many more” means to subtract, we’re taking the thinking out of the problem altogether, allowing them to go on autopilot without truly solving the problem or using their comprehension skills to visualize it. 

3. Revisit ‘representation’

The word “representation” can be misleading. It seems like something to do after the process of solving. When students think they have to go straight to solving, they may not realize that they need a step in between to be able to support their understanding of what’s actually happening in the problem first.

Using an anchor chart like one of these ( lower grade , upper grade ) can help students to choose a representation that most closely matches what they’re visualizing in their mind. Once they sketch it out, it can give them a clearer picture of different ways they could solve the problem.

Think about this problem: “Varush went on a trip with his family to his grandmother’s house. It was 710 miles away. On the way there, three people took turns driving. His mom drove 214 miles. His dad drove 358 miles. His older sister drove the rest. How many miles did his sister drive?”

If we were to show this student the anchor chart, they would probably choose a number line or a strip diagram to help them understand what’s happening.

If we tell students they must always draw base 10 blocks in a place value chart, that doesn’t necessarily match the concept of this problem. When we ask students to match our way of thinking, we rob them of critical thinking practice and sometimes confuse them in the process. 

4. Give time to process

Sometimes as educators, we can feel rushed to get to everyone and everything that’s required. When solving a complex problem, students need time to just sit with a problem and wrestle with it, maybe even leaving it and coming back to it after a period of time.

This might mean we need to give them fewer problems but go deeper with those problems we give them. We can also speed up processing time when we allow for collaboration and talk time with peers on problem-solving tasks. 

5. Ask questions that let Students do the thinking

Questions or prompts during problem-solving should be very open-ended to promote thinking. Telling a student to reread the problem or to think about what tools or resources would help them solve it is a way to get them to try something new but not take over their thinking.

These skills are also transferable across content, and students will be reminded, “Good readers and mathematicians reread.” 

6. Spiral concepts so students frequently use problem-solving skills

When students don’t have to switch gears in between concepts, they’re not truly using deep problem-solving skills. They already kind of know what operation it might be or that it’s something they have at the forefront of their mind from recent learning. Being intentional within their learning stations and assessments about having a variety of rigorous problem-solving skills will refine their critical thinking abilities while building more and more resilience throughout the school year as they retain content learning in the process. 

Problem-solving skills are so abstract, and it can be tough to pinpoint exactly what students need. Sometimes we have to go slow to go fast. Slowing down and helping students have tools when they get stuck and enabling them to be critical thinkers will prepare them for life and allow them multiple ways to get to their own destination.

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

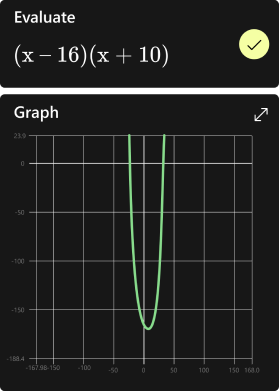
Graph your math problems

Practice, practice, practice

Get math help in your language

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

5 Teaching Mathematics Through Problem Solving

Janet Stramel

In his book “How to Solve It,” George Pólya (1945) said, “One of the most important tasks of the teacher is to help his students. This task is not quite easy; it demands time, practice, devotion, and sound principles. The student should acquire as much experience of independent work as possible. But if he is left alone with his problem without any help, he may make no progress at all. If the teacher helps too much, nothing is left to the student. The teacher should help, but not too much and not too little, so that the student shall have a reasonable share of the work.” (page 1)

What is a problem  in mathematics? A problem is “any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method” (Hiebert, et. al., 1997). Problem solving in mathematics is one of the most important topics to teach; learning to problem solve helps students develop a sense of solving real-life problems and apply mathematics to real world situations. It is also used for a deeper understanding of mathematical concepts. Learning “math facts” is not enough; students must also learn how to use these facts to develop their thinking skills.

According to NCTM (2010), the term “problem solving” refers to mathematical tasks that have the potential to provide intellectual challenges for enhancing students’ mathematical understanding and development. When you first hear “problem solving,” what do you think about? Story problems or word problems? Story problems may be limited to and not “problematic” enough. For example, you may ask students to find the area of a rectangle, given the length and width. This type of problem is an exercise in computation and can be completed mindlessly without understanding the concept of area. Worthwhile problems  includes problems that are truly problematic and have the potential to provide contexts for students’ mathematical development.

There are three ways to solve problems: teaching for problem solving, teaching about problem solving, and teaching through problem solving.

Teaching for problem solving begins with learning a skill. For example, students are learning how to multiply a two-digit number by a one-digit number, and the story problems you select are multiplication problems. Be sure when you are teaching for problem solving, you select or develop tasks that can promote the development of mathematical understanding.

Teaching about problem solving begins with suggested strategies to solve a problem. For example, “draw a picture,” “make a table,” etc. You may see posters in teachers’ classrooms of the “Problem Solving Method” such as: 1) Read the problem, 2) Devise a plan, 3) Solve the problem, and 4) Check your work. There is little or no evidence that students’ problem-solving abilities are improved when teaching about problem solving. Students will see a word problem as a separate endeavor and focus on the steps to follow rather than the mathematics. In addition, students will tend to use trial and error instead of focusing on sense making.

Teaching through problem solving  focuses students’ attention on ideas and sense making and develops mathematical practices. Teaching through problem solving also develops a student’s confidence and builds on their strengths. It allows for collaboration among students and engages students in their own learning.

Consider the following worthwhile-problem criteria developed by Lappan and Phillips (1998):

• The problem has important, useful mathematics embedded in it.
• The problem requires high-level thinking and problem solving.
• The problem contributes to the conceptual development of students.
• The problem creates an opportunity for the teacher to assess what his or her students are learning and where they are experiencing difficulty.
• The problem can be approached by students in multiple ways using different solution strategies.
• The problem has various solutions or allows different decisions or positions to be taken and defended.
• The problem encourages student engagement and discourse.
• The problem connects to other important mathematical ideas.
• The problem promotes the skillful use of mathematics.
• The problem provides an opportunity to practice important skills.

Of course, not every problem will include all of the above. Sometimes, you will choose a problem because your students need an opportunity to practice a certain skill.

Key features of a good mathematics problem includes:

• It must begin where the students are mathematically.
• The feature of the problem must be the mathematics that students are to learn.
• It must require justifications and explanations for both answers and methods of solving.

Problem solving is not a  neat and orderly process. Think about needlework. On the front side, it is neat and perfect and pretty.

But look at the b ack.

It is messy and full of knots and loops. Problem solving in mathematics is also like this and we need to help our students be “messy” with problem solving; they need to go through those knots and loops and learn how to solve problems with the teacher’s guidance.

When you teach through problem solving , your students are focused on ideas and sense-making and they develop confidence in mathematics!

Mathematics Tasks and Activities that Promote Teaching through Problem Solving

Choosing the Right Task

Selecting activities and/or tasks is the most significant decision teachers make that will affect students’ learning. Consider the following questions:

• Teachers must do the activity first. What is problematic about the activity? What will you need to do BEFORE the activity and AFTER the activity? Additionally, think how your students would do the activity.
• What mathematical ideas will the activity develop? Are there connections to other related mathematics topics, or other content areas?
• Can the activity accomplish your learning objective/goals?

Low Floor High Ceiling Tasks

By definition, a “ low floor/high ceiling task ” is a mathematical activity where everyone in the group can begin and then work on at their own level of engagement. Low Floor High Ceiling Tasks are activities that everyone can begin and work on based on their own level, and have many possibilities for students to do more challenging mathematics. One gauge of knowing whether an activity is a Low Floor High Ceiling Task is when the work on the problems becomes more important than the answer itself, and leads to rich mathematical discourse [Hover: ways of representing, thinking, talking, agreeing, and disagreeing; the way ideas are exchanged and what the ideas entail; and as being shaped by the tasks in which students engage as well as by the nature of the learning environment].

The strengths of using Low Floor High Ceiling Tasks:

• Allows students to show what they can do, not what they can’t.
• Provides differentiation to all students.
• Promotes a positive classroom environment.
• Advances a growth mindset in students
• Aligns with the Standards for Mathematical Practice

Examples of some Low Floor High Ceiling Tasks can be found at the following sites:

• YouCubed – under grades choose Low Floor High Ceiling
• NRICH Creating a Low Threshold High Ceiling Classroom
• Inside Mathematics Problems of the Month

Math in 3-Acts

Math in 3-Acts was developed by Dan Meyer to spark an interest in and engage students in thought-provoking mathematical inquiry. Math in 3-Acts is a whole-group mathematics task consisting of three distinct parts:

Act One is about noticing and wondering. The teacher shares with students an image, video, or other situation that is engaging and perplexing. Students then generate questions about the situation.

In Act Two , the teacher offers some information for the students to use as they find the solutions to the problem.

Act Three is the “reveal.” Students share their thinking as well as their solutions.

“Math in 3 Acts” is a fun way to engage your students, there is a low entry point that gives students confidence, there are multiple paths to a solution, and it encourages students to work in groups to solve the problem. Some examples of Math in 3-Acts can be found at the following websites:

• Dan Meyer’s Three-Act Math Tasks
• Graham Fletcher3-Act Tasks ]
• Math in 3-Acts: Real World Math Problems to Make Math Contextual, Visual and Concrete

Number Talks

Number talks are brief, 5-15 minute discussions that focus on student solutions for a mental math computation problem. Students share their different mental math processes aloud while the teacher records their thinking visually on a chart or board. In addition, students learn from each other’s strategies as they question, critique, or build on the strategies that are shared.. To use a “number talk,” you would include the following steps:

• The teacher presents a problem for students to solve mentally.
• Provide adequate “ wait time .”
• The teacher calls on a students and asks, “What were you thinking?” and “Explain your thinking.”
• For each student who volunteers to share their strategy, write their thinking on the board. Make sure to accurately record their thinking; do not correct their responses.
• Invite students to question each other about their strategies, compare and contrast the strategies, and ask for clarification about strategies that are confusing.

“Number Talks” can be used as an introduction, a warm up to a lesson, or an extension. Some examples of Number Talks can be found at the following websites:

• Inside Mathematics Number Talks
• Number Talks Build Numerical Reasoning

Saying “This is Easy”

“This is easy.” Three little words that can have a big impact on students. What may be “easy” for one person, may be more “difficult” for someone else. And saying “this is easy” defeats the purpose of a growth mindset classroom, where students are comfortable making mistakes.

When the teacher says, “this is easy,” students may think,

• “Everyone else understands and I don’t. I can’t do this!”
• Students may just give up and surrender the mathematics to their classmates.
• Students may shut down.

Instead, you and your students could say the following:

• “I think I can do this.”
• “I have an idea I want to try.”
• “I’ve seen this kind of problem before.”

Tracy Zager wrote a short article, “This is easy”: The Little Phrase That Causes Big Problems” that can give you more information. Read Tracy Zager’s article here.

Using “Worksheets”

Do you want your students to memorize concepts, or do you want them to understand and apply the mathematics for different situations?

What is a “worksheet” in mathematics? It is a paper and pencil assignment when no other materials are used. A worksheet does not allow your students to use hands-on materials/manipulatives [Hover: physical objects that are used as teaching tools to engage students in the hands-on learning of mathematics]; and worksheets are many times “naked number” with no context. And a worksheet should not be used to enhance a hands-on activity.

Students need time to explore and manipulate materials in order to learn the mathematics concept. Worksheets are just a test of rote memory. Students need to develop those higher-order thinking skills, and worksheets will not allow them to do that.

One productive belief from the NCTM publication, Principles to Action (2014), states, “Students at all grade levels can benefit from the use of physical and virtual manipulative materials to provide visual models of a range of mathematical ideas.”

You may need an “activity sheet,” a “graphic organizer,” etc. as you plan your mathematics activities/lessons, but be sure to include hands-on manipulatives. Using manipulatives can

• Provide your students a bridge between the concrete and abstract
• Serve as models that support students’ thinking
• Provide another representation
• Support student engagement
• Give students ownership of their own learning.

Adapted from “ The Top 5 Reasons for Using Manipulatives in the Classroom ”.

any task or activity for which the students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific ‘correct’ solution method

should be intriguing and contain a level of challenge that invites speculation and hard work, and directs students to investigate important mathematical ideas and ways of thinking toward the learning

involves teaching a skill so that a student can later solve a story problem

when we teach students how to problem solve

teaching mathematics content through real contexts, problems, situations, and models

a mathematical activity where everyone in the group can begin and then work on at their own level of engagement

20 seconds to 2 minutes for students to make sense of questions

Mathematics Methods for Early Childhood Copyright © 2021 by Janet Stramel is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book

Problem Solving in Mathematics Education

• Open Access
• First Online: 28 June 2016

Cite this chapter

You have full access to this open access chapter

• Peter Liljedahl 6 ,
• Manuel Santos-Trigo 7 ,
• Uldarico Malaspina 8 &
• Regina Bruder 9  

Part of the book series: ICME-13 Topical Surveys ((ICME13TS))

91k Accesses

14 Citations

Problem solving in mathematics education has been a prominent research field that aims at understanding and relating the processes involved in solving problems to students’ development of mathematical knowledge and problem solving competencies. The accumulated knowledge and field developments include conceptual frameworks to characterize learners’ success in problem solving activities, cognitive, metacognitive, social and affective analysis, curriculum proposals, and ways to foster problem solving approaches. In the survey, four interrelated areas are reviewed: (i) the relevance of heuristics in problem solving approaches—why are they important and what research tells us about their use? (ii) the need to characterize and foster creative problem solving approaches—what type of heuristics helps learners think of and practice creative solutions? (iii) the importance for learners to formulate and pursue their own problems; and (iv) the role played by the use of both multiple purpose and ad hoc mathematical action types of technologies in problem solving activities—what ways of reasoning do learners construct when they rely on the use of digital technologies and how technology and technology approaches can be reconciled?

You have full access to this open access chapter,  Download chapter PDF

• Mathematical Problem
• Prospective Teacher
• Creative Process
• Digital Technology
• Mathematical Task

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Mathematical problem solving has long been seen as an important aspect of mathematics, the teaching of mathematics, and the learning of mathematics. It has infused mathematics curricula around the world with calls for the teaching of problem solving as well as the teaching of mathematics through problem solving. And as such, it has been of interest to mathematics education researchers for as long as our field has existed. More relevant, mathematical problem solving has played a part in every ICME conference, from 1969 until the forthcoming meeting in Hamburg, wherein mathematical problem solving will reside most centrally within the work of Topic Study 19: Problem Solving in Mathematics Education. This booklet is being published on the occasion of this Topic Study Group.

To this end, we have assembled four summaries looking at four distinct, yet inter-related, dimensions of mathematical problem solving. The first summary, by Regina Bruder, is a nuanced look at heuristics for problem solving. This notion of heuristics is carried into Peter Liljedahl’s summary, which looks specifically at a progression of heuristics leading towards more and more creative aspects of problem solving. This is followed by Luz Manuel Santos Trigo’s summary introducing us to problem solving in and with digital technologies. The last summary, by Uldarico Malaspina Jurado, documents the rise of problem posing within the field of mathematics education in general and the problem solving literature in particular.

Each of these summaries references in some critical and central fashion the works of George Pólya or Alan Schoenfeld. To the initiated researchers, this is no surprise. The seminal work of these researchers lie at the roots of mathematical problem solving. What is interesting, though, is the diverse ways in which each of the four aforementioned contributions draw on, and position, these works so as to fit into the larger scheme of their respective summaries. This speaks to not only the depth and breadth of these influential works, but also the diversity with which they can be interpreted and utilized in extending our thinking about problem solving.

Taken together, what follows is a topical survey of ideas representing the diversity of views and tensions inherent in a field of research that is both a means to an end and an end onto itself and is unanimously seen as central to the activities of mathematics.

1 Survey on the State-of-the-Art

1.1 role of heuristics for problem solving—regina bruder.

The origin of the word heuristic dates back to the time of Archimedes and is said to have come out of one of the famous stories told about this great mathematician and inventor. The King of Syracuse asked Archimedes to check whether his new wreath was really made of pure gold. Archimedes struggled with this task and it was not until he was at the bathhouse that he came up with the solution. As he entered the tub he noticed that he had displaced a certain amount of water. Brilliant as he was, he transferred this insight to the issue with the wreath and knew he had solved the problem. According to the legend, he jumped out of the tub and ran from the bathhouse naked screaming, “Eureka, eureka!”. Eureka and heuristic have the same root in the ancient Greek language and so it has been claimed that this is how the academic discipline of “heuristics” dealing with effective approaches to problem solving (so-called heurisms) was given its name. Pólya ( 1964 ) describes this discipline as follows:

Heuristics deals with solving tasks. Its specific goals include highlighting in general terms the reasons for selecting those moments in a problem the examination of which could help us find a solution. (p. 5)

This discipline has grown, in part, from examining the approaches to certain problems more in detail and comparing them with each other in order to abstract similarities in approach, or so-called heurisms. Pólya ( 1949 ), but also, inter alia, Engel ( 1998 ), König ( 1984 ) and Sewerin ( 1979 ) have formulated such heurisms for mathematical problem tasks. The problem tasks examined by the authors mentioned are predominantly found in the area of talent programmes, that is, they often go back to mathematics competitions.

In 1983 Zimmermann provided an overview of heuristic approaches and tools in American literature which also offered suggestions for mathematics classes. In the German-speaking countries, an approach has established itself, going back to Sewerin ( 1979 ) and König ( 1984 ), which divides school-relevant heuristic procedures into heuristic tools, strategies and principles, see also Bruder and Collet ( 2011 ).

Below is a review of the conceptual background of heuristics, followed by a description of the effect mechanisms of heurisms in problem-solving processes.

1.1.1 Research Review on the Promotion of Problem Solving

In the 20th century, there has been an advancement of research on mathematical problem solving and findings about possibilities to promote problem solving with varying priorities (c.f. Pehkonen 1991 ). Based on a model by Pólya ( 1949 ), in a first phase of research on problem solving, particularly in the 1960s and the 1970s, a series of studies on problem-solving processes placing emphasis on the importance of heuristic strategies (heurisms) in problem solving has been carried out. It was assumed that teaching and learning heuristic strategies, principles and tools would provide students with an orientation in problem situations and that this could thus improve students’ problem-solving abilities (c.f. for instance, Schoenfeld 1979 ). This approach, mostly researched within the scope of talent programmes for problem solving, was rather successful (c.f. for instance, Sewerin 1979 ). In the 1980s, requests for promotional opportunities in everyday teaching were given more and more consideration: “ problem solving must be the focus of school mathematics in the 1980s ” (NCTM 1980 ). For the teaching and learning of problem solving in regular mathematics classes, the current view according to which cognitive, heuristic aspects were paramount, was expanded by certain student-specific aspects, such as attitudes, emotions and self-regulated behaviour (c.f. Kretschmer 1983 ; Schoenfeld 1985 , 1987 , 1992 ). Kilpatrick ( 1985 ) divided the promotional approaches described in the literature into five methods which can also be combined with each other.

Osmosis : action-oriented and implicit imparting of problem-solving techniques in a beneficial learning environment

Memorisation : formation of special techniques for particular types of problem and of the relevant questioning when problem solving

Imitation : acquisition of problem-solving abilities through imitation of an expert

Cooperation : cooperative learning of problem-solving abilities in small groups

Reflection : problem-solving abilities are acquired in an action-oriented manner and through reflection on approaches to problem solving.

Kilpatrick ( 1985 ) views as success when heuristic approaches are explained to students, clarified by means of examples and trained through the presentation of problems. The need of making students aware of heuristic approaches is by now largely accepted in didactic discussions. Differences in varying approaches to promoting problem-solving abilities rather refer to deciding which problem-solving strategies or heuristics are to imparted to students and in which way, and not whether these should be imparted at all or not.

1.1.2 Heurisms as an Expression of Mental Agility

The activity theory, particularly in its advancement by Lompscher ( 1975 , 1985 ), offers a well-suited and manageable model to describe learning activities and differences between learners with regard to processes and outcomes in problem solving (c.f. Perels et al. 2005 ). Mental activity starts with a goal and the motive of a person to perform such activity. Lompscher divides actual mental activity into content and process. Whilst the content in mathematical problem-solving consists of certain concepts, connections and procedures, the process describes the psychological processes that occur when solving a problem. This course of action is described in Lompscher by various qualities, such as systematic planning, independence, accuracy, activity and agility. Along with differences in motivation and the availability of expertise, it appears that intuitive problem solvers possess a particularly high mental agility, at least with regard to certain contents areas.

According to Lompscher, “flexibility of thought” expresses itself

… by the capacity to change more or less easily from one aspect of viewing to another one or to embed one circumstance or component into different correlations, to understand the relativity of circumstances and statements. It allows to reverse relations, to more or less easily or quickly attune to new conditions of mental activity or to simultaneously mind several objects or aspects of a given activity (Lompscher 1975 , p. 36).

These typical manifestations of mental agility can be focused on in problem solving by mathematical means and can be related to the heurisms known from the analyses of approaches by Pólya et al. (c.f. also Bruder 2000 ):

Reduction : Successful problem solvers will intuitively reduce a problem to its essentials in a sensible manner. To achieve such abstraction, they often use visualisation and structuring aids, such as informative figures, tables, solution graphs or even terms. These heuristic tools are also very well suited to document in retrospect the approach adopted by the intuitive problem solvers in a way that is comprehensible for all.

Reversibility : Successful problem solvers are able to reverse trains of thought or reproduce these in reverse. They will do this in appropriate situations automatically, for instance, when looking for a key they have mislaid. A corresponding general heuristic strategy is working in reverse.

Minding of aspects : Successful problem solvers will mind several aspects of a given problem at the same time or easily recognise any dependence on things and vary them in a targeted manner. Sometimes, this is also a matter of removing barriers in favour of an idea that appears to be sustainable, that is, by simply “hanging on” to a certain train of thought even against resistance. Corresponding heurisms are, for instance, the principle of invariance, the principle of symmetry (Engel 1998 ), the breaking down or complementing of geometric figures to calculate surface areas, or certain terms used in binomial formulas.

Change of aspects : Successful problem solvers will possibly change their assumptions, criteria or aspects minded in order to find a solution. Various aspects of a given problem will be considered intuitively or the problem be viewed from a different perspective, which will prevent “getting stuck” and allow for new insights and approaches. For instance, many elementary geometric propositions can also be proved in an elegant vectorial manner.

Transferring : Successful problem solvers will be able more easily than others to transfer a well-known procedure to another, sometimes even very different context. They recognise more easily the “framework” or pattern of a given task. Here, this is about own constructions of analogies and continual tracing back from the unknown to the known.

Intuitive, that is, untrained good problem solvers, are, however, often unable to access these flexibility qualities consciously. This is why they are also often unable to explain how they actually solved a given problem.

To be able to solve problems successfully, a certain mental agility is thus required. If this is less well pronounced in a certain area, learning how to solve problems means compensating by acquiring heurisms. In this case, insufficient mental agility is partly “offset” through the application of knowledge acquired by means of heurisms. Mathematical problem-solving competences are thus acquired through the promotion of manifestations of mental agility (reduction, reversibility, minding of aspects and change of aspects). This can be achieved by designing sub-actions of problem solving in connection with a (temporarily) conscious application of suitable heurisms. Empirical evidence for the success of the active principle of heurisms has been provided by Collet ( 2009 ).

Against such background, learning how to solve problems can be established as a long-term teaching and learning process which basically encompasses four phases (Bruder and Collet 2011 ):

Intuitive familiarisation with heuristic methods and techniques.

Making aware of special heurisms by means of prominent examples (explicit strategy acquisition).

Short conscious practice phase to use the newly acquired heurisms with differentiated task difficulties.

Expanding the context of the strategies applied.

In the first phase, students are familiarised with heurisms intuitively by means of targeted aid impulses and questions (what helped us solve this problem?) which in the following phase are substantiated on the basis of model tasks, are given names and are thus made aware of their existence. The third phase serves the purpose of a certain familiarisation with the new heurisms and the experience of competence through individualised practising at different requirement levels, including in the form of homework over longer periods. A fourth and delayed fourth phase aims at more flexibility through the transfer to other contents and contexts and the increasingly intuitive use of the newly acquired heurisms, so that students can enrich their own problem-solving models in a gradual manner. The second and third phases build upon each other in close chronological order, whilst the first phase should be used in class at all times.

All heurisms can basically be described in an action-oriented manner by means of asking the right questions. The way of asking questions can thus also establish a certain kind of personal relation. Even if the teacher presents and suggests the line of basic questions with a prototypical wording each time, students should always be given the opportunity to find “their” wording for the respective heurism and take a note of it for themselves. A possible key question for the use of a heuristic tool would be: How to illustrate and structure the problem or how to present it in a different way?

Unfortunately, for many students, applying heuristic approaches to problem solving will not ensue automatically but will require appropriate early and long-term promoting. The results of current studies, where promotion approaches to problem solving are connected with self-regulation and metacognitive aspects, demonstrate certain positive effects of such combination on students. This field of research includes, for instance, studies by Lester et al. ( 1989 ), Verschaffel et al. ( 1999 ), the studies on teaching method IMPROVE by Mevarech and Kramarski ( 1997 , 2003 ) and also the evaluation of a teaching concept on learning how to solve problems by the gradual conscious acquisition of heurisms by Collet and Bruder ( 2008 ).

1.2 Creative Problem Solving—Peter Liljedahl

There is a tension between the aforementioned story of Archimedes and the heuristics presented in the previous section. Archimedes, when submersing himself in the tub and suddenly seeing the solution to his problem, wasn’t relying on osmosis, memorisation, imitation, cooperation, or reflection (Kilpatrick 1985 ). He wasn’t drawing on reduction, reversibility, minding of aspects, change of aspect, or transfer (Bruder 2000 ). Archimedes was stuck and it was only, in fact, through insight and sudden illumination that he managed to solve his problem. In short, Archimedes was faced with a problem that the aforementioned heuristics, and their kind, would not help him to solve.

According to some, such a scenario is the definition of a problem. For example, Resnick and Glaser ( 1976 ) define a problem as being something that you do not have the experience to solve. Mathematicians, in general, agree with this (Liljedahl 2008 ).

Any problem in which you can see how to attack it by deliberate effort, is a routine problem, and cannot be an important discover. You must try and fail by deliberate efforts, and then rely on a sudden inspiration or intuition or if you prefer to call it luck. (Dan Kleitman, participant cited in Liljedahl 2008 , p. 19).

Problems, then, are tasks that cannot be solved by direct effort and will require some creative insight to solve (Liljedahl 2008 ; Mason et al. 1982 ; Pólya 1965 ).

1.2.1 A History of Creativity in Mathematics Education

In 1902, the first half of what eventually came to be a 30 question survey was published in the pages of L’Enseignement Mathématique , the journal of the French Mathematical Society. The authors, Édouard Claparède and Théodore Flournoy, were two Swiss psychologists who were deeply interested in the topics of mathematical discovery, creativity and invention. Their hope was that a widespread appeal to mathematicians at large would incite enough responses for them to begin to formulate some theories about this topic. The first half of the survey centered on the reasons for becoming a mathematician (family history, educational influences, social environment, etc.), attitudes about everyday life, and hobbies. This was eventually followed, in 1904, by the publication of the second half of the survey pertaining, in particular, to mental images during periods of creative work. The responses were sorted according to nationality and published in 1908.

During this same period Henri Poincaré (1854–1912), one of the most noteworthy mathematicians of the time, had already laid much of the groundwork for his own pursuit of this same topic and in 1908 gave a presentation to the French Psychological Society in Paris entitled L’Invention mathématique —often mistranslated to Mathematical Creativity Footnote 1 (c.f. Poincaré 1952 ). At the time of the presentation Poincaré stated that he was aware of Claparède and Flournoy’s work, as well as their results, but expressed that they would only confirm his own findings. Poincaré’s presentation, as well as the essay it spawned, stands to this day as one of the most insightful, and thorough treatments of the topic of mathematical discovery, creativity, and invention.

Just at this time, I left Caen, where I was living, to go on a geological excursion under the auspices of the School of Mines. The incident of the travel made me forget my mathematical work. Having reached Coutances, we entered an omnibus to go some place or other. At the moment when I put my foot on the step, the idea came to me, without anything in my former thoughts seeming to have paved the way for it, that the transformations I had used to define the Fuschian functions were identical with those of non-Euclidean geometry. I did not verify the idea; I should not have had the time, as, upon taking my seat in the omnibus, I went on with the conversation already commenced, but I felt a perfect certainty. On my return to Caen, for conscience’ sake, I verified the results at my leisure. (Poincaré 1952 , p. 53)

So powerful was his presentation, and so deep were his insights into his acts of invention and discovery that it could be said that he not so much described the characteristics of mathematical creativity, as defined them. From that point forth mathematical creativity, or even creativity in general, has not been discussed seriously without mention of Poincaré’s name.

Inspired by this presentation, Jacques Hadamard (1865–1963), a contemporary and a friend of Poincaré’s, began his own empirical investigation into this fascinating phenomenon. Hadamard had been critical of Claparède and Flournoy’s work in that they had not adequately treated the topic on two fronts. As exhaustive as the survey appeared to be, Hadamard felt that it failed to ask some key questions—the most important of which was with regard to the reason for failures in the creation of mathematics. This seemingly innocuous oversight, however, led directly to his second and “most important criticism” (Hadamard 1945 ). He felt that only “first-rate men would dare to speak of” (p. 10) such failures. So, inspired by his good friend Poincaré’s treatment of the subject Hadamard retooled the survey and gave it to friends of his for consideration—mathematicians such as Henri Poincaré and Albert Einstein, whose prominence were beyond reproach. Ironically, the new survey did not contain any questions that explicitly dealt with failure. In 1943 Hadamard gave a series of lectures on mathematical invention at the École Libre des Hautes Études in New York City. These talks were subsequently published as The Psychology of Mathematical Invention in the Mathematical Field (Hadameard 1945 ).

Hadamard’s classic work treats the subject of invention at the crossroads of mathematics and psychology. It provides not only an entertaining look at the eccentric nature of mathematicians and their rituals, but also outlines the beliefs of mid twentieth-century mathematicians about the means by which they arrive at new mathematics. It is an extensive exploration and extended argument for the existence of unconscious mental processes. In essence, Hadamard took the ideas that Poincaré had posed and, borrowing a conceptual framework for the characterization of the creative process from the Gestaltists of the time (Wallas 1926 ), turned them into a stage theory. This theory still stands as the most viable and reasonable description of the process of mathematical creativity.

1.2.2 Defining Mathematical Creativity

The phenomena of mathematical creativity, although marked by sudden illumination, actually consist of four separate stages stretched out over time, of which illumination is but one stage. These stages are initiation, incubation, illumination, and verification (Hadamard 1945 ). The first of these stages, the initiation phase, consists of deliberate and conscious work. This would constitute a person’s voluntary, and seemingly fruitless, engagement with a problem and be characterized by an attempt to solve the problem by trolling through a repertoire of past experiences. This is an important part of the inventive process because it creates the tension of unresolved effort that sets up the conditions necessary for the ensuing emotional release at the moment of illumination (Hadamard 1945 ; Poincaré 1952 ).

Following the initiation stage the solver, unable to come up with a solution stops working on the problem at a conscious level and begins to work on it at an unconscious level (Hadamard 1945 ; Poincaré 1952 ). This is referred to as the incubation stage of the inventive process and can last anywhere from several minutes to several years. After the period of incubation a rapid coming to mind of a solution, referred to as illumination , may occur. This is accompanied by a feeling of certainty and positive emotions (Poincaré 1952 ). Although the processes of incubation and illumination are shrouded behind the veil of the unconscious there are a number of things that can be deduced about them. First and foremost is the fact that unconscious work does, indeed, occur. Poincaré ( 1952 ), as well as Hadamard ( 1945 ), use the very real experience of illumination, a phenomenon that cannot be denied, as evidence of unconscious work, the fruits of which appear in the flash of illumination. No other theory seems viable in explaining the sudden appearance of solution during a walk, a shower, a conversation, upon waking, or at the instance of turning the conscious mind back to the problem after a period of rest (Poincaré 1952 ). Also deducible is that unconscious work is inextricably linked to the conscious and intentional effort that precedes it.

There is another remark to be made about the conditions of this unconscious work: it is possible, and of a certainty it is only fruitful, if it is on the one hand preceded and on the other hand followed by a period of conscious work. These sudden inspirations never happen except after some days of voluntary effort which has appeared absolutely fruitless and whence nothing good seems to have come … (Poincaré 1952 , p. 56)

Hence, the fruitless efforts of the initiation phase are only seemingly so. They not only set up the aforementioned tension responsible for the emotional release at the time of illumination, but also create the conditions necessary for the process to enter into the incubation phase.

Illumination is the manifestation of a bridging that occurs between the unconscious mind and the conscious mind (Poincaré 1952 ), a coming to (conscious) mind of an idea or solution. What brings the idea forward to consciousness is unclear, however. There are theories of the aesthetic qualities of the idea, effective surprise/shock of recognition, fluency of processing, or breaking functional fixedness. For reasons of brevity I will only expand on the first of these.

Poincaré proposed that ideas that were stimulated during initiation remained stimulated during incubation. However, freed from the constraints of conscious thought and deliberate calculation, these ideas would begin to come together in rapid and random unions so that “their mutual impacts may produce new combinations” (Poincaré 1952 ). These new combinations, or ideas, would then be evaluated for viability using an aesthetic sieve, which allows through to the conscious mind only the “right combinations” (Poincaré 1952 ). It is important to note, however, that good or aesthetic does not necessarily mean correct. Correctness is evaluated during the verification stage.

The purpose of verification is not only to check for correctness. It is also a method by which the solver re-engages with the problem at the level of details. That is, during the unconscious work the problem is engaged with at the level of ideas and concepts. During verification the solver can examine these ideas in closer details. Poincaré succinctly describes both of these purposes.

As for the calculations, themselves, they must be made in the second period of conscious work, that which follows the inspiration, that in which one verifies the results of this inspiration and deduces their consequences. (Poincaré 1952 , p. 62)

Aside from presenting this aforementioned theory on invention, Hadamard also engaged in a far-reaching discussion on a number of interesting, and sometimes quirky, aspects of invention and discovery that he had culled from the results of his empirical study, as well as from pertinent literature. This discussion was nicely summarized by Newman ( 2000 ) in his commentary on the elusiveness of invention.

The celebrated phrenologist Gall said mathematical ability showed itself in a bump on the head, the location of which he specified. The psychologist Souriau, we are told, maintained that invention occurs by “pure chance”, a valuable theory. It is often suggested that creative ideas are conjured up in “mathematical dreams”, but this attractive hypothesis has not been verified. Hadamard reports that mathematicians were asked whether “noises” or “meteorological circumstances” helped or hindered research [..] Claude Bernard, the great physiologist, said that in order to invent “one must think aside”. Hadamard says this is a profound insight; he also considers whether scientific invention may perhaps be improved by standing or sitting or by taking two baths in a row. Helmholtz and Poincaré worked sitting at a table; Hadamard’s practice is to pace the room (“Legs are the wheels of thought”, said Emile Angier); the chemist J. Teeple was the two-bath man. (p. 2039)

1.2.3 Discourses on Creativity

Creativity is a term that can be used both loosely and precisely. That is, while there exists a common usage of the term there also exists a tradition of academic discourse on the subject. A common usage of creative refers to a process or a person whose products are original, novel, unusual, or even abnormal (Csíkszentmihályi 1996 ). In such a usage, creativity is assessed on the basis of the external and observable products of the process, the process by which the product comes to be, or on the character traits of the person doing the ‘creating’. Each of these usages—product, process, person—is the roots of the discourses (Liljedahl and Allan 2014 ) that I summarize here, the first of which concerns products.

Consider a mother who states that her daughter is creative because she drew an original picture. The basis of such a statement can lie either in the fact that the picture is unlike any the mother has ever seen or unlike any her daughter has ever drawn before. This mother is assessing creativity on the basis of what her daughter has produced. However, the standards that form the basis of her assessment are neither consistent nor stringent. There does not exist a universal agreement as to what she is comparing the picture to (pictures by other children or other pictures by the same child). Likewise, there is no standard by which the actual quality of the picture is measured. The academic discourse that concerns assessment of products, on the other hand, is both consistent and stringent (Csíkszentmihályi 1996 ). This discourse concerns itself more with a fifth, and as yet unmentioned, stage of the creative process; elaboration . Elaboration is where inspiration becomes perspiration (Csíkszentmihályi 1996 ). It is the act of turning a good idea into a finished product, and the finished product is ultimately what determines the creativity of the process that spawned it—that is, it cannot be a creative process if nothing is created. In particular, this discourse demands that the product be assessed against other products within its field, by the members of that field, to determine if it is original AND useful (Csíkszentmihályi 1996 ; Bailin 1994 ). If it is, then the product is deemed to be creative. Note that such a use of assessment of end product pays very little attention to the actual process that brings this product forth.

The second discourse concerns the creative process. The literature pertaining to this can be separated into two categories—a prescriptive discussion of the creativity process and a descriptive discussion of the creativity process. Although both of these discussions have their roots in the four stages that Wallas ( 1926 ) proposed makes up the creative process, they make use of these stages in very different ways. The prescriptive discussion of the creative process is primarily focused on the first of the four stages, initiation , and is best summarized as a cause - and - effect discussion of creativity, where the thinking processes during the initiation stage are the cause and the creative outcome are the effects (Ghiselin 1952 ). Some of the literature claims that the seeds of creativity lie in being able to think about a problem or situation analogically. Other literature claims that utilizing specific thinking tools such as imagination, empathy, and embodiment will lead to creative products. In all of these cases, the underlying theory is that the eventual presentation of a creative idea will be precipitated by the conscious and deliberate efforts during the initiation stage. On the other hand, the literature pertaining to a descriptive discussion of the creative process is inclusive of all four stages (Kneller 1965 ; Koestler 1964 ). For example, Csíkszentmihályi ( 1996 ), in his work on flow attends to each of the stages, with much attention paid to the fluid area between conscious and unconscious work, or initiation and incubation. His claim is that the creative process is intimately connected to the enjoyment that exists during times of sincere and consuming engagement with a situation, the conditions of which he describes in great detail.

The third, and final, discourse on creativity pertains to the person. This discourse is space dominated by two distinct characteristics, habit and genius. Habit has to do with the personal habits as well as the habits of mind of people that have been deemed to be creative. However, creative people are most easily identified through their reputation for genius. Consequently, this discourse is often dominated by the analyses of the habits of geniuses as is seen in the work of Ghiselin ( 1952 ), Koestler ( 1964 ), and Kneller ( 1965 ) who draw on historical personalities such as Albert Einstein, Henri Poincaré, Vincent Van Gogh, D.H. Lawrence, Samuel Taylor Coleridge, Igor Stravinsky, and Wolfgang Amadeus Mozart to name a few. The result of this sort of treatment is that creative acts are viewed as rare mental feats, which are produced by extraordinary individuals who use extraordinary thought processes.

These different discourses on creativity can be summed up in a tension between absolutist and relativist perspectives on creativity (Liljedahl and Sriraman 2006 ). An absolutist perspective assumes that creative processes are the domain of genius and are present only as precursors to the creation of remarkably useful and universally novel products. The relativist perspective, on the other hand, allows for every individual to have moments of creativity that may, or may not, result in the creation of a product that may, or may not, be either useful or novel.

Between the work of a student who tries to solve a problem in geometry or algebra and a work of invention, one can say there is only a difference of degree. (Hadamard 1945 , p. 104).

Regardless of discourse, however, creativity is not “part of the theories of logical forms” (Dewey 1938 ). That is, creativity is not representative of the lock-step logic and deductive reasoning that mathematical problem solving is often presumed to embody (Bibby 2002 ; Burton 1999 ). Couple this with the aforementioned demanding constraints as to what constitutes a problem, where then does that leave problem solving heuristics? More specifically, are there creative problem solving heuristics that will allow us to resolve problems that require illumination to solve? The short answer to this question is yes—there does exist such problem solving heuristics. To understand these, however, we must first understand the routine problem solving heuristics they are built upon. In what follows, I walk through the work of key authors and researchers whose work offers us insights into progressively more creative problem solving heuristics for solving true problems.

1.2.4 Problem Solving by Design

In a general sense, design is defined as the algorithmic and deductive approach to solving a problem (Rusbult 2000 ). This process begins with a clearly defined goal or objective after which there is a great reliance on relevant past experience, referred to as repertoire (Bruner 1964 ; Schön 1987 ), to produce possible options that will lead towards a solution of the problem (Poincaré 1952 ). These options are then examined through a process of conscious evaluations (Dewey 1933 ) to determine their suitability for advancing the problem towards the final goal. In very simple terms, problem solving by design is the process of deducing the solution from that which is already known.

Mayer ( 1982 ), Schoenfeld ( 1982 ), and Silver ( 1982 ) state that prior knowledge is a key element in the problem solving process. Prior knowledge influences the problem solver’s understanding of the problem as well as the choice of strategies that will be called upon in trying to solve the problem. In fact, prior knowledge and prior experiences is all that a solver has to draw on when first attacking a problem. As a result, all problem solving heuristics incorporate this resource of past experiences and prior knowledge into their initial attack on a problem. Some heuristics refine these ideas, and some heuristics extend them (c.f. Kilpatrick 1985 ; Bruder 2000 ). Of the heuristics that refine, none is more influential than the one created by George Pólya (1887–1985).

1.2.5 George Pólya: How to Solve It

In his book How to Solve It (1949) Pólya lays out a problem solving heuristic that relies heavily on a repertoire of past experience. He summarizes the four-step process of his heuristic as follows:

Understanding the Problem

First. You have to understand the problem.

What is the unknown? What are the data? What is the condition?

Is it possible to satisfy the condition? Is the condition sufficient to determine the unknown? Or is it insufficient? Or redundant? Or contradictory?

Draw a figure. Introduce suitable notation.

Separate the various parts of the condition. Can you write them down?

Devising a Plan

Second. Find the connection between the data and the unknown. You may be obliged to consider auxiliary problems if an immediate connection cannot be found. You should obtain eventually a plan of the solution.

Have you seen it before? Or have you seen the same problem in a slightly different form?

Do you know a related problem? Do you know a theorem that could be useful?

Look at the unknown! And try to think of a familiar problem having the same or a similar unknown.

Here is a problem related to yours and solved before. Could you use it? Could you use its result? Could you use its method? Should you introduce some auxiliary element in order to make its use possible?

Could you restate the problem? Could you restate it still differently? Go back to definitions.

If you cannot solve the proposed problem try to solve first some related problem. Could you imagine a more accessible related problem? A more general problem? A more special problem? An analogous problem? Could you solve a part of the problem? Keep only a part of the condition, drop the other part; how far is the unknown then determined, how can it vary? Could you derive something useful from the data? Could you think of other data appropriate to determine the unknown? Could you change the unknown or data, or both if necessary, so that the new unknown and the new data are nearer to each other?

Did you use all the data? Did you use the whole condition? Have you taken into account all essential notions involved in the problem?

Carrying Out the Plan

Third. Carry out your plan.

Carrying out your plan of the solution, check each step. Can you see clearly that the step is correct? Can you prove that it is correct?

Looking Back

Fourth. Examine the solution obtained.

Can you check the result? Can you check the argument?

Can you derive the solution differently? Can you see it at a glance?

Can you use the result, or the method, for some other problem?

The emphasis on auxiliary problems, related problems, and analogous problems that are, in themselves, also familiar problems is an explicit manifestation of relying on a repertoire of past experience. This use of familiar problems also requires an ability to deduce from these related problems a recognizable and relevant attribute that will transfer to the problem at hand. The mechanism that allows for this transfer of knowledge between analogous problems is known as analogical reasoning (English 1997 , 1998 ; Novick 1988 , 1990 , 1995 ; Novick and Holyoak 1991 ) and has been shown to be an effective, but not always accessible, thinking strategy.

Step four in Pólya’s heuristic, looking back, is also a manifestation of utilizing prior knowledge to solve problems, albeit an implicit one. Looking back makes connections “in memory to previously acquired knowledge [..] and further establishes knowledge in long-term memory that may be elaborated in later problem-solving encounters” (Silver 1982 , p. 20). That is, looking back is a forward-looking investment into future problem solving encounters, it sets up connections that may later be needed.

Pólya’s heuristic is a refinement on the principles of problem solving by design. It not only makes explicit the focus on past experiences and prior knowledge, but also presents these ideas in a very succinct, digestible, and teachable manner. This heuristic has become a popular, if not the most popular, mechanism by which problem solving is taught and learned.

1.2.6 Alan Schoenfeld: Mathematical Problem Solving

The work of Alan Schoenfeld is also a refinement on the principles of problem solving by design. However, unlike Pólya ( 1949 ) who refined these principles at a theoretical level, Schoenfeld has refined them at a practical and empirical level. In addition to studying taught problem solving strategies he has also managed to identify and classify a variety of strategies, mostly ineffectual, that students invoke naturally (Schoenfeld 1985 , 1992 ). In so doing, he has created a better understanding of how students solve problems, as well as a better understanding of how problems should be solved and how problem solving should be taught.

For Schoenfeld, the problem solving process is ultimately a dialogue between the problem solver’s prior knowledge, his attempts, and his thoughts along the way (Schoenfeld 1982 ). As such, the solution path of a problem is an emerging and contextually dependent process. This is a departure from the predefined and contextually independent processes of Pólya’s ( 1949 ) heuristics. This can be seen in Schoenfeld’s ( 1982 ) description of a good problem solver.

To examine what accounts for expertise in problem solving, you would have to give the expert a problem for which he does not have access to a solution schema. His behavior in such circumstances is radically different from what you would see when he works on routine or familiar “non-routine” problems. On the surface his performance is no longer proficient; it may even seem clumsy. Without access to a solution schema, he has no clear indication of how to start. He may not fully understand the problem, and may simply “explore it for a while until he feels comfortable with it. He will probably try to “match” it to familiar problems, in the hope it can be transformed into a (nearly) schema-driven solution. He will bring up a variety of plausible things: related facts, related problems, tentative approaches, etc. All of these will have to be juggled and balanced. He may make an attempt solving it in a particular way, and then back off. He may try two or three things for a couple of minutes and then decide which to pursue. In the midst of pursuing one direction he may go back and say “that’s harder than it should be” and try something else. Or, after the comment, he may continue in the same direction. With luck, after some aborted attempts, he will solve the problem. (p. 32-33)

Aside from demonstrating the emergent nature of the problem solving process, this passage also brings forth two consequences of Schoenfeld’s work. The first of these is the existence of problems for which the solver does not have “access to a solution schema”. Unlike Pólya ( 1949 ), who’s heuristic is a ‘one size fits all (problems)’ heuristic, Schoenfeld acknowledges that problem solving heuristics are, in fact, personal entities that are dependent on the solver’s prior knowledge as well as their understanding of the problem at hand. Hence, the problems that a person can solve through his or her personal heuristic are finite and limited.

The second consequence that emerges from the above passage is that if a person lacks the solution schema to solve a given problem s/he may still solve the problem with the help of luck . This is an acknowledgement, if only indirectly so, of the difference between problem solving in an intentional and mechanical fashion verses problem solving in a more creative fashion, which is neither intentional nor mechanical (Pehkonen 1997 ).

1.2.7 David Perkins: Breakthrough Thinking

As mentioned, many consider a problem that can be solved by intentional and mechanical means to not be worthy of the title ‘problem’. As such, a repertoire of past experiences sufficient for dealing with such a ‘problem’ would disqualify it from the ranks of ‘problems’ and relegate it to that of ‘exercises’. For a problem to be classified as a ‘problem’, then, it must be ‘problematic’. Although such an argument is circular it is also effective in expressing the ontology of mathematical ‘problems’.

Perkins ( 2000 ) also requires problems to be problematic. His book Archimedes’ Bathtub: The Art and Logic of Breakthrough Thinking (2000) deals with situations in which the solver has gotten stuck and no amount of intentional or mechanical adherence to the principles of past experience and prior knowledge is going to get them unstuck. That is, he deals with problems that, by definition, cannot be solved through a process of design [or through the heuristics proposed by Pólya ( 1949 ) and Schoenfeld ( 1985 )]. Instead, the solver must rely on the extra-logical process of what Perkins ( 2000 ) calls breakthrough thinking .

Perkins ( 2000 ) begins by distinguishing between reasonable and unreasonable problems. Although both are solvable, only reasonable problems are solvable through reasoning. Unreasonable problems require a breakthrough in order to solve them. The problem, however, is itself inert. It is neither reasonable nor unreasonable. That quality is brought to the problem by the solver. That is, if a student cannot solve a problem by direct effort then that problem is deemed to be unreasonable for that student. Perkins ( 2000 ) also acknowledges that what is an unreasonable problem for one person is a perfectly reasonable problem for another person; reasonableness is dependent on the person.

This is not to say that, once found, the solution cannot be seen as accessible through reason. During the actual process of solving, however, direct and deductive reasoning does not work. Perkins ( 2000 ) uses several classic examples to demonstrate this, the most famous being the problem of connecting nine dots in a 3 × 3 array with four straight lines without removing pencil from paper, the solution to which is presented in Fig.  1 .

Nine dots—four lines problem and solution

To solve this problem, Perkins ( 2000 ) claims that the solver must recognize that the constraint of staying within the square created by the 3 × 3 array is a self-imposed constraint. He further claims that until this is recognized no amount of reasoning is going to solve the problem. That is, at this point in the problem solving process the problem is unreasonable. However, once this self-imposed constraint is recognized the problem, and the solution, are perfectly reasonable. Thus, the solution of an, initially, unreasonable problem is reasonable.

The problem solving heuristic that Perkins ( 2000 ) has constructed to deal with solvable, but unreasonable, problems revolves around the idea of breakthrough thinking and what he calls breakthrough problems . A breakthrough problem is a solvable problem in which the solver has gotten stuck and will require an AHA! to get unstuck and solve the problem. Perkins ( 2000 ) poses that there are only four types of solvable unreasonable problems, which he has named wilderness of possibilities , the clueless plateau , narrow canyon of exploration , and oasis of false promise . The names for the first three of these types of problems are related to the Klondike gold rush in Alaska, a time and place in which gold was found more by luck than by direct and systematic searching.

The wilderness of possibilities is a term given to a problem that has many tempting directions but few actual solutions. This is akin to a prospector searching for gold in the Klondike. There is a great wilderness in which to search, but very little gold to be found. The clueless plateau is given to problems that present the solver with few, if any, clues as to how to solve it. The narrow canyon of exploration is used to describe a problem that has become constrained in such a way that no solution now exists. The nine-dot problem presented above is such a problem. The imposed constraint that the lines must lie within the square created by the array makes a solution impossible. This is identical to the metaphor of a prospector searching for gold within a canyon where no gold exists. The final type of problem gets its name from the desert. An oasis of false promise is a problem that allows the solver to quickly get a solution that is close to the desired outcome; thereby tempting them to remain fixed on the strategy that they used to get this almost-answer. The problem is, that like the canyon, the solution does not exist at the oasis; the solution strategy that produced an almost-answer is incapable of producing a complete answer. Likewise, a desert oasis is a false promise in that it is only a reprieve from the desolation of the dessert and not a final destination.

Believing that there are only four ways to get stuck, Perkins ( 2000 ) has designed a problem solving heuristic that will “up the chances” of getting unstuck. This heuristic is based on what he refers to as “the logic of lucking out” (p. 44) and is built on the idea of introspection. By first recognizing that they are stuck, and then recognizing that the reason they are stuck can only be attributed to one of four reasons, the solver can access four strategies for getting unstuck, one each for the type of problem they are dealing with. If the reason they are stuck is because they are faced with a wilderness of possibilities they are to begin roaming far, wide, and systematically in the hope of reducing the possible solution space to one that is more manageable. If they find themselves on a clueless plateau they are to begin looking for clues, often in the wording of the problem. When stuck in a narrow canyon of possibilities they need to re-examine the problem and see if they have imposed any constraints. Finally, when in an oasis of false promise they need to re-attack the problem in such a way that they stay away from the oasis.

Of course, there are nuances and details associated with each of these types of problems and the strategies for dealing with them. However, nowhere within these details is there mention of the main difficulty inherent in introspection; that it is much easier for the solver to get stuck than it is for them to recognize that they are stuck. Once recognized, however, the details of Perkins’ ( 2000 ) heuristic offer the solver some ways for recognizing why they are stuck.

1.2.8 John Mason, Leone Burton, and Kaye Stacey: Thinking Mathematically

The work of Mason et al. in their book Thinking Mathematically ( 1982 ) also recognizes the fact that for each individual there exists problems that will not yield to their intentional and mechanical attack. The heuristic that they present for dealing with this has two main processes with a number of smaller phases, rubrics, and states. The main processes are what they refer to as specializing and generalizing. Specializing is the process of getting to know the problem and how it behaves through the examination of special instances of the problem. This process is synonymous with problem solving by design and involves the repeated oscillation between the entry and attack phases of Mason et al. ( 1982 ) heuristic. The entry phase is comprised of ‘getting started’ and ‘getting involved’ with the problem by using what is immediately known about it. Attacking the problem involves conjecturing and testing a number of hypotheses in an attempt to gain greater understanding of the problem and to move towards a solution.

At some point within this process of oscillating between entry and attack the solver will get stuck, which Mason et al. ( 1982 ) refer to as “an honourable and positive state, from which much can be learned” (p. 55). The authors dedicate an entire chapter to this state in which they acknowledge that getting stuck occurs long before an awareness of being stuck develops. They proposes that the first step to dealing with being stuck is the simple act of writing STUCK!

The act of expressing my feelings helps to distance me from my state of being stuck. It frees me from incapacitating emotions and reminds me of actions that I can take. (p. 56)

The next step is to reengage the problem by examining the details of what is known, what is wanted, what can be introduced into the problem, and what has been introduced into the problem (imposed assumptions). This process is engaged in until an AHA!, which advances the problem towards a solution, is encountered. If, at this point, the problem is not completely solved the oscillation is then resumed.

At some point in this process an attack on the problem will yield a solution and generalizing can begin. Generalizing is the process by which the specifics of a solution are examined and questions as to why it worked are investigated. This process is synonymous with the verification and elaboration stages of invention and creativity. Generalization may also include a phase of review that is similar to Pólya’s ( 1949 ) looking back.

1.2.9 Gestalt: The Psychology of Problem Solving

The Gestalt psychology of learning believes that all learning is based on insights (Koestler 1964 ). This psychology emerged as a response to behaviourism, which claimed that all learning was a response to external stimuli. Gestalt psychologists, on the other hand, believed that there was a cognitive process involved in learning as well. With regards to problem solving, the Gestalt school stands firm on the belief that problem solving, like learning, is a product of insight and as such, cannot be taught. In fact, the theory is that not only can problem solving not be taught, but also that attempting to adhere to any sort of heuristic will impede the working out of a correct solution (Krutestkii 1976 ). Thus, there exists no Gestalt problem solving heuristic. Instead, the practice is to focus on the problem and the solution rather than on the process of coming up with a solution. Problems are solved by turning them over and over in the mind until an insight, a viable avenue of attack, presents itself. At the same time, however, there is a great reliance on prior knowledge and past experiences. The Gestalt method of problem solving, then, is at the same time very different and very similar to the process of design.

Gestalt psychology has not fared well during the evolution of cognitive psychology. Although it honours the work of the unconscious mind it does so at the expense of practicality. If learning is, indeed, entirely based on insight then there is little point in continuing to study learning. “When one begins by assuming that the most important cognitive phenomena are inaccessible, there really is not much left to talk about” (Schoenfeld 1985 , p. 273). However, of interest here is the Gestalt psychologists’ claim that focus on problem solving methods creates functional fixedness (Ashcraft 1989 ). Mason et al. ( 1982 ), as well as Perkins ( 2000 ) deal with this in their work on getting unstuck.

1.2.10 Final Comments

Mathematics has often been characterized as the most precise of all sciences. Lost in such a misconception is the fact that mathematics often has its roots in the fires of creativity, being born of the extra-logical processes of illumination and intuition. Problem solving heuristics that are based solely on the processes of logical and deductive reasoning distort the true nature of problem solving. Certainly, there are problems in which logical deductive reasoning is sufficient for finding a solution. But these are not true problems. True problems need the extra-logical processes of creativity, insight, and illumination, in order to produce solutions.

Fortunately, as elusive as such processes are, there does exist problem solving heuristics that incorporate them into their strategies. Heuristics such as those by Perkins ( 2000 ) and Mason et al. ( 1982 ) have found a way of combining the intentional and mechanical processes of problem solving by design with the extra-logical processes of creativity, illumination, and the AHA!. Furthermore, they have managed to do so without having to fully comprehend the inner workings of this mysterious process.

1.3 Digital Technologies and Mathematical Problem Solving—Luz Manuel Santos-Trigo

Mathematical problem solving is a field of research that focuses on analysing the extent to which problem solving activities play a crucial role in learners’ understanding and use of mathematical knowledge. Mathematical problems are central in mathematical practice to develop the discipline and to foster students learning (Pólya 1945 ; Halmos 1994 ). Mason and Johnston-Wilder ( 2006 ) pointed out that “The purpose of a task is to initiate mathematically fruitful activity that leads to a transformation in what learners are sensitized to notice and competent to carry out” (p. 25). Tasks are essential for learners to elicit their ideas and to engage them in mathematical thinking. In a problem solving approach, what matters is the learners’ goals and ways to interact with the tasks. That is, even routine tasks can be a departure point for learners to extend initial conditions and transform them into some challenging activities.

Thus, analysing and characterizing ways in which mathematical problems are formulated (Singer et al. 2015 ) and the process involved in pursuing and solving those problems generate important information to frame and structure learning environments to guide and foster learners’ construction of mathematical concepts and problem solving competences (Santos-Trigo 2014 ). Furthermore, mathematicians or discipline practitioners have often been interested in unveiling and sharing their own experience while developing the discipline. As a results, they have provided valuable information to characterize mathematical practices and their relations to what learning processes of the discipline entails. It is recognized that the work of Pólya ( 1945 ) offered not only bases to launch several research programs in problem solving (Schoenfeld 1992 ; Mason et al. 1982 ); but also it became an essential resource for teachers to orient and structure their mathematical lessons (Krulik and Reys 1980 ).

1.3.1 Research Agenda

A salient feature of a problem solving approach to learn mathematics is that teachers and students develop and apply an enquiry or inquisitive method to delve into mathematical concepts and tasks. How are mathematical problems or concepts formulated? What types of problems are important for teachers/learners to discuss and engage in mathematical reasoning? What mathematical processes and ways of reasoning are involved in understanding mathematical concepts and solving problems? What are the features that distinguish an instructional environment that fosters problem-solving activities? How can learners’ problem solving competencies be assessed? How can learners’ problem solving competencies be characterized and explained? How can learners use digital technologies to understand mathematics and to develop problem-solving competencies? What ways of reasoning do learners construct when they use digital technologies in problem solving approaches? These types of questions have been important in the problem solving research agenda and delving into them has led researchers to generate information and results to support and frame curriculum proposals and learning scenarios. The purpose of this section is to present and discuss important themes that emerged in problem solving approaches that rely on the systematic use of several digital technologies.

In the last 40 years, the accumulated knowledge in the problem solving field has shed lights on both a characterization of what mathematical thinking involves and how learners can construct a robust knowledge in problem solving environments (Schoenfeld 1992 ). In this process, the field has contributed to identify what types of transformations traditional learning scenarios might consider when teachers and students incorporate the use of digital technologies in mathematical classrooms. In this context, it is important to briefly review what main themes and developments the field has addressed and achieved during the last 40 years.

1.3.2 Problem Solving Developments

There are traces of mathematical problems and solutions throughout the history of civilization that explain the humankind interest for identifying and exploring mathematical relations (Kline 1972 ). Pólya ( 1945 ) reflects on his own practice as a mathematician to characterize the process of solving mathematical problems through four main phases: Understanding the problem, devising a plan, carrying out the plan, and looking back. Likewise, Pólya ( 1945 ) presents and discusses the role played by heuristic methods throughout all problem solving phases. Schoenfeld ( 1985 ) presents a problem solving research program based on Pólya’s ( 1945 ) ideas to investigate the extent to which problem solving heuristics help university students to solve mathematical problems and to develop a way of thinking that shows consistently features of mathematical practices. As a result, he explains the learners’ success or failure in problem solving activities can be characterized in terms their mathematical resources and ways to access them, cognitive and metacognitive strategies used to represent and explore mathematical tasks, and systems of beliefs about mathematics and solving problems. In addition, Schoenfeld ( 1992 ) documented that heuristics methods as illustrated in Pólya’s ( 1945 ) book are ample and general and do not include clear information and directions about how learners could assimilate, learn, and use them in their problem solving experiences. He suggested that students need to discuss what it means, for example, to think of and examining special cases (one important heuristic) in finding a closed formula for series or sequences, analysing relationships of roots of polynomials, or focusing on regular polygons or equilateral/right triangles to find general relations about these figures. That is, learners need to work on examples that lead them to recognize that the use of a particular heuristic often involves thinking of different type of cases depending on the domain or content involved. Lester and Kehle ( 2003 ) summarize themes and methodological shifts in problem solving research up to 1995. Themes include what makes a problem difficult for students and what it means to be successful problem solvers; studying and contrasting experts and novices’ problem solving approaches; learners’ metacognitive, beliefs systems and the influence of affective behaviours; and the role of context; and social interactions in problem solving environments. Research methods in problem solving studies have gone from emphasizing quantitative or statistical design to the use of cases studies and ethnographic methods (Krutestkii ( 1976 ). Teaching strategies also evolved from being centred on teachers to the active students’ engagement and collaboration approaches (NCTM 2000 ). Lesh and Zawojewski ( 2007 ) propose to extend problem solving approaches beyond class setting and they introduce the construct “model eliciting activities” to delve into the learners’ ideas and thinking as a way to engage them in the development of problem solving experiences. To this end, learners develop and constantly refine problem-solving competencies as a part of a learning community that promotes and values modelling construction activities. Recently, English and Gainsburg ( 2016 ) have discussed the importance of modeling eliciting activities to prepare and develop students’ problem solving experiences for 21st Century challenges and demands.

Törner et al. ( 2007 ) invited mathematics educators worldwide to elaborate on the influence and developments of problem solving in their countries. Their contributions show a close relationship between countries mathematical education traditions and ways to frame and implement problem solving approaches. In Chinese classrooms, for example, three instructional strategies are used to structure problem solving lessons: one problem multiple solutions , multiple problems one solution , and one problem multiple changes . In the Netherlands, the realistic mathematical approach permeates the students’ development of problem solving competencies; while in France, problem solving activities are structured in terms of two influential frameworks: The theory of didactical situations and anthropological theory of didactics.

In general, problem solving frameworks and instructional approaches came from analysing students’ problem solving experiences that involve or rely mainly on the use of paper and pencil work. Thus, there is a need to re-examined principles and frameworks to explain what learners develop in learning environments that incorporate systematically the coordinated use of digital technologies (Hoyles and Lagrange 2010 ). In this perspective, it becomes important to briefly describe and identify what both multiple purpose and ad hoc technologies can offer to the students in terms of extending learning environments and representing and exploring mathematical tasks. Specifically, a task is used to identify features of mathematical reasoning that emerge through the use digital technologies that include both mathematical action and multiple purpose types of technologies.

1.3.3 Background

Digital technologies are omnipresent and their use permeates and shapes several social and academic events. Mobile devices such as tablets or smart phones are transforming the way people communicate, interact and carry out daily activities. Churchill et al. ( 2016 ) pointed out that mobile technologies provide a set of tools and affordances to structure and support learning environments in which learners continuously interact to construct knowledge and solve problems. The tools include resources or online materials, efficient connectivity to collaborate and discuss problems, ways to represent, explore and store information, and analytical and administration tools to management learning activities. Schmidt and Cohen ( 2013 ) stated that nowadays it is difficult to imagine a life without mobile devices, and communication technologies are playing a crucial role in generating both cultural and technical breakthroughs. In education, the use of mobile artefacts and computers offers learners the possibility of continuing and extending peers and groups’ mathematical discussions beyond formal settings. In this process, learners can also consult online materials and interact with experts, peers or more experienced students while working on mathematical tasks. In addition, dynamic geometry systems (GeoGebra) provide learners a set of affordances to represent and explore dynamically mathematical problems. Leung and Bolite-Frant ( 2015 ) pointed out that tools help activate an interactive environment in which teachers and students’ mathematical experiences get enriched. Thus, the digital age brings new challenges to the mathematics education community related to the changes that technologies produce to curriculum, learning scenarios, and ways to represent, explore mathematical situations. In particular, it is important to characterize the type of reasoning that learners can develop as a result of using digital technologies in their process of learning concepts and solving mathematical problems.

1.3.4 A Focus on Mathematical Tasks

Mathematical tasks are essential elements for engaging learners in mathematical reasoning which involves representing objects, identifying and exploring their properties in order to detect invariants or relationships and ways to support them. Watson and Ohtani ( 2015 ) stated that task design involves discussions about mathematical content and students’ learning (cognitive perspective), about the students’ experiences to understand the nature of mathematical activities; and about the role that tasks played in teaching practices. In this context, tasks are the vehicle to present and discuss theoretical frameworks for supporting the use of digital technology, to analyse the importance of using digital technologies in extending learners’ mathematical discussions beyond formal settings, and to design ways to foster and assess the use of technologies in learners’ problem solving environments. In addition, it is important to discuss contents, concepts, representations and strategies involved in the process of using digital technologies in approaching the tasks. Similarly, it becomes essential to discuss what types of activities students will do to learn and solve the problems in an environment where the use of technologies fosters and values the participation and collaboration of all students. What digital technologies are important to incorporate in problem solving approaches? Dynamic Geometry Systems can be considered as a milestone in the development of digital technologies. Objects or mathematical situations can be represented dynamically through the use of a Dynamic Geometry System and learners or problem solvers can identify and examine mathematical relations that emerge from moving objects within the dynamic model (Moreno-Armella and Santos-Trigo 2016 ).

Leung and Bolite-Frant ( 2015 ) stated that “dynamic geometry software can be used in task design to cover a large epistemic spectrum from drawing precise robust geometrical figures to exploration of new geometric theorems and development of argumentation discourse” (p. 195). As a result, learners not only need to develop skills and strategies to construct dynamic configuration of problems; but also ways of relying on the tool’s affordances (quantifying parameters or objects attributes, generating loci, graphing objects behaviours, using sliders, or dragging particular elements within the configuration) in order to identify and support mathematical relations. What does it mean to represent and explore an object or mathematical situation dynamically?

A simple task that involves a rhombus and its inscribed circle is used to illustrate how a dynamic representation of these objects and embedded elements can lead learners to identify and examine mathematical properties of those objects in the construction of the configuration. To this end, learners are encouraged to pose and pursue questions to explain the behaviours of parameters or attributes of the family of objects that is generated as a result of moving a particular element within the configuration.

1.3.5 A Task: A Dynamic Rhombus

Figure  2 represents a rhombus APDB and its inscribed circle (O is intersection of diagonals AD and BP and the radius of the inscribed circle is the perpendicular segment from any side of the rhombus to point O), vertex P lies on a circle c centred at point A. Circle c is only a heuristic to generate a family of rhombuses. Thus, point P can be moved along circle c to generate a family of rhombuses. Indeed, based on the symmetry of the circle it is sufficient to move P on the semicircle B’CA to draw such a family of rhombuses.

A dynamic construction of a rhombus

1.3.6 Posing Questions

A goal in constructing a dynamic model or configuration of problems is always to identify and explore mathematical properties and relations that might result from moving objects within the model. How do the areas of both the rhombus and the inscribed circle behave when point P is moved along the arc B’CB? At what position of point P does the area of the rhombus or inscribed circle reach the maximum value? The coordinates of points S and Q (Fig.  3 ) are the x -value of point P and as y -value the corresponding area values of rhombus ABDP and the inscribed circle respectively. Figure  2 shows the loci of points S and Q when point P is moved along arc B’CB. Here, finding the locus via the use of GeoGebra is another heuristic to graph the area behaviour without making explicit the algebraic model of the area.

Graphic representation of the area variation of the family of rhombuses and inscribed circles generated when P is moved through arc B’CB

The area graphs provide information to visualize that in that family of generated rhombuses the maximum area value of the inscribed circle and rhombus is reached when the rhombus becomes a square (Fig.  4 ). That is, the controlled movement of particular objects is an important strategy to analyse the area variation of the family of rhombuses and their inscribed circles.

Visualizing the rhombus and the inscribed circle with maximum area

It is important to observe the identification of points P and Q in terms of the position of point P and the corresponding areas and the movement of point P was sufficient to generate both area loci. That is, the graph representation of the areas is achieved without having an explicit algebraic expression of the area variation. Clearly, the graphic representations provide information regarding the increasing or decreasing interval of both areas; it is also important to explore what properties both graphic representations hold. The goal is to argue that the area variation of the rhombus represents an ellipse and the area of the inscribed circle represents a parabola. An initial argument might involve selecting five points on each locus and using the tool to draw the corresponding conic section (Fig.  5 ). In this case, the tool affordances play an important role in generating the graphic representation of the areas’ behaviours and in identifying properties of those representations. In this context, the use of the tool can offer learners the opportunity to problematize (Santos-Trigo 2007 ) a simple mathematical object (rhombus) as a means to search for mathematical relations and ways to support them.

Drawing the conic section that passes through five points

1.3.7 Looking for Different Solutions Methods

Another line of exploration might involve asking for ways to construct a rhombus and its inscribed circle: Suppose that the side of the rhombus and the circle are given, how can you construct the rhombus that has that circle inscribed? Figure  6 shows the given data, segment A 1 B 1 and circle centred at O and radius OD. The initial goal is to draw the circle tangent to the given segment. To this end, segment AB is congruent to segment A 1 B 1 and on this segment a point P is chosen and a perpendicular to segment AB that passes through point P is drawn. Point C is on this perpendicular and the centre of a circle with radius OD and h is the perpendicular to line PC that passes through point C. Angle ACB changes when point P is moved along segment AB and point E and F are the intersection of line h and the circle with centre M the midpoint of AB and radius MA (Fig.  6 ).

Drawing segment AB tangent to the given circle

Figure  7 a shows the right triangle AFB as the base to construct the rhombus and the inscribed circle and Fig.  7 b shows the second solution based on triangle AEB.

a Drawing the rhombus and the inscribed circle. b Drawing the second solution

Another approach might involve drawing the given circle centred at the origin and the segment as EF with point E on the y-axis. Line OC is perpendicular to segment EF and the locus of point C when point E moves along the y-axis intersects the given circle (Fig.  8 a, b). Both figures show two solutions to draw the rhombus that circumscribe the given circle.

a and b Another solution that involves finding a locus of point C

In this example, the GeoGebra affordances not only are important to construct a dynamic model of the task; but also offer learners and opportunity to explore relations that emerge from moving objects within the model. As a result, learners can rely on different concepts and strategies to solve the tasks. The idea in presenting this rhombus task is to illustrate that the use of a Dynamic Geometry System provides affordances for learners to construct dynamic representation of mathematical objects or problems, to move elements within the representation to pose questions or conjectures to explain invariants or patterns among involved parameters; to search for arguments to support emerging conjectures, and to develop a proper language to communicate results.

1.3.8 Looking Back

Conceptual frameworks used to explain learners’ construction of mathematical knowledge need to capture or take into account the different ways of reasoning that students might develop as a result of using a set of tools during the learning experiences. Figure  9 show some digital technologies that learners can use for specific purpose at the different stages of problem solving activities.

The coordinated use of digital tools to engage learners in problem solving experiences

The use of a dynamic system (GeoGebra) provides a set of affordances for learners to conceptualize and represent mathematical objects and tasks dynamically. In this process, affordances such as moving objects orderly (dragging), finding loci of objects, quantifying objects attributes (lengths, areas, angles, etc.), using sliders to vary parameters, and examining family of objects became important to look for invariance or objects relationships. Likewise, analysing the parameters or objects behaviours within the configuration might lead learners to identify properties to support emerging mathematical relations. Thus, with the use of the tool, learners might conceptualize mathematical tasks as an opportunity for them to engage in mathematical activities that include constructing dynamic models of tasks, formulating conjectures, and always looking for different arguments to support them. Similarly, learners can use an online platform to share their ideas, problem solutions or questions in a digital wall and others students can also share ideas or solution methods and engaged in mathematical discussions that extend mathematical classroom activities.

1.4 Problem Posing: An Overview for Further Progress—Uldarico Malaspina Jurado

Problem posing and problem solving are two essential aspects of the mathematical activity; however, researchers in mathematics education have not emphasized their attention on problem posing as much as problem solving. In that sense, due to its importance in the development of mathematical thinking in students since the first grades, we agree with Ellerton’s statement ( 2013 ): “for too long, successful problem solving has been lauded as the goal; the time has come for problem posing to be given a prominent but natural place in mathematics curricula and classrooms” (pp. 100–101); and due to its importance in teacher training, with Abu-Elwan’s statement ( 1999 ):

While teacher educators generally recognize that prospective teachers require guidance in mastering the ability to confront and solve problems, what is often overlooked is the critical fact that, as teachers, they must be able to go beyond the role as problem solvers. That is, in order to promote a classroom situation where creative problem solving is the central focus, the practitioner must become skillful in discovering and correctly posing problems that need solutions. (p. 1)

Scientists like Einstein and Infeld ( 1938 ), recognized not only for their notable contributions in the fields they worked, but also for their reflections on the scientific activity, pointed out the importance of problem posing; thus it is worthwhile to highlight their statement once again:

The formulation of a problem is often more essential than its solution, which may be merely a matter of mathematical or experimental skills. To raise new questions, new possibilities, to regard old questions from a new angle, requires creative imagination and marks real advance in science. (p. 92)

Certainly, it is also relevant to remember mathematician Halmos’s statement ( 1980 ): “I do believe that problems are the heart of mathematics, and I hope that as teachers (…) we will train our students to be better problem posers and problem solvers than we are” (p. 524).

An important number of researchers in mathematics education has focused on the importance of problem posing, and we currently have numerous, very important publications that deal with different aspects of problem posing related to the mathematics education of students in all educational levels and to teacher training.

1.4.1 A Retrospective Look

Kilpatrick ( 1987 ) marked a historical milestone in research related to problem posing and points out that “problem formulating should be viewed not only as a goal of instruction but also as a means of instruction” (Kilpatrick 1987 , p. 123); and he also emphasizes that, as part of students’ education, all of them should be given opportunities to live the experience of discovering and posing their own problems. Drawing attention to the few systematic studies on problem posing performed until then, Kilpatrick contributes defining some aspects that required studying and investigating as steps prior to a theoretical building, though he warns, “attempts to teach problem-formulating skills, of course, need not await a theory” (p. 124).

Kilpatrick refers to the “Source of problems” and points out how virtually all problems students solve have been posed by another person; however, in real life “many problems, if not most, must be created or discovered by the solver, who gives the problem an initial formulation” (p. 124). He also points out that problems are reformulated as they are being solved, and he relates this to investigation, reminding us what Davis ( 1985 ) states that, “what typically happens in a prolonged investigation is that problem formulation and problem solution go hand in hand, each eliciting the other as the investigation progresses” (p. 23). He also relates it to the experiences of software designers, who formulate an appropriate sequence of sub-problems to solve a problem. He poses that a subject to be examined by teachers and researchers “is whether, by drawing students’ attention to the reformulating process and given them practice in it, we can improve their problem solving performance” (p. 130). He also points out that problems may be a mathematical formulation as a result of exploring a situation and, in that sense, “school exercises in constructing mathematical models of a situation presented by the teacher are intended to provide students with experiences in formulating problems.” (p. 131).

Another important section of Kilpatrick’s work ( 1987 ) is Processes of Problem Formulating , in which he considers association, analogy, generalization and contradiction. He believes the use of concept maps to represent concept organization, as cognitive scientists Novak and Gowin suggest, might help to comprehend such concepts, stimulate creative thinking about them, and complement the ideas Brown and Walter ( 1983 ) give for problem posing by association. Further, in the section “Understanding and developing problem formulating abilities”, he poses several questions, which have not been completely answered yet, like “Perhaps the central issue from the point of view of cognitive science is what happens when someone formulates the problem? (…) What is the relation between problem formulating, problem solving and structured knowledge base? How rich a knowledge base is needed for problem formulating? (…) How does experience in problem formulating add to knowledge base? (…) What metacognitive processes are needed for problem formulating?”

It is interesting to realize that some of these questions are among the unanswered questions proposed and analyzed by Cai et al. ( 2015 ) in Chap. 1 of the book Mathematical Problem Posing (Singer et al. 2015 ). It is worth stressing the emphasis on the need to know the cognitive processes in problem posing, an aspect that Kilpatrick had already posed in 1987, as we just saw.

1.4.2 Researches and Didactic Experiences

Currently, there are a great number of publications related to problem posing, many of which are research and didactic experiences that gather the questions posed by Kilpatrick, which we just commented. Others came up naturally as reflections raised in the framework of problem solving, facing the natural requirement of having appropriate problems to use results and suggestions of researches on problem solving, or as a response to a thoughtful attitude not to resign to solving and asking students to solve problems that are always created by others. Why not learn and teach mathematics posing one’s own problems?

1.4.3 New Directions of Research

Singer et al. ( 2013 ) provides a broad view about problem posing that links problem posing experiences to general mathematics education; to the development of abilities, attitudes and creativity; and also to its interrelation with problem solving, and studies on when and how problem-solving sessions should take place. Likewise, it provides information about research done regarding ways to pose new problems and about the need for teachers to develop abilities to handle complex situations in problem posing contexts.

Singer et al. ( 2013 ) identify new directions in problem posing research that go from problem-posing task design to the development of problem-posing frameworks to structure and guide teachers and students’ problem posing experiences. In a chapter of this book, Leikin refers to three different types of problem posing activities, associated with school mathematics research: (a) problem posing through proving; (b) problem posing for investigation; and (c) problem posing through investigation. This classification becomes evident in the problems posed in a course for prospective secondary school mathematics teachers by using a dynamic geometry environment. Prospective teachers posed over 25 new problems, several of which are discussed in the article. The author considers that, by developing this type of problem posing activities, prospective mathematics teachers may pose different problems related to a geometric object, prepare more interesting lessons for their students, and thus gradually develop their mathematical competence and their creativity.

1.4.4 Final Comments

This overview, though incomplete, allows us to see a part of what problem posing experiences involve and the importance of this area in students mathematical learning. An important task is to continue reflecting on the questions posed by Kilpatrick ( 1987 ), as well as on the ones that come up in the different researches aforementioned. To continue progressing in research on problem posing and contribute to a greater consolidation of this research line, it will be really important that all mathematics educators pay more attention to problem posing, seek to integrate approaches and results, and promote joint and interdisciplinary works. As Singer et al. ( 2013 ) say, going back to Kilpatrick’s proposal ( 1987 ),

Problem posing is an old issue. What is new is the awareness that problem posing needs to pervade the education systems around the world, both as a means of instruction (…) and as an object of instruction (…) with important targets in real-life situations. (p. 5)

Although it can be argued that there is a difference between creativity, discovery, and invention (see Liljedahl and Allan 2014 ) for the purposes of this book these will be assumed to be interchangeable.

Abu-Elwan, R. (1999). The development of mathematical problem posing skills for prospective middle school teachers. In A. Rogerson (Ed.), Proceedings of the International Conference on Mathematical Education into the 21st century: Social Challenges, Issues and Approaches , (Vol. 2, pp. 1–8), Cairo, Egypt.

Google Scholar  

Ashcraft, M. (1989). Human memory and cognition . Glenview, Illinois: Scott, Foresman and Company.

Bailin, S. (1994). Achieving extraordinary ends: An essay on creativity . Norwood, NJ: Ablex Publishing Corporation.

Bibby, T. (2002). Creativity and logic in primary-school mathematics: A view from the classroom. For the Learning of Mathematics, 22 (3), 10–13.

Brown, S., & Walter, M. (1983). The art of problem posing . Philadelphia: Franklin Institute Press.

Bruder, R. (2000). Akzentuierte Aufgaben und heuristische Erfahrungen. In W. Herget & L. Flade (Eds.), Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen (pp. 69–78). Berlin: Volk und Wissen.

Bruder, R. (2005). Ein aufgabenbasiertes anwendungsorientiertes Konzept für einen nachhaltigen Mathematikunterricht—am Beispiel des Themas “Mittelwerte”. In G. Kaiser & H. W. Henn (Eds.), Mathematikunterricht im Spannungsfeld von Evolution und Evaluation (pp. 241–250). Hildesheim, Berlin: Franzbecker.

Bruder, R., & Collet, C. (2011). Problemlösen lernen im Mathematikunterricht . Berlin: CornelsenVerlag Scriptor.

Bruner, J. (1964). Bruner on knowing . Cambridge, MA: Harvard University Press.

Burton, L. (1999). Why is intuition so important to mathematicians but missing from mathematics education? For the Learning of Mathematics, 19 (3), 27–32.

Cai, J., Hwang, S., Jiang, C., & Silber, S. (2015). Problem posing research in mathematics: Some answered and unanswered questions. In F.M. Singer, N. Ellerton, & J. Cai (Eds.), Mathematical problem posing: From research to effective practice (pp.3–34). Springer.

Churchill, D., Fox, B., & King, M. (2016). Framework for designing mobile learning environments. In D. Churchill, J. Lu, T. K. F. Chiu, & B. Fox (Eds.), Mobile learning design (pp. 20–36)., lecture notes in educational technology NY: Springer.

Chapter   Google Scholar  

Collet, C. (2009). Problemlösekompetenzen in Verbindung mit Selbstregulation fördern. Wirkungsanalysen von Lehrerfortbildungen. In G. Krummheuer, & A. Heinze (Eds.), Empirische Studien zur Didaktik der Mathematik , Band 2, Münster: Waxmann.

Collet, C., & Bruder, R. (2008). Longterm-study of an intervention in the learning of problem-solving in connection with self-regulation. In O. Figueras, J. L. Cortina, S. Alatorre, T. Rojano, & A. Sepúlveda (Eds.), Proceedings of the Joint Meeting of PME 32 and PME-NA XXX, (Vol. 2, pp. 353–360).

Csíkszentmihályi, M. (1996). Creativity: Flow and the psychology of discovery and invention . New York: Harper Perennial.

Davis, P. J. (1985). What do I know? A study of mathematical self-awareness. College Mathematics Journal, 16 (1), 22–41.

Article   Google Scholar  

Dewey, J. (1933). How we think . Boston, MA: D.C. Heath and Company.

Dewey, J. (1938). Logic: The theory of inquiry . New York, NY: Henry Holt and Company.

Einstein, A., & Infeld, L. (1938). The evolution of physics . New York: Simon and Schuster.

Ellerton, N. (2013). Engaging pre-service middle-school teacher-education students in mathematical problem posing: Development of an active learning framework. Educational Studies in Math, 83 (1), 87–101.

Engel, A. (1998). Problem-solving strategies . New York, Berlin und Heidelberg: Springer.

English, L. (1997). Children’s reasoning processes in classifying and solving comparison word problems. In L. D. English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 191–220). Mahwah, NJ: Lawrence Erlbaum Associates Inc.

English, L. (1998). Reasoning by analogy in solving comparison problems. Mathematical Cognition, 4 (2), 125–146.

English, L. D. & Gainsburg, J. (2016). Problem solving in a 21st- Century mathematics education. In L. D. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (pp. 313–335). NY: Routledge.

Ghiselin, B. (1952). The creative process: Reflections on invention in the arts and sciences . Berkeley, CA: University of California Press.

Hadamard, J. (1945). The psychology of invention in the mathematical field . New York, NY: Dover Publications.

Halmos, P. (1980). The heart of mathematics. American Mathematical Monthly, 87 , 519–524.

Halmos, P. R. (1994). What is teaching? The American Mathematical Monthly, 101 (9), 848–854.

Hoyles, C., & Lagrange, J.-B. (Eds.). (2010). Mathematics education and technology–Rethinking the terrain. The 17th ICMI Study . NY: Springer.

Kilpatrick, J. (1985). A retrospective account of the past 25 years of research on teaching mathematical problem solving. In E. Silver (Ed.), Teaching and learning mathematical problem solving: Multiple research perspectives (pp. 1–15). Hillsdale, New Jersey: Lawrence Erlbaum.

Kilpatrick, J. (1987). Problem formulating: Where do good problem come from? In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 123–147). Hillsdale, NJ: Erlbaum.

Kline, M. (1972). Mathematical thought from ancient to modern times . NY: Oxford University Press.

Kneller, G. (1965). The art and science of creativity . New York, NY: Holt, Reinhart, and Winstone Inc.

Koestler, A. (1964). The act of creation . New York, NY: The Macmillan Company.

König, H. (1984). Heuristik beim Lösen problemhafter Aufgaben aus dem außerunterrichtlichen Bereich . Technische Hochschule Chemnitz, Sektion Mathematik.

Kretschmer, I. F. (1983). Problemlösendes Denken im Unterricht. Lehrmethoden und Lernerfolge . Dissertation. Frankfurt a. M.: Peter Lang.

Krulik, S. A., & Reys, R. E. (Eds.). (1980). Problem solving in school mathematics. Yearbook of the national council of teachers of mathematics . Reston VA: NCTM.

Krutestkii, V. A. (1976). The psychology of mathematical abilities in school children . University of Chicago Press.

Lesh, R., & Zawojewski, J. S. (2007). Problem solving and modeling. In F. K. Lester, Jr. (Ed.), The second handbook of research on mathematics teaching and learning (pp. 763–804). National Council of Teachers of Mathematics, Charlotte, NC: Information Age Publishing.  

Lester, F., & Kehle, P. E. (2003). From problem solving to modeling: The evolution of thinking about research on complex mathematical activity. In R. Lesh & H. Doerr (Eds.), Beyond constructivism: Models and modeling perspectives on mathematics problem solving, learning and teaching (pp. 501–518). Mahwah, NJ: Lawrence Erlbaum.

Lester, F. K., Garofalo, J., & Kroll, D. (1989). The role of metacognition in mathematical problem solving: A study of two grade seven classes. Final report to the National Science Foundation, NSF Project No. MDR 85-50346. Bloomington: Indiana University, Mathematics Education Development Center.

Leung, A., & Bolite-Frant, J. (2015). Designing mathematical tasks: The role of tools. In A. Watson & M. Ohtani (Eds.), Task design in mathematics education (pp. 191–225). New York: Springer.

Liljedahl, P. (2008). The AHA! experience: Mathematical contexts, pedagogical implications . Saarbrücken, Germany: VDM Verlag.

Liljedahl, P., & Allan, D. (2014). Mathematical discovery. In E. Carayannis (Ed.), Encyclopedia of creativity, invention, innovation, and entrepreneurship . New York, NY: Springer.

Liljedahl, P., & Sriraman, B. (2006). Musings on mathematical creativity. For the Learning of Mathematics, 26 (1), 20–23.

Lompscher, J. (1975). Theoretische und experimentelle Untersuchungen zur Entwicklung geistiger Fähigkeiten . Berlin: Volk und Wissen. 2. Auflage.

Lompscher, J. (1985). Die Lerntätigkeit als dominierende Tätigkeit des jüngeren Schulkindes. In L. Irrlitz, W. Jantos, E. Köster, H. Kühn, J. Lompscher, G. Matthes, & G. Witzlack (Eds.), Persönlichkeitsentwicklung in der Lerntätigkeit . Berlin: Volk und Wissen.

Mason, J., & Johnston-Wilder, S. (2006). Designing and using mathematical tasks . St. Albans: Tarquin Publications.

Mason, J., Burton, L., & Stacey, K. (1982). Thinking mathematically . Harlow: Pearson Prentice Hall.

Mayer, R. (1982). The psychology of mathematical problem solving. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 1–13). Philadelphia, PA: Franklin Institute Press.

Mevarech, Z. R., & Kramarski, B. (1997). IMPROVE: A multidimensional method for teaching mathematics in heterogeneous classrooms. American Educational Research Journal, 34 (2), 365–394.

Mevarech, Z. R., & Kramarski, B. (2003). The effects of metacognitive training versus worked-out examples on students’ mathematical reasoning. British Journal of Educational Psychology, 73 , 449–471.

Moreno-Armella, L., & Santos-Trigo, M. (2016). The use of digital technologies in mathematical practices: Reconciling traditional and emerging approaches. In L. English & D. Kirshner (Eds.), Handbook of international research in mathematics education (3rd ed., pp. 595–616). New York: Taylor and Francis.

National Council of Teachers of Mathematics (NCTM). (1980). An agenda for action . Reston, VA: NCTM.

National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics . Reston, VA: National Council of Teachers of Mathematics.

Newman, J. (2000). The world of mathematics (Vol. 4). New York, NY: Dover Publishing.

Novick, L. (1988). Analogical transfer, problem similarity, and expertise. Journal of Educational Psychology: Learning, Memory, and Cognition, 14 (3), 510–520.

Novick, L. (1990). Representational transfer in problem solving. Psychological Science, 1 (2), 128–132.

Novick, L. (1995). Some determinants of successful analogical transfer in the solution of algebra word problems. Thinking & Reasoning, 1 (1), 5–30.

Novick, L., & Holyoak, K. (1991). Mathematical problem solving by analogy. Journal of Experimental Psychology, 17 (3), 398–415.

Pehkonen, E. K. (1991). Developments in the understanding of problem solving. ZDM—The International Journal on Mathematics Education, 23 (2), 46–50.

Pehkonen, E. (1997). The state-of-art in mathematical creativity. Analysis, 97 (3), 63–67.

Perels, F., Schmitz, B., & Bruder, R. (2005). Lernstrategien zur Förderung von mathematischer Problemlösekompetenz. In C. Artelt & B. Moschner (Eds.), Lernstrategien und Metakognition. Implikationen für Forschung und Praxis (pp. 153–174). Waxmann education.

Perkins, D. (2000). Archimedes’ bathtub: The art of breakthrough thinking . New York, NY: W.W. Norton and Company.

Poincaré, H. (1952). Science and method . New York, NY: Dover Publications Inc.

Pólya, G. (1945). How to solve It . Princeton NJ: Princeton University.

Pólya, G. (1949). How to solve It . Princeton NJ: Princeton University.

Pólya, G. (1954). Mathematics and plausible reasoning . Princeton: Princeton University Press.

Pólya, G. (1964). Die Heuristik. Versuch einer vernünftigen Zielsetzung. Der Mathematikunterricht , X (1), 5–15.

Pólya, G. (1965). Mathematical discovery: On understanding, learning and teaching problem solving (Vol. 2). New York, NY: Wiley.

Resnick, L., & Glaser, R. (1976). Problem solving and intelligence. In L. B. Resnick (Ed.), The nature of intelligence (pp. 230–295). Hillsdale, NJ: Lawrence Erlbaum Associates.

Rusbult, C. (2000). An introduction to design . http://www.asa3.org/ASA/education/think/intro.htm#process . Accessed January 10, 2016.

Santos-Trigo, M. (2007). Mathematical problem solving: An evolving research and practice domain. ZDM—The International Journal on Mathematics Education , 39 (5, 6): 523–536.

Santos-Trigo, M. (2014). Problem solving in mathematics education. In S. Lerman (Ed.), Encyclopedia of mathematics education (pp. 496–501). New York: Springer.

Schmidt, E., & Cohen, J. (2013). The new digital age. Reshaping the future of people nations and business . NY: Alfred A. Knopf.

Schoenfeld, A. H. (1979). Explicit heuristic training as a variable in problem-solving performance. Journal for Research in Mathematics Education, 10 , 173–187.

Schoenfeld, A. H. (1982). Some thoughts on problem-solving research and mathematics education. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 27–37). Philadelphia: Franklin Institute Press.

Schoenfeld, A. H. (1985). Mathematical problem solving . Orlando, Florida: Academic Press Inc.

Schoenfeld, A. H. (1987). What’s all the fuss about metacognition? In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 189–215). Hillsdale, NJ: Lawrence Erlbaum Associates.

Schoenfeld, A. H. (1992). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). New York, NY: Simon and Schuster.

Schön, D. (1987). Educating the reflective practitioner . San Fransisco, CA: Jossey-Bass Publishers.

Sewerin, H. (1979): Mathematische Schülerwettbewerbe: Beschreibungen, Analysen, Aufgaben, Trainingsmethoden mit Ergebnissen . Umfrage zum Bundeswettbewerb Mathematik. München: Manz.

Silver, E. (1982). Knowledge organization and mathematical problem solving. In F. K. Lester & J. Garofalo (Eds.), Mathematical problem solving: Issues in research (pp. 15–25). Philadelphia: Franklin Institute Press.

Singer, F., Ellerton, N., & Cai, J. (2013). Problem posing research in mathematics education: New questions and directions. Educational Studies in Mathematics, 83 (1), 9–26.

Singer, F. M., Ellerton, N. F., & Cai, J. (Eds.). (2015). Mathematical problem posing. From research to practice . NY: Springer.

Törner, G., Schoenfeld, A. H., & Reiss, K. M. (2007). Problem solving around the world: Summing up the state of the art. ZDM—The International Journal on Mathematics Education, 39 (1), 5–6.

Verschaffel, L., de Corte, E., Lasure, S., van Vaerenbergh, G., Bogaerts, H., & Ratinckx, E. (1999). Learning to solve mathematical application problems: A design experiment with fifth graders. Mathematical Thinking and Learning, 1 (3), 195–229.

Wallas, G. (1926). The art of thought . New York: Harcourt Brace.

Watson, A., & Ohtani, M. (2015). Themes and issues in mathematics education concerning task design: Editorial introduction. In A. Watson & M. Ohtani (Eds.), Task design in mathematics education, an ICMI Study 22 (pp. 3–15). NY: Springer.

Zimmermann, B. (1983). Problemlösen als eine Leitidee für den Mathematikunterricht. Ein Bericht über neuere amerikanische Beiträge. Der Mathematikunterricht, 3 (1), 5–45.

Further Reading

Boaler, J. (1997). Experiencing school mathematics: Teaching styles, sex, and setting . Buckingham, PA: Open University Press.

Borwein, P., Liljedahl, P., & Zhai, H. (2014). Mathematicians on creativity. Mathematical Association of America.

Burton, L. (1984). Thinking things through . London, UK: Simon & Schuster Education.

Feynman, R. (1999). The pleasure of finding things out . Cambridge, MA: Perseus Publishing.

Gardner, M. (1978). Aha! insight . New York, NY: W. H. Freeman and Company.

Gardner, M. (1982). Aha! gotcha: Paradoxes to puzzle and delight . New York, NY: W. H. Freeman and Company.

Gardner, H. (1993). Creating minds: An anatomy of creativity seen through the lives of Freud, Einstein, Picasso, Stravinsky, Eliot, Graham, and Ghandi . New York, NY: Basic Books.

Glas, E. (2002). Klein’s model of mathematical creativity. Science & Education, 11 (1), 95–104.

Hersh, D. (1997). What is mathematics, really? . New York, NY: Oxford University Press.

Root-Bernstein, R., & Root-Bernstein, M. (1999). Sparks of genius: The thirteen thinking tools of the world’s most creative people . Boston, MA: Houghton Mifflin Company.

Zeitz, P. (2006). The art and craft of problem solving . New York, NY: Willey.

Download references

Author information

Authors and affiliations.

Faculty of Education, Simon Fraser University, Burnaby, BC, Canada

Peter Liljedahl

Mathematics Education Department, Cinvestav-IPN, Centre for Research and Advanced Studies, Mexico City, Mexico

Manuel Santos-Trigo

Pontificia Universidad Católica del Perú, Lima, Peru

Uldarico Malaspina

Technical University Darmstadt, Darmstadt, Germany

Regina Bruder

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Peter Liljedahl .

Rights and permissions

Open Access This chapter is distributed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, a link is provided to the Creative Commons license and any changes made are indicated.

The images or other third party material in this chapter are included in the work’s Creative Commons license, unless indicated otherwise in the credit line; if such material is not included in the work’s Creative Commons license and the respective action is not permitted by statutory regulation, users will need to obtain permission from the license holder to duplicate, adapt or reproduce the material.

Reprints and permissions

Copyright information

© 2016 The Author(s)

About this chapter

Liljedahl, P., Santos-Trigo, M., Malaspina, U., Bruder, R. (2016). Problem Solving in Mathematics Education. In: Problem Solving in Mathematics Education. ICME-13 Topical Surveys. Springer, Cham. https://doi.org/10.1007/978-3-319-40730-2_1

Download citation

DOI : https://doi.org/10.1007/978-3-319-40730-2_1

Published : 28 June 2016

Publisher Name : Springer, Cham

Print ISBN : 978-3-319-40729-6

Online ISBN : 978-3-319-40730-2

eBook Packages : Education Education (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Math Solver

Geogebra math solver.

Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

Fluency, Reasoning and Problem Solving: What This Looks Like In Every Math Lesson

Neil Almond

Fluency, reasoning and problem solving are central strands of mathematical competency, as recognized by the National Council of Teachers of Mathematics (NCTM) and the National Research Council’s report ‘Adding It Up’.

They are key components to the Standards of Mathematical Practice, standards that are interwoven into every mathematics lesson. Here we look at how these three approaches or elements of math can be interwoven in a child’s math education through elementary and middle school.

We look at what fluency, reasoning and problem solving are, how to teach them, and how to know how a child is progressing in each – as well as what to do when they’re not, and what to avoid.

The hope is that this blog will help elementary and middle school teachers think carefully about their practice and the pedagogical choices they make around the teaching of what the common core refers to as ‘mathematical practices’, and reasoning and problem solving in particular.

Before we can think about what this would look like in Common Core math examples and other state-specific math frameworks, we need to understand the background to these terms.

What is fluency in math?

What is reasoning in math, what is problem solving in math, mathematical problem solving is a learned skill, performance vs learning: what to avoid when teaching fluency, reasoning, and problem solving.

• What IS ‘performance vs learning’?
• Teaching to “cover the curriculum” hinders development of strong problem solving skills.
• Fluency and reasoning – Best practice in a lesson, a unit, and a semester

Best practice for problem solving in a lesson, a unit, and a semester 

Fluency, reasoning and problem solving should not be taught by rote .

The Ultimate Guide to Problem Solving Techniques

Develop problem solving skills in the classroom with this free, downloadable worksheet

Fluency in math is a fairly broad concept. The basics of mathematical fluency – as defined by the Common Core State Standards for math – involve knowing key mathematical skills and being able to carry them out flexibly, accurately and efficiently.

But true fluency in math (at least up to middle school) means being able to apply the same skill to multiple contexts, and being able to choose the most appropriate method for a particular task.

Fluency in math lessons means we teach the content using a range of representations, to ensure that all students understand and have sufficient time to practice what is taught.

Read more: How the best schools develop math fluency

Reasoning in math is the process of applying logical thinking to a situation to derive the correct math strategy for problem solving  for a question, and using this method to develop and describe a solution.

Put more simply, mathematical reasoning is the bridge between fluency and problem solving. It allows students to use the former to accurately carry out the latter.

Read more: Developing math reasoning: the mathematical skills required and how to teach them .

It’s sometimes easier to start off with what problem solving is not. Problem solving is not necessarily just about answering word problems in math. If a child already has a readily available method to solve this sort of problem, problem solving has not occurred. Problem solving in math is finding a way to apply knowledge and skills you have to answer unfamiliar types of problems.

Read more: Math problem solving: strategies and resources for primary school teachers .

We are all problem solvers

First off, problem solving should not be seen as something that some students can do and some cannot. Every single person is born with an innate level of problem-solving ability.

Early on as a species on this planet, we solved problems like recognizing faces we know, protecting ourselves against other species, and as babies the problem of getting food (by crying relentlessly until we were fed).

All these scenarios are a form of what the evolutionary psychologist David Geary (1995) calls biologically primary knowledge. We have been solving these problems for millennia and they are so ingrained in our DNA that we learn them without any specific instruction.

Why then, if we have this innate ability, does actually teaching problem solving seem so hard?

As you might have guessed, the domain of mathematics is far from innate. Math doesn’t just happen to us; we need to learn it. It needs to be passed down from experts that have the knowledge to novices who do not.

This is what Geary calls biologically secondary knowledge. Solving problems (within the domain of math) is a mixture of both primary and secondary knowledge.

The issue is that problem solving in domains that are classified as biologically secondary knowledge (like math) can only be improved by practicing elements of that domain.

So there is no generic problem-solving skill that can be taught in isolation and transferred to other areas.

This will have important ramifications for pedagogical choices, which I will go into more detail about later on in this blog.

The educationalist Dylan Wiliam had this to say on the matter: ‘for…problem solving, the idea that students can learn these skills in one context and apply them in another is essentially wrong.’ (Wiliam, 2018) So what is the best method of teaching problem solving to elementary and middle school math students?

The answer is that we teach them plenty of domain specific biological secondary knowledge – in this case, math. Our ability to successfully problem solve requires us to have a deep understanding of content and fluency of facts and mathematical procedures.

Here is what cognitive psychologist Daniel Willingham (2010) has to say:

‘Data from the last thirty years leads to a conclusion that is not scientifically challengeable: thinking well requires knowing facts, and that’s true not simply because you need something to think about.

The very processes that teachers care about most—critical thinking processes such as reasoning and problem solving—are intimately intertwined with factual knowledge that is stored in long-term memory (not just found in the environment).’

Colin Foster (2019), a reader in Mathematics Education in the Mathematics Education Center at Loughborough University, UK, says, ‘I think of fluency and mathematical reasoning, not as ends in themselves, but as means to support students in the most important goal of all: solving problems.’

In that paper he produces this pyramid:

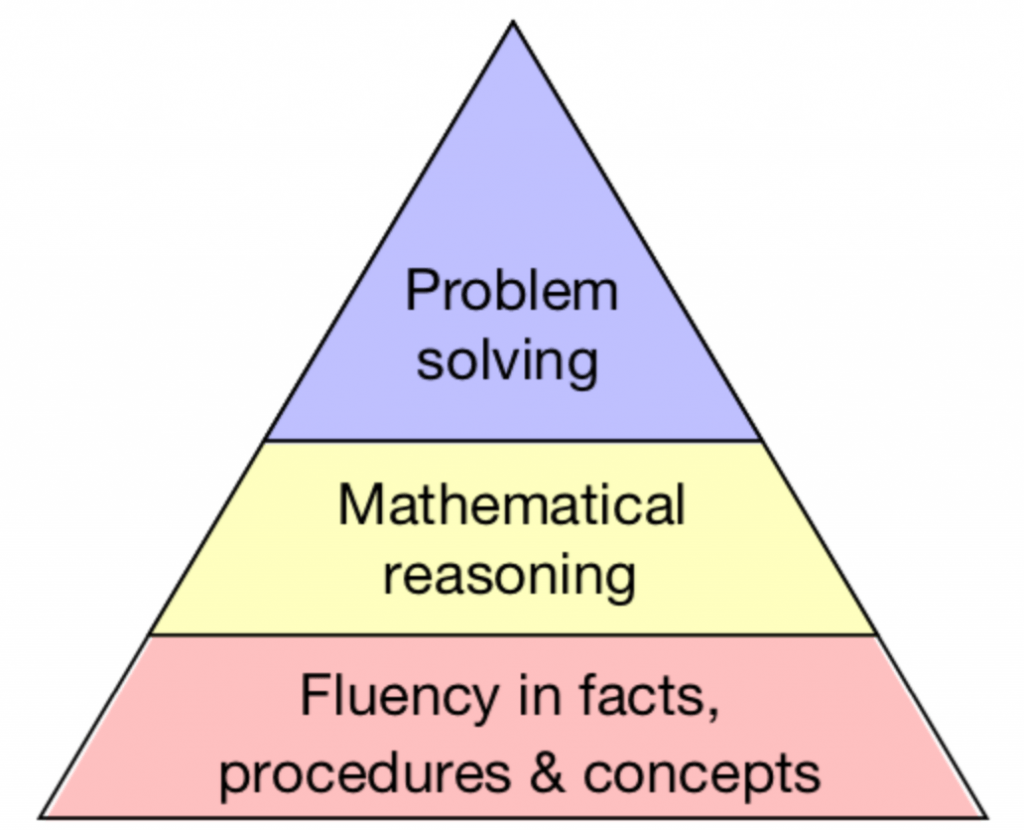
This is important for two reasons:

1)    It splits up reasoning skills and problem solving into two different entities

2)    It demonstrates that fluency is not something to be rushed through to get to the ‘problem solving’ stage but is rather the foundation of problem solving.

In my own work I adapt this model and turn it into a cone shape, as education seems to have a problem with pyramids and gross misinterpretation of them (think Bloom’s taxonomy).

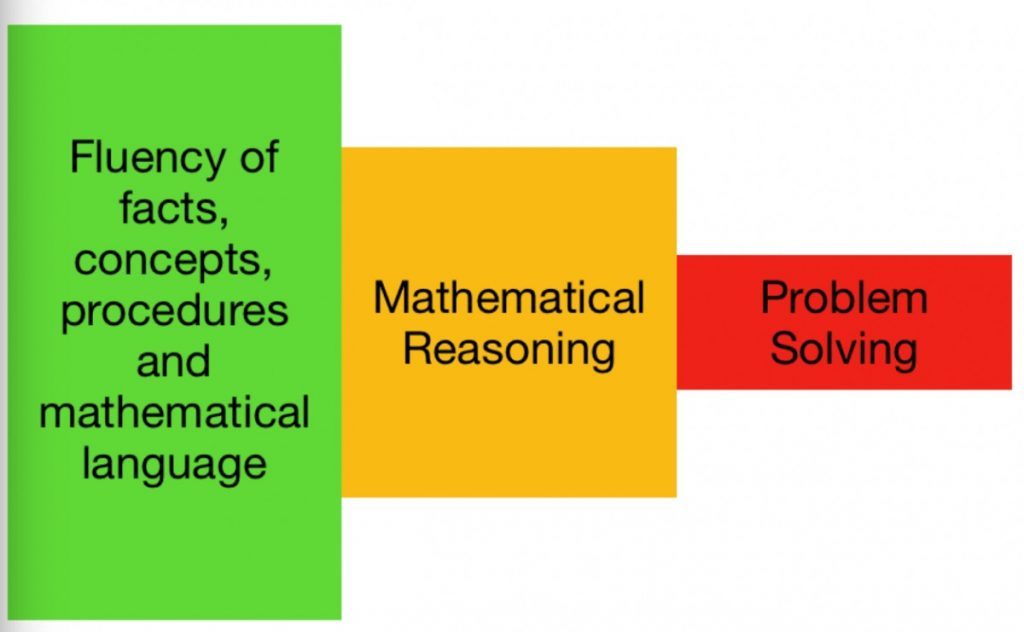
Notice how we need plenty of fluency of facts, concepts, procedures and mathematical language.

Having this fluency will help with improving logical reasoning skills, which will then lend themselves to solving mathematical problems – but only if it is truly learnt and there is systematic retrieval of this information carefully planned across the curriculum.

I mean to make no sweeping generalization here; this was my experience both at university when training and from working in schools.

At some point, schools become obsessed with the ridiculous notion of moving students through content at an accelerated rate. I have heard it used in all manner of educational contexts while training and being a teacher. ‘You will need to show ‘accelerated progress in math’ in this lesson,’ ‘School officials will be looking for ‘accelerated progress’ etc.

I have no doubt that all of this came from a good place and from those wanting the best possible outcomes – but it is misguided.

I remember being told that we needed to get students onto the problem solving questions as soon as possible to demonstrate this mystical ‘accelerated progress’.

This makes sense; you have a group of students and you have taken them from not knowing something to working out pretty sophisticated 2-step or multi-step word problems within an hour. How is that not ‘accelerated progress?’

This was a frequent feature of my lessons up until last academic year: teach a mathematical procedure; get the students to do about 10 of them in their books; mark these and if the majority were correct, model some reasoning/problem solving questions from the same content as the fluency content; give the students some reasoning and word problem questions and that was it.

I wondered if I was the only one who had been taught this while at university so I did a quick poll on Twitter and found that was not the case.

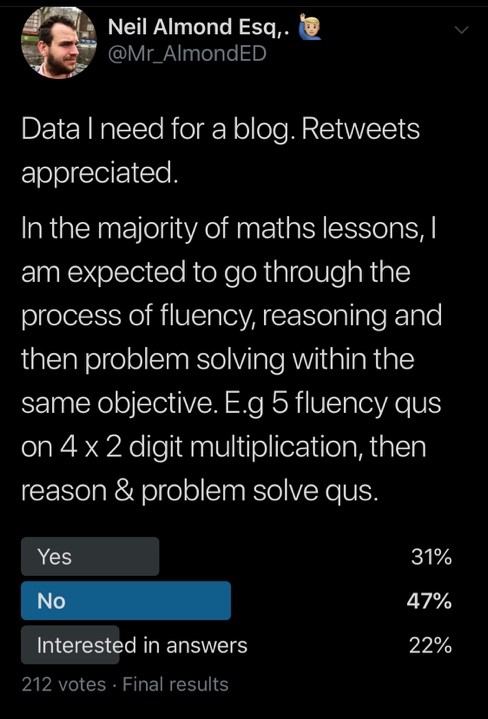
I know these numbers won’t be big enough for a representative sample but it still shows that others are familiar with this approach.

The issue with the lesson framework I mentioned above is that it does not take into account ‘performance vs learning.’

What IS ‘performance vs learning’?

The premise is that performance in a lesson is not a good proxy for learning.

Yes, those students were performing well after I had modeled a mathematical procedure for them, and managed to get questions correct.

But if problem solving depends on a deep knowledge of mathematics, this approach to lesson structure is going to be very ineffective.

As mentioned earlier, the reasoning and problem solving questions were based on the same math content as the fluency exercises, making it more likely that students would solve problems correctly whether they fully understood them or not.

Chances are that all they’d need to do is find the numbers in the questions and use the same method they used in the fluency section to get their answers (a process referred to as “number plucking”) – not exactly high level problem solving skills.

Teaching to “cover the curriculum” hinders development of strong problem solving skills.

This is one of my worries with ‘math mastery schemes’ that block content so that, in some circumstances, it is not looked at again until the following year (and with new objectives).

The pressure for teachers to ‘get through the curriculum’ results in many opportunities to revisit content being missed in the classroom.

Students are unintentionally forced to skip ahead in the fluency, reasoning, problem solving chain without proper consolidation of the earlier processes.

As David Didau (2019) puts it, ‘When novices face a problem for which they do not have a conveniently stored solution, they have to rely on the costlier means-end analysis.

This is likely to lead to cognitive overload because it involves trying to work through and hold in mind multiple possible solutions.

It’s a bit like trying to juggle five objects at once without previous practice. Solving problems is an inefficient way to get better at problem solving.’

Fluency and reasoning – Best practice in a lesson, a unit, and a semester

By now I hope you have realized that when it comes to problem solving, fluency is king. As such we should look to mastery math based teaching to ensure that the fluency that students need is there.

The answer to what fluency looks like will obviously depend on many factors, including the content being taught and the grade you find yourself teaching.

But we should not consider rushing them on to problem solving or logical reasoning in the early stages of this new content as it has not been learnt, only performed.

I would say that in the early stages of learning, content that requires the end goal of being fluent should take up the majority of lesson time – approximately 60%. The rest of the time should be spent rehearsing and retrieving other knowledge that is at risk of being forgotten about.

This blog on mental math strategies students should learn at each grade level is a good place to start when thinking about the core aspects of fluency that students should achieve.

Little and often is a good mantra when we think about fluency, particularly when revisiting the key mathematical skills of number bond fluency or multiplication fluency. So when it comes to what fluency could look like throughout the day, consider all the opportunities to get students practicing.

They could chant multiplication facts when transitioning. If a lesson in another subject has finished earlier than expected, use that time to quiz students on number bonds. Have fluency exercises as part of the morning work.

Read more: How to teach multiplication for instant recall

What about best practice over a longer period?

Thinking about what fluency could look like across a unit of work would again depend on the unit itself.

Look at this unit below from a popular scheme of work.

They recommend 20 days to cover 9 objectives. One of these specifically mentions problem solving so I will forget about that one at the moment – so that gives 8 objectives.

I would recommend that the fluency of this unit look something like this:

This type of structure is heavily borrowed from Mark McCourt’s phased learning idea from his book ‘Teaching for Mastery.’

This should not be seen as something set in stone; it would greatly depend on the needs of the class in front of you. But it gives an idea of what fluency could look like across a unit of lessons – though not necessarily all math lessons.

When we think about a semester, we can draw on similar ideas to the one above except that your lessons could also pull on content from previous units from that semester.

So lesson one may focus 60% on the new unit and 40% on what was learnt in the previous unit.

The structure could then follow a similar pattern to the one above.

When an adult first learns something new, we cannot solve a problem with it straight away. We need to become familiar with the idea and practice before we can make connections, reason and problem solve with it.

The same is true for students. Indeed, it could take up to two years ‘between the mathematics a student can use in imitative exercises and that they have sufficiently absorbed and connected to use autonomously in non-routine problem solving.’ (Burkhardt, 2017).

Practice with facts that are secure

So when we plan for reasoning and problem solving, we need to be looking at content from 2 years ago to base these questions on.

You could get students in 3rd grade to solve complicated place value problems with the numbers they should know from 1st or 2nd grade. This would lessen the cognitive load , freeing up valuable working memory so they can actually focus on solving the problems using content they are familiar with.

Increase complexity gradually

Once they practice solving these types of problems, they can draw on this knowledge later when solving problems with more difficult numbers.

This is what Mark McCourt calls the ‘Behave’ phase. In his book he writes:

‘Many teachers find it an uncomfortable – perhaps even illogical – process to plan the ‘Behave’ phase as one that relates to much earlier learning rather than the new idea, but it is crucial to do so if we want to bring about optimal gains in learning, understanding and long term recall.’  (Mark McCourt, 2019)

This just shows the fallacy of ‘accelerated progress’; in the space of 20 minutes some teachers are taught to move students from fluency through to non-routine problem solving, or we are somehow not catering to the needs of the child.

When considering what problem solving lessons could look like, here’s an example structure based on the objectives above.

It is important to reiterate that this is not something that should be set in stone. Key to getting the most out of this teaching for mastery approach is ensuring your students (across abilities) are interested and engaged in their work.

Depending on the previous attainment and abilities of the children in your class, you may find that a few have come across some of the mathematical ideas you have been teaching, and so they are able to problem solve effectively with these ideas.

Equally likely is encountering students on the opposite side of the spectrum, who may not have fully grasped the concept of place value and will need to go further back than 2 years and solve even simpler problems.

In order to have the greatest impact on class performance, you will have to account for these varying experiences in your lessons.

Read more: 

• Math Mastery Toolkit : A Practical Guide To Mastery Teaching And Learning
• Problem Solving and Reasoning Questions and Answers
• Get to Grips with Math Problem Solving For Elementary Students
• Mixed Ability Teaching for Mastery: Classroom How To
• 21 Math Challenges To Really Stretch Your More Able Students
• Why You Should Be Incorporating Stem Sentences Into Your Elementary Math Teaching

Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?

The content in this article was originally written by primary school lead teacher Neil Almond and has since been revised and adapted for US schools by elementary math teacher Jaclyn Wassell.

Related articles

20 Effective Math Strategies To Approach Problem-Solving 

Why Student Centered Learning Is Important: A Guide For Educators

13 Effective Learning Strategies: A Guide to Using them in your Math Classroom

Differentiated Instruction: 9 Differentiated Curriculum And Instruction Strategies For Teachers 

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• Practice, practice, practice Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing...

Please add a message.

Message received. Thanks for the feedback.

• Skip to main content
• Skip to primary sidebar
• Skip to footer

Additional menu

Khan Academy Blog

Free Math Worksheets — Over 100k free practice problems on Khan Academy

Looking for free math worksheets.

You’ve found something even better!

That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!

Just choose your grade level or topic to get access to 100% free practice questions:

Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.

• Trigonometry

Statistics and probability

High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.

• Addition and subtraction
• Place value (tens and hundreds)
• Addition and subtraction within 20
• Addition and subtraction within 100
• Addition and subtraction within 1000
• Measurement and data
• Counting and place value
• Measurement and geometry
• Place value
• Measurement, data, and geometry
• Add and subtract within 20
• Add and subtract within 100
• Add and subtract within 1,000
• Money and time
• Measurement
• Intro to multiplication
• 1-digit multiplication
• Addition, subtraction, and estimation
• Intro to division
• Understand fractions
• Equivalent fractions and comparing fractions
• More with multiplication and division
• Arithmetic patterns and problem solving
• Quadrilaterals
• Represent and interpret data
• Multiply by 1-digit numbers
• Multiply by 2-digit numbers
• Factors, multiples and patterns
• Add and subtract fractions
• Multiply fractions
• Understand decimals
• Plane figures
• Measuring angles
• Area and perimeter
• Units of measurement
• Decimal place value
• Add decimals
• Subtract decimals
• Multi-digit multiplication and division
• Divide fractions
• Multiply decimals
• Divide decimals
• Powers of ten
• Coordinate plane
• Algebraic thinking
• Converting units of measure
• Properties of shapes
• Ratios, rates, & percentages
• Arithmetic operations
• Negative numbers
• Properties of numbers
• Variables & expressions
• Equations & inequalities introduction
• Data and statistics
• Negative numbers: addition and subtraction
• Negative numbers: multiplication and division
• Fractions, decimals, & percentages
• Rates & proportional relationships
• Expressions, equations, & inequalities
• Numbers and operations
• Solving equations with one unknown
• Linear equations and functions
• Systems of equations
• Geometric transformations
• Data and modeling
• Volume and surface area
• Pythagorean theorem
• Transformations, congruence, and similarity
• Arithmetic properties
• Factors and multiples
• Reading and interpreting data
• Negative numbers and coordinate plane
• Ratios, rates, proportions
• Equations, expressions, and inequalities
• Exponents, radicals, and scientific notation
• Foundations
• Algebraic expressions
• Linear equations and inequalities
• Graphing lines and slope
• Expressions with exponents
• Quadratics and polynomials
• Equations and geometry
• Algebra foundations
• Solving equations & inequalities
• Working with units
• Linear equations & graphs
• Forms of linear equations
• Inequalities (systems & graphs)
• Absolute value & piecewise functions
• Exponents & radicals
• Exponential growth & decay
• Quadratics: Multiplying & factoring
• Quadratic functions & equations
• Irrational numbers
• Performing transformations
• Transformation properties and proofs
• Right triangles & trigonometry
• Non-right triangles & trigonometry (Advanced)
• Analytic geometry
• Conic sections
• Solid geometry
• Polynomial arithmetic
• Complex numbers
• Polynomial factorization
• Polynomial division
• Polynomial graphs
• Rational exponents and radicals
• Exponential models
• Transformations of functions
• Rational functions
• Trigonometric functions
• Non-right triangles & trigonometry
• Trigonometric equations and identities
• Analyzing categorical data
• Displaying and comparing quantitative data
• Summarizing quantitative data
• Modeling data distributions
• Exploring bivariate numerical data
• Study design
• Probability
• Counting, permutations, and combinations
• Random variables
• Sampling distributions
• Confidence intervals
• Significance tests (hypothesis testing)
• Two-sample inference for the difference between groups
• Inference for categorical data (chi-square tests)
• Advanced regression (inference and transforming)
• Analysis of variance (ANOVA)
• Scatterplots
• Data distributions
• Two-way tables
• Binomial probability
• Normal distributions
• Displaying and describing quantitative data
• Inference comparing two groups or populations
• Chi-square tests for categorical data
• More on regression
• Prepare for the 2020 AP®︎ Statistics Exam
• AP®︎ Statistics Standards mappings
• Polynomials
• Composite functions
• Probability and combinatorics
• Limits and continuity
• Derivatives: definition and basic rules
• Derivatives: chain rule and other advanced topics
• Applications of derivatives
• Analyzing functions
• Parametric equations, polar coordinates, and vector-valued functions
• Applications of integrals
• Differentiation: definition and basic derivative rules
• Differentiation: composite, implicit, and inverse functions
• Contextual applications of differentiation
• Applying derivatives to analyze functions
• Integration and accumulation of change
• Applications of integration
• AP Calculus AB solved free response questions from past exams
• AP®︎ Calculus AB Standards mappings
• Infinite sequences and series
• AP Calculus BC solved exams
• AP®︎ Calculus BC Standards mappings
• Integrals review
• Integration techniques
• Thinking about multivariable functions
• Derivatives of multivariable functions
• Applications of multivariable derivatives
• Integrating multivariable functions
• Green’s, Stokes’, and the divergence theorems
• First order differential equations
• Second order linear equations
• Laplace transform
• Vectors and spaces
• Matrix transformations
• Alternate coordinate systems (bases)

Frequently Asked Questions about Khan Academy and Math Worksheets

Why is khan academy even better than traditional math worksheets.

Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.

What do Khan Academy’s interactive math worksheets look like?

Here’s an example:

What are teachers saying about Khan Academy’s interactive math worksheets?

“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”

Is Khan Academy free?

Khan Academy’s practice questions are 100% free—with no ads or subscriptions.

What do Khan Academy’s interactive math worksheets cover?

Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.

Is Khan Academy a company?

Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.

Want to get even more out of Khan Academy?

Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.

Get Khanmigo

The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo. 

For learners     For teachers     For parents

Check Out the New Website Shop!

Novels & Picture Books

Anchor Charts

• Critical Thinking

How To Encourage Critical Thinking in Math

By Mary Montero

Share This Post:

• Facebook Share
• Twitter Share
• Pinterest Share
• Email Share

Critical thinking is more than just a buzzword… It’s an essential skill that helps students develop problem-solving abilities and make logical connections between different concepts. By encouraging critical thinking in math, students learn to approach problems more thoughtfully, they learn to analyze and evaluate math concepts, identify patterns and relationships, and explore different strategies for finding the solution. Critical thinking also involves a great deal of persistence. Those are critical life skills!

When you think about it, students are typically asked to solve math problems and find the answer. Showing their work is frequently stressed too, which is important, but not the end. Instead, students need to be able to look at math in different ways in order to truly grasp a complete understanding of math concepts. Mathematics requires logical reasoning, problem-solving, and abstract thinking.

What Does Critical Thinking in Math Look Like?

When I think about critical thinking in math, I focus on:

• Solving problems through logical thinking . Students learn how to break down complex problems, analyze the different parts, and understand how they fit together logically.
• Identifying patterns and making connections. Students learn how to identify patterns across different math concepts, make connections between seemingly unrelated topics, and develop a more in-depth understanding of how math works.
• Evaluating and comparing solutions. Students learn to evaluate which solution is best for a given problem and identify any flaws in their reasoning or others’ reasoning when looking at different solutions

Mathematician Posters

These FREE Marvelous Mathematician posters have been a staple in my classroom for the last 8+ years! I first started using a version from MissMathDork and adapted them for my classroom over the years. 

I print, laminate, and add magnetic stickers on the back. At the beginning of the year, I only put one or two up at a time depending on our area of focus. Now, they are all hanging on my board, and I’ll pull out different ones depending on our area of focus. They are so empowering to my mathematicians and help them stay on track!

A Marvelous Mathematician:

• knows that quicker doesn’t mean better
• looks for patterns
• knows mistakes happen and keeps going
• makes sense of the most important details
• embraces challenges and works through frustrations
• uses proper math vocabulary to explain their thinking
• shows their work and models their thinking
• discusses solutions and evaluates reasonableness
• gives context by labeling answers
• applies mathematical knowledge to similar situations
• checks for errors (computational and conceptual)

Critical Thinking Math Activities

Here are a few of my favorite critical thinking activities. 

Square Of Numbers

I love to incorporate challenge problems (use Nrich and Openmiddle to get started) because they teach my students so much more than how to solve a math problem. They learn important lessons in teamwork, persistence, resiliency, and growth mindset. We talk about strategies for tackling difficult problems and the importance of not giving up when things get hard.

This square of numbers challenge was a hit!

ALL kids need to feel and learn to embrace challenge. Oftentimes, kids I see have rarely faced an academic challenge. Things have just come easy to them, so when it doesn’t, they can lack strategies that will help them. In fact, they will often give up before they even get started.

I tell them it’s my job to make sure I’m helping them stretch and grow their brain by giving them challenges. They don’t love it at first, but they eventually do! 

This domino challenge was another one from Nrich . I’m always on the hunt for problems like this!!  How would you guide students toward an answer??

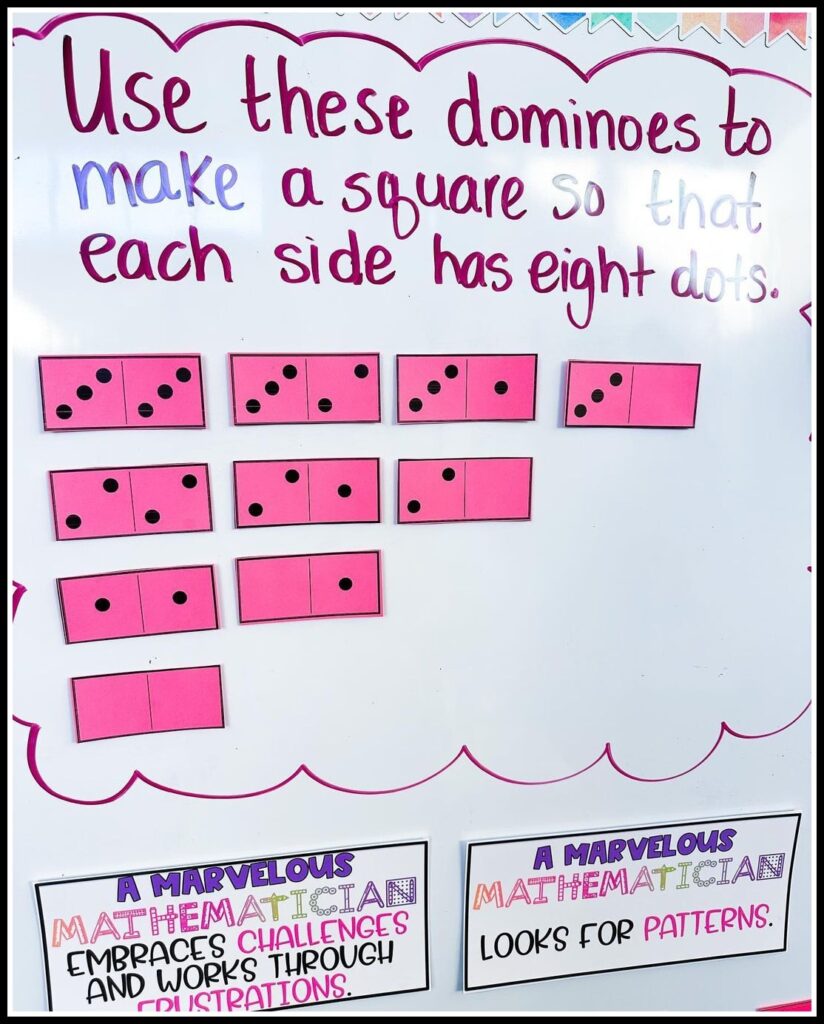
Fifteen Cards

This is a well-loved math puzzle with my students, and it’s amazing for encouraging students to consider all options when solving a math problem.

We have number cards 1-15 (one of each number) and only seven are laid out. With the given clues, students need to figure out which seven cards should be put out and in what order. My students love these, and after they’ve done a few, they enjoy creating their own, too! Use products, differences, and quotients to increase the challenge.

This is also adapted from Nrich, which is an AMAZING resource for math enrichment!

This is one of my favorite fraction lessons that I’ve done for years! Huge shout out to Meg from The Teacher Studio for this one. I give each child a slip of paper with this figure and they have to silently write their answer and justification. Then I tally up the answers and have students take a side and DEBATE with their reasoning! It’s an AMAZING conversation, and I highly recommend trying it with your students. 

Sometimes we leave it hanging overnight and work on visual models to make some proofs. 

Logic Puzzles

Logic puzzles are always a hit too! You can enrich and extend your math lessons with these ‘Math Mystery’ logic puzzles that are the perfect challenge for 4th, 5th, and 6th grades. The puzzles are skills-based, so they integrate well with almost ANY math lesson. You can use them to supplement instruction or challenge your fast-finishers and gifted students… all while encouraging critical thinking about important math skills!

Three levels are included, so they’re perfect to use for differentiation.

• Introductory logic puzzles are great for beginners (4th grade and up!)
• Advanced logic puzzles are great for students needing an extra challenge
• Extra Advanced logic puzzles are perfect for expert solvers… we dare you to figure these puzzles out! 

Do you have a group of students who are ready for more of a fraction challenge? My well-loved fraction puzzlers are absolutely perfect for fraction enrichment. They’ll motivate your students to excel at even the most challenging tasks! 

Math Projects

Math projects are another way to differentiation while building critical thinking skills. Math projects hold so much learning power with their real-world connections, differentiation options, collaborative learning opportunities, and numerous avenues for cross curricular learning too. 

If you’re new to math projects, I shared my best tips and tricks for using math projects in this blog post . They’re perfect for cumulative review, seasonal practice, centers, early finisher work, and more.

I use both concept-based math projects to focus on specific standards and seasonal math projects that integrate several skills.

Error Analysis

Finally, error analysis is always a challenging way to encourage critical thinking. When we use error analysis, we encourage students to analyze their own mistakes to prevent making the same mistakes in the future.

For my gifted students, I use error analysis tasks as an assessment when they have shown mastery of a unit during other tasks. For students in the regular classroom needing enrichment, I usually have them complete the tasks in a center or with a partner.

For students needing extra support, we complete error analysis in small groups.  We go step-by-step through the concept and they are always able to eventually identify what the error is. It is so empowering to students when they finally figure out the error AND it helps prevent them from making the same error in the future!

My FREE addition error analysis is a good place to start, no matter the grade level. I show them the process of walking through the problem and how best to complete an error analysis task.

When you’re ready for more, this bundle of error analysis tasks contains more than 240 tasks to engage and enrich your students in critical thinking practice.

If you want to dig even deeper, visit this conceptual vs computational error analysis post to learn more about using error analysis in the classroom. 

Related Critical Thinking Posts

• How to Increase Critical Thinking and Creativity in Your “Spare” Time
• More Tips to Increase Critical Thinking

Critical thinking is essential for students to develop a deeper understanding of math concepts, problem-solving skills, and a stronger ability to reason logically. When you learn how to encourage critical thinking in math, you’re setting your students up for success not only in more advanced math subjects they’ll encounter, but also in life. 

How do you integrate critical thinking in your classroom? Come share your ideas with us in our FREE Inspired In Upper Elementary Facebook group .

Mary Montero

I’m so glad you are here. I’m a current gifted and talented teacher in a small town in Colorado, and I’ve been in education since 2009. My passion (other than my family and cookies) is for making teachers’ lives easier and classrooms more engaging.

You might also like…

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

One Comment

Mary Thankyou for your inspirational activities. I have just read and loved the morning talk activities. I do have meetings with my students but usually at end of day. What time do you

©2023 Teaching With a Mountain View . All Rights Reserved | Designed by Ashley Hughes

Username or Email Address

Remember Me

Lost your password?

Review Cart

No products in the cart.

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

• Open supplemental data
• Reference Manager
• Simple TEXT file

People also looked at

Original research article, mathematical problem-solving through cooperative learning—the importance of peer acceptance and friendships.

• 1 Department of Education, Uppsala University, Uppsala, Sweden
• 2 Department of Education, Culture and Communication, Malardalen University, Vasteras, Sweden
• 3 School of Natural Sciences, Technology and Environmental Studies, Sodertorn University, Huddinge, Sweden
• 4 Faculty of Education, Gothenburg University, Gothenburg, Sweden

Mathematical problem-solving constitutes an important area of mathematics instruction, and there is a need for research on instructional approaches supporting student learning in this area. This study aims to contribute to previous research by studying the effects of an instructional approach of cooperative learning on students’ mathematical problem-solving in heterogeneous classrooms in grade five, in which students with special needs are educated alongside with their peers. The intervention combined a cooperative learning approach with instruction in problem-solving strategies including mathematical models of multiplication/division, proportionality, and geometry. The teachers in the experimental group received training in cooperative learning and mathematical problem-solving, and implemented the intervention for 15 weeks. The teachers in the control group received training in mathematical problem-solving and provided instruction as they would usually. Students (269 in the intervention and 312 in the control group) participated in tests of mathematical problem-solving in the areas of multiplication/division, proportionality, and geometry before and after the intervention. The results revealed significant effects of the intervention on student performance in overall problem-solving and problem-solving in geometry. The students who received higher scores on social acceptance and friendships for the pre-test also received higher scores on the selected tests of mathematical problem-solving. Thus, the cooperative learning approach may lead to gains in mathematical problem-solving in heterogeneous classrooms, but social acceptance and friendships may also greatly impact students’ results.

Introduction

The research on instruction in mathematical problem-solving has progressed considerably during recent decades. Yet, there is still a need to advance our knowledge on how teachers can support their students in carrying out this complex activity ( Lester and Cai, 2016 ). Results from the Program for International Student Assessment (PISA) show that only 53% of students from the participating countries could solve problems requiring more than direct inference and using representations from different information sources ( OECD, 2019 ). In addition, OECD (2019) reported a large variation in achievement with regard to students’ diverse backgrounds. Thus, there is a need for instructional approaches to promote students’ problem-solving in mathematics, especially in heterogeneous classrooms in which students with diverse backgrounds and needs are educated together. Small group instructional approaches have been suggested as important to promote learning of low-achieving students and students with special needs ( Kunsch et al., 2007 ). One such approach is cooperative learning (CL), which involves structured collaboration in heterogeneous groups, guided by five principles to enhance group cohesion ( Johnson et al., 1993 ; Johnson et al., 2009 ; Gillies, 2016 ). While CL has been well-researched in whole classroom approaches ( Capar and Tarim, 2015 ), few studies of the approach exist with regard to students with special educational needs (SEN; McMaster and Fuchs, 2002 ). This study contributes to previous research by studying the effects of the CL approach on students’ mathematical problem-solving in heterogeneous classrooms, in which students with special needs are educated alongside with their peers.

Group collaboration through the CL approach is structured in accordance with five principles of collaboration: positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing ( Johnson et al., 1993 ). First, the group tasks need to be structured so that all group members feel dependent on each other in the completion of the task, thus promoting positive interdependence. Second, for individual accountability, the teacher needs to assure that each group member feels responsible for his or her share of work, by providing opportunities for individual reports or evaluations. Third, the students need explicit instruction in social skills that are necessary for collaboration. Fourth, the tasks and seat arrangements should be designed to promote interaction among group members. Fifth, time needs to be allocated to group processing, through which group members can evaluate their collaborative work to plan future actions. Using these principles for cooperation leads to gains in mathematics, according to Capar and Tarim (2015) , who conducted a meta-analysis on studies of cooperative learning and mathematics, and found an increase of .59 on students’ mathematics achievement scores in general. However, the number of reviewed studies was limited, and researchers suggested a need for more research. In the current study, we focused on the effect of CL approach in a specific area of mathematics: problem-solving.

Mathematical problem-solving is a central area of mathematics instruction, constituting an important part of preparing students to function in modern society ( Gravemeijer et al., 2017 ). In fact, problem-solving instruction creates opportunities for students to apply their knowledge of mathematical concepts, integrate and connect isolated pieces of mathematical knowledge, and attain a deeper conceptual understanding of mathematics as a subject ( Lester and Cai, 2016 ). Some researchers suggest that mathematics itself is a science of problem-solving and of developing theories and methods for problem-solving ( Hamilton, 2007 ; Davydov, 2008 ).

Problem-solving processes have been studied from different perspectives ( Lesh and Zawojewski, 2007 ). Problem-solving heuristics Pólya, (1948) has largely influenced our perceptions of problem-solving, including four principles: understanding the problem, devising a plan, carrying out the plan, and looking back and reflecting upon the suggested solution. Schoenfield, (2016) suggested the use of specific problem-solving strategies for different types of problems, which take into consideration metacognitive processes and students’ beliefs about problem-solving. Further, models and modelling perspectives on mathematics ( Lesh and Doerr, 2003 ; Lesh and Zawojewski, 2007 ) emphasize the importance of engaging students in model-eliciting activities in which problem situations are interpreted mathematically, as students make connections between problem information and knowledge of mathematical operations, patterns, and rules ( Mousoulides et al., 2010 ; Stohlmann and Albarracín, 2016 ).

Not all students, however, find it easy to solve complex mathematical problems. Students may experience difficulties in identifying solution-relevant elements in a problem or visualizing appropriate solution to a problem situation. Furthermore, students may need help recognizing the underlying model in problems. For example, in two studies by Degrande et al. (2016) , students in grades four to six were presented with mathematical problems in the context of proportional reasoning. The authors found that the students, when presented with a word problem, could not identify an underlying model, but rather focused on superficial characteristics of the problem. Although the students in the study showed more success when presented with a problem formulated in symbols, the authors pointed out a need for activities that help students distinguish between different proportional problem types. Furthermore, students exhibiting specific learning difficulties may need additional support in both general problem-solving strategies ( Lein et al., 2020 ; Montague et al., 2014 ) and specific strategies pertaining to underlying models in problems. The CL intervention in the present study focused on supporting students in problem-solving, through instruction in problem-solving principles ( Pólya, 1948 ), specifically applied to three models of mathematical problem-solving—multiplication/division, geometry, and proportionality.

Students’ problem-solving may be enhanced through participation in small group discussions. In a small group setting, all the students have the opportunity to explain their solutions, clarify their thinking, and enhance understanding of a problem at hand ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ). In fact, small group instruction promotes students’ learning in mathematics by providing students with opportunities to use language for reasoning and conceptual understanding ( Mercer and Sams, 2006 ), to exchange different representations of the problem at hand ( Fujita et al., 2019 ), and to become aware of and understand groupmates’ perspectives in thinking ( Kazak et al., 2015 ). These opportunities for learning are created through dialogic spaces characterized by openness to each other’s perspectives and solutions to mathematical problems ( Wegerif, 2011 ).

However, group collaboration is not only associated with positive experiences. In fact, studies show that some students may not be given equal opportunities to voice their opinions, due to academic status differences ( Langer-Osuna, 2016 ). Indeed, problem-solvers struggling with complex tasks may experience negative emotions, leading to uncertainty of not knowing the definite answer, which places demands on peer support ( Jordan and McDaniel, 2014 ; Hannula, 2015 ). Thus, especially in heterogeneous groups, students may need additional support to promote group interaction. Therefore, in this study, we used a cooperative learning approach, which, in contrast to collaborative learning approaches, puts greater focus on supporting group cohesion through instruction in social skills and time for reflection on group work ( Davidson and Major, 2014 ).

Although cooperative learning approach is intended to promote cohesion and peer acceptance in heterogeneous groups ( Rzoska and Ward, 1991 ), previous studies indicate that challenges in group dynamics may lead to unequal participation ( Mulryan, 1992 ; Cohen, 1994 ). Peer-learning behaviours may impact students’ problem-solving ( Hwang and Hu, 2013 ) and working in groups with peers who are seen as friends may enhance students’ motivation to learn mathematics ( Deacon and Edwards, 2012 ). With the importance of peer support in mind, this study set out to investigate whether the results of the intervention using the CL approach are associated with students’ peer acceptance and friendships.

The Present Study

In previous research, the CL approach has shown to be a promising approach in teaching and learning mathematics ( Capar and Tarim, 2015 ), but fewer studies have been conducted in whole-class approaches in general and students with SEN in particular ( McMaster and Fuchs, 2002 ). This study aims to contribute to previous research by investigating the effect of CL intervention on students’ mathematical problem-solving in grade 5. With regard to the complexity of mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach in this study was combined with problem-solving principles pertaining to three underlying models of problem-solving—multiplication/division, geometry, and proportionality. Furthermore, considering the importance of peer support in problem-solving in small groups ( Mulryan, 1992 ; Cohen, 1994 ; Hwang and Hu, 2013 ), the study investigated how peer acceptance and friendships were associated with the effect of the CL approach on students’ problem-solving abilities. The study aimed to find answers to the following research questions:

a) What is the effect of CL approach on students’ problem-solving in mathematics?

b) Are social acceptance and friendship associated with the effect of CL on students’ problem-solving in mathematics?

Participants

The participants were 958 students in grade 5 and their teachers. According to power analyses prior to the start of the study, 1,020 students and 51 classes were required, with an expected effect size of 0.30 and power of 80%, provided that there are 20 students per class and intraclass correlation is 0.10. An invitation to participate in the project was sent to teachers in five municipalities via e-mail. Furthermore, the information was posted on the website of Uppsala university and distributed via Facebook interest groups. As shown in Figure 1 , teachers of 1,165 students agreed to participate in the study, but informed consent was obtained only for 958 students (463 in the intervention and 495 in the control group). Further attrition occurred at pre- and post-measurement, resulting in 581 students’ tests as a basis for analyses (269 in the intervention and 312 in the control group). Fewer students (n = 493) were finally included in the analyses of the association of students’ social acceptance and friendships and the effect of CL on students’ mathematical problem-solving (219 in the intervention and 274 in the control group). The reasons for attrition included teacher drop out due to sick leave or personal circumstances (two teachers in the control group and five teachers in the intervention group). Furthermore, some students were sick on the day of data collection and some teachers did not send the test results to the researchers.

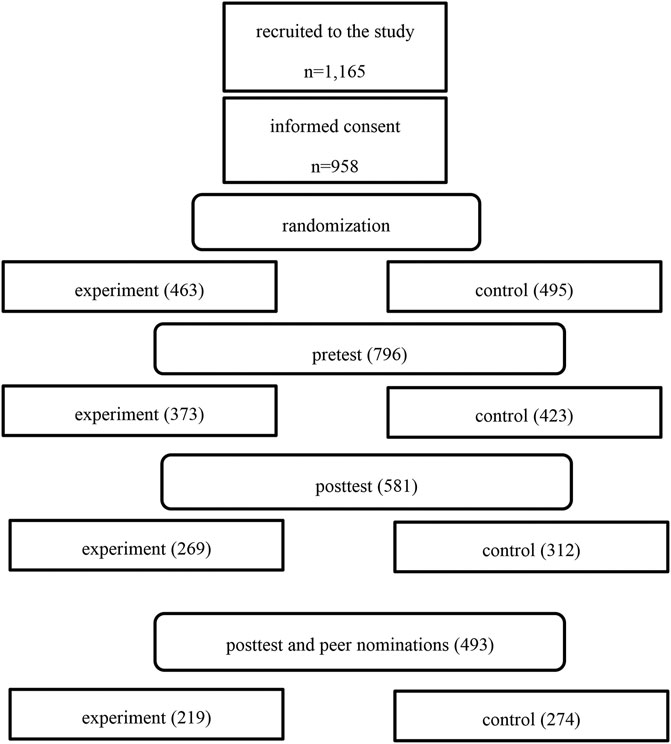
FIGURE 1 . Flow chart for participants included in data collection and data analysis.

As seen in Table 1 , classes in both intervention and control groups included 27 students on average. For 75% of the classes, there were 33–36% of students with SEN. In Sweden, no formal medical diagnosis is required for the identification of students with SEN. It is teachers and school welfare teams who decide students’ need for extra adaptations or special support ( Swedish National Educational Agency, 2014 ). The information on individual students’ type of SEN could not be obtained due to regulations on the protection of information about individuals ( SFS 2009 ). Therefore, the information on the number of students with SEN on class level was obtained through teacher reports.

TABLE 1 . Background characteristics of classes and teachers in intervention and control groups.

Intervention

The intervention using the CL approach lasted for 15 weeks and the teachers worked with the CL approach three to four lessons per week. First, the teachers participated in two-days training on the CL approach, using an especially elaborated CL manual ( Klang et al., 2018 ). The training focused on the five principles of the CL approach (positive interdependence, individual accountability, explicit instruction in social skills, promotive interaction, and group processing). Following the training, the teachers introduced the CL approach in their classes and focused on group-building activities for 7 weeks. Then, 2 days of training were provided to teachers, in which the CL approach was embedded in activities in mathematical problem-solving and reading comprehension. Educational materials containing mathematical problems in the areas of multiplication and division, geometry, and proportionality were distributed to the teachers ( Karlsson and Kilborn, 2018a ). In addition to the specific problems, adapted for the CL approach, the educational materials contained guidance for the teachers, in which problem-solving principles ( Pólya, 1948 ) were presented as steps in problem-solving. Following the training, the teachers applied the CL approach in mathematical problem-solving lessons for 8 weeks.

Solving a problem is a matter of goal-oriented reasoning, starting from the understanding of the problem to devising its solution by using known mathematical models. This presupposes that the current problem is chosen from a known context ( Stillman et al., 2008 ; Zawojewski, 2010 ). This differs from the problem-solving of the textbooks, which is based on an aim to train already known formulas and procedures ( Hamilton, 2007 ). Moreover, it is important that students learn modelling according to their current abilities and conditions ( Russel, 1991 ).

In order to create similar conditions in the experiment group and the control group, the teachers were supposed to use the same educational material ( Karlsson and Kilborn, 2018a ; Karlsson and Kilborn, 2018b ), written in light of the specified view of problem-solving. The educational material is divided into three areas—multiplication/division, geometry, and proportionality—and begins with a short teachers’ guide, where a view of problem solving is presented, which is based on the work of Polya (1948) and Lester and Cai (2016) . The tasks are constructed in such a way that conceptual knowledge was in focus, not formulas and procedural knowledge.

Implementation of the Intervention

To ensure the implementation of the intervention, the researchers visited each teachers’ classroom twice during the two phases of the intervention period, as described above. During each visit, the researchers observed the lesson, using a checklist comprising the five principles of the CL approach. After the lesson, the researchers gave written and oral feedback to each teacher. As seen in Table 1 , in 18 of the 23 classes, the teachers implemented the intervention in accordance with the principles of CL. In addition, the teachers were asked to report on the use of the CL approach in their teaching and the use of problem-solving activities embedding CL during the intervention period. As shown in Table 1 , teachers in only 11 of 23 classes reported using the CL approach and problem-solving activities embedded in the CL approach at least once a week.

Control Group

The teachers in the control group received 2 days of instruction in enhancing students’ problem-solving and reading comprehension. The teachers were also supported with educational materials including mathematical problems Karlsson and Kilborn (2018b) and problem-solving principles ( Pólya, 1948 ). However, none of the activities during training or in educational materials included the CL approach. As seen in Table 1 , only 10 of 25 teachers reported devoting at least one lesson per week to mathematical problem-solving.

Tests of Mathematical Problem-Solving

Tests of mathematical problem-solving were administered before and after the intervention, which lasted for 15 weeks. The tests were focused on the models of multiplication/division, geometry, and proportionality. The three models were chosen based on the syllabus of the subject of mathematics in grades 4 to 6 in the Swedish National Curriculum ( Swedish National Educational Agency, 2018 ). In addition, the intention was to create a variation of types of problems to solve. For each of these three models, there were two tests, a pre-test and a post-test. Each test contained three tasks with increasing difficulty ( Supplementary Appendix SA ).

The tests of multiplication and division (Ma1) were chosen from different contexts and began with a one-step problem, while the following two tasks were multi-step problems. Concerning multiplication, many students in grade 5 still understand multiplication as repeated addition, causing significant problems, as this conception is not applicable to multiplication beyond natural numbers ( Verschaffel et al., 2007 ). This might be a hindrance in developing multiplicative reasoning ( Barmby et al., 2009 ). The multi-step problems in this study were constructed to support the students in multiplicative reasoning.

Concerning the geometry tests (Ma2), it was important to consider a paradigm shift concerning geometry in education that occurred in the mid-20th century, when strict Euclidean geometry gave way to other aspects of geometry like symmetry, transformation, and patterns. van Hiele (1986) prepared a new taxonomy for geometry in five steps, from a visual to a logical level. Therefore, in the tests there was a focus on properties of quadrangles and triangles, and how to determine areas by reorganising figures into new patterns. This means that structure was more important than formulas.

The construction of tests of proportionality (M3) was more complicated. Firstly, tasks on proportionality can be found in many different contexts, such as prescriptions, scales, speeds, discounts, interest, etc. Secondly, the mathematical model is complex and requires good knowledge of rational numbers and ratios ( Lesh et al., 1988 ). It also requires a developed view of multiplication, useful in operations with real numbers, not only as repeated addition, an operation limited to natural numbers ( Lybeck, 1981 ; Degrande et al., 2016 ). A linear structure of multiplication as repeated addition leads to limitations in terms of generalization and development of the concept of multiplication. This became evident in a study carried out in a Swedish context ( Karlsson and Kilborn, 2018c ). Proportionality can be expressed as a/b = c/d or as a/b = k. The latter can also be expressed as a = b∙k, where k is a constant that determines the relationship between a and b. Common examples of k are speed (km/h), scale, and interest (%). An important pre-knowledge in order to deal with proportions is to master fractions as equivalence classes like 1/3 = 2/6 = 3/9 = 4/12 = 5/15 = 6/18 = 7/21 = 8/24 … ( Karlsson and Kilborn, 2020 ). It was important to take all these aspects into account when constructing and assessing the solutions of the tasks.

The tests were graded by an experienced teacher of mathematics (4 th author) and two students in their final year of teacher training. Prior to grading, acceptable levels of inter-rater reliability were achieved by independent rating of students’ solutions and discussions in which differences between the graders were resolved. Each student response was to be assigned one point when it contained a correct answer and two points when the student provided argumentation for the correct answer and elaborated on explanation of his or her solution. The assessment was thus based on quality aspects with a focus on conceptual knowledge. As each subtest contained three questions, it generated three student solutions. So, scores for each subtest ranged from 0 to 6 points and for the total scores from 0 to 18 points. To ascertain that pre- and post-tests were equivalent in degree of difficulty, the tests were administered to an additional sample of 169 students in grade 5. Test for each model was conducted separately, as students participated in pre- and post-test for each model during the same lesson. The order of tests was switched for half of the students in order to avoid the effect of the order in which the pre- and post-tests were presented. Correlation between students’ performance on pre- and post-test was .39 ( p < 0.000) for tests of multiplication/division; .48 ( p < 0.000) for tests of geometry; and .56 ( p < 0.000) for tests of proportionality. Thus, the degree of difficulty may have differed between pre- and post-test.

Measures of Peer Acceptance and Friendships

To investigate students’ peer acceptance and friendships, peer nominations rated pre- and post-intervention were used. Students were asked to nominate peers who they preferred to work in groups with and who they preferred to be friends with. Negative peer nominations were avoided due to ethical considerations raised by teachers and parents ( Child and Nind, 2013 ). Unlimited nominations were used, as these are considered to have high ecological validity ( Cillessen and Marks, 2017 ). Peer nominations were used as a measure of social acceptance, and reciprocated nominations were used as a measure of friendship. The number of nominations for each student were aggregated and divided by the number of nominators to create a proportion of nominations for each student ( Velásquez et al., 2013 ).

Statistical Analyses

Multilevel regression analyses were conducted in R, lme4 package Bates et al. (2015) to account for nestedness in the data. Students’ classroom belonging was considered as a level 2 variable. First, we used a model in which students’ results on tests of problem-solving were studied as a function of time (pre- and post) and group belonging (intervention and control group). Second, the same model was applied to subgroups of students who performed above and below median at pre-test, to explore whether the CL intervention had a differential effect on student performance. In this second model, the results for subgroups of students could not be obtained for geometry tests for subgroup below median and for tests of proportionality for subgroup above median. A possible reason for this must have been the skewed distribution of the students in these subgroups. Therefore, another model was applied that investigated students’ performances in math at both pre- and post-test as a function of group belonging. Third, the students’ scores on social acceptance and friendships were added as an interaction term to the first model. In our previous study, students’ social acceptance changed as a result of the same CL intervention ( Klang et al., 2020 ).

The assumptions for the multilevel regression were assured during the analyses ( Snijders and Bosker, 2012 ). The assumption of normality of residuals were met, as controlled by visual inspection of quantile-quantile plots. For subgroups, however, the plotted residuals deviated somewhat from the straight line. The number of outliers, which had a studentized residual value greater than ±3, varied from 0 to 5, but none of the outliers had a Cook’s distance value larger than 1. The assumption of multicollinearity was met, as the variance inflation factors (VIF) did not exceed a value of 10. Before the analyses, the cases with missing data were deleted listwise.

What Is the Effect of the CL Approach on Students’ Problem-Solving in Mathematics?

As seen in the regression coefficients in Table 2 , the CL intervention had a significant effect on students’ mathematical problem-solving total scores and students’ scores in problem solving in geometry (Ma2). Judging by mean values, students in the intervention group appeared to have low scores on problem-solving in geometry but reached the levels of problem-solving of the control group by the end of the intervention. The intervention did not have a significant effect on students’ performance in problem-solving related to models of multiplication/division and proportionality.

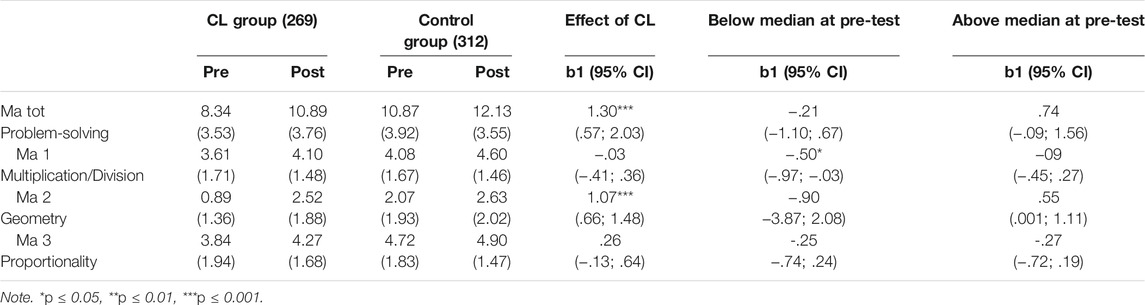
TABLE 2 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving.

The question is, however, whether CL intervention affected students with different pre-test scores differently. Table 2 includes the regression coefficients for subgroups of students who performed below and above median at pre-test. As seen in the table, the CL approach did not have a significant effect on students’ problem-solving, when the sample was divided into these subgroups. A small negative effect was found for intervention group in comparison to control group, but confidence intervals (CI) for the effect indicate that it was not significant.

Is Social Acceptance and Friendships Associated With the Effect of CL on Students’ Problem-Solving in Mathematics?

As seen in Table 3 , students’ peer acceptance and friendship at pre-test were significantly associated with the effect of the CL approach on students’ mathematical problem-solving scores. Changes in students’ peer acceptance and friendships were not significantly associated with the effect of the CL approach on students’ mathematical problem-solving. Consequently, it can be concluded that being nominated by one’s peers and having friends at the start of the intervention may be an important factor when participation in group work, structured in accordance with the CL approach, leads to gains in mathematical problem-solving.

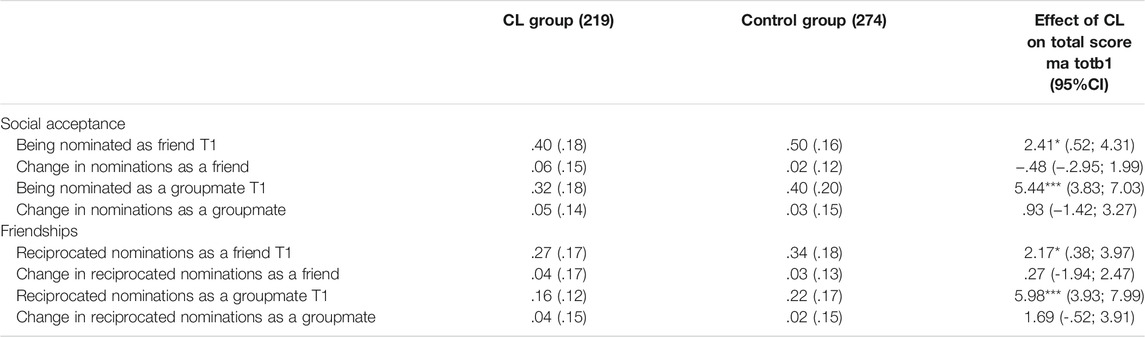
TABLE 3 . Mean scores (standard deviation in parentheses) and unstandardized multilevel regression estimates for tests of mathematical problem-solving, including scores of social acceptance and friendship in the model.

In light of the limited number of studies on the effects of CL on students’ problem-solving in whole classrooms ( Capar and Tarim, 2015 ), and for students with SEN in particular ( McMaster and Fuchs, 2002 ), this study sought to investigate whether the CL approach embedded in problem-solving activities has an effect on students’ problem-solving in heterogeneous classrooms. The need for the study was justified by the challenge of providing equitable mathematics instruction to heterogeneous student populations ( OECD, 2019 ). Small group instructional approaches as CL are considered as promising approaches in this regard ( Kunsch et al., 2007 ). The results showed a significant effect of the CL approach on students’ problem-solving in geometry and total problem-solving scores. In addition, with regard to the importance of peer support in problem-solving ( Deacon and Edwards, 2012 ; Hwang and Hu, 2013 ), the study explored whether the effect of CL on students’ problem-solving was associated with students’ social acceptance and friendships. The results showed that students’ peer acceptance and friendships at pre-test were significantly associated with the effect of the CL approach, while change in students’ peer acceptance and friendships from pre- to post-test was not.

The results of the study confirm previous research on the effect of the CL approach on students’ mathematical achievement ( Capar and Tarim, 2015 ). The specific contribution of the study is that it was conducted in classrooms, 75% of which were composed of 33–36% of students with SEN. Thus, while a previous review revealed inconclusive findings on the effects of CL on student achievement ( McMaster and Fuchs, 2002 ), the current study adds to the evidence of the effect of the CL approach in heterogeneous classrooms, in which students with special needs are educated alongside with their peers. In a small group setting, the students have opportunities to discuss their ideas of solutions to the problem at hand, providing explanations and clarifications, thus enhancing their understanding of problem-solving ( Yackel et al., 1991 ; Webb and Mastergeorge, 2003 ).

In this study, in accordance with previous research on mathematical problem-solving ( Lesh and Zawojewski, 2007 ; Degrande et al., 2016 ; Stohlmann and Albarracín, 2016 ), the CL approach was combined with training in problem-solving principles Pólya (1948) and educational materials, providing support in instruction in underlying mathematical models. The intention of the study was to provide evidence for the effectiveness of the CL approach above instruction in problem-solving, as problem-solving materials were accessible to teachers of both the intervention and control groups. However, due to implementation challenges, not all teachers in the intervention and control groups reported using educational materials and training as expected. Thus, it is not possible to draw conclusions of the effectiveness of the CL approach alone. However, in everyday classroom instruction it may be difficult to separate the content of instruction from the activities that are used to mediate this content ( Doerr and Tripp, 1999 ; Gravemeijer, 1999 ).

Furthermore, for successful instruction in mathematical problem-solving, scaffolding for content needs to be combined with scaffolding for dialogue ( Kazak et al., 2015 ). From a dialogical perspective ( Wegerif, 2011 ), students may need scaffolding in new ways of thinking, involving questioning their understandings and providing arguments for their solutions, in order to create dialogic spaces in which different solutions are voiced and negotiated. In this study, small group instruction through CL approach aimed to support discussions in small groups, but the study relies solely on quantitative measures of students’ mathematical performance. Video-recordings of students’ discussions may have yielded important insights into the dialogic relationships that arose in group discussions.

Despite the positive findings of the CL approach on students’ problem-solving, it is important to note that the intervention did not have an effect on students’ problem-solving pertaining to models of multiplication/division and proportionality. Although CL is assumed to be a promising instructional approach, the number of studies on its effect on students’ mathematical achievement is still limited ( Capar and Tarim, 2015 ). Thus, further research is needed on how CL intervention can be designed to promote students’ problem-solving in other areas of mathematics.

The results of this study show that the effect of the CL intervention on students’ problem-solving was associated with students’ initial scores of social acceptance and friendships. Thus, it is possible to assume that students who were popular among their classmates and had friends at the start of the intervention also made greater gains in mathematical problem-solving as a result of the CL intervention. This finding is in line with Deacon and Edwards’ study of the importance of friendships for students’ motivation to learn mathematics in small groups ( Deacon and Edwards, 2012 ). However, the effect of the CL intervention was not associated with change in students’ social acceptance and friendship scores. These results indicate that students who were nominated by a greater number of students and who received a greater number of friends did not benefit to a great extent from the CL intervention. With regard to previously reported inequalities in cooperation in heterogeneous groups ( Cohen, 1994 ; Mulryan, 1992 ; Langer Osuna, 2016 ) and the importance of peer behaviours for problem-solving ( Hwang and Hu, 2013 ), teachers should consider creating inclusive norms and supportive peer relationships when using the CL approach. The demands of solving complex problems may create negative emotions and uncertainty ( Hannula, 2015 ; Jordan and McDaniel, 2014 ), and peer support may be essential in such situations.

Limitations

The conclusions from the study must be interpreted with caution, due to a number of limitations. First, due to the regulation of protection of individuals ( SFS 2009 ), the researchers could not get information on type of SEN for individual students, which limited the possibilities of the study for investigating the effects of the CL approach for these students. Second, not all teachers in the intervention group implemented the CL approach embedded in problem-solving activities and not all teachers in the control group reported using educational materials on problem-solving. The insufficient levels of implementation pose a significant challenge to the internal validity of the study. Third, the additional investigation to explore the equivalence in difficulty between pre- and post-test, including 169 students, revealed weak to moderate correlation in students’ performance scores, which may indicate challenges to the internal validity of the study.

Implications

The results of the study have some implications for practice. Based on the results of the significant effect of the CL intervention on students’ problem-solving, the CL approach appears to be a promising instructional approach in promoting students’ problem-solving. However, as the results of the CL approach were not significant for all subtests of problem-solving, and due to insufficient levels of implementation, it is not possible to conclude on the importance of the CL intervention for students’ problem-solving. Furthermore, it appears to be important to create opportunities for peer contacts and friendships when the CL approach is used in mathematical problem-solving activities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Uppsala Ethical Regional Committee, Dnr. 2017/372. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.

Author Contributions

NiK was responsible for the project, and participated in data collection and data analyses. NaK and WK were responsible for intervention with special focus on the educational materials and tests in mathematical problem-solving. PE participated in the planning of the study and the data analyses, including coordinating analyses of students’ tests. MK participated in the designing and planning the study as well as data collection and data analyses.

The project was funded by the Swedish Research Council under Grant 2016-04,679.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to teachers who participated in the project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.710296/full#supplementary-material

Barmby, P., Harries, T., Higgins, S., and Suggate, J. (2009). The array representation and primary children's understanding and reasoning in multiplication. Educ. Stud. Math. 70 (3), 217–241. doi:10.1007/s10649-008-914510.1007/s10649-008-9145-1

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2015). Fitting Linear Mixed-Effects Models Usinglme4. J. Stat. Soft. 67 (1), 1–48. doi:10.18637/jss.v067.i01

Capar, G., and Tarim, K. (2015). Efficacy of the cooperative learning method on mathematics achievement and attitude: A meta-analysis research. Educ. Sci-theor Pract. 15 (2), 553–559. doi:10.12738/estp.2015.2.2098

Child, S., and Nind, M. (2013). Sociometric methods and difference: A force for good - or yet more harm. Disabil. Soc. 28 (7), 1012–1023. doi:10.1080/09687599.2012.741517

Cillessen, A. H. N., and Marks, P. E. L. (2017). Methodological choices in peer nomination research. New Dir. Child Adolesc. Dev. 2017, 21–44. doi:10.1002/cad.20206

PubMed Abstract | CrossRef Full Text | Google Scholar

Clarke, B., Cheeseman, J., and Clarke, D. (2006). The mathematical knowledge and understanding young children bring to school. Math. Ed. Res. J. 18 (1), 78–102. doi:10.1007/bf03217430

Cohen, E. G. (1994). Restructuring the classroom: Conditions for productive small groups. Rev. Educ. Res. 64 (1), 1–35. doi:10.3102/00346543064001001

Davidson, N., and Major, C. H. (2014). Boundary crossings: Cooperative learning, collaborative learning, and problem-based learning. J. Excell. Coll. Teach. 25 (3-4), 7.

Google Scholar

Davydov, V. V. (2008). Problems of developmental instructions. A Theoretical and experimental psychological study . New York: Nova Science Publishers, Inc .

Deacon, D., and Edwards, J. (2012). Influences of friendship groupings on motivation for mathematics learning in secondary classrooms. Proc. Br. Soc. Res. into Learn. Math. 32 (2), 22–27.

Degrande, T., Verschaffel, L., and van Dooren, W. (2016). “Proportional word problem solving through a modeling lens: a half-empty or half-full glass?,” in Posing and Solving Mathematical Problems, Research in Mathematics Education . Editor P. Felmer.

Doerr, H. M., and Tripp, J. S. (1999). Understanding how students develop mathematical models. Math. Thinking Learn. 1 (3), 231–254. doi:10.1207/s15327833mtl0103_3

Fujita, T., Doney, J., and Wegerif, R. (2019). Students' collaborative decision-making processes in defining and classifying quadrilaterals: a semiotic/dialogic approach. Educ. Stud. Math. 101 (3), 341–356. doi:10.1007/s10649-019-09892-9

Gillies, R. (2016). Cooperative learning: Review of research and practice. Ajte 41 (3), 39–54. doi:10.14221/ajte.2016v41n3.3

Gravemeijer, K. (1999). How Emergent Models May Foster the Constitution of Formal Mathematics. Math. Thinking Learn. 1 (2), 155–177. doi:10.1207/s15327833mtl0102_4

Gravemeijer, K., Stephan, M., Julie, C., Lin, F.-L., and Ohtani, M. (2017). What mathematics education may prepare students for the society of the future? Int. J. Sci. Math. Educ. 15 (S1), 105–123. doi:10.1007/s10763-017-9814-6

Hamilton, E. (2007). “What changes are needed in the kind of problem-solving situations where mathematical thinking is needed beyond school?,” in Foundations for the Future in Mathematics Education . Editors R. Lesh, E. Hamilton, and Kaput (Mahwah, NJ: Lawrence Erlbaum ), 1–6.

Hannula, M. S. (2015). “Emotions in problem solving,” in Selected Regular Lectures from the 12 th International Congress on Mathematical Education . Editor S. J. Cho. doi:10.1007/978-3-319-17187-6_16

Hwang, W.-Y., and Hu, S.-S. (2013). Analysis of peer learning behaviors using multiple representations in virtual reality and their impacts on geometry problem solving. Comput. Edu. 62, 308–319. doi:10.1016/j.compedu.2012.10.005

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (2009). Circle of Learning: Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Johnson, D. W., Johnson, R. T., and Johnson Holubec, E. (1993). Cooperation in the Classroom . Gurgaon: Interaction Book Company .

Jordan, M. E., and McDaniel, R. R. (2014). Managing uncertainty during collaborative problem solving in elementary school teams: The role of peer influence in robotics engineering activity. J. Learn. Sci. 23 (4), 490–536. doi:10.1080/10508406.2014.896254

Karlsson, N., and Kilborn, W. (2018a). Inclusion through learning in group: tasks for problem-solving. [Inkludering genom lärande i grupp: uppgifter för problemlösning] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2018c). It's enough if they understand it. A study of teachers 'and students' perceptions of multiplication and the multiplication table [Det räcker om de förstår den. En studie av lärares och elevers uppfattningar om multiplikation och multiplikationstabellen]. Södertörn Stud. Higher Educ. , 175.

Karlsson, N., and Kilborn, W. (2018b). Tasks for problem-solving in mathematics. [Uppgifter för problemlösning i matematik] . Uppsala: Uppsala University .

Karlsson, N., and Kilborn, W. (2020). “Teacher’s and student’s perception of rational numbers,” in Interim Proceedings of the 44 th Conference of the International Group for the Psychology of Mathematics Education , Interim Vol., Research Reports . Editors M. Inprasitha, N. Changsri, and N. Boonsena (Khon Kaen, Thailand: PME ), 291–297.

Kazak, S., Wegerif, R., and Fujita, T. (2015). Combining scaffolding for content and scaffolding for dialogue to support conceptual breakthroughs in understanding probability. ZDM Math. Edu. 47 (7), 1269–1283. doi:10.1007/s11858-015-0720-5

Klang, N., Olsson, I., Wilder, J., Lindqvist, G., Fohlin, N., and Nilholm, C. (2020). A cooperative learning intervention to promote social inclusion in heterogeneous classrooms. Front. Psychol. 11, 586489. doi:10.3389/fpsyg.2020.586489

Klang, N., Fohlin, N., and Stoddard, M. (2018). Inclusion through learning in group: cooperative learning [Inkludering genom lärande i grupp: kooperativt lärande] . Uppsala: Uppsala University .

Kunsch, C. A., Jitendra, A. K., and Sood, S. (2007). The effects of peer-mediated instruction in mathematics for students with learning problems: A research synthesis. Learn. Disabil Res Pract 22 (1), 1–12. doi:10.1111/j.1540-5826.2007.00226.x

Langer-Osuna, J. M. (2016). The social construction of authority among peers and its implications for collaborative mathematics problem solving. Math. Thinking Learn. 18 (2), 107–124. doi:10.1080/10986065.2016.1148529

Lein, A. E., Jitendra, A. K., and Harwell, M. R. (2020). Effectiveness of mathematical word problem solving interventions for students with learning disabilities and/or mathematics difficulties: A meta-analysis. J. Educ. Psychol. 112 (7), 1388–1408. doi:10.1037/edu0000453

Lesh, R., and Doerr, H. (2003). Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning and Teaching . Mahwah, NJ: Erlbaum .

Lesh, R., Post, T., and Behr, M. (1988). “Proportional reasoning,” in Number Concepts and Operations in the Middle Grades . Editors J. Hiebert, and M. Behr (Hillsdale, N.J.: Lawrence Erlbaum Associates ), 93–118.

Lesh, R., and Zawojewski, (2007). “Problem solving and modeling,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor L. F. K. Lester (Charlotte, NC: Information Age Pub ), vol. 2.

Lester, F. K., and Cai, J. (2016). “Can mathematical problem solving be taught? Preliminary answers from 30 years of research,” in Posing and Solving Mathematical Problems. Research in Mathematics Education .

Lybeck, L. (1981). “Archimedes in the classroom. [Arkimedes i klassen],” in Göteborg Studies in Educational Sciences (Göteborg: Acta Universitatis Gotoburgensis ), 37.

McMaster, K. N., and Fuchs, D. (2002). Effects of Cooperative Learning on the Academic Achievement of Students with Learning Disabilities: An Update of Tateyama-Sniezek's Review. Learn. Disabil Res Pract 17 (2), 107–117. doi:10.1111/1540-5826.00037

Mercer, N., and Sams, C. (2006). Teaching children how to use language to solve maths problems. Lang. Edu. 20 (6), 507–528. doi:10.2167/le678.0

Montague, M., Krawec, J., Enders, C., and Dietz, S. (2014). The effects of cognitive strategy instruction on math problem solving of middle-school students of varying ability. J. Educ. Psychol. 106 (2), 469–481. doi:10.1037/a0035176

Mousoulides, N., Pittalis, M., Christou, C., and Stiraman, B. (2010). “Tracing students’ modeling processes in school,” in Modeling Students’ Mathematical Modeling Competencies . Editor R. Lesh (Berlin, Germany: Springer Science+Business Media ). doi:10.1007/978-1-4419-0561-1_10

Mulryan, C. M. (1992). Student passivity during cooperative small groups in mathematics. J. Educ. Res. 85 (5), 261–273. doi:10.1080/00220671.1992.9941126

OECD (2019). PISA 2018 Results (Volume I): What Students Know and Can Do . Paris: OECD Publishing . doi:10.1787/5f07c754-en

CrossRef Full Text

Pólya, G. (1948). How to Solve it: A New Aspect of Mathematical Method . Princeton, N.J.: Princeton University Press .

Russel, S. J. (1991). “Counting noses and scary things: Children construct their ideas about data,” in Proceedings of the Third International Conference on the Teaching of Statistics . Editor I. D. Vere-Jones (Dunedin, NZ: University of Otago ), 141–164., s.

Rzoska, K. M., and Ward, C. (1991). The effects of cooperative and competitive learning methods on the mathematics achievement, attitudes toward school, self-concepts and friendship choices of Maori, Pakeha and Samoan Children. New Zealand J. Psychol. 20 (1), 17–24.

Schoenfeld, A. H. (2016). Learning to think mathematically: Problem solving, metacognition, and sense making in mathematics (reprint). J. Edu. 196 (2), 1–38. doi:10.1177/002205741619600202

SFS 2009:400. Offentlighets- och sekretesslag. [Law on Publicity and confidentiality] . Retrieved from https://www.riksdagen.se/sv/dokument-lagar/dokument/svensk-forfattningssamling/offentlighets--och-sekretesslag-2009400_sfs-2009-400 on the 14th of October .

Snijders, T. A. B., and Bosker, R. J. (2012). Multilevel Analysis. An Introduction to Basic and Advanced Multilevel Modeling . 2nd Ed. London: SAGE .

Stillman, G., Brown, J., and Galbraith, P. (2008). Research into the teaching and learning of applications and modelling in Australasia. In H. Forgasz, A. Barkatas, A. Bishop, B. Clarke, S. Keast, W. Seah, and P. Sullivan (red.), Research in Mathematics Education in Australasiae , 2004-2007 , p.141–164. Rotterdam: Sense Publishers .doi:10.1163/9789087905019_009

Stohlmann, M. S., and Albarracín, L. (2016). What is known about elementary grades mathematical modelling. Edu. Res. Int. 2016, 1–9. doi:10.1155/2016/5240683

Swedish National Educational Agency (2014). Support measures in education – on leadership and incentives, extra adaptations and special support [Stödinsatser I utbildningen – om ledning och stimulans, extra anpassningar och särskilt stöd] . Stockholm: Swedish National Agency of Education .

Swedish National Educational Agency (2018). Syllabus for the subject of mathematics in compulsory school . Retrieved from https://www.skolverket.se/undervisning/grundskolan/laroplan-och-kursplaner-for-grundskolan/laroplan-lgr11-for-grundskolan-samt-for-forskoleklassen-och-fritidshemmet?url=-996270488%2Fcompulsorycw%2Fjsp%2Fsubject.htm%3FsubjectCode%3DGRGRMAT01%26tos%3Dgr&sv.url=12.5dfee44715d35a5cdfa219f ( on the 32nd of July, 2021).

van Hiele, P. (1986). Structure and Insight. A Theory of Mathematics Education . London: Academic Press .

Velásquez, A. M., Bukowski, W. M., and Saldarriaga, L. M. (2013). Adjusting for Group Size Effects in Peer Nomination Data. Soc. Dev. 22 (4), a–n. doi:10.1111/sode.12029

Verschaffel, L., Greer, B., and De Corte, E. (2007). “Whole number concepts and operations,” in Second Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics . Editor F. K. Lester (Charlotte, NC: Information Age Pub ), 557–628.

Webb, N. M., and Mastergeorge, A. (2003). Promoting effective helping behavior in peer-directed groups. Int. J. Educ. Res. 39 (1), 73–97. doi:10.1016/S0883-0355(03)00074-0

Wegerif, R. (2011). “Theories of Learning and Studies of Instructional Practice,” in Theories of learning and studies of instructional Practice. Explorations in the learning sciences, instructional systems and Performance technologies . Editor T. Koschmann (Berlin, Germany: Springer ). doi:10.1007/978-1-4419-7582-9

Yackel, E., Cobb, P., and Wood, T. (1991). Small-group interactions as a source of learning opportunities in second-grade mathematics. J. Res. Math. Edu. 22 (5), 390–408. doi:10.2307/749187

Zawojewski, J. (2010). Problem Solving versus Modeling. In R. Lesch, P. Galbraith, C. R. Haines, and A. Hurford (red.), Modelling student’s mathematical modelling competencies: ICTMA , p. 237–243. New York, NY: Springer .doi:10.1007/978-1-4419-0561-1_20

Keywords: cooperative learning, mathematical problem-solving, intervention, heterogeneous classrooms, hierarchical linear regression analysis

Citation: Klang N, Karlsson N, Kilborn W, Eriksson P and Karlberg M (2021) Mathematical Problem-Solving Through Cooperative Learning—The Importance of Peer Acceptance and Friendships. Front. Educ. 6:710296. doi: 10.3389/feduc.2021.710296

Received: 15 May 2021; Accepted: 09 August 2021; Published: 24 August 2021.

Reviewed by:

Copyright © 2021 Klang, Karlsson, Kilborn, Eriksson and Karlberg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Nina Klang, [email protected]

Along with Stanford news and stories, show me:

• Student information
• Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

• Share full article

Advertisement

Supported by

The Algebra Problem: How Middle School Math Became a National Flashpoint

Top students can benefit greatly by being offered the subject early. But many districts offer few Black and Latino eighth graders a chance to study it.

By Troy Closson

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system. Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly four in five poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class. San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’s administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12 percent of Black and Latino eighth graders do, compared with roughly 24 percent of white pupils, a federal report found .

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research . A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Mass., the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside of school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, Mr. de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80 percent from 60 percent. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s current schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won both support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Mr. Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Mr. Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100 percent, yes,” he added. “That was not something that I could live with.”

Troy Closson reports on K-12 schools in New York City for The Times. More about Troy Closson

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Today's news
• Reviews and deals
• Climate change
• 2024 election
• Fall allergies
• Health news
• Mental health
• Sexual health
• Family health
• So mini ways
• Unapologetically
• Buying guides

Entertainment

• How to Watch
• My watchlist
• Stock market
• Biden economy
• Personal finance
• Stocks: most active
• Stocks: gainers
• Stocks: losers
• Trending tickers
• World indices
• US Treasury bonds
• Top mutual funds
• Highest open interest
• Highest implied volatility
• Currency converter
• Basic materials
• Communication services
• Consumer cyclical
• Consumer defensive
• Financial services
• Industrials
• Real estate
• Mutual funds
• Credit cards
• Balance transfer cards
• Cash back cards
• Rewards cards
• Travel cards
• Online checking
• High-yield savings
• Money market
• Home equity loan
• Personal loans
• Student loans
• Options pit
• Fantasy football
• Pro Pick 'Em
• College Pick 'Em
• Fantasy baseball
• Fantasy hockey
• Fantasy basketball
• Download the app
• Daily fantasy
• Scores and schedules
• GameChannel
• World Baseball Classic
• Premier League
• CONCACAF League
• Champions League
• Motorsports
• Horse racing
• Newsletters

New on Yahoo

• Privacy Dashboard

The Algebra Problem: How Middle School Math Became a National Flashpoint

From suburbs in the Northeast to major cities on the West Coast, a surprising subject is prompting ballot measures, lawsuits and bitter fights among parents: algebra.

Students have been required for decades to learn to solve for the variable x, and to find the slope of a line. Most complete the course in their first year of high school. But top-achievers are sometimes allowed to enroll earlier, typically in eighth grade.

The dual pathways inspire some of the most fiery debates over equity and academic opportunity in American education.

Sign up for The Morning newsletter from the New York Times

Do bias and inequality keep Black and Latino children off the fast track? Should middle schools eliminate algebra to level the playing field? What if standout pupils lose the chance to challenge themselves?

The questions are so fraught because algebra functions as a crucial crossroads in the education system.

Students who fail it are far less likely to graduate. Those who take it early can take calculus by 12th grade, giving them a potential edge when applying to elite universities and lifting them toward society’s most high-status and lucrative professions.

But racial and economic gaps in math achievement are wide in the United States, and grew wider during the pandemic. In some states, nearly 4 in 5 poor children do not meet math standards.

To close those gaps, New York City’s previous mayor, Bill de Blasio, adopted a goal embraced by many districts elsewhere. Every middle school would offer algebra, and principals could opt to enroll all of their eighth graders in the class.

San Francisco took an opposite approach: If some children could not reach algebra by middle school, no one would be allowed to take it.

The central mission in both cities was to help disadvantaged students. But solving the algebra dilemma can be more complex than solving the quadratic formula.

New York’s dream of “algebra for all” was never fully realized, and Mayor Eric Adams’ administration changed the goal to improving outcomes for ninth graders taking algebra. In San Francisco, dismantling middle-school algebra did little to end racial inequities among students in advanced math classes. After a huge public outcry, the district decided to reverse course.

“You wouldn’t think that there could be a more boring topic in the world,” said Thurston Domina, a professor at the University of North Carolina. “And yet, it’s this place of incredibly high passions.”

“Things run hot,” he said.

In some cities, disputes over algebra have been so intense that parents have sued school districts, protested outside mayors’ offices and campaigned for the ouster of school board members.

Teaching math in middle school is a challenge for educators in part because that is when the material becomes more complex, with students moving from multiplication tables to equations and abstract concepts. Students who have not mastered the basic skills can quickly become lost, and it can be difficult for them to catch up.

Many school districts have traditionally responded to divergent achievement levels by simply separating children into distinct pathways, placing some in general math classes while offering others algebra as an accelerated option. Such sorting, known as tracking, appeals to parents who want their children to reach advanced math as quickly as possible.

But tracking has cast an uncomfortable spotlight on inequality. Around a quarter of all students in the United States take algebra in middle school. But only about 12% of Black and Latino eighth graders do, compared with roughly 24% of white pupils, a federal report found.

“That’s why middle school math is this flashpoint,” said Joshua Goodman, an associate professor of education and economics at Boston University. “It’s the first moment where you potentially make it very obvious and explicit that there are knowledge gaps opening up.”

In the decades-long war over math, San Francisco has emerged as a prominent battleground.

California once required that all eighth graders take algebra. But lower-performing middle school students often struggle when forced to enroll in the class, research shows. San Francisco later stopped offering the class in eighth grade. But the ban did little to close achievement gaps in more advanced math classes, recent research has found.

As the pendulum swung, the only constant was anger. Leading Bay Area academics disparaged one another’s research. A group of parents even sued the district last spring. “Denying students the opportunity to skip ahead in math when their intellectual ability clearly allows for it greatly harms their potential for future achievement,” their lawsuit said.

The city is now back to where it began: Middle school algebra — for some, not necessarily for all — will return in August. The experience underscored how every approach carries risks.

“Schools really don’t know what to do,” said Jon R. Star, an educational psychologist at Harvard who has studied algebra education. “And it’s just leading to a lot of tension.”

In Cambridge, Massachusetts, the school district phased out middle school algebra before the pandemic. But some argued that the move had backfired: Families who could afford to simply paid for their children to take accelerated math outside school.

“It’s the worst of all possible worlds for equity,” Jacob Barandes, a Cambridge parent, said at a school board meeting.

Elsewhere, many students lack options to take the class early: One of Philadelphia’s most prestigious high schools requires students to pass algebra before enrolling, preventing many low-income children from applying because they attend middle schools that do not offer the class.

In New York, de Blasio sought to tackle the disparities when he announced a plan in 2015 to offer algebra — but not require it — in all of the city’s middle schools. More than 15,000 eighth graders did not have the class at their schools at the time.

Since then, the number of middle schools that offer algebra has risen to about 80% from 60%. But white and Asian American students still pass state algebra tests at higher rates than their peers.

The city’s schools chancellor, David Banks, also shifted the system’s algebra focus to high schools, requiring the same ninth-grade curriculum at many schools in a move that has won support and backlash from educators.

And some New York City families are still worried about middle school. A group of parent leaders in Manhattan recently asked the district to create more accelerated math options before high school, saying that many young students must seek out higher-level instruction outside the public school system.

In a vast district like New York — where some schools are filled with children from well-off families and others mainly educate homeless children — the challenge in math education can be that “incredible diversity,” said Pedro A. Noguera, the dean of the University of Southern California’s Rossier School of Education.

“You have some kids who are ready for algebra in fourth grade, and they should not be denied it,” Noguera said. “Others are still struggling with arithmetic in high school, and they need support.”

Many schools are unequipped to teach children with disparate math skills in a single classroom. Some educators lack the training they need to help students who have fallen behind, while also challenging those working at grade level or beyond.

Some schools have tried to find ways to tackle the issue on their own. KIPP charter schools in New York have added an additional half-hour of math time to many students’ schedules, to give children more time for practice and support so they can be ready for algebra by eighth grade.

At Middle School 50 in Brooklyn, where all eighth graders take algebra, teachers rewrote lesson plans for sixth- and seventh-grade students to lay the groundwork for the class.

The school’s principal, Ben Honoroff, said he expected that some students would have to retake the class in high school. But after starting a small algebra pilot program a few years ago, he came to believe that exposing children early could benefit everyone — as long as students came into it well prepared.

Looking around at the students who were not enrolling in the class, Honoroff said, “we asked, ‘Are there other kids that would excel in this?’”

“The answer was 100%, yes,” he added. “That was not something that I could live with.”

c.2024 The New York Times Company

Recommended Stories

Birmingham-southern baseball advances to diii college world series, as school shuts down.

The Birmingham-Southern baseball team will play in the Division III College World Series as the school itself is shutting down due to financial difficulties.

Elon Musk is reportedly planning an xAI supercomputer to power a better version of Grok

Musk recently presented plans for a ‘gigafactory of compute’ to investors, The Information reports. This would power a future, smarter version of Grok and require at least 100,000 NVIDIA H100 GPUs.

Scarlett Johansson brought receipts to the OpenAI controversy

OpenAI announced this week that it’s removing Sky, one of the voices used by its new GPT-4o model, after users found it sounded eerily similar to Scarlett Johansson’s AI character in “Her.” While the company claims the voice was not based on Johansson’s, the actress said OpenAI had previously approached her about using her voice for the model. The U.S. Department of Justice and 30 state attorneys general filed a lawsuit against Live Nation Entertainment, Ticketmaster’s parent company, for alleged monopolistic practices.

3 Americans accused of involvement in Congo coup attempt. Here's what we know about what happened.

A spokesperson for the Congo army said three Americans from Utah were detained following the foiled coup on May 19.

Grayson Murray, two-time PGA Tour winner, dead at 30

Murray won two PGA tournaments, including the Sony Hawaii Open this past January.

AI tutors are quietly changing how kids in the US study, and the leading apps are from China

Evan, a high school sophomore from Houston, was stuck on a calculus problem. Within a few seconds, Answer AI had generated an answer alongside a step-by-step process of solving the problem. A year ago, Evan would be scouring through long YouTube videos in hopes of tackling his homework challenges.

Junkyard Gem: 1977 Dodge Aspen Wagon

A 1977 Dodge Aspen station wagon, sibling to the Plymouth Volaré station wagon, found in a Colorado self-service wrecking yard.

Amazon's secret overstock section is bursting with huge savings for Memorial Day — starting at $6

Save big on amazing hidden deals, from knives to patio string lights and more.

Women in AI: Sarah Myers West says we should ask, 'Why build AI at all?'

To give AI-focused women academics and others their well-deserved — and overdue — time in the spotlight, TechCrunch has been publishing a series of interviews focused on remarkable women who’ve contributed to the AI revolution. Sarah Myers West is managing director at the AI Now institute, an American research institute studying the social implications of AI and policy research that addresses the concentration of power in the tech industry. Early in my career, I had a front row seat observing how U.S. tech companies showed up around the world in ways that changed the political landscape — in Southeast Asia, China, the Middle East and elsewhere — and wrote a book delving in to how industry lobbying and regulation shaped the origins of the surveillance business model for the internet despite technologies that offered alternatives in theory that in practice failed to materialize.

SpaceX Raptor engine test ends in a fiery explosion

A SpaceX testing stand at the company's McGregor, Texas facilities went up in flames during a test of its Raptor 2 engines on the afternoon of May 23.

I'm a fashion writer and these are the best Memorial Day sales I've found at Amazon, Walmart, Hoka and more

Save up to 70% on staples like flattering swimsuits, fan-favorite shorts, top-selling sneakers and a breezy cooling bra.

Nordstrom Rack's Clear the Rack sale is here and it's major — save up to 80% on flowy dresses, sandals and more

Thousands of items including designer brands are marked down by an extra 25%.

Meta and Activision face lawsuit by families of Uvalde school shooting victims

A lawsuit by the families of the Uvalde school shooting victims accuse Meta and Call of Duty publisher Activision of exposing the shooter to the weapon he used.

Austin Pedal Car reemerges in new, bespoke form

Austin Pedals cars offers a new 'J40 Continuation' version of an old classic 'toy' as bespoke offering in partnership with tailor Holland & Sherry.

No one gets in trouble owning too many tech stocks: Chart of the Week

More and more funds bought tech stocks over the past 12 months, with GLP-1 maker Eli Lilly the only non-tech cracking the top 10 stocks that saw increased ownership.

CD rates today, May 25, 2024 (best account provides 5.15% APY)

If you’re searching for today’s best CD rates, we’ve narrowed down some of the top offers. Learn more about CD rates today.

Mortgage rates today, May 25, 2024: Rates ease up

These are today's mortgage rates. Though rates may continue to tick down throughout 2024, they probably won't plummet drastically. Lock in your rate today.

Bulls' Lonzo Ball reveals he underwent rare meniscus transplant procedure on left knee

Ball's plan is to be ready at the start of next season.

This $13 outlet extender solves the problem of 'too many devices, not enough space' — it's over 30% off

It's a no-brainer in a tech-heavy household, plus it has a 12-month replacement period.

Doctor Who: 73 Yards review: Don’t stand so close to me

'73 Yards' offers a darker twist on the Doctor-lite episode.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 7: Medium: Problem solving and data analysis

About this unit.

This unit tackles the medium-difficulty problem solving and data analysis questions on the SAT Math test. Work through each skill, taking quizzes and the unit test to level up your mastery progress.

Ratios, rates, and proportions: medium

• Ratios, rates, and proportions | SAT lesson (Opens a modal)
• Ratios, rates, and proportions — Basic example (Opens a modal)
• Ratios, rates, and proportions — Harder example (Opens a modal)
• Ratios, rates, and proportions: medium Get 3 of 4 questions to level up!

Unit conversion: medium

• Unit conversion | Lesson (Opens a modal)
• Units — Basic example (Opens a modal)
• Units — Harder example (Opens a modal)
• Unit conversion: medium Get 3 of 4 questions to level up!

Percentages: medium

• Percentages | Lesson (Opens a modal)
• Percents — Basic example (Opens a modal)
• Percents — Harder example (Opens a modal)
• Percentages: medium Get 3 of 4 questions to level up!

Center, spread, and shape of distributions: medium

• Center, spread, and shape of distributions | Lesson (Opens a modal)
• Center, spread, and shape of distributions — Basic example (Opens a modal)
• Center, spread, and shape of distributions — Harder example (Opens a modal)
• Center, spread, and shape of distributions: medium Get 3 of 4 questions to level up!

Data representations: medium

• Data representations | Lesson (Opens a modal)
• Key features of graphs — Basic example (Opens a modal)
• Key features of graphs — Harder example (Opens a modal)
• Data representations: medium Get 3 of 4 questions to level up!

Scatterplots: medium

• Scatterplots | Lesson (Opens a modal)
• Scatterplots — Basic example (Opens a modal)
• Scatterplots — Harder example (Opens a modal)
• Scatterplots: medium Get 3 of 4 questions to level up!

Linear and exponential growth: medium

• Linear and exponential growth | Lesson (Opens a modal)
• Linear and exponential growth — Basic example (Opens a modal)
• Linear and exponential growth — Harder example (Opens a modal)
• Linear and exponential growth: medium Get 3 of 4 questions to level up!

Probability and relative frequency: medium

• Probability and relative frequency | Lesson (Opens a modal)
• Table data — Basic example (Opens a modal)
• Table data — Harder example (Opens a modal)
• Probability and relative frequency: medium Get 3 of 4 questions to level up!

Data inferences: medium

• Data inferences | Lesson (Opens a modal)
• Data inferences — Basic example (Opens a modal)
• Data inferences — Harder example (Opens a modal)
• Data inferences: medium Get 3 of 4 questions to level up!

Evaluating statistical claims: medium

• Evaluating statistical claims | Lesson (Opens a modal)
• Data collection and conclusions — Basic example (Opens a modal)
• Data collection and conclusions — Harder example (Opens a modal)
• Evaluating statistical claims: medium Get 3 of 4 questions to level up!

share this!

May 21, 2024

This article has been reviewed according to Science X's editorial process and policies . Editors have highlighted the following attributes while ensuring the content's credibility:

fact-checked

trusted source

The case for 'math-ish' thinking

by Stanford University

For everyone whose relationship with mathematics is distant or broken, Jo Boaler, a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start—to approach the subject with playfulness and curiosity, not anxiety or dread.

"Most people have only ever experienced what I call narrow mathematics—a set of procedures they need to follow, at speed," Boaler says. "Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience."

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed, a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math, the first massive open online course (MOOC) on mathematics education . She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, " Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics ," Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls "ishing" a math problem can help students make better sense of the answer.

What do you mean by 'math-ish' thinking?

It's a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport—these are generally answered with what I call "ish" numbers, and that's very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They're given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2—but the most common answer 13-year-olds gave was 19. The second most common was 21.

I'm not surprised, because when students learn fractions, they often don't learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don't you also risk sending the message that mathematical precision isn't important?

I'm not saying precision isn't important. What I'm suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they'll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, "Isn't 'ishing' just estimating?" It is, but when we ask students to estimate, they often groan, thinking it's yet another mathematical method. But when we ask them to "ish" a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things—all of that contributes to our understanding of how it works.

There's an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik's Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they'd done that activity in our summer camp and asked what had stayed with them. One student said, "I'm in geometry class now, and I still remember that sugar cube, what it looked like and felt like." His class had been asked to estimate the volume of their shoes, and he said he'd imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don't get to see and manipulate them. When we learn about square roots, we don't take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That's the thing—elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it's all symbolic. There's a myth that there's a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There's an example in the book where you've asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn't it be easier to teach students one standard method?

That narrow, rigid version of mathematics where there's only one right approach is what most students experience, and it's a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they're not developing number sense.

They don't learn how to use numbers flexibly in different situations. It also makes students who think differently believe there's something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics.

When we bring those forms of diversity together, it's powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

Provided by Stanford University

Explore further

Feedback to editors

NASA launches ground-breaking climate change satellite

4 hours ago

Dyson spheres: Astronomers report potential candidates for alien structures, and evidence against their existence

5 hours ago

You leave a 'microbe fingerprint' on every piece of clothing you wear—and it could help forensic scientists solve crimes

9 hours ago

Saturday Citations: The cheapness horizon of electric batteries; the battle-worthiness of ancient armor; scared animals

12 hours ago

Cosmic leap: NASA Swift satellite and AI unravel the distance of the farthest gamma-ray bursts

14 hours ago

Scientists discover CO₂ and CO ices in outskirts of solar system

Charge your laptop in a minute? Supercapacitors can help; new research offers clues

15 hours ago

New study discovers tiny target on RNA to short-circuit inflammation

Researchers develop organic photoredox catalysts with enhanced stability and recyclability

May 24, 2024

Theory and experiment combine to shine a new light on proton spin

Relevant physicsforums posts, memorizing trigonometric identities, conformal flatness of ellipsoid, graphing trip efficiency - distance over time.

May 20, 2024

Help with Recurrence Equation

May 18, 2024

Numerically how to approximate exponential decay in a discrete signal

May 16, 2024

Flat surface to curved surface

May 13, 2024

More from General Math

Related Stories

Changing students' attitudes to mathematics improves test scores

May 10, 2018

Math degrees are becoming less accessible—and this is a problem for business, government and innovation

May 5, 2024

Former math teacher explains why some students are 'good' at math and others lag behind

Nov 3, 2022

Studies recommend increased research into achievement, engagement to raise student math scores

Feb 15, 2024

5 tips to get your children excited about math

Jan 17, 2020

Future teachers often think memorization is the best way to teach math and science – until they learn a different way

Sep 17, 2020

Recommended for you

Math discovery provides new method to study cell activity, aging

First-generation medical students face unique challenges and need more targeted support, say researchers

Mechanistic model shows how much gossip is needed to foster social cooperation

May 15, 2024

Random processes shape science and math: Researchers propose a unified, probabilistic framework

May 9, 2024

Study of new method used to preserve privacy with US census data suggests accuracy has suffered

May 6, 2024

New study is first to use statistical physics to corroborate 1940s social balance theory

May 3, 2024

Let us know if there is a problem with our content

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter

• {{subColumn.name}}

AIMS Mathematics

• {{newsColumn.name}}
• Share facebook twitter google linkedin

Randomized symmetric Gauss-Seidel method for solving linear least squares problems

• Fan Sha 1 ,  ,  , 
• Jianbing Zhang 2
• 1. School of Mathematics, East China Normal University, Shanghai 200241, China
• 2. School of Artificial Intelligence, Nanjing University, Nanjing 210023, China
• Received: 30 March 2024 Revised: 08 May 2024 Accepted: 14 May 2024 Published: 23 May 2024

MSC : 65F10

• Full Text(HTML)
• Download PDF

We introduced a random symmetric Gauss-Seidel (RSGS) method, which was designed to handle large scale linear least squares problems involving tall coefficient matrices. This RSGS method projected the approximate residual onto the subspace spanned by two symmetric columns at each iteration. These columns were sampled from the coefficient matrix based on an effective probability criterion. Our theoretical analysis indicated that RSGS converged when the coefficient matrix had full column rank. Furthermore, numerical experiments demonstrated that RSGS outperformed the baseline algorithms in terms of iteration steps and CPU time.

• randomized symmetric Gauss-Seidel ,
• linear least squares ,
• randomized sampling ,
• converge in expectation ,
• probability criterion

Citation: Fan Sha, Jianbing Zhang. Randomized symmetric Gauss-Seidel method for solving linear least squares problems[J]. AIMS Mathematics, 2024, 9(7): 17453-17463. doi: 10.3934/math.2024848

Related Papers:

• This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->

Supplements

Access history.

• Corresponding author: Email: [email protected] ; 

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 29 ) PDF downloads( 4 ) Cited by( 0 )

Figures and Tables

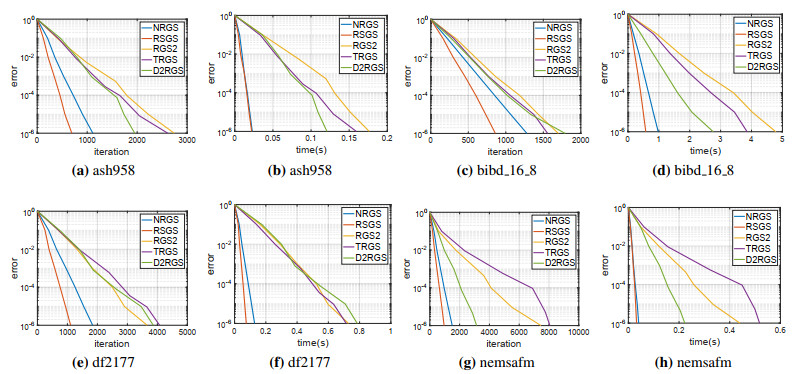
Figures( 2 )  /  Tables( 1 )

Associated material

Other articles by authors.

• Jianbing Zhang

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File

• Figure 1. Compasions of different baselines in terms of iteration and running time on Florida sparse matrices
• Figure 2. Compasions of different baselines in terms of iteration and running time on dense matrices