multiplication and division of decimals problem solving

Multiplying/Dividing by Decimals Practice Questions

Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Pre-Algebra >
• Decimals >

Decimal Word Problem Worksheets

Extensive decimal word problems are presented in these sets of worksheets, which require the learner to perform addition, subtraction, multiplication, and division operations. This batch of printable decimal word problem worksheets is curated for students of grade 3 through grade 7. Free worksheets are included.

Adding Decimals Word Problems

Decimal word problems presented here help the children learn decimal addition based on money, measurement and other real-life units.

• Download the set

Subtracting Decimals Word Problems

These decimal word problem worksheets reinforce the real-life subtraction skills such as tender the exact change, compare the height, the difference between the quantities and more.

Decimals: Addition and Subtraction

It's review time for grade 4 and grade 5 students. Take these printable worksheets that help you reinforce the knowledge in adding and subtracting decimals. There are five word problems in each pdf worksheet.

Multiplying Decimals Whole Numbers

Reduce the chaos and improve clarity in your decimal multiplication skill using this collection of no-prep, printable worksheets. A must-have resource for young learners looking to ace their class!

Decimal Division Whole Numbers

Revive your decimal division skills with a host of interesting lifelike word problems involving whole numbers. Keep up with consistent practice and you’ll fly high in the topic in no time!

Multiplying Decimals Word Problems

Each decimal word problem involves multiplication of a whole number with a decimal number. 5th grade students are expected to find the product and check their answer using the answer key provided in the second page.

Dividing Decimals Word Problems

These division word problems require children to divide the decimals with the whole numbers. Ask the 6th graders to perform the division to find the quotient by applying long division method. Avoid calculator.

Decimals: Multiplication and Division

These decimal worksheets emphasize decimal multiplication and division. The perfect blend of word problems makes the grade 6 and grade 7 children stronger in performing the multiplication and division operation.

Related Worksheets

» Fraction Word Problems

» Ratio Word Problems

» Division Word Problems

Become a Member

Membership Information

Privacy Policy

What's New?

Printing Help

Testimonial

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

Fun teaching resources & tips to help you teach math with confidence

{FREE} Multiplying Decimals Word Problems Set

Whether our kids want to admit it or not, decimals are a part of our everyday life. And it’s important that they feel confident doing basic computations with decimals. Even if they start to use a calculator, they still need to understand how to rightly apply operations with decimals to solve real world problems. If they don’t know whether to multiply or add, using a calculator isn’t going to help. So I hope this free set of multiplying decimals word problems provides a chance for some quick, low-prep practice.

* Please Note : This post contains affiliate links which support the work of this site. Read our full disclosure here .*

Multiplying Decimals Word Problems:

This set of word problems is actually a sample from my ‘Making Sense of Word Problems’ course . In that course, I explain the different types and structures for word problems .

When you consider multiplication and division problems, there are actually 9 different types or problem structures for a multiplication/division problem.

This set of 27 decimal word problems covers all the different structures, which kids can solve using multiplication and division.

Each page includes 3 problems , with space for kids to write out their thinking and solution. However, you could also cut the pages into strips to assign one problem at a time.

The download also includes an answer key , making it easy for you to print and use with your students.

Ways to Incorporate More Word Problem Practice:

There are a lot of different ways you can include word problem practice into your math routine, but here are some ideas to get you started. Or just provide some ideas you may not have thought of.

• At the start of a new unit: Although most curricula or textbooks will save word problems for last, I actually think you should begin a unit by presenting a problem for kids to solve. This does not necessarily have to be a word problem, but with multiplication and division involving fractions and decimals, I think these skills are best learned in context . So even if you have not given students an example or method for solving, this will encourage them to think and apply what they know to come up with their own ideas and strategies.
• As a daily challenge problem: Another idea is to have a ‘problem of the day’ word problem for kids, perhaps when they come into class. This is a great way to not only work on word problems, but also review skills, because this doesn’t necessarily need to be related to your lesson that day. This set of word problems can easily be cut into strips so kids can glue the problem into their notebook or math journal each day.
• Math practice for a sub day: Not sure what to plan for your substitute while you’re out? Why not give kids a set of related word problems? Let them work independently or in small groups . Then when you return you can discuss the different problems, how to multiply and divide decimals or different strategies kids used.
•  As homework: Lastly, assigning a small set of related word problems as homework provides practice for kids independently, but not an overwhelming amount.

But however you include word problems as you explore multiplying decimals or dividing decimals , I hope this set of 27 problems provides a quick and easy resource for you.

{Click HERE to go to my shop and grab the FREE set of Multiplying Decimals Word Problems}

*pssst: looking for even more word problem resources check out the complete course to help you and your students make sense of word problems., find more free word problem resources below:.

• Word problem solving templates
• I Notice…I Wonder Routine for solving problems | Journal for kids
• Pythagorean Theorem word problems
• Lemonade stand word problems | time & money
• Two step problems set | multiplication & subtraction of whole numbers

One Comment

• Pingback: 50 Decimal Activities to Strengthen Decimal Sense

Comments are closed.

Similar Posts

December Problem of the Day Calendars {FREE}

Add & Subtract Decimals on a Number Line {FREE Printable Number Lines!}

Understanding Data: FREE Mean Median & Mode Lesson

Printable Math Manipulatives | FREE Download

Swim Meet Printable Rounding Game {FREE}

Want a Unique Tangram Game to Challenge Your Kids?

Find more resources to help make math engaging, join 165k+ parents & teachers.

Who learn new tips and strategies, as well as receive engaging resources to make math fun!

• Privacy Policy

Math Time Doesn't Have to End in Tears

Join 165,000+ parents and teachers who learn new tips and strategies, as well as receive engaging resources to make math fun. Plus, receive my guide, "5 Games You Can Play Today to Make Math Fun," as my free gift to get you started!

Multiplying Decimals

Multiply without the decimal point, then re-insert it in the correct spot!

How to Multiply Decimals

Just follow these steps:

• Multiply normally, ignoring the decimal points.
• Then put the decimal point in the answer - it will have as many decimal places as the two original numbers combined.

In other words, just count up how many numbers are after the decimal point in both numbers you are multiplying, then the answer should have that many numbers after its decimal point.

Example: Multiply 0.03 by 1.1

How does it work.

Because when you multiply without the decimal point, you are really shifting the decimal point to the right to get it out of the way :

Then we do the (now easy) multiplication:

3. × 11. = 33.

But remember, we did 3 Moves of the decimal point, so we need to undo that:

Here are some more examples:

Example: Multiply 0.25 by 0.2

Example: multiply 102 by 0.22, common sense.

As a final check you can put your "common sense" hat on and think "is that the right size?" , because you don't want to pay ten times too much for anything, nor get only one-tenth of what you need!

And that's all.

Just remember: the answer should have the same number of decimal places as are in both the numbers you are multiplying.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.2.2: Multiplying and Dividing Decimals

• Last updated
• Save as PDF
• Page ID 62047

• The NROC Project

Learning Objectives

• Multiply two or more decimals.
• Multiply a decimal by a power of 10.
• Divide by a decimal.
• Divide a decimal by a power of 10.
• Solve application problems that require decimal multiplication or division.

Introduction

As with whole numbers, sometimes you run into situations where you need to multiply or divide decimals. And just as there is a correct way to multiply and divide whole numbers, so, too, there is a correct way to multiply and divide decimals.

Imagine that a couple eats dinner at a Japanese steakhouse. The bill for the meal is $58.32 —which includes a tax of $4.64. To calculate the tip, they can double the tax. So if they know how to multiply $4.64 by 2, the couple can figure out how much they should leave for the tip.

Here’s another problem. Andy just sold his van that averaged 20 miles per gallon of gasoline. He bought a new pickup truck and took it on a trip of 614.25 miles. He used 31.5 gallons of gas to make it that far. Did Andy get better gas mileage with the new truck?

Both of these problems can be solved by multiplying or dividing decimals. Here’s how to do it.

Multiplying Decimals

Multiplying decimals is the same as multiplying whole numbers except for the placement of the decimal point in the answer. When you multiply decimals, the decimal point is placed in the product so that the number of decimal places in the product is the sum of the decimal places in the factors .

Let’s compare two multiplication problems that look similar: \(\ 214 \cdot 36\) and \(\ 21.4 \cdot 3.6\).

\(\ \begin{array}{r} 214 \\ \times \quad 36 \\ \hline 1284 \\ 6420 \\ \hline \mathbf{7 , 7 0 4} \end{array}\) \(\ \begin{array}{r} 21.4 \\ \times \quad 3.6 \\ \hline 1284 \\ 6420 \\ \hline \mathbf{7 7 . 0 4} \end{array}\)

Notice how the digits in the two solutions are exactly the same: 7, 7, 0, and 4. The multiplication does not change at all. The difference lies in the placement of the decimal point in the final answers: \(\ 214 \cdot 36=7,704\), and \(\ 21.4 \cdot 3.6=77.04\).

To find out where to put the decimal point in a decimal multiplication problem, count the total number of decimal places in each of the factors.

21.4 the first factor has one decimal place

3.6 the second factor has one decimal place

77.04 the product will have 1+1=2 decimal places

Note that the decimal points do not have to be aligned as for addition and subtraction.

\(\ 3.04 \cdot 6.1=?\)

\(\ 3.04 \cdot 6.1=18.544\)

Sometimes you may need to insert zeros in front of the product so that you have the right number of decimal places. See the final answer in the example below:

0.037 \cdot 0.08=?

If one or more zeros occur on the right in the product, they are not dropped until after the decimal point is inserted.

\(\ 2.04 \cdot 1.95=?\)

To multiply decimals:

• Set up and multiply the numbers as you do with whole numbers.
• Count the total number of decimal places in both of the factors.
• Place the decimal point in the product so that the number of decimal places in the product is the sum of the decimal places in the factors.
• Keep all zeros in the product when you place the decimal point. You can drop the zeros on the right once the decimal point has been placed in the product. If the number of decimal places is greater than the number of digits in the product, you can insert zeros in front of the product.

Multiply. \(\ 51.2 \cdot 3.08\)

• Incorrect. Pay attention to the placement of the decimal point. The correct answer is 157.696.
• Correct. To find the product, multiply \(\ 512 \cdot 308=157696\). Count the total number of decimal places in the factors, 3, and then place a decimal point in the product so that the product has three decimal places as well. The answer is 157.696.

Multiplying by Tens

Take a moment to multiply 4.469 by 10. Now do \(\ 4.469 \cdot 100\). Finally, do \(\ 4.469 \cdot 1,000\). Notice any patterns in your products?

\(\ \begin{array}{r} 4.469 \\ \times \quad 10 \\ \hline 44.690 \end{array}\) \(\ \begin{array}{r} 4.469 \\ \times \quad 100 \\ \hline 446.900 \end{array}\) \(\ \begin{array}{r} 4.469 \\ \times \quad 1000 \\ \hline 4469.000 \end{array}\)

Notice that the products keep getting greater by one place value as the multiplier (10, 100, and 1,000) increases. In fact, the decimal point moves to the right by the same number of zeros in the power of ten multiplier.

\(\ 4.469 \cdot 10=44.69 \quad\quad 4.469 \cdot 100=446.9 \quad\quad 4.469 \cdot 1,000=4469\)

You can use this observation to help you quickly multiply any decimal by a power of ten (10, 100, 1,000, etc).

\(\ 0.03 \cdot 100=?\)

\(\ 0.03 \cdot 100=3\)

Multiplying a Decimal by a Power of Ten

To multiply a decimal number by a power of ten (such as 10, 100, 1,000, etc.), count the number of zeros in the power of ten. Then move the decimal point that number of places to the right.

For example, \(\ 0.054 \cdot 100=5.4\). The multiplier 100 has two zeros, so you move the decimal point in 0.054 two places to the right—for a product of 5.4.

Dividing Decimals

To divide decimals, you will once again apply the methods you use for dividing whole numbers. Look at the two problems below. How are the methods similar?

\(\ \begin{array}{r} 867\ \\ 3\longdiv{2601}\\ -24\ \ \ \ \ \\ \hline 20\ \ \ \\ -18\ \ \ \\ \hline 21\ \\ -21\ \\ \hline 0\ \end{array}\) \(\ \begin{array}{r} 8.67\ \\ 3\longdiv{26.01}\\ -24\ \ \ \ \ \ \\ \hline 2\ 0\ \ \ \\ -1\ 8\ \ \ \\ \hline 21\ \\ -21\ \\ \hline 0\ \end{array}\)

Notice that the division occurs in the same way—the only difference is the placement of the decimal point in the quotient .

\(\ 18.32 \div 8=?\)

\(\ 18.32 \div 8=2.29\)

But what about a case where you are dividing by a decimal, as in the problem below?

\(\ 0.3\longdiv{260.1}\)

In cases like this, you can use powers of 10 to help create an easier problem to solve. In this case, you can multiply the divisor , 0.3, by 10 to move the decimal point 1 place to the right. If you multiply the divisor by 10, then you also have to multiply the dividend by 10 to keep the quotient the same. The new problem, with its solution, is shown below.

\(\ 260.1 \div 0.3=?\)

\(\ 260.1 \div 0.3=867\)

Often, the dividend will still be a decimal after multiplying by a power of 10. In this case, the placement of the decimal point must align with the decimal point in the dividend.

\(\ 15.275 \div 3.25=?\)

\(\ 15.275 \div 3.25=4.7\)

Dividing Decimals by Whole Numbers

Divide as you would with whole numbers. Then place the decimal point in the quotient directly above the decimal point in the dividend.

To divide by a decimal, multiply the divisor by a power of ten to make the divisor a whole number. Then multiply the dividend by the same power of ten. You can think of this as moving the decimal point in the dividend the same number of places to the right as you move the decimal point in the divisor.

Then place the decimal point in the quotient directly over the decimal point in the dividend. Finally, divide as you would with whole numbers.

Divide: \(\ 25.095 \div 0.5\).

• Incorrect. Multiply both the divisor and the dividend by 10 (this will change 0.5 into a whole number), and then divide. Then place the decimal point in the quotient directly over the decimal point in the dividend. The correct answer is 50.19.
• Correct. This problem can be set up as \(\ 250.95 \div 5\); the quotient is 50.19.
• Incorrect. Remember that when you divide, you do not count the total number of decimal places in the divisor and dividend. You change the divisor to a whole number, then move the decimal point in the dividend the same number of places and divide. Finally, place the decimal point in the quotient directly over the decimal point in the dividend. The correct answer is 50.19.

Dividing by Tens

Recall that when you multiply a decimal by a power of ten (10, 100, 1,000, etc.), the placement of the decimal point in the product will move to the right according to the number of zeros in the power of ten. For instance, \(\ 4.12 \cdot 10=41.2\).

Multiplication and division are inverse operations, so you can expect that if you divide a decimal by a power of ten, the decimal point in the quotient will also correspond to the number of zeros in the power of ten. The difference is that the decimal point moves to the right when you multiply; it moves to the left when you divide.

\(\ \begin{array}{r} .4469\ \\ 10\longdiv{4.4690}\\ -4\ 0\ \ \ \ \ \ \ \\ \hline 46\ \ \ \ \ \\ -40\ \ \ \ \ \\ \hline 69\ \ \ \\ -60\ \ \ \\ \hline 90 \ \\ -90 \ \\ \hline 0\ \end{array}\) \(\ \begin{array}{r} .04469\ \\ 100\longdiv{4.46900}\\ -4 \ 00\ \ \ \ \ \ \\ \hline 469\ \ \ \ \\ -400\ \ \ \ \\ \hline 690\ \ \\ -600\ \ \\ \hline 900\\ -900\\ \hline 0 \end{array}\) \(\ \begin{array}{r} .004469\ \\ 1000\longdiv{4.469000}\\ -4\ 000\ \ \ \ \ \ \ \\ \hline 4690\ \ \ \ \ \\ -4000\ \ \ \ \ \\ \hline 6900\ \ \ \\ -6000\ \ \ \\ \hline 9000\ \\ -9000\ \\ \hline 0\ \end{array}\)

In the examples above, notice that each quotient still contains the digits 4469—but as another 0 is added to the end of each power of ten in the divisor, the decimal point moves an additional place to the left in the quotient.

Dividing by Powers of Ten

To divide a decimal by a power of ten (10, 100, 1,000, ect.), count the number of zeros in the divisor. Then move the decimal point in the dividend that number of decimal places to the left; this will be your quotient.

\(\ 31.05 \div 10=?\)

\(\ 31.05 \div 10=3.105\)

Divide. \(\ 0.045 \div 100\)

• Correct. There are two zeros in the divisor, 100, so to find the quotient, take the dividend, 0.045, and move the decimal point two places to the left. The quotient is 0.00045.
• Incorrect. 0.045 is the dividend in the problem; it cannot be the quotient unless the divisor is 1. The correct answer is 0.00045.
• Incorrect. 4.5 would be the correct answer if you multiplied 0.045 by 100, not divided it by 100. The correct answer is 0.00045.
• Incorrect. 4,500 would be the correct answer if you multiplied 0.045 by 100,000, not divided it by 100. The correct answer is 0.00045.

Solving Problems by Multiplying or Dividing Decimals

Now let’s return to the two problems from the beginning of this section. You know how to multiply and divide with decimals now. Let’s put that knowledge to the test.

A couple eats dinner at a Japanese steakhouse. The bill for the meal totals $58.32—which includes a tax of $4.64. To calculate the tip, they can double the tax. How much tip should the couple leave?

The couple should leave a tip of $9.28.

Andy just sold his van that averaged 20 miles per gallon of gasoline. He bought a new pickup truck and took it on a trip of 614.25 miles. He used 31.5 gallons of gas for the trip. Did Andy get better gas mileage with the new truck?

Andy gets 19.5 miles per gallon now. He used to get 20 miles per gallon. He does not get better gas mileage with the new truck.

Learning to multiply and divide with decimals is an important skill. In both cases, you work with the decimals as you have worked with whole numbers, but you have to figure out where the decimal point goes. When multiplying decimals, the number of decimal places in the product is the sum of the decimal places in the factors. When dividing by decimals, move the decimal point in the dividend the same number of places to the right as you move the decimal point in the divisor. Then place the decimal point in the quotient above the decimal point in the dividend.

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Perform Operations of Decimals: Word Problems

Greetings, budding mathematicians! Today, we're going to jump into an adventure with decimals. Working with decimals is a fundamental math skill that you'll use in many aspects of life, from managing money to measuring distances.

Introduction to Decimal Operations

First things first, let’s talk about decimals. A decimal is a way of representing a number that’s less than one, or a number that’s a whole and a fraction together. When you work with decimals, the same rules apply as when you’re working with whole numbers, but the decimal point plays a crucial role.

There are four major operations that you can perform on decimals:

• Subtraction
• Multiplication

Now, let’s tackle some word problems involving decimal operations.

Step-By-Step Guide to Solving Word Problems with Decimal Operations

Step 1: understand the problem.

First and foremost, carefully read through the problem. Identify what you know and what you need to find out.

Step 2: Plan the Solution

Next, decide which operation (addition, subtraction, multiplication, or division) will help you solve the problem. This will depend on what the problem is asking.

Step 3: Carry Out the Operation

Perform the operation on the decimals. Remember to align the decimal points when you’re adding or subtracting, and apply the rules for multiplication and division of decimals correctly.

Step 4: Check the Answer

Finally, check if your answer makes sense in the context of the problem.

Consider this problem: Laura bought \(2.3\) kilograms of apples and \(1.5\) kilograms of grapes. How many kilograms of fruit did she buy in total?

Step 1: Understand that you know the weight of apples and grapes separately, and you need to find the total weight.

Step 2: Realize that to find the total, you need to add the weights together.

Step 3: Add the weights: \(2.3\ kg + 1.5\ kg = 3.8\ kg\).

Step 4: Check that the answer makes sense. Laura bought \(2.3\ kg\) of apples and \(1.5\ kg\) of grapes, so it makes sense that she bought \(3.8\ kg\) in total.

Keep practicing with different word problems, and you’ll get the hang of decimal operations in no time. Remember, the more you practice, the better you’ll get. Happy calculating!

by: Effortless Math Team about 10 months ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• 10 Most Common DAT Quantitative Reasoning Math Questions
• Linear, Quadratic, and Exponential Models
• What does PSAT Stand for?
• 4th Grade STAAR Math FREE Sample Practice Questions
• 6th Grade MEAP Math Worksheets: FREE & Printable
• The Ultimate 6th Grade NHSAS Math Course (+FREE Worksheets)
• How to Create a Proportion? (+FREE Worksheet!)
• Top 10 Accuplacer Math Prep Books (Our 2023 Favorite Picks)
• How to Find Complex Roots of the Quadratic Equation?
• 6th Grade SBAC Math Worksheets: FREE & Printable

What people say about "How to Perform Operations of Decimals: Word Problems - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems

Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

• Child Login
• Number Sense
• Measurement
• Pre Algebra
• Figurative Language
• Reading Comprehension
• Reading and Writing
• Science Worksheets
• Social Studies Worksheets
• Math Worksheets
• ELA Worksheets
• Online Worksheets

Browse By Grade

• Become a Member

• Kindergarten

• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even Numbers
• Prime and Composite Numbers
• Roman Numerals
• Ordinal Numbers

• Big vs Small
• Long vs Short
• Tall vs Short
• Heavy vs Light
• Full and Empty
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature

• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem and Leaf Plot
• Box and Whisker Plot
• Permutations
• Combinations

• Lines, Rays, and Line Segments
• Points, Lines, and Planes
• Transformation
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel and Perpendicular Lines
• Surface Area
• Pythagorean Theorem

• Significant Figures
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Scientific Notation
• Absolute Value

• Translating Algebraic Phrases
• Simplifying Algebraic Expressions
• Evaluating Algebraic Expressions
• Systems of Equations
• Slope of a Line
• Equation of a Line
• Quadratic Equations
• Polynomials
• Inequalities
• Determinants
• Arithmetic Sequence
• Arithmetic Series
• Geometric Sequence
• Complex Numbers
• Trigonometry

Multiplying Decimals Word Problems Worksheets

• Pre-Algebra >
• Decimals >
• Multiplication >

If children and our free, printable multiplying decimals word problems worksheets have found harmony with each other, children and a desire to excel have found harmony with each other. The promise is an inexhaustible supply of real-world problems on decimal multiplication! Make the most of the resources presenting you with umpteen real-life scenarios on multiplying decimals by whole numbers and multiplying two decimals. Read the scenarios, boil them down to the multiplicand and multiplier, and determine the product. Get ready to tackle this pdf collection!

We recommend our decimal multiplication word problems worksheets pdf for 5th grade, 6th grade, and 7th grade kids.

Multiplying Decimals by Whole Numbers Word Problems | Customary

Lucy dropped $0.67 into a charity box. If James dropped six times the money, how much did he donate? It's $4.02. These exercises, featuring decimals and whole numbers with customary units, have more such questions.

Multiplying Decimals by Whole Numbers Word Problems | Metric

Can you imagine money, measurement, and more without decimals? The answer is a resounding "No". Let grade 5 and grade 6 kids tackle word problems involving decimals, whole numbers, and metric units.

Multiplying Decimals Word Problems | Customary

Watch grade 7 learners tackle multiplying decimals with different decimal places. Show off your skills by solving these printable multiplying decimals word problems worksheets featuring customary units.

Multiplying Decimals Word Problems | Metric

The more you practice these printable worksheets, the smarter you become at figuring out problems on multiplying two decimals. Be mindful of placing the decimal point in the product. These exercises feature metric units.

Related Printable Worksheets

▶ Multiplying Decimals Using Number Lines

▶ Multiplying Decimals by Powers of Ten

▶ Multiplying Decimals by Whole Numbers

Tutoringhour

What we offer, information.

• Membership Benefits
• How to Use Online Worksheets
• How to Use Printable Worksheets
• Printing Help
• Testimonial
• Privacy Policy
• Refund Policy

Copyright © 2024 - Tutoringhour

You must be a member to unlock this feature!

Sign up now for only $29.95/year — that's just 8 cents a day!

Printable Worksheets

• 20,000+ Worksheets Across All Subjects
• Access to Answer Key
• Add Worksheets to "My Collections"
• Create Custom Workbooks

Digitally Fillable Worksheets

• 1100+ Math and ELA Worksheets
• Preview and Assign Worksheets
• Create Groups and Add Children
• Track Progress

Addition (Basic)

Addition (Multi-Digit)

Algebra & Pre-Algebra

Comparing Numbers

Daily Math Review

Division (Basic)

Division (Long Division)

Hundreds Charts

Measurement

Multiplication (Basic)

Multiplication (Multi-Digit)

Order of Operations

Place Value

Probability

Skip Counting

Subtraction

Telling Time

Word Problems (Daily)

More Math Worksheets

Reading Comprehension

Reading Comprehension Gr. 1

Reading Comprehension Gr. 2

Reading Comprehension Gr. 3

Reading Comprehension Gr. 4

Reading Comprehension Gr. 5

Reading Comprehension Gr. 6

Reading & Writing

Reading Worksheets

Cause & Effect

Fact & Opinion

Fix the Sentences

Graphic Organizers

Synonyms & Antonyms

Writing Prompts

Writing Story Pictures

Writing Worksheets

More ELA Worksheets

Consonant Sounds

Vowel Sounds

Consonant Blends

Consonant Digraphs

Word Families

More Phonics Worksheets

Early Literacy

Build Sentences

Sight Word Units

Sight Words (Individual)

More Early Literacy

Punctuation

Subjects and Predicates

More Grammar Worksheets

Spelling Lists

Spelling Grade 1

Spelling Grade 2

Spelling Grade 3

Spelling Grade 4

Spelling Grade 5

Spelling Grade 6

More Spelling Worksheets

Chapter Books

Charlotte's Web

Magic Tree House #1

Boxcar Children

More Literacy Units

Animal (Vertebrate) Groups

Butterfly Life Cycle

Electricity

Matter (Solid, Liquid, Gas)

Simple Machines

Space - Solar System

More Science Worksheets

Social Studies

Maps (Geography)

Maps (Map Skills)

More Social Studies

Mother's Day

Father's Day

More Holiday Worksheets

Puzzles & Brain Teasers

Brain Teasers

Logic:  Addition Squares

Mystery Graph Pictures

Number Detective

Lost in the USA

More Thinking Puzzles

Teacher Helpers

Teaching Tools

Award Certificates

More Teacher Helpers

Pre-K and Kindergarten

Alphabet (ABCs)

Numbers and Counting

Shapes (Basic)

More Kindergarten

Worksheet Generator

Word Search Generator

Multiple Choice Generator

Fill-in-the-Blanks Generator

More Generator Tools

Full Website Index

Dividing Decimals

The printable math worksheets on this page can be used to practice dividing decimal numbers.

Decimal Division Patterns

Logged in members can use the Super Teacher Worksheets filing cabinet to save their favorite worksheets.

Quickly access your most used files AND your custom generated worksheets!

Please login to your account or become a member and join our community today to utilize this helpful feature.

Decimals in the Dividends (Level: Basic)

Decimals in the divisors and dividends (level: basic), decimals in the divisors and dividends (level: intermediate), decimals in the divisor and dividend (level: advanced).

Practice adding and subtracting decimal numbers with these printable worksheets.

Practice solving multiplication problems with decimals as factors.

Learn to read, write, and interpret basic decimal numbers with these printable worksheets.

Sample Worksheet Images

PDF with answer key:

PDF no answer key:

Singapore math support and resources

Problem Solving – 5th Grade Dividing and Multiplying Decimals

Here’s a problem in 5 th grade that involves all of the following:

• Problem Solving
• Bar Modeling
• Dividing Decimals
• Multiplying Decimals

Rey had 5 times as much money as James at first. When Rey gave James $12.50, both of them have the same amount of money. How much money does Rey have at first?

Here’s a solution using Bar Model.

A Note on Bar Modeling

Interpreting the problem in bar model heuristic is the first step to solve this problem. Often, students misunderstand the meaning of “5 times as much money as”. Thinking that 5 times means 5 units more in the bar model, they might draw:

Instead Rey’s bar model should have 5 times the number of units:

Related Resources

For more related resources, please refer to our Bar Models page.

Leave a Comment Cancel Reply

Your email address will not be published. Required fields are marked *

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Distance Word Problems

Algebra topics  -, distance word problems, algebra topics distance word problems.

Algebra Topics: Distance Word Problems

Lesson 10: distance word problems.

/en/algebra-topics/introduction-to-word-problems/content/

What are distance word problems?

Distance word problems are a common type of algebra word problems. They involve a scenario in which you need to figure out how fast , how far , or how long one or more objects have traveled. These are often called train problems because one of the most famous types of distance problems involves finding out when two trains heading toward each other cross paths.

In this lesson, you'll learn how to solve train problems and a few other common types of distance problems. But first, let's look at some basic principles that apply to any distance problem.

The basics of distance problems

There are three basic aspects to movement and travel: distance , rate , and time . To understand the difference among these, think about the last time you drove somewhere.

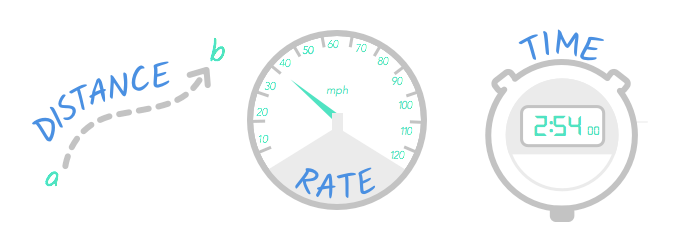
The distance is how far you traveled. The rate is how fast you traveled. The time is how long the trip took.

The relationship among these things can be described by this formula:

distance = rate x time d = rt

In other words, the distance you drove is equal to the rate at which you drove times the amount of time you drove. For an example of how this would work in real life, just imagine your last trip was like this:

• You drove 25 miles—that's the distance .
• You drove an average of 50 mph—that's the rate .
• The drive took you 30 minutes, or 0 .5 hours—that's the time .

According to the formula, if we multiply the rate and time , the product should be our distance.

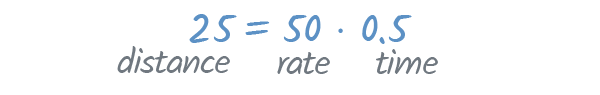
And it is! We drove 50 mph for 0.5 hours—and 50 ⋅ 0.5 equals 25 , which is our distance.

What if we drove 60 mph instead of 50? How far could we drive in 30 minutes? We could use the same formula to figure this out.

60 ⋅ 0.5 is 30, so our distance would be 30 miles.

Solving distance problems

When you solve any distance problem, you'll have to do what we just did—use the formula to find distance , rate , or time . Let's try another simple problem.

On his day off, Lee took a trip to the zoo. He drove an average speed of 65 mph, and it took him two-and-a-half hours to get from his house to the zoo. How far is the zoo from his house?

First, we should identify the information we know. Remember, we're looking for any information about distance, rate, or time. According to the problem:

• The rate is 65 mph.
• The time is two-and-a-half hours, or 2.5 hours.
• The distance is unknown—it's what we're trying to find.

You could picture Lee's trip with a diagram like this:

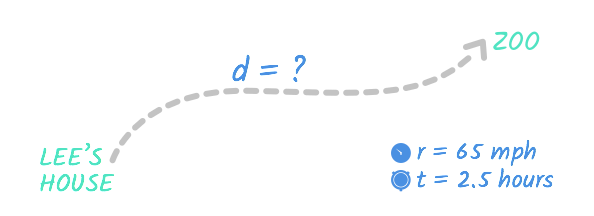
This diagram is a start to understanding this problem, but we still have to figure out what to do with the numbers for distance , rate , and time . To keep track of the information in the problem, we'll set up a table. (This might seem excessive now, but it's a good habit for even simple problems and can make solving complicated problems much easier.) Here's what our table looks like:

We can put this information into our formula: distance = rate ⋅ time .

We can use the distance = rate ⋅ time formula to find the distance Lee traveled.

The formula d = rt looks like this when we plug in the numbers from the problem. The unknown distance is represented with the variable d .

d = 65 ⋅ 2.5

To find d , all we have to do is multiply 65 and 2.5. 65 ⋅ 2.5 equals 162.5 .

We have an answer to our problem: d = 162.5. In other words, the distance Lee drove from his house to the zoo is 162.5 miles.

Be careful to use the same units of measurement for rate and time. It's possible to multiply 65 miles per hour by 2.5 hours because they use the same unit: an hour . However, what if the time had been written in a different unit, like in minutes ? In that case, you'd have to convert the time into hours so it would use the same unit as the rate.

Solving for rate and time

In the problem we just solved we calculated for distance , but you can use the d = rt formula to solve for rate and time too. For example, take a look at this problem:

After work, Janae walked in her neighborhood for a half hour. She walked a mile-and-a-half total. What was her average speed in miles per hour?

We can picture Janae's walk as something like this:

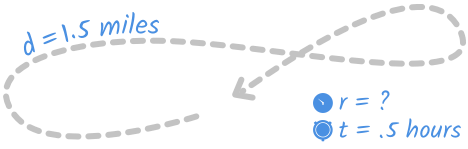
And we can set up the information from the problem we know like this:

The table is repeating the facts we already know from the problem. Janae walked one-and-a-half miles or 1.5 miles in a half hour, or 0.5 hours.

As always, we start with our formula. Next, we'll fill in the formula with the information from our table.

The rate is represented by r because we don't yet know how fast Janae was walking. Since we're solving for r , we'll have to get it alone on one side of the equation.

1.5 = r ⋅ 0.5

Our equation calls for r to be multiplied by 0.5, so we can get r alone on one side of the equation by dividing both sides by 0.5: 1.5 / 0.5 = 3 .

r = 3 , so 3 is the answer to our problem. Janae walked 3 miles per hour.

In the problems on this page, we solved for distance and rate of travel, but you can also use the travel equation to solve for time . You can even use it to solve certain problems where you're trying to figure out the distance, rate, or time of two or more moving objects. We'll look at problems like this on the next few pages.

Two-part and round-trip problems

Do you know how to solve this problem?

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, then he drove on the interstate at an average of 70 mph. The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

This problem is a classic two-part trip problem because it's asking you to find information about one part of a two-part trip. This problem might seem complicated, but don't be intimidated!

You can solve it using the same tools we used to solve the simpler problems on the first page:

• The travel equation d = rt
• A table to keep track of important information

Let's start with the table . Take another look at the problem. This time, the information relating to distance , rate , and time has been underlined.

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph , then he drove on the interstate at an average of 70 mph . The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

If you tried to fill in the table the way we did on the last page, you might have noticed a problem: There's too much information. For instance, the problem contains two rates— 30 mph and 70 mph . To include all of this information, let's create a table with an extra row. The top row of numbers and variables will be labeled in town , and the bottom row will be labeled interstate .

We filled in the rates, but what about the distance and time ? If you look back at the problem, you'll see that these are the total figures, meaning they include both the time in town and on the interstate. So the total distance is 225 . This means this is true:

Interstate distance + in-town distance = Total distance

Together, the interstate distance and in-town distance are equal to the total distance. See?

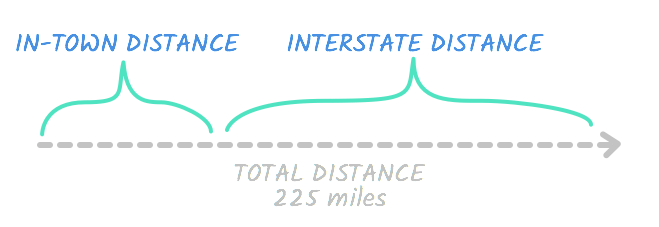
In any case, we're trying to find out how far Bill drove on the interstate , so let's represent this number with d . If the interstate distance is d , it means the in-town distance is a number that equals the total, 225 , when added to d . In other words, it's equal to 225 - d .

We can fill in our chart like this:

We can use the same technique to fill in the time column. The total time is 3.5 hours . If we say the time on the interstate is t , then the remaining time in town is equal to 3.5 - t . We can fill in the rest of our chart.

Now we can work on solving the problem. The main difference between the problems on the first page and this problem is that this problem involves two equations. Here's the one for in-town travel :

225 - d = 30 ⋅ (3.5 - t)

And here's the one for interstate travel :

If you tried to solve either of these on its own, you might have found it impossible: since each equation contains two unknown variables, they can't be solved on their own. Try for yourself. If you work either equation on its own, you won't be able to find a numerical value for d . In order to find the value of d , we'll also have to know the value of t .

We can find the value of t in both problems by combining them. Let's take another look at our travel equation for interstate travel.

While we don't know the numerical value of d , this equation does tell us that d is equal to 70 t .

Since 70 t and d are equal , we can replace d with 70 t . Substituting 70 t for d in our equation for interstate travel won't help us find the value of t —all it tells us is that 70 t is equal to itself, which we already knew.

But what about our other equation, the one for in-town travel?

When we replace the d in that equation with 70 t , the equation suddenly gets much easier to solve.

225 - 70t = 30 ⋅ (3.5 - t)

Our new equation might look more complicated, but it's actually something we can solve. This is because it only has one variable: t . Once we find t , we can use it to calculate the value of d —and find the answer to our problem.

To simplify this equation and find the value of t , we'll have to get the t alone on one side of the equals sign. We'll also have to simplify the right side as much as possible.

Let's start with the right side: 30 times (3.5 - t ) is 105 - 30 t .

225 - 70t = 105 - 30t

Next, let's cancel out the 225 next to 70 t . To do this, we'll subtract 225 from both sides. On the right side, it means subtracting 225 from 105 . 105 - 225 is -120 .

- 70t = -120 - 30t

Our next step is to group like terms—remember, our eventual goal is to have t on the left side of the equals sign and a number on the right . We'll cancel out the -30 t on the right side by adding 30 t to both sides. On the right side, we'll add it to -70 t . -70 t + 30 t is -40 t .

- 40t = -120

Finally, to get t on its own, we'll divide each side by its coefficient: -40. -120 / - 40 is 3 .

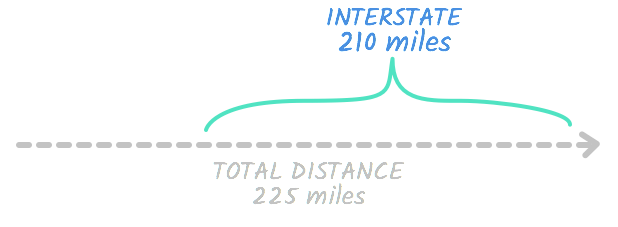
So t is equal to 3 . In other words, the time Bill traveled on the interstate is equal to 3 hours . Remember, we're ultimately trying to find the distanc e Bill traveled on the interstate. Let's look at the interstate row of our chart again and see if we have enough information to find out.

It looks like we do. Now that we're only missing one variable, we should be able to find its value pretty quickly.

To find the distance, we'll use the travel formula distance = rate ⋅ time .

We now know that Bill traveled on the interstate for 3 hours at 70 mph , so we can fill in this information.

d = 3 ⋅ 70

Finally, we finished simplifying the right side of the equation. 3 ⋅ 70 is 210 .

So d = 210 . We have the answer to our problem! The distance is 210 . In other words, Bill drove 210 miles on the interstate.

Solving a round-trip problem

It might have seemed like it took a long time to solve the first problem. The more practice you get with these problems, the quicker they'll go. Let's try a similar problem. This one is called a round-trip problem because it describes a round trip—a trip that includes a return journey. Even though the trip described in this problem is slightly different from the one in our first problem, you should be able to solve it the same way. Let's take a look:

Eva drove to work at an average speed of 36 mph. On the way home, she hit traffic and only drove an average of 27 mph. Her total time in the car was 1 hour and 45 minutes, or 1.75 hours. How far does Eva live from work?

If you're having trouble understanding this problem, you might want to visualize Eva's commute like this:

As always, let's start by filling in a table with the important information. We'll make a row with information about her trip to work and from work .

1.75 - t to describe the trip from work. (Remember, the total travel time is 1.75 hours , so the time to work and from work should equal 1.75 .)

From our table, we can write two equations:

• The trip to work can be represented as d = 36 t .
• The trip from work can be represented as d = 27 (1.75 - t ) .

In both equations, d represents the total distance. From the diagram, you can see that these two equations are equal to each other—after all, Eva drives the same distance to and from work .

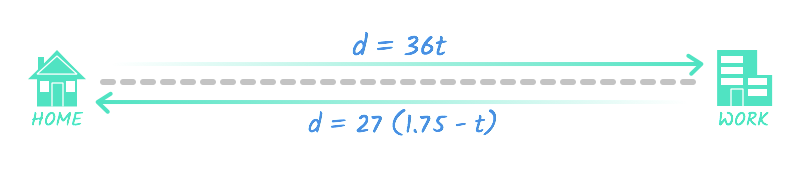
Just like with the last problem we solved, we can solve this one by combining the two equations.

We'll start with our equation for the trip from work .

d = 27 (1.75 - t)

Next, we'll substitute in the value of d from our to work equation, d = 36 t . Since the value of d is 36 t , we can replace any occurrence of d with 36 t .

36t = 27 (1.75 - t)

Now, let's simplify the right side. 27 ⋅(1.75 - t ) is 47.25 .

36t = 47.25 - 27t

Next, we'll cancel out -27 t by adding 27 t to both sides of the equation. 36 t + 27 t is 63 t .

63t = 47.25

Finally, we can get t on its own by dividing both sides by its coefficient: 63 . 47.25 / 63 is .75 .

t is equal to .75 . In other words, the time it took Eva to drive to work is .75 hours . Now that we know the value of t , we'll be able to can find the distance to Eva's work.

If you guessed that we were going to use the travel equation again, you were right. We now know the value of two out of the three variables, which means we know enough to solve our problem.

First, let's fill in the values we know. We'll work with the numbers for the trip to work . We already knew the rate : 36 . And we just learned the time : .75 .

d = 36 ⋅ .75

Now all we have to do is simplify the equation: 36 ⋅ .75 = 27 .

d is equal to 27 . In other words, the distance to Eva's work is 27 miles . Our problem is solved.

Intersecting distance problems

An intersecting distance problem is one where two things are moving toward each other. Here's a typical problem:

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading to Springfield at the same time a train leaves Springfield heading to Pawnee. One train is moving at a speed of 45 mph, and the other is moving 60 mph. How long will they travel before they meet?

This problem is asking you to calculate how long it will take these two trains moving toward each other to cross paths. This might seem confusing at first. Even though it's a real-world situation, it can be difficult to imagine distance and motion abstractly. This diagram might help you get a sense of what this situation looks like:

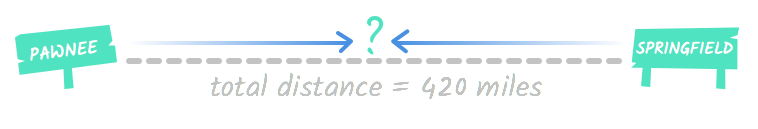
If you're still confused, don't worry! You can solve this problem the same way you solved the two-part problems on the last page. You'll just need a chart and the travel formula .

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading toward Springfield at the same time a train leaves Springfield heading toward Pawnee. One train is moving at a speed of 45 mph , and the other is moving 60 mph . How long will they travel before they meet?

Let's start by filling in our chart. Here's the problem again, this time with the important information underlined. We can start by filling in the most obvious information: rate . The problem gives us the speed of each train. We'll label them fast train and slow train . The fast train goes 60 mph . The slow train goes only 45 mph .

We can also put this information into a table:

We don't know the distance each train travels to meet the other yet—we just know the total distance. In order to meet, the trains will cover a combined distance equal to the total distance. As you can see in this diagram, this is true no matter how far each train travels.

This means that—just like last time—we'll represent the distance of one with d and the distance of the other with the total minus d. So the distance for the fast train will be d , and the distance for the slow train will be 420 - d .

Because we're looking for the time both trains travel before they meet, the time will be the same for both trains. We can represent it with t .

The table gives us two equations: d = 60 t and 420 - d = 45 t . Just like we did with the two-part problems, we can combine these two equations.

The equation for the fast train isn't solvable on its own, but it does tell us that d is equal to 60 t .

The other equation, which describes the slow train, can't be solved alone either. However, we can replace the d with its value from the first equation.

420 - d = 45t

Because we know that d is equal to 60 t , we can replace the d in this equation with 60 t . Now we have an equation we can solve.

420 - 60t = 45t

To solve this equation, we'll need to get t and its coefficients on one side of the equals sign and any other numbers on the other. We can start by canceling out the -60 t on the left by adding 60 t to both sides. 45 t + 60 t is 105 t .

Now we just need to get rid of the coefficient next to t . We can do this by dividing both sides by 105 . 420 / 105 is 4 .

t = 4 . In other words, the time it takes the trains to meet is 4 hours . Our problem is solved!

If you want to be sure of your answer, you can check it by using the distance equation with t equal to 4 . For our fast train, the equation would be d = 60 ⋅ 4 . 60 ⋅ 4 is 240 , so the distance our fast train traveled would be 240 miles. For our slow train, the equation would be d = 45 ⋅ 4 . 45 ⋅ 4 is 180 , so the distance traveled by the slow train is 180 miles . Remember how we said the distance the slow train and fast train travel should equal the total distance? 240 miles + 180 miles equals 420 miles , which is the total distance from our problem. Our answer is correct.

Practice problem 1

Here's another intersecting distance problem. It's similar to the one we just solved. See if you can solve it on your own. When you're finished, scroll down to see the answer and an explanation.

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove an average of 70 mph. How long did they drive before they met up?

Problem 1 answer

Here's practice problem 1:

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove 70 mph. How long did they drive before they met up?

Answer: 2 hours .

Let's solve this problem like we solved the others. First, try making the chart. It should look like this:

Here's how we filled in the chart:

• Distance: Together, Dani and Jon will have covered the total distance between them by the time they meet up. That's 270 . Jon's distance is represented by d , so Dani's distance is 270 - d .
• Rate: The problem tells us Dani and Jon's speeds. Dani drives 65 mph , and Jon drives 70 mph .
• Time: Because Jon and Dani drive the same amount of time before they meet up, both of their travel times are represented by t .

Now we have two equations. The equation for Jon's travel is d = 65 t . The equation for Dani's travel is 270 - d = 70 t . To solve this problem, we'll need to combine them.

The equation for Jon tells us that d is equal to 65 t . This means we can combine the two equations by replacing the d in Dani's equation with 65 t .

270 - 65t = 70t

Let's get t on one side of the equation and a number on the other. The first step to doing this is to get rid of -65 t on the left side. We'll cancel it out by adding 65 t to both sides: 70 t + 65 t is 135 t .

All that's left to do is to get rid of the 135 next to the t . We can do this by dividing both sides by 135 : 270 / 135 is 2 .

That's it. t is equal to 2 . We have the answer to our problem: Dani and Jon drove 2 hours before they met up.

Overtaking distance problems

The final type of distance problem we'll discuss in this lesson is a problem in which one moving object overtakes —or passes —another. Here's a typical overtaking problem:

The Hill family and the Platter family are going on a road trip. The Hills left 3 hours before the Platters, but the Platters drive an average of 15 mph faster. If it takes the Platter family 13 hours to catch up with the Hill family, how fast are the Hills driving?

You can picture the moment the Platter family left for the road trip a little like this:

The problem tells us that the Platter family will catch up with the Hill family in 13 hours and asks us to use this information to find the Hill family's rate . Like some of the other problems we've solved in this lesson, it might not seem like we have enough information to solve this problem—but we do. Let's start making our chart. The distance can be d for both the Hills and the Platters—when the Platters catch up with the Hills, both families will have driven the exact same distance.

Filling in the rate and time will require a little more thought. We don't know the rate for either family—remember, that's what we're trying to find out. However, we do know that the Platters drove 15 mph faster than the Hills. This means if the Hill family's rate is r , the Platter family's rate would be r + 15 .

Now all that's left is the time. We know it took the Platters 13 hours to catch up with the Hills. However, remember that the Hills left 3 hours earlier than the Platters—which means when the Platters caught up, they'd been driving 3 hours more than the Platters. 13 + 3 is 16 , so we know the Hills had been driving 16 hours by the time the Platters caught up with them.

Our chart gives us two equations. The Hill family's trip can be described by d = r ⋅ 16 . The equation for the Platter family's trip is d = ( r + 15) ⋅ 13 . Just like with our other problems, we can combine these equations by replacing a variable in one of them.

The Hill family equation already has the value of d equal to r ⋅ 16. So we'll replace the d in the Platter equation with r ⋅ 16 . This way, it will be an equation we can solve.

r ⋅ 16 = (r + 15) ⋅ 13

First, let's simplify the right side: r ⋅ 16 is 16 r .

16r = (r + 15) ⋅ 13

Next, we'll simplify the right side and multiply ( r + 15) by 13 .

16r = 13r + 195

We can get both r and their coefficients on the left side by subtracting 13 r from 16 r : 16 r - 13 r is 3 r .

Now all that's left to do is get rid of the 3 next to the r . To do this, we'll divide both sides by 3: 195 / 3 is 65 .

So there's our answer: r = 65. The Hill family drove an average of 65 mph .

You can solve any overtaking problem the same way we solved this one. Just remember to pay special attention when you're setting up your chart. Just like the Hill family did in this problem, the person or vehicle who started moving first will always have a greater travel time.

Practice problem 2

Try solving this problem. It's similar to the problem we just solved. When you're finished, scroll down to see the answer and an explanation.

A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?

Problem 2 answer

Here's practice problem 2:

Answer: 4 p.m.

To solve this problem, start by making a chart. Here's how it should look:

Here's an explanation of the chart:

• Distance: Both trains will have traveled the same distance by the time the fast train catches up with the slow one, so the distance for both is d .
• Rate: The problem tells us how fast each train was going. The fast train has a rate of 80 mph , and the slow train has a rate of 60 mph .
• Time: We'll use t to represent the fast train's travel time before it catches up. Because the slow train started an hour before the fast one, it will have been traveling one hour more by the time the fast train catches up. It's t + 1 .

Now we have two equations. The equation for the fast train is d = 80 t . The equation for the slow train is d = 60 ( t + 1) . To solve this problem, we'll need to combine the equations.

The equation for the fast train says d is equal to 80 t . This means we can combine the two equations by replacing the d in the slow train's equation with 80 t .

80t = 60 (t + 1)

First, let's simplify the right side of the equation: 60 ⋅ ( t + 1) is 60 t + 60 .

80t = 60t + 60

To solve the equation, we'll have to get t on one side of the equals sign and a number on the other. We can get rid of 60 t on the right side by subtracting 60 t from both sides: 80 t - 60 t is 20 t .

Finally, we can get rid of the 20 next to t by dividing both sides by 20 . 60 divided by 20 is 3 .

So t is equal to 3 . The fast train traveled for 3 hours . However, it's not the answer to our problem. Let's look at the original problem again. Pay attention to the last sentence, which is the question we're trying to answer.

Our problem doesn't ask how long either of the trains traveled. It asks what time the second train catches up with the first.

The problem tells us that the slow train left at noon and the fast one left an hour later. This means the fast train left at 1 p.m . From our equations, we know the fast train traveled 3 hours . 1 + 3 is 4 , so the fast train caught up with the slow one at 4 p.m . The answer to the problem is 4 p.m .

/en/algebra-topics/algebra-quiz/content/

Long Multiplication Calculator

How do you multiply decimals, how to do long multiplication, long multiplication with decimals, how to multiply big numbers multiplication algorithm in practice, how (and when) to use the long multiplication calculator.

Welcome to the long multiplication calculator – a great tool that helps you solve multiplication yourself. If you ever asked yourself: How do you multiply decimals? or How to multiply big numbers? , here is the right place to find the answer.

Knowledge of the basic multiplication algorithm makes it possible to deal with more complex problems like multiplying fractions or matrices. Furthermore, if you learn how to do long multiplication and also practice with long division calculator , it will make math exercises with operations on numbers as simple as never before!

If you'd like to try an alternative approach to multiplying large numbers, check out Omni's partial products calculator !

Let's begin from the basics – multiplication is a compact way of writing the addition of repeating numbers. If we want to solve a problem like 6×2 , it would be the same as if we have to add 2 six times, 2+2+2+2+2+2 . In that meaning, multiplication is extremely useful, especially for big numbers.

Mathematicians call the first number in the multiplication the multiplier and the second one the multiplicand . The result of the multiplication is the product .

💡 Multiplication is commutative . It means that we can change the multiplier and multiplicand places , and the outcome wouldn't change.

From the beginning of our education, we all learn how to multiply numbers from one to ten – most pupils' nightmare, isn't it? But, actually, it's all you need to know about how to multiply big numbers or how long multiplication with decimals works!

So, how do you multiply decimals? In short, forget about the decimal dot and perform the multiplication with whole numbers. Next, add up the decimal places in the multiplier and the multiplicand . The sum is the number of decimal places in the product. We describe the whole process in detail in the dedicated section below .

We can describe the long multiplication algorithm in a few steps:

• Set both numbers one under the other and align them to the right so that the first significant digits are the first ones from the right.

🙋 It's a good practice to set the longer number as the multiplier and the shorter one as the multiplicand. It doesn't change the product, but it does reduce the number of steps .

Start multiplying the multiplier by the first digit (from the right) of the multiplicand, digit by digit. Anytime you finish with a number larger than 9, write down the digit of ones and carry the digit of tens to the next step (e.g. 7×5=35 , so write 5 and carry 3 ).

Repeat for the rest of the digits of the multiplier. Whenever you carry a number, add it to the product (e.g. 1×5 and 3 carried from the previous step gives us 8 ).

When you finish with the first digit of the multiplicand, you obtain a first intermediate product .

Repeat the same procedure for the rest of the digits from the multiplicand, each time starting one place further from the right (as you multiply by tens, hundreds, and so on). You can also write trailing zeros if you like.

🙋 If you face any 0 digits in the multiplicand, you can skip the step , as the product of zero and any other number is always zero.

When you're done with all of the intermediate products, add them up .

The result is your final product. Now you know how to do long multiplication!

Let's step up to the next level and find out how to multiply decimals using the long multiplication method. As for an example, let's multiply 4.37 by 8.5 . It turns out that we can treat it as a 3- and 2-digit multiplication problem. To get the answer, we can follow these steps:

Count the number of decimal digits in both numbers . There are two decimals in the first one and a single decimal in the second one.

The sum of decimal digits in the multiplier and the multiplicand is three ( 2+1 ). We will have three decimals in the product as well.

At this point, we can forget about decimal dots and perform the multiplication 437 × 85 .

The product of 437 and 5 is 2185 .

The product of 437 and 8 is 3496 . Remember to start writing it one place further from the right. Alternatively, you can add one 0 at the end, so the product becomes 34960 , and both numbers are right-aligned then.

Evaluate the sum of these two intermediate products. 2185 + 34960 = 37145 .

Finally, apply the decimal dot in the product . We know there should be three decimal digits , so our outcome equals 37.145 .

If you have any doubts, get lost at some point, or simply want to check the answer, you can always use our long multiplication calculator!

The good thing about long multiplication is that it doesn't make a problem significantly more difficult for larger numbers. What matters is the length of the numbers rather than the values themselves. Moreover, it may be even simpler to multiply big numbers if any of them (or both) ends with several trailing zeros. Why?

We can simply skip trailing zeros for multiplication , as any intermediate products would equal zero. We can add trailing zeros from both the multiplier and the multiplicand and write them next to the product . The procedure is very similar to the one with decimals.

Let's apply the long multiplication algorithm for two big numbers, let's say 34000 and 2870 :

Count the number of trailing zeros in both cases . There are three of them in the first number and a single zero in the second one.

Now, our new values are 34 and 287 , respectively. Note that in this case, the first number is shorter than the second one (in contrast to the initial numbers). We can swap them and work out the multiplication 287 times 34 .

The first intermediate product is 1148 , and the second one is 861 (remember about shifting this number one digit to the left). Summing them up, we receive 9758 .

That's the right time to apply missing trailing zeros to the product . We have four of them in total.

The final result of long multiplication is 97,580,000 . We can even write it as 9.758×10⁷ using scientific notation.

Have you ever tried to add or subtract fractions? If so, you're probably familiar with the concept of finding the least common denominator. Simply speaking, it's all about finding the least common multiple of two (or multiple) numbers. The process involves a certain skill in multiplication. This situation is where our long multiplication calculator becomes handy, especially for fractions containing decimals or big numbers.

The good thing is that our tool is pretty straightforward to use. As you already know how to do long multiplication with decimals by hand from previous sections, let's see how to do the same using the long multiplication calculator:

Type the first number as the multiplier, e.g., 0.00367 .

Input the second number as the multiplicand, e.g., 449300 .

And that's all! As a result, you receive an answer, which is 1648.931 . Additionally, you also get explanations and hints on how to deal with multiplying big numbers and decimals.

If you like this long multiplication calculator, make sure to check our distributive property calculator as well!

BMR - Harris-Benedict equation

Helium balloons.

• Biology (100)
• Chemistry (100)
• Construction (144)
• Conversion (295)
• Ecology (30)
• Everyday life (262)
• Finance (570)
• Health (440)
• Physics (510)
• Sports (105)
• Statistics (183)
• Other (182)
• Discover Omni (40)

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 8: Multiply decimals

About this unit.

When it comes to multiplying decimals, there's more than one way to get the job done. Explore different strategies in this unit and find the one that works best for you. From estimation, to area models, to grids, one of these is bound to help you master decimals multiplication.

Multiplying decimals and whole numbers

• Estimating with multiplying decimals and whole numbers (Opens a modal)
• Multiplying decimals and whole numbers with visuals (Opens a modal)
• Strategies for multiplying decimals and whole numbers (Opens a modal)
• Strategies for multiplying multi-digit decimals by whole numbers (Opens a modal)
• Estimating with multiplying decimals and whole numbers Get 3 of 4 questions to level up!
• Multiply decimals and whole numbers visually Get 5 of 7 questions to level up!
• Multiply whole numbers by 0.1 and 0.01 Get 3 of 4 questions to level up!
• Multiply whole numbers and decimals less than 1 Get 3 of 4 questions to level up!
• Multiply whole numbers and decimals Get 3 of 4 questions to level up!

Multiplying decimals strategies

• Estimating decimal multiplication (Opens a modal)
• Developing strategies for multiplying decimals (Opens a modal)
• Decimal multiplication with grids (Opens a modal)
• Understanding decimal multiplication (Opens a modal)
• Multiplying decimals using estimation (Opens a modal)
• Estimating with multiplying decimals Get 3 of 4 questions to level up!
• Represent decimal multiplication with grids and area models Get 3 of 4 questions to level up!
• Understand multiplying decimals Get 3 of 4 questions to level up!

Multiplying decimals

• Developing strategies for multiplying 2-digit decimals (Opens a modal)
• Multiplying decimals (no standard algorithm) (Opens a modal)
• Multiply decimals: FAQ (Opens a modal)
• Multiply decimals tenths Get 5 of 7 questions to level up!
• Multiply decimals (1&2-digit factors) Get 3 of 4 questions to level up!
• Multiply decimals (up to 4-digit factors) Get 3 of 4 questions to level up!

Sciencing_Icons_Science SCIENCE

Sciencing_icons_biology biology, sciencing_icons_cells cells, sciencing_icons_molecular molecular, sciencing_icons_microorganisms microorganisms, sciencing_icons_genetics genetics, sciencing_icons_human body human body, sciencing_icons_ecology ecology, sciencing_icons_chemistry chemistry, sciencing_icons_atomic & molecular structure atomic & molecular structure, sciencing_icons_bonds bonds, sciencing_icons_reactions reactions, sciencing_icons_stoichiometry stoichiometry, sciencing_icons_solutions solutions, sciencing_icons_acids & bases acids & bases, sciencing_icons_thermodynamics thermodynamics, sciencing_icons_organic chemistry organic chemistry, sciencing_icons_physics physics, sciencing_icons_fundamentals-physics fundamentals, sciencing_icons_electronics electronics, sciencing_icons_waves waves, sciencing_icons_energy energy, sciencing_icons_fluid fluid, sciencing_icons_astronomy astronomy, sciencing_icons_geology geology, sciencing_icons_fundamentals-geology fundamentals, sciencing_icons_minerals & rocks minerals & rocks, sciencing_icons_earth scructure earth structure, sciencing_icons_fossils fossils, sciencing_icons_natural disasters natural disasters, sciencing_icons_nature nature, sciencing_icons_ecosystems ecosystems, sciencing_icons_environment environment, sciencing_icons_insects insects, sciencing_icons_plants & mushrooms plants & mushrooms, sciencing_icons_animals animals, sciencing_icons_math math, sciencing_icons_arithmetic arithmetic, sciencing_icons_addition & subtraction addition & subtraction, sciencing_icons_multiplication & division multiplication & division, sciencing_icons_decimals decimals, sciencing_icons_fractions fractions, sciencing_icons_conversions conversions, sciencing_icons_algebra algebra, sciencing_icons_working with units working with units, sciencing_icons_equations & expressions equations & expressions, sciencing_icons_ratios & proportions ratios & proportions, sciencing_icons_inequalities inequalities, sciencing_icons_exponents & logarithms exponents & logarithms, sciencing_icons_factorization factorization, sciencing_icons_functions functions, sciencing_icons_linear equations linear equations, sciencing_icons_graphs graphs, sciencing_icons_quadratics quadratics, sciencing_icons_polynomials polynomials, sciencing_icons_geometry geometry, sciencing_icons_fundamentals-geometry fundamentals, sciencing_icons_cartesian cartesian, sciencing_icons_circles circles, sciencing_icons_solids solids, sciencing_icons_trigonometry trigonometry, sciencing_icons_probability-statistics probability & statistics, sciencing_icons_mean-median-mode mean/median/mode, sciencing_icons_independent-dependent variables independent/dependent variables, sciencing_icons_deviation deviation, sciencing_icons_correlation correlation, sciencing_icons_sampling sampling, sciencing_icons_distributions distributions, sciencing_icons_probability probability, sciencing_icons_calculus calculus, sciencing_icons_differentiation-integration differentiation/integration, sciencing_icons_application application, sciencing_icons_projects projects, sciencing_icons_news news.

• Share Tweet Email Print
• Home ⋅
• Science ⋅
• Nature ⋅

What Kinds of Plants & Animals Live in the Region of Moscow, Russia?

Bernie's Got a Green New Deal – Here's What's In It

Moscow, the capital of Russia, is also the nation's most populous city. However, simply because it's an urban center with a large population does not mean that the city and the immediate area are devoid of nature and wildlife. The Moscow region is in a mixed forest area, which means that it is rich in flora and fauna, especially as one moves away from the densest areas of the city and into the suburbs and rural areas surrounding the capital.

Area Vegetation

Moscow's position in the center of the country means that it lies between ecosystems that exist in Russia's north and south. The city and its surrounding region fall into a band of mixed forest approximately 500 kilometers wide. This means that broad-leaf birch and other warmer-weather, deciduous trees mix with the vegetation of the taiga, including the northern pine, fir, and spruce trees, which dominate in the north until the barren tundra. Willows and larch trees also grow in abundance around Moscow.

Regional Wildlife

Like any large city, the center of Moscow does not have many large animals, but the Elk Island National Nature Park sits just on the boundary of the city and its northwestern suburbs, meaning that wildlife thrives close to the capital. More than 200 animal species make their home in the park, including wild boar, dappled and roe deer and elk, along with beavers and otters that live in the area's waterways. Area birds include partridges, pheasants and egrets.

The park's Alexeev Copse is also home to 200-year-old pine trees and spruce trees as old as 170 years. Eighty-five percent of the area is forested.

Environmental Issues

Moscow's plants and animals depend on a healthy environment. Naturally, given Moscow's status as a political and economic powerhouse, the city's population is growing, which means a larger population pushing into the surrounding areas and greater industrial activity, both of which can have a negative effect on the environment and the species that live within it. However, the government is making efforts to protect its natural resources. Approximately 17,700 hectares of Moscow territory enjoy special protection, and the city hopes to increase that amount to 24,800 hectares, or a full 20% of its total area, by the year 2020.

Increasing public awareness and corporate responsibility, including greener technologies, are encouraging signs as well. Still, decreasing government regulation is a concern, while growing demand for land and natural resources mean that the future of Moscow's natural habitats and flora and fauna continue to be in question.

Related Articles

Landforms near chicago, how to find the radius of a sector, climate in the regions of kentucky, sierra nevada mountain facts for kids, about the four natural regions of texas, facts on the atlantic coastal plains, list of natural resources in vermont, ecosystems in missouri, facts on colorado state for kids, how to calculate average revenue, how to calculate a population density, how to get the percentage of an area, how to calculate the grand mean, animals in the mediterranean forest, native plants & animals of france, how to calculate percent relative range, the impact of natural disasters, how to report z-score results, what countries are in the polar zone.

• Russian Flora & Fauna
• Central Russia: Moscow Region
• Elk Island National Nature Park

About the Author

Terry Mann has worked as a professional journalist for the last five years. Her work as appeared online and in print, in such publications as "The Philadelphia Inquirer" and "The Wall Street Journal."

Photo Credits

Moscow image by Alexander Sinitsyn from Fotolia.com

Find Your Next Great Science Fair Project! GO