how to write hypothesis for goodness of fit

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

2.4 - goodness-of-fit test.

A goodness-of-fit test, in general, refers to measuring how well do the observed data correspond to the fitted (assumed) model. We will use this concept throughout the course as a way of checking the model fit. Like in linear regression, in essence, the goodness-of-fit test compares the observed values to the expected (fitted or predicted) values.

A goodness-of-fit statistic tests the following hypothesis:

\(H_0\colon\) the model \(M_0\) fits

\(H_A\colon\) the model \(M_0\) does not fit (or, some other model \(M_A\) fits)

Most often the observed data represent the fit of the saturated model, the most complex model possible with the given data. Thus, most often the alternative hypothesis \(\left(H_A\right)\) will represent the saturated model \(M_A\) which fits perfectly because each observation has a separate parameter. Later in the course, we will see that \(M_A\) could be a model other than the saturated one. Let us now consider the simplest example of the goodness-of-fit test with categorical data.

In the setting for one-way tables, we measure how well an observed variable X corresponds to a \(Mult\left(n, \pi\right)\) model for some vector of cell probabilities, \(\pi\). We will consider two cases:

• when vector \(\pi\) is known, and
• when vector \(\pi\) is unknown.

In other words, we assume that under the null hypothesis data come from a \(Mult\left(n, \pi\right)\) distribution, and we test whether that model fits against the fit of the saturated model. The rationale behind any model fitting is the assumption that a complex mechanism of data generation may be represented by a simpler model. The goodness-of-fit test is applied to corroborate our assumption.

Consider our dice example from Lesson 1. We want to test the hypothesis that there is an equal probability of six faces by comparing the observed frequencies to those expected under the assumed model: \(X \sim Multi(n = 30, \pi_0)\), where \(\pi_0=(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)\). We can think of this as simultaneously testing that the probability in each cell is being equal or not to a specified value:

\(H_0:\pi =\pi_0\)

where the alternative hypothesis is that any of these elements differ from the null value. There are two statistics available for this test.

Test Statistics Section  

Pearson goodness-of-fit test statistic.

The Pearson goodness-of-fit statistic is

\(X^2=\sum\limits_{j=1}^k \dfrac{(X_j-n\pi_{0j})^2}{n\pi_{0j}}\)

An easy way to remember it is

\(X^2=\sum\limits_{j=1}^k \dfrac{(O_j-E_j)^2}{E_j}\)

where \(O_j = X_j\) is the observed count in cell \(j\), and \(E_j=E(X_j)=n\pi_{0j}\) is the expected count in cell \(j\) under the assumption that null hypothesis is true.

Deviance Test Statistic

The deviance statistic is

\(G^2=2\sum\limits_{j=1}^k X_j \log\left(\dfrac{X_j}{n\pi_{0j}}\right) =2\sum\limits_j O_j \log\left(\dfrac{O_j}{E_j}\right)\)

In some texts, \(G^2\) is also called the likelihood-ratio test (LRT) statistic, for comparing the loglikelihoods \(L_0\) and \(L_1\) of two models under \(H_0\) (reduced model) and \(H_A\) (full model), respectively:

Likelihood-ratio Test Statistic

\(G^2 = -2\log\left(\dfrac{\ell_0}{\ell_1}\right) = -2\left(L_0 - L_1\right)\)

Note that \(X^2\) and \(G^2\) are both functions of the observed data \(X\) and a vector of probabilities \(\pi_0\). For this reason, we will sometimes write them as \(X^2\left(x, \pi_0\right)\) and \(G^2\left(x, \pi_0\right)\), respectively; when there is no ambiguity, however, we will simply use \(X^2\) and \(G^2\). We will be dealing with these statistics throughout the course in the analysis of 2-way and \(k\)-way tables and when assessing the fit of log-linear and logistic regression models.

Testing the Goodness-of-Fit Section  

\(X^2\) and \(G^2\) both measure how closely the model, in this case \(Mult\left(n,\pi_0\right)\) "fits" the observed data. And both have an approximate chi-square distribution with \(k-1\) degrees of freedom when \(H_0\) is true. This allows us to use the chi-square distribution to find critical values and \(p\)-values for establishing statistical significance.

• If the sample proportions \(\hat{\pi}_j\) (i.e., saturated model) are exactly equal to the model's \(\pi_{0j}\) for cells \(j = 1, 2, \dots, k,\) then \(O_j = E_j\) for all \(j\), and both \(X^2\) and \(G^2\) will be zero. That is, the model fits perfectly.
• If the sample proportions \(\hat{\pi}_j\) deviate from the \(\pi_{0j}\)s, then \(X^2\) and \(G^2\) are both positive. Large values of \(X^2\) and \(G^2\) mean that the data do not agree well with the assumed/proposed model \(M_0\).

Example: Dice Rolls Section  

Suppose that we roll a die 30 times and observe the following table showing the number of times each face ends up on top.

We want to test the null hypothesis that the die is fair. Under this hypothesis, \(X \sim Mult\left(n = 30, \pi_0\right)\) where \(\pi_{0j} = 1/6\), for \(j=1,\ldots,6\). This is our assumed model, and under this \(H_0\), the expected counts are \(E_j = 30/6= 5\) for each cell. We now have what we need to calculate the goodness-of-fit statistics:

\begin{eqnarray*} X^2 &= & \dfrac{(3-5)^2}{5}+\dfrac{(7-5)^2}{5}+\dfrac{(5-5)^2}{5}\\ & & +\dfrac{(10-5)^2}{5}+\dfrac{(2-5)^2}{5}+\dfrac{(3-5)^2}{5}\\ &=& 9.2 \end{eqnarray*}

\begin{eqnarray*} G^2 &=& 2\left(3\text{log}\dfrac{3}{5}+7\text{log}\dfrac{7}{5}+5\text{log}\dfrac{5}{5}\right.\\ & & \left.+ 10\text{log}\dfrac{10}{5}+2\text{log}\dfrac{2}{5}+3\text{log}\dfrac{3}{5}\right)\\ &=& 8.8 \end{eqnarray*}

Note that even though both have the same approximate chi-square distribution, the realized numerical values of \(Χ^2\) and \(G^2\) can be different. The \(p\)-values are \(P\left(\chi^{2}_{5} \ge 9.2\right) = .10\) and \(P\left(\chi^{2}_{5} \ge 8.8\right) = .12\). Given these \(p\)-values, with the significance level of \(\alpha=0.05\), we fail to reject the null hypothesis. But rather than concluding that \(H_0\) is true, we simply don't have enough evidence to conclude it's false. That is, the fair-die model doesn't fit the data exactly, but the fit isn't bad enough to conclude that the die is unfair, given our significance threshold of 0.05.

Next, we show how to do this in SAS and R.

The following SAS code will perform the goodness-of-fit test for the example above.

The FREQ Procedure

Sample Size = 30

Notice that this SAS code only computes the Pearson chi-square statistic and not the deviance statistic.

-->  Stop and Think!

Can you identify the relevant statistics and the \(p\)-value in the output? What does the column labeled "Percent" represent?

The following R code, dice_rolls.R will perform the same analysis as in SAS. The output will be saved into two files, dice_rolls.out and dice_rolls_Results.

Can you identify the relevant statistics and the \(p\)-value in the output? What does the column labeled "Percentage" in dice_rolls.out represent?

Example: Tomato Phenotypes Section  

Tall cut-leaf tomatoes were crossed with dwarf potato-leaf tomatoes, and n = 1611 offspring were classified by their phenotypes.

Genetic theory says that the four phenotypes should occur with relative frequencies 9 : 3 : 3 : 1, and thus are not all equally as likely to be observed. The dwarf potato-leaf is less likely to observed than the others. Do the observed data support this theory?

Under the null hypothesis, the probabilities are

\(\pi_1 = 9/16 , \pi_2 = \pi_3 = 3/16 , \pi_4 = 1/16\)

and the expected frequencies are

\(E_1 = 1611(9/16) = 906.2, E_2 = E_3 = 1611(3/16) = 302.1,\text{ and }E_4 = 1611(1/16) = 100.7\).

We calculate the fit statistics and find that \(X^2 = 1.47\) and \(G^2 = 1.48\), which are nearly identical. The \(p\)-values based on the \(\chi^2\) distribution with 3 degrees of freedom are approximately equal to 0.69. Therefore, we fail to reject the null hypothesis and accept (by default) that the data are consistent with the genetic theory.

Here is the above analysis done in SAS.

The SAS System

Sample Size = 1611

Here is how to do the computations in R using the following code :

This has step-by-step calculations and also uses chisq.test() to produce output with Pearson and deviance residuals.

Do you recall what the residuals are from linear regression? How would you define them in this context? What do they tell you about the tomato example?

Module 11: The Chi Square Distribution

Goodness-of-fit test, learning outcomes.

• Conduct and interpret chi-square goodness-of-fit hypothesis tests

In this type of hypothesis test, you determine whether the data “fit” a particular distribution or not. For example, you may suspect your unknown data fit a binomial distribution. You use a chi-square test (meaning the distribution for the hypothesis test is chi-square) to determine if there is a fit or not. The null and the alternative hypotheses for this test may be written in sentences or may be stated as equations or inequalities.

The test statistic for a goodness-of-fit test is: [latex]\displaystyle{\sum_{k}}\frac{{({O}-{E})}^{{2}}}{{E}}[/latex]

• O = observed values (data)
• E = expected values (from theory)
• k = the number of different data cells or categories

The observed values are the data values and the expected values are the values you would expect to get if the null hypothesis were true. There are  n terms of the form [latex]\displaystyle\frac{{({O}-{E})}^{{2}}}{{E}}[/latex].

The number of degrees of freedom is  df = (number of categories – 1).

The goodness-of-fit test is almost always right-tailed. If the observed values and the corresponding expected values are not close to each other, then the test statistic can get very large and will be way out in the right tail of the chi-square curve.

Note:  The expected value for each cell needs to be at least five in order for you to use this test.

Absenteeism of college students from math classes is a major concern to math instructors because missing class appears to increase the drop rate. Suppose that a study was done to determine if the actual student absenteeism rate follows faculty perception. The faculty expected that a group of 100 students would miss class according to this table.

A random survey across all mathematics courses was then done to determine the actual number  (observed) of absences in a course. The chart in this table displays the results of that survey.

Determine the null and alternative hypotheses needed to conduct a goodness-of-fit test.

H 0 : Student absenteeism fits faculty perception.

The alternative hypothesis is the opposite of the null hypothesis.

H a : Student absenteeism does not fit faculty perception.

• Can you use the information as it appears in the charts to conduct the goodness-of-fit test?
• What is the number of degrees of freedom ( df )?
• There are four “cells” or categories in each of the new tables. df = number of cells – 1 = 4 – 1 = 3

A factory manager needs to understand how many products are defective versus how many are produced. The number of expected defects is listed in the table.

A random sample was taken to determine the actual number of defects. This table shows the results of the survey.

State the null and alternative hypotheses needed to conduct a goodness-of-fit test, and state the degrees of freedom.

H 0 : The number of defaults fits expectations.

H a : The number of defaults does not fit expectations.

Employers want to know which days of the week employees are absent in a five-day work week. Most employers would like to believe that employees are absent equally during the week. Suppose a random sample of 60 managers were asked on which day of the week they had the highest number of employee absences. The results were distributed as in the table below. For the population of employees, do the days for the highest number of absences occur with equal frequencies during a five-day work week? Test at a 5% significance level.

Day of the Week Employees were Most Absent

The null and alternative hypotheses are:

• H 0 : The absent days occur with equal frequencies, that is, they fit a uniform distribution.
• H a : The absent days occur with unequal frequencies, that is, they do not fit a uniform distribution.

If the absent days occur with equal frequencies, then, out of 60 absent days (the total in the sample: 15 + 12 + 9 + 9 + 15 = 60), there would be 12 absences on Monday, 12 on Tuesday, 12 on Wednesday, 12 on Thursday, and 12 on Friday. These numbers are the expected ( E ) values. The values in the table are the observed ( O ) values or data.

This time, calculate the  χ 2 test statistic by hand. Make a chart with the following headings and fill in the columns:

• Expected ( E ) values (12, 12, 12, 12, 12)
• Observed ( O ) values (15, 12, 9, 9, 15)
• ( O – E ) 2
• [latex]\displaystyle\frac{{({O}-{E})}^{{2}}}{{E}}[/latex]

Now add (sum) the last column. The sum is three. This is the  χ 2 test statistic.

To find the  p -value, calculate P ( χ 2 > 3). This test is right-tailed. (Use a computer or calculator to find the p -value. You should get p -value = 0.5578.)

The  dfs are the number of cells – 1 = 5 – 1 = 4

Press  2nd DISTR . Arrow down to  χ2cdf . Press ENTER . Enter (3,10^99,4) . Rounded to four decimal places, you should see 0.5578, which is the p-value.

Next, complete a graph like the following one with the proper labeling and shading. (You should shade the right tail.)

The decision is not to reject the null hypothesis.

Conclusion: At a 5% level of significance, from the sample data, there is not sufficient evidence to conclude that the absent days do not occur with equal frequencies.

TI-83+ and some TI-84 calculators do not have a special program for the test statistic for the goodness-of-fit test. The next example has the calculator instructions. The newer TI-84 calculators have in  STAT TESTS the test Chi2 GOF . To run the test, put the observed values (the data) into a first list and the expected values (the values you expect if the null hypothesis is true) into a second list. Press STAT TESTS  and Chi2 GOF . Enter the list names for the Observed list and the Expected list. Enter the degrees of freedom and press  calculate or draw . Make sure you clear any lists before you start. To Clear Lists in the calculators: Go into  STAT EDIT and arrow up to the list name area of the particular list. Press  CLEAR and then arrow down. The list will be cleared. Alternatively, you can press STAT and press 4 (for  ClrList ). Enter the list name and press ENTER .

Teachers want to know which night each week their students are doing most of their homework. Most teachers think that students do homework equally throughout the week. Suppose a random sample of 49 students were asked on which night of the week they did the most homework. The results were distributed as in the table.

From the population of students, do the nights for the highest number of students doing the majority of their homework occur with equal frequencies during a week? What type of hypothesis test should you use?

p -value = 0.6093

We decline to reject the null hypothesis. There is not enough evidence to support that students do not do the majority of their homework equally throughout the week.

One study indicates that the number of televisions that American families have is distributed (this is the  given distribution for the American population) as in the table.

The table contains expected ( E ) percents.

A random sample of 600 families in the far western United States resulted in the data in this table.

The table contains observed ( O ) frequency values.

At the 1% significance level, does it appear that the distribution “number of televisions” of far western United States families is different from the distribution for the American population as a whole?

This problem asks you to test whether the far western United States families distribution fits the distribution of the American families. This test is always right-tailed.

The first table contains expected percentages. To get expected ( E ) frequencies, multiply the percentage by 600. The expected frequencies are shown in this table.

Therefore, the expected frequencies are 60, 96, 330, 66, and 48. In the TI calculators, you can let the calculator do the math. For example, instead of 60, enter 0.10*600.

H 0 : The “number of televisions” distribution of far western United States families is the same as the “number of televisions” distribution of the American population.

H a : The “number of televisions” distribution of far western United States families is different from the “number of televisions” distribution of the American population.

Distribution for the test: [latex]\displaystyle\chi^{2}_{4}[/latex] where df = (the number of cells) – 1 = 5 – 1 = 4.

Note : [latex]df\neq600-1[/latex]

Calculate the test statistic: χ 2 = 29.65

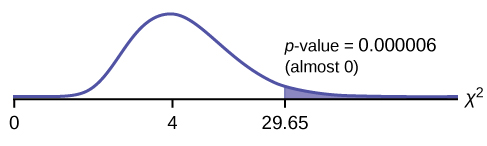
Probability statement: p -value = P ( χ 2 > 29.65) = 0.000006

Compare α and the p -value:

α = 0.01 p -value = 0.000006

So, α > p -value.

Make a decision: Since α > p -value, reject H o .

This means you reject the belief that the distribution for the far western states is the same as that of the American population as a whole.

Conclusion: At the 1% significance level, from the data, there is sufficient evidence to conclude that the “number of televisions” distribution for the far western United States is different from the “number of televisions” distribution for the American population as a whole.

Press STAT and ENTER . Make sure to clear lists L1 , L2 , and L3 if they have data in them (see the note at the end of Example 2). Into L1 , put the observed frequencies 66 , 119 , 349 , 60 , 15 . Into L2 , put the expected frequencies .10*600, .16*600 , .55*600 , .11*600 , .08*600 . Arrow over to list L3 and up to the name area L3 . Enter (L1-L2)^2/L2 and ENTER . Press 2nd QUIT . Press 2nd LIST and arrow over to MATH . Press 5 . You should see "sum" (Enter L3) . Rounded to 2 decimal places, you should see 29.65 . Press 2nd DISTR . Press 7 or Arrow down to 7:χ2cdf and press ENTER . Enter (29.65,1E99,4) . Rounded to four places, you should see 5.77E-6 = .000006  (rounded to six decimal places), which is the p-value.

The newer TI-84 calculators have in STAT TESTS the test Chi2 GOF . To run the test, put the observed values (the data) into a first list and the expected values (the values you expect if the null hypothesis is true) into a second list. Press STAT TESTS and Chi2 GOF . Enter the list names for the Observed list and the Expected list. Enter the degrees of freedom and press calculate or draw . Make sure you clear any lists before you start.

The expected percentage of the number of pets students have in their homes is distributed (this is the given distribution for the student population of the United States) as in this table.

A random sample of 1,000 students from the Eastern United States resulted in the data in the table below.

At the 1% significance level, does it appear that the distribution “number of pets” of students in the Eastern United States is different from the distribution for the United States student population as a whole? What is the p -value?

Suppose you flip two coins 100 times. The results are 20 HH , 27 HT , 30 TH , and 23 TT . Are the coins fair? Test at a 5% significance level.

This problem can be set up as a goodness-of-fit problem. The sample space for flipping two fair coins is { HH , HT , TH , TT }. Out of 100 flips, you would expect 25 HH , 25 HT , 25 TH , and 25 TT . This is the expected distribution. The question, “Are the coins fair?” is the same as saying, “Does the distribution of the coins (20 HH , 27 HT , 30 TH , 23 TT ) fit the expected distribution?”

Random Variable: Let X = the number of heads in one flip of the two coins. X takes on the values 0, 1, 2. (There are 0, 1, or 2 heads in the flip of two coins.) Therefore, the number of cells is three . Since X = the number of heads, the observed frequencies are 20 (for two heads), 57 (for one head), and 23 (for zero heads or both tails). The expected frequencies are 25 (for two heads), 50 (for one head), and 25 (for zero heads or both tails). This test is right-tailed.

H 0 : The coins are fair.

H a : The coins are not fair.

Distribution for the test:  [latex]\chi^2_2[/latex] where df = 3 – 1 = 2.

Calculate the test statistic: χ 2 = 2.14

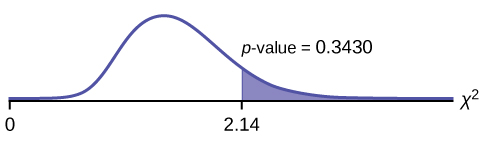
Probability statement: p -value = P ( χ 2 > 2.14) = 0.3430

α < p -value.

Make a decision: Since α < p -value, do not reject H 0 .

Conclusion: There is insufficient evidence to conclude that the coins are not fair.

Press STAT and ENTER . Make sure you clear lists L1 , L2 , and L3 if they have data in them. Into L1 , put the observed frequencies 20 , 57 , 23 . Into L2 , put the expected frequencies 25 , 50 , 25 . Arrow over to list L3 and up to the name area "L3" . Enter (L1-L2)^2/L2 and ENTER . Press 2nd QUIT . Press 2nd LIST and arrow over to MATH . Press 5 . You should see "sum" . Enter L3 . Rounded to two decimal places, you should see 2.14 . Press 2nd DISTR . Arrow down to 7:χ2cdf (or press 7 ). Press ENTER . Enter 2.14,1E99,2) . Rounded to four places, you should see .3430 , which is the p-value.

Students in a social studies class hypothesize that the literacy rates across the world for every region are 82%. This table shows the actual literacy rates across the world broken down by region. What are the test statistic and the degrees of freedom?

chi 2 test statistic = 26.38

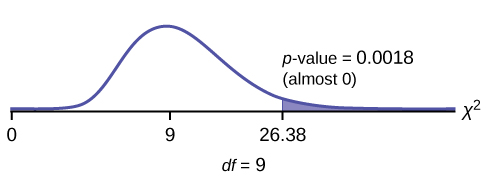
Press STAT and ENTER . Make sure you clear lists L1, L2, and L3 if they have data in them. Into L1, put the observed frequencies 99, 99.5, 67.3, 62.5, 91, 93.8, 61.9, 91.9, 84.5, 66.4 . Into L2 , put the expected frequencies 82, 82, 82, 82, 82, 82, 82, 82, 82, 82 . Arrow over to list L3 and up to the name area L3 . Enter (L1-L2)^2/L2 and ENTER . Press 2nd QUIT . Press 2nd LIST and arrow over to MATH . Press 5 . You should see "sum" . Enter L3 . Rounded to two decimal places, you should see 26.38 . Press 2nd DISTR . Arrow down to 7:χ2cdf (or press 7 ). Press ENTER . Enter 26.38,1E99,9) . Rounded to four places, you should see .0018 , which is the p -value.

• OpenStax College, Introductory Statistics. Located at : . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Pearson's chi square test (goodness of fit) | Probability and Statistics | Khan Academy . Authored by : Khan Academy. Located at : https://www.youtube.com/embed/2QeDRsxSF9M . License : All Rights Reserved . License Terms : Standard YouTube License