hypothesis testing one way anova

One-way ANOVA

What is this test for.

The one-way analysis of variance (ANOVA) is used to determine whether there are any statistically significant differences between the means of three or more independent (unrelated) groups. This guide will provide a brief introduction to the one-way ANOVA, including the assumptions of the test and when you should use this test. If you are familiar with the one-way ANOVA, but would like to carry out a one-way ANOVA analysis, go to our guide: One-way ANOVA in SPSS Statistics .

What does this test do?

The one-way ANOVA compares the means between the groups you are interested in and determines whether any of those means are statistically significantly different from each other. Specifically, it tests the null hypothesis:

where µ = group mean and k = number of groups. If, however, the one-way ANOVA returns a statistically significant result, we accept the alternative hypothesis (H A ), which is that there are at least two group means that are statistically significantly different from each other.

At this point, it is important to realize that the one-way ANOVA is an omnibus test statistic and cannot tell you which specific groups were statistically significantly different from each other, only that at least two groups were. To determine which specific groups differed from each other, you need to use a post hoc test . Post hoc tests are described later in this guide.

When might you need to use this test?

If you are dealing with individuals, you are likely to encounter this situation using two different types of study design:

One study design is to recruit a group of individuals and then randomly split this group into three or more smaller groups (i.e., each participant is allocated to one, and only one, group). You then get each group to undertake different tasks (or put them under different conditions) and measure the outcome/response on the same dependent variable. For example, a researcher wishes to know whether different pacing strategies affect the time to complete a marathon. The researcher randomly assigns a group of volunteers to either a group that (a) starts slow and then increases their speed, (b) starts fast and slows down or (c) runs at a steady pace throughout. The time to complete the marathon is the outcome (dependent) variable. This study design is illustrated schematically in the diagram below:

When you might use this test is continued on the next page .

13.1 One-Way ANOVA

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test uses variances to help determine if the means are equal or not. To perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:

• Each population from which a sample is taken is assumed to be normal.
• All samples are randomly selected and independent.
• The populations are assumed to have equal standard deviations (or variances).
• The factor is a categorical variable.
• The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are k groups

H 0 : μ 1 = μ 2 = μ 3 = ... = μ k

H a : At least two of the group means μ 1 , μ 2 , μ 3 , ..., μ k are not equal. That is, μ i ≠ μ j for some i ≠ j .

The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), H 0 : μ 1 = μ 2 = μ 3 and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.

If the null hypothesis is false, then the variance of the combined data is larger, which is caused by the different means as shown in the second graph (green box plots).

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

• Authors: Barbara Illowsky, Susan Dean
• Publisher/website: OpenStax
• Book title: Statistics
• Publication date: Mar 27, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/statistics/pages/1-introduction
• Section URL: https://openstax.org/books/statistics/pages/13-1-one-way-anova

© Jan 23, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

JMP | Statistical Discovery.™ From SAS.

Statistics Knowledge Portal

A free online introduction to statistics

One-Way ANOVA

What is one-way anova.

One-way analysis of variance (ANOVA) is a statistical method for testing for differences in the means of three or more groups.

How is one-way ANOVA used?

One-way ANOVA is typically used when you have a single independent variable, or factor , and your goal is to investigate if variations, or different levels  of that factor have a measurable effect on a dependent variable.

What are some limitations to consider?

One-way ANOVA can only be used when investigating a single factor and a single dependent variable. When comparing the means of three or more groups, it can tell us if at least one pair of means is significantly different, but it can’t tell us which pair. Also, it requires that the dependent variable be normally distributed in each of the groups and that the variability within groups is similar across groups.

One-way ANOVA is a test for differences in group means

See how to perform a one-way anova using statistical software.

• Download JMP to follow along using the sample data included with the software.
• To see more JMP tutorials, visit the JMP Learning Library .

One-way ANOVA is a statistical method to test the null hypothesis ( H 0 ) that three or more population means are equal vs. the alternative hypothesis ( H a ) that at least one mean is different. Using the formal notation of statistical hypotheses, for k means we write:

$ H_0:\mu_1=\mu_2=\cdots=\mu_k $

$ H_a:\mathrm{not\mathrm{\ }all\ means\ are\ equal} $

where $\mu_i$ is the mean of the i -th level of the factor.

Okay, you might be thinking, but in what situations would I need to determine if the means of multiple populations are the same or different? A common scenario is you suspect that a particular independent process variable is a driver of an important result of that process. For example, you may have suspicions about how different production lots, operators or raw material batches are affecting the output (aka a quality measurement) of a production process.

To test your suspicion, you could run the process using three or more variations (aka levels) of this independent variable (aka factor), and then take a sample of observations from the results of each run. If you find differences when comparing the means from each group of observations using an ANOVA, then (assuming you’ve done everything correctly!) you have evidence that your suspicion was correct—the factor you investigated appears to play a role in the result!

A one-way ANOVA example

Let's work through a one-way ANOVA example in more detail. Imagine you work for a company that manufactures an adhesive gel that is sold in small jars. The viscosity of the gel is important: too thick and it becomes difficult to apply; too thin and its adhesiveness suffers. You've received some feedback from a few unhappy customers lately complaining that the viscosity of your adhesive is not as consistent as it used to be. You've been asked by your boss to investigate.

You decide that a good first step would be to examine the average viscosity of the five most recent production lots. If you find differences between lots, that would seem to confirm the issue is real. It might also help you begin to form hypotheses about factors that could cause inconsistencies between lots.

You measure viscosity using an instrument that rotates a spindle immersed in the jar of adhesive. This test yields a measurement called torque resistance. You test five jars selected randomly from each of the most recent five lots. You obtain the torque resistance measurement for each jar and plot the data.

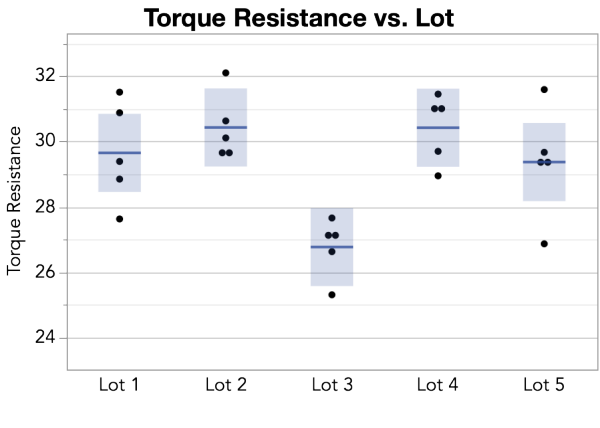
From the plot of the data, you observe that torque measurements from the Lot 3 jars tend to be lower than the torque measurements from the samples taken from the other lots. When you calculate the means from all your measurements, you see that the mean torque for Lot 3 is 26.77—much lower than the other four lots, each with a mean of around 30.

Table 1: Mean torque measurements from tests of five lots of adhesive

The anova table.

ANOVA results are typically displayed in an ANOVA table. An ANOVA table includes:

• Source: the sources of variation including the factor being examined (in our case, lot), error and total.
• DF: degrees of freedom for each source of variation.
• Sum of Squares: sum of squares (SS) for each source of variation along with the total from all sources.
• Mean Square: sum of squares divided by its associated degrees of freedom.
• F Ratio: the mean square of the factor (lot) divided by the mean square of the error.
• Prob > F: the p-value.

Table 2: ANOVA table with results from our torque measurements

We'll explain how the components of this table are derived below. One key element in this table to focus on for now is the p-value. The p-value is used to evaluate the validity of the null hypothesis that all the means are the same. In our example, the p-value (Prob > F) is 0.0012. This small p-value can be taken as evidence that the means are not all the same. Our samples provide evidence that there is a difference in the average torque resistance values between one or more of the five lots.

What is a p-value?

A p-value is a measure of probability used for hypothesis testing. The goal of hypothesis testing is to determine whether there is enough evidence to support a certain hypothesis about your data. Recall that with ANOVA, we formulate two hypotheses: the null hypothesis that all the means are equal and the alternative hypothesis that the means are not all equal.

Because we’re only examining random samples of data pulled from whole populations, there’s a risk that the means of our samples are not representative of the means of the full populations. The p-value gives us a way to quantify that risk. It is the probability that any variability in the means of your sample data is the result of pure chance; more specifically, it’s the probability of observing variances in the sample means at least as large as what you’ve measured when in fact the null hypothesis is true (the full population means are, in fact, equal).

A small p-value would lead you to reject the null hypothesis. A typical threshold for rejection of a null hypothesis is 0.05. That is, if you have a p-value less than 0.05, you would reject the null hypothesis in favor of the alternative hypothesis that at least one mean is different from the rest.

Based on these results, you decide to hold Lot 3 for further testing. In your report you might write: The torque from five jars of product were measured from each of the five most recent production lots. An ANOVA analysis found that the observations support a difference in mean torque between lots (p = 0.0012). A plot of the data shows that Lot 3 had a lower mean (26.77) torque as compared to the other four lots. We will hold Lot 3 for further evaluation.

Remember, an ANOVA test will not tell you which mean or means differs from the others, and (unlike our example) this isn't always obvious from a plot of the data. One way to answer questions about specific types of differences is to use a multiple comparison test. For example, to compare group means to the overall mean, you can use analysis of means (ANOM). To compare individual pairs of means, you can use the Tukey-Kramer multiple comparison test.

One-way ANOVA calculation

Now let’s consider our torque measurement example in more detail. Recall that we had five lots of material. From each lot we randomly selected five jars for testing. This is called a one-factor design. The one factor, lot, has five levels. Each level is replicated (tested) five times. The results of the testing are listed below.

Table 3: Torque measurements by Lot

To explore the calculations that resulted in the ANOVA table above (Table 2), let's first establish the following definitions:

$n_i$ = Number of observations for treatment $i$ (in our example, Lot $i$)

$N$ = Total number of observations

$Y_{ij}$ = The j th observation on the i th treatment

$\overline{Y}_i$ = The sample mean for the i th treatment

$\overline{\overline{Y}}$ = The mean of all observations (grand mean)

Sum of Squares

With these definitions in mind, let's tackle the Sum of Squares column from the ANOVA table. The sum of squares gives us a way to quantify variability in a data set by focusing on the difference between each data point and the mean of all data points in that data set. The formula below partitions the overall variability into two parts: the variability due to the model or the factor levels, and the variability due to random error.  

$$ \sum_{i=1}^{a}\sum_{j=1}^{n_i}(Y_{ij}-\overline{\overline{Y}})^2\;=\;\sum_{i=1}^{a}n_i(\overline{Y}_i-\overline{\overline{Y}})^2+\sum_{i=1}^{a}\sum_{j=1}^{n_i}(Y_{ij}-\overline{Y}_i)^2 $$

$$ SS(Total)\;     =     \;SS(Factor)\;     +     \;SS(Error) $$

While that equation may seem complicated, focusing on each element individually makes it much easier to grasp. Table 4 below lists each component of the formula and then builds them into the squared terms that make up the sum of squares. The first column of data ($Y_{ij}$) contains the torque measurements we gathered in Table 3 above.

Another way to look at sources of variability: between group variation and within group variation

Recall that in our ANOVA table above (Table 2), the Source column lists two sources of variation: factor (in our example, lot) and error. Another way to think of those two sources is between group variation (which corresponds to variation due to the factor or treatment) and within group variation (which corresponds to variation due to chance or error). So using that terminology, our sum of squares formula is essentially calculating the sum of variation due to differences between the groups (the treatment effect) and variation due to differences within each group (unexplained differences due to chance).  

Table 4: Sum of squares calculation

Degrees of freedom (df).

Associated with each sum of squares is a quantity called degrees of freedom (DF). The degrees of freedom indicate the number of independent pieces of information used to calculate each sum of squares. For a one factor design with a factor at k levels (five lots in our example) and a total of N observations (five jars per lot for a total of 25), the degrees of freedom are as follows:

Table 5: Determining degrees of freedom

Mean squares (ms) and f ratio.

We divide each sum of squares by the corresponding degrees of freedom to obtain mean squares. When the null hypothesis is true (i.e. the means are equal), MS (Factor) and MS (Error) are both estimates of error variance and would be about the same size. Their ratio, or the F ratio, would be close to one. When the null hypothesis is not true then the MS (Factor) will be larger than MS (Error) and their ratio greater than 1. In our adhesive testing example, the computed F ratio, 6.90, presents significant evidence against the null hypothesis that the means are equal.

Table 6: Calculating mean squares and F ratio

The ratio of MS(factor) to MS(error)—the F ratio—has an F distribution. The F distribution is the distribution of F values that we'd expect to observe when the null hypothesis is true (i.e. the means are equal). F distributions have different shapes based on two parameters, called the numerator and denominator degrees of freedom. For an ANOVA test, the numerator is the MS(factor), so the degrees of freedom are those associated with the MS(factor). The denominator is the MS(error), so the denominator degrees of freedom are those associated with the MS(error).

If your computed F ratio exceeds the expected value from the corresponding F distribution, then, assuming a sufficiently small p-value, you would reject the null hypothesis that the means are equal. The p-value in this case is the probability of observing a value greater than the F ratio from the F distribution when in fact the null hypothesis is true.

Module 13: F-Distribution and One-Way ANOVA

One-way anova, learning outcomes.

• Conduct and interpret one-way ANOVA

The purpose of a one-way ANOVA test is to determine the existence of a statistically significant difference among several group means. The test actually uses variances to help determine if the means are equal or not. In order to perform a one-way ANOVA test, there are five basic assumptions to be fulfilled:

• Each population from which a sample is taken is assumed to be normal.
• All samples are randomly selected and independent.
• The populations are assumed to have equal standard deviations (or variances) .
• The factor is a categorical variable.
• The response is a numerical variable.

The Null and Alternative Hypotheses

The null hypothesis is simply that all the group population means are the same. The alternative hypothesis is that at least one pair of means is different. For example, if there are k groups:

H 0 : μ 1 = μ 2 = μ 3 = … = μ k

H a : At least two of the group means μ 1 , μ 2 , μ 3 , …, μ k are not equal.

The graphs, a set of box plots representing the distribution of values with the group means indicated by a horizontal line through the box, help in the understanding of the hypothesis test. In the first graph (red box plots), H 0 : μ 1 = μ 2 = μ 3 and the three populations have the same distribution if the null hypothesis is true. The variance of the combined data is approximately the same as the variance of each of the populations.

If the null hypothesis is false, then the variance of the combined data is larger which is caused by the different means as shown in the second graph (green box plots).

(b) H 0 is not true. All means are not the same; the differences are too large to be due to random variation.

Concept Review

Analysis of variance extends the comparison of two groups to several, each a level of a categorical variable (factor). Samples from each group are independent, and must be randomly selected from normal populations with equal variances. We test the null hypothesis of equal means of the response in every group versus the alternative hypothesis of one or more group means being different from the others. A one-way ANOVA hypothesis test determines if several population means are equal. The distribution for the test is the F distribution with two different degrees of freedom.

Assumptions:

• The populations are assumed to have equal standard deviations (or variances).
• OpenStax, Statistics, One-Way ANOVA. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Completing a simple ANOVA table. Authored by : masterskills. Located at : https://youtu.be/OXA-bw9tGfo . License : All Rights Reserved . License Terms : Standard YouTube License

Hypothesis Testing - Analysis of Variance (ANOVA)

Lisa Sullivan, PhD

Professor of Biostatistics

Boston University School of Public Health

Introduction

This module will continue the discussion of hypothesis testing, where a specific statement or hypothesis is generated about a population parameter, and sample statistics are used to assess the likelihood that the hypothesis is true. The hypothesis is based on available information and the investigator's belief about the population parameters. The specific test considered here is called analysis of variance (ANOVA) and is a test of hypothesis that is appropriate to compare means of a continuous variable in two or more independent comparison groups. For example, in some clinical trials there are more than two comparison groups. In a clinical trial to evaluate a new medication for asthma, investigators might compare an experimental medication to a placebo and to a standard treatment (i.e., a medication currently being used). In an observational study such as the Framingham Heart Study, it might be of interest to compare mean blood pressure or mean cholesterol levels in persons who are underweight, normal weight, overweight and obese.  

The technique to test for a difference in more than two independent means is an extension of the two independent samples procedure discussed previously which applies when there are exactly two independent comparison groups. The ANOVA technique applies when there are two or more than two independent groups. The ANOVA procedure is used to compare the means of the comparison groups and is conducted using the same five step approach used in the scenarios discussed in previous sections. Because there are more than two groups, however, the computation of the test statistic is more involved. The test statistic must take into account the sample sizes, sample means and sample standard deviations in each of the comparison groups.

If one is examining the means observed among, say three groups, it might be tempting to perform three separate group to group comparisons, but this approach is incorrect because each of these comparisons fails to take into account the total data, and it increases the likelihood of incorrectly concluding that there are statistically significate differences, since each comparison adds to the probability of a type I error. Analysis of variance avoids these problemss by asking a more global question, i.e., whether there are significant differences among the groups, without addressing differences between any two groups in particular (although there are additional tests that can do this if the analysis of variance indicates that there are differences among the groups).

The fundamental strategy of ANOVA is to systematically examine variability within groups being compared and also examine variability among the groups being compared.

Learning Objectives

After completing this module, the student will be able to:

• Perform analysis of variance by hand
• Appropriately interpret results of analysis of variance tests
• Distinguish between one and two factor analysis of variance tests
• Identify the appropriate hypothesis testing procedure based on type of outcome variable and number of samples

The ANOVA Approach

Consider an example with four independent groups and a continuous outcome measure. The independent groups might be defined by a particular characteristic of the participants such as BMI (e.g., underweight, normal weight, overweight, obese) or by the investigator (e.g., randomizing participants to one of four competing treatments, call them A, B, C and D). Suppose that the outcome is systolic blood pressure, and we wish to test whether there is a statistically significant difference in mean systolic blood pressures among the four groups. The sample data are organized as follows:

The hypotheses of interest in an ANOVA are as follows:

• H 0 : μ 1 = μ 2 = μ 3 ... = μ k
• H 1 : Means are not all equal.

where k = the number of independent comparison groups.

In this example, the hypotheses are:

• H 0 : μ 1 = μ 2 = μ 3 = μ 4
• H 1 : The means are not all equal.

The null hypothesis in ANOVA is always that there is no difference in means. The research or alternative hypothesis is always that the means are not all equal and is usually written in words rather than in mathematical symbols. The research hypothesis captures any difference in means and includes, for example, the situation where all four means are unequal, where one is different from the other three, where two are different, and so on. The alternative hypothesis, as shown above, capture all possible situations other than equality of all means specified in the null hypothesis.

Test Statistic for ANOVA

The test statistic for testing H 0 : μ 1 = μ 2 = ... =   μ k is:

and the critical value is found in a table of probability values for the F distribution with (degrees of freedom) df 1 = k-1, df 2 =N-k. The table can be found in "Other Resources" on the left side of the pages.

NOTE: The test statistic F assumes equal variability in the k populations (i.e., the population variances are equal, or s 1 2 = s 2 2 = ... = s k 2 ). This means that the outcome is equally variable in each of the comparison populations. This assumption is the same as that assumed for appropriate use of the test statistic to test equality of two independent means. It is possible to assess the likelihood that the assumption of equal variances is true and the test can be conducted in most statistical computing packages. If the variability in the k comparison groups is not similar, then alternative techniques must be used.

The F statistic is computed by taking the ratio of what is called the "between treatment" variability to the "residual or error" variability. This is where the name of the procedure originates. In analysis of variance we are testing for a difference in means (H 0 : means are all equal versus H 1 : means are not all equal) by evaluating variability in the data. The numerator captures between treatment variability (i.e., differences among the sample means) and the denominator contains an estimate of the variability in the outcome. The test statistic is a measure that allows us to assess whether the differences among the sample means (numerator) are more than would be expected by chance if the null hypothesis is true. Recall in the two independent sample test, the test statistic was computed by taking the ratio of the difference in sample means (numerator) to the variability in the outcome (estimated by Sp).  

The decision rule for the F test in ANOVA is set up in a similar way to decision rules we established for t tests. The decision rule again depends on the level of significance and the degrees of freedom. The F statistic has two degrees of freedom. These are denoted df 1 and df 2 , and called the numerator and denominator degrees of freedom, respectively. The degrees of freedom are defined as follows:

df 1 = k-1 and df 2 =N-k,

where k is the number of comparison groups and N is the total number of observations in the analysis.   If the null hypothesis is true, the between treatment variation (numerator) will not exceed the residual or error variation (denominator) and the F statistic will small. If the null hypothesis is false, then the F statistic will be large. The rejection region for the F test is always in the upper (right-hand) tail of the distribution as shown below.

Rejection Region for F   Test with a =0.05, df 1 =3 and df 2 =36 (k=4, N=40)

For the scenario depicted here, the decision rule is: Reject H 0 if F > 2.87.

The ANOVA Procedure

We will next illustrate the ANOVA procedure using the five step approach. Because the computation of the test statistic is involved, the computations are often organized in an ANOVA table. The ANOVA table breaks down the components of variation in the data into variation between treatments and error or residual variation. Statistical computing packages also produce ANOVA tables as part of their standard output for ANOVA, and the ANOVA table is set up as follows: 

where  

• X = individual observation,
• k = the number of treatments or independent comparison groups, and
• N = total number of observations or total sample size.

The ANOVA table above is organized as follows.

• The first column is entitled "Source of Variation" and delineates the between treatment and error or residual variation. The total variation is the sum of the between treatment and error variation.
• The second column is entitled "Sums of Squares (SS)" . The between treatment sums of squares is

and is computed by summing the squared differences between each treatment (or group) mean and the overall mean. The squared differences are weighted by the sample sizes per group (n j ). The error sums of squares is:

and is computed by summing the squared differences between each observation and its group mean (i.e., the squared differences between each observation in group 1 and the group 1 mean, the squared differences between each observation in group 2 and the group 2 mean, and so on). The double summation ( SS ) indicates summation of the squared differences within each treatment and then summation of these totals across treatments to produce a single value. (This will be illustrated in the following examples). The total sums of squares is:

and is computed by summing the squared differences between each observation and the overall sample mean. In an ANOVA, data are organized by comparison or treatment groups. If all of the data were pooled into a single sample, SST would reflect the numerator of the sample variance computed on the pooled or total sample. SST does not figure into the F statistic directly. However, SST = SSB + SSE, thus if two sums of squares are known, the third can be computed from the other two.

• The third column contains degrees of freedom . The between treatment degrees of freedom is df 1 = k-1. The error degrees of freedom is df 2 = N - k. The total degrees of freedom is N-1 (and it is also true that (k-1) + (N-k) = N-1).
• The fourth column contains "Mean Squares (MS)" which are computed by dividing sums of squares (SS) by degrees of freedom (df), row by row. Specifically, MSB=SSB/(k-1) and MSE=SSE/(N-k). Dividing SST/(N-1) produces the variance of the total sample. The F statistic is in the rightmost column of the ANOVA table and is computed by taking the ratio of MSB/MSE.  

A clinical trial is run to compare weight loss programs and participants are randomly assigned to one of the comparison programs and are counseled on the details of the assigned program. Participants follow the assigned program for 8 weeks. The outcome of interest is weight loss, defined as the difference in weight measured at the start of the study (baseline) and weight measured at the end of the study (8 weeks), measured in pounds.  

Three popular weight loss programs are considered. The first is a low calorie diet. The second is a low fat diet and the third is a low carbohydrate diet. For comparison purposes, a fourth group is considered as a control group. Participants in the fourth group are told that they are participating in a study of healthy behaviors with weight loss only one component of interest. The control group is included here to assess the placebo effect (i.e., weight loss due to simply participating in the study). A total of twenty patients agree to participate in the study and are randomly assigned to one of the four diet groups. Weights are measured at baseline and patients are counseled on the proper implementation of the assigned diet (with the exception of the control group). After 8 weeks, each patient's weight is again measured and the difference in weights is computed by subtracting the 8 week weight from the baseline weight. Positive differences indicate weight losses and negative differences indicate weight gains. For interpretation purposes, we refer to the differences in weights as weight losses and the observed weight losses are shown below.

Is there a statistically significant difference in the mean weight loss among the four diets?  We will run the ANOVA using the five-step approach.

• Step 1. Set up hypotheses and determine level of significance

H 0 : μ 1 = μ 2 = μ 3 = μ 4 H 1 : Means are not all equal              α=0.05

• Step 2. Select the appropriate test statistic.  

The test statistic is the F statistic for ANOVA, F=MSB/MSE.

• Step 3. Set up decision rule.  

The appropriate critical value can be found in a table of probabilities for the F distribution(see "Other Resources"). In order to determine the critical value of F we need degrees of freedom, df 1 =k-1 and df 2 =N-k. In this example, df 1 =k-1=4-1=3 and df 2 =N-k=20-4=16. The critical value is 3.24 and the decision rule is as follows: Reject H 0 if F > 3.24.

• Step 4. Compute the test statistic.  

To organize our computations we complete the ANOVA table. In order to compute the sums of squares we must first compute the sample means for each group and the overall mean based on the total sample.  

We can now compute

So, in this case:

Next we compute,

SSE requires computing the squared differences between each observation and its group mean. We will compute SSE in parts. For the participants in the low calorie diet:  

For the participants in the low fat diet:  

For the participants in the low carbohydrate diet:  

For the participants in the control group:

We can now construct the ANOVA table .

• Step 5. Conclusion.  

We reject H 0 because 8.43 > 3.24. We have statistically significant evidence at α=0.05 to show that there is a difference in mean weight loss among the four diets.    

ANOVA is a test that provides a global assessment of a statistical difference in more than two independent means. In this example, we find that there is a statistically significant difference in mean weight loss among the four diets considered. In addition to reporting the results of the statistical test of hypothesis (i.e., that there is a statistically significant difference in mean weight losses at α=0.05), investigators should also report the observed sample means to facilitate interpretation of the results. In this example, participants in the low calorie diet lost an average of 6.6 pounds over 8 weeks, as compared to 3.0 and 3.4 pounds in the low fat and low carbohydrate groups, respectively. Participants in the control group lost an average of 1.2 pounds which could be called the placebo effect because these participants were not participating in an active arm of the trial specifically targeted for weight loss. Are the observed weight losses clinically meaningful?

Another ANOVA Example

Calcium is an essential mineral that regulates the heart, is important for blood clotting and for building healthy bones. The National Osteoporosis Foundation recommends a daily calcium intake of 1000-1200 mg/day for adult men and women. While calcium is contained in some foods, most adults do not get enough calcium in their diets and take supplements. Unfortunately some of the supplements have side effects such as gastric distress, making them difficult for some patients to take on a regular basis.  

 A study is designed to test whether there is a difference in mean daily calcium intake in adults with normal bone density, adults with osteopenia (a low bone density which may lead to osteoporosis) and adults with osteoporosis. Adults 60 years of age with normal bone density, osteopenia and osteoporosis are selected at random from hospital records and invited to participate in the study. Each participant's daily calcium intake is measured based on reported food intake and supplements. The data are shown below.   

Is there a statistically significant difference in mean calcium intake in patients with normal bone density as compared to patients with osteopenia and osteoporosis? We will run the ANOVA using the five-step approach.

H 0 : μ 1 = μ 2 = μ 3 H 1 : Means are not all equal                            α=0.05

In order to determine the critical value of F we need degrees of freedom, df 1 =k-1 and df 2 =N-k.   In this example, df 1 =k-1=3-1=2 and df 2 =N-k=18-3=15. The critical value is 3.68 and the decision rule is as follows: Reject H 0 if F > 3.68.

To organize our computations we will complete the ANOVA table. In order to compute the sums of squares we must first compute the sample means for each group and the overall mean.  

 If we pool all N=18 observations, the overall mean is 817.8.

We can now compute:

Substituting:

SSE requires computing the squared differences between each observation and its group mean. We will compute SSE in parts. For the participants with normal bone density:

For participants with osteopenia:

For participants with osteoporosis:

We do not reject H 0 because 1.395 < 3.68. We do not have statistically significant evidence at a =0.05 to show that there is a difference in mean calcium intake in patients with normal bone density as compared to osteopenia and osterporosis. Are the differences in mean calcium intake clinically meaningful? If so, what might account for the lack of statistical significance?

One-Way ANOVA in R

The video below by Mike Marin demonstrates how to perform analysis of variance in R. It also covers some other statistical issues, but the initial part of the video will be useful to you.

Two-Factor ANOVA

The ANOVA tests described above are called one-factor ANOVAs. There is one treatment or grouping factor with k > 2 levels and we wish to compare the means across the different categories of this factor. The factor might represent different diets, different classifications of risk for disease (e.g., osteoporosis), different medical treatments, different age groups, or different racial/ethnic groups. There are situations where it may be of interest to compare means of a continuous outcome across two or more factors. For example, suppose a clinical trial is designed to compare five different treatments for joint pain in patients with osteoarthritis. Investigators might also hypothesize that there are differences in the outcome by sex. This is an example of a two-factor ANOVA where the factors are treatment (with 5 levels) and sex (with 2 levels). In the two-factor ANOVA, investigators can assess whether there are differences in means due to the treatment, by sex or whether there is a difference in outcomes by the combination or interaction of treatment and sex. Higher order ANOVAs are conducted in the same way as one-factor ANOVAs presented here and the computations are again organized in ANOVA tables with more rows to distinguish the different sources of variation (e.g., between treatments, between men and women). The following example illustrates the approach.

Consider the clinical trial outlined above in which three competing treatments for joint pain are compared in terms of their mean time to pain relief in patients with osteoarthritis. Because investigators hypothesize that there may be a difference in time to pain relief in men versus women, they randomly assign 15 participating men to one of the three competing treatments and randomly assign 15 participating women to one of the three competing treatments (i.e., stratified randomization). Participating men and women do not know to which treatment they are assigned. They are instructed to take the assigned medication when they experience joint pain and to record the time, in minutes, until the pain subsides. The data (times to pain relief) are shown below and are organized by the assigned treatment and sex of the participant.

Table of Time to Pain Relief by Treatment and Sex

The analysis in two-factor ANOVA is similar to that illustrated above for one-factor ANOVA. The computations are again organized in an ANOVA table, but the total variation is partitioned into that due to the main effect of treatment, the main effect of sex and the interaction effect. The results of the analysis are shown below (and were generated with a statistical computing package - here we focus on interpretation). 

 ANOVA Table for Two-Factor ANOVA

There are 4 statistical tests in the ANOVA table above. The first test is an overall test to assess whether there is a difference among the 6 cell means (cells are defined by treatment and sex). The F statistic is 20.7 and is highly statistically significant with p=0.0001. When the overall test is significant, focus then turns to the factors that may be driving the significance (in this example, treatment, sex or the interaction between the two). The next three statistical tests assess the significance of the main effect of treatment, the main effect of sex and the interaction effect. In this example, there is a highly significant main effect of treatment (p=0.0001) and a highly significant main effect of sex (p=0.0001). The interaction between the two does not reach statistical significance (p=0.91). The table below contains the mean times to pain relief in each of the treatments for men and women (Note that each sample mean is computed on the 5 observations measured under that experimental condition).  

Mean Time to Pain Relief by Treatment and Gender

Treatment A appears to be the most efficacious treatment for both men and women. The mean times to relief are lower in Treatment A for both men and women and highest in Treatment C for both men and women. Across all treatments, women report longer times to pain relief (See below).  

Notice that there is the same pattern of time to pain relief across treatments in both men and women (treatment effect). There is also a sex effect - specifically, time to pain relief is longer in women in every treatment.  

Suppose that the same clinical trial is replicated in a second clinical site and the following data are observed.

Table - Time to Pain Relief by Treatment and Sex - Clinical Site 2

The ANOVA table for the data measured in clinical site 2 is shown below.

Table - Summary of Two-Factor ANOVA - Clinical Site 2

Notice that the overall test is significant (F=19.4, p=0.0001), there is a significant treatment effect, sex effect and a highly significant interaction effect. The table below contains the mean times to relief in each of the treatments for men and women.  

Table - Mean Time to Pain Relief by Treatment and Gender - Clinical Site 2

Notice that now the differences in mean time to pain relief among the treatments depend on sex. Among men, the mean time to pain relief is highest in Treatment A and lowest in Treatment C. Among women, the reverse is true. This is an interaction effect (see below).  

Notice above that the treatment effect varies depending on sex. Thus, we cannot summarize an overall treatment effect (in men, treatment C is best, in women, treatment A is best).    

When interaction effects are present, some investigators do not examine main effects (i.e., do not test for treatment effect because the effect of treatment depends on sex). This issue is complex and is discussed in more detail in a later module. 

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

11.4 One-Way ANOVA and Hypothesis Tests for Three or More Population Means

Learning objectives.

• Conduct and interpret hypothesis tests for three or more population means using one-way ANOVA.

The purpose of a one-way ANOVA (analysis of variance) test is to determine the existence of a statistically significant difference among the means of three or more populations.  The test actually uses variances to help determine if the population means are equal or not.

Throughout this section, we will use subscripts to identify the values for the means, sample sizes, and standard deviations for the populations:

[latex]k[/latex] is the number of populations under study, [latex]n[/latex] is the total number of observations in all of the samples combined, and [latex]\overline{\overline{x}}[/latex] is the mean of the sample means.

[latex]\begin{eqnarray*} n & = & n_1+n_2+\cdots+n_k \\ \\ \overline{\overline{x}} & = & \frac{n_1 \times \overline{x}_1 +n_2 \times \overline{x}_2 +\cdots+n_k \times \overline{x}_k}{n} \end{eqnarray*}[/latex]

One-Way ANOVA

A predictor variable is called a factor or independent variable .  For example age, temperature, and gender are factors.  The groups or samples are often referred to as treatments .  This terminology comes from the use of ANOVA procedures in medical and psychological research to determine if there is a difference in the effects of different treatments.

A local college wants to compare the mean GPA for players on four of its sports teams:  basketball, baseball, hockey, and lacrosse.  A random sample of players was taken from each team and their GPA recorded in the table below.

In this example, the factor is the sports team.

[latex]\begin{eqnarray*} k & = & 4 \\ \\ n & = & n_1+n_2+n_3+n_4 \\ & = & 5+5+5+5 \\ & = & 20 \\ \\ \overline{\overline{x}} & = & \frac{n_1 \times \overline{x}_1+n_2 \times \overline{x}_2+n_3 \times \overline{x}_3+n_4 \times \overline{x}_4}{n} \\ & = & \frac{5 \times 3.22+5 \times 3.02+5 \times 3+5 \times 2.94}{20}  \\& = & 3.045 \end{eqnarray*}[/latex]

The following assumptions are required to use a one-way ANOVA test:

• Each population from which a sample is taken is normally distributed.
• All samples are randomly selected and independently taken from the populations.
• The populations are assumed to have equal variances.
• The population data is numerical (interval or ratio level).

The logic behind one-way ANOVA is to compare population means based on two independent estimates of the (assumed) equal variance [latex]\sigma^2[/latex] between the populations:

• One estimate of the equal variance [latex]\sigma^2[/latex] is based on the variability among the sample means themselves (called the between-groups estimate of population variance).
• One estimate of the equal variance [latex]\sigma^2[/latex] is based on the variability of the data within each sample (called the within-groups estimate of population variance).

The one-way ANOVA procedure compares these two estimates of the population variance [latex]\sigma^2[/latex] to determine if the population means are equal or if there is a difference in the population means.  Because ANOVA involves the comparison of two estimates of variance, an [latex]F[/latex]-distribution is used to conduct the ANOVA test.  The test statistic is an [latex]F[/latex]-score that is the ratio of the two estimates of population variance:

[latex]\displaystyle{F=\frac{\mbox{variance between groups}}{\mbox{variance within groups}}}[/latex]

The degrees of freedom for the [latex]F[/latex]-distribution are [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex] where [latex]k[/latex] is the number of populations and [latex]n[/latex] is the total number of observations in all of the samples combined.

The variance between groups estimate of the population variance is called the mean square due to treatment , [latex]MST[/latex].  The [latex]MST[/latex] is the estimate of the population variance determined by the variance of the sample means from the overall sample mean [latex]\overline{\overline{x}}[/latex].  When the population means are equal, [latex]MST[/latex] provides an unbiased estimate of the population variance.  When the population means are not equal, [latex]MST[/latex] provides an overestimate of the population variance.

[latex]\begin{eqnarray*} SST & = & n_1 \times (\overline{x}_1-\overline{\overline{x}})^2+n_2\times (\overline{x}_2-\overline{\overline{x}})^2+ \cdots +n_k \times (\overline{x}_k-\overline{\overline{x}})^2 \\  \\ MST & =& \frac{SST}{k-1} \end{eqnarray*}[/latex]

The variance within groups estimate of the population variance is called the mean square due to error , [latex]MSE[/latex].  The [latex]MSE[/latex] is the pooled estimate of the population variance using the sample variances as estimates for the population variance.  The [latex]MSE[/latex] always provides an unbiased estimate of the population variance because it is not affected by whether or not the population means are equal.

[latex]\begin{eqnarray*} SSE & = & (n_1-1) \times s_1^2+ (n_2-1) \times s_2^2+ \cdots + (n_k-1) \times s_k^2\\  \\ MSE & =& \frac{SSE}{n -k} \end{eqnarray*}[/latex]

The one-way ANOVA test depends on the fact that the variance between groups [latex]MST[/latex] is influenced by differences between the population means, which results in [latex]MST[/latex] being either an unbiased or overestimate of the population variance.  Because the variance within groups [latex]MSE[/latex] compares values of each group to its own group mean, [latex]MSE[/latex] is not affected by differences between the population means and is always an unbiased estimate of the population variance.

The null hypothesis in a one-way ANOVA test is that the population means are all equal and the alternative hypothesis is that there is a difference in the population means.  The [latex]F[/latex]-score for the one-way ANOVA test is [latex]\displaystyle{F=\frac{MST}{MSE}}[/latex] with [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex].  The p -value for the test is the area in the right tail of the [latex]F[/latex]-distribution, to the right of the [latex]F[/latex]-score.

• When the variance between groups [latex]MST[/latex] and variance within groups [latex]MSE[/latex] are close in value, the [latex]F[/latex]-score is close to 1 and results in a large p -value.  In this case, the conclusion is that the population means are equal.
• When the variance between groups [latex]MST[/latex] is significantly larger than the variability within groups [latex]MSE[/latex], the [latex]F[/latex]-score is large and results in a small p -value.  In this case, the conclusion is that there is a difference in the population means.

Steps to Conduct a Hypothesis Test for Three or More Population Means

• Verify that the one-way ANOVA assumptions are met.

[latex]\begin{eqnarray*} \\ H_0: &  &  \mu_1=\mu_2=\cdots=\mu_k\end{eqnarray*}[/latex].

[latex]\begin{eqnarray*} \\ H_a: &  & \mbox{at least one population mean is different from the others} \\ \\ \end{eqnarray*}[/latex]

• Collect the sample information for the test and identify the significance level [latex]\alpha[/latex].

[latex]\begin{eqnarray*}F & = & \frac{MST}{MSE} \\ \\ df_1 & = & k-1 \\ \\ df_2 &  = & n-k \\ \\ \end{eqnarray*}[/latex]

• The results of the sample data are significant.  There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
• The results of the sample data are not significant.  There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
• Write down a concluding sentence specific to the context of the question.

Assume the populations are normally distributed and have equal variances.  At the 5% significance level, is there a difference in the average GPA between the sports team.

Let basketball be population 1, let baseball be population 2, let hockey be population 3, and let lacrosse be population 4. From the question we have the following information:

Previously, we found [latex]k=4[/latex], [latex]n=20[/latex], and [latex]\overline{\overline{x}}=3.045[/latex].

Hypotheses:

[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3=\mu_4 \\   H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]

To calculate out the [latex]F[/latex]-score, we need to find [latex]MST[/latex] and [latex]MSE[/latex].

[latex]\begin{eqnarray*} SST & = & n_1 \times (\overline{x}_1-\overline{\overline{x}})^2+n_2\times (\overline{x}_2-\overline{\overline{x}})^2+n_3 \times (\overline{x}_3-\overline{\overline{x}})^2  +n_4 \times (\overline{x}_4-\overline{\overline{x}})^2\\  & = & 5 \times (3.22-3.045)^2+5 \times (3.02-3.045)^2+5 \times (3-3.045)^2 \\ &  & +5 \times (2.94 -3.045)^2 \\ & = & 0.2215 \\ \\ MST & = & \frac{SST}{k-1} \\ & = & \frac{0.2215 }{4-1} \\ & = & 0.0738...\\ \\  SSE & = & (n_1-1) \times s_1^2+ (n_2-1) \times s_2^2+  (n_3-1) \times s_3^2+ (n_4-1) \times s_4^2\\  & = &( 5-1) \times 0.277+(5-1) \times 0.487+(5-1) \times 0.56 +(5-1)\times 0.623 \\ & = & 7.788 \\ \\ MSE & = & \frac{SSE}{n-k} \\ & = & \frac{7.788 }{20-4} \\ & = & 0.48675\end{eqnarray*}[/latex]

The p -value is the area in the right tail of the [latex]F[/latex]-distribution.  To use the f.dist.rt  function, we need to calculate out the [latex]F[/latex]-score and the degrees of freedom:

[latex]\begin{eqnarray*} F & = &\frac{MST}{MSE} \\ & = & \frac{0.0738...}{0.48675} \\ & = & 0.15168... \\ \\ df_1 & = & k-1 \\ & = & 4-1 \\ & = & 3 \\ \\df_2 & = & n-k \\ & = & 20-4 \\ & = & 16\end{eqnarray*}[/latex]

So the p -value[latex]=0.9271[/latex].

Conclusion:

Because p -value[latex]=0.9271 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is  enough evidence to suggest that the mean GPA for the sports teams are the same.

• The null hypothesis [latex]\mu_1=\mu_2=\mu_3=\mu_4[/latex] is the claim that the mean GPA for the sports teams are all equal.
• The alternative hypothesis is the claim that at least one of the population means is not equal to the others.  The alternative hypothesis does not say that all of the population means are not equal, only that at least one of them is not equal to the others.
• The function is f.dist.rt because we are finding the area in the right tail of an [latex]F[/latex]-distribution.
• Field 1 is the value of [latex]F[/latex].
• Field 2 is the value of [latex]df_1[/latex].
• Field 3 is the value of [latex]df_2[/latex].
• The p -value of 0.9271 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the population means are all equal.

ANOVA Summary Tables

The calculation of the [latex]MST[/latex], [latex]MSE[/latex], and the [latex]F[/latex]-score for a one-way ANOVA test can be time consuming, even with the help of software like Excel.  However, Excel has a built-in one-way ANOVA summary table that not only generates the averages, variances, [latex]MST[/latex] and [latex]MSE[/latex], but also calculates the required [latex]F[/latex]-score and p -value for the test.

USING EXCEL TO CREATE A ONE-WAY ANOVA SUMMARY TABLE

In order to create a one-way ANOVA summary table, we need to use the Analysis ToolPak.  Follow these instructions to add the Analysis ToolPak.

• Enter the data into an Excel worksheet.
• Go to the Data tab and click on Data Analysis .  If you do not see Data Analysis in the Data tab, you will need to install the Analysis ToolPak.
• In the Data Analysis window, select Anova:  Single Factor .  Click OK .
• In the Inpu t range, enter the cell range for the data.
• In the Grouped By box, select rows if your data is entered as rows (the default is columns).
• Click on Labels in first row if the you included the column headings in the input range.
• In the Alpha box, enter the significance level for the test.
• From the Output Options , select the location where you want the output to appear.

This website provides additional information on using Excel to create a one-way ANOVA summary table.

Because we are using the p -value approach to hypothesis testing, it is not crucial that we enter the actual significance level we are using for the test.  The p -value (the area in the right tail of the [latex]F[/latex]-distribution) is not affected by significance level.  For the critical-value approach to hypothesis testing, we must enter the correct significance level for the test because the critical value does depend on the significance level.

Let basketball be population 1, let baseball be population 2, let hockey be population 3, and let lacrosse be population 4.

The ANOVA summary table generated by Excel is shown below:

The p -value for the test is in the P -value column of the between groups row .  So the p -value[latex]=0.9271[/latex].

• In the top part of the ANOVA summary table (under the Summary heading), we have the averages and variances for each of the groups (basketball, baseball, hockey, and lacrosse).
• The value of [latex]SST[/latex] (in the SS column of the between groups row).
• The value of [latex]MST[/latex] (in the MS column of the between group s row).
• The value of [latex]SSE[/latex] (in the SS column of the within groups row).
• The value of [latex]MSE[/latex] (in the MS column of the within groups row).
• The value of the [latex]F[/latex]-score (in the F column of the between groups row).
• The p -value (in the p -value column of the between groups row).

A fourth grade class is studying the environment.  One of the assignments is to grow bean plants in different soils.  Tommy chose to grow his bean plants in soil found outside his classroom mixed with dryer lint.  Tara chose to grow her bean plants in potting soil bought at the local nursery.  Nick chose to grow his bean plants in soil from his mother’s garden.  No chemicals were used on the plants, only water.  They were grown inside the classroom next to a large window.  Each child grew five plants.  At the end of the growing period, each plant was measured, producing the data (in inches) in the table below.

Assume the heights of the plants are normally distribution and have equal variance.  At the 5% significance level, does it appear that the three media in which the bean plants were grown produced the same mean height?

Let Tommy’s plants be population 1, let Tara’s plants be population 2, and let Nick’s plants be population 3.

[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3 \\   H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]

So the p -value[latex]=0.8760[/latex].

Because p -value[latex]=0.8760 \gt 0.05=\alpha[/latex], we do not reject the null hypothesis.  At the 5% significance level there is  enough evidence to suggest that the mean heights of the plants grown in three media are the same.

• The null hypothesis [latex]\mu_1=\mu_2=\mu_3[/latex] is the claim that the mean heights of the plants grown in the three different media are all equal.
• The p -value of 0.8760 is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true.  This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis.  In other words, the population means are all equal.

A statistics professor wants to study the average GPA of students in four different programs: marketing, management, accounting, and human resources.  The professor took a random sample of GPAs of students in those programs at the end of the past semester.  The data is recorded in the table below.

Assume the GPAs of the students are normally distributed and have equal variance.  At the 5% significance level, is there a difference in the average GPA of the students in the different programs?

Let marketing be population 1, let management be population 2, let accounting be population 3, and let human resources be population 4.

[latex]\begin{eqnarray*} H_0: & & \mu_1=\mu_2=\mu_3=\mu_4\\   H_a: & & \mbox{at least one population mean is different from the others} \end{eqnarray*}[/latex]

So the p -value[latex]=0.0462[/latex].

Because p -value[latex]=0.0462 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 5% significance level there is enough evidence to suggest that there is a difference in the average GPA of the students in the different programs.

A manufacturing company runs three different production lines to produce one of its products.  The company wants to know if the average production rate is the same for the three lines.  For each production line, a sample of eight hour shifts was taken and the number of items produced during each shift was recorded in the table below.

Assume the numbers of items produced on each line during an eight hour shift are normally distributed and have equal variance.  At the 1% significance level, is there a difference in the average production rate for the three lines?

Let Line 1 be population 1, let Line 2 be population 2, and let Line 3 be population 3.

So the p -value[latex]=0.0073[/latex].

Because p -value[latex]=0.0073 \lt 0.01=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis.  At the 1% significance level there is enough evidence to suggest that there is a difference in the average production rate of the three lines.

Concept Review

A one-way ANOVA hypothesis test determines if several population means are equal.  In order to conduct a one-way ANOVA test, the following assumptions must be met:

• Each population from which a sample is taken is assumed to be normal.
• All samples are randomly selected and independent.

The analysis of variance procedure compares the variation between groups [latex]MST[/latex] to the variation within groups [latex]MSE[/latex]. The ratio of these two estimates of variance is the [latex]F[/latex]-score from an [latex]F[/latex]-distribution with [latex]df_1=k-1[/latex] and [latex]df_2=n-k[/latex].  The p -value for the test is the area in the right tail of the [latex]F[/latex]-distribution.  The statistics used in an ANOVA test are summarized in the ANOVA summary table generated by Excel.

The one-way ANOVA hypothesis test for three or more population means is a well established process:

• Write down the null and alternative hypotheses in terms of the population means.  The null hypothesis is the claim that the population means are all equal and the alternative hypothesis is the claim that at least one of the population means is different from the others.
• Collect the sample information for the test and identify the significance level.
• The p -value is the area in the right tail of the [latex]F[/latex]-distribution.  Use the ANOVA summary table generated by Excel to find the p -value.
• Compare the  p -value to the significance level and state the outcome of the test.

Attribution

“ 13.1   One-Way ANOVA “  and “ 13.2   The F Distribution and the F-Ratio “ in Introductory Statistics by OpenStax  is licensed under a  Creative Commons Attribution 4.0 International License .

Introduction to Statistics Copyright © 2022 by Valerie Watts is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

• Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
• Duis aute irure dolor in reprehenderit in voluptate
• Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

10.2 - a statistical test for one-way anova.

Before we go into the details of the test, we need to determine the null and alternative hypotheses. Recall that for a test for two independent means, the null hypothesis was \(\mu_1=\mu_2\). In one-way ANOVA, we want to compare \(t\) population means, where \(t>2\). Therefore, the null hypothesis for analysis of variance for \(t\) population means is:

\(H_0\colon \mu_1=\mu_2=...\mu_t\)

The alternative, however, cannot be set up similarly to the two-sample case. If we wanted to see if two population means are different, the alternative would be \(\mu_1\ne\mu_2\). With more than two groups, the research question is “Are some of the means different?." If we set up the alternative to be \(\mu_1\ne\mu_2\ne…\ne\mu_t\), then we would have a test to see if ALL the means are different. This is not what we want. We need to be careful how we set up the alternative. The mathematical version of the alternative is...

\(H_a\colon \mu_i\ne\mu_j\text{ for some }i \text{ and }j \text{ where }i\ne j\)

This means that at least one of the pairs is not equal. The more common presentation of the alternative is:

\(H_a\colon \text{ at least one mean is different}\) or \(H_a\colon \text{ not all the means are equal}\)

Recall that when we compare the means of two populations for independent samples, we use a 2-sample t -test with pooled variance when the population variances can be assumed equal.

For more than two populations, the test statistic, \(F\), is the ratio of between group sample variance and the within-group-sample variance. That is,

\(F=\dfrac{\text{between group variance}}{\text{within group variance}}\)

Under the null hypothesis (and with certain assumptions), both quantities estimate the variance of the random error, and thus the ratio should be close to 1. If the ratio is large, then we have evidence against the null, and hence, we would reject the null hypothesis.

In the next section, we present the assumptions for this test. In the following section, we present how to find the between group variance, the within group variance, and the F-statistic in the ANOVA table.

Statistics Made Easy

Understanding the Null Hypothesis for ANOVA Models

A one-way ANOVA is used to determine if there is a statistically significant difference between the mean of three or more independent groups.

A one-way ANOVA uses the following null and alternative hypotheses:

• H 0 :  μ 1  = μ 2  = μ 3  = … = μ k  (all of the group means are equal)
• H A : At least one group mean is different   from the rest

To decide if we should reject or fail to reject the null hypothesis, we must refer to the p-value in the output of the ANOVA table.

If the p-value is less than some significance level (e.g. 0.05) then we can reject the null hypothesis and conclude that not all group means are equal.

A two-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups that have been split on two variables (sometimes called “factors”).

A two-way ANOVA tests three null hypotheses at the same time:

• All group means are equal at each level of the first variable
• All group means are equal at each level of the second variable
• There is no interaction effect between the two variables

To decide if we should reject or fail to reject each null hypothesis, we must refer to the p-values in the output of the two-way ANOVA table.

The following examples show how to decide to reject or fail to reject the null hypothesis in both a one-way ANOVA and two-way ANOVA.

Example 1: One-Way ANOVA

Suppose we want to know whether or not three different exam prep programs lead to different mean scores on a certain exam. To test this, we recruit 30 students to participate in a study and split them into three groups.

The students in each group are randomly assigned to use one of the three exam prep programs for the next three weeks to prepare for an exam. At the end of the three weeks, all of the students take the same exam. 

The exam scores for each group are shown below:

When we enter these values into the One-Way ANOVA Calculator , we receive the following ANOVA table as the output:

Notice that the p-value is 0.11385 .

For this particular example, we would use the following null and alternative hypotheses:

• H 0 :  μ 1  = μ 2  = μ 3 (the mean exam score for each group is equal)

Since the p-value from the ANOVA table is not less than 0.05, we fail to reject the null hypothesis.

This means we don’t have sufficient evidence to say that there is a statistically significant difference between the mean exam scores of the three groups.

Example 2: Two-Way ANOVA

Suppose a botanist wants to know whether or not plant growth is influenced by sunlight exposure and watering frequency.

She plants 40 seeds and lets them grow for two months under different conditions for sunlight exposure and watering frequency. After two months, she records the height of each plant. The results are shown below:

In the table above, we see that there were five plants grown under each combination of conditions.

For example, there were five plants grown with daily watering and no sunlight and their heights after two months were 4.8 inches, 4.4 inches, 3.2 inches, 3.9 inches, and 4.4 inches:

She performs a two-way ANOVA in Excel and ends up with the following output:

We can see the following p-values in the output of the two-way ANOVA table:

• The p-value for watering frequency is 0.975975 . This is not statistically significant at a significance level of 0.05.
• The p-value for sunlight exposure is 3.9E-8 (0.000000039) . This is statistically significant at a significance level of 0.05.
• The p-value for the interaction between watering  frequency and sunlight exposure is 0.310898 . This is not statistically significant at a significance level of 0.05.

These results indicate that sunlight exposure is the only factor that has a statistically significant effect on plant height.

And because there is no interaction effect, the effect of sunlight exposure is consistent across each level of watering frequency.

That is, whether a plant is watered daily or weekly has no impact on how sunlight exposure affects a plant.

Additional Resources

The following tutorials provide additional information about ANOVA models:

How to Interpret the F-Value and P-Value in ANOVA How to Calculate Sum of Squares in ANOVA What Does a High F Value Mean in ANOVA?

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

13.E: F Distribution and One-Way ANOVA (Exercises)

• Last updated
• Save as PDF
• Page ID 1154

These are homework exercises to accompany the Textmap created for "Introductory Statistics" by OpenStax.

13.1: Introduction

13.2: one-way anova.

Three different traffic routes are tested for mean driving time. The entries in the table are the driving times in minutes on the three different routes. The one-way \(ANOVA\) results are shown in Table.

State \(SS_{\text{between}}\), \(SS_{\text{within}}\), and the \(F\) statistic.

\(SS_{\text{between}} = 26\)

\(SS_{\text{within}} = 441\)

\(F = 0.2653\)

Suppose a group is interested in determining whether teenagers obtain their drivers licenses at approximately the same average age across the country. Suppose that the following data are randomly collected from five teenagers in each region of the country. The numbers represent the age at which teenagers obtained their drivers licenses.

State the hypotheses.

\(H_{0}\): ____________

\(H_{a}\): ____________

13.3: The F-Distribution and the F-Ratio

Use the following information to answer the next five exercises. There are five basic assumptions that must be fulfilled in order to perform a one-way \(ANOVA\) test. What are they?

Exercise 13.2.1

Write one assumption.

Each population from which a sample is taken is assumed to be normal.

Exercise 13.2.2

Write another assumption.

Exercise 13.2.3

Write a third assumption.

The populations are assumed to have equal standard deviations (or variances).

Exercise 13.2.4

Write a fourth assumption.

Exercise 13.2.5

Write the final assumption.

The response is a numerical value.

Exercise 13.2.6

State the null hypothesis for a one-way \(ANOVA\) test if there are four groups.

Exercise 13.2.7

State the alternative hypothesis for a one-way \(ANOVA\) test if there are three groups.

\(H_{a}: \text{At least two of the group means } \mu_{1}, \mu_{2}, \mu_{3} \text{ are not equal.}\)

Exercise 13.2.8

When do you use an \(ANOVA\) test?

Use the following information to answer the next three exercises. Suppose a group is interested in determining whether teenagers obtain their drivers licenses at approximately the same average age across the country. Suppose that the following data are randomly collected from five teenagers in each region of the country. The numbers represent the age at which teenagers obtained their drivers licenses.

\(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4} = \mu_{5}\)

\(H_{a}\): At least any two of the group means \(\mu_{1} , \mu_{2}, \dotso, \mu_{5}\) are not equal.

degrees of freedom – numerator: \(df(\text{num}) =\) _________

degrees of freedom – denominator: \(df(\text{denom}) =\) ________

\(df(\text{denom}) = 15\)

\(F\) statistic = ________

13.4: Facts About the F Distribution

Exercise 13.4.4

An \(F\) statistic can have what values?

Exercise 13.4.5

What happens to the curves as the degrees of freedom for the numerator and the denominator get larger?

The curves approximate the normal distribution.

Use the following information to answer the next seven exercise. Four basketball teams took a random sample of players regarding how high each player can jump (in inches). The results are shown in Table.

Exercise 13.4.6

What is the \(df(\text{num})\)?

Exercise 13.4.7

What is the \(df(\text{denom})\)?

Exercise 13.4.8

What are the Sum of Squares and Mean Squares Factors?

Exercise 13.4.9

What are the Sum of Squares and Mean Squares Errors?

\(SS = 237.33; MS = 23.73\)

Exercise 13.4.10

What is the \(F\) statistic?

Exercise 13.4.11

What is the \(p\text{-value}\)?

Exercise 13.4.12

At the 5% significance level, is there a difference in the mean jump heights among the teams?

Use the following information to answer the next seven exercises. A video game developer is testing a new game on three different groups. Each group represents a different target market for the game. The developer collects scores from a random sample from each group. The results are shown in Table

Exercise 13.4.13

Exercise 13.4.14

Exercise 13.4.15

What are the \(SS_{\text{between}}\) and \(MS_{\text{between}}\)?

\(SS_{\text{between}} = 5,700.4\);

\(MS_{\text{between}} = 2,850.2\)

Exercise 13.4.16

What are the \(SS_{\text{within}}\) and \(MS_{\text{within}}\)?

Exercise 13.4.17

What is the \(F\) Statistic?

Exercise 13.4.18

Exercise 13.4.19

At the 10% significance level, are the scores among the different groups different?

Yes, there is enough evidence to show that the scores among the groups are statistically significant at the 10% level.

Enter the data into your calculator or computer.

Exercise 13.4.20

\(p\text{-value} =\) ______

State the decisions and conclusions (in complete sentences) for the following preconceived levels of \(\alpha\).

Exercise 13.4.21

\(\alpha = 0.05\)

• Decision: ____________________________
• Conclusion: ____________________________

Exercise 13.4.22

\(\alpha = 0.01\)

Use the following information to answer the next eight exercises. Groups of men from three different areas of the country are to be tested for mean weight. The entries in the table are the weights for the different groups. The one-way \(ANOVA\) results are shown in Table .

Exercise 13.3.2

What is the Sum of Squares Factor?

Exercise 13.3.3

What is the Sum of Squares Error?

Exercise 13.3.4

What is the \(df\) for the numerator?

Exercise 13.3.5

What is the \(df\) for the denominator?

Exercise 13.3.6

What is the Mean Square Factor?

Exercise 13.3.7

What is the Mean Square Error?

Exercise 13.3.8

Use the following information to answer the next eight exercises. Girls from four different soccer teams are to be tested for mean goals scored per game. The entries in the table are the goals per game for the different teams. The one-way \(ANOVA\) results are shown in Table .

Exercise 13.3.9

What is \(SS_{\text{between}}\)?

Exercise 13.3.10

Exercise 13.3.11

What is \(MS_{\text{between}}\)?

Exercise 13.3.12

What is \(SS_{\text{within}}\)?

Exercise 13.3.13

Exercise 13.3.14

What is \(MS_{\text{within}}\)?

Exercise 13.3.15

Exercise 13.3.16

Judging by the \(F\) statistic, do you think it is likely or unlikely that you will reject the null hypothesis?

Because a one-way \(ANOVA\) test is always right-tailed, a high \(F\) statistic corresponds to a low \(p\text{-value}\), so it is likely that we will reject the null hypothesis.

Use a solution sheet to conduct the following hypothesis tests. The solution sheet can be found in [link] .

Three students, Linda, Tuan, and Javier, are given five laboratory rats each for a nutritional experiment. Each rat's weight is recorded in grams. Linda feeds her rats Formula A, Tuan feeds his rats Formula B, and Javier feeds his rats Formula C. At the end of a specified time period, each rat is weighed again, and the net gain in grams is recorded. Using a significance level of 10%, test the hypothesis that the three formulas produce the same mean weight gain.

• \(H_{0}: \mu_{L} = \mu_{T} = \mu_{J}\)
• at least any two of the means are different
• \(df(\text{num}) = 2; df(\text{denom}) = 12\)
• \(F\) distribution
• Check student’s solution.
• Decision: Do not reject null hypothesis; Conclusion: There is insufficient evidence to conclude that the means are different.

A grassroots group opposed to a proposed increase in the gas tax claimed that the increase would hurt working-class people the most, since they commute the farthest to work. Suppose that the group randomly surveyed 24 individuals and asked them their daily one-way commuting mileage. The results are in Table . Using a 5% significance level, test the hypothesis that the three mean commuting mileages are the same.

Examine the seven practice laps from [link] . Determine whether the mean lap time is statistically the same for the seven practice laps, or if there is at least one lap that has a different mean time from the others.

• \(H_{0}: \mu_{1} = \mu_{2} = \mu_{3} = \mu_{4} = \mu_{5} = \mu_{6} = \mu_{T}\)
• At least two mean lap times are different.
• \(df(\text{num}) = 6; df(\text{denom}) = 98\)
• Decision: Do not reject null hypothesis; Conclusion: There is insufficient evidence to conclude that the mean lap times are different.

Use the following information to answer the next two exercises. Table lists the number of pages in four different types of magazines.

Using a significance level of 5%, test the hypothesis that the four magazine types have the same mean length.

Eliminate one magazine type that you now feel has a mean length different from the others. Redo the hypothesis test, testing that the remaining three means are statistically the same. Use a new solution sheet. Based on this test, are the mean lengths for the remaining three magazines statistically the same?

• \(H_{a}: \mu_{d} = \mu_{n} = \mu_{h}\)
• At least any two of the magazines have different mean lengths.
• \(df(\text{num}) = 2, df(\text{denom}) = 12\)
• \(F\) distribtuion
• \(F = 15.28\)
• \(p\text{-value} = 0.001\)
• \(\alpha: 0.05\)
• Decision: Reject the Null Hypothesis.
• Reason for decision: \(p\text{-value} < \alpha\)
• Conclusion: There is sufficient evidence to conclude that the mean lengths of the magazines are different.

A researcher wants to know if the mean times (in minutes) that people watch their favorite news station are the same. Suppose that Table shows the results of a study.

Assume that all distributions are normal, the four population standard deviations are approximately the same, and the data were collected independently and randomly. Use a level of significance of 0.05.

Are the means for the final exams the same for all statistics class delivery types? Table shows the scores on final exams from several randomly selected classes that used the different delivery types.

• \(H_{0}: \mu_{o} = \mu_{h} = \mu_{f}\)
• At least two of the means are different.
• \(df(\text{n}) = 2, df(\text{d}) = 13\)
• \(F_{2,13}\)
• Decision: Do not reject the null hypothesis.
• Conclusion: The mean scores of different class delivery are not different.

Are the mean number of times a month a person eats out the same for whites, blacks, Hispanics and Asians? Suppose that Table shows the results of a study.

Are the mean numbers of daily visitors to a ski resort the same for the three types of snow conditions? Suppose that Table shows the results of a study.

• \(H_{0}: \mu_{p} = \mu_{m} = \mu_{h}\)
• At least any two of the means are different.
• \(df(\text{n}) = 2, df(\text{d}) = 12\)
• \(F_{2,12}\)
• Conclusion: There is not sufficient evidence to conclude that the mean numbers of daily visitors are different.

Sanjay made identical paper airplanes out of three different weights of paper, light, medium and heavy. He made four airplanes from each of the weights, and launched them himself across the room. Here are the distances (in meters) that his planes flew.

Figure 13.4.1.

• Take a look at the data in the graph. Look at the spread of data for each group (light, medium, heavy). Does it seem reasonable to assume a normal distribution with the same variance for each group? Yes or No.
• Why is this a balanced design?
• Calculate the sample mean and sample standard deviation for each group.
• variance of the group means __________
• \(MS_{\text{between}} =\) ___________
• mean of the three sample variances ___________
• \(MS_{\text{within}} =\) _____________
• \(F\) statistic = ____________
• \(df(\text{num}) =\) __________, \(df(\text{denom}) =\) ___________
• number of groups _______
• number of observations _______
• \(p\text{-value} =\) __________ (\(P(F >\) _______\() =\) __________)
• Graph the \(p\text{-value}\).
• decision: _______________________
• conclusion: _______________________________________________________________

DDT is a pesticide that has been banned from use in the United States and most other areas of the world. It is quite effective, but persisted in the environment and over time became seen as harmful to higher-level organisms. Famously, egg shells of eagles and other raptors were believed to be thinner and prone to breakage in the nest because of ingestion of DDT in the food chain of the birds.

An experiment was conducted on the number of eggs (fecundity) laid by female fruit flies. There are three groups of flies. One group was bred to be resistant to DDT (the RS group). Another was bred to be especially susceptible to DDT (SS). Finally there was a control line of non-selected or typical fruitflies (NS). Here are the data:

The values are the average number of eggs laid daily for each of 75 flies (25 in each group) over the first 14 days of their lives. Using a 1% level of significance, are the mean rates of egg selection for the three strains of fruitfly different? If so, in what way? Specifically, the researchers were interested in whether or not the selectively bred strains were different from the nonselected line, and whether the two selected lines were different from each other.

Here is a chart of the three groups:

The data appear normally distributed from the chart and of similar spread. There do not appear to be any serious outliers, so we may proceed with our ANOVA calculations, to see if we have good evidence of a difference between the three groups.

\(H_{0}: \mu_{1} = \mu_{2} = \mu_{3}\);

\(H_{a}: \mu_{i} \neq \mu_{j}\) some \(i \neq j\).

Define \(\mu_{1}, \mu_{2}, \mu_{3}\), as the population mean number of eggs laid by the three groups of fruit flies.

\(F\) statistic \(= 8.6657\);

\(p\text{-value} = 0.0004\)

Decision: Since the \(p\text{-value}\) is less than the level of significance of 0.01, we reject the null hypothesis.

Conclusion: We have good evidence that the average number of eggs laid during the first 14 days of life for these three strains of fruitflies are different.

Interestingly, if you perform a two sample \(t\)-test to compare the RS and NS groups they are significantly different (\(p = 0.0013\)). Similarly, SS and NS are significantly different (\(p = 0.0006\)). However, the two selected groups, RS and SS are not significantly different (\(p = 0.5176\)). Thus we appear to have good evidence that selection either for resistance or for susceptibility involves a reduced rate of egg production (for these specific strains) as compared to flies that were not selected for resistance or susceptibility to DDT. Here, genetic selection has apparently involved a loss of fecundity.

The data shown is the recorded body temperatures of 130 subjects as estimated from available histograms.

Traditionally we are taught that the normal human body temperature is 98.6 F. This is not quite correct for everyone. Are the mean temperatures among the four groups different?

Calculate 95% confidence intervals for the mean body temperature in each group and comment about the confidence intervals.

13.5: Test of Two Variances

Use the following information to answer the next two exercises. There are two assumptions that must be true in order to perform an \(F\) test of two variances.

Exercise 13.5.2

Name one assumption that must be true.

The populations from which the two samples are drawn are normally distributed.

Exercise 13.5.3

What is the other assumption that must be true?

Use the following information to answer the next five exercises. Two coworkers commute from the same building. They are interested in whether or not there is any variation in the time it takes them to drive to work. They each record their times for 20 commutes. The first worker’s times have a variance of 12.1. The second worker’s times have a variance of 16.9. The first worker thinks that he is more consistent with his commute times and that his commute time is shorter. Test the claim at the 10% level.

Exercise 13.5.4

State the null and alternative hypotheses.

\(H_{0}: \sigma_{1} = \sigma_{2}\)

\(H_{a}: \sigma_{1} < \sigma_{2}\)

• \(H_{0}: \sigma^{2}_{1} = \sigma^{2}_{2}\)

\(H_{a}: \sigma^{2}_{1} < \sigma^{2}_{2}\)

Exercise 13.5.5

What is \(s_{1}\) in this problem?

Exercise 13.5.6

What is \(s_{2}\) in this problem?

Exercise 13.5.7

What is \(n\)?

Exercise 13.5.8

Exercise 13.5.9

Exercise 13.5.10

Is the claim accurate?

No, at the 10% level of significance, we do not reject the null hypothesis and state that the data do not show that the variation in drive times for the first worker is less than the variation in drive times for the second worker.

Use the following information to answer the next four exercises. Two students are interested in whether or not there is variation in their test scores for math class. There are 15 total math tests they have taken so far. The first student’s grades have a standard deviation of 38.1. The second student’s grades have a standard deviation of 22.5. The second student thinks his scores are lower.

Exercise 13.5.11

Exercise 13.5.12

Exercise 13.5.13

Exercise 13.5.14

At the 5% significance level, do we reject the null hypothesis?

Reject the null hypothesis. There is enough evidence to say that the variance of the grades for the first student is higher than the variance in the grades for the second student.

Use the following information to answer the next three exercises. Two cyclists are comparing the variances of their overall paces going uphill. Each cyclist records his or her speeds going up 35 hills. The first cyclist has a variance of 23.8 and the second cyclist has a variance of 32.1. The cyclists want to see if their variances are the same or different.

Exercise 13.5.15

Exercise 13.5.16

Exercise 13.5.17

At the 5% significance level, what can we say about the cyclists’ variances?

Three students, Linda, Tuan, and Javier, are given five laboratory rats each for a nutritional experiment. Each rat’s weight is recorded in grams. Linda feeds her rats Formula A, Tuan feeds his rats Formula B, and Javier feeds his rats Formula C. At the end of a specified time period, each rat is weighed again and the net gain in grams is recorded.

Determine whether or not the variance in weight gain is statistically the same among Javier’s and Linda’s rats. Test at a significance level of 10%.

• \(H_{a}: \sigma^{2}_{1} \neq \sigma^{2}_{1}\)
• \(df(\text{num}) = 4; df(\text{denom}) = 4\)
• \(F_{4, 4}\)
• \(2(0.1563) = 0.3126\). Using the TI-83+/84+ function 2-SampFtest, you get the test statistic as 2.9986 and p -value directly as 0.3127. If you input the lists in a different order, you get a test statistic of 0.3335 but the \(p\text{-value}\) is the same because this is a two-tailed test.
• Check student't solution.
• Decision: Do not reject the null hypothesis; Conclusion: There is insufficient evidence to conclude that the variances are different.

A grassroots group opposed to a proposed increase in the gas tax claimed that the increase would hurt working-class people the most, since they commute the farthest to work. Suppose that the group randomly surveyed 24 individuals and asked them their daily one-way commuting mileage. The results are as follows.

Determine whether or not the variance in mileage driven is statistically the same among the working class and professional (middle income) groups. Use a 5% significance level.

Refer to the data from [link] .

Examine practice laps 3 and 4. Determine whether or not the variance in lap time is statistically the same for those practice laps.

Use the following information to answer the next two exercises. The following table lists the number of pages in four different types of magazines.

• \(df(\text{n}) = 19, df(\text{d}) = 19\)
• \(F_{19,19}\)
• Reason for decision: \(p\text{-value} > \alpha\)
• Conclusion: There is not sufficient evidence to conclude that the variances are different.

Which two magazine types do you think have the same variance in length?

Which two magazine types do you think have different variances in length?

The answers may vary. Sample answer: Home decorating magazines and news magazines have different variances.

Is the variance for the amount of money, in dollars, that shoppers spend on Saturdays at the mall the same as the variance for the amount of money that shoppers spend on Sundays at the mall? Suppose that the Table shows the results of a study.

Are the variances for incomes on the East Coast and the West Coast the same? Suppose that Table shows the results of a study. Income is shown in thousands of dollars. Assume that both distributions are normal. Use a level of significance of 0.05.

• \(df(\text{n}) = 7, df(\text{d}) = 6\)
• \(F_{7,6}\)

Thirty men in college were taught a method of finger tapping. They were randomly assigned to three groups of ten, with each receiving one of three doses of caffeine: 0 mg, 100 mg, 200 mg. This is approximately the amount in no, one, or two cups of coffee. Two hours after ingesting the caffeine, the men had the rate of finger tapping per minute recorded. The experiment was double blind, so neither the recorders nor the students knew which group they were in. Does caffeine affect the rate of tapping, and if so how?

Here are the data:

King Manuel I, Komnenus ruled the Byzantine Empire from Constantinople (Istanbul) during the years 1145 to 1180 A.D. The empire was very powerful during his reign, but declined significantly afterwards. Coins minted during his era were found in Cyprus, an island in the eastern Mediterranean Sea. Nine coins were from his first coinage, seven from the second, four from the third, and seven from a fourth. These spanned most of his reign. We have data on the silver content of the coins:

Did the silver content of the coins change over the course of Manuel’s reign?

Here are the means and variances of each coinage. The data are unbalanced.

Here is a strip chart of the silver content of the coins:

While there are differences in spread, it is not unreasonable to use \(ANOVA\) techniques. Here is the completed \(ANOVA\) table:

\(P(F > 26.272) = 0\);

Reject the null hypothesis for any alpha. There is sufficient evidence to conclude that the mean silver content among the four coinages are different. From the strip chart, it appears that the first and second coinages had higher silver contents than the third and fourth.

The American League and the National League of Major League Baseball are each divided into three divisions: East, Central, and West. Many years, fans talk about some divisions being stronger (having better teams) than other divisions. This may have consequences for the postseason. For instance, in 2012 Tampa Bay won 90 games and did not play in the postseason, while Detroit won only 88 and did play in the postseason. This may have been an oddity, but is there good evidence that in the 2012 season, the American League divisions were significantly different in overall records? Use the following data to test whether the mean number of wins per team in the three American League divisions were the same or not. Note that the data are not balanced, as two divisions had five teams, while one had only four.

Here is a stripchart of the number of wins for the 14 teams in the AL for the 2012 season.

While the spread seems similar, there may be some question about the normality of the data, given the wide gaps in the middle near the 0.500 mark of 82 games (teams play 162 games each season in MLB). However, one-way \(ANOVA\) is robust.

Here is the \(ANOVA\) table for the data:

\(P(F > 1.5521) = 0.2548\)

Since the \(p\text{-value}\) is so large, there is not good evidence against the null hypothesis of equal means. We decline to reject the null hypothesis. Thus, for 2012, there is not any have any good evidence of a significant difference in mean number of wins between the divisions of the American League.

13.6: Lab: One-Way ANOVA

• Salary & Income Tax Calculators
• Mortgage Calculators
• Retirement Calculators
• Depreciation Calculators
• Statistics and Analysis Calculators
• Date and Time Calculators
• Contractor Calculators
• Budget & Savings Calculators
• Loan Calculators
• Forex Calculators
• Real Function Calculators
• Engineering Calculators
• Tax Calculators
• Volume Calculators
• 2D Shape Calculators
• 3D Shape Calculators
• Logistics Calculators
• HRM Calculators
• Sales & Investments Calculators
• Grade & GPA Calculators
• Conversion Calculators
• Ratio Calculators
• Sports & Health Calculators
• Other Calculators

ANOVA Calculator: One-Way Analysis of Variance Calculator

This One-way ANOVA Test Calculator helps you to quickly and easily produce a one-way analysis of variance (ANOVA) table that includes all relevant information from the observation data set including sums of squares, mean squares, degrees of freedom, F- and P-values.

To use the One-way ANOVA Calculator, input the observation data, separating the numbers with a comma, line break, or space for every group and then click on the "Calculate" button to generate the results.

Group 1 5,1,11,2,8

Group 2 0,1,4,6,3

Group 3 13,9,8,15,7

+ Add Group   − Delete Group  

ANOVA Formulas

Between Groups Degrees of Freedom: DF = k − 1 , where k is the number of groups

Within Groups Degrees of Freedom: DF = N − k , where N is the total number of subjects

Total Degrees of Freedom: DF = N − 1

Sum of Squares Between Groups: SS B = S k i=1 n i ( x i − x ) 2 , where n i is the number of subjects in the i-th group

Sum of Squares Within Groups: SS W = S k i=1 (n i − 1) S i 2 , where S i is the standard deviation of the i-th group

Total Sum of Squares: SS T = SS B + SS W

Mean Square Between Groups: MS B = SS B / (k − 1)

Mean Square Within Groups: MS W = SS W / (N − k)

F-Statistic (or F-ratio): F = MS B / MS W

• Currently 4.79/5

Rating: 4.8 /5 (1019 votes)

How do I perform a One-Way ANOVA in Google Sheets?

Table of Contents

A One-Way ANOVA (Analysis of Variance) is a statistical test used to compare the means of three or more groups. This test can be performed in Google Sheets by following a few simple steps. First, organize your data into columns, with each column representing a different group. Then, go to the “Data” tab and select “Data analysis” from the drop-down menu. Choose “ANOVA: Single Factor” and input the range of data for each group. Finally, click “OK” to view the results, which will include the F-statistic and p-value. This test can help determine if there is a significant difference between the means of the groups.

One-Way ANOVA in Google Sheets (Step-by-Step)

A one-way ANOVA is used to determine whether or not there is a statistically significant difference between the means of three or more independent groups.

This tutorial provides a step-by-step example of how to perform a one-way ANOVA in Google Sheets.

Step 1: Install the XLMiner Analysis ToolPak

To perform a one-way ANOVA in Google Sheets, we need to first install the free XLMiner Analysis Toolpak.

To do so, click  Add-ons > Get add-ons :

Next, type  XLMiner Analysis ToolPak in the search bar and click the icon that appears:

Lastly, click the  Install button.

Step 2: Enter the Data

Next, we need to enter the data to use for the one-way ANOVA.

For this example, suppose a researcher recruits 30 students to participate in a study. The students are randomly assigned to use one of three studying methods to prepare for an exam. The exam results for each student are shown below:

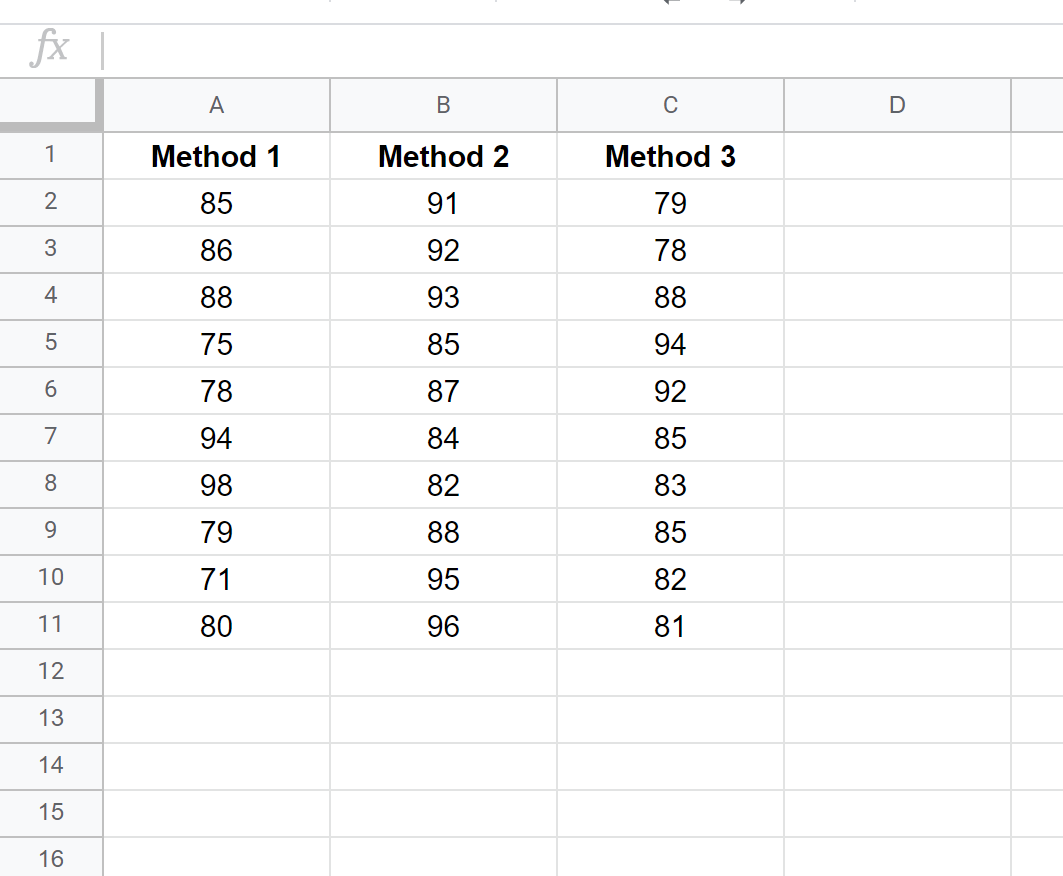
Step 3: Perform the One-Way ANOVA

To perform a one-way ANOVA on this dataset, click Add-ons > XLMiner Analysis ToolPak > Start . The Analysis ToolPak will appear on the right side of the screen.

Click  Anova: Single Factor and fill in the following information:

Step 4: Interpret the Results

Once you click  OK , the results of the one-way ANOVA will appear starting in the cell you specified in  Output Range . In our case, we chose to display the results starting in cell E1:

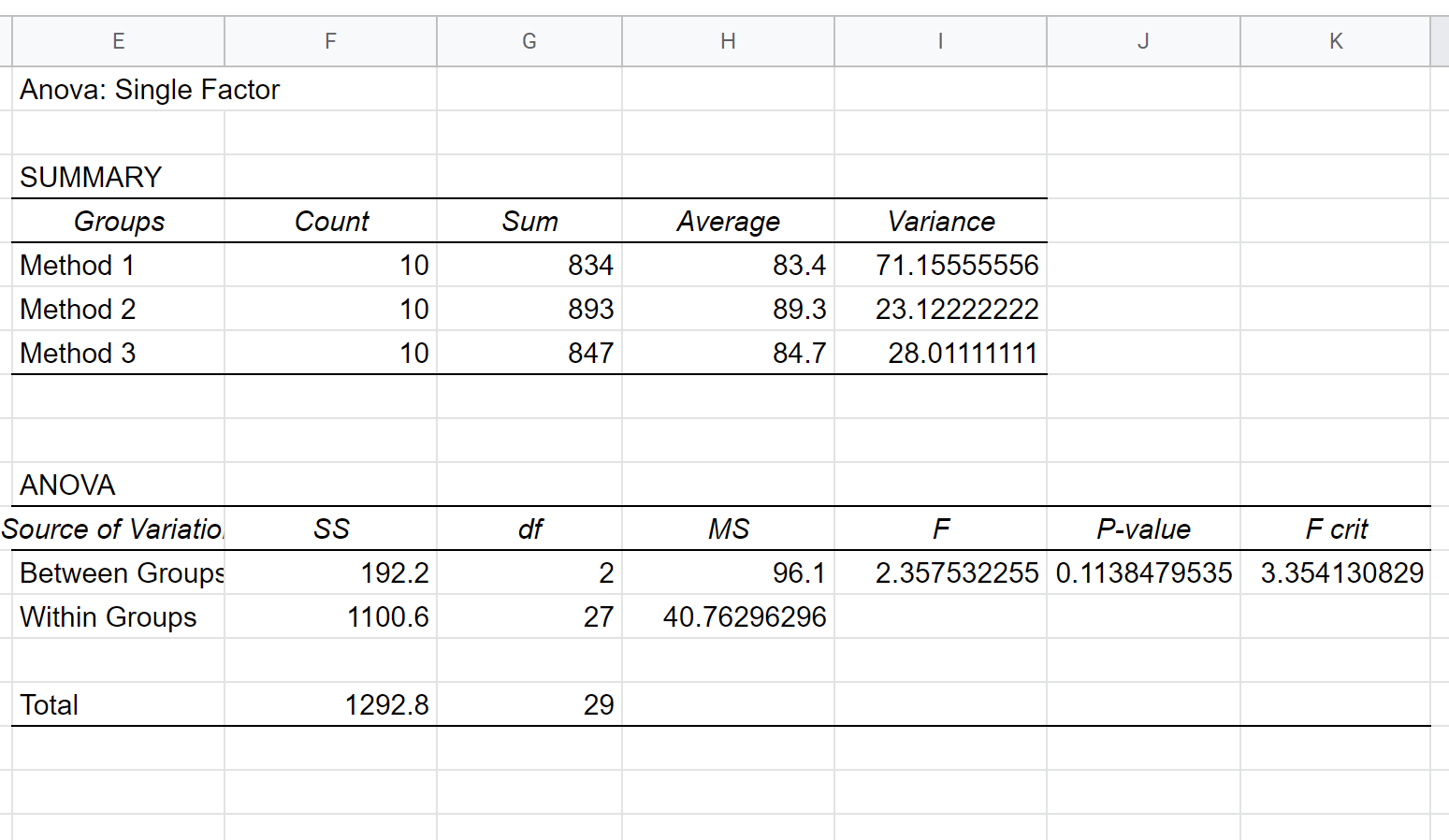
There are two tables shown in the output.

The first table shows the count, sum, average, and variance of the test scores for each of the three groups.

The second table displays the results of the one-way ANOVA, including:

• F-statistic: 2.3575
• F Critical value : 3.3541
• P-value: 0.1138

Recall that a one-way ANOVA has the following null and alternative hypotheses:

• H 0  (null hypothesis): All group means are equal.
• H A (alternative hypothesis): At least one group mean is different   from the rest.

Since the p-value in the ANOVA table (.1138) is not less than .05, we do not have sufficient evidence to reject the null hypothesis.

Thus, we don’t have evidence to say that the three different studying methods lead to different exam scores.

Additional Resources

How to Perform a One-Way ANOVA in Excel How to Perform a One-Way ANOVA by Hand One-Way ANOVA Calculator

Related terms:

• Difference between One-Way ANOVA and Repeated Measures ANOVA
• What Does a High F Value Mean in ANOVA? what does the f value mean in anova
• When should one use a one-way ANOVA and when should one use a two-way ANOVA?
• How do I run a Repeated Measures ANOVA in Google Sheets?
• Count Specific Characters in Google Sheets How to count specific characters in google sheets?
• How can I perform a Repeated Measures ANOVA in Excel?
• “How do you perform a Two-Way ANOVA in Excel?”
• How do you perform a one-way ANOVA by hand?
• How do you perform a One-Way ANOVA in SPSS?
• How do you perform a Two-Way ANOVA in SPSS?