theory of teaching essay passing score 8

A Theory of Teaching

• Open Access
• First Online: 07 June 2023

Cite this chapter

You have full access to this open access chapter

• Alan H. Schoenfeld 3  

4818 Accesses

4 Citations

1 Altmetric

Whether one can claim to have a theory of teaching depends on what one takes to constitute teaching and what one means by theory. This chapter characterizes both. Given those characterizations, I claim that we already have a theory of teaching, which specifies that teachers’ in-the-moment classroom decisions can be modeled by attending to three major factors: the resources at the teachers’ disposal (both their knowledge and material resources), their orientations (beliefs, preferences, values, etc.), and their goals (which exist at multiple levels and change dynamically according to evolving events). Beyond that, the Teaching for Robust Understanding (TRU) framework indicates that the following five dimensions of learning environments are consequential and comprehensive – the degree to which the environment: (1) offers affordances for rich engagement with content; (2) operates within the students’ zone of proximal development; (3) supports all students in engaging with core content; (4) provides opportunities for students to contribute to classroom discourse and develop a sense of agency and disciplinary identity; and, (5) reveals and responds to student thinking. Combining these two theoretical frames yields a theoretical specification of what has been called “ambitious teaching.” There is much more to be concerned with, however. In general, the field’s understanding of relevant knowledge and resources for ambitious teaching is weak, a problem exacerbated by the widespread adoption of virtual instruction due to the presence of Covid-19. Moreover, little is understood regarding teachers’ developmental trajectories. Such knowledge will be necessary to establish effective long-term professional development efforts.

• Ambitious instruction
• Models of teaching
• Teaching for robust understanding
• Teachers’ decision making
• Theories of teaching

Download chapter PDF

Similar content being viewed by others

Processes of Building Theories of Learning: Three Contrasting Cases

Taking Teaching Philosophies Seriously: Pedagogical Identity, Philosophy of Education, and New Opportunities for Publication

Connecting Theory to Concept Building: Designing Instruction for Learning

1 introduction and overview.

This essay grapples with the framing questions offered by the book’s editors:

What is a theory (of teaching)?

What should it contain and why?

Can such a theory accommodate differences across subject matters and student populations taught? If so, how? If not, why?

Do we already have a theory/theories on teaching? If so, which are they?

In the future, in what ways might it be possible, if at all, to create a (more comprehensive) theory of teaching?

In a concluding discussion I also address some of the larger issues of context raised in Hill and Lampert’s foreword

For the purposes of this paper I will use the standard dictionary definition of what it means to teach. The Merriam-Webster dictionary ( 2020 ) defines “teach” as follows: “to cause to know something… to guide the studies of… to impart the knowledge of (e.g., teach algebra) to instruct by precept, example, or experience… to conduct instruction regularly in teach school” ( https://www.merriam-webster.com/dictionary/teach ). It goes without saying that there is more to the totality of teaching than this – for example, planning, creating materials, and meeting with students outside of class, to name but a few. But the common-sense definition of teaching is “the act of instructing students in the classroom.” That definition frames most of what follows.

To put my theoretical cards on the table: There does exist a theory of human in-the-moment decision making in complex social contexts (Schoenfeld, 2011 ). This empirically validated theory includes as a subset the decision making by teachers during the act of instruction– that is, “teaching” in the sense characterized above. As elaborated in Sect. 2 , the theory says that it suffices to understand teachers’ resources, orientations, and goals in order to model teachers’ choices during instruction. Hence, we already have a theory of teaching. I suspect, however, that such a value-neutral question was not the sole intention of the editors. The question most people are interested in is, do we have a theory of “good teaching” (or, as characterized below, “teaching for robust understanding”)?

A theory of teaching as framed above does not address the question of what the appropriate goals for instruction should be, or how to achieve them. By analogy, consider the fact that there has been a theory of internal combustion engines for almost two centuries: Samuel Brown obtained a patent for an internal combustion engine suitable for industrial use in 1823, and Gottlieb Daimler and Karl Benz patented gasoline engines in the late 1870s. Thus in a sense, there was a “theory of cars” a century and a half ago. Nonetheless, the contexts in which automobiles operate and the goals for automotive performance have evolved continuously over the decades. The relevant question for automobiles is, what are current or emerging performance goals (including safety, etc.) and how can they be achieved?

With regard to teaching then, the question is what goals are appropriate for learning environments – in the sense that if learning environments attain those goals, students will emerge from them being knowledgeable and agentive thinkers and problem solvers. Notice the fundamental shift in frame. The key question is not “what should a teacher do,” which is teacher-focused, but “what properties should the learning environment have?”, which focuses on the experiences of students. It goes without saying that the teacher is the key agent in establishing and maintaining the learning environment – but the goals for the teacher are then focused on how students experience it.

Here too, there exists a theoretical framing that addresses the issue in principle. The Teaching for Robust Understanding (TRU) Framework (Schoenfeld, 2014 ; Teaching for Robust Understanding Project, 2018 ) identifies key dimensions of productive learning environments. As such it serves to establish appropriate teaching goals. See Sect. 3 .

Such a theoretical framing, however, leaves much work to be done. There are questions of how to frame materials and learning experiences for teachers, so they can develop the resources to attain the goals specified in Sect. 3 . And there are questions about next steps in an R&D agenda that pursues these issues. See Sect. 4 .

2 A Theory of In-The-Moment Decision Making

I begin with a characterization of “theory.” The web definition provides a good start: “a supposition or a system of ideas intended to explain something, especially one based on general principles independent of the thing to be explained.” Footnote 1 The implied generality in this definition is important, in that a theory applies to a class of objects, actions, and relations: “under certain circumstances, specific objects interact in specific ways.” The National Academy of Sciences ( 1999 , p. 2) elaborates, “Theory: In science, a well-substantiated explanation of some aspect of the natural world that can incorporate facts, laws, inferences, and tested hypotheses.” Popper ( 1963 ) goes further, arguing that theories should be falsifiable. The idea is that ( pace Schrödinger) most theories should enable predictions in a wide range of cases. With each confirmation, if it comes, there is more reason to believe in the robustness of the theory.

With these characterizations in mind I discuss the idea of a theory of teaching – more generally, a theory of knowledge-based decision making in complex social contexts. The general question is as follows. Suppose you are trying to explain/predict the decisions made by an individual while they are engaged in a “well practiced” endeavor – something they’re been doing for a while, so they have a body of knowledge and routines at their disposal. In general, what would you have to know about that person, and the context, in order to explain/predict that person’s decision making? Specifically in the case of teaching, what would you have to know about a teacher in order to explain or predict what a teacher does when confronted by various circumstances as instructional activities unfold?

The key idea is that human decision-making is goal oriented and can be modeled as such . In-the-moment decision making in any context can be modeled as a function of three categories of things:

The decision maker’s goals in that context at that time.

The decision maker’s orientations (beliefs, preferences, values, tastes, biases, etc.), which shape the choice and prioritizing of goals and

The resources (mostly knowledge, but also material resources) available in the context where the decision making is taking place.

The fundamental mechanism governing decision makers’ choices is outlined in Fig. 6.1 .

How people make decisions, in outline Reprinted with permission from Schoenfeld ( 2011 , p. 18)

A comprehensive case for this theoretical framing is provided in Schoenfeld ( 2011 ), which offers a series of models of teachers’ decision making. A few examples will convey the ways in which goals, orientations and resources operate.

First, goals operate at multiple levels and multiple goals may be activated at the same time. A teacher may want to cover the curriculum, teach for understanding, prepare students for an upcoming test, create a welcoming environment, help students become reflective learners, and more (see, e.g., Lampert, 2001 ). Second, prior to entering the classroom, the teacher may have a plan that establishes top-level goals and subgoals: “I want to introduce this material today. I’ll review the homework, spend the bulk of time on the new material, and close by assigning homework.”

The selection of goals and their prioritization is shaped by the teacher’s orientations (primarily belief systems, which evolve over time), as is the set of resources the teacher will bring to bear in any context. For example, one teacher taught a particular class in a very procedural manner: “Step 1, do this. Step 2, do this…” Asked if he would consider asking the students an open question, his response was “Not these students, it would confuse them. I do that with my honors students.” That is, his beliefs about appropriate pedagogies for students with different “abilities” resulted in his choosing different pedagogies for teaching them (Schoenfeld, 1988 ). Footnote 2 Equity-oriented goals may result in the prioritization of particular classroom routines, as will goals of “teaching for understanding” rather than being “mastery oriented.” At a more fine-grained level, seeing a typically quiet student volunteer may lead the teacher to call on that student and frame the interaction with the student in ways that support the student differently than the teacher would approach an interaction with a student who is more voluble. Thus, goals are very much context-dependent, grounded in history and immediate constraints. (And, I note, they are grounded in the teacher’s perceptions of what is possible given their understanding of the environment. That’s the issue of beliefs, discussed immediately below.) Nonetheless, the evidence is clear that the set of highly activated goals at any particular time is the fundamental shaper of which resources will be selected and employed.

Belief systems and orientations develop slowly over time, and they are developed (often unconsciously) as a result of experience (see, e.g., Cooney, 1985 ; Kuhn, 1996 ; Patterson & Norwood, 2004 ; Philipp, 2007 ; Richardson, 1996 ; Thompson, 1985 , 1992 ; Usó-Doménech & Nescolarde-Selva, 2016 ). Likewise, the establishment of a rich body of knowledge for teaching develops slowly over time. The very notion of pedagogical content knowledge (Shulman, 1986 , 1987 ) is testimony to the evolution of a special teaching-specific kind of learning: beginning teachers who are at first surprised by a student writing “(a + b) 2  = a 2  + b 2 ” will, after a few years of teaching experience, have a repertoire of responses to choose from.

Moreover, as elaborated below, belief systems and pedagogical resources are interwoven in development. A classic example of this is “Mrs. Oublier” (Cohen, 1990 ), a teacher who aspired to implement “reform” ideas but some of whose pedagogical practices were so grounded in established networks of beliefs that her ongoing teaching did not yet reflect those aspirations. For all of these reasons, change is hard – a topic to which we will return toward the end of this chapter. For the moment, however, the key point is that a goal-oriented architecture, as described in Schoenfeld ( 2011 ), provides the foundation of a theory of teaching. The next question is, what is a relevant set of goals, orientations, and resources that produces desirable teaching outcomes ?

Before proceeding, however, it is essential to note that this question, as important as it is, is different from a theory of teaching. A theory of teaching describes the mechanisms by which teaching takes place. As such, the theory is value-neutral: it should enable one to characterize teaching that one finds laudable but also teaching that one finds problematic. Once one asks about “ambitious” or “effective” teaching – whatever one’s definition of those terms may be – one is asking a different type of question. Footnote 3 One way to frame the question of ambitious or effective teaching is, “what kinds of actions on the part of teachers result in powerful learning? As will be seen below, I believe it is much more profitable to address that question in stages.

One can first ask, what are the properties of learning environments from which students emerge as knowledgeable and agentive learners? This is a theoretical question, which can result in a theory of learning environments. Then, one can reframe ambitious teaching as the decisions make while creating and maintaining productive learning environments. With that framing, one can revisit the theory of decision making described above and ask, what sets of goals, resources and orientations result in the creation of powerful learning environments – environments from which learners emerge as knowledgeable and agentive thinkers and problem solvers? That is the approach taken here.

3 Establishing Goals for “Ambitious Teaching” (Key Dimensions of Productive Learning Environments) and Thinking About the Development of Orientations and Resources

We begin with a discussion of the goals for teaching. Historically the focus of instruction has been on disciplinary content. That is a desired aspect of learning, of course, but this framing is far too narrow. For one thing, goals for mathematics instruction have expanded from “mastering” content to becoming proficient at both the content and the practices that typify rich mathematical understanding (Common Core State Standards Initiative, 2010 ; National Council of Teachers of Mathematics, 1989 , 2000 ). But this is just a start: it is in our classrooms that students develop their beliefs about the nature of mathematics and their relationship to it; where they come to see themselves as agentive (or not) in mathematics; where they develop their sense of mathematical identity; where they are positioned by others; and much more. When thinking about learning as a whole, it is best to think about the opportunities the learning environment provides for growth along all these dimensions. The teacher is responsible for orchestrating all of this. Hence a more encompassing definition of “ambitious” teaching or “teaching for robust understanding” is: Teaching for robust understanding is the shaping of learning environments and interactions in them, in ways aimed at enhancing student learning.

The key question for powerful learning – for teaching for robust understanding – then becomes:

What are the attributes of powerful learning environments – learning environments from which students emerge as agentive, knowledgeable and resourceful thinkers and problem solvers?

An answer to this question provides the goals for a theory of productive teaching (a theory of teaching aimed at desirable teaching outcomes, as suggested in Sect. 2 ).

To cut to the chase, the Teaching for Robust Understanding (TRU) Framework (Schoenfeld, 2013 , 2014 ; Teaching for Robust Understanding Project, 2018 ) provides the answer to the key question above. Here as in Sect. 2 the discussion will be telegraphic, with references to sources that provide the analytic and empirical justifications of the claims made.

Schoenfeld ( 2013 , 2014 ) documents the process by which the extensive literature on “what counts” in ambitious teaching was distilled into five essential dimensions of classroom practice and subjected to empirical testing. The result of that work, the Teaching for Robust Understanding (TRU) Framework, provides evidence that students will emerge from learning environments as powerful, agentive, and empowered thinkers and learners to the degree that the five dimensions highlighted in Fig. 6.2 are consistently reflected in instructional practice.

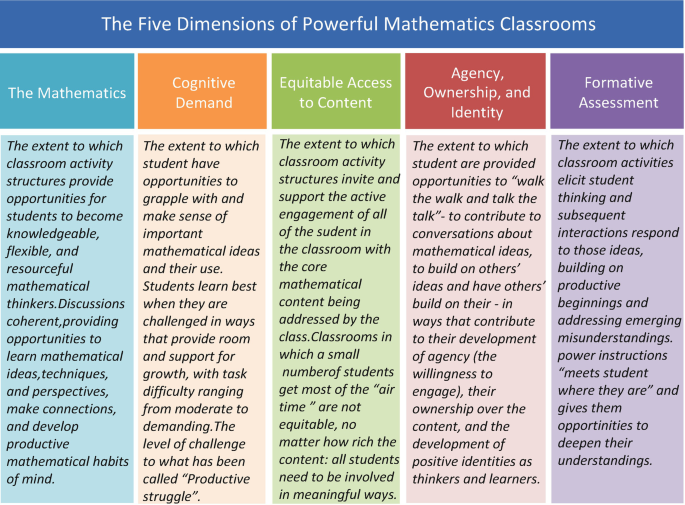
Five dimensions of powerful mathematics classrooms. (Reproduced with permission from the TRU Observation Guide, p. 1)

Before incorporating the substance of Fig. 6.2 (and Fig. 6.3 to come) into a theory of powerful teaching, I briefly summarize some of the properties of the framework. For extensive detail, see the TRU Framework web site ( https://truframework.org/ ).

For purposes of specificity and because of its historical origins, Fig. 6.2 describes powerful learning environments in mathematics. In fact, the framework is general: replace “mathematics” by “X” and the TRU framework provides a characterization of learning environments from which participants emerge aspowerful and agentive learners and practitioners of X.

All five dimensions are necessary, and learning outcomes will be significantly weakened if the learning environment does not do well along any of those dimensions. That is: If the mathematics is not rich; if activities are not crafted in ways that support all students in engageing productive struggle; if some students are not engaged with core content; if some students do not have opportunities co contribute to discussions and the mutual refinement of ideas; or if the environment does not adapt in meaningful ways to what students reveal of their thinking, then at least some students will be significantly shortchanged.

The five dimensions are sufficient for the desired outcomes, a fact that comes from the derivation of the framework (Schoenfeld, 2013 , 2014 ; Schoenfeld et al., 2018 ) and from empirical testing (Prediger & Neugebauer, 2021 ; Schoenfeld, 2016 , 2018 ).

There is no claim that the five dimensions reflect a unique distillation of the literature. They are best thought of as analogous to “basis vectors,” spanning the space of powerful (or if you prefer, “ambitious”) teaching. Other decompositions are possible, and they might highlight different aspects of teaching. One feature of this choice of five dimensions, however, is that they have been chosen in ways that they can each be the focus of meaningful professional development.

The description of each dimension with a short phrase that is given in Fig. 6.2 provides merely the briefest characterization of the explicit and implied contents of the dimension. For instance, “students feeling safe to venture ideas” is a necessary condition for Dimension 4, opportunities for the development of agency, ownership over content, and the development of positive disciplinary identities. Likewise, much more can be said about the richness of disciplinary content (e.g., the role of mathematical representations, mathematics as a language, what it means to understand content deeply, etc.) or any of the other dimensions.

The framework is not prescriptive. That is, it does not imply that one must teach in any particular way in order to achieve positive outcomes. (We have all observed wonderful teachers whose styles and classroom routines are very different.) Rather, the five dimensions of TRU can be seen as representing five key principles underlying ambitious, powerful, or robust instruction. There are as many ways to live up to those principles as there are superb teachers.

Again, it is essential to note that the TRU framework focuses on the attributes of the learning environment and the affordances it offers students for their learning and development. Figure 6.3 is useful in reminding us of the goals of instruction, when seen from the student’s perspective.

Framing lesson goals, from the student perspective. (Reproduced with permission from the TRU Observation Guide, p. 2)

With this as background, it is now possible to begin to flesh out some of the goal structure for a theory of ambitious (mathematics) teaching. Footnote 4 In what follows I will focus on decisions during the act of teaching – but as elaborated in Sect. 4 , these goals are relevant both in planning instruction and in reviewing instructional events afterward. Once again, this discussion will be somewhat terse; more detail can be found in Schoenfeld ( 2020b ).

3.1.1 Mathematics-Related Goals

First, let us consider goals for the student’s engagement with mathematics. High priority goals include that the student will experience/learn about, and come to internalize:

Mathematics as a sense-making discipline, not one of memorizing facts and procedures

Big mathematical ideas – that students see “what counts” and don’t get lost in minutia

Reasoning and problem solving

Ties between concepts and procedures

Multiple representations

Productive patterns of mathematical thinking (Schoenfeld, 2017 )

Moreover, these goals operate at multiple levels: the student should experience these at the micro-level when engaging in any day’s lesson, and experience them at aggregate (topic and unit) levels. Ultimately, students should come to see (and experience) mathematics as a sense making enterprise.

Once again, I stress that these are the very top-level versions of the goals. In any particular context (say a particular day’s instruction), they would be elaborated with regard to that day’s instruction – e.g., “what are the opportunities for sense making with regard to today’s content, and how can students be positioned to experience them?; how can the lesson support students in engaging with and understanding the big ideas?”, etc.

These are just the beginnings of questions. In Sect. 4 we will introduce the TRU Conversation Guide (Louie et al., 2016 ) and the TRU Observation guide (Schoenfeld and the Teaching for Robust Understanding Project, 2016 ), which elaborate on the bullet points immediately above. Each of those can be used to generate a more refined set of goals regarding the students’ mathematical experience.

3.1.2 Cognitive Demand-Related Goals

The top-level goal for cognitive demand (see Fig. 6.2 ) is that students should be in a position to engage productively with the central mathematical ideas of the lesson – with the level of challenge being such that the students are stretched, and that they grow from their sense making experience. The key idea is to sustain “productive struggle.” Some subgoals can be inferred from Fig. 6.3 : giving students time to engage with the challenges, providing scaffolding in ways that keep tasks within reach but don’t turn them into rote exercises; asking for explanations rather than simply for answers.

The challenge is to maintain cognitive demand in the moment, as students are working together. This can implicate task design, in planning – for example, a task that has multiple entry points or employs multiple representations can be approachable in different ways, and these different handholds can allow students to find places to engage meaningfully with the mathematics. Likewise, different classroom activity structures can offer different affordances for meaningful engagement. Of course, most of these goals are emergent – it’s when one sees a student bored or struggling in what seems to be an unproductive way that the goals for cognitive demand get activated.

3.1.3 Equitable Access-Related Goals

One key point with regard to dimension 3 is that the equity-related goal is not simply to keep students engaged; it is for all students to be engaged with the core content of the lesson. A classroom is not equitable if, by virtue of the activities they engage with, the “rich get richer and the poor get poorer.” So, the goal in that regard is to find and implement activities that engage every student meaningfully with the big ideas. A second key point, of course, is that there are various ways to participate in classroom activities: responding to questions, participating in discussions, volunteering ideas, and more. As implied by Fig. 6.2 , all students should have opportunities for significant amounts of “air time” – a top-level goal not just for whole class discussions but for small group activities as well. And as implied by Fig. 6.3 , another major goal is for all students (even those who are initially reluctant) to be supported in engaging meaningfully.

As in the case of all of the TRU dimensions, some of the more fine-grained questions elaborating the top-level goals can be found in the TRU Conversation guide (Louie et al., 2016 ). For example, the first few reflection questions related to agency, ownership and identity,

What is the range of ways that students can and do participate in the mathematical work of the class (talking, writing, leaning in, listening hard; manipulating symbols, making diagrams, interpreting text, using manipulatives, connecting different ideas, etc.)?

Which students participate in which ways?

Which students are most active, and when?

In what ways can particular students’ strengths or preferences be used to engage them in the mathematical activity of the class? (TRU Conversation guide, page 8)

give rise to opportunities for lesson planning and for modifying the lesson as a lesson unfolds.

3.1.4 Agency, Ownership, and Identity-Related Goals

There is a large literature documenting the negative impacts of mathematics instruction – the very existence of “math anxiety” as a phenomenon (see https://en.wikipedia.org/wiki/Mathematical_anxiety ) gives testimony to the often negative impact that mathematics instruction has on students. Goals related to Dimension 4 move in precisely opposite directions:

One goal is for students to feel mathematical agentive: “I can do mathematics, and I’m willing to jump in and give it my best.”

Another is for them to take possession of knowledge by making it their own – “I figured this out; it makes sense; it’s not simply what ‘they’ told me is true.”

A third is for their mathematical Identities to flower: “I like math and look forward to doing it – it makes sense and I can figure things out.”

It goes without saying that the development of positive agency/ownership/identity hinges on having had some degree of success in facing and working on mathematical challenges – not necessarily solving all of them, but having frequent opportunities to venture ideas, critique and build on others’ ideas, and have one’s own ideas both critiqued and built upon. Thus, highly dialogic classrooms are essential (see, e.g., Mercer et al., 2019 ); top-level goals are to create and sustain classroom practices that provide all (cf. dimension 3) students opportunities to generate, expand on, and explain their own ideas, responding in kind to the ideas of others. Additional goals (again, see the TRU Conversation Guide) include developing students’ capacity to do so, by opening up the kinds of ideas students have opportunities to generate and share (concerning, for example, strategies, connections, partial understandings, prior knowledge, and representations), placing responsibilities of evaluation and response more in students’ hands, and increasing the depth of expected explanations.

3.1.5 Formative Assessment-Related Goals

For an extended discussion of formative assessment see Burkhardt & Schoenfeld ( 2019 ). The first major goal related to formative assessment is to elicit student thinking and have it become public. This provides a clear example of how goals and subgoals cascade: students who fear being embarrassed by incorrect answers are not going to venture away from safe territory, so top-level goals for formative assessment activate a series of subgoals regarding classroom climate. Finding ways to reveal what students think is also a major component of dimension 2: it’s hard to know what level of cognitive demand to aim for if you have little idea of what students are thinking! A second major goal is for those student thoughts to be pursued in ways that advance individuals’, groups’, and the whole class’s mathematical agenda. Some of this is suggested by the last row of Fig. 6.3 . But there is more. One misconception regarding formative assessment is that once student misunderstandings are revealed, it is the teacher’s responsibility to set everything straight. (One teacher with whom we worked complained that, now that she was aware of student misconceptions, she felt like she was playing whack-a-mole: as soon as she addressed one student’s misconception, another cropped up!) This framing neglects the fact that the students themselves can serve as tremendous resources for each other. They can often “hear” each other’s misunderstandings in ways that the teacher, who is trying to attend to all of the students in the class, may not hear them, and they can respond in student language and often at each other’s level. Regarding formative assessment, student goals from the TRU Observation Guide include:

Taking ownership of the learning process in planning, monitoring, and reflecting on individual and/or collective work

Asking questions and making suggestions that support analyzing, evaluating, applying and synthesizing ideas

Building on the contributions of others and helping others see or make connections

Holding classmates and themselves accountable for justifying their positions, through the use of evidence and/or elaborating on their reasoning. (TRU Observation Guide, p. 4)

Thus, another major goal for formative assessment is for the teacher to create an environment in which students become skilled in working toward the goals above.

3.2 Orientations

The task of identifying high priority goals – the focus of Sect. 3.1 – is relatively easy. It should be noted, however, that the goals highlighted in Sect. 3.1 reflect a particular set of values, those embodied by the TRU framework. The premises that:

mathematics learning should result in deep and connected understandings, above and beyond a set of well honed skills

the learning environment should be tailored to support all students as opposed to letting “natural ability” separate those who should pursue mathematics from those who should not

all students should have opportunities to engage meaningfully with mathematics, at all levels

a major goal of mathematics instruction should be the development of productive mathematical identities

teachers are responsible for ongoing monitoring of student understanding and adjusting their instruction so that students have maximal opportunities for sense making, as opposed to being responsible for presenting the mathematics clearly (with the responsibility for making sense of the mathematics, once presented, falling on the shoulders of the students)

are consistent with the idea of “ambitious” or “powerful” instruction and are consonant with much of the “reform” movement in the U.S., but they are not universally shared. Footnote 5 That said, suppose we stipulate the kinds of goals discussed in Sect. 3.1 . That is still the easy part: the challenge is the development of orientations and resources that enable the implementation of activities to attain those goals.

As explained in Schoenfeld ( 2011 ), there are multiple interactions between goals, orientations, and resources. For purposes of exposition, I have chosen to begin with goals. Part of what makes things challenging, however, is the fact that (cf. Fig. 6.1 ) the goals one establishes in the moment are a function of one’s beliefs and orientations, which are a function of one’s history – and beliefs are formed over time, often unconsciously. Recall the teacher who taught his regular students in a very step-by-step manner, because anything less rigid would “confuse” them. That’s a matter of beliefs. Moreover, beliefs operate as parts of belief systems , but specific beliefs may be triggered by specific events and override other beliefs.

For example, Cohen ( 1990 ) tells the story of “Mrs. Oublier,” who espouses the rhetoric of reform but doesn’t live up to it. The point I wish to make is that this kind of situation is not only natural, but to be expected. The decisions that teachers make are a complex combination of their goals, their belief systems and orientations, and the mental and material resources at their disposal.

Consider a teacher in transition, akin to Mrs. Oublier. This teacher wants to do less “telling” and open up her classroom to contributions from students, as suggested by the literature and the professional development she has experienced. She has students discuss their work in groups and has students come to the board to present their work. So far, so good. But then, what a student writes on the board is incorrect – say a typical error such as “(a + b) 2 = a 2 + b 2 ”. Now what does the teacher do?

This teacher may have a previously established set of beliefs and orientations that get triggered by this error, and a set of goals and actions that correspond to them. For example, the teacher may have a cluster of beliefs related to the idea that “it’s bad to have incorrect mathematics written on the board, especially because students may copy it into their notebooks.” As a result, the teacher may move almost automatically to have the student erase the incorrect statement from the board. This action, so natural for the pre-transition teacher, well may undermine the teacher’s currently espoused goal of having students engage in mathematical sense making.

When things function smoothly in decision making, it’s because nested clusters of goals and subgoals are largely consistent with comparably nested clusters of beliefs and orientations, and the teacher’s repertoire of techniques (resources) includes a collection of actions consonant with those orientations and goals. That’s the baseline for “well practiced” behavior as captured in Fig. 6.1 .

It goes without saying that building a (mostly) coherent repertoire of linked resources, goals, and orientations is a long and slow process. That, in part, is what lies behind the notion of “pedagogical content knowledge” (Shulman, 1986 , 1987 ), the idea that “mere” content knowledge is far from enough for effective teaching. Shulman’s key idea was that the wisdom of practice is represented by the accumulation, over time, of ways to respond to student understandings. The first time a teacher sees a student make a particular error, the teacher may be floored, and make up something on the spot. Over time, the teacher builds a repertoire of responses, and chooses from them when the need arises.

What goes beyond Shulman’s notion, however, is that the different responses serve different goals and orientations. The teacher who is invested and well practiced in “mastery” may well provide a reminder of the formula, possibly with a justification for it, and give students some practice so that they are more likely to remember the formula. The teacher who is invested and well practiced in “teaching for understanding” may ask the student to check the formula and then work through something like an area model to build or strengthen the linkage between the distributive law and underlying representations of it. That is, different resources are not value-neutral: the decision to call upon them is tied to clusters of orientations and goals. For the well practiced teacher in a familiar content arena, these clusters cohere and the chain of decisions described in Fig. 6.1 proceeds smoothly. For the novice teacher, sparse resources can lead to challenges (Schoenfeld, 2011 ). For the teacher in transition, the challenge is not only to construct the relevant resource-orientation-goal clusters, but to supplant some of the clusters that are already well engrained.

That said, we can return to the question of orientations and resources relevant for teaching for robust understanding. In the remainder of this section I point to challenges in characterizing them. In the following section I discuss some tools that hold promise for progress.

A key issue about beliefs and orientations is that they are formed slowly over time. They may be held unconsciously, and thus challenging to address – it can be hard to alter an orientation you are not aware of! (Schoenfeld, 1985 ). Thus, either consistent experience for an extended period of time or an eye-opening experience that casts some currently held beliefs into doubt are the catalysts for change.

As a thought experiment, consider the set of goals identified in Sect. 3.1 . At the very top level, teaching for robust understanding requires a fundamental shift in perspective, from thinking about the central question of teaching being “what activities do I prepare for my students?” to “how are my students experiencing the classroom activities and environment? This is a major shift, which entails changes in beliefs and orientations in all five dimensions of TRU. To mention just one example regarding Dimension 1, consider beliefs regarding the nature of problem solving and the kinds of experiences that would enable students to make progress on problems that they have not been shown how to solve. Understanding that this is a major curricular goal and that it requires a different kind of student experience is not only challenging at the top level, but (as discussed above) requires families of context- and content-specific beliefs and orientations consistent with that perspective. (For example, what is the appropriate kind of response when students run into difficulty?) Employing formative assessment (Dimension 5) in order to adjust the level of cognitive demand (Dimension 2) requires some faith in students’ abilities to figure things out by themselves (recall the teacher who said that he would give his honors students room to explore, but not his regular students – “it would just confuse them”) and the belief that students can serve as meaningful resources for each other (Black & Wiliam, 1998 ; Burkhardt & Schoenfeld, 2019 ; Swan, 2006 ). Likewise, there are huge numbers of beliefs about race, tracking, differentiation, deficit perspectives, and more that impede the consideration and implementation of activities that could enhance equitable access to core content for all students. Constructing an environment that is conducive to the development of agency, ownership, and identity means believing that students are capable of making progress on complex issues, that they can be supported in making conjectures, building on each other’s ideas, etc. Believing that there is value in handing over some of the responsibility for learning to the students, and that – appropriately supported – they can interact in ways that lead not only to understanding rich mathematical content but becoming agentive and “owning” the content they generate, can require a significant leap of faith. In short, identifying and then supporting the development of beliefs and orientations that support teaching for robust understanding is a decidedly significant challenge. Developing them is that much more of a challenge.

3.3 Resources

Some key points with regard to resources are as follows. It should be noted that although some teaching routines (obviously central resources) are general, for example asking students “Can you tell me what you’re thinking,” the vast majority of resources are content- and context-specific. I touched on content-specificity with regard to the algebra error “(a + b) 2  = a 2  + b 2 ”. That error springs from a particular small grain-size piece of content. There are thousands of such, as, to give but one example, Brown & Burton’s ( 1978 ) pioneering error analyses in elementary subtraction indicate. Context and history matter, in that what was said yesterday may shape how one interprets what students say today.

In Schoenfeld ( 2019 ) I considered the issue of resources raised by the TRU Framework, highlighting issues that could profit from investigation. What follows are some of the main ideas.

3.3.1 Mathematics-Related Resources

At least two major issues regarding the practice of mathematics need to be addressed. First, although more that 30 years have passed since the NCTM ( 1989 ) Standards called for an increased emphasis on mathematical processes such as problem solving and reasoning, there is not nearly as much attention given to supporting students as reasoners and problem solvers – and in engaging more generally in powerful patterns of mathematical thinking (PPMT) such as problem solving, habits of mind, representation and modeling, abstracting, reasoning and proof as there should be (Schoenfeld, 2017 ). Far less attention is given to mathematical processes and practices than should be the case (Schoenfeld, 2020a ). Teachers need both material resources (curricular support) and rich experiences in problem solving, conjecturing and proving, and abstracting and generalizing in order to develop those mathematical habits of mind and the wherewithal to teach them.

Second, mathematics instruction, abetted by standards and testing, tends to emphasize a rather fine-grained level of curriculum and instruction – “this list (e.g., the Common Core State Standards for Instruction, 2010 ) identifies the skills we will teach and hold students accountable for.” This has long been a problem, as evidenced by what has been called the “summer slump,” the fact that students forget so much of what they learned the previous year over the few summer months they are away from school. The details don’t necessarily matter; the ideas behind them do.

For example, there are classical “work problems” such as this:

Pipe A can fill a swimming pool in 6 h. Pipe B can fill it in 8 h. How long does it take to fill the pool if both pipes are open simultaneously? If you don’t remember the formula, think about the problem.

Many years ago my research group included a graduate student who had recently been a high school teacher and an established mathematician visiting on sabbatical. The graduate student said “You use the following formula for problems like this” as found the answer in no time. The mathematician said, “I haven’t worked problems like this in 40 years. There’s a formula, but I don’t have a clue what it is.” Then he thought about what he could combine. Not hours, not pools, but… rates do combine. In 1 h, Pipe A fills 1/6 of the pool; in 1 h, pipe B fills 1/8 of the pool; hence the two together fill (1/6 + 1/8) = 7/24 of the pool. So, it takes 24/7 h to fill the pool.

The key point to observe is that the mathematician’s knowledge was generative . Unlike “summer slump” students who are at a loss when something falls out of memory, the mathematician remembered central ideas and principles that enabled him to regenerate the formula when he needed it.

A quick look through the curriculum yields myriad examples where the memory load placed on students is immense, and an understanding of key underlying ideas could ease that burden substantially. For example, many students memorize a range of formulas for determining the equation of a line in the plane: the two-point formula, the point-slope formula, the general formula, etc. It’s much more useful to understand that any two non-redundant pieces of information determine a line, and that one can find any of the formulas from any of the others.

It’s an open question as to what the most robust understandings of any body of content could or should be based on, and how to put these at the center of mathematics instruction.

3.3.2 Cognitive Demand-Related Resources

The goal for the cognitive demand dimension is “productive struggle,” based on the idea that if students are working productively within their zone of proximal development (Vygotsky, 1962 , 1978 ), they will build the kinds of knowledge that extends what they know in meaningful ways.

The challenge, then, is to arrange the environment so that each student has opportunities to make reasonable and reasoned progress. The word environment is stressed for multiple reasons. It includes both the tasks and the ways the students are set up to engage with them. For example, tasks that are simple exercises provide little opportunity for growth. The same is the case for tasks that are not within reach. However, a lot of this challenge can be mitigated both by task design and by classroom activity structures. If a task can only be solved in one way, then the solution is either within reach or not. But if a problem can be approached in multiple ways, or can be illuminated by employing multiple representations, then there are a range of ways in which students can engage with it profitably. Yet this is only the beginning, because the framing thus far invokes the image of an individual students working on the task in isolation. Things get much richer when students work on problems in collaborative groups. For one thing – and this can’t be stressed enough – students can serve as resources for each other. An individual teacher can only devote limited time to any student, but that student’s classmates are much more available. There is much to be learned from asking questions of or explaining to one’s classmates, and even more when one is collaborating with them. If a group of students is probing or building on each other’s ideas, the students are much more likely to be working within their zones of proximal development. In addition, comparing and contrasting the approaches they have taken to problems that support multiple approaches enhances the mathematical richness of the conversations. Thus crafting and using tasks that support rich conversations and implementing classroom activity structures that engage students productively with their fellow students are some of the cognitive demand-related resources teachers need to develop. (Cohen & Lotan, 2014 ; Cohen et al., 1999 ; Mercer et al., 2019 ).

3.3.3 Equitable Access-Related Resources

The key idea is that every student must have ample opportunity to engage meaningfully with the central mathematical content that is the focus of the lesson or unit. That means much more than some, perhaps peripheral, engagement with the topic. For example, the Wikipedia definition of “differentiated instruction” Footnote 6 says:

Differentiated classrooms have also been described as ones that respond to student variety in readiness levels, interests, and learning profiles. It is a classroom that includes and allows all students to be successful. To do this, a teacher sets different expectations for task completion for students, specifically based upon their individual needs.

The difficulty here lies in the phrase “a teacher sets different expectations for task completion for students.” If some students in a classroom are practicing factoring whole numbers while others are factoring quadratic polynomials, or some do just the first step of a procedure while others are expected to complete it, the students may all be engaged, but not in ways that does justice to each and everyone. The challenge is that there are many hidden biases, as revealed for example in the classic AAUW volume How schools shortchange girls (American Association of University Women,  1992 ). Data from that volume indicate that girls were called on less frequently than boys and asked lower-level questions. Bias and discrimination can be subtle or overt and occur across all ethnic and racial, gender and gender orientation, linguistic proficiency, and untold numbers of other categories. There are a wide range of equity-oriented tools and practices, including Complex Instruction (Cohen & Lotan, 2014 ; Cohen et al., 1999 ), Equity Pedagogy (Banks & Banks, 1995 ) and Equity Analytics (Reinholz & Shah, 2018 ). A first challenge is to become aware of such resources, a second to build classroom cultures that make productive use of them. This is highly context-sensitive. And it’s just the beginning, given the close links between Dimensions 3 and 4.

3.3.4 Agency, Ownership, and Identity-Related Resources

As noted in Sect. 3.1 , ambitious instruction aims for students to be agentive; for them to learn the mathematics in ways that gives them ownership over it; and for them to develop positive mathematical identities. The path to AOI lies in successful mathematical experiences, so the relevant resources consist of ways of crafting the learning environment in ways that are likely to improve them. Some of those resources include those mentioned for Dimension 2 – rich mathematical tasks with multiple entry points and classroom activity structures that support students in venturing and building on ideas are relevant. Likewise, the activity structures mentioned in Dimension 3, which focus on making sure that all students are engaged in significant ways, set the stage for AOI. Ultimately, however, supporting students’ development of AOI depend on a large set of resources deployed in the moment. Consider the questions given in Fig. 6.4 , drawn from the TRU conversation guide (Louie et al., 2016 ). Many can be planned for in advance, but many require real-time decision making based on what the teacher sees in classroom interactions. That brings us to Dimension 5.

Things to think about, re AOI. (Reprinted with permission from the TRU Conversation Guide, p. 10)

3.3.5 Formative Assessment-Related Resources

As indicated by Fig. 6.5 , Formative Assessment can be thought of as the glue that holds everything together in classrooms from which students emerge as mathematically powerful thinkers and learners.

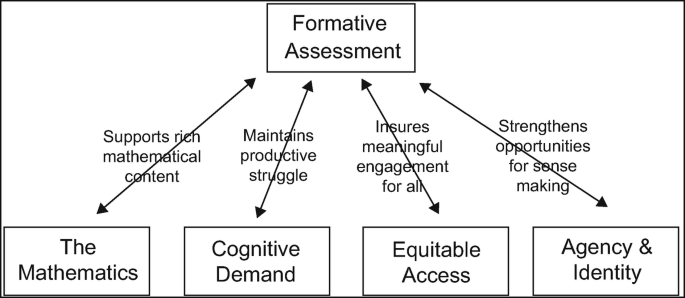
The key roles of Formative Assessment. (Reprinted with permission from Burkhardt & Schoenfeld, 2019 , p. 43)

Learning mathematics means not only understanding content, but equally important, becoming proficient at mathematical processes and practices (conjecturing, reasoning and proving, problem solving, etc.). Supporting students to become effective mathematical thinkers (TRU Dimension 1) requires making their thinking available to others and interacting with it in the moment – the very definition of formative assessment. Similarly, cognitive demand (Dimension 2) is impossible to adjust unless student thinking is made public; providing equitable access (Dimension 3) requires constant attention; and as discussed immediately above, equitable access is only the gateway to the kinds of opportunities for sense making that support students in developing agency, ownership over content, and positive mathematical identities (Dimension 4).

As with the other dimensions, there are both material and pedagogical resources to be marshalled in the service of formative assessment. One set of material resources is the Formative Assessment Lessons (FALs) produced by the Mathematics Assessment project. These lessons, also known as classroom challenges, are available at no cost from https://www.map.mathshell.org/ . Independent evaluations of the FALs indicated that including 10–12 days worth of FAL-based instruction in the mathematics curriculum resulted, on average, in 4.6 months of learning gains (Herman et al., 2014 , Research for Action, 2015 ) – a gain likely attributable to the inference that teachers’ pedagogy during their regular lessons changed as a result of their being supported in different pedagogical practices while teaching using the FALs. But one should not give the impression that building the knowledge and pedagogical habits to employ formative assessment is straightforward. The FALs had the impact they did as the result of a quarter century of research and development, including content-specifics regarding typical student misconceptions and productive ways to structure classroom interactions to counter them. Developing such pedagogical content knowledge on one’s own is a long, slow process, as is developing the habits of mind that orient one to such knowledge (Black & Wiliam, 1998 ; Burkhardt & Schoenfeld, 2019 ).

4 Summary and Next Steps

This concluding discussion summarizes the main theoretical points in this chapter. I revisit the issues raised by the editors, pointing also to some resources and next steps in a research and development agenda.

4.1 What Is a Theory (of Teaching)?

I hope to have addressed that question thoroughly – well, as thoroughly as one can in a few pages – in Sect. 2 . My book How We Think (Schoenfeld, 2011 ) offers a comprehensive theory of knowledge intensive and socially intensive in-the-moment decision making. That theory is a theory in the scientific sense. It specifies objects and the relations between them, specifying a mechanism by which in-the-moment decisions are made. The theory described in Sect. 2 is general, and it supports the creation of models that test the theory.

4.2 What Should It Contain and Why? Do We Already Have a Theory/Theories on Teaching? If So, Which Are They?

As noted in Sect. 2 , an individual’s in-the-moment decision making can be characterized and modelled by focusing on that individual’s resources, orientations, and goals, using a decision mechanism akin to (but obviously more detailed and fine-grained than) Fig. 6.1 . In that sense there does exist a robust and empirically verified theory of teaching. As discussed in Schoenfeld ( 2011 ), this theory is general; it generates models of particular teachers that apply in a wide range of situations.

As noted, however, I suspect that the editors really intended for the authors of this volume to address the issue of “ambitious” or “powerful” teaching – instruction from which students emerge as knowledgeable, resourceful, and agentive thinkers and problem solvers. This is a very different question, because what one takes as important depends on one’s goals and values; it is no longer simply a question of theory. To invoke the automotive metaphor once again: one can have a theory of internal combustion engines (and theories of aerodynamics, etc.) but one will build very different cars if one’s goal is (a) to win the Indy 500, where cost is no object, or (b) to build a comfortable and profitable family sedan.

That said, there is an empirically validated theory of “teaching for robust understanding” and a framework that identifies what matters in ambitious instruction. As described in Sect. 3 , the TRU framework (Teaching for robust understanding project, 2018 ) indicates that a learning environment will be successful in producing powerful thinkers and learners to the degree that (1) the content and practices with which students engage is disciplinarily rich; (2) students engage in sense making within their zones of proximal development; (3) all students engage with core content and practices; (4) students have opportunities to contribute to discussions and progress in ways that support the development of agency, ownership over content, and the development of disciplinary identity; and (5) student thinking is made public and the learning environment adjusts accordingly.

It should be clear that there is no one “right” way to teach; teachers with very different styles and routines may be successful along all five dimensions of the TRU framework, just as somewhat different automobiles can vie for “best in class.”

Nonetheless, the combination of the theory of decision making in Sect. 2 and the TRU framework as discussed in Sect. 3 provides the mechanism for constructing a theory of ambitious teaching, a.k.a. Teaching for Robust Understanding. The question is, what are combinations (note the plural) of resources, orientations, and goals that would support teachers in constructing learning environments that do well in the five TRU dimensions? This was the issue pursued in at least some depth in Sect. 3 . That discussion just scratches the surface. It will be pursued in Sect. 4.4 , which identifies directions for further work.

4.3 Can Such a Theory Accommodate Differences Across Subject Matters and Student Populations Taught? If So, How? If Not, Why?

In a word, yes. The theory of decision making elaborated in Sect. 2 applies to well-practiced decision making in all knowledge-intensive domains. Schoenfeld ( 2011 ) provided detailed models of beginning and experienced teachers at the elementary and secondary levels, an indication that neither level of expertise nor grade level is a theoretical obstacle. The TRU framework was developed in mathematics, but it is domain general – it is a theory of powerful learning environments, independent of content domain and age level. That is not so say that content specifics or student population don’t matter. To create a powerful learning environment in physics, chemistry, or English Language Arts, one needs to have a rich sense of the content and practices in those domains. To be an effective teacher of any group of students, one needs to know those particular students and have a sense of what supports their learning. But those are details – the details of the resources, orientations, and goals relevant for any particular model one wishes to build in detail. That is a huge empirical challenge, but it is not a theoretical challenge.

4.4 (From the Editors:) In the Future, In What Ways Might It Be Possible, If at All, to Create a (More Comprehensive) Theory of Teaching?

As indicated above, the issues facing us as a field are not theoretical: the theory of in-the-moment decision making during teaching and the TRU framework, together, provide a comprehensive theoretical framework regarding teaching for robust understanding. The issue before us is: what would be useful to know in order to flesh out the details of that theoretical framework and provide mechanisms to help teachers move in productive directions? Thus, I would reframe question 4.4as:

4.5 (Reframed:) In the Future, In What Ways Might It Be Possible, If at All, to Elaborate and Support the Mechanisms of Teaching for Robust Understanding, and to Understand the Impact of the Contexts Within Which Teaching Takes Place?

In the balance of this section I briefly identify four arenas essential for progress.

4.5.1 Research and Development on Resources for Teaching for Robust Understanding

Section 3.3 characterized some of the cognitive resources that can support teachers in teaching for robust understanding. The list in that section is just a “starter set” – as noted above, pedagogical content knowledge comes with experience, and is tied very specifically to the content that one teaches. A major question is how to catalyze the development of such resources.

That question is intimately tied to the issues of material resources and professional development. As an example of the former, consider the Formative Assessment Lessons (FALs) available at https://www.map.mathshell.org/ . Each these 100 lessons provides direct curricular support for teaching key content using formative assessment. The lessons are aimed at unearthing student thinking related to the content and building on it. The support materials included as part of the lessons (which take 2 to 3 days each to implement) include diagnostic tasks that reveal student misunderstandings to teachers, tables of “common student issues” and ways to lead students to address them, and very detailed lesson plans. The lessons themselves bolster content and process understandings for teachers. By virtue of orienting teachers to common student misunderstandings and providing mechanisms for addressing them, the lessons scaffold the development of teachers’ pedagogical knowledge. In fact, each of the FALs embodies pedagogical content knowledge with regard to the content and practices at hand. (See Swan, 2006 , 2017 ; Swan & Burkhardt, 2012 , 2014 ). A major issue is scaling up: the FALs, which required a highly skilled design team, were based on decades of research and cost upwards of $6 M USD to produce, only address a subset of the central topics in the high school curriculum.

But there is more to be said about the FALs. The lessons were designed to help teachers learn key aspects of formative assessment, in the expectation that some of the productive pedagogical habits learned by teaching the FALs would become parts of the teachers’ general repertoire. Although the evidence to date is still thin, it appears that that is the case. Kim ( 2017 ) documents the changes over the course of a year as a teacher taught five of the FALs. After the first FAL, there was little or no change in the teacher’s pedagogy: the lesson she taught the next day very closely resembled in style the lessons she had taught before teaching the FAL. However, there were some slight changes after the teacher taught the second FAL, and by the end of the year the teacher was doing significantly less “telling” and providing students with a great deal more time to raise questions and discuss them among themselves. This experience was hardly an unalloyed success; the loss of the previously rigid structure the teacher had employed resulted in challenges in classroom management, for example. But the fact that the pedagogical strategies implemented in the FALs influenced the teacher’s regular lessons indicates that it is possible for such materials to have an impact on teachers’ pedagogical practices. Indeed, such “travel” is the most likely explanation for the findings in Herman et al. ( 2014 ), that Kentucky teachers who taught 10–12 days of FALs saw their students gain an additional 4.6 months in terms of mathematics learning. The students only experienced 10–12 days of FAL content, but they most likely experienced a significant amount of FAL-related (and TRU-consistent) pedagogy.

Note that these are largely conjectures at this point, and a great deal more needs to be studied.

Along similar lines but not on nearly as large a scale, the Teaching for Robust Understanding project has created a number of tools for teachers’ professional development: see https://truframework.org/ . Figures 6.2 and 6.3 were drawn from the TRU Observation Guide (Schoenfeld & the Teaching for Robust Understanding Project, 2016 ), and Fig. 6.4 from TRU conversation Guide (Louie et al., 2016 ). These tools have been used in a wide range of professional development projects (See Schoenfeld et al., 2020 , ; see also Schoenfeld et al., 2019 for a description of Teaching for Robust Understanding with Lesson Study.) These projects, in general, are aimed at helping teachers develop richer pedagogical resources and orientations consistent with the TRU Framework. Two new books (Schoenfeld et al., 2023a , b ) provide additional tools and support for professional learning communities.

Over time, it will be valuable to flesh out the knowledge and orientation base that supports teaching for robust understanding. This is both a theoretical and engineering exercise. For example, there is much to be learned about how belief systems are formed and operate (e.g., how orientations prioritize resources) and how to unpack and support student thinking (the what and how of content-specific formative assessment). For a more detailed view of desirable R&D, see Schoenfeld ( 2020b ) and Burkhardt & Schoenfeld ( 2019 ).

4.5.2 Issues of Developmental Trajectories

The field lacks good data on how teachers grow with regard to the key dimensions of TRU, especially in environments meant to foster their growth. There is a literature on teacher growth. In broad brush strokes, that literature (see, for example, Fuller, 1969 ; Hord et al., 1987 ; Ryan, 1986 ; Smith, 2000 ) suggests that teachers tend to spend the first few years of their careers mastering issues of classroom management, after which they increasingly get involved in using and sometimes developing engaging mathematical activities. Along the way they develop pedagogical content knowledge (in the arenas they teach, consistent with their orientations and practices) and some small percentage of teachers become adept at focusing on student thinking.

Such trajectories are hardly inevitable, however. Management is an issue if students are not engaged. Thus, an early focus on rich and engaging materials and activities may both lessen challenges of classroom management and hasten the growth of pedagogical content knowledge. Moreover, having your teacher focus on your thinking and ideas is very engaging for students – so teachers whose classrooms feature formative assessment early on may display (currently) non-normative developmental trajectories. Studies of how teachers’ understandings and practices develop, under what conditions, could help to optimize professional development.

4.5.3 Theoretical and Pragmatic Challenges in an Increasingly Virtual Instructional World

The coronavirus pandemic has thrown teachers around the world headlong into virtual instruction, whether they were ready for it or not – and few were. We thus face the massive challenge of reconceiving teaching within a radically different social, technological, and instructional context. The key point I wish to make here is that two things remain the same as we consider these changes. The first is that the mechanisms of decision making during instruction remain the same. What teachers will do in the moment is a function of their goals, the resources available, and their orientations. Without doubt, the material and social resources available in virtual environments differ substantially from those in in-person instruction. But what a teacher chooses to do will be a function of that teacher’s resources, orientations, and goals. Second and perhaps more important in this context, the teaching for Robust Understanding Framework applies to all learning environments, including virtual learning environments. What that means is that TRU can be used to problematize virtual learning. The key questions to confront are:

How can whatever mode of instruction teachers are employing – whether it is in-person, virtual, or blended – be configured so that …

students engage in deep ways with disciplinary content and practices

cognitive demand is adjusted so that students engage in productive struggle

all students are meaningfully engaged with core content

all students have opportunities to contribute to exchanges in ways that support the development of agency, ownership over content, and the growth of positive disciplinary identities and identities as learners

student thinking is made public and instruction responds in ways that supports the first four bullets above?

This is a huge challenge in in-person instruction and will be that much more of a challenge as we take on the new challenges of virtual instruction. But the framing given above highlights what is important and points us to the research and development that will help us to address the challenge.

4.5.4 Broader Issues of Context

The focus of this chapter has been on elaborating a theory of what the teacher does, inside the walls of the classroom. It goes without saying that everything that takes place inside schools is shaped by myriad societal forces. Issues susch as the “savage inequalities” of school funding (Kozol, 1992 ) and pervasive racism, to name just two, are critically important. For a preliminary discussion of the impact of such issues and how to link them to the issues discussed in this chapter, see Schoenfeld ( 2022 ).

See Google “define theory”.

Please not that I am not endorsing this perspective, just reporting it.

Such questions are value-laden, depending on what one considers to be important student learning outcomes. My stance is made clear in the next paragraph.

Analogous characterizations can be developed for every discipline.

In fact, the “math wars” were the result of opposing positions on points such as these. (Schoenfeld, 2004 )

https://en.wikipedia.org/wiki/Differentiated_instruction

American Association of University Women. (1992). How schools shortchange girls . AAUW and NEA.

Google Scholar  

Banks, C. A. M., & Banks, J. A. (1995). Equity pedagogy: An essential component of multicultural education. Theory Into Practice, 34 (3), 152–158. https://doi.org/10.1080/00405849509543674

Article   Google Scholar  

Black, P. J., & Wiliam, D. (1998). Assessment and classroom learning. Assessment in Education, 5 , 7–74.

Brown, J. S., & Burton, R. R. (1978). Diagnostic models for procedural bugs in basic mathematical skills. Cognitive Science, 2 (2), 155–192.

Burkhardt, H., & Schoenfeld, A. H. (2019). Formative assessment in mathematics. In R. Bennett, H. Andrade, & G. Cizek (Eds.), Handbook of formative assessment in the disciplines (pp. 35–67). Routledge.

Chapter   Google Scholar  

Cohen, D. K. (1990). A revolution in one classroom: The case of Mrs. Oublier. Educational Evaluation and Policy Analysis, 12 , 311–330.

Cohen, E. G., & Lotan, R. A. (2014). Designing groupwork: Strategies for the heterogeneous classroom (3rd ed.). Teachers College Press.

Cohen, E. G., Lotan, R. A., Scarloss, B. A., & Arellano, A. R. (1999). Complex instruction: Equity in cooperative learning classrooms. Theory Into Practice, 38 (2), 80–86. https://doi.org/10.1080/00405849909543836

Common Core State Standards Initiative (2010). Common core state standards for mathematics. http://www.corestandards.org/wp-content/uploads/Math_Standards.pdf

Cooney, T. (1985). A beginning teacher’s view of problem solving. Journal for Research in Mathematics Education, 16 (5), 324–336.

Fuller, F. (1969). Concerns of teachers: A developmental conceptualization. American Educational Research Journal, 6 , 207–226.

Herman, J., Epstein, S., Leon, S., La Torre Matrundola, D., Reber, S., & Choi, K. (2014). Implementation and effects of LDC and MDC in Kentucky districts (CRESST policy brief no. 13). University of California, National Center for Research on Evaluation, Standards, and Student Testing (CRESST).

Hord, S. M., Rutherford, W. L., Huling-Austin, L., & Hall, G. E. (1987). Taking charge of change . Association for Supervision and Curriculum Development.

Kim, H.-J. (2017). Teacher learning opportunities provided by implementing formative assessment lessons: Becoming responsive to student mathematical thinking. International Journal of Science and Math Education, 17 (2), 341–363. https://doi.org/10.1007/s10763-017-9866-7

Kozol, J. (1992). Savage inequalities . Harper Perennial.

Kuhn, T. S. (1996). The structure of scientific revolutions (3rd ed.). University of Chicago Press.

Book   Google Scholar  

Lampert, M. (2001). Teaching problems and the problems of teaching . Yale University Press.

Louie, N. L., Baldinger, E. M., & The Algebra Teaching Study and Mathematics Assessment Project. (2016). The TRU conversation guide: A tool for teacher learning and growth . Graduate School of Education, University of California, Berkeley & College of Education, Michigan State University. Retrieved from http://truframework.org

Mercer, N., Wegerif, R., & Major, L. (Eds.). (2019). The Routledge international handbook of research on dialogic education . Routledge.

Merriam-Webster online dictionary (2020). https://www.merriam-webster.com/ .

National Academy of Sciences. (1999). Science and creationism: A view from the national academy of sciences (2nd ed.). The National Academies Press. https://doi.org/10.17226/6024

National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics . Author.

National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics . Author.

Patterson, N. D., & Norwood, K. S. (2004). A case study of teacher beliefs on students’ beliefs about multiple representations. International Journal of Science and Mathematics Education, 2 , 5–23.

Philipp, R. A. (2007). Mathematics teachers’ beliefs and affect. In F. K. Lester Jr. (Ed.), Second handbook of research on mathematics teaching and learning (pp. 257–315). National Council of Teachers of Mathematics.

Popper, K. (1963). Conjectures and refutations . Routledge and Kegan Paul.

Prediger, S., & Neugebauer, P. (2021). Capturing teaching practices in language-responsive mathematics classrooms – Extending the TRU framework “teaching for robust understanding” to L-TRU. ZDM, 53 , 289–304. https://doi.org/10.1007/s11858-020-01187-1

Reinholz, D. L., & Shah, N. (2018). Equity analytics: A methodological approach for quantifying participation patterns in mathematics classroom discourse. Journal for Research in Mathematics Education, 49 (2), 140–177.

Research for Action. (2015). MDC’s influence on teaching and learning . Author. Retrieved from https://www.researchforaction.org/publications/mdcs-influence-on-teaching-and-learning/

Richardson, V. (1996). The role of attitudes and beliefs in learning to teach. In J. Sikula (Ed.), Handbook of research on teacher education (2nd ed., pp. 102–119). Macmillan.

Ryan, K. (1986). The induction of new teachers. Fastback of Phi Delta Kappa Educational Foundation (No. 237).

Schoenfeld, A. H. (1985). Mathematical problem solving . Academic.

Schoenfeld, A. H. (1988). When good teaching leads to bad results: The disasters of well taught mathematics classes. Educational Psychologist, 23 (2), 145–166.

Schoenfeld, A. H. (2004). The math wars. Educational Policy, 18 (1), 253–286.

Schoenfeld, A. H. (2011). How we think: A theory of goal-oriented decision making and its educational applications . Routledge.

Schoenfeld, A. H. (2013). Classroom observations in theory and practice. ZDM, the International Journal of Mathematics Education, 45 , 607–621. https://doi.org/10.1007/s11858-012-0483-1 .

Schoenfeld, A.H. (2014, November). What makes for powerful classrooms, and how can we support teachers in creating them? Educational Researcher, 43 (8), 404–412. https://doi.org/10.3102/0013189X1455 .

Schoenfeld, A. H. (2016). Making sense of teaching. ZDM, the International Journal of Mathematics Education, 48 (1/2), 239–246. https://doi.org/10.1007/s11858-016-0762-3

Schoenfeld, A. H. (2017). Teaching for robust understanding of essential mathematics. In T. McDougal (Ed.), Essential mathematics for the next generation: What and how students should learn (pp. 104–129). Tokyo Gagukei University.

Schoenfeld, A. H. (2018). Video analyses for research and professional development: The Teaching for Robust Understanding (TRU) framework. In C. Y. Charalambous & A.-K. Praetorius (Eds.), Studying Instructional Quality in Mathematics through Different Lenses: In Search of Common Ground . An issue of ZDM: Mathematics Education. Manuscript available at https://doi.org/10.1007/s11858-017-0908-y

Schoenfeld, A. H. (2020a). Mathematical practices, in theory and practice. ZDM, 52 , 1163–1175. https://doi.org/10.1007/s11858-020-01162-w

Schoenfeld, A. H. (2020b). Reframing teacher knowledge: A research and development agenda. ZDM, 52 (2), 359–376. https://doi.org/10.1007/s11858-019-01057-5

Schoenfeld, A. (2022). Why are Learning and Teaching Mathematics so Difficult? In M. Danesi, (Ed.), Handbook of cognitive mathematics (pp. 763–798). Springer Nature. https://doi.org/10.1007/978-3-030-44982-7_10-1 . eBook ISBN 978-3-031-03945-4, Print ISBN 978-3-031-03944-7

Schoenfeld, A. H., & The Teaching for Robust Understanding Project. (2016). The Teaching for Robust Understanding (TRU) observation guide: A tool for teachers, coaches, administrators, and professional learning communities . Graduate School of Education, University of California, Berkeley. Retrieved from https://truframework.org/

Schoenfeld, A. H., Floden, R. B., & The algebra teaching study and mathematics assessment projects. (2018). On classroom observations. Journal of STEM Education Research, 1 (1), 34–59. https://doi.org/10.1007/s41979-018-0001-7

Schoenfeld, A., Dosalmas, A., Fink, H., Sayavedra, A., Weltman, A., Zarkh, A., Tran, K., & Zuniga-Ruiz, S. (2019). Teaching for robust understanding with lesson study. In R. Huang, A. Takahashi, & J. P. Ponte (Eds.), Theory and practices of lesson study in mathematics: An international perspective (pp. 136–162). Springer. ISBN 978-3-030-04031-4.

Schoenfeld, A. H., Baldinger, E., Disston, J., Donovan, S., Dosalmas, A., Driskill, M., Fink, H., Foster, D., Haumersen, R., Lewis, C., Louie, N., Mertens, A., Murray, E., Narasimhan, L., Ortega, C., Reed, M., Ruiz, S., Sayavedra, A., Sola, T., Tran, K., Weltman, A., Wilson, D., & Zarkh, A. (2020). Learning with and from TRU: Teacher educators and the teaching for robust understanding framework. In K. Beswick (Ed.), The mathematics teacher educator as a developing professional (International handbook of mathematics teacher education) (Vol. 4). Sense Publishers.

Schoenfeld, A. H., Fink, H., Ruiz, S., Huang, S., Wei, X., & Chirinda, B. (2023a). Helping students become powerful mathematics thinkers: Case studies of teaching for robust understanding . Routledge. ISBN 9781032441689.

Schoenfeld, A. H., Fink, H., Ruiz, S., Sayavedra, A., & Weltman, A. (2023b). Mathematics teaching ontarget: A TRU guide for enriching mathematics teaching at all grade levels . Routledge. ISBN 9781032441672.

Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 17 (1), 4–14.

Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57 , 1–22.

Smith, B. P. (2000). Emerging themes in problems experienced by student teachers: A framework for analysis. College Student Journal. Downloaded April 20, 2009, from http://findarticles.com/p/articles/mi_m0FCR/is_4_34/ai_69750211/

Swan, M. (2006). Collaborative learning in mathematics: A challenge to our beliefs and practices . : National Institute for Advanced and Continuing Education (NIACE) for the National Research and Development Centre for Adult Literacy and Numeracy (NRDC).

Swan, M. (2017). Towards a task-based curriculum: Frameworks for task design and pedagogy. In T. McDougal (Ed.), Essential mathematics for the next generation: What and how students should learn (pp. 29–60). Tokyo Gakugei University.

Swan, M., & Burkhardt, H. (2012). A designer speaks. Educational Designer, 2 (5) Retrieved from: http://www.educationaldesigner.org/ed/volume2/issue5/article19

Swan, M., & Burkhardt, H. (2014). Lesson design for formative assessment. Educational Designer, 2 (7) Retrieved from: http://www.educationaldesigner.org/ed/volume2/issue7/article24/

Teaching for Robust Understanding Project. (2018). https://truframework.org/

Thompson, A. G. (1985). Teachers’ conceptions of mathematics and the teaching of problem solving. In E. A. Silver (Ed.), Teaching and learning mathematical problem solving: Multiple research perspectives (pp. 281–294). Erlbaum.

Thompson, A. G. (1992). Teachers’ beliefs and conceptions: A synthesis of the research. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 127–146). Macmillan.

Usó-Doménech, J. L., & Nescolarde-Selva, J. (2016). What are belief systems? Foundations of Science, 21 , 147–152. https://doi.org/10.1007/s10699-015-9409-z

Vygotsky, L. S. (1962). Thought and language (E. Hanfmann & G. Vakar, Trans.). MIT Press.

Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes . Harvard University Press.

Download references

Acknowledgments

The ideas discussed here have evolved over many years and profited immensely from refinement by the Functions Group, the Mathematics Assessment Project, and the Teaching for Robust Understanding Project, among others. This paper was produced with support from the U.S. National Science Foundation Grant 1503454, “TRUmath and Lesson Study: Supporting Fundamental and Sustainable Improvement in High School Mathematics Teaching,” a partnership between the Oakland Unified School District, Mills College, the SERP Institute, and the University of California at Berkeley.

Author information

Authors and affiliations.

Graduate School of Education, University of California, Berkeley, CA, USA

Alan H. Schoenfeld

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Alan H. Schoenfeld .

Editor information

Editors and affiliations.

Res on Learning, Instruction & Didactics, University of Zurich, Zurich, Switzerland

Anna-Katharina Praetorius

Department of Education, University of Cyprus, Nicosia, Cyprus

Charalambos Y. Charalambous

Rights and permissions

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License ( http://creativecommons.org/licenses/by/4.0/ ), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

Reprints and permissions

Copyright information

© 2023 The Author(s)

About this chapter

Schoenfeld, A.H. (2023). A Theory of Teaching. In: Praetorius, AK., Charalambous, C.Y. (eds) Theorizing Teaching. Springer, Cham. https://doi.org/10.1007/978-3-031-25613-4_6

Download citation

DOI : https://doi.org/10.1007/978-3-031-25613-4_6

Published : 07 June 2023

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-25612-7

Online ISBN : 978-3-031-25613-4

eBook Packages : Education Education (R0)

Share this chapter

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 2: The nature of knowledge and the implications for teaching

Purpose of the chapter.

This chapter discusses the relationship between our views on the nature of knowledge and the way we decide to teach.

After reading this chapter you should be able to:

• recognize your own epistemological/philosophical position that determines the way you are currently teaching;
• reflect on the similarities or differences between academic and everyday knowledge;
• decide whether technology changes the nature of knowledge, and consider the implications for teaching;
• describe in broad terms the main theories of learning and discuss their implications for teaching;
• identify different levels and types of learning and decide which is most appropriate for your subject area/students;
• integrate these ideas into a personal strategy or philosophy for the teaching of your subject;
• decide on whether or not to change your overall approach to teaching in the light of the issues raised in this chapter.

What is covered in this chapter

In this chapter, I will be discussing different beliefs about the nature of knowledge, and how that influences teaching and learning.

In particular, this chapter covers the following topics:

• Scenario C: A pre-dinner party discussion
• 2.1: Art, theory, research, and best practices in teaching
• 2.2 Epistemology and theories of learning
• 2.3 Objectivism and behaviourism
• 2.4 Cognitivism
• 2.5 Constructivism
• 2.6 Connectivism
• 2.7 Is the nature of knowledge changing?
• 2.8 Summary

Also in this chapter you will find the following activities:

• Activity 2.1 What do you think makes a good teacher??
• Activity 2.3  Defining t h e limits of behaviourism
• Activity 2.4 Defining the limits of cognitivism
• Activity 2.5  Defining t h e limits of constructivism
• Activity 2.6  Defining t h e limits of connectivism
• Activity 2.7 Epistemology and academic knowledge

Key Takeaways

1. Teaching is a highly complex occupation, which needs to adapt to a great deal of variety in context, subject matter and learners. It does not lend itself to broad generalizations. Nevertheless it is possible to provide guidelines or principles based on best practices, theory and research, that must then be adapted or modified to local conditions.

2. Our underlying beliefs and values, usually shared by other experts in a subject domain, shape our approach to teaching. These underlying beliefs and values are often implicit and are often not directly shared with our students, even though they are seen as essential components of becoming an ‘expert’ in a particular subject domain.

3. Different theories of learning reflect different views on the nature of knowledge.

4. Every teacher starts from some epistemological or theoretical position, even if it is not explicit, or even if the teacher is not fully aware of their beliefs.

5. With the possible exception of connectivism, there is some form of empirical evidence to support each of the theories of learning outlined here. The difference then is as much about values and beliefs about knowledge as it is about the effectiveness of each theory.

6. It is argued that academic knowledge is different from other forms of knowledge, and is even more relevant today in a digital age.

7. However, academic knowledge is not the only kind of knowledge that is important in today’s society, and as teachers we have to be aware of other forms of knowledge and their potential importance to our students, and make sure that we are providing the full range of contents and skills needed for students in a digital age.

Teaching in a Digital Age Copyright © 2015 by Anthony William (Tony) Bates is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License , except where otherwise noted.

Share This Book