lesson 12.2 problem solving with right triangles

Right Triangles

Rules, Formula and more

Pythagorean Theorem

The sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse .

Usually, this theorem is expressed as $$ A^2 + B^2 = C^2 $$ .

Right Triangle Properties

A right triangle has one $$ 90^{\circ} $$ angle ($$ \angle $$ B in the picture on the left) and a variety of often-studied formulas such as:

• The Pythagorean Theorem
• Trigonometry Ratios (SOHCAHTOA)
• Pythagorean Theorem vs Sohcahtoa (which to use)

SOHCAHTOA only applies to right triangles ( more here ) .

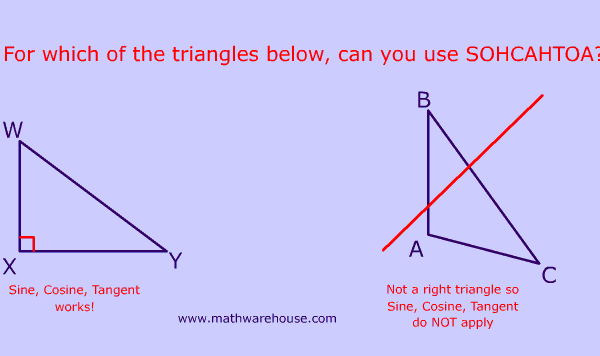
A Right Triangle's Hypotenuse

The hypotenuse is the largest side in a right triangle and is always opposite the right angle.

In the triangle above, the hypotenuse is the side AB which is opposite the right angle, $$ \angle C $$.

Online tool calculates the hypotenuse (or a leg) using the Pythagorean theorem.

Practice Problems

Below are several practice problems involving the Pythagorean theorem, you can also get more detailed lesson on how to use the Pythagorean theorem here .

Find the length of side t in the triangle on the left.

Substitute the two known sides into the Pythagorean theorem's formula : A² + B² = C²

What is the value of x in the picture on the left?

Set up the Pythagorean Theorem : 14 2 + 48 2 = x 2 2,500 = X 2

$$ x = \sqrt{2500} = 50 $$

$$ x^2 = 21^2 + 72^2 \\ x^2= 5625 \\ x = \sqrt{5625} \\ x =75 $$

Find the length of side X in the triangle on on the left?

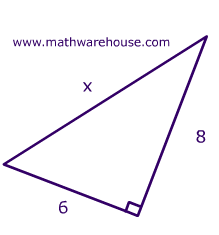
Substitue the two known sides into the pythagorean theorem's formula : $$ A^2 + B^2 = C^2 \\ 8^2 + 6^2 = x^2 \\ x = \sqrt{100}=10 $$

What is x in the triangle on the left?

x 2 + 4 2 = 5 2 x 2 + 16 = 25 x 2 = 25 - 16 = 9 x = 3

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Chapter 12 - Lesson 12.2 Problem Solving with Right Triangles

Nov 19, 2014

390 likes | 783 Views

Chapter 12 - Lesson 12.2 Problem Solving with Right Triangles. HW: 12.2/1-20. Finding the Sides of a Triangle. Remember: SOHCAHTOA. Review: Trig Ratios. First we will find the Sine, Cosine and Tangent ratios for Angle P. P.

Share Presentation

• step 5 solve
• 5 ft tall theodolite

Presentation Transcript

Chapter 12 - Lesson 12.2 Problem Solving with Right Triangles HW: 12.2/1-20

Finding the Sides of a Triangle Remember: SOHCAHTOA

Review: Trig Ratios First we will find the Sine, Cosine and Tangent ratios for Angle P. P Next we will find the Sine, Cosine, and Tangent ratios for Angle Q 20 12 Adjacent Q 16 Opposite Remember SohCahToa

Solving Right Triangles Every right triangle has one right angle, two acute angles, one hypotenuse, and two legs. To Solve a Right Triangle means to determine the measures of all six parts.

Missing sides r and s, and angle S.

But what if you don’t know either of the acute angles? To solve those triangle we must use Inverse Trig Functions

Missing side….

What are the angles of elevation and depression and what is their relationship to right triangles?

ANGLE OF DEPRESSION Looking down from the horizontal observer Eye level Angle of depression cliffs object Sea level

ANGLE OF ELEVATION Looking up from the horizontal observer Eye level cliffs Angle of elevation object Sea level

If an observer sights an object above, the angle between a horizontal line and his or her line of sight is called an angle of elevation. If the line of sight is below the horizontal it is called the angle of depression. Angle of Depression Angle of Elevation

eye - level line of sight eye - level

The angles are equal – they are alternate interior angles eye - level line of sight eye - level

Angles of Elevation and Depression Top Horizontal Angle of Depression Line of Sight Angle of Elevation Bottom Horizontal Since the two horizontal lines are parallel, by Alternate Interior Angles the angle of depression must be equal to the angle of elevation.

Angles of Elevation and Depression line of sight

B h 250 A 21 m Example 1 The angle of elevation of building A to building B is 250. The distance between the buildings is 21 meters. Calculate how much taller Building B is than building A. Step 1: Draw a right angled triangle with the given information. Angle of elevation Step 2: Take care with placement of the angle of elevation Step 3: Set up the trig equation. Step 4: Solve the trig equation.

 80 m  60 m A boat is 60 meters out to sea. Madge is standing on a cliff 80 meters high. What is the angle of depression from the top of the cliff to the boat? Example 2 Step 1: Draw a right angled triangle with the given information. Angle of depression Step 2: Alternate interior angles place  inside the triangle. Step 3: Decide which trig ratio to use. Step 4: Use calculator to find the value of the unknown.

Plane 25 km h Marty is standing on level ground when he sees a plane directly overhead. The angle of elevation of the plane after it has travelled 25 km is 200. Calculate the altitude of the plane at this time. Example 3 Step 1: Draw a right angled triangle with the given information. 200 Step 2:Alternate interior angles places 200 inside the triangle. Angle of elevation 200 Step 3: Decide which trig ratio to use. Step 4: Use calculator to find the value of the unknown. (nearest km)

5m 650 450 P K p k Example 4 Kate and Petra are on opposite sides of a tree. The angle of elevation to the top of the tree from Kate is 45o and from Petra is 65o. If the tree is 5 m tall, who is closer to the tree, Kate or Petra? Kate Petra Answer Therefore, Petra is closer to the tree, since the distance is shorter.

Bird 400 200 2 m Car Example 5 Maryann is peering outside her window. From her window she sees her car and a bird hovering above her car. The angle of depression of Maryann’s car is 200 whilst the angle of elevation to the bird is 400. If Maryann’s window is 2m off the ground, what is the bird’s altitude at that moment? Step 1: Draw a diagram Step 2: Set up the trig equations in two parts. Find d first, then b. Step 3: Solve the equations and answer the question. b d Therefore, The bird is 6.6 m (2 + 4.6) from the ground at that moment.

Your Turn 1: You sight a rock climber on a cliff at a 32oangle of elevation. The horizontal ground distance to the cliff is 1000 ft. Find the line of sight distance to the rock climber. x 1000 ft

Your Turn 2: An airplane pilots sights a life raft at a 26o angle of depression. The airplane’s altitude is 3 km. What is the airplane’s surface distance dfrom the raft? 3 km d

FYI: Theodolite Theodolite is a precision instrument for measuring angles in the horizontal and vertical planes. Theodolites are mainly used for surveying applications, and have been adapted for specialized purposes in fields like meteorology and rocket launch technology. When the telescope is pointed at a target object, the angle of each of these axes can be measured with great precision Theodolites are still used today for ultra high precision optical alignment and measurement

x 200 tan 35° = x = 200 • tan 35° Your Turn 3: A surveyor stands 200 ft from a building to measure its height with a 5-ft tall theodolite. The angle of elevation to the top of the building is 35°. How tall is the building? So x ≈ 140 To find the height of the building, add the height of the Theodolite, which is 5 ft tall. The building is about 140 ft + 5 ft, or 145 ft tall.

Your Turn 4: 3500 x ft sin 2° = 3500 ft sin 2° x ft = An airplane flying 3500 ft above ground begins a 2° descent to land at an airport. How many miles from the airport is the airplane when it starts its descent? x ft ≈ 100,287.9792 ft x miles ≈ 18.9939 miles ≈ 19 miles The airplane is about 19 mi from the airport when it starts its descent.

Your Turn 5: A 6-ft man stands 12 ft from the base of a tree. The angle of elevation from his eyes to the top of the tree is 40°. 1. About how tall is the tree? 2. If the man releases a pigeon that flies directly to the top of the tree, about how far will it fly? 3. What is the angle of depression from the treetop to the man’s eyes? about 16 ft about 15.7 ft 40°

Your Turn 6: Step 1: Draw a triangle to fit problem Step 3: Identify trig function to use 30.5 = 25 + 5.5 Step 2: Label sides from angle’s view opp Step 4: Set up equation 27° adj x 30.5 tan 27° = ------- x Step 5: Solve for variable S  O / H C  A / H T  O / A x tan 27° = 30.5 x = (30.5) / (tan 27°) x = 59.9 CIRCUS ACTS. At the circus, a person in the audience watches the high-wire routine. A 5-foot-6-inch tall acrobat is standing on a platform that is 25 feet off the ground. How far is the audience member from the base of the platform, if the angle of elevation from the audience member’s line of sight to the top of the acrobat is 27°?

Your Turn 7: 37 = 32 + 6 x° 45 = 50 - 5 DIVING At a diving competition, a 6-foot-tall diver stands atop the 32-foot platform. The front edge of the platform projects 5 feet beyond the ends of the pool. The pool itself is 50 feet in length. A camera is set up at the opposite end of the pool even with the pool’s edge. If the camera is angled so that its line of sight extends to the top of the diver’s head, what is the camera’s angle of elevation to the nearest degree?

Your Turn 8: From a point 80m from the base of a tower, the angle of elevation is 28˚. How tall is the tower to the nearest meter? x 28˚ 80m tan 28˚ = 80 (tan 28˚) = x 80 (.5317) = x x ≈ 42.5m is the height of the tower

Your Turn 8: A ladder that is 20 ft is leaning against the side of a building. If the angle formed between the ladder and ground is 75˚, how far is the bottom of the ladder from the base of the building? 20 building ladder 75˚ x cos 75˚ = 20 (cos 75˚) = x 20 (.2588) = x x ≈ 5.2ft from the base of the building

Your Turn 9: When the sun is 62˚ above the horizon, a building casts a shadow 18m long. How tall is the building? x 62˚ 18 shadow tan 62˚ = 18 (tan 62˚) = x 18 (1.8807) = x x ≈ 33.9m is the height of the building

Your Turn 10: A kite is flying at an angle of elevation of about 55˚. Ignoring the sag in the string, find the height of the kite if 85m of string have been let out. kite 85 x string 55˚ sin 55˚ = 85 (sin 55˚) = x 85 (.8192) = x x ≈ 69.6m is the height of the kite

Your Turn 11: A 5.5 foot person standing 10 feet from a street light casts a 14 foot shadow. What is the height of the streetlight? 5.5 x˚ 10 14 shadow 1st find the angle of elevation 2nd use the angle to find the height of the light. tan x˚ = x° ≈ 21.45° height = 9.43 feet

Your Turn 12: The angle of depression from the top of a tower to a boulder on the ground is 38º. If the tower is 25m high, how far from the base of the tower is the boulder? 38º angle of depression 25 Alternate Interior Angles are congruent 38º x

• More by User

9.6 Solving Right Triangles

9.6 Solving Right Triangles. Geometry Mrs. Spitz Spring 2005. Objectives/Assignment. Solve a right triangle. Use right triangles to solve real-life problems, such as finding the glide angle and altitude of a space shuttle.

313 views • 16 slides

Solving Right Triangles

Solving Right Triangles. Geometry Mrs. Spitz Spring 2005. Objectives/Assignment. Solve a right triangle. Use right triangles to solve real-life problems, such as finding the glide angle and altitude of a space shuttle.

158 views • 14 slides

Chapter 12 - Lesson 12.2 Problem Solving with Right Triangles. HW: 12.2/1-20 . Finding the Sides of a Triangle. Remember: SOHCAHTOA. Review: Trig Ratios. First we will find the Sine, Cosine and Tangent ratios for Angle P. P.

391 views • 38 slides

Lesson 9.1 Use Trigonometry with Right Triangles

Lesson 9.1 Use Trigonometry with Right Triangles. Standard Accessed: Students will prove, apply, and model trigonometric functions and ratios. Warm-Up. Lesson Presentation. Lesson Quiz. Warm-Up.

558 views • 13 slides

Trigonometry Functions And Solving Right Triangles

Trigonometry Functions And Solving Right Triangles. Next Slide. Title Page. Table OF Contents. Table of Content s. What are the Trigonometry Functions and how are they used. What do you need to solve a right Triangle using Trig. Functions. Sine Function. Cosine Function.

400 views • 24 slides

5-5 Solving Right Triangles

5-5 Solving Right Triangles. Find Sin Ѳ = 0. Find Cos Ѳ = .7. Inverses of Trigonometric Functions. Arccosine relation – the inverse of y = cos x Arcsine relation – the inverse of y = sin x Arctangent relation – the inverse of y = tan x. y = sin x y = cos x y = tan x.

374 views • 28 slides

Lesson 12.2

Lesson 12.2. Matrix Multiplication. Row and Column Order. The rows in a matrix are usually indexed 1 to m from top to bottom. The columns are usually indexed 1 to n from left to right. Elements are indexed by row, then column. Scalar Multiplication of Matrices.

396 views • 22 slides

Lesson 9 – Problem Solving with Relative Motion

Lesson 9 – Problem Solving with Relative Motion. August 12, 2013. Learning Goals. The student will learn effective problem solving tactics in physics The student will be able to solve problems related to relative motion, by adding and subtracting vector quantities by using a variety of methods.

294 views • 11 slides

1.5 Solving Right Triangles

1.5 Solving Right Triangles. JMerrill, 2005 Revised 2009. Recall from Last Week. SOH-CAH-TOA Sine: abbreviation: s in = Cosine: abbreviation: c os = Tangent: abbreviation: t an = These are the ratios of 2 sides. . Evaluating with a Calculator When .

242 views • 12 slides

8.3 Solving Right Triangles

8.3 Solving Right Triangles. Examples:. Use the trigonometric ratio to determine which angle of the triangle is  A. Examples:. Use the given trigonometric ratio to determine which angle of the triangle is  A. Examples:.

301 views • 10 slides

Solving Right Triangles. How do you solve right triangles?. M2 Unit 2: Day 6. To solve a right triangle you need…. Every right triangle has one right angle, two acute angles, one hypotenuse, and two legs. To SOLVE A RIGHT TRIANGLE means to find all 6 parts.

392 views • 16 slides

GEOMETRY Solving Right Triangles

GEOMETRY Solving Right Triangles. Warm Up. Use your calculator to find each trigonometric ratio. Round to the nearest hundredth. 1) sin 63˚ 2) cos 27˚ 3) tan 64˚. Right Triangles. You can use trigonometric ratios to change a percent grade to an angle measure.

455 views • 31 slides

Solving Right Triangles. Section 3.3. N. Solve a Right Triangle. The Tunnel of Samos. An island has a spring at point S , on one side of a mountain, M. A city at point C , on the other side of the mountain, needs the water.

316 views • 14 slides

2.5 Solving Right Triangles

2.5 Solving Right Triangles. OBJ: Find missing sides and angles of a right triangle. sin(74  8  14 ) sin(74 + 8 60 + 14 3600) = .962 74.137  sin (74.137  ). sin 0 0 sin 30 .5 sin 60 .87 sin 90 1

317 views • 12 slides

5-5: Solving Right Triangles

Alexis Mathis Aaron Goode Jessica Anderson. 5-5: Solving Right Triangles. Unit Circle. Pythagorean theorem. a²+b²=c² Used to determine the sides of a right triangle. Unit chart. Soh - Cah -Toa. Right triangle basics. Internal angle=180 Right angle=90

328 views • 16 slides

5.5 Solving Right Triangles

5.5 Solving Right Triangles. How do we find missing angle measurements? How do we evaluate inverse trig functions?. If I told you what could be? If I told you what could be? If I told you what could be? We can do this without the table too.

227 views • 11 slides

Solving right triangles

Solving right triangles. Warm Up Use ∆ ABC for Exercises 1–3. 1. If a = 8 and b = 5, find c . 2. If a = 60 and c = 61, find b . 3. If b = 6 and c = 10, find sin B . Find AB. 4. A (8, 10), B (3, 0) 5. A (1, –2), B (2, 6). 11. 0.6. Objective.

395 views • 26 slides

9.6 Solving Right Triangles. Objectives/Assignment. Solve a right triangle Use right triangles to solve problems Assignment: 2-36 even, 48-64 even. Solving a right triangle.

221 views • 14 slides

SOLVING RIGHT TRIANGLES

SOLVING RIGHT TRIANGLES. We will be given information about a triangle and then have to find the remaining sides and angles. We will develop new ways to find the area of triangles. We will apply the law of sines and law of cosines. SOH CAH TOA. PYTHAGOREAN THEOREM. SOH CAH TOA. B.

413 views • 10 slides

189 views • 16 slides

Chapter 12 12.1-12.2

Chapter 12 12.1-12.2. Geology and nonrenewable minerals Matt Healy. Case Study: The General Mining Law of 1872. Designed to encourage mineral exploration and the mining of hard rock minerals (gold, silver, zinc, etc) on US public lands and help to develop the then sparsely populated West.

386 views • 38 slides

Solving Right Triangles. How do you solve right triangles?. Day 53. Lesson 5.4. Sunday, January 5, 2020. Every right triangle has one right angle, two acute angles, one hypotenuse, and two legs. To SOLVE A RIGHT TRIANGLE means to find all 6 parts. Find the measure of the missing angle.

301 views • 26 slides

• Anatomy & Physiology
• Astrophysics
• Earth Science
• Environmental Science
• Organic Chemistry
• Precalculus
• Trigonometry
• English Grammar
• U.S. History
• World History

... and beyond

• Socratic Meta
• Featured Answers

• Solving Right Triangles

Key Questions

In Triangle #ABC# with the right angle at #C# , let #a# , #b# , and #c# be the opposite, the adjacent, and the hypotenuse of #angle A# . Then, we have

#sin A=a/c Rightarrow "m"angle A=sin^{-1}(a/c)#

#sin B=b/c Rightarrow "m"angle B=sin^{-1}(b/c)#

I hope that this was helpful.

Chapter 2: Trigonometric Ratios

Exercises: 2.2 Right Triangle Trigonometry

Exercises homework 2.2.

• Use measurements to calculate the trigonometric ratios for acute angles #1-10, 57-60
• Use trigonometric ratios to find unknown sides of right triangles #11-26
• Solve problems using trigonometric ratios #27-34, 41-46
• Use trig ratios to write equations relating the sides of a right triangle #35-40
• Use relationships among the trigonometric ratios #47-56, 61-68

Suggested Homework Problems

Here are two right triangles with a [latex]65 °[/latex] angle.

• Measure the sides [latex]AB[/latex] and [latex]BC[/latex] with a ruler. Use the lengths to estimate [latex]\sin 65°{.}[/latex]
• Measure the sides [latex]AD[/latex] and [latex]DE[/latex] with a ruler. Use the lengths to estimate [latex]\sin 65°{.}[/latex]
• Use your calculator to look up [latex]\sin 65°{.}[/latex] Compare your answers. How close were your estimates?

Use the figure in Problem 1 to calculate two estimates each for the cosine and tangent of [latex]65 °{.}[/latex] Compare your estimates to your calculator’s values for [latex]\cos 65°[/latex] and [latex]\tan 65°{.}[/latex]

Here are two right triangles with a [latex]40 °[/latex] angle.

• Measure the sides [latex]AB[/latex] and [latex]AC[/latex] with a ruler. Use the lengths to estimate [latex]\cos 40°{.}[/latex]
• Measure the sides [latex]AD[/latex] and [latex]AE[/latex] with a ruler. Use the lengths to estimate [latex]\cos 40°{.}[/latex]
• Use your calculator to look up [latex]\cos 40°{.}[/latex] Compare your answers. How close were your estimates?

Use the figure in Problem 2 to calculate two estimates each for the cosine and tangent of [latex]40 °{.}[/latex] Compare your estimates to your calculator’s values for [latex]\sin 40°[/latex] and [latex]\tan 40°{.}[/latex]

Exercise Group

For the right triangles in Problems 5–10,

• Find the length of the unknown side.
• Find the sine, cosine, and tangent of [latex]\theta \text{.}[/latex] Round your answers to four decimal places.

For Problems 11–16,

• Sketch and label the sides of a right triangle with angle [latex]\theta\text{.}[/latex]
• Sketch and label another right triangle with angle [latex]\theta[/latex] and longer sides.

[latex]\cos \theta = \dfrac{3}{5}[/latex]

[latex]\tan \theta = \dfrac{7}{2}[/latex]

[latex]\tan \theta = \dfrac{11}{4}[/latex]

[latex]\sin \theta = \dfrac{4}{9}[/latex]

[latex]\sin \theta = \dfrac{1}{9}[/latex]

[latex]\cos \theta = \dfrac{7}{8}[/latex]

For Problems 17–22, use one of the three trigonometric ratios to find the unknown side of the triangle. Round your answer to hundredths.

For Problems 23–26, sketch and label a right triangle with the given properties.

One angle is [latex]40°{,}[/latex] the side opposite that angle is 8 inches

One angle is [latex]65°{,}[/latex] the side adjacent to that angle is 30 yards

One angle is [latex]28°{,}[/latex] the hypotenuse is 56 feet

One leg is [latex]15[/latex] meters, the hypotenuse is [latex]18[/latex] meters

For Problems 27–34,

• Sketch a right triangle that illustrates the situation. Label your sketch with the given information.
• Choose the appropriate trig ratio and write an equation, then solve the problem.

To measure the height of cloud cover, airport controllers fix a searchlight to shine a vertical beam on the clouds. The searchlight is [latex]120[/latex] yards from the office. A technician in the office measures the angle of elevation to the light on the cloud cover at [latex]54.8°{.}[/latex] What is the height of the cloud cover?

To measure the distance across a canyon, Evel first sights an interesting rock directly opposite on the other side. He then walks [latex]200[/latex] yards down the rim of the canyon and sights the rock again, this time at an angle of [latex]18.5°[/latex] from the canyon rim. What is the width of the canyon?

A salvage ship is searching for the wreck of a pirate vessel on the ocean floor. Using sonar, they locate the wreck at an angle of depression of [latex]36.2°{.}[/latex] The depth of the ocean at their location is [latex]260[/latex] feet. How far should they move so that they are directly above the wrecked vessel?

Ramps for wheelchairs should be no steeper than an angle of [latex]6°{.}[/latex] How much horizontal distance should be allowed for a ramp that rises [latex]5[/latex] feet in height?

The radio signal from a weather balloon indicates that it is [latex]1500[/latex] meters from a meteorologist on the ground. The angle of elevation to the balloon is [latex]48°{.}[/latex] What is the balloon’s altitude?

According to Chinese legend, around 200 BC, the general Han Xin used a kite to determine the distance from his location to an enemy palace. He then dug a secret tunnel which emerged inside the palace. When the kite was directly above the palace, its angle of elevation was [latex]27°[/latex] and the string to the kite was [latex]1850[/latex] feet long. How far did Han Xin’s troops have to dig?

A cable car on a ski lift traverses a horizontal distance of [latex]1800[/latex] meters at an angle of [latex]38°{.}[/latex] How long is the cable?

Zelda is building the loft on her summer cottage. At its central point, the height of the loft is [latex]8[/latex] feet, and the pitch of the roof should be [latex]24°{.}[/latex] How long should the rafters be?

For Problems 35–40, use a trig ratio to write an equation for [latex]x[/latex] in terms of [latex]\theta{.}[/latex]

For Problems 41–44, find the altitude of the triangle. Round your answer to two decimal places.

For Problems 45 and 46, find the length of the chord [latex]AB{.}[/latex] Round your answer to two decimal places.

For Problems 47–50, fill in the table.

• In each of the figures for Problems 47-50, what is the relationship between the angles [latex]\theta[/latex] and [latex]\phi{?}[/latex]
• Study the tables for Problems 47-50. What do you notice about the values of sine and cosine for the angles [latex]\theta[/latex] and [latex]\phi{?}[/latex] Explain why this is true.

There is a relationship between the tangent, the sine, and the cosine of any angle. Study the tables for Problems 47-50 to discover this relationship. Write your answer as an equation.

• Use the figure to explain what happens to [latex]\tan \theta[/latex] as [latex]\theta[/latex] increases, and why.
• Use the figure to explain what happens to [latex]\cos \theta[/latex] as [latex]\theta[/latex] increases, and why.
• What happens to [latex]\tan \theta[/latex] as [latex]\theta[/latex] increases?
• What value does your calculator give for [latex]\tan 90°{?}[/latex] Why?

Explain why it makes sense that [latex]\sin 0° = 0[/latex] and [latex]\sin 90° = 1{.}[/latex] Use a figure to illustrate your explanation.

Explain why it makes sense that [latex]\cos 0° = 1[/latex] and [latex]\cos 90° = 0{.}[/latex] Use a figure to illustrate your explanation

For Problems 57–60, explain why the trigonometric ratio is not correct.

[latex]\sin \theta = \dfrac{5}{9}[/latex]

[latex]\tan \theta = \dfrac{4}{7}[/latex]

[latex]\cos \theta = \dfrac{21}{20}[/latex]

[latex]\sin \theta = \dfrac{8}{10}[/latex]

For Problems 61–64, sketch and label a right triangle, then fill in the blank.

If [latex]\sin \theta = 0.2358\text{,}[/latex]  then [latex]\cos (90^{o} - \theta)=\underline{\qquad} \text{,}[/latex]

• If [latex]\cos \alpha = \dfrac{3}{11} \text{,}[/latex] then [latex]\underline{\qquad} (90° - \alpha) = \dfrac{3}{11}\text{.}[/latex]
• If [latex]\sin 42° = n\text{,}[/latex] then [latex]\cos \underline{\qquad} = n\text{.}[/latex]
• If [latex]\cos 13° = z\text{,}[/latex] then [latex]\sin \underline{\qquad} = z\text{.}[/latex]
• If [latex]\cos \beta = \dfrac{2}{\sqrt{7}}{,}[/latex] then [latex]\sin (90° - \beta) =\underline{\qquad} {.}[/latex]
• If [latex]\sin \phi = 0.693{,}[/latex] then [latex](90° - \phi) = 0.693{.}[/latex]
• If [latex]\cos 87° = p{,}[/latex] then [latex]\sin \underline{\qquad} = p{.}[/latex]
• If [latex]\sin 59° =w{,}[/latex] then [latex]\cos \underline{\qquad} = w{.}[/latex]
• If [latex]\sin \phi = \dfrac{5}{13}[/latex] and [latex]\cos \phi = \dfrac{12}{13}{,}[/latex] then [latex]\tan \phi =\underline{\qquad} {.}[/latex]
• If [latex]\cos \beta = \dfrac{1}{\sqrt{10}}{,}[/latex] and [latex]\sin \beta = \dfrac{3}{\sqrt{10}}{,}[/latex] then [latex]\tan \beta = \underline{\qquad}{.}[/latex]
• If [latex]\tan B = \dfrac{2}{\sqrt{5}}[/latex] and [latex]\cos B = \dfrac{\sqrt{5}}{3}{,}[/latex] then [latex]\sin B =\underline{\qquad}{.}[/latex]
• If [latex]\sin W = \sqrt{\dfrac{3}{7}}[/latex] and [latex]\tan W = \dfrac{\sqrt{3}}{2}{,}[/latex] then [latex]\cos W =\underline{\qquad}{.}[/latex]
• If [latex]\cos \theta = \dfrac{2}{\sqrt{10}}[/latex] and [latex]\sin \theta = \sqrt{\dfrac{3}{5}}{,}[/latex] then [latex]\tan \theta = \underline{\qquad}{.}[/latex]
• If [latex]\sin \alpha = \dfrac{\sqrt{2}}{4}{,}[/latex] and [latex]\cos \alpha =\dfrac{\sqrt{14}}{4}{,}[/latex] then [latex]\tan \alpha = \underline{\qquad}{.}[/latex]
• If [latex]\tan A = \dfrac{\sqrt{7}}{3}[/latex] and [latex]\cos A = \dfrac{3}{4}{,}[/latex] then [latex]\sin A =\underline{\qquad}{.}[/latex]
• If [latex]\sin V = \sqrt{\dfrac{10}{5}}[/latex] and [latex]\tan V = \dfrac{2}{5}{,}[/latex] then [latex]\cos V =\underline{\qquad}{.}[/latex]

Explain why the cosine of a [latex]73°[/latex] angle is always the same, no matter what size triangle the angle is in. Illustrate your explanation with a sketch.

• If you plotted the points in your table, would they lie on a straight line? Why or why not?
• What is the slope of the line through the origin and point [latex]P{?}[/latex]
• What is the tangent of the angle [latex]\theta{?}[/latex]
• On the same grid, sketch an angle whose tangent is [latex]\dfrac{8}{5}.[/latex]
• Use your calculator to complete the table. Round your answers to hundredths.
• Use the values of tan [latex]\theta[/latex] to sketch all the angles listed in the table. Locate the vertex of each angle at the origin and the initial side along the positive [latex]x[/latex]-axis.

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.1: Right triangles

• Last updated
• Save as PDF
• Page ID 89299

• Matthew Boelkins, David Austin & Steven Schlicker
• Grand Valley State University via ScholarWorks @Grand Valley State University

Motivating Questions

• How can we view \(\cos(\theta)\) and \(\sin(\theta)\) as side lengths in right triangles with hypotenuse \(1\text{?}\)
• Why can both \(\cos(\theta)\) and \(\sin(\theta)\) be thought of as ratios of certain side lengths in any right triangle?
• What is the minimum amount of information we need about a right triangle in order to completely determine all of its sides and angles?

In Section 2.3 , we defined the cosine and sine functions as the functions that track the location of a point traversing the unit circle counterclockwise from \((1,0)\text{.}\) In particular, for a central angle of radian measure \(t\) that passes through the point \((1,0)\text{,}\) we define \(\cos(t)\) as the \(x\)-coordinate of the point where the other side of the angle intersects the unit circle, and \(\sin(t)\) as the \(y\)-coordinate of that same point, as pictured in Figure \(\PageIndex{1}\)

By changing our perspective slightly, we can see that it is equivalent to think of the values of the sine and cosine function as representing the lengths of legs in right triangles. Specifically, given a central angle  1  \(\theta\text{,}\) if we think of the right triangle with vertices \((\cos(\theta),0)\text{,}\) \((0,0)\text{,}\) and \((\cos(\theta), \sin(\theta))\text{,}\) then the length of the horizontal leg is \(\cos(\theta)\) and the length of the vertical leg is \(\sin(\theta)\text{,}\) as seen in Figure \(\PageIndex{2}\)

This right triangle perspective enables us to use the sine and cosine functions to determine missing information in certain right triangles. The field of mathematics that studies relationships among the angles and sides of triangles is called trigonometry . In addition, it's important to recall both the Pythagorean Theorem and the Fundamental Trigonometric Identity. The former states that in any right triangle with legs of length \(a\) and \(b\) and hypotenuse of length \(c\text{,}\) it follows \(a^2 + b^2 = c^2\text{.}\) The latter, which is a special case of the Pythagorean Theorem, says that for any angle \(\theta\text{,}\) \(\cos^2(\theta) + \sin^2(\theta) = 1\text{.}\)

Preview Activity \(\PageIndex{1}\)

For each of the following situations, sketch a right triangle that satisfies the given conditions, and then either determine the requested missing information in the triangle or explain why you don't have enough information to determine it. Assume that all angles are being considered in radian measure.

• The length of the other leg of a right triangle with hypotenuse of length \(1\) and one leg of length \(\frac{3}{5}\text{.}\)
• The lengths of the two legs in a right triangle with hypotenuse of length \(1\) where one of the non-right angles measures \(\frac{\pi}{3}\text{.}\)
• The length of the other leg of a right triangle with hypotenuse of length \(7\) and one leg of length \(6\text{.}\)
• The lengths of the two legs in a right triangle with hypotenuse \(5\) and where one of the non-right angles measures \(\frac{\pi}{4}\text{.}\)
• The length of the other leg of a right triangle with hypotenuse of length \(1\) and one leg of length \(\cos(0.7)\text{.}\)
• The measures of the two angles in a right triangle with hypotenuse of length \(1\) where the two legs have lengths \(\cos(1.1)\) and \(\sin(1.1)\text{,}\) respectively.

The geometry of triangles

In the study of functions, linear functions are the simplest of all and form a foundation for our understanding of functions that have other shapes. In the study of geometric shapes (polygons, circles, and more), the simplest figure of all is the triangle, and understanding triangles is foundational to understanding many other geometric ideas. To begin, we list some familiar and important facts about triangles.

• Any triangle has \(6\) important features: \(3\) sides and \(3\) angles.
• In any triangle in the Cartesian plane, the sum of the measures of the interior angles is \(\pi\) radians (or equivalently, \(180^\circ\)).
• In any triangle in the plane, knowing three of the six features of a triangle is often enough information to determine the missing three features.  2 

The situation is especially nice for right triangles, because then we only have five unknown features since one of the angles is \(\frac{\pi}{2}\) radians (or \(90^\circ\)), as demonstrated in Figure \(\PageIndex{3}\) If we know one of the two non-right angles, then we know the other as well. Moreover, if we know any two sides, we can immediately deduce the third, because of the Pythagorean Theorem. As we saw in Preview Activity \(\PageIndex{1}\) , the cosine and sine functions offer additional help in determining missing information in right triangles. Indeed, while the functions \(\cos(t)\) and \(\sin(t)\) have many important applications in modeling periodic phenomena such as osciallating masses on springs, they also find powerful application in settings involving right triangles, such as in navigation and surveying.

Because we know the values of the cosine and sine functions from the unit circle, right triangles with hypotentuse \(1\) are the easiest ones in which to determine missing information. In addition, we can relate any other right triangle to a right triangle with hypotenuse \(1\) through the concept of similarity . Recall that two triangles are similar provided that one is a magnification of the other. More precisely, two triangles are similar whenever there is some constant \(k\) such that every side in one triangle is \(k\) times as long as the corresponding side in the other and the corresponding angles in the two triangles are equal. An important result from geometry tells us that if two triangles are known to have all three of their corresponding angles equal, then it follows that the two triangles are similar, and therefore their corresponding sides must be proportionate to one another.

Activity \(\PageIndex{2}\)

Consider right triangle \(OPQ\) given in Figure \(\PageIndex{4}\) , and assume that the length of the hypotenuse is \(OP = r\) for some constant \(r \gt 1\text{.}\) Let point \(M\) lie on \(\overline{OP}\) between \(O\) and \(P\) in such a way that \(OM = 1\text{,}\) and let point \(N\) lie on \(\overline{OQ}\) so that \(\angle ONM\) is a right angle, as pictured. In addition, assume that point \(O\) corresponds to \((0,0)\text{,}\) point \(Q\) to \((x,0)\text{,}\) and point \(P\) to \((x,y)\) so that \(OQ = x\) and \(PQ = y\text{.}\) Finally, let \(\theta\) be the measure of \(\angle POQ\text{.}\)

• Explain why \(\triangle OPQ\) and \(\triangle OMN\) are similar triangles.
• What is the value of the ratio \(\frac{OP}{OM}\text{?}\) What does this tell you about the ratios \(\frac{OQ}{ON}\) and \(\frac{PQ}{MN}\text{?}\)
• What is the value of \(ON\) in terms of \(\theta\text{?}\) What is the value of \(MN\) in terms of \(\theta\text{?}\)
• Use your conclusions in (b) and (c) to express the values of \(x\) and \(y\) in terms of \(r\) and \(\theta\text{.}\)

Ratios of sides in right triangles

A right triangle with a hypotenuse of length \(1\) can be viewed as lying in standard position in the unit circle, with one vertex at the origin and one leg along the positive \(x\)-axis. If we let the angle formed by the hypotenuse and the horizontal leg have measure \(\theta\text{,}\) then the right triangle with hypotenuse \(1\) has horizontal leg of length \(\cos(\theta)\) and vertical leg of length \(\sin(\theta)\text{.}\) If we consider now consider a similar right triangle with hypotenuse of length \(r \ne 1\text{,}\) we can view that triangle as a magnification of a triangle with hypotenuse \(1\text{.}\) These observations, combined with our work in Activity \(\PageIndex{2}\) , show us that the horizontal legs of the right triangle with hypotenuse \(r\) have measure \(r\cos(\theta)\) and \(r\sin(\theta)\text{,}\) as pictured in Figure \(\PageIndex{5}\)

From the similar triangles in Figure \(\PageIndex{5}\) , we can make an important observation about ratios in right triangles. Because the triangles are similar, the ratios of corresponding sides must be equal, so if we consider the two hypotenuses and the two horizontal legs, we have

If we rearrange Equation (4.1.1) by dividing both sides by \(r\) and multiplying both sides by \(\cos(\theta)\text{,}\) we see that

From a geometric perspective, Equation (4.1.2) tells us that the ratio of the horizontal leg of a right triangle to the hypotenuse of the triangle is always the same (regardless of \(r\)) and that the value of that ratio is \(\cos(\theta)\text{,}\) where \(\theta\) is the angle adjacent to the horizontal leg. In an analogous way, the equation involving the hypotenuses and vertical legs of the similar triangles is

which can be rearranged to

Equation (4.1.4) shows that the ratio of the vertical leg of a right triangle to the hypotenuse of the triangle is always the same (regardless of \(r\)) and that the value of that ratio is \(\sin(\theta)\text{,}\) where \(\theta\) is the angle opposite the vertical leg. We summarize these recent observations as follows.

Ratios in right triangles.

In a right triangle where one of the non-right angles is \(\theta\text{,}\) and “adj” denotes the length of the leg adjacent to \(\theta\text{,}\) “opp” the length the side opposite \(\theta\text{,}\) and “hyp” the length of the hypotenuse,

\[ \cos(\theta) = \frac{\text{adj}}{\text{hyp}} \text{ and } \sin(\theta) = \frac{\text{opp}}{\text{hyp}}\text{.} \nonumber \]

Activity \(\PageIndex{3}\)

In each of the following scenarios involving a right triangle, determine the exact values of as many of the remaining side lengths and angle measures (in radians) that you can. If there are quantities that you cannot determine, explain why. For every prompt, draw a labeled diagram of the situation.

• A right triangle with hypotenuse \(7\) and one non-right angle of measure \(\frac{\pi}{7}\text{.}\)
• A right triangle with non-right angle \(\alpha\) that satisfies \(\sin(\alpha) = \frac{3}{5}\text{.}\)
• A right triangle where one of the non-right angles is \(\beta = 1.2\) and the hypotenuse has length \(2.7\text{.}\)
• A right triangle with hypotenuse \(13\) and one leg of length \(6.5\text{.}\)
• A right triangle with legs of length \(5\) and \(12\text{.}\)
• A right triangle where one of the non-right angles is \(\beta = \frac{\pi}{5}\) and the leg opposite this angle has length \(4\text{.}\)

Using a ratio involving sine and cosine

In Activity \(\PageIndex{3}\) , we found that in many cases where we have a right triangle, knowing two additional pieces of information enables us to find the remaining three unknown quantities in the triangle. At this point in our studies, the following general principles hold.

Missing information in right triangles.

In any right triangle,

• if we know one of the non-right angles and the length of the hypotenuse, we can find both the remaining non-right angle and the lengths of the two legs;
• if we know the length of two sides of the triangle, then we can find the length of the other side;
• if we know the measure of one non-right angle, then we can find the measure of the remaining angle.

In scenario (1.), all \(6\) features of the triangle are not only determined, but we are able to find their values. In (2.), the triangle is uniquely determined by the given information, but as in Activity 4.1.3 parts (d) and (e), while we know the values of the sine and cosine of the angles in the triangle, we haven't yet developed a way to determine the measures of those angles. Finally, in scenario (3.), the triangle is not uniquely determined, since any magnified version of the triangle will have the same three angles as the given one, and thus we need more information to determine side length.

We will revisit scenario (2) in our future work. Now, however, we want to consider a situation that is similar to (1), but where it is one leg of the triangle instead of the hypotenuse that is known. We encountered this in Activity 4.1.3 part (f): a right triangle where one of the non-right angles is \(\beta = \frac{\pi}{5}\) and the leg opposite this angle has length \(4\text{.}\)

Example \(\PageIndex{6}\)

Consider a right triangle in which one of the non-right angles is \(\beta = \frac{\pi}{5}\) and the leg opposite \(\beta\) has length \(4\text{.}\)

Determine (both exactly and approximately) the measures of all of the remaining sides and angles in the triangle.

From the fact that \(\beta = \frac{\pi}{5}\text{,}\) it follows that \(\alpha = \frac{\pi}{2} - \frac{\pi}{5} = \frac{3\pi}{10}\text{.}\) In addition, we know that

\[ \sin\left(\frac{\pi}{5}\right) = \frac{4}{h}\label{eq-right-sin-ratio}\tag{4.1.5} \] and

\[ \cos\left(\frac{\pi}{5}\right) = \frac{x}{h}\label{eq-right-cos-ratio}\tag{4.1.6} \] Solving Equation (4.1.5) for \(h\text{,}\) we see that

\[ h = \frac{4}{\sin\left(\frac{\pi}{5}\right)}\text{,}\label{eq-right-sin-ratio-2}\tag{4.1.7} \] which is the exact numerical value of \(h\text{.}\) Substituting this result in Equation (4.1.6), solving for \(h\) we find that

\[ \cos\left(\frac{\pi}{5}\right) = \frac{x}{\frac{4}{\sin\left(\frac{\pi}{5}\right)}}\text{.}\label{eq-right-cos-ratio-2}\tag{4.1.8} \] Solving this equation for the single unknown \(x\) shows that

\[ x = \frac{4 \cos\left(\frac{\pi}{5}\right)}{\sin\left(\frac{\pi}{5}\right)}\text{.} \nonumber \] The approximate values of \(x\) and \(h\) are \(x \approx 5.506\) and \(h \approx 6.805\text{.}\)

Example \(\PageIndex{6}\) demonstrates that a ratio of values of the sine and cosine function can be needed in order to determine the value of one of the missing sides of a right triangle, and also that we may need to work with two unknown quantities simultaneously in order to determine both of their values.

Activity \(\PageIndex{4}\)

We want to determine the distance between two points \(A\) and \(B\) that are directly across from one another on opposite sides of a river, as pictured in Figure \(\PageIndex{8}\) We mark the locations of those points and walk \(50\) meters downstream from \(B\) to point \(P\) and use a sextant to measure \(\angle BPA\text{.}\) If the measure of \(\angle BPA\) is \(56.4^{\circ}\text{,}\) how wide is the river? What other information about the situation can you determine?

• In a right triangle with hypotenuse \(1\text{,}\) we can view \(\cos(\theta)\) as the length of the leg adjacent to \(\theta\) and \(\sin(\theta)\) as the length of the leg opposite \(\theta\text{,}\) as seen in Figure 4.1.2. This is simply a change in perspective achieved by focusing on the triangle as opposed to the unit circle.
• Because a right triangle with hypotenuse of length \(r\) can be thought of as a scaled version of a right triangle with hypotenuse of length \(1\text{,}\) we can conclude that in a right triangle with hypotenuse of length \(r\text{,}\) the leg adjacent to angle \(\theta\) has length \(r\cos(\theta)\text{,}\) and the leg opposite \(\theta\) has length \(r\sin(\theta)\text{,}\) as seen in Figure 4.1.5. Moreover, in any right triangle with angle \(\theta\text{,}\) we know that \[ \cos(\theta) = \frac{\text{adj}}{\text{hyp}} \text{ and } \sin(\theta) = \frac{\text{opp}}{\text{hyp}}\text{.} \nonumber \]
• In a right triangle, there are five additional characteristics: the measures of the two non-right angles and the lengths of the three sides. In general, if we know one of those two angles and one of the three sides, we can determine all of the remaining pieces.

A person standing \(50\) feet away from a streetlight observes that they cast a shadow that is \(14\) feet long. If a ray of light from the streetlight to the tip of the person's shadow forms an angle of \(27.5^\circ\) with the ground, how tall is the person and how tall is the streetlight? What other information about the situation can you determine?

A person watching a rocket launch uses a laser range-finder to measure the distance from themselves to the rocket. The range-finder also reports the angle at which the finder is being elevated from horizontal. At a certain instant, the range-finder reports that it is elevated at an angle of \(17.4^\circ\) from horizontal and that the distance to the rocket is \(1650\) meters. How high off the ground is the rocket? Assuming a straight-line vertical path for the rocket that is perpendicular to the earth, how far away was the rocket from the range-finder at the moment it was launched?

A trough is constructed by bending a \(4' \times 24'\) rectangular sheet of metal. Two symmetric folds \(2\) feet apart are made parallel to the longest side of the rectangle so that the trough has cross-sections in the shape of a trapezoid, as pictured in Figure \(\PageIndex{9}\) Determine a formula for \(V(\theta)\text{,}\) the volume of the trough as a function of \(\theta\text{.}\)

The volume of the trough is the area of a cross-section times the length of the trough.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

High school geometry

Course: high school geometry   >   unit 5.

• Triangle similarity & the trigonometric ratios

Trigonometric ratios in right triangles

• (Choice A)   3 5 ‍   A 3 5 ‍  
• (Choice B)   4 5 ‍   B 4 5 ‍  
• (Choice C)   3 4 ‍   C 3 4 ‍  
• (Choice D)   4 3 ‍   D 4 3 ‍  

Right Triangle Calculator

Please provide 2 values below to calculate the other values of a right triangle. If radians are selected as the angle unit, it can take values such as pi/3, pi/4, etc.

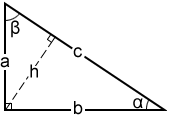
Related Triangle Calculator | Pythagorean Theorem Calculator

Right triangle

A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry.

In a right triangle, the side that is opposite of the 90° angle is the longest side of the triangle, and is called the hypotenuse. The sides of a right triangle are commonly referred to with the variables a, b, and c, where c is the hypotenuse and a and b are the lengths of the shorter sides. Their angles are also typically referred to using the capitalized letter corresponding to the side length: angle A for side a, angle B for side b, and angle C (for a right triangle this will be 90°) for side c, as shown below. In this calculator, the Greek symbols α (alpha) and β (beta) are used for the unknown angle measures. h refers to the altitude of the triangle, which is the length from the vertex of the right angle of the triangle to the hypotenuse of the triangle. The altitude divides the original triangle into two smaller, similar triangles that are also similar to the original triangle.

If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle. In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. Examples include: 3, 4, 5; 5, 12, 13; 8, 15, 17, etc.

Area and perimeter of a right triangle are calculated in the same way as any other triangle. The perimeter is the sum of the three sides of the triangle and the area can be determined using the following equation:

Special Right Triangles

30°-60°-90° triangle:

The 30°-60°-90° refers to the angle measurements in degrees of this type of special right triangle. In this type of right triangle, the sides corresponding to the angles 30°-60°-90° follow a ratio of 1:√ 3 :2. Thus, in this type of triangle, if the length of one side and the side's corresponding angle is known, the length of the other sides can be determined using the above ratio. For example, given that the side corresponding to the 60° angle is 5, let a be the length of the side corresponding to the 30° angle, b be the length of the 60° side, and c be the length of the 90° side.:

Angles: 30°: 60°: 90°

Ratio of sides: 1:√ 3 :2

Side lengths: a:5:c

Then using the known ratios of the sides of this special type of triangle:

As can be seen from the above, knowing just one side of a 30°-60°-90° triangle enables you to determine the length of any of the other sides relatively easily. This type of triangle can be used to evaluate trigonometric functions for multiples of π/6.

45°-45°-90° triangle:

The 45°-45°-90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°-45°-90°, follow a ratio of 1:1:√ 2 . Like the 30°-60°-90° triangle, knowing one side length allows you to determine the lengths of the other sides of a 45°-45°-90° triangle.

Angles: 45°: 45°: 90°

Ratio of sides: 1:1:√ 2

Side lengths: a:a:c

Given c= 5:

45°-45°-90° triangles can be used to evaluate trigonometric functions for multiples of π/4.