problem solving literature review

To read this content please select one of the options below:

Please note you do not have access to teaching notes, systematic problem-solving and its antecedents: a synthesis of the literature.

Management Research Review

ISSN : 2040-8269

Article publication date: 4 February 2020

Issue publication date: 31 August 2020

This study aims at determining the factors that favor a systematic approach to deal with complex operational and strategic problems. Management literature on problem-solving makes a clear distinction between either fixing a problem temporarily by eliminating its symptoms or solving it by diagnosing and altering underlying causes. Adopting a cognitive perspective of the dual-processing theory, this study labels these two approaches intuitive problem-solving and systematic problem-solving (SPS). While the superior effectiveness of SPS in fostering organizational learning is widely documented, existing literature fails to provide an overview of the conditions that support the adoption of SPS.

Design/methodology/approach

This paper presents a systematic literature review to shed light on the main supporting factors of SPS in operational as well as strategic domains.

Seven supporting factors of SPS (namely, nature of the problem, time availability, information availability, collaborative culture, transformational leadership, organizational learning infrastructure and environmental dynamism) are first identified and then discussed in an integrative model.

Originality/value

This work is an original attempt to inclusively address organizational, environmental and problem nature-related factors that favor SPS adoption. By determining the SPS supporting factors, this study highlights why many organizations fail or struggle to implement and sustain SPS over time.

• Organizational behavior
• Co-citation analysis
• Systematic literature review
• Dual-process theory
• Intuitive problem-solving
• Systematic problem-solving

Mohaghegh, M. and Furlan, A. (2020), "Systematic problem-solving and its antecedents: a synthesis of the literature", Management Research Review , Vol. 43 No. 9, pp. 1033-1062. https://doi.org/10.1108/MRR-06-2019-0284

Emerald Publishing Limited

Copyright © 2020, Emerald Publishing Limited

Related articles

We’re listening — tell us what you think, something didn’t work….

Report bugs here

All feedback is valuable

Please share your general feedback

Join us on our journey

Platform update page.

Visit emeraldpublishing.com/platformupdate to discover the latest news and updates

Questions & More Information

Answers to the most commonly asked questions here

Paradigms and problem-solving: a literature review

• PMID: 6748029
• DOI: 10.1097/00001888-198408000-00002

Thomas Kuhn's conceptions of the influence of paradigms on the progress of science from the framework for analyzing how medical educators have approached research on medical problem-solving. Kuhn's ideas help to explain the often conflicting research results that have appeared over the last 20 years. Specifically, underlying assumptions about the problem-solving process are explored in light of data that demonstrate (a) low correlations between different measures of problem-solving, (b) inconsistent relationships between the amount of clinical experience and problem-solving ability, and (c) case specificity of performance. A new paradigm emphasizing multiple types of problems with varied solution strategies is proposed.

• Clinical Competence
• Education, Medical
• Educational Measurement
• Problem Solving*
• Teaching / methods

An official website of the United States government

The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

• Publications
• Account settings

Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .

• Advanced Search
• Journal List
• HHS Author Manuscripts

Solving Word Problems using Schemas: A Review of the Literature

Sarah r. powell.

Vanderbilt University

Solving word problems is a difficult task for students at-risk for or with learning disabilities (LD). One instructional approach that has emerged as a valid method for helping students at-risk for or with LD to become more proficient at word-problem solving is using schemas. A schema is a framework for solving a problem. With a schema, students are taught to recognize problems as falling within word-problem types and to apply a problem solution method that matches that problem type. This review highlights two schema approaches for 2 nd - and 3 rd -grade students at-risk for or with LD: schema-based instruction and schema-broadening instruction. A total of 12 schema studies were reviewed and synthesized. Both types of schema approaches enhanced the word-problem skill of students at-risk for or with LD. Based on the review, suggestions are provided for incorporating word-problem instruction using schemas.

Since Pólya (1945) introduced four steps for solving word problems (understand the question, devise a plan, carry out the plan, and look back and check), teachers have been encouraged to provide more systematic instruction on problem solving in mathematics. Word-problem instruction has become vital for students. High-stakes standardized tests like the National Assessment of Educational Progress (NAEP; National Assessment Governing Board, 2009 ) place heavy emphasis on mathematics word problems and national educational organizations like the National Council of Teachers of Mathematics ( NCTM; 2000 ) heavily value the teaching of problem solving across grades K through 12. Many researchers have investigated methods for teaching problem solving to general-education students ( Marshall, 1995 ; Schoenfeld, 1992 ; Shavelson, Webb, Stasz, & McArthur, 1988 ) and, in more recent years, to students with learning disabilities (LD) (e.g., Case, Harris, & Graham, 1992 ; Mastropieri, Scruggs, & Shiah, 1997 ; Miller & Mercer, 1993 ).

Over the last two decades, a sizeable literature has begun to accumulate with an emphasis on helping students develop schemas to solve word problems in mathematics (e.g., Fuchs, Fuchs, Finelli, Courey, & Hamlett, 2004 ; Fuchs, Seethaler, et al., 2008 ; Griffin & Jitendra, 2009 ; Jitendra & Hoff, 1996 ; Willis & Fuson, 1988 ). A schema is a framework, outline, or plan for solving a problem ( Marshall, 1995 ). In mathematics, students can use schemas to organize information from a word problem in ways that represent the underlying structure of a problem type. Pictures or diagrams, as well as number sentences or equations, can be used to represent schemas.

Often, word problems can be differentiated into types of problems. The problem type is determined by what is happening in the word-problem narrative. For example, students may be given the following information: There are 7 blue birds and 4 red birds sitting on a tree . If, however, students are asked, How many birds are on the tree? , the problem type is combining or totaling (the birds). If students are asked, Five blue birds flew away, how many blue birds are left sitting in the tree? , the problem type is finding the change (in the number of blue birds). Combining or totaling is different from finding a change in that the examples represent two distinct problem types. Two distinct schemas can be used to solve the problems. Once students determine the problem type, they can apply a schema (i.e., diagram, equation, or plan) to assist in solving the word problem. In the elementary grades, most word problems can be sorted into only a few types ( Riley & Greeno, 1988 ). If students know a schema for each type, and understand how to sort problems into the problem types and apply the solution method for each schema, then students should be able to solve most word problems ( Cooper & Sweller, 1987 ).

The first purpose of the present paper was to review and synthesize the literature on schemas within word-problem instruction to determine (a) what schemas were taught to elementary students at-risk for or with LD, (b) how these schemas were taught, and (c) what effects were associated with solving word problems using schemas. The second purpose was to provide suggestions for classroom teachers on how to teach students to use schemas to solve word problems.

Word-Problem Difficulty

Students at-risk for or with LD often struggle with word-problem solving ( Parmar, Cawley, & Frazita, 1996 ). For example, Wilson and Sindelar (1991) worked with second- through fifth-graders with LD. On a test of addition and subtraction word problems, these students performed significantly below third-grade students without LD. At second- and fourth-grade, Englert, Culatta, and Horn (1987) tested 24 students with LD on 16 addition word problems. When compared to grade-level peers, the students with LD demonstrated significantly lower accuracy on word-problem solutions. More recently, Jordan and Hanich (2000) administered 14 addition and subtraction word problems to 20 second-grade students at-risk for or with mathematics LD and 29 second-grade students without LD. Students at-risk for or with LD answered fewer word problems correct than students without LD and employed less efficient strategies. These findings were corroborated with a larger group of second-grade ( Hanich, Jordan, Kaplan, & Dick, 2001 ) and third-grade students ( Jordan & Montani, 1997 ). Moving beyond simple word problems, Fuchs and Fuchs (2002) administered 10 word problems comprising four types (i.e., shopping list, buying bags, half, and pictograph) and 10 multi-step word problems with tables and graphs to fourth-grade students. The performance of 40 students with LD was compared to normative data collected from typical fourth-grade students. On both word problem sets, students with LD scored significantly lower than students in the normative group with effect sizes (ESs) ranging from 0.49 to 1.10 favoring the normative group.

Word problems may pose a challenge for students at-risk for or with LD because numerous steps and skills are necessary to solve a word problem ( Parmar et al., 1996 ). Additionally, students may struggle with comprehension of the text of the word problem ( Cummins, Kintsch, Reusser, & Weimer, 1988 ). Many students with LD struggle with mathematics and reading difficulty; therefore, embedding mathematics within a linguistic context may challenge students who also have reading deficits ( Fuchs, Fuchs, Stuebing, et al., 2008 ). To solve a word problem, students must use the text to identify missing information, derive a plan for solving for the missing information, and perform a calculation to find the missing information. Even when complex calculations are not required, students with LD struggle with problem solving compared to their average-performing peers ( Pellegrino & Goldman, 1987 ).

Instruction for Students with LD

To help students at-risk for or with LD become more efficient and accurate word-problem solvers, explicit word-problem instruction may be warranted ( Parmar et al., 1996 ). For example, Kroesbergen, Van Luit, and Maas (2004) randomly assigned 265 8- to 11-year-old students with LD or behavior disorders to receive constructivist multiplication instruction, explicit multiplication instruction, or regular classroom instruction (control). Students in the constructivist and explicit conditions received 30 lessons over 4 to 5 months. Intervention focused on multiplication automaticity and problem solving. In the constructivist condition, students were encouraged to discuss different approaches to solving a multiplication problem and then determine whether they could use one of these approaches to solve the problem. In the explicit condition, students were told how a problem should be solved and were provided examples of good problem-solving strategies. Students were always told which strategies to use. In the control condition, students followed the school's regular mathematics curriculum which included instruction on multiplication. At posttest, explicit instruction students significantly outperformed constructivist and control students on a computation multiplication measure and a measure of multiplication word problems. Kroesbergen et al. concluded that explicit or direct mathematics instruction, but not discovery or constructivist learning, may benefit lower-performing students.

Several explicit approaches exist for teaching students at-risk for or with LD to solve word problems ( Jitendra & Xin, 1997 ). These include diagramming or drawing the word problem ( van Garderen, 2007 ); identifying key words in a word problem and solving the problem based on the key word; utilizing computer-assisted instruction with explicit step-by-step work ( Mastropieri et al., 1997 ); using a mnemonic device to guide word-problem solving ( Miller & Mercer, 1993 ); learning metacognitive strategies to monitor word problem-solving progress ( Case et al., 1992 ); and using a checklist of steps to solve word problems along with monitoring work with metacognitive strategies ( Montague, Warger, & Morgan, 2000 ). An additional approach to teaching word-problem solving to students at-risk for or with LD, which has been developed over the last 20 years, is using schemas to solve word problems (e.g., Fuchs, Fuchs, Finelli, et al., 2004 ; Jitendra & Hoff, 1996 ). Word-problem instruction using schemas differs from typical word-problem instruction (e.g., key words, checklist of steps) because students first identify a word problem as belonging to a problem type and then use a specific problem-type schema to solve the problem. In conventional word-problem instruction, students may organize word-problem information or follow a mnemonic device to work step-by-step through the problem; however, students are not taught to determine a problem type and solve word problems according to a problem-type schema. In this paper, the research conducted to evaluate using schemas in word-problem solving was reviewed and synthesized.

Literature Search

The studies selected for this literature review met four criteria. First, the implemented treatments incorporated explicit instruction on solving a word problem though a schema. Second, studies needed to include, but not necessarily be limited to, students at-risk for or with LD. Third, study participants comprised students in second or third grade. These were the target grades because this is often when identification of students with LD occurs ( Fletcher, Lyon, Fuchs, & Barnes, 2006 ) and when written word-problem solving is a major focus of the curriculum as opposed to less formal, oral problems presented in kindergarten and first grade. Fourth, studies needed to be published in a peer-reviewed journal. I conducted searches in electronic databases including ERIC, PsycInfo, and ProQuest using the following terms: schema, word problem, story problem , and problem solving . Then, I read the titles and abstracts of articles to identify studies that fit the four criteria resulting in 12 word-problem solving studies. In all 12 studies, instruction focused on addition and subtraction word problems, which are the two operations most commonly found in second- and third-grade instruction and on standardized tests ( Hudson & Miller, 2006 ).

Overview of Included Studies

Each schema study reviewed in this paper is outlined in Table 1 . Study publication dates ranged from 1996 to 2009. Across studies, almost 4000 students were included. Of these students, 411 were at-risk for LD and 173 were identified as receiving special education services. Jitendra and colleagues tended to work with students with LD whereas Fuchs and colleagues generally worked with students at-risk for LD. The researchers utilized a variety of experimental designs: single subject (1), group teaching without assignment to treatment conditions (1), student random assignment (4), matched pairs random assignment (2), and classroom random assignment (5). Instruction occurred during school hours in individual settings (3), in small groups (2), and in large groups (8). Assessments for determining instructional effects were experimenter-designed in all 12 studies. Two of the studies included standardized assessments as well as experimenter-designed measures in the testing battery. In ten of the studies, more than one assessment was administered.

Two Approaches to Schema Instruction

In this section, two approaches to schema instruction are discussed. The first, referred to as schema-based instruction , teaches students to use schematic diagrams to solve addition and subtraction word problems ( Jitendra, Griffin, Deatline-Buchman, & Sczesniak, 2007 ; Jitendra & Hoff, 1996 ). The student reads a word problem, selects a schema diagram into which the word problem fits, and uses the structure of the diagram to solve the problem. In more recent studies, students are taught to use a mathematical equation (i.e., 4 + ? = 7), after filling in a schematic diagram, to solve the problem ( Griffin & Jitendra, 2009 ). The work by Jitendra and colleagues uses schema-based instruction. By contrast, Fuchs et al. (2003) uses a second approach to schema instruction, schema-broadening instruction . Schema-broadening instruction is similar to schema-based instruction in that students read the word problem and select a schema (from the taught schema) to solve word problems. Schema-broadening instruction differs from schema-based instruction because students are taught to transfer their knowledge of problem types to recognize problems with novel features (e.g., different format, additional question, irrelevant information, unfamiliar vocabulary, or information presented in charts, graphs, or pictures) as belonging to a problem type for which they know a solution. As with Jitendra and colleagues, Fuchs and colleagues also teach students to set up and solve mathematical equations (e.g., X – 3 = 7) representing the structure of problem types ( Fuchs et al., 2009 ).

In terms of schema instruction, the schema-based instruction of Jitendra and colleagues differs from the schema-broadening instruction of Fuchs and colleagues in one primary way. With schema-broadening (but not schema-based) instruction, students receive explicit instruction on transfer to novel problems. The schemas that Jitendra and colleagues used rely on diagrams for organizing word-problem work. (See Figure 1 for an example.) Fuchs and colleagues, in contrast, teach students to organize word-problem information in sections or in mathematical equations. (See Figures 2 and ​ and3 3 for examples.)

Schema-Based Instruction

To understand how schema-based instruction may benefit students with LD, Jitendra and Hoff (1996) worked with three third- and fourth-grade students with LD. During 13 to 16 days of intervention, students learned to recognize defining features of addition and subtraction word-problem types, classify problems in terms of problem types, map the word problem information onto the schema's diagram, and use the diagram to solve the problem. Jitendra and Hoff taught three schemas: change, group, and compare. All three students demonstrated positive growth as the study progressed and maintained skills 2 to 3 weeks after the final intervention session, with only a slight decline in scores. Through this multiple-baseline, single-subject design, Jitendra and Hoff demonstrated the possible benefit of using schemas for teaching word-problem solving to students with LD.

Working with a larger number of students, Jitendra et al. (1998) recruited 34 second- to fifth-grade students who performed below the 60 th percentile on a word-problem measure. Students were randomly assigned to receive small-group schema instruction or small-group traditional instruction during 17 to 20 sessions. Schema instruction focused on change, group, and compare problems. Students learned how to identify the schema for a word problem and to use a schema diagram to organize the problem's information. The traditional instruction followed a basal mathematics program focused on general mathematics skills and was implemented to control for tutoring time. At posttest, students participating in schema tutoring outperformed students in the traditional tutoring on experimenter-designed measures of word problems. A delayed posttest, administered one week after tutoring commenced, continued to favor schema students over traditional students. Jitendra et al. also recruited 24 average-performing third graders to serve as a normative sample. At posttest, the schema-tutoring students performed comparably to students in the normative sample, whereas traditional-tutoring students did not. These results favoring schema instruction led Jitendra et al. to conclude that word-problem instruction using schemas is more advantageous to students at-risk for LD than traditional word-problem instruction.

In the next phase of this research program, Jitendra moved from small-group schema intervention to whole-class schema-based instruction. Jitendra, Griffin, Deatline-Buchman, et al. (2007) provided schema-based instruction similar to Jitendra and Hoff (1996) with students receiving instruction on using schematic diagrams to solve change, combine or group, and compare problems. Students were taught to fill word-problem information into a problem type's corresponding schematic diagram and then generate a mathematical equation (i.e., a number sentence with missing information) to help solve the problem. A question mark was used to mark the missing information (i.e., ? + 5 = 10). Across three classrooms, 38 lower-performing third-grade students, 9 of whom were identified with LD, received schema-based instruction. Instruction lasted 15 weeks with three 30-min sessions per week. On two experimenter-designed word-problem posttests, students in the three classrooms demonstrated improvement from pretest although the improvement was not significant. Jitendra, Griffin, Deatline-Buchman, et al. concluded that lower-performing students and students with LD need and benefit from explicit word problem-solving instruction focused around schemas. With the absence of control classrooms for comparison purposes or significant growth from pre- to posttest, Jitendra, Griffin, Deatline-Buchman, et al. indicated, but did not verify, that schema instruction may be beneficial for students at-risk for or with LD.

Comparing schema-based instruction to another word-problem solving approach, Jitendra, Griffin, Haria, et al. (2007) randomly assigned 88 third-grade students to two conditions: schema-based instruction and general-strategy instruction. Four of the 88 participants were identified with LD. Schema-based instruction focused on the change, combine, and compare problem types as in Jitendra, Griffin, Deatline-Buchman, et al., (2007) whereas students receiving general-strategy instruction were taught four steps to solve a word problem (i.e., read and understand, plan, solve, and check) along with four strategies to assist in solving a word problem (i.e., use manipulatives, act it out or draw a diagram, write a number sentence, and use information from a graph). Similar to Jitendra, Griffin, Deatline-Buchman, et al., students receiving schema instruction learned to identify the schema of a word problem, fill word-problem information into a schematic diagram, and then generate an equation to help solve the word problem. Students used different schematic diagrams for each of the three problem types, and the use of schematic diagrams was faded toward the end of instruction on each problem type. Many students, however, continued to draw schematic diagrams independently. After all three problem types were introduced, tutors taught the students to solve two-step problems that combined two schemas. All students received 41 lessons, each lasting approximately 25 min. From pre- to posttest, students in the schema-based condition outperformed students in the general-strategy condition on an experimenter-designed word-problem measure, with an ES of 0.52. The same measure, administered six weeks after posttest, again showed students in the schema-based condition outperforming general-strategy condition students (ES = 0.69). The number of students with LD was small ( n = 4), so results for students with disabilities were not presented by Jitendra, Griffin, Deatline-Buchman, et al. separate from the main analysis. Therefore, conclusions about the benefit of schema-based instruction for students with LD could not be inferred.

Interestingly, Griffin and Jitendra (2009) also compared schema-based instruction to general-strategy instruction with third-grade students but did not replicate the results from Jitendra, Griffin, Haria, et al. (2007) . Students from three classrooms ( n = 60; 5 with LD) were matched based on performance on a standardized mathematics test and then the pairs were randomly assigned to schema-based or general-strategy instruction. Schema-based and general-strategy instruction were similar to that provided in Jitendra, Griffin, Haria, et al., except that instruction was provided in 20 lessons lasting 100 min each. Schema instruction included completing schematic diagrams and generating equations. The final four lessons comprised instruction on two-step problems where tutors taught students to solve problems using two schemas. On an experimenter-designed word-problem measure, there were no significant differences between the two groups at posttest or at 12-week maintenance (even though both groups demonstrated growth from pretest to posttest to maintenance). On a measure of word-problem solving fluency administered three times throughout instruction, there were significant differences favoring schema-based instruction at the beginning of treatment. These effects, however, faded over the course of the study: At posttest, schema-based and general-strategy groups performed similarly. Griffin and Jitendra attributed the inconsistency of this finding to the fact that instruction was provided in 100-min sessions and once a week rather than shorter sessions occurring several times a week.

Jitendra and colleagues' program of research on schema-based instruction is impressive and demonstrates that students at-risk for or with LD may benefit from explicit schema instruction. These researchers taught students to use three schemas (i.e., change, combine or group, and compare) on different types of word problems with two operations (i.e., addition and subtraction). Even though the specific nature of schema-based instruction varied in small ways from study to study, the majority of students benefitted from learning about different schema and applying the schema to solve word problems. Across studies, two instructional design features were consistently incorporated within schema-based instruction. First, interventions were of long duration (13 to 45 lessons), and second, explicit instruction focused on recognizing a problem's schema, using a diagram based on the schema, and solving the problem. The research by Jitendra and colleagues offers a solid foundation for future schema-based investigations and provides strategies that teachers can use to enhance the performance of their students with LD on word problems.

Schema-Broadening Instruction

As in Jitendra and colleagues' schema-based instruction, schema-broadening instruction relies on schemas for conceptualizing word problems. Some of Fuchs and colleagues' schema-broadening instruction comprises problem types (i.e., shopping list, half, buying bags, pictograph) that are notably different from the problem types used by Jitendra and colleagues. Other schema-broadening problem types of Fuchs and colleagues (i.e., total, difference, and change) are similar to the combine, compare, and change problem types of Jitendra and colleagues. Schema-broadening instruction includes a focus on transfer features to help students expand their conceptualization of the schema. Thus, schema-broadening instruction helps students recognize a novel problem (with unfamiliar problem features such as different format, additional question, irrelevant information, unfamiliar vocabulary, or information presented in charts, graphs, or pictures) as belonging to the schema for which they know a problem solution strategy.

To pinpoint the effects of explicit transfer instruction within schema-broadening instruction, Fuchs et al. (2003) randomly assigned 24 third-grade classrooms ( n = 375) to four conditions: problem-solution instruction, partial-problem-solution-with-transfer instruction (to control for instructional time), full problem-solution-with-transfer-instruction, or control, business-as-usual instruction with a 6-lesson introductory general-problem solving unit that all 24 classrooms received. Students receiving special education services ( n = 23) were distributed across the four conditions. After this introductory unit, problem-solution instruction was presented over the next 20 lessons, in which students were explicitly taught to understand and recognize four schema (i.e., shopping list, half, buying bags, and pictograph) and to apply rules for solving problems for each schema. Students in the partial-problem-solution-plus-transfer condition received only 10 solution lessons but also received 10 transfer lessons. The transfer lessons included explicit instruction on the meaning of transfer and instruction to broaden schema to address problems with different formats, unfamiliar vocabulary, additional questions, and broader problem-solving contexts. Students in the full-problem-solution-plus-transfer condition received all 20 solution lessons and all 10 transfer lessons. In terms of classroom performance from pre- to posttest, students in the problem-solution, partial-problem-solution-with-transfer, and full-problem-solution-with-transfer classrooms outperformed control classrooms on an experimenter-designed immediate-transfer measure (ESs = 2.61, 2.15, and 1.82, respectively). On a far-transfer measure, students who received the partial- or full-solution-plus-transfer-instruction significantly outperformed control classrooms. Additionally, classrooms that received the full-solution-plus-transfer instruction improved more than classrooms that received the solution instruction alone. For students with disabilities, however, the results were not as promising. In the partial-problem-solution condition, 60-80% of the students were unresponsive to treatment. Students in the problem-solution and full-problem-solution-with-transfer conditions demonstrated greater levels of response. This study, as well as a similar study conducted with 24 classrooms of 366 students by Fuchs, Fuchs, Prentice, et al. (2004) , demonstrated the added value of schema instruction with an explicit focus on transfer schemas. Interestingly, in Fuchs, Fuchs, Prentice, et al. students in special education demonstrated significant gains over control students with ESs of 0.87 to 1.96.

To further extend this research program on schema-broadening instruction, Fuchs, Fuchs, Finelli, et al. (2004) randomly assigned 24 classrooms, with 351 students, to three conditions: schema-broadening instruction that addressed three transfer features, schema-broadening instruction that addressed six transfer features, and business-as-usual control. Twenty-nine students received special education services. All classrooms received six sessions about generic word problem-solving steps. Schema-broadening classrooms also received 28 lessons focused on the four schemas taught in Fuchs et al. (2003) . The schema-broadening instruction condition addressed three transfer features (i.e., different format, different question, or different vocabulary). The six-feature schema-broadening instruction condition addressed different format, different question, different vocabulary, irrelevant information, combined problem types, and mixing of transfer features. On experimenter-designed measures with the shortest transfer distance (unfamiliar problems but without novel features), students participating in both schema-broadening instruction conditions performed comparably but significantly better than control (ESs = 3.69 and 3.72, respectively). On measures assessing word problems with medium transfer distance (i.e., different format, question, or vocabulary transfer features), again there were no significant differences between the two schema-broadening instruction conditions, which outperformed the control group (ESs = 1.98 and 2.71, respectively). However, on the measure assessing the greatest transfer distance (i.e., involving all six transfer features), students in the schema-broadening instruction condition that incorporated all six transfer features demonstrated a significant advantage with an ES of 2.71 over control students and an ES of 0.72 over students in the narrower schema-broadening instruction treatment. Students with disabilities demonstrated similar gains to those of students without disabilities. Fuchs, Fuchs, Finelli, et al. demonstrated that students benefit from explicit schema-broadening instruction focused on a wide variety of transfer features.

In an expansion of Fuchs, Fuchs, Finelli, et al. (2004) , Fuchs and colleagues tested how real-life problem-solving skills might provide added benefit to schema-broadening instruction ( Fuchs et al., 2006 ). From 30 classrooms, 445 third-grade students (34 of whom received special education services) were randomly assigned by classroom to schema-broadening instruction, schema-broadening and real-life instruction, or business-as-usual control. All 30 classrooms received six 40-min sessions on general problem-solving strategies. Both schema-broadening treatments received an additional 30 sessions on four problem types. Additionally, schema-broadening plus real-life instruction classrooms received explicit instruction via video on real-life problem solving skills (i.e., review the problem, determine extra steps necessary for solving the problem, find important information without number, figure out important information not provided within the problem, reread, and ignore irrelevant information). On experimenter-designed measures of immediate and medium word-problem transfer, both schema-broadening treatments outperformed control classrooms with ESs ranging from 3.59 to 6.84. On a far transfer task, the added benefit of explicit real-life problem solving emerged on an open-ended question about what the student could buy. Students could use information from a pictograph, a price chart, or their own experiences to answer the question. On this question, the schema-broadening plus real-life students outperformed schema-broadening students (ES = 1.83). In this way, Fuchs et al. (2006) demonstrated how the combination of schema-broadening and real-life problem-solving instruction is beneficial for solving word problems. Results for students with disabilities, however, were not disaggregated from the entire sample, thus it was unclear if these students performed in a similar manner.

To investigate the effect of schema-broadening instruction for students at-risk for LD, Fuchs, Fuchs, Craddock, et al. (2008) randomly assigned 119 classrooms to receive schema-broadening instruction or to participate in a business-as-usual control group. Then, within each whole-class condition, 243 students at-risk for or with LD were randomly assigned to receive small-group schema-broadening tutoring or to remain in their whole-class condition without tutoring. In this way, 28 students received business-as-usual whole-class instruction and no schema-broadening tutoring, 51 students received whole-class schema-broadening instruction but no schema-broadening tutoring, 56 students received business-as-usual whole-class instruction with schema-broadening tutoring, and 108 students received whole-class schema-broadening instruction plus schema-broadening tutoring. The schema-broadening instruction at the classroom level provided explicit instruction on solving the four problem types (i.e., shopping list, half, buying bags, and pictograph) over 16 weeks. Tutoring occurred 3 times a week for 13 weeks following completion of three weeks of whole-class instruction. Tutoring sessions lasted 20 to 30 min in small groups of two to four students. For students who received whole-class schema-broadening instruction, tutored students outperformed students who did not receive tutoring on experimenter-designed measures (ES = 1.13). In a similar way, for students in business-as-usual classrooms, tutored students outperformed students who did not receive tutoring (ES = 1.34). Importantly, students who received two tiers of schema-broadening instruction (whole class and small-group tutoring) significantly outperformed students who received schema-broadening tutoring without whole-class schema-broadening instruction. This finding suggests that the combination of whole-class instruction and small-group tutoring provided the best outcome for students struggling with word problems. Whole-class instruction was beneficial alone as was small-group tutoring; however, the combination proved better than one or the other.

Two other studies in the Fuchs's program of research ( Fuchs et al., 2009 ; Fuchs, Seethaler, et al., 2008 ) rely on schema-broadening instruction but with problem types (i.e., change, total, and difference) that parallel those used by Jitendra and colleagues (i.e., change, combine, and compare). In these tutoring studies (conducted on a one-to-one basis), however, students were also explicitly taught to set up and solve mathematical equations that represent the underlying schema of the word problems similar to Griffin and Jitendra (2009) , Jitendra, Griffin, Deatline-Buchman, et al. (2007) , and Jitendra, Griffin, Haria, et al. (2009). In a pilot study, Fuchs, Seethaler, et al. (2008) randomly assigned 35 third-grade students at-risk for or with LD to two conditions: schema-broadening instruction tutoring with mathematical equations or no-tutoring control. All students performed below the 26 th percentile on global math and reading tests. Students in the schema-broadening condition received individual instruction over 12 weeks with sessions conducted 3 times a week, 30 min per session. Instruction focused on the three problem types with three transfer features (irrelevant information, important information embedded within charts, graphs, or pictures, and double-digit numbers). First, students learned to understand and identify the three schemas (i.e., problem types), to set up an equation to represent each schema (i.e., 3 + X = 9), and to solve equations. Then, explicit instruction to broaden schema to the three transfer features occurred. Students receiving schema-broadening tutoring demonstrated significantly better growth than control students on an experimenter-designed test of word problems (ES = 1.80) and on a test of word problems designed by a research team not affiliated with the study (ES = 0.69). On a standardized test of problem solving, however, there were no significant differences.

Expanding the pilot study to focus on the effects of treatment as a function of difficulty subtype (i.e., students at-risk for or with mathematics LD alone versus students at-risk for or with mathematics and reading LD) and controlling for tutoring time with a contrasting math tutoring condition, Fuchs et al. (2009) randomly assigned 133 third-grade students, blocking by difficulty subtype and by site (i.e., Nashville vs. Houston) to three conditions: number combinations tutoring, schema-broadening word-problem tutoring, or no-tutoring control. Students in the two tutoring conditions received individual tutoring on word problems or on number combinations 3 times a week for 15 weeks, each time for 20 to 30 min. Word-problem tutoring relied on schema-broadening instruction with mathematical equations similar to Fuchs, Seethaler, et al. (2008) . Growth from pre- to posttest on an experimenter-designed word-problem measure, including problems that required transfer, indicated that students in word-problem tutoring significantly outperformed students in number-combinations tutoring and in the control group (ESs = 0.83 and 0.79, respectively). On a standardized test of problem solving, students in word-problem tutoring significantly outperformed students in the control group (ES = 0.28). Additionally, difficulty subtype did not moderate the effect of schema-broadening instruction with equations. That is, students at-risk for or with mathematics and reading LD and students at-risk for mathematics without reading LD responded comparably well to the treatments.

Expanding beyond whole-class, schema-broadening instruction to incorporate mathematical equations, the research conducted by Fuchs et al. (2009) and Fuchs, Seethaler, et al. (2008) revealed how students at-risk for or with LD may benefit from tutoring that combines schema-broadening instruction with instruction on setting up and solving addition and subtraction mathematical equations. Because students did not receive concurrent whole-class instruction and individual word-problem tutoring as in Fuchs, Fuchs, Craddock, et al. (2008) , future research may investigate the added value of such a combination with schema-broadening plus mathematical equations instruction provided at the whole-class and small-group or individual tutoring levels.

A Framework for Teaching Word Problems in the Primary Grades

Across the two lines of work applying schema theory to word-problem solving, Jitendra and colleagues and Fuchs and colleagues provide evidence that students, including those at-risk for or with LD, may benefit from this explicit approach to word-problem instruction at the classroom and tutoring levels. In the schema-based instruction of Jitendra and colleagues, students learned to use schematic diagrams to solve word problems. In Jitendra's more recent research, students also learned to set up and solve an equation to find the word-problem answer after filling in a schematic diagram. The schema-broadening instruction of Fuchs and colleagues incorporated explicit schema instruction about word problem transfer features so students could learn how to recognize novel problems as belonging to the schemas they learned, but without reliance on schematic diagrams. Additionally, in the schema-broadening instruction of Fuchs et al. (2009) and Fuchs, Seethaler, et al. (2008) , students learned to use mathematical equations to represent the structure of a word problem.

Limitations

Before proceeding, it is important to discuss a few limitations across the two lines of schema work. First, and perhaps most importantly, many of the measures used to determine treatment effects were designed by the experimenters conducting the research. Some measures included word problems almost identical to those presented to students during instruction, perhaps raising questions about the generalizability of the word-problem instruction. When standardized tests of problem solving were administered, effects were either not significant or not as large as on the experimenter-designed measures. Second, a few of the studies, especially those by Fuchs and colleagues, included students at-risk for LD and not necessarily students with identified LD. Some of these students at-risk for LD received special education services; most did not. Within these studies for students at-risk for LD, the results for students with disabilities were not disaggregated from the primary sample. The same holds true for some of the other studies conducted by both Fuchs and colleagues and Jitendra and colleagues ( Fuchs et al., 2006 ; Fuchs et al., 2009 ; Fuchs, Fuchs, Craddock, et al., 2008 ; Fuchs, Seethaler, et al., 2008 ; Griffin & Jitendra, 2009 ). Therefore, it remains unclear if the interventions benefit students at-risk for LD, students with LD, or both.

Implications for Practice

Other schema investigations (e.g., Jitendra, DiPipi, & Perron-Jones, 2002 ; Jitendra, Hoff, & Beck, 1999 ; Xin, Jitendra, & Deatline-Buchman, 2005 ; Xin & Zhang, 2009 ) suggest using schema to solve word problems in the intermediate grades. That aside, the focus of the present literature review was on the primary grades, where the literature provides the basis for conceptualizing a framework for teaching word problems to students at-risk for or with LD that comprises the following features. First, instruction should be explicit. Across the two lines of schema work, schema were introduced in an explicit manner, and teachers or tutors often modeled or provided worked examples of word problems using each schema. It is not surprising that students at-risk for or with LD benefitted from explicit instruction, given that other mathematics researchers not focused on schema instruction (e.g., Kroesbergen et al., 2004 ; Mercer, Jordan, & Miller, 1996 ) have demonstrated the benefits of explicit instruction for students at-risk for or with LD. Across all the schema studies at the primary grades, students learned one word-problem schema at a time and had adequate practice (i.e., for days or weeks) on the schema before learning another schema.

Next, word-problem instruction should be organized. Students with LD profited from organizing word problems via schemas and having an explicit method for conceptualizing their solutions for each schema. This solution method could be a schematic diagram ( Jitendra et al., 1998 ), a mathematical equation ( Fuchs et al., 2009 ; Griffin & Jitendra, 2009 ), or a way of organizing information ( Fuchs, Fuchs, Finelli, et al., 2004 ). Because methods that work for one student may not work for another, it is important that teachers familiarize themselves with various explicit methods for helping students learn schema approaches to word problems so they can best help their students.

A schematic diagram may help some students organize their word-problem work, as in Figure 1 . With a schematic diagram, students fill in the relevant numbers from the word problem. The area of the schematic diagram that represents the question of the word problem (i.e., the word-problem solution) is left blank or filled in with a question mark. Students then learn how to solve for the blank space in the diagram to solve the word problem by calculating the answer. For example, the following is a typical elementary-school word problem: A classroom has 15 students. If 6 of the students are boys, how many students are girls? Using the schemas employed by Jitendra et al. (1998) , this word problem falls under the “group” schema because there is a larger set (i.e., the classroom) with smaller sets (i.e., boys and girls) within the larger set. The larger set (15) and one of the smaller sets (6) are defined within the text of the word problem. The other smaller set is the missing information needed to answer the word-problem question. After a student selects the word-problem schema (i.e., group), they fill in a schematic diagram. The schematic diagrams assist in organizing the word-problem information in pictorial fashion, which, as Jitendra and colleagues have demonstrated, may be beneficial for students at-risk for or with LD.

Another approach that may assist students in organizing word-problem work is to decide on a problem's schema and then use a mathematical equation to represent the underlying structure of the schema. Working with the word problem just discussed: A classroom has 15 students. If 6 of the students are boys, how many students are girls? , Fuchs et al. (2009) categorized this problem as falling within a “total” schema. In a “total” schema, parts are put together for a total. Instead of using a schematic diagram, students are taught a mathematical equation (i.e., P1 + P2 = T) that represents the two parts (i.e., P1, P2) put together for a total (i.e., T). After students decide the word problem's schema, they write the mathematical equation to help organize their word-problem work. (See Figure 2 for a worked example.) Students fill in the relevant numbers from the word problem and write an X for the missing part of the equation. Students then solve for X (i.e., solve the word-problem question). As demonstrated by Fuchs and Jitendra, using an equation to represent the schema is also an effective approach for strengthening the word-problem skill of students at-risk for or with LD.

For more difficult word problems, Fuchs and colleagues (e.g., Fuchs, Fuchs, Finelli, et al., 2004 ) have demonstrated how students can organize their word-problem work without a schematic diagram or mathematical equation, while relying on their knowledge of the problem schema. The word problem, Maya wants to buy 2 bags of pencils for $3 each, 4 notebooks for $2 each, and 6 folders for $1 each. How much will Maya spend? , would fall under the “shopping list” schema because multiple items of various prices are purchased. Instead of using a schematic diagram or equation for a “shopping list” problem, students draw vertical lines on their paper to organize their work. (See Figure 3 for a worked example.) Students calculate one part or step of the shopping list problem (i.e., pencils, notebooks, folders) in each section and calculate the overall cost of items in the right-most section. The vertical lines assist students in organizing the word-problem information and their work, but drawing the lines is not a necessity. That is, students could use their knowledge of schemas to solve the word problem with or without the lines.

Several other dimensions of a word-problem teaching framework using schema theory also emerge across the two lines of schema. These include practice in sorting word problems into schema, many instructional sessions, and multiple settings (i.e., whole class, small group, individual) for schema instruction to occur. With regard to sorting word problems into schema, both Jitendra and colleagues and Fuchs and colleagues made a point of mixing word-problem types so students had to differentiate what problems belonged to which schema. Some of this practice was explicit via flash cards ( Fuchs, Seethaler, et al., 2008 ). Some of the schema identification practice was embedded within the lesson, whereby teachers and tutors presented students with word problems, students had to decide which schema represented the word problem, and then use the structure of the schema to solve the word problem.

Across schema studies, the number of instructional sessions varied from 13 to 45 sessions. For all studies but one, students were taught or tutored multiple times each week, and students demonstrated significant gains from the schema instruction. Only the results of Griffin and Jitendra (2009) proved disappointing, with the absence of significant differences between the schema-based instruction and a comparison group. The authors attributed this lack of significance to the fact that instruction was provided once a week instead of multiple times each week. The significant results from the other 11 studies highlighted in this review suggest that instruction should be of sufficient duration (i.e., weeks and months, not days) and occur multiple times each week.

Finally, in the body of work reviewed in this paper, schema instruction occurred in whole-class, small-group tutoring, and individual tutoring settings. Students at-risk for or with LD benefitted from the schema instruction in all three of these settings. One study ( Fuchs, Fuchs, Craddock, et al., 2008 ) isolated the effects of conducted schema instruction provided in whole-class arrangement versus small-group tutoring settings. They concluded that the combination of both whole-class teaching and small-group tutoring may optimally enhance outcomes for students at risk for LD and that tutoring was essential for promoting strong outcomes. Teachers, therefore, should be mindful that whole-class instruction may not be enough for students with or at risk for LD, and additional tutoring (i.e., Tier 2 or 3 within a Response to Intervention framework) may be necessary to improve the word-problem outcomes of students with LD.

The linking features of these two schema approaches require students to (a) read a word problem, (b) recognize the underlying structure of the word problem as belonging to a specific schema, and (c) solve the word problem using a solution method that represents a schema. Whether students use schematic diagrams, mathematical equations, or another method to help them apply their knowledge of the word-problem schema, the research conducted by Jitendra and colleagues and Fuchs and colleagues demonstrates that students at-risk for or with LD may benefit from explicit word-problem instruction that incorporates schemas.

Acknowledgments

This research was supported by Award Number R01HD059179 from the Eunice Kennedy Shriver National Institute of Child Health & Human Development to Vanderbilt University. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Eunice Kennedy Shriver National Institute Of Child Health & Human Development or the National Institutes of Health.

• Case LP, Harris KR, Graham S. Improving the mathematical problem-solving skills of students with learning disabilities: Self-regulated strategy development. Journal of Special Education. 1992; 26 :1–19. [ Google Scholar ]
• Cooper G, Sweller J. Effects of schema acquisition and rule automation on mathematical problem-solving transfer. Journal of Educational Psychology. 1987; 79 :347–362. [ Google Scholar ]
• Cummins DD, Kintsch W, Reusser K, Weimer R. The role of understanding in word problems. Cognitive Psychology. 1988; 20 :405–438. [ Google Scholar ]
• Englert CS, Culatta BE, Horn DG. Influence of irrelevant information in addition word problems on problem solving. Learning Disability Quarterly. 1987; 10 :29–36. [ Google Scholar ]
• Fletcher JM, Lyon GR, Fuchs LS, Barnes MA. Learning disabilities: From identification to intervention. New York, NY: Guilford Press; 2006. [ Google Scholar ]
• Fuchs LS, Fuchs D. Mathematical problem-solving profiles of students with mathematics disabilities with and without comorbid reading disabilities. Journal of Learning Disabilities. 2002; 35 :563–573. [ PubMed ] [ Google Scholar ]
• Fuchs LS, Fuchs D, Craddock C, Hollenbeck KN, Hamlett CL, Schatschneider C. Effects of small-group tutoring with and without validated classroom instruction on at-risk students' math problem solving: Are two tiers of preventions better than one? Journal of Educational Psychology. 2008; 100 :491–509. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Fuchs LS, Fuchs D, Finelli R, Courey SJ, Hamlett CL. Expanding schema-based transfer instruction to help third graders solve real-life mathematical problems. American Educational Research Journal. 2004; 41 :419–445. [ Google Scholar ]
• Fuchs LS, Fuchs D, Finelli R, Courey SJ, Hamlett CL, Sones EM, Hope SK. Teaching third graders about real-life mathematical problem solving: A randomized control trial. The Elementary School Journal. 2006; 106 :293–311. [ Google Scholar ]
• Fuchs LS, Fuchs D, Prentice K, Burch M, Hamlett CL, Owen R, et al.Jancek D. Explicitly teaching for transfer: Effects on third-grade students' mathematical problem solving. Journal of Educational Psychology. 2003; 95 :293–305. [ Google Scholar ]
• Fuchs LS, Fuchs D, Prentice K, Hamlett CL, Finelli R, Courey SJ. Enhancing mathematical problem solving among third-grade students with schema-based instruction. Journal of Educational Psychology. 2004; 96 :635–647. [ Google Scholar ]
• Fuchs LS, Fuchs D, Stuebing K, Fletcher J, Hamlett CL, Lambert W. Problem-solving and computational skill: Are they shared or distinct aspects of mathematical cognition? Journal of Educational Psychology. 2008; 100 :30–47. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Fuchs LS, Powell SR, Seethaler PM, Cirino PT, Fletcher JM, Fuchs D, et al.Zumeta RO. Remediating number combination and word problem deficits among students with mathematics difficulties: A randomized control trial. Journal of Educational Psychology. 2009; 101 :561–576. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Fuchs LS, Seethaler PS, Powell SR, Fuchs D, Hamlett CL, Fletcher JM. Effects of preventative tutoring on the mathematical problem solving of third-grade students with math and reading difficulties. Exceptional Children. 2008; 74 :155–173. [ PMC free article ] [ PubMed ] [ Google Scholar ]
• Griffin CC, Jitendra AK. Word problem-solving instruction in inclusive third-grade classrooms. The Journal of Educational Research. 2009; 102 :187–201. [ Google Scholar ]
• Hanich LB, Jordan NC, Kaplan D, Dick J. Performance across different areas of mathematical cognition in children with learning difficulties. Journal of Educational Psychology. 2001; 93 :615–626. [ Google Scholar ]
• Hudson P, Miller SP. Designing and implementing mathematics instruction for students with diverse learning needs. Boston, MA: Allyn & Bacon; 2006. [ Google Scholar ]
• Jitendra A, DiPipi CM, Perron-Jones N. An exploratory study of schema-based word-problem-solving instruction for middle school students with learning disabilities: An emphasis on conceptual and procedural understanding. The Journal of Special Education. 2002; 36 :23–38. [ Google Scholar ]
• Jitendra AK, Griffin CC, Deatline-Buchman A, Sczesniak E. Mathematical problem solving in third-grade classrooms. Journal of Educational Research. 2007; 100 :283–302. [ Google Scholar ]
• Jitendra AK, Griffin CC, Haria P, Leh J, Adams A, Kaduvettoor A. A comparison of single and multiple strategy instruction on third-grade students' mathematical problem solving. Journal of Educational Psychology. 2007; 99 :115–127. [ Google Scholar ]
• Jitendra AK, Griffin CC, McGoey K, Gardill MC, Bhat P, Riley T. Effects of mathematical word problem solving by students at risk or with mild disabilities. The Journal of Educational Research. 1998; 91 :345–355. [ Google Scholar ]
• Jitendra AK, Hoff K. The effects of schema-based instruction on mathematical word-problem-solving performance of students with learning disabilities. Journal of Learning Disabilities. 1996; 29 :422–431. [ PubMed ] [ Google Scholar ]
• Jitendra AK, Hoff K, Beck MM. Teaching middle school students with learning disabilities to solve word problems using a schema-based approach. Remedial and Special Education. 1999; 20 :50–64. [ Google Scholar ]
• Jitendra A, Xin YP. Mathematical word problem-solving instruction for students with mild disabilities and students at risk for math failure: A research synthesis. The Journal of Special Education. 1997; 30 :412–438. [ Google Scholar ]
• Jordan NC, Hanich LB. Mathematical thinking in second-grade children with different forms of LD. Journal of Learning Disabilities. 2000; 33 :567–578. [ PubMed ] [ Google Scholar ]
• Jordan NC, Montani TO. Cognitive arithmetic and problem solving: A comparison of children with specific and general mathematics difficulties. Journal of Learning Disabilities. 1997; 30 :624–634. [ PubMed ] [ Google Scholar ]
• Kroesbergen EH, Van Luit JEH, Maas CTM. Effectiveness of explicit and constructivist mathematics instruction for low-achieving students in the Netherlands. The Elementary School Journal. 2004; 104 :233–251. [ Google Scholar ]
• Marshall SP. Schemas in Problem Solving. New York, NY: Cambridge University Press; 1995. [ Google Scholar ]
• Mastropieri MA, Scruggs TE, Shiah R. Can computers teach problem-solving strategies to students with mild mental retardation? Remedial and Special Education. 1997; 18 :157–165. [ Google Scholar ]
• Mercer CD, Jordan L, Miller SP. Constructivistic math instruction for diverse learners. Learning Disabilities Research & Practice. 1996; 11 :147–156. [ Google Scholar ]
• Miller SP, Mercer CD. Mnemonics: Enhancing the math performance of students with learning difficulties. Intervention in School and Clinic. 1993; 29 :78–82. [ Google Scholar ]
• Montague M, Warger C, Morgan TH. Solve it! Strategy instruction to improve mathematical problem solving. Learning Disabilities Research & Practice. 2000; 15 :110–116. [ Google Scholar ]
• National Assessment Governing Board . National assessment of educational progress. Washington, DC: Institute of Education Sciences; 2009. [ Google Scholar ]
• National Council of Teachers of Mathematics . Principles and standards for school mathematics. Reston, VA: Author; 2000. [ Google Scholar ]
• Parmar RS, Cawley JF, Frazita RR. Word problem-solving by students with and without mild disabilities. Exceptional Children. 1996; 62 :415–429. [ Google Scholar ]
• Pellegrino JW, Goldman SR. Information processing and elementary mathematics. Journal of Learning Disabilities. 1987; 20 :23–32. 57. [ PubMed ] [ Google Scholar ]
• Pólya G. How to solve it. Princeton, NJ: Princeton University Press; 1945. [ Google Scholar ]
• Riley MS, Greeno JG. Developmental analysis of understanding language about quantities and of solving problems. Cognition and Instruction. 1988; 5 :49–101. [ Google Scholar ]
• Schoenfeld AH. Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In: Grouws D, editor. Handbook for research on mathematics teaching and learning. New York, NY: MacMillan; 1992. pp. 334–370. [ Google Scholar ]
• Shavelson RJ, Webb NM, Stasz C, McArthur D. Teaching mathematical problem solving: Insights from teachers and tutors. In: Charles RI, Silver EA, editors. The teaching and assessing of mathematical problem solving. Reston, VA: The National council of Teachers of Mathematics, Inc.; 1988. pp. 203–231. [ Google Scholar ]
• van Garderen D. Teaching students with LD to use diagrams to solve mathematical word problems. Journal of Learning Disabilities. 2007; 40 :540–553. [ PubMed ] [ Google Scholar ]
• Willis GB, Fuson KC. Teaching children to use schematic drawings to solve addition and subtraction word problems. Journal of Educational Psychology. 1988; 80 :192–201. [ Google Scholar ]
• Wilson CL, Sindelar PT. Direct instruction in math word problems: Students with learning disabilities. Exceptional Children. 1991; 57 :512–519. [ PubMed ] [ Google Scholar ]
• Xin YP, Jitendra AK, Deatline-Buchman A. Effects of mathematical word problem-solving instruction on middle-school students with learning problems. The Journal of Special Education. 2005; 39 :181–192. [ Google Scholar ]
• Xin YP, Zhang D. Exploring a conceptual model-based approach to teaching situated word problems. The Journal of Educational Research. 2009; 102 :427–441. [ Google Scholar ]

Academia.edu no longer supports Internet Explorer.

To browse Academia.edu and the wider internet faster and more securely, please take a few seconds to  upgrade your browser .

Enter the email address you signed up with and we'll email you a reset link.

• We're Hiring!
• Help Center

Collaborative Problem Solving Literature Review & Research

Collaborative Problem Solving (CPS) applications will be examined from the ecological perspectives; however, the transactional models will also be discussed regarding helpful strategies and useful approaches that mental health professionals utilize when dealing with challenging behavior. CPS is a well-known approach to effectively addressing challenging behavior in children without using traditional approaches applied in Behaviorism. CPS avoids using Behaviorism approaches because it emphasizes the belief that a child’s challenging behavior is not because of their misbehavior, but a result of their cognitive limitation. CPS also avoids Behaviorism approaches because it utilizes a rewards and punishment system that may engender fear of punishment within children if they are noncompliant. Behaviorism places no emphasis on cognitive limitations or learning disabilities, rather it views children as “manipulative, mischievous, and resistant” to change their misbehavior. Consequently, children being treated with this/her approach frequently experience even more confusion and frustration when relating to adults while living with the fear of being punished. In short, CPS provides more humane, compassionate, and effective care to challenging children and provides a new understanding of these children’s identities and needs for success. CPS is a well-known transactional model that has extraordinary results in reducing challenging behaviors observed in children while simultaneously assisting them to build skills in adaptability, frustration tolerance, and problem-solving. CPS also builds and enhances healthy child-adult relationships without having to face prescriptive consequences for their misbehavior.

Related Papers

Journal of Psychosomatic Research

Ross Greene

Child & Family Behavior Therapy

Journal of Consulting and Clinical Psychology

Michael Monuteaux

Patricia Kerig

Marina Fiori

The goal of this study is twofold: (1) to assess brain anatomical differences between children meeting diagnostic criteria for oppositional defiant disorder (ODD) and healthy controls, and (2) to investigate whether morphological brain characteristics associated with ODD differ in boys and girls. Eight-year-old participants (N = 38) were scanned using magnetic resonance imaging. ODD symptoms were assessed using the Dominic-R interactive. In ODD participants, we observed a significant reduction of gray matter density in the left orbitofrontal cortex—a prefrontal region that plays a pivotal role in emotional self-regulation and impulse control—and, conversely, an increase in the left temporal area—an area that has been associated with aggressive, impulsive, and antisocial personality. Furthermore, ODD boys showed a reduction of both gray matter density in the left orbitofrontal cortex and of white matter density in the left superior frontal area. The structural abnormalities found in the present study, in particular, the correlation between ODD symptoms and reduction of gray matter density in the left orbitofrontal cortex, may present some evidence for the existence of neuropathology associated with ODD symptoms during childhood. Furthermore, our findings indicate morphometric differences between boys and girls with ODD, which may be associated with gender differences in social behavior in children showing ODD symptoms.

Clinical child and family psychology review

Alysa Doyle , Ross Greene

The conceptualization and treatment of oppositional defiant disorder (ODD) has been characterized by surprising homogeneity. In this paper evidence is presented to underscore the heterogeneity within ODD, including research demonstrating (a) the distinction between reactive and proactive forms of aggression; (b) the importance of affective modulation and self-regulation, and associated cognitive skills, in the development of the skill of compliance; and (c) high levels of comorbidity between ODD and other disorders. The disparate pathways that give rise to oppositional behavior suggest that different children with ODD may require different forms of intervention. The necessity of a transactional conceptualization, of achieving a comprehensive understanding of the factors underlying the difficulties of individual children with ODD, and of matching intervention ingredients to the specific needs of different children and families is discussed.

Child Psychiatry & Human Development

We examined the association of callous-unemotional (C/U) traits with length of psychiatric hospitalization among two samples each with 50 participants: a group of 7–11 year-olds (39 males and 11 females) receiving services on a children’s unit, and a group of 12–17 year-olds (27 males and 23 females) receiving services on an adolescent unit. Our analyses focused on the additionally predictive value of C/U traits above and beyond the influence of pre-established risk factors for length of stay, including age, gender, ethnicity, overall levels of functioning and psychopathology, and the diagnosis of a Conduct Disorder or Oppositional Defiant Disorder. In both samples, hierarchic regression analyses indicated that C/U traits were associated with longer lengths of stay, whereas none of the previously identified risk factors were significant. The discussion of these results focuses on the importance of developing non-coercive and non-confrontational therapeutic treatment regimens for youth with C/U traits receiving inpatient psychiatric services.

American Journal of Orthopsychiatry

Journal of Child and Family Studies

We present a general model for intervention with children diagnosed with ADHD that emphasizes the nature of the dyadic interaction between parent and child as the critical focus of concern. Conventional treatment outcome research designs, however, do not easily permit the testing of this or any other generative model. We explain why, and critique the clinical value of certain research

George Holden , Joan E Durrant

This commentary addresses the critique by Larzelere, Gunnoe, Roberts, and Ferguson (2017: Marriage & Family Review, 53, 24–35) ostensibly concerning the quality of research on “positive parenting” but actually critiquing physical punishment research. The critique revealed that the authors have a poor understanding of positive parenting. After explicating the different meanings of that term and describing what positive parenting is, we then address each of their four critiques of the physical punishment research. Each critique was flawed in multiple ways. After identifying their errors and correcting misinformation, we then raise broader issues about children’s right not to be hit and how professional organizations are increasingly recognizing the need and calling for an end to all physical punishment of children.

RELATED PAPERS

Maria Isabel Capuchino

Journal of Pediatric Psychology

Elizabeth D'Amico

Journal of Developmental and Physical Disabilities

Julie Leclerc , Jacques Forget

April Fletcher

Pratiques Psychologiques

Clinical Psychology Review

Thomas Ollendick

Journal of Psychiatric and Mental Health Nursing

M. Zywicki , Yulia Y. Semeniuk , Susan Riesch , Jeffrey Henriques

Geoffrey Goodman , Vera Regina Rohnelt Ramires

American Journal of Psychiatry

Jessica Malmberg

Journal of child and adolescent psychiatric nursing : official publication of the Association of Child and Adolescent Psychiatric Nurses, Inc

kathleen Delaney

Madelaine Hittos

Melanie Barwick

Joy Bustrum

Cognitive therapy with children …

Rebecca A Burwell

David DuBois

Elias Kourkoutas

Holly Grason , Deborah Perry

Quenette Walton , Tyreasa Washington , Dr.Joan M Blakey

Clinical Psychologist

Mohsen Shokoohiyekta , Ameneh Shahaeian

Vicki Cowling

Journal of Affective Disorders

Edward Craighead

Journal of the American Academy of Child & Adolescent Psychiatry

Denis Sukhodolsky

Developmental Psychology

Rebecca Bulotsky-shearer , Paul McDermott

Exceptional children

Teresa Nesman

Journal of Attention Disorders

Peter Jensen , Howard Abikoff

Orlando Mpafa

Cognition, Intelligence, and Achievement

David Tzuriel , Gilat Trabelsi

David Miklowitz

Educational Researcher

Jeffrey Sprague , David Osher

Child and Adolescent Psychiatry and Mental Health

Josephine Johnston

Halima Al-Khattab

Clinical Child and Family Psychology Review

Caroline Murphy

Development and Psychopathology

Stephanie Stepp

Child Maltreatment

Assaf Oshri , Jody Manly

Manny Cokerschwimmer

Mimi du Soleil

Aaron Frost

School Psychology Quarterly

Daniel Olympia

RELATED TOPICS

•   We're Hiring!
•   Help Center
• Find new research papers in:
• Health Sciences
• Earth Sciences
• Cognitive Science
• Mathematics
• Computer Science
• Academia ©2024

The Workforce Scheduling Problem (WSP): A Review of the Literature

• Conference paper
• First Online: 26 April 2024
• Cite this conference paper

• Efraín Pérez-Cubero 6 ,
• Raul Poler 7 &
• Eduardo Vicens 7  

Part of the book series: Lecture Notes on Data Engineering and Communications Technologies ((LNDECT,volume 206))

Included in the following conference series:

• International Conference on Industrial Engineering and Industrial Management (ICIEIM) – Congreso de Ingeniería de Organización

The aim of this article is to identify and analyse the methods that are being used to solve the Workforce Scheduling Problem (WSP) through a systematic review of the publications on this problem. This study aims to provide researchers with a starting point to advance in the approaches to solving the problem and in enriching the WSP with additional variables that complement it in a natural way. Finally, the most promising lines of research for the future are identified.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Institutional subscriptions

Ayough, A., Zandieh, M., Farsijani, H.: GA and ICA approaches to job rotation scheduling problem: considering employee’s boredom. Int. J. Adv. Manuf. Technol. 60 (5–8), 651–666 (2012). https://doi.org/10.1007/s00170-011-3641-7

Article   Google Scholar  

Berman, O., Larson, R.C., Pinker, E.: Scheduling workforce and workflow in a high volume factory. Manag. Sci. 43 (2), 158–172 (1997). https://doi.org/10.1287/mnsc.43.2.158

Chu, X., et al.: Worker assignment with learning-forgetting effect in cellular manufacturing system using adaptive memetic differential search algorithm. Comput. Ind. Eng. 136 (July), 381–396 (2019). https://doi.org/10.1016/j.cie.2019.07.028

Eurofund. Working conditions in sectors. Publications Office of the European Union, Luxembourg (2020). https://www.eurofound.europa.eu/publications/report/2020/working-conditions-in-sectors

Hillier, F.S., Lieberman, G.J.: Introduction to Operations Research, 10 edn. McGraw-Hill, Stanford (2015)

Google Scholar  

Pérez-Cubero, E., Poler, R.: Aplicación de algoritmos de aprendizaje automático a la programación de órdenes de producción en talleres de trabajo: Una revisión de la literatura reciente. Direccion y Organizacion 72 (72), 82–94 (2021). https://doi.org/10.37610/DYO.V0I72.588

Rinaldi, M., et al.: Workforce scheduling incorporating worker skills and ergonomic constraints. Comput. Ind. Eng. 168 (2021). https://doi.org/10.1016/j.cie.2022.108107

Sabar, M., Montreuil, B., Frayret, J.M.: A multi-agent-based approach for personnel scheduling in assembly centers. Eng. Appl. Artif. Intell. 22 (7), 1080–1088 (2009). https://doi.org/10.1016/j.engappai.2009.02.009

Savino, M.M., Riccio, C., Menanno, M.: Empirical study to explore the impact of ergonomics on workforce scheduling. Int. J. Prod. Res. 58 (2), 415–433 (2020). https://doi.org/10.1080/00207543.2019.1591645

Wu, L., et al.: Cross-trained worker assignment problem in cellular manufacturing system using swarm intelligence metaheuristics. Math. Probl. Eng. 2018 (2018). https://doi.org/10.1155/2018/4302062

Xin, B., et al.: An adaptive BPSO algorithm for multi-skilled workers assignment problem in aircraft assembly lines. Assem. Autom. 35 (4), 317–328 (2015). https://doi.org/10.1108/AA-06-2015-051

Download references

Author information

Authors and affiliations.

University of Costa Rica, Alajuela Campus, Alajuela, Costa Rica

Efraín Pérez-Cubero

Universitat Politècnica de València, Production Engineering and Management Research Center. Camino de Vera S/N, Valencia, Spain

Raul Poler & Eduardo Vicens

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Efraín Pérez-Cubero .

Editor information

Editors and affiliations.

ETSEIB, Universitat Politècnica de Catalunya, Barcelona, Spain

Joaquín Bautista-Valhondo

Manuel Mateo-Doll

Rafael Pastor-Moreno

Rights and permissions

Reprints and permissions

Copyright information

© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Cite this paper.

Pérez-Cubero, E., Poler, R., Vicens, E. (2024). The Workforce Scheduling Problem (WSP): A Review of the Literature. In: Bautista-Valhondo, J., Mateo-Doll, M., Lusa, A., Pastor-Moreno, R. (eds) Proceedings of the 17th International Conference on Industrial Engineering and Industrial Management (ICIEIM) – XXVII Congreso de Ingeniería de Organización (CIO2023). CIO 2023. Lecture Notes on Data Engineering and Communications Technologies, vol 206. Springer, Cham. https://doi.org/10.1007/978-3-031-57996-7_55

Download citation

DOI : https://doi.org/10.1007/978-3-031-57996-7_55

Published : 26 April 2024

Publisher Name : Springer, Cham

Print ISBN : 978-3-031-57995-0

Online ISBN : 978-3-031-57996-7

eBook Packages : Engineering Engineering (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 10 April 2024

A hybrid particle swarm optimization algorithm for solving engineering problem

• Jinwei Qiao 1 , 2 ,
• Guangyuan Wang 1 , 2 ,
• Zhi Yang 1 , 2 ,
• Xiaochuan Luo 3 ,
• Jun Chen 1 , 2 ,
• Kan Li 4 &
• Pengbo Liu 1 , 2  

Scientific Reports volume  14 , Article number:  8357 ( 2024 ) Cite this article

408 Accesses

Metrics details

• Computational science
• Mechanical engineering

To overcome the disadvantages of premature convergence and easy trapping into local optimum solutions, this paper proposes an improved particle swarm optimization algorithm (named NDWPSO algorithm) based on multiple hybrid strategies. Firstly, the elite opposition-based learning method is utilized to initialize the particle position matrix. Secondly, the dynamic inertial weight parameters are given to improve the global search speed in the early iterative phase. Thirdly, a new local optimal jump-out strategy is proposed to overcome the "premature" problem. Finally, the algorithm applies the spiral shrinkage search strategy from the whale optimization algorithm (WOA) and the Differential Evolution (DE) mutation strategy in the later iteration to accelerate the convergence speed. The NDWPSO is further compared with other 8 well-known nature-inspired algorithms (3 PSO variants and 5 other intelligent algorithms) on 23 benchmark test functions and three practical engineering problems. Simulation results prove that the NDWPSO algorithm obtains better results for all 49 sets of data than the other 3 PSO variants. Compared with 5 other intelligent algorithms, the NDWPSO obtains 69.2%, 84.6%, and 84.6% of the best results for the benchmark function ( \({f}_{1}-{f}_{13}\) ) with 3 kinds of dimensional spaces (Dim = 30,50,100) and 80% of the best optimal solutions for 10 fixed-multimodal benchmark functions. Also, the best design solutions are obtained by NDWPSO for all 3 classical practical engineering problems.

Similar content being viewed by others

Physics-informed machine learning

Principal component analysis

Bayesian statistics and modelling

Introduction.

In the ever-changing society, new optimization problems arise every moment, and they are distributed in various fields, such as automation control 1 , statistical physics 2 , security prevention and temperature prediction 3 , artificial intelligence 4 , and telecommunication technology 5 . Faced with a constant stream of practical engineering optimization problems, traditional solution methods gradually lose their efficiency and convenience, making it more and more expensive to solve the problems. Therefore, researchers have developed many metaheuristic algorithms and successfully applied them to the solution of optimization problems. Among them, Particle swarm optimization (PSO) algorithm 6 is one of the most widely used swarm intelligence algorithms.

However, the basic PSO has a simple operating principle and solves problems with high efficiency and good computational performance, but it suffers from the disadvantages of easily trapping in local optima and premature convergence. To improve the overall performance of the particle swarm algorithm, an improved particle swarm optimization algorithm is proposed by the multiple hybrid strategy in this paper. The improved PSO incorporates the search ideas of other intelligent algorithms (DE, WOA), so the improved algorithm proposed in this paper is named NDWPSO. The main improvement schemes are divided into the following 4 points: Firstly, a strategy of elite opposition-based learning is introduced into the particle population position initialization. A high-quality initialization matrix of population position can improve the convergence speed of the algorithm. Secondly, a dynamic weight methodology is adopted for the acceleration coefficients by combining the iterative map and linearly transformed method. This method utilizes the chaotic nature of the mapping function, the fast convergence capability of the dynamic weighting scheme, and the time-varying property of the acceleration coefficients. Thus, the global search and local search of the algorithm are balanced and the global search speed of the population is improved. Thirdly, a determination mechanism is set up to detect whether the algorithm falls into a local optimum. When the algorithm is “premature”, the population resets 40% of the position information to overcome the local optimum. Finally, the spiral shrinking mechanism combined with the DE/best/2 position mutation is used in the later iteration, which further improves the solution accuracy.

The structure of the paper is given as follows: Sect. “ Particle swarm optimization (PSO) ” describes the principle of the particle swarm algorithm. Section “ Improved particle swarm optimization algorithm ” shows the detailed improvement strategy and a comparison experiment of inertia weight is set up for the proposed NDWPSO. Section “ Experiment and discussion ” includes the experimental and result discussion sections on the performance of the improved algorithm. Section “ Conclusions and future works ” summarizes the main findings of this study.

Literature review

This section reviews some metaheuristic algorithms and other improved PSO algorithms. A simple discussion about recently proposed research studies is given.

Metaheuristic algorithms

A series of metaheuristic algorithms have been proposed in recent years by using various innovative approaches. For instance, Lin et al. 7 proposed a novel artificial bee colony algorithm (ABCLGII) in 2018 and compared ABCLGII with other outstanding ABC variants on 52 frequently used test functions. Abed-alguni et al. 8 proposed an exploratory cuckoo search (ECS) algorithm in 2021 and carried out several experiments to investigate the performance of ECS by 14 benchmark functions. Brajević 9 presented a novel shuffle-based artificial bee colony (SB-ABC) algorithm for solving integer programming and minimax problems in 2021. The experiments are tested on 7 integer programming problems and 10 minimax problems. In 2022, Khan et al. 10 proposed a non-deterministic meta-heuristic algorithm called Non-linear Activated Beetle Antennae Search (NABAS) for a non-convex tax-aware portfolio selection problem. Brajević et al. 11 proposed a hybridization of the sine cosine algorithm (HSCA) in 2022 to solve 15 complex structural and mechanical engineering design optimization problems. Abed-Alguni et al. 12 proposed an improved Salp Swarm Algorithm (ISSA) in 2022 for single-objective continuous optimization problems. A set of 14 standard benchmark functions was used to evaluate the performance of ISSA. In 2023, Nadimi et al. 13 proposed a binary starling murmuration optimization (BSMO) to select the effective features from different important diseases. In the same year, Nadimi et al. 14 systematically reviewed the last 5 years' developments of WOA and made a critical analysis of those WOA variants. In 2024, Fatahi et al. 15 proposed an Improved Binary Quantum-based Avian Navigation Optimizer Algorithm (IBQANA) for the Feature Subset Selection problem in the medical area. Experimental evaluation on 12 medical datasets demonstrates that IBQANA outperforms 7 established algorithms. Abed-alguni et al. 16 proposed an Improved Binary DJaya Algorithm (IBJA) to solve the Feature Selection problem in 2024. The IBJA’s performance was compared against 4 ML classifiers and 10 efficient optimization algorithms.

Improved PSO algorithms

Many researchers have constantly proposed some improved PSO algorithms to solve engineering problems in different fields. For instance, Yeh 17 proposed an improved particle swarm algorithm, which combines a new self-boundary search and a bivariate update mechanism, to solve the reliability redundancy allocation problem (RRAP) problem. Solomon et al. 18 designed a collaborative multi-group particle swarm algorithm with high parallelism that was used to test the adaptability of Graphics Processing Units (GPUs) in distributed computing environments. Mukhopadhyay and Banerjee 19 proposed a chaotic multi-group particle swarm optimization (CMS-PSO) to estimate the unknown parameters of an autonomous chaotic laser system. Duan et al. 20 designed an improved particle swarm algorithm with nonlinear adjustment of inertia weights to improve the coupling accuracy between laser diodes and single-mode fibers. Sun et al. 21 proposed a particle swarm optimization algorithm combined with non-Gaussian stochastic distribution for the optimal design of wind turbine blades. Based on a multiple swarm scheme, Liu et al. 22 proposed an improved particle swarm optimization algorithm to predict the temperatures of steel billets for the reheating furnace. In 2022, Gad 23 analyzed the existing 2140 papers on Swarm Intelligence between 2017 and 2019 and pointed out that the PSO algorithm still needs further research. In general, the improved methods can be classified into four categories:

Adjusting the distribution of algorithm parameters. Feng et al. 24 used a nonlinear adaptive method on inertia weights to balance local and global search and introduced asynchronously varying acceleration coefficients.

Changing the updating formula of the particle swarm position. Both papers 25 and 26 used chaotic mapping functions to update the inertia weight parameters and combined them with a dynamic weighting strategy to update the particle swarm positions. This improved approach enables the particle swarm algorithm to be equipped with fast convergence of performance.

The initialization of the swarm. Alsaidy and Abbood proposed 27 a hybrid task scheduling algorithm that replaced the random initialization of the meta-heuristic algorithm with the heuristic algorithms MCT-PSO and LJFP-PSO.

Combining with other intelligent algorithms: Liu et al. 28 introduced the differential evolution (DE) algorithm into PSO to increase the particle swarm as diversity and reduce the probability of the population falling into local optimum.

Particle swarm optimization (PSO)

The particle swarm optimization algorithm is a population intelligence algorithm for solving continuous and discrete optimization problems. It originated from the social behavior of individuals in bird and fish flocks 6 . The core of the PSO algorithm is that an individual particle identifies potential solutions by flight in a defined constraint space adjusts its exploration direction to approach the global optimal solution based on the shared information among the group, and finally solves the optimization problem. Each particle \(i\) includes two attributes: velocity vector \({V}_{i}=\left[{v}_{i1},{v}_{i2},{v}_{i3},{...,v}_{ij},{...,v}_{iD},\right]\) and position vector \({X}_{i}=[{x}_{i1},{x}_{i2},{x}_{i3},...,{x}_{ij},...,{x}_{iD}]\) . The velocity vector is used to modify the motion path of the swarm; the position vector represents a potential solution for the optimization problem. Here, \(j=\mathrm{1,2},\dots ,D\) , \(D\) represents the dimension of the constraint space. The equations for updating the velocity and position of the particle swarm are shown in Eqs. ( 1 ) and ( 2 ).

Here \({Pbest}_{i}^{k}\) represents the previous optimal position of the particle \(i\) , and \({Gbest}\) is the optimal position discovered by the whole population. \(i=\mathrm{1,2},\dots ,n\) , \(n\) denotes the size of the particle swarm. \({c}_{1}\) and \({c}_{2}\) are the acceleration constants, which are used to adjust the search step of the particle 29 . \({r}_{1}\) and \({r}_{2}\) are two random uniform values distributed in the range \([\mathrm{0,1}]\) , which are used to improve the randomness of the particle search. \(\omega\) inertia weight parameter, which is used to adjust the scale of the search range of the particle swarm 30 . The basic PSO sets the inertia weight parameter as a time-varying parameter to balance global exploration and local seeking. The updated equation of the inertia weight parameter is given as follows:

where \({\omega }_{max}\) and \({\omega }_{min}\) represent the upper and lower limits of the range of inertia weight parameter. \(k\) and \(Mk\) are the current iteration and maximum iteration.

Improved particle swarm optimization algorithm

According to the no free lunch theory 31 , it is known that no algorithm can solve every practical problem with high quality and efficiency for increasingly complex and diverse optimization problems. In this section, several improvement strategies are proposed to improve the search efficiency and overcome this shortcoming of the basic PSO algorithm.

Improvement strategies

The optimization strategies of the improved PSO algorithm are shown as follows:

The inertia weight parameter is updated by an improved chaotic variables method instead of a linear decreasing strategy. Chaotic mapping performs the whole search at a higher speed and is more resistant to falling into local optimal than the probability-dependent random search 32 . However, the population may result in that particles can easily fly out of the global optimum boundary. To ensure that the population can converge to the global optimum, an improved Iterative mapping is adopted and shown as follows:

Here \({\omega }_{k}\) is the inertia weight parameter in the iteration \(k\) , \(b\) is the control parameter in the range \([\mathrm{0,1}]\) .

The acceleration coefficients are updated by the linear transformation. \({c}_{1}\) and \({c}_{2}\) represent the influential coefficients of the particles by their own and population information, respectively. To improve the search performance of the population, \({c}_{1}\) and \({c}_{2}\) are changed from fixed values to time-varying parameter parameters, that are updated by linear transformation with the number of iterations:

where \({c}_{max}\) and \({c}_{min}\) are the maximum and minimum values of acceleration coefficients, respectively.

The initialization scheme is determined by elite opposition-based learning . The high-quality initial population will accelerate the solution speed of the algorithm and improve the accuracy of the optimal solution. Thus, the elite backward learning strategy 33 is introduced to generate the position matrix of the initial population. Suppose the elite individual of the population is \({X}=[{x}_{1},{x}_{2},{x}_{3},...,{x}_{j},...,{x}_{D}]\) , and the elite opposition-based solution of \(X\) is \({X}_{o}=[{x}_{{\text{o}}1},{x}_{{\text{o}}2},{x}_{{\text{o}}3},...,{x}_{oj},...,{x}_{oD}]\) . The formula for the elite opposition-based solution is as follows:

where \({k}_{r}\) is the random value in the range \((\mathrm{0,1})\) . \({ux}_{oij}\) and \({lx}_{oij}\) are dynamic boundaries of the elite opposition-based solution in \(j\) dimensional variables. The advantage of dynamic boundary is to reduce the exploration space of particles, which is beneficial to the convergence of the algorithm. When the elite opposition-based solution is out of bounds, the out-of-bounds processing is performed. The equation is given as follows:

After calculating the fitness function values of the elite solution and the elite opposition-based solution, respectively, \(n\) high quality solutions were selected to form a new initial population position matrix.

The position updating Eq. ( 2 ) is modified based on the strategy of dynamic weight. To improve the speed of the global search of the population, the strategy of dynamic weight from the artificial bee colony algorithm 34 is introduced to enhance the computational performance. The new position updating equation is shown as follows:

Here \(\rho\) is the random value in the range \((\mathrm{0,1})\) . \(\psi\) represents the acceleration coefficient and \({\omega }{\prime}\) is the dynamic weight coefficient. The updated equations of the above parameters are as follows:

where \(f(i)\) denotes the fitness function value of individual particle \(i\) and u is the average of the population fitness function values in the current iteration. The Eqs. ( 11 , 12 ) are introduced into the position updating equation. And they can attract the particle towards positions of the best-so-far solution in the search space.

New local optimal jump-out strategy is added for escaping from the local optimal. When the value of the fitness function for the population optimal particles does not change in M iterations, the algorithm determines that the population falls into a local optimal. The scheme in which the population jumps out of the local optimum is to reset the position information of the 40% of individuals within the population, in other words, to randomly generate the position vector in the search space. M is set to 5% of the maximum number of iterations.

New spiral update search strategy is added after the local optimal jump-out strategy. Since the whale optimization algorithm (WOA) was good at exploring the local search space 35 , the spiral update search strategy in the WOA 36 is introduced to update the position of the particles after the swarm jumps out of local optimal. The equation for the spiral update is as follows:

Here \(D=\left|{x}_{i}\left(k\right)-Gbest\right|\) denotes the distance between the particle itself and the global optimal solution so far. \(B\) is the constant that defines the shape of the logarithmic spiral. \(l\) is the random value in \([-\mathrm{1,1}]\) . \(l\) represents the distance between the newly generated particle and the global optimal position, \(l=-1\) means the closest distance, while \(l=1\) means the farthest distance, and the meaning of this parameter can be directly observed by Fig.  1 .

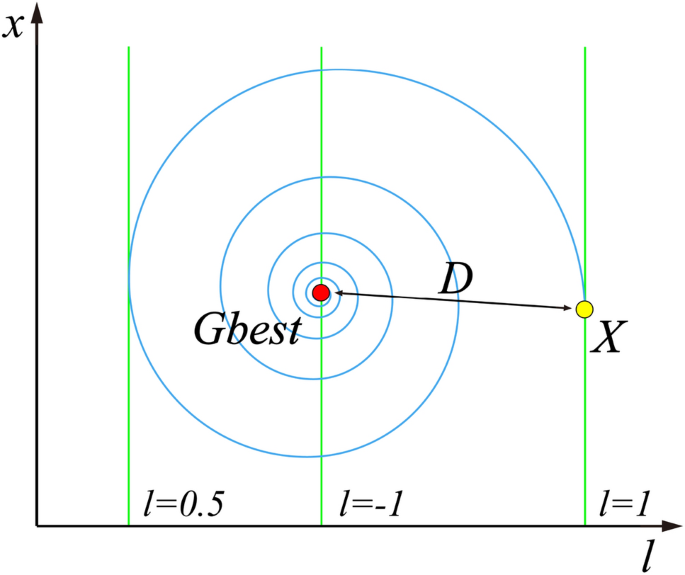
Spiral updating position.

The DE/best/2 mutation strategy is introduced to form the mutant particle. 4 individuals in the population are randomly selected that differ from the current particle, then the vector difference between them is rescaled, and the difference vector is combined with the global optimal position to form the mutant particle. The equation for mutation of particle position is shown as follows:

where \({x}^{*}\) is the mutated particle, \(F\) is the scale factor of mutation, \({r}_{1}\) , \({r}_{2}\) , \({r}_{3}\) , \({r}_{4}\) are random integer values in \((0,n]\) and not equal to \(i\) , respectively. Specific particles are selected for mutation with the screening conditions as follows:

where \(Cr\) represents the probability of mutation, \(rand\left(\mathrm{0,1}\right)\) is a random number in \(\left(\mathrm{0,1}\right)\) , and \({i}_{rand}\) is a random integer value in \((0,n]\) .

The improved PSO incorporates the search ideas of other intelligent algorithms (DE, WOA), so the improved algorithm proposed in this paper is named NDWPSO. The pseudo-code for the NDWPSO algorithm is given as follows:

The main procedure of NDWPSO.

Comparing the distribution of inertia weight parameters

There are several improved PSO algorithms (such as CDWPSO 25 , and SDWPSO 26 ) that adopt the dynamic weighted particle position update strategy as their improvement strategy. The updated equations of the CDWPSO and the SDWPSO algorithm for the inertia weight parameters are given as follows:

where \({\text{A}}\) is a value in \((\mathrm{0,1}]\) . \({r}_{max}\) and \({r}_{min}\) are the upper and lower limits of the fluctuation range of the inertia weight parameters, \(k\) is the current number of algorithm iterations, and \(Mk\) denotes the maximum number of iterations.

Considering that the update method of inertia weight parameters by our proposed NDWPSO is comparable to the CDWPSO, and SDWPSO, a comparison experiment for the distribution of inertia weight parameters is set up in this section. The maximum number of iterations in the experiment is \(Mk=500\) . The distributions of CDWPSO, SDWPSO, and NDWPSO inertia weights are shown sequentially in Fig.  2 .

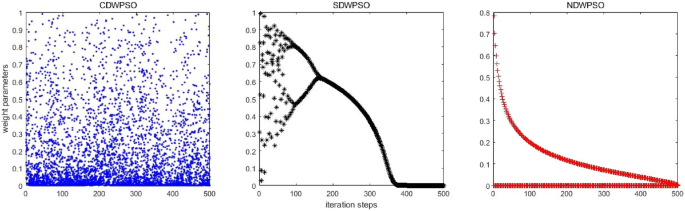
The inertial weight distribution of CDWPSO, SDWPSO, and NDWPSO.

In Fig.  2 , the inertia weight value of CDWPSO is a random value in (0,1]. It may make individual particles fly out of the range in the late iteration of the algorithm. Similarly, the inertia weight value of SDWPSO is a value that tends to zero infinitely, so that the swarm no longer can fly in the search space, making the algorithm extremely easy to fall into the local optimal value. On the other hand, the distribution of the inertia weights of the NDWPSO forms a gentle slope by two curves. Thus, the swarm can faster lock the global optimum range in the early iterations and locate the global optimal more precisely in the late iterations. The reason is that the inertia weight values between two adjacent iterations are inversely proportional to each other. Besides, the time-varying part of the inertial weight within NDWPSO is designed to reduce the chaos characteristic of the parameters. The inertia weight value of NDWPSO avoids the disadvantages of the above two schemes, so its design is more reasonable.

Experiment and discussion

In this section, three experiments are set up to evaluate the performance of NDWPSO: (1) the experiment of 23 classical functions 37 between NDWPSO and three particle swarm algorithms (PSO 6 , CDWPSO 25 , SDWPSO 26 ); (2) the experiment of benchmark test functions between NDWPSO and other intelligent algorithms (Whale Optimization Algorithm (WOA) 36 , Harris Hawk Algorithm (HHO) 38 , Gray Wolf Optimization Algorithm (GWO) 39 , Archimedes Algorithm (AOA) 40 , Equilibrium Optimizer (EO) 41 and Differential Evolution (DE) 42 ); (3) the experiment for solving three real engineering problems (welded beam design 43 , pressure vessel design 44 , and three-bar truss design 38 ). All experiments are run on a computer with Intel i5-11400F GPU, 2.60 GHz, 16 GB RAM, and the code is written with MATLAB R2017b.

The benchmark test functions are 23 classical functions, which consist of indefinite unimodal (F1–F7), indefinite dimensional multimodal functions (F8–F13), and fixed-dimensional multimodal functions (F14–F23). The unimodal benchmark function is used to evaluate the global search performance of different algorithms, while the multimodal benchmark function reflects the ability of the algorithm to escape from the local optimal. The mathematical equations of the benchmark functions are shown and found as Supplementary Tables S1 – S3 online.

Experiments on benchmark functions between NDWPSO, and other PSO variants

The purpose of the experiment is to show the performance advantages of the NDWPSO algorithm. Here, the dimensions and corresponding population sizes of 13 benchmark functions (7 unimodal and 6 multimodal) are set to (30, 40), (50, 70), and (100, 130). The population size of 10 fixed multimodal functions is set to 40. Each algorithm is repeated 30 times independently, and the maximum number of iterations is 200. The performance of the algorithm is measured by the mean and the standard deviation (SD) of the results for different benchmark functions. The parameters of the NDWPSO are set as: \({[{\omega }_{min},\omega }_{max}]=[\mathrm{0.4,0.9}]\) , \(\left[{c}_{max},{c}_{min}\right]=\left[\mathrm{2.5,1.5}\right],{V}_{max}=0.1,b={e}^{-50}, M=0.05\times Mk, B=1,F=0.7, Cr=0.9.\) And, \(A={\omega }_{max}\) for CDWPSO; \({[r}_{max},{r}_{min}]=[\mathrm{4,0}]\) for SDWPSO.

Besides, the experimental data are retained to two decimal places, but some experimental data will increase the number of retained data to pursue more accuracy in comparison. The best results in each group of experiments will be displayed in bold font. The experimental data is set to 0 if the value is below 10 –323 . The experimental parameter settings in this paper are different from the references (PSO 6 , CDWPSO 25 , SDWPSO 26 , so the final experimental data differ from the ones within the reference.

As shown in Tables 1 and 2 , the NDWPSO algorithm obtains better results for all 49 sets of data than other PSO variants, which include not only 13 indefinite-dimensional benchmark functions and 10 fixed-multimodal benchmark functions. Remarkably, the SDWPSO algorithm obtains the same accuracy of calculation as NDWPSO for both unimodal functions f 1 –f 4 and multimodal functions f 9 –f 11 . The solution accuracy of NDWPSO is higher than that of other PSO variants for fixed-multimodal benchmark functions f 14 -f 23 . The conclusion can be drawn that the NDWPSO has excellent global search capability, local search capability, and the capability for escaping the local optimal.

In addition, the convergence curves of the 23 benchmark functions are shown in Figs. 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 and 19 . The NDWPSO algorithm has a faster convergence speed in the early stage of the search for processing functions f1-f6, f8-f14, f16, f17, and finds the global optimal solution with a smaller number of iterations. In the remaining benchmark function experiments, the NDWPSO algorithm shows no outstanding performance for convergence speed in the early iterations. There are two reasons of no outstanding performance in the early iterations. On one hand, the fixed-multimodal benchmark function has many disturbances and local optimal solutions in the whole search space. on the other hand, the initialization scheme based on elite opposition-based learning is still stochastic, which leads to the initial position far from the global optimal solution. The inertia weight based on chaotic mapping and the strategy of spiral updating can significantly improve the convergence speed and computational accuracy of the algorithm in the late search stage. Finally, the NDWPSO algorithm can find better solutions than other algorithms in the middle and late stages of the search.

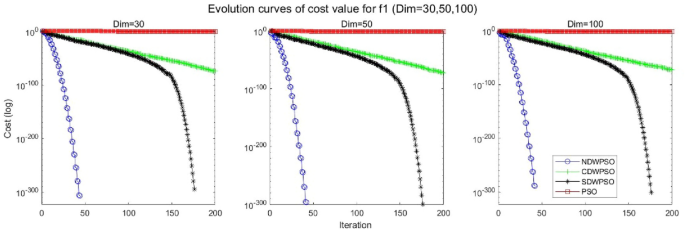
Evolution curve of NDWPSO and other PSO algorithms for f1 (Dim = 30,50,100).

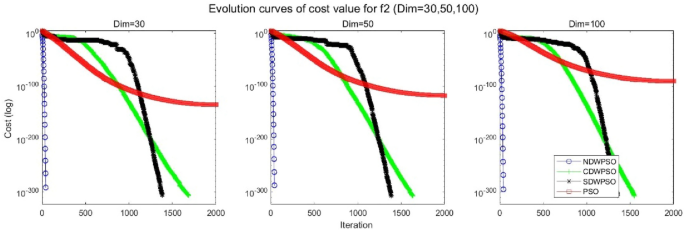
Evolution curve of NDWPSO and other PSO algorithms for f2 (Dim = 30,50,100).

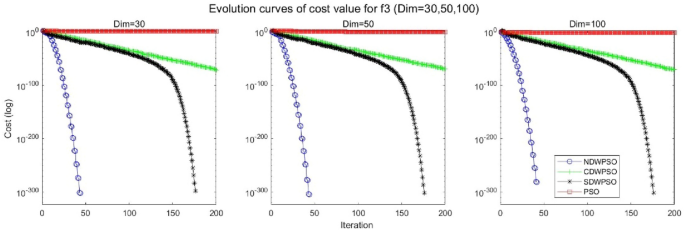
Evolution curve of NDWPSO and other PSO algorithms for f3 (Dim = 30,50,100).

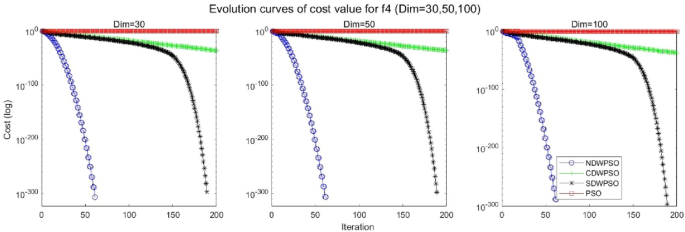
Evolution curve of NDWPSO and other PSO algorithms for f4 (Dim = 30,50,100).

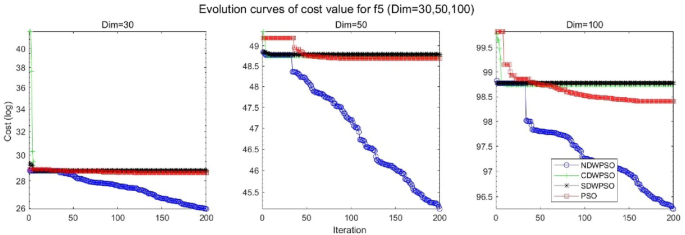
Evolution curve of NDWPSO and other PSO algorithms for f5 (Dim = 30,50,100).

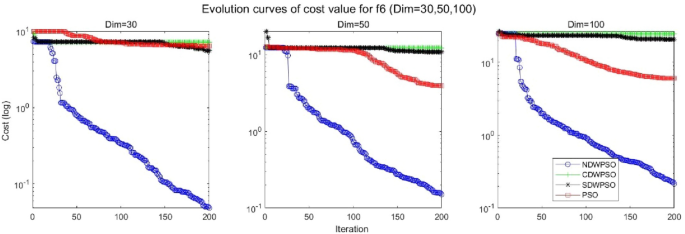
Evolution curve of NDWPSO and other PSO algorithms for f6 (Dim = 30,50,100).

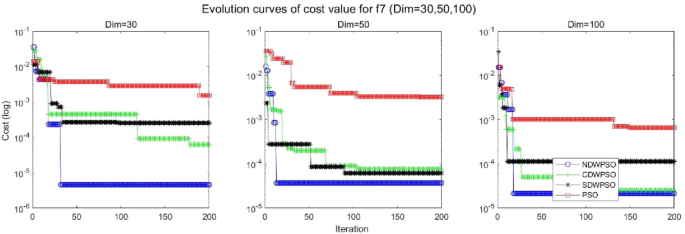
Evolution curve of NDWPSO and other PSO algorithms for f7 (Dim = 30,50,100).

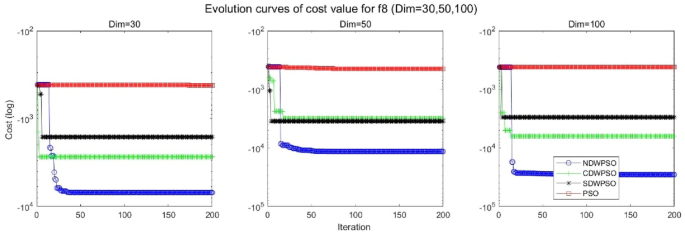
Evolution curve of NDWPSO and other PSO algorithms for f8 (Dim = 30,50,100).

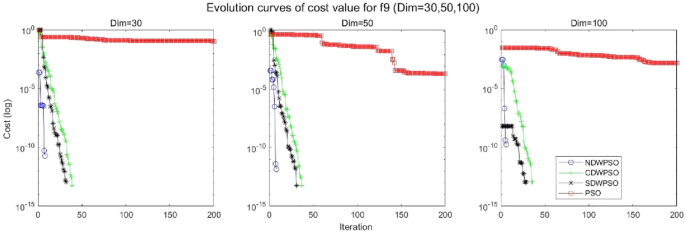
Evolution curve of NDWPSO and other PSO algorithms for f9 (Dim = 30,50,100).

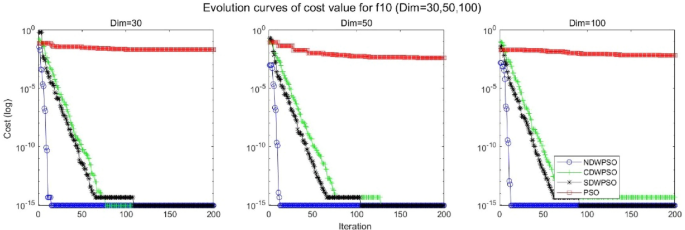
Evolution curve of NDWPSO and other PSO algorithms for f10 (Dim = 30,50,100).

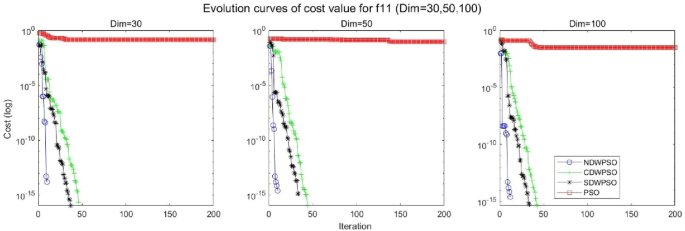
Evolution curve of NDWPSO and other PSO algorithms for f11(Dim = 30,50,100).

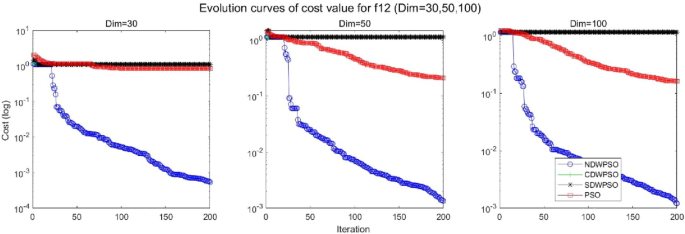
Evolution curve of NDWPSO and other PSO algorithms for f12 (Dim = 30,50,100).

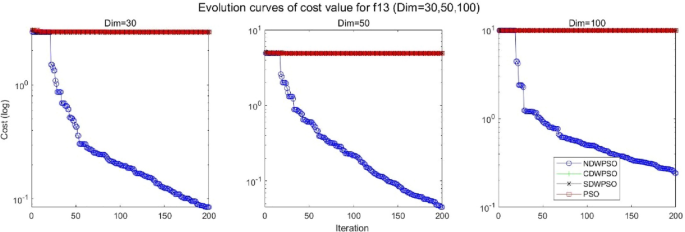
Evolution curve of NDWPSO and other PSO algorithms for f13 (Dim = 30,50,100).

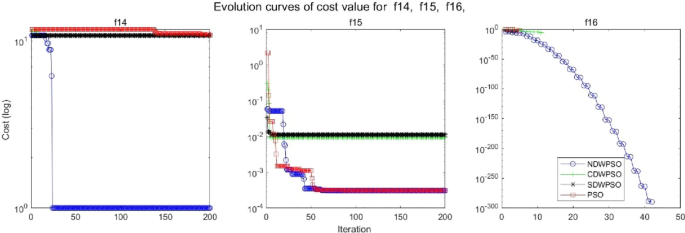
Evolution curve of NDWPSO and other PSO algorithms for f14, f15, f16.

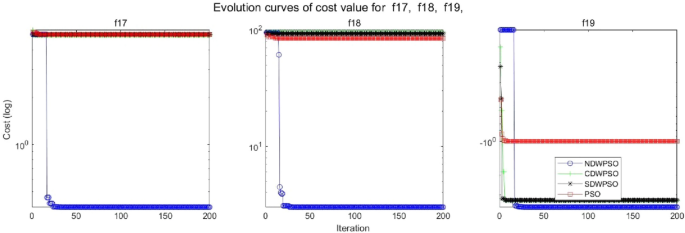
Evolution curve of NDWPSO and other PSO algorithms for f17, f18, f19.

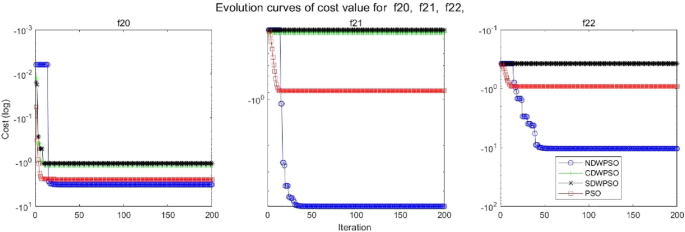
Evolution curve of NDWPSO and other PSO algorithms for f20, f21, f22.

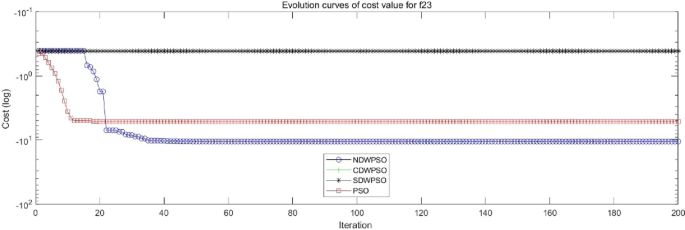
Evolution curve of NDWPSO and other PSO algorithms for f23.

To evaluate the performance of different PSO algorithms, a statistical test is conducted. Due to the stochastic nature of the meta-heuristics, it is not enough to compare algorithms based on only the mean and standard deviation values. The optimization results cannot be assumed to obey the normal distribution; thus, it is necessary to judge whether the results of the algorithms differ from each other in a statistically significant way. Here, the Wilcoxon non-parametric statistical test 45 is used to obtain a parameter called p -value to verify whether two sets of solutions are different to a statistically significant extent or not. Generally, it is considered that p  ≤ 0.5 can be considered as a statistically significant superiority of the results. The p -values calculated in Wilcoxon’s rank-sum test comparing NDWPSO and other PSO algorithms are listed in Table  3 for all benchmark functions. The p -values in Table  3 additionally present the superiority of the NDWPSO because all of the p -values are much smaller than 0.5.

In general, the NDWPSO has the fastest convergence rate when finding the global optimum from Figs. 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 and 19 , and thus we can conclude that the NDWPSO is superior to the other PSO variants during the process of optimization.

Comparison experiments between NDWPSO and other intelligent algorithms

Experiments are conducted to compare NDWPSO with several other intelligent algorithms (WOA, HHO, GWO, AOA, EO and DE). The experimental object is 23 benchmark functions, and the experimental parameters of the NDWPSO algorithm are set the same as in Experiment 4.1. The maximum number of iterations of the experiment is increased to 2000 to fully demonstrate the performance of each algorithm. Each algorithm is repeated 30 times individually. The parameters of the relevant intelligent algorithms in the experiments are set as shown in Table 4 . To ensure the fairness of the algorithm comparison, all parameters are concerning the original parameters in the relevant algorithm literature. The experimental results are shown in Tables 5 , 6 , 7 and 8 and Figs. 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 and 36 .

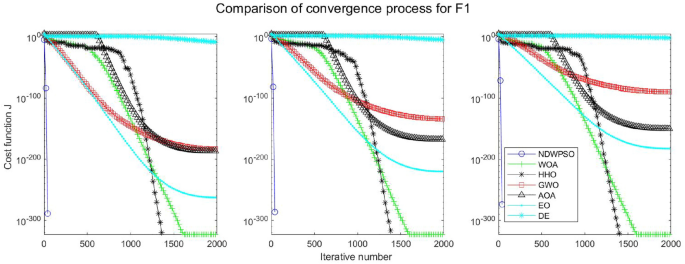
Evolution curve of NDWPSO and other algorithms for f1 (Dim = 30,50,100).

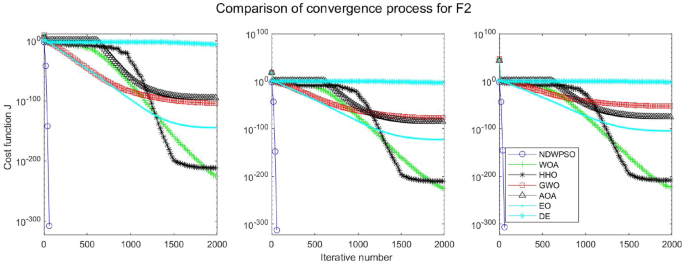
Evolution curve of NDWPSO and other algorithms for f2 (Dim = 30,50,100).

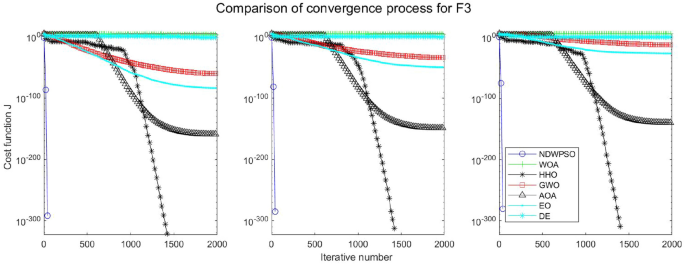
Evolution curve of NDWPSO and other algorithms for f3(Dim = 30,50,100).

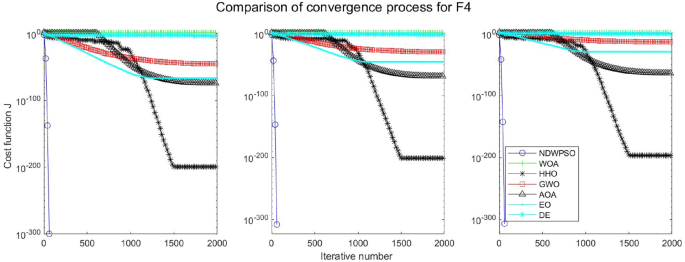
Evolution curve of NDWPSO and other algorithms for f4 (Dim = 30,50,100).

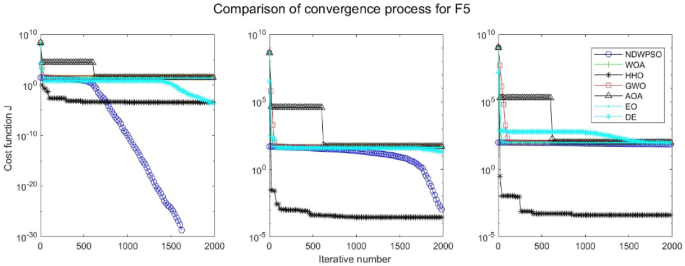
Evolution curve of NDWPSO and other algorithms for f5 (Dim = 30,50,100).

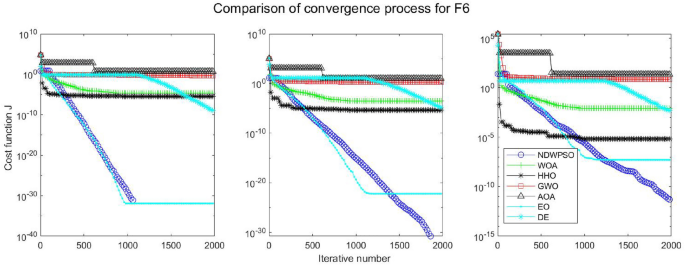
Evolution curve of NDWPSO and other algorithms for f6 (Dim = 30,50,100).

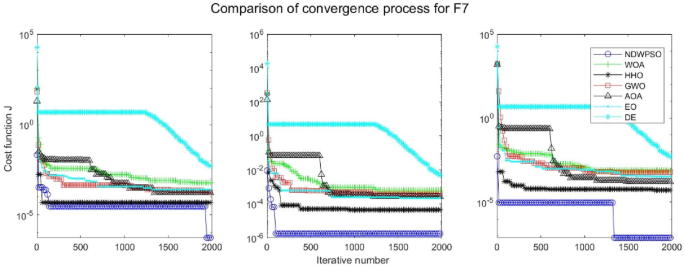
Evolution curve of NDWPSO and other algorithms for f7 (Dim = 30,50,100).

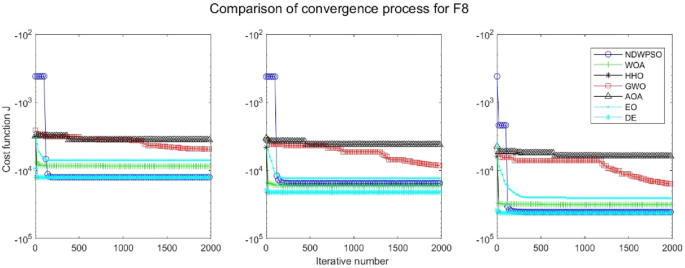
Evolution curve of NDWPSO and other algorithms for f8 (Dim = 30,50,100).

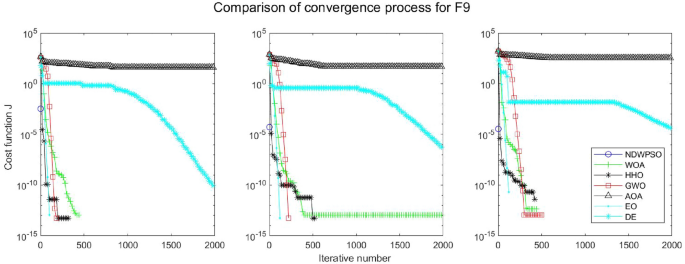
Evolution curve of NDWPSO and other algorithms for f9(Dim = 30,50,100).

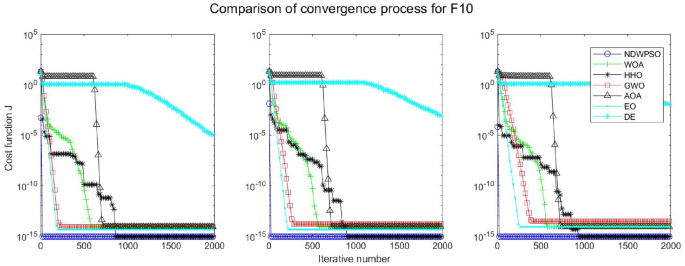
Evolution curve of NDWPSO and other algorithms for f10 (Dim = 30,50,100).

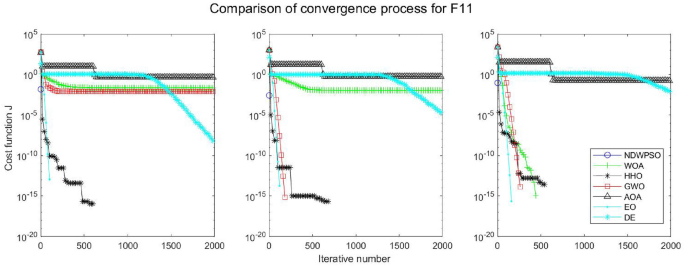
Evolution curve of NDWPSO and other algorithms for f11 (Dim = 30,50,100).

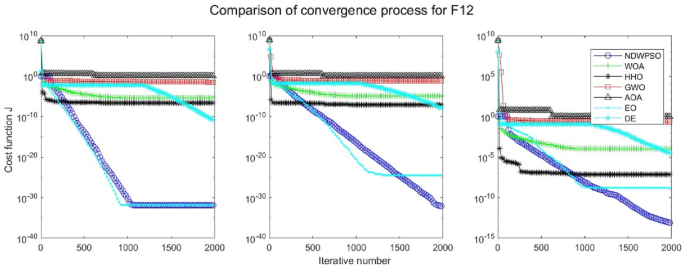
Evolution curve of NDWPSO and other algorithms for f12 (Dim = 30,50,100).

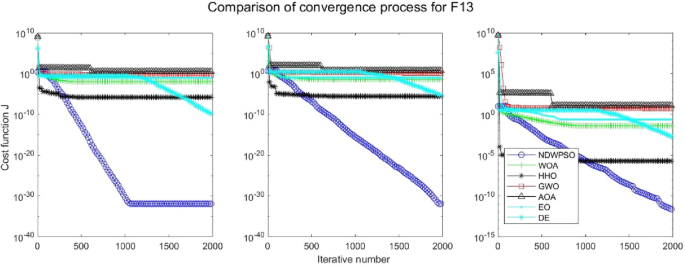
Evolution curve of NDWPSO and other algorithms for f13 (Dim = 30,50,100).

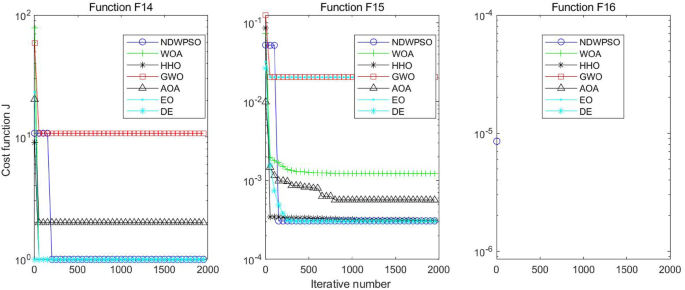
Evolution curve of NDWPSO and other algorithms for f14, f15, f16.

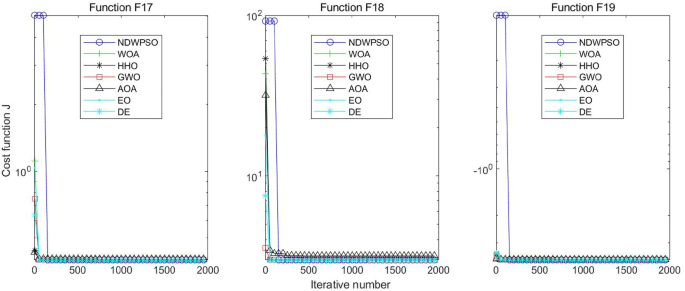
Evolution curve of NDWPSO and other algorithms for f17, f18, f19.

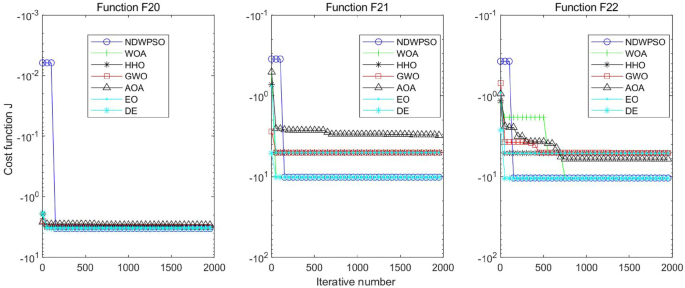
Evolution curve of NDWPSO and other algorithms for f20, f21, f22.

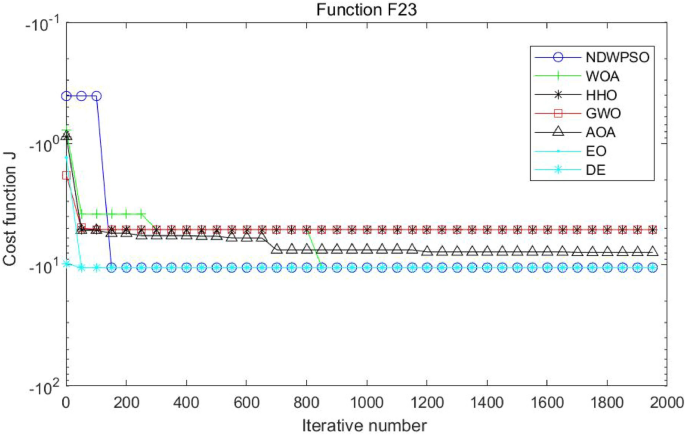
Evolution curve of NDWPSO and other algorithms for f23.

The experimental data of NDWPSO and other intelligent algorithms for handling 30, 50, and 100-dimensional benchmark functions ( \({f}_{1}-{f}_{13}\) ) are recorded in Tables 8 , 9 and 10 , respectively. The comparison data of fixed-multimodal benchmark tests ( \({f}_{14}-{f}_{23}\) ) are recorded in Table 11 . According to the data in Tables 5 , 6 and 7 , the NDWPSO algorithm obtains 69.2%, 84.6%, and 84.6% of the best results for the benchmark function ( \({f}_{1}-{f}_{13}\) ) in the search space of three dimensions (Dim = 30, 50, 100), respectively. In Table 8 , the NDWPSO algorithm obtains 80% of the optimal solutions in 10 fixed-multimodal benchmark functions.

The convergence curves of each algorithm are shown in Figs. 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 and 36 . The NDWPSO algorithm demonstrates two convergence behaviors when calculating the benchmark functions in 30, 50, and 100-dimensional search spaces. The first behavior is the fast convergence of NDWPSO with a small number of iterations at the beginning of the search. The reason is that the Iterative-mapping strategy and the position update scheme of dynamic weighting are used in the NDWPSO algorithm. This scheme can quickly target the region in the search space where the global optimum is located, and then precisely lock the optimal solution. When NDWPSO processes the functions \({f}_{1}-{f}_{4}\) , and \({f}_{9}-{f}_{11}\) , the behavior can be reflected in the convergence trend of their corresponding curves. The second behavior is that NDWPSO gradually improves the convergence accuracy and rapidly approaches the global optimal in the middle and late stages of the iteration. The NDWPSO algorithm fails to converge quickly in the early iterations, which is possible to prevent the swarm from falling into a local optimal. The behavior can be demonstrated by the convergence trend of the curves when NDWPSO handles the functions \({f}_{6}\) , \({f}_{12}\) , and \({f}_{13}\) , and it also shows that the NDWPSO algorithm has an excellent ability of local search.

Combining the experimental data with the convergence curves, it is concluded that the NDWPSO algorithm has a faster convergence speed, so the effectiveness and global convergence of the NDWPSO algorithm are more outstanding than other intelligent algorithms.

Experiments on classical engineering problems

Three constrained classical engineering design problems (welded beam design, pressure vessel design 43 , and three-bar truss design 38 ) are used to evaluate the NDWPSO algorithm. The experiments are the NDWPSO algorithm and 5 other intelligent algorithms (WOA 36 , HHO, GWO, AOA, EO 41 ). Each algorithm is provided with the maximum number of iterations and population size ( \({\text{Mk}}=500,\mathrm{ n}=40\) ), and then repeats 30 times, independently. The parameters of the algorithms are set the same as in Table 4 . The experimental results of three engineering design problems are recorded in Tables 9 , 10 and 11 in turn. The result data is the average value of the solved data.

Welded beam design

The target of the welded beam design problem is to find the optimal manufacturing cost for the welded beam with the constraints, as shown in Fig.  37 . The constraints are the thickness of the weld seam ( \({\text{h}}\) ), the length of the clamped bar ( \({\text{l}}\) ), the height of the bar ( \({\text{t}}\) ) and the thickness of the bar ( \({\text{b}}\) ). The mathematical formulation of the optimization problem is given as follows:

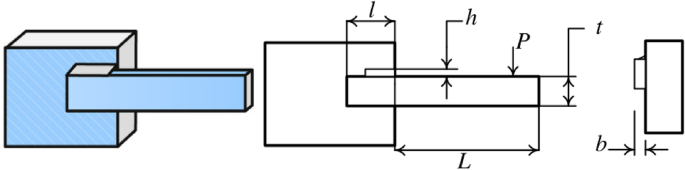
Welded beam design.

In Table 9 , the NDWPSO, GWO, and EO algorithms obtain the best optimal cost. Besides, the standard deviation (SD) of t NDWPSO is the lowest, which means it has very good results in solving the welded beam design problem.

Pressure vessel design

Kannan and Kramer 43 proposed the pressure vessel design problem as shown in Fig.  38 to minimize the total cost, including the cost of material, forming, and welding. There are four design optimized objects: the thickness of the shell \({T}_{s}\) ; the thickness of the head \({T}_{h}\) ; the inner radius \({\text{R}}\) ; the length of the cylindrical section without considering the head \({\text{L}}\) . The problem includes the objective function and constraints as follows:

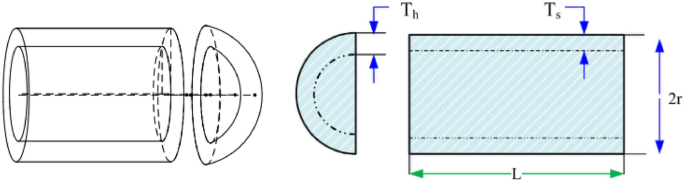
Pressure vessel design.

The results in Table 10 show that the NDWPSO algorithm obtains the lowest optimal cost with the same constraints and has the lowest standard deviation compared with other algorithms, which again proves the good performance of NDWPSO in terms of solution accuracy.

Three-bar truss design

This structural design problem 44 is one of the most widely-used case studies as shown in Fig.  39 . There are two main design parameters: the area of the bar1 and 3 ( \({A}_{1}={A}_{3}\) ) and area of bar 2 ( \({A}_{2}\) ). The objective is to minimize the weight of the truss. This problem is subject to several constraints as well: stress, deflection, and buckling constraints. The problem is formulated as follows:

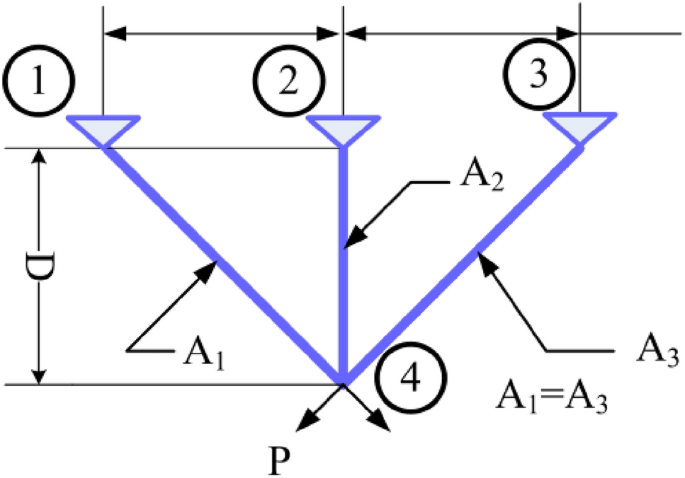
Three-bar truss design.

From Table 11 , NDWPSO obtains the best design solution in this engineering problem and has the smallest standard deviation of the result data. In summary, the NDWPSO can reveal very competitive results compared to other intelligent algorithms.

Conclusions and future works

An improved algorithm named NDWPSO is proposed to enhance the solving speed and improve the computational accuracy at the same time. The improved NDWPSO algorithm incorporates the search ideas of other intelligent algorithms (DE, WOA). Besides, we also proposed some new hybrid strategies to adjust the distribution of algorithm parameters (such as the inertia weight parameter, the acceleration coefficients, the initialization scheme, the position updating equation, and so on).

23 classical benchmark functions: indefinite unimodal (f1-f7), indefinite multimodal (f8-f13), and fixed-dimensional multimodal(f14-f23) are applied to evaluate the effective line and feasibility of the NDWPSO algorithm. Firstly, NDWPSO is compared with PSO, CDWPSO, and SDWPSO. The simulation results can prove the exploitative, exploratory, and local optima avoidance of NDWPSO. Secondly, the NDWPSO algorithm is compared with 5 other intelligent algorithms (WOA, HHO, GWO, AOA, EO). The NDWPSO algorithm also has better performance than other intelligent algorithms. Finally, 3 classical engineering problems are applied to prove that the NDWPSO algorithm shows superior results compared to other algorithms for the constrained engineering optimization problems.

Although the proposed NDWPSO is superior in many computation aspects, there are still some limitations and further improvements are needed. The NDWPSO performs a limit initialize on each particle by the strategy of “elite opposition-based learning”, it takes more computation time before speed update. Besides, the” local optimal jump-out” strategy also brings some random process. How to reduce the random process and how to improve the limit initialize efficiency are the issues that need to be further discussed. In addition, in future work, researchers will try to apply the NDWPSO algorithm to wider fields to solve more complex and diverse optimization problems.

Data availability

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.

Sami, F. Optimize electric automation control using artificial intelligence (AI). Optik 271 , 170085 (2022).

Article   ADS   Google Scholar  

Li, X. et al. Prediction of electricity consumption during epidemic period based on improved particle swarm optimization algorithm. Energy Rep. 8 , 437–446 (2022).

Article   Google Scholar  

Sun, B. Adaptive modified ant colony optimization algorithm for global temperature perception of the underground tunnel fire. Case Stud. Therm. Eng. 40 , 102500 (2022).

Bartsch, G. et al. Use of artificial intelligence and machine learning algorithms with gene expression profiling to predict recurrent nonmuscle invasive urothelial carcinoma of the bladder. J. Urol. 195 (2), 493–498 (2016).

Article   PubMed   Google Scholar  

Bao, Z. Secure clustering strategy based on improved particle swarm optimization algorithm in internet of things. Comput. Intell. Neurosci. 2022 , 1–9 (2022).

Google Scholar  

Kennedy, J. & Eberhart, R. Particle swarm optimization. In: Proceedings of ICNN'95-International Conference on Neural Networks . IEEE, 1942–1948 (1995).

Lin, Q. et al. A novel artificial bee colony algorithm with local and global information interaction. Appl. Soft Comput. 62 , 702–735 (2018).

Abed-alguni, B. H. et al. Exploratory cuckoo search for solving single-objective optimization problems. Soft Comput. 25 (15), 10167–10180 (2021).

Brajević, I. A shuffle-based artificial bee colony algorithm for solving integer programming and minimax problems. Mathematics 9 (11), 1211 (2021).

Khan, A. T. et al. Non-linear activated beetle antennae search: A novel technique for non-convex tax-aware portfolio optimization problem. Expert Syst. Appl. 197 , 116631 (2022).

Brajević, I. et al. Hybrid sine cosine algorithm for solving engineering optimization problems. Mathematics 10 (23), 4555 (2022).

Abed-Alguni, B. H., Paul, D. & Hammad, R. Improved Salp swarm algorithm for solving single-objective continuous optimization problems. Appl. Intell. 52 (15), 17217–17236 (2022).

Nadimi-Shahraki, M. H. et al. Binary starling murmuration optimizer algorithm to select effective features from medical data. Appl. Sci. 13 (1), 564 (2022).

Nadimi-Shahraki, M. H. et al. A systematic review of the whale optimization algorithm: Theoretical foundation, improvements, and hybridizations. Archiv. Comput. Methods Eng. 30 (7), 4113–4159 (2023).

Fatahi, A., Nadimi-Shahraki, M. H. & Zamani, H. An improved binary quantum-based avian navigation optimizer algorithm to select effective feature subset from medical data: A COVID-19 case study. J. Bionic Eng. 21 (1), 426–446 (2024).

Abed-alguni, B. H. & AL-Jarah, S. H. IBJA: An improved binary DJaya algorithm for feature selection. J. Comput. Sci. 75 , 102201 (2024).

Yeh, W.-C. A novel boundary swarm optimization method for reliability redundancy allocation problems. Reliab. Eng. Syst. Saf. 192 , 106060 (2019).

Solomon, S., Thulasiraman, P. & Thulasiram, R. Collaborative multi-swarm PSO for task matching using graphics processing units. In: Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation 1563–1570 (2011).

Mukhopadhyay, S. & Banerjee, S. Global optimization of an optical chaotic system by chaotic multi swarm particle swarm optimization. Expert Syst. Appl. 39 (1), 917–924 (2012).

Duan, L. et al. Improved particle swarm optimization algorithm for enhanced coupling of coaxial optical communication laser. Opt. Fiber Technol. 64 , 102559 (2021).

Sun, F., Xu, Z. & Zhang, D. Optimization design of wind turbine blade based on an improved particle swarm optimization algorithm combined with non-gaussian distribution. Adv. Civ. Eng. 2021 , 1–9 (2021).

Liu, M. et al. An improved particle-swarm-optimization algorithm for a prediction model of steel slab temperature. Appl. Sci. 12 (22), 11550 (2022).

Article   MathSciNet   CAS   Google Scholar  

Gad, A. G. Particle swarm optimization algorithm and its applications: A systematic review. Archiv. Comput. Methods Eng. 29 (5), 2531–2561 (2022).

Article   MathSciNet   Google Scholar  

Feng, H. et al. Trajectory control of electro-hydraulic position servo system using improved PSO-PID controller. Autom. Constr. 127 , 103722 (2021).

Chen, Ke., Zhou, F. & Liu, A. Chaotic dynamic weight particle swarm optimization for numerical function optimization. Knowl. Based Syst. 139 , 23–40 (2018).

Bai, B. et al. Reliability prediction-based improved dynamic weight particle swarm optimization and back propagation neural network in engineering systems. Expert Syst. Appl. 177 , 114952 (2021).

Alsaidy, S. A., Abbood, A. D. & Sahib, M. A. Heuristic initialization of PSO task scheduling algorithm in cloud computing. J. King Saud Univ. –Comput. Inf. Sci. 34 (6), 2370–2382 (2022).

Liu, H., Cai, Z. & Wang, Y. Hybridizing particle swarm optimization with differential evolution for constrained numerical and engineering optimization. Appl. Soft Comput. 10 (2), 629–640 (2010).

Deng, W. et al. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 23 , 2445–2462 (2019).

Huang, M. & Zhen, L. Research on mechanical fault prediction method based on multifeature fusion of vibration sensing data. Sensors 20 (1), 6 (2019).

Article   ADS   PubMed   PubMed Central   Google Scholar  

Wolpert, D. H. & Macready, W. G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1 (1), 67–82 (1997).

Gandomi, A. H. et al. Firefly algorithm with chaos. Commun. Nonlinear Sci. Numer. Simul. 18 (1), 89–98 (2013).

Article   ADS   MathSciNet   Google Scholar  

Zhou, Y., Wang, R. & Luo, Q. Elite opposition-based flower pollination algorithm. Neurocomputing 188 , 294–310 (2016).

Li, G., Niu, P. & Xiao, X. Development and investigation of efficient artificial bee colony algorithm for numerical function optimization. Appl. Soft Comput. 12 (1), 320–332 (2012).

Xiong, G. et al. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Solar Energy 176 , 742–761 (2018).

Mirjalili, S. & Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 95 , 51–67 (2016).

Yao, X., Liu, Y. & Lin, G. Evolutionary programming made faster. IEEE Trans. Evol. Comput. 3 (2), 82–102 (1999).

Heidari, A. A. et al. Harris hawks optimization: Algorithm and applications. Fut. Gener. Comput. Syst. 97 , 849–872 (2019).

Mirjalili, S., Mirjalili, S. M. & Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 69 , 46–61 (2014).

Hashim, F. A. et al. Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Appl. Intell. 51 , 1531–1551 (2021).

Faramarzi, A. et al. Equilibrium optimizer: A novel optimization algorithm. Knowl. -Based Syst. 191 , 105190 (2020).

Pant, M. et al. Differential evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 90 , 103479 (2020).

Coello, C. A. C. Use of a self-adaptive penalty approach for engineering optimization problems. Comput. Ind. 41 (2), 113–127 (2000).

Kannan, B. K. & Kramer, S. N. An augmented lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. J. Mech. Des. 116 , 405–411 (1994).

Derrac, J. et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 1 (1), 3–18 (2011).

Download references

Acknowledgements

This work was supported by Key R&D plan of Shandong Province, China (2021CXGC010207, 2023CXGC01020); First batch of talent research projects of Qilu University of Technology in 2023 (2023RCKY116); Introduction of urgently needed talent projects in Key Supported Regions of Shandong Province; Key Projects of Natural Science Foundation of Shandong Province (ZR2020ME116); the Innovation Ability Improvement Project for Technology-based Small- and Medium-sized Enterprises of Shandong Province (2022TSGC2051, 2023TSGC0024, 2023TSGC0931); National Key R&D Program of China (2019YFB1705002), LiaoNing Revitalization Talents Program (XLYC2002041) and Young Innovative Talents Introduction & Cultivation Program for Colleges and Universities of Shandong Province (Granted by Department of Education of Shandong Province, Sub-Title: Innovative Research Team of High Performance Integrated Device).

Author information

Authors and affiliations.

School of Mechanical and Automotive Engineering, Qilu University of Technology (Shandong Academy of Sciences), Jinan, 250353, China

Jinwei Qiao, Guangyuan Wang, Zhi Yang, Jun Chen & Pengbo Liu

Shandong Institute of Mechanical Design and Research, Jinan, 250353, China

School of Information Science and Engineering, Northeastern University, Shenyang, 110819, China

Xiaochuan Luo

Fushun Supervision Inspection Institute for Special Equipment, Fushun, 113000, China

You can also search for this author in PubMed   Google Scholar

Contributions

Z.Y., J.Q., and G.W. wrote the main manuscript text and prepared all figures and tables. J.C., P.L., K.L., and X.L. were responsible for the data curation and software. All authors reviewed the manuscript.

Corresponding author

Correspondence to Zhi Yang .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary information., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Qiao, J., Wang, G., Yang, Z. et al. A hybrid particle swarm optimization algorithm for solving engineering problem. Sci Rep 14 , 8357 (2024). https://doi.org/10.1038/s41598-024-59034-2

Download citation

Received : 11 January 2024

Accepted : 05 April 2024

Published : 10 April 2024

DOI : https://doi.org/10.1038/s41598-024-59034-2

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Particle swarm optimization
• Elite opposition-based learning
• Iterative mapping
• Convergence analysis

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.