solving quadratic inequalities in one variable assignment quizlet

Solving Quadratic Inequalities

... and more ...

A Quadratic Equation (in Standard Form) looks like:

The above is an equation (=) but sometimes we need to solve inequalities like these:

Solving inequalities is very like solving equations ... we do most of the same things.

So this is what we do:

• find the "=0" points
• greater than zero (>0), or
• less than zero (<0)
• then pick a test value to find out which it is (>0 or <0)

Here is an example:

Example: x 2 − x − 6 < 0

x 2 − x − 6 has these simple factors (what luck!):

(x+2)(x−3) < 0

Firstly , let us find where it is equal to zero:

(x+2)(x−3) = 0

It is equal to zero when x = −2 or x = +3 because when x = −2, then (x+2) is zero or when x = +3, then (x−3) is zero

So between −2 and +3, the function will either be

• always greater than zero, or
• always less than zero

We don't know which ... yet!

Let's pick a value in-between (say x=0) and test it:

So between x=−2 and x=+3, the function is less than zero.

And that is the region we want, so...

x 2 − x − 6 < 0 in the interval (−2, 3)

Note: x 2 − x − 6 > 0   in the interval (−∞,−2) and (3, +∞)

Also try the Inequality Grapher .

What If It Doesn't Go Through Zero?

A "real world" example, a stuntman will jump off a 20 m building. a high-speed camera is ready to film him between 15 m and 10 m above the ground..

When should the camera film him?

We can use this formula for distance and time:

d = 20 − 5t 2

• d = distance above ground (m), and
• t = time from jump (seconds)

(Note: if you are curious about the formula, it is simplified from d = d 0 + v 0 t + ½a 0 t 2 , where d 0 =20 , v 0 =0 , and a 0 =−9.81 the acceleration due to gravity.)

OK, let's go.

First , let us sketch the question:

The distance we want is from 10 m to 15 m :

10 < d < 15

And we know the formula for d :

10 < 20 − 5t 2 < 15

Now let's solve it!

First, let's subtract 20 from both sides:

−10 < −5t 2 <−5

 Now multiply both sides by −(1/5). But because we are multiplying by a negative number, the inequalities will change direction ... read Solving Inequalities to see why.

2 > t 2 > 1

To be neat, the smaller number should be on the left, and the larger on the right. So let's swap them over (and make sure the inequalities still point correctly):

1 < t 2 < 2

 Lastly, we can safely take square roots, since all values are greater then zero:

√1 < t < √2

We can tell the film crew:

"Film from 1.0 to 1.4 seconds after jumping"

Higher Than Quadratic

The same ideas can help us solve more complicated inequalities:

Example: x 3 + 4 ≥ 3x 2 + x

First, let's put it in standard form:

x 3 − 3x 2 − x + 4 ≥ 0

This is a cubic equation (the highest exponent is a cube, i.e. x 3 ), and is hard to solve, so let us graph it instead:

The zero points are approximately :

And from the graph we can see the intervals where it is greater than (or equal to) zero:

• From −1.1 to 1.3, and
• From 2.9 on

In interval notation we can write:

Approximately: [−1.1, 1.3] U [2.9, +∞)

• Study Guides
• Quiz: Solving Quadratic Inequalities
• Linear Equations
• Quiz: Linear Equations
• Quiz: Formulas
• Absolute Value Equations
• Quiz: Absolute Value Equations
• Linear Inequalities
• Quiz: Linear Inequalities
• Compound Inequalities
• Quiz: Compound Inequalities
• Absolute Value Inequalities
• Quiz: Absolute Value Inequalities
• Rectangular Coordinate System
• Quiz: Rectangular Coordinate System
• Distance Formula
• Quiz: Distance Formula
• Midpoint Formula
• Quiz: Midpoint Formula
• Slope of a Line
• Quiz: Slope of a Line
• Slopes of Parallel and Perpendicular Lines
• Quiz: Slopes of Parallel and Perpendicular Lines
• Equations of Lines
• Quiz: Equations of Lines
• Graphs of Linear Inequalities
• Quiz: Graphs of Linear Inequalities
• Linear Equations: Solutions Using Graphing with Two Variables
• Quiz: Linear Equations: Solutions Using Graphing with Two Variables
• Linear Equations: Solutions Using Substitution with Two Variables
• Quiz: Linear Equations: Solutions Using Substitution with Two Variables
• Linear Equations: Solutions Using Elimination with Two Variables
• Quiz: Linear Equations: Solutions Using Elimination with Two Variables
• Linear Equations: Solutions Using Matrices with Two Variables
• Quiz: Linear Equations: Solutions Using Matrices with Two Variables
• Linear Equations: Solutions Using Determinants with Two Variables
• Quiz: Linear Equations: Solutions Using Determinants with Two Variables
• Linear Inequalities: Solutions Using Graphing with Two Variables
• Quiz: Linear Inequalities: Solutions Using Graphing with Two Variables
• Quiz: Linear Equations: Solutions Using Elimination with Three Variables
• Linear Equations: Solutions Using Elimination with Three Variables
• Linear Equations: Solutions Using Matrices with Three Variables
• Quiz: Linear Equations: Solutions Using Matrices with Three Variables
• Linear Equations: Solutions Using Determinants with Three Variables
• Quiz: Linear Equations: Solutions Using Determinants with Three Variables
• Adding and Subtracting Polynomials
• Quiz: Adding and Subtracting Polynomials
• Multiplying Polynomials
• Quiz: Multiplying Polynomials
• Special Products of Binomials
• Quiz: Special Products of Binomials
• Dividing Polynomials
• Quiz: Dividing Polynomials
• Synthetic Division
• Quiz: Synthetic Division
• Greatest Common Factor
• Quiz: Greatest Common Factor
• Difference of Squares
• Quiz: Difference of Squares
• Sum or Difference of Cubes
• Quiz: Sum or Difference of Cubes
• Trinomials of the Form x^2 + bx + c
• Quiz: Trinomials of the Form x^2 + bx + c
• Trinomials of the Form ax^2 + bx + c
• Quiz: Trinomials of the Form ax^2 + bx + c
• Square Trinomials
• Quiz: Square Trinomials
• Factoring by Regrouping
• Quiz: Factoring by Regrouping
• Summary of Factoring Techniques
• Solving Equations by Factoring
• Quiz: Solving Equations by Factoring
• Examples of Rational Expressions
• Quiz: Examples of Rational Expressions
• Simplifying Rational Expressions
• Quiz: Simplifying Rational Expressions
• Multiplying Rational Expressions
• Quiz: Multiplying Rational Expressions
• Dividing Rational Expressions
• Quiz: Dividing Rational Expressions
• Adding and Subtracting Rational Expressions
• Quiz: Adding and Subtracting Rational Expressions
• Complex Fractions
• Quiz: Complex Fractions
• Solving Rational Equations
• Quiz: Solving Rational Equations
• Proportion, Direct Variation, Inverse Variation, Joint Variation
• Quiz: Proportion, Direct Variation, Inverse Variation, Joint Variation
• Graphing Rational Functions
• Quiz: Graphing Rational Functions
• Basic Definitions
• Quiz: Basic Definitions
• Function Notation
• Quiz: Function Notation
• Compositions of Functions
• Quiz: Compositions of Functions
• Algebra of Functions
• Quiz: Algebra of Functions
• Inverse Functions
• Quiz: Inverse Functions
• Polynomial Function
• Quiz: Polynomial Function
• Remainder Theorem
• Quiz: Remainder Theorem
• Factor Theorem
• Quiz: Factor Theorem
• Zeros of a Function
• Quiz: Zeros of a Function
• Rational Zero Theorem
• Quiz: Rational Zero Theorem
• Graphing Polynomial Functions
• Quiz: Graphing Polynomial Functions
• What Are Radicals?
• Quiz: Radicals
• Simplifying Radicals
• Quiz: Simplifying Radicals
• Adding and Subtracting Radical Expressions
• Quiz: Adding and Subtracting Radical Expressions
• Multiplying Radical Expressions
• Quiz: Multiplying Radical Expressions
• Dividing Radical Expressions
• Quiz: Dividing Radical Expressions
• Rational Exponents
• Quiz: Rational Exponents
• Complex Numbers
• Quiz: Complex Numbers
• Quadratic Equations
• Solving Quadratics by Factoring
• Quiz: Solving Quadratics by Factoring
• Solving Quadratics by the Square Root Property
• Quiz: Solving Quadratics by the Square Root Property
• Solving Quadratics by Completing the Square
• Quiz: Solving Quadratics by Completing the Square
• Solving Quadratics by the Quadratic Formula
• Quiz: Solving Quadratics by the Quadratic Formula
• Solving Equations in Quadratic Form
• Quiz: Solving Equations in Quadratic Form
• Solving Radical Equations
• Quiz: Solving Radical Equations
• Solving Quadratic Inequalities
• The Four Conic Sections
• Quiz: The Four Conic Sections
• Quiz: Circle
• Quiz: Parabola
• Quiz: Ellipse
• Quiz: Hyperbola
• Systems of Equations Solved Algebraically
• Quiz: Systems of Equations Solved Algebraically
• Systems of Equations Solved Graphically
• Quiz: Systems of Equations Solved Graphically
• Systems of Inequalities Solved Graphically
• Exponential Functions
• Quiz: Exponential Functions
• Logarithmic Functions
• Quiz: Logarithmic Functions
• Properties of Logarithms
• Quiz: Properties of Logarithms
• Exponential and Logarithmic Equations
• Quiz: Exponential and Logarithmic Equations
• Definition and Examples of Sequences
• Quiz: Definition and Examples of Sequences
• Arithmetic Sequence
• Quiz: Arithmetic Sequence
• Arithmetic Series
• Quiz: Arithmetic Series
• Geometric Sequence
• Quiz: Geometric Sequence
• Geometric Series
• Quiz: Geometric Series
• Summation Notation
• Quiz: Summation Notation
• Quiz: Factorials
• Binomial Coefficients and the Binomial Theorem
• Quiz: Binomial Coefficients and the Binomial Theorem
• Permutations
• Quiz: Permutations
• Combinations
• Quiz: Combinations
• General Strategy
• Simple Interest
• Quiz: Simple Interest
• Compound Interest
• Quiz: Compound Interest
• Quiz: Mixture
• Quiz: Motion
• Arithmetic/Geometric Series
• Quiz: Arithmetic/Geometric Series
• Algebra II Quiz

Previous Solving Quadratic Inequalities

Next The Four Conic Sections

• Online Quizzes for CliffsNotes Algebra II Quick Review, 2nd Edition

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.9: Solve Quadratic Inequalities

• Last updated
• Save as PDF
• Page ID 18867

Learning Objectives

By the end of this section, you will be able to:

• Solve quadratic inequalities graphically
• Solve quadratic inequalities algebraically

Before you get started, take this readiness quiz.

• Solve: \(2x−3=0\). If you missed this problem, review Example 2.2.
• Solve: \(2y^{2}+y=15\). If you missed this problem, review Example 6.45.
• Solve \(\frac{1}{x^{2}+2 x-8}>0\) If you missed this problem, review Example 7.56.

We have learned how to solve linear inequalities and rational inequalities previously. Some of the techniques we used to solve them were the same and some were different. We will now learn to solve inequalities that have a quadratic expression. We will use some of the techniques from solving linear and rational inequalities as well as quadratic equations. We will solve quadratic inequalities two ways—both graphically and algebraically.

Solve Quadratic Inequalities Graphically

A quadratic equation is in standard form when written as \(ax^{2}+bx+c=0\). If we replace the equal sign with an inequality sign, we have a quadratic inequality in standard form.

Definition \(\PageIndex{1}\): Quadratic Inequality

A quadratic inequality is an inequality that contains a quadratic expression. The standard form of a quadratic inequality is written:

\(\begin{array}{ll}{a x^{2}+b x+c<0} & {a x^{2}+b x+c \leq 0} \\ {a x^{2}+b x+c>0} & {a x^{2}+b x+c \geq 0}\end{array}\)

The graph of a quadratic function \(f(x)=a x^{2}+b x+c=0\) is a parabola. When we ask when is \(a x^{2}+b x+c<0\), we are asking when is \(f(x)<0\). We want to know when the parabola is below the \(x\)-axis.

When we ask when is \(a x^{2}+b x+c>0\), we are asking when is \(f(x)>0\). We want to know when the parabola is above the \(y\)-axis.

Example \(\PageIndex{1}\): How to Solve a Quadratic Inequality Graphically

Solve \(x^{2}−6x+8<0\) graphically. Write the solution in interval notation.

Step 1 : Write the quadratic inequality in standard form.

The inequality is in standard form.

\(x^{2}-6 x+8<0\)

Step 2 : Graph the function \(f(x)=a x^{2}+b x+c\) using properties or transformations.

We will graph using the properties.

\(f(x)=x^{2}-6 x+8\)

Look at \(a\) in the equation.

\(\color{red}{a=1, b=-6, c=8}\)

Since \(a\) is positive, the parabola opens upward.

The parabola opens upward.

The axis of symmetry is the line \(x=-\frac{b}{2 a}\).

Axis of Symmetry

\(x=-\frac{b}{2 a}\)

\(\begin{array}{l}{x=-\frac{(-6)}{2 \cdot 1}} \\ {x=3}\end{array}\)

The axis of symmetry is the line \(x=3\).

The vertex is on the axis of symmetry. Substitute \(x=3\) into the function.

\(\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8} \\ {f(3)=-1}\end{array}\)

The vertex is \((3,-1)\).

We find \(f(0)\)

\(y\)-intercept

\(\begin{array}{l}{f(x)=x^{2}-6 x+8} \\ {f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8} \\ {f(0)=8}\end{array}\)

The \(y\)-intercept is \((0,8)\).

We use the axis of symmetry to find a point symmetric to the \(y\)-intercept. The \(y\)-intercept is \(3\) units left of the axis of symmetry, \(x=3\). A point \(3\) units to the right of the axis of symmetry has \(x=6\).

Point symmetric to \(y\)-intercept

The point is \((6,8)\).

We solve \(f(x)=0\).

\(x\)-intercepts

We can solve this quadratic equation by factoring.

\(\begin{aligned} f(x) &=x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}x^{2}-6 x+8 \\ \color{red}{0} &\color{black}{=}(x-2)(x-4) \\ x &=2 \text { or } x=4 \end{aligned}\)

The \(x\)-intercepts are \((2,0)\) and \((4,0)\).

We graph the vertex, intercepts, and the point symmetric to the \(y\)-intercept. We connect these \(5\) points to sketch the parabola.

Step 3 : Determine the solution from the graph.

The inequality asks for the values of \(x\) which make the function less than \(0\). Which values of \(x\) make the parabola below the \(x\)-axis.

We do not include the values \(2\), \(4\) as the inequality is less than only.

The solution, in interval notation, is \((2,4)\).

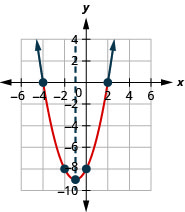
Exercise \(\PageIndex{1}\)

• Solve \(x^{2}+2 x-8<0\) graphically
• Write the solution in interval notation

Exercise \(\PageIndex{2}\)

• Solve \(x^{2}-8 x+12 \geq 0\) graphically

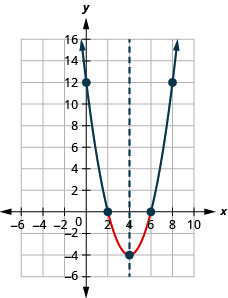
• \((-\infty, 2] \cup[6, \infty)\)

We list the steps to take to solve a quadratic inequality graphically.

Solve a Quadratic Inequality Graphically

• Write the quadratic inequality in standard form.
• Graph the function \(f(x)=ax^{2}+bx+c\).
• Determine the solution from the graph.

In the last example, the parabola opened upward and in the next example, it opens downward. In both cases, we are looking for the part of the parabola that is below the \(x\)-axis but note how the position of the parabola affects the solution.

Example \(\PageIndex{2}\)

Solve \(-x^{2}-8 x-12 \leq 0\) graphically. Write the solution in interval notation.

Exercise \(\PageIndex{3}\)

• Solve \(-x^{2}-6 x-5>0\) graphically

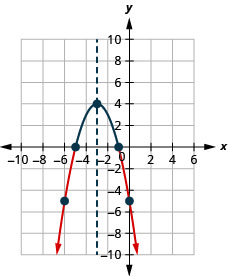
• \((-5,-1)\)

Exercise \(\PageIndex{4}\)

• Solve \(−x^{2}+10x−16≤0\) graphically

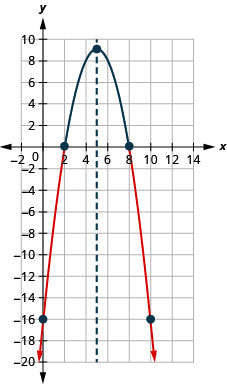
• \((-\infty, 2] \cup[8, \infty)\)

Solve Quadratic Inequalities Algebraically

The algebraic method we will use is very similar to the method we used to solve rational inequalities. We will find the critical points for the inequality, which will be the solutions to the related quadratic equation. Remember a polynomial expression can change signs only where the expression is zero.

We will use the critical points to divide the number line into intervals and then determine whether the quadratic expression will be positive or negative in the interval. We then determine the solution for the inequality.

Example \(\PageIndex{3}\): How to Solve Quadratic Inequalities Algebraically

Solve \(x^{2}-x-12 \geq 0\) algebraically. Write the solution in interval notation.

Exercise \(\PageIndex{5}\)

Solve \(x^{2}+2x−8≥0\) algebraically. Write the solution in interval notation.

\((-\infty,-4] \cup[2, \infty)\)

Exercise \(\PageIndex{6}\)

Solve \(x^{2}−2x−15≤0\) algebraically. Write the solution in interval notation.

In this example, since the expression \(x^{2}−x−12\) factors nicely, we can also find the sign in each interval much like we did when we solved rational inequalities. We find the sign of each of the factors, and then the sign of the product. Our number line would like this:

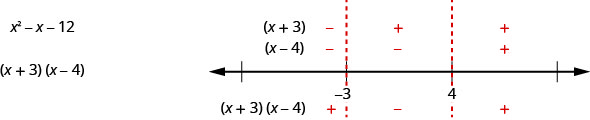
The result is the same as we found using the other method.

We summarize the steps here.

Solve a Quadratic Inequality Algebraically

• Determine the critical points—the solutions to the related quadratic equation.
• Use the critical points to divide the number line into intervals.
• Above the number line show the sign of each quadratic expression using test points from each interval substituted into the original inequality.
• Determine the intervals where the inequality is correct. Write the solution in interval notation.

Example \(\PageIndex{4}\)

Solve \(x^{2}+6x−7≥0\) algebraically. Write the solution in interval notation.

Exercise \(\PageIndex{7}\)

Solve \(−x^{2}+2x+1≥0\) algebraically. Write the solution in interval notation.

\([-1-\sqrt{2},-1+\sqrt{2}]\)

Exercise \(\PageIndex{8}\)

Solve \(−x^{2}+8x−14<0\) algebraically. Write the solution in interval notation.

\((-\infty, 4-\sqrt{2}) \cup(4+\sqrt{2}, \infty)\)

The solutions of the quadratic inequalities in each of the previous examples, were either an interval or the union of two intervals. This resulted from the fact that, in each case we found two solutions to the corresponding quadratic equation \(ax^{2}+bx+c=0\). These two solutions then gave us either the two \(x\) - intercepts for the graph or the two critical points to divide the number line into intervals.

This correlates to our previous discussion of the number and type of solutions to a quadratic equation using the discriminant.

For a quadratic equation of the form \(ax^{2}+bc+c=0, a≠0\).

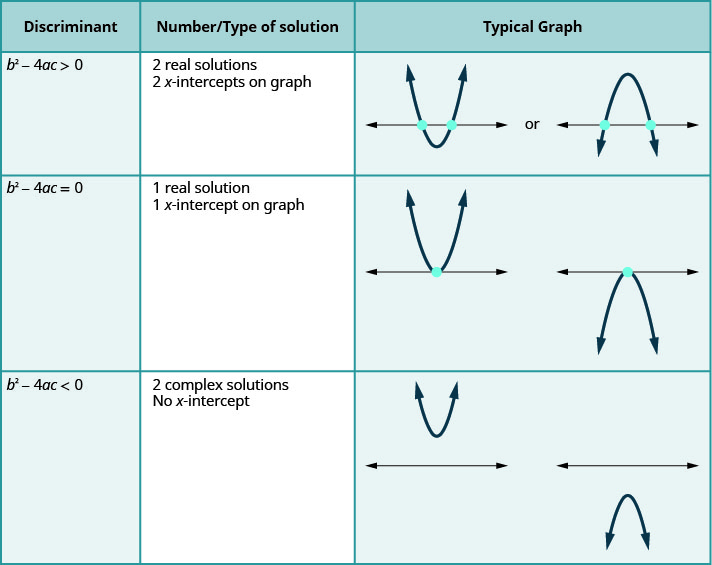
The last row of the table shows us when the parabolas never intersect the \(x\)-axis. Using the Quadratic Formula to solve the quadratic equation, the radicand is a negative. We get two complex solutions.

In the next example, the quadratic inequality solutions will result from the solution of the quadratic equation being complex.

Example \(\PageIndex{5}\)

Solve, writing any solution in interval notation:

• \(x^{2}-3 x+4>0\)

\(x^{2}-3 x+4 \leq 0\)

We are to find the solution to \(x^{2}−3x+4>0\). Since for all values of \(x\) the graph is above the \(x\)-axis, all values of \(x\) make the inequality true. In interval notation we write \((−∞,∞)\).

b. Write the quadratic inequality in standard form.

Determine the critical points by solving the related quadratic equation.

\(x^{2}-3 x+4=0\)

Since the corresponding quadratic equation is the same as in part (a), the parabola will be the same. The parabola opens upward and is completely above the \(x\)-axis—no part of it is below the \(x\)-axis.

We are to find the solution to \(x^{2}−3x+4≤0\). Since for all values of \(x\) the graph is never below the \(x\)-axis, no values of \(x\) make the inequality true. There is no solution to the inequality.

Exercise \(\PageIndex{9}\)

Solve and write any solution in interval notation:

• \(-x^{2}+2 x-4 \leq 0\)
• \(-x^{2}+2 x-4 \geq 0\)
• \((-\infty, \infty)\)
• no solution

Exercise \(\PageIndex{10}\)

• \(x^{2}+3 x+3<0\)
• \(x^{2}+3 x+3>0\)

Key Concepts

• Graph the function \(f(x)=ax^{2}+bx+c\) using properties or transformations.
• Determine the critical points -- the solutions to the related quadratic equation.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Quadratic Inequalities – Explanation & Examples

Solving Quadratic Inequalities – Explanation & Examples

A quadratic inequality is an equation of second degree that uses an inequality sign instead of an equal sign.

The solutions to quadratic inequality always give the two roots. The nature of the roots may differ and can be determined by discriminant (b 2 – 4ac).

The general forms of the quadratic inequalities are:

ax 2 + bx + c < 0

ax 2 + bx + c ≤ 0

ax 2 + bx + c > 0

ax 2 + bx + c ≥ 0

Examples of quadratic inequalities are:

x 2 – 6x – 16 ≤ 0, 2x 2  – 11x + 12 > 0, x 2  + 4 > 0, x 2  – 3x + 2 ≤ 0 etc.

How to Solve Quadratic Inequalities?

Examples of quadratic inequalities are: x 2 – 6x – 16 ≤ 0, 2x 2  – 11x + 12 > 0, x 2  + 4 > 0, x 2  – 3x + 2 ≤ 0 etc.

Solving a quadratic inequality in Algebra is similar to solving a quadratic equation. The only exception is that, with quadratic equations, you equate the expressions to zero, but with inequalities, you’re interested in knowing what’s on either side of the zero i.e. negatives and positives.

Quadratic equations can be solved by either the factorization method or by use of the quadratic formula . Before we can learn how to solve quadratic inequalities, let’s recall how quadratic equations are solved by handling a few examples.

How Quadratic Equations are Solved by Factorization Method?

Since we know we can similarly solve quadratic inequalities as quadratic equations, it is useful to understand how to factorize the given equation or inequality.

Let’s see a few examples here.

• 6x 2 – 7x + 2 = 0

⟹ 6x 2  – 4x – 3x + 2 = 0

Factorize the expression;

⟹ 2x (3x – 2) – 1(3x – 2) = 0

⟹ (3x – 2) (2x – 1) = 0

⟹ 3x – 2 = 0 or 2x – 1 = 0

⟹ 3x = 2 or 2x = 1

⟹ x = 2/3 or x = 1/2

Therefore, x = 2/3, ½

• Solve 3x 2 – 6x + 4x – 8 = 0

Factorize the expression on the left-hand side.

⟹ 3x 2  – 6x + 4x – 8 = 0

⟹ 3x (x – 2) + 4(x – 2) = 0

⟹ (x – 2) (3x + 4) = 0

⟹ x – 2 = 0 or 3x + 4 = 0

⟹ x = 2 or x = -4/3

Therefore, the roots of the quadratic equation are, x = 2, -4/3.

• Solve 2(x 2 + 1) = 5x

2x 2 + 2 = 5x

⟹ 2x 2  – 5x + 2 = 0

⟹ 2x 2  – 4x – x + 2 = 0

⟹ 2x (x – 2) – 1(x – 2) = 0

⟹ (x – 2) (2x – 1) = 0

⟹ x – 2 = 0 or 2x – 1 = 0

⟹ x = 2 or x = 1/2

Therefore, the solutions are x = 2, 1/2.

• (2x – 3) 2 = 25

Expand and factorize the expression.

(2x – 3) 2  = 25

⟹ 4x 2  – 12x + 9 – 25 = 0

⟹ 4x 2  – 12x – 16 = 0

⟹ x 2  – 3x – 4 = 0

⟹ (x – 4) (x + 1) = 0

⟹ x = 4 or x = -1

• Solve x 2 + (4 – 3y) x – 12y = 0

Expand the equation;

x 2  + 4x – 3xy – 12y = 0

⟹ x (x + 4) – 3y (x + 4) = 0

x + 4) (x – 3y) = 0

⟹ x + 4 = 0 or x – 3y = 0

⟹ x = -4 or x = 3y

Thus, x = -4 or x = 3y

To solve a quadratic inequality, we also apply the same method as illustrated in the procedure below:

• Write the quadratic inequality in standard form: ax 2  + bx + c where a, b and are coefficients and a ≠ 0
• Determine the roots of the inequality.
• Write the solution in inequality notation or interval notation.

Solve the inequality x 2  – 4x > –3

First, make one side one side of the inequality zero by adding both sides by 3.

x 2  – 4x > –3 ⟹ x 2  – 4x + 3 > 0

Factor the left side of the inequality.

x 2  – 4x + 3 > 0 ⟹ (x – 3) (x – 1) > 0

Solve for all the zeroes for the inequality;

For, (x – 1) > 0 ⟹ x > 1 and for, (x – 3) > 0 ⟹ x>3

Since y is positive, we therefore choose the values of x which the curve will be above the x-axis. x < 1 or x > 3

Solve the inequality x 2  – x > 12.

To write the inequality in standard form, subtract both sides of the inequality by 12.

x 2  – x > 12 ⟹ x 2  – x – 12 > 0.

Factorize the quadratic inequality to get to;

( x  – 4) ( x  + 3) > 0

For, (x + 3) > 0 ⟹ x > -3

For x – 4 > 0 ⟹ x > 4

The values x < –3 or x > 4 are therefore the solution of this quadratic inequality.

Solve 2x 2  < 9x + 5

Write the inequality in standard form by making one side of the inequality zero.

2x 2  < 9x + 5 ⟹ 2x 2  – 9x – 5 < 0

Factor the left side of the quadratic inequality.

2x 2  – 9x – 5 < 0 ⟹ (2x + 1) (x – 5) < 0

Solve for all the zeroes for the inequality

For, (x – 5) < 0 ⟹ x < 5 and for (2x + 1) < 0 ⟹ x < -1/2

Since y is negative for the equation 2x 2  – 9x – 5 < 0, we therefore choose the values of x which the curve will be below the x axis.

Therefore, the solution is   -1/2 < x < 5

Solve – x 2 + 4 < 0.

Since the inequality is already in standard form, we therefore factor the expression.

-x 2 + 4 < 0 ⟹ (x + 2) (x – 2) < 0

For, (x + 2) < 0 ⟹ x < -2 and for, (x – 2) < 0 ⟹ x < 2

The y for –x 2 + 4 < 0 is negative; therefore, we choose the values of x in which the curve will below the x- axis: –2 < x > 2

Solve 2x 2  + x − 15 ≤ 0.

Factor the quadratic equation.

2x 2  + x − 15 = 0

2x 2  + 6x – 5x− 15 = 0

2x (x + 3) – 5(x + 3) = 0

(2x – 5) (x + 3) = 0

For, 2x – 5 = 0 ⟹ x= 5/2 and for, x + 3= 0 ⟹ x = -3

Since the y for 2x 2  + x − 15 ≤ 0 is negative, the we choose the values of x in which the curve will be below the x axis. Therefore, x ≤ -3 or x ≥5/2 is the solution.

Solve – x 2  + 3x − 2 ≥ 0

Multiply the quadratic equation by -1 and remember to change the sign.

x 2  – 3x + 2 = 0

x 2  – 1x – 2x + 2 = 0

x (x – 1) – 2(x – 1) = 0

(x – 2) (x – 1) = 0

For, x – 2 = 0 ⟹ x = 2 and for, x – 1= 0 ⟹x=1

Therefore, the solution to the quadratic inequality is 1 ≤ x ≤ 2

Solve x 2 − 3x + 2 > 0

Factorize the expression to get;

x 2 − 3x + 2 > 0 ⟹ (x − 2) (x − 1) > 0

Now solve for the roots of the inequality as;

(x − 2) > 0 ⟹ x > 2

(x − 1) > 0 ⟹x > 1

The curve for x 2 − 3x + 2 > 0 has positive y, therefore which choose the values of x in which the curve will be above the x-axis. The solution is hence, x < 1 or x > 2.

Solve −2x 2 + 5x + 12 ≥ 0

Multiply the entire expression by -1 and change the inequality sign

−2x 2 + 5x + 12 ≥ 0 ⟹2x 2 − 5x − 12 ≤ 0

(2x + 3) (x − 4) ≤ 0.

Solve the roots;

(2x + 3) ≤ 0 ⟹ x ≤ -3/2.

(x − 4) ≤ 0 ⟹ x ≤ 4.

By applying the rule; (x – a) (x – b) ≥ 0, then a ≤ x ≤ b, we can comfortably write the solutions of this quadratic inequality as:

-3/2 ≤ x ≤ 4.

x 2  − x − 6 < 0

Factorize x 2  − x − 6 to get;

(x + 2) (x − 3) < 0

Find the roots of the equation as;

(x + 2) (x − 3) = 0

x = −2 or x = +3 Because y is negative for x 2  − x − 6 < 0, then we choose an interval in which the curve will be below the x axis. Therefore, -2 < x < 3 is the solution.

Practice Questions

Previous lesson  |  main page | next lesson.