stokes hypothesis wikipedia

Physical Review E

Covering statistical, nonlinear, biological, and soft matter physics.

• Collections
• Editorial Team

Discussion of Stokes' hypothesis through the smoothed particle hydrodynamics model

Andrea colagrossi, danilo durante, josep bonet avalos, and antonio souto-iglesias, phys. rev. e 96 , 023101 – published 8 august 2017.

• Citing Articles (15)
• INTRODUCTION
• MODELING FLUIDS AS MACROSCOPIC SYSTEMS…
• DISCRETIZATION OF THE NEWTONIAN VISCOUS…
• CONCLUSIONS
• ACKNOWLEDGMENTS

Stokes' hypothesis, the zeroing of the bulk viscosity in a Newtonian fluid, is discussed in this paper. To this aim, a continuum macroscopic fluid domain is initially modeled as a Hamiltonian system of discrete particles, for which the interparticle dissipative forces are required to be radial in order to conserve the angular momentum. The resulting system of particles is then reconverted to the continuum domain via the framework of the smoothed particle hydrodynamics (SPH) model. Since an SPH-consistent approximation of the Newtonian viscous term in the momentum equation incorporates interparticle radial as well as nonradial terms, it is postulated that the latter must be null. In the present work it is shown that this constraint implies that first and second viscosities are equal, resulting in a positive value for the bulk viscosity, in contradiction to the cited Stokes' hypothesis. Moreover, it is found that this postulate leads to bulk viscosity coefficients close to values found in the experimental literature for monoatomic gases and common liquids such as water.

• Received 3 January 2017

DOI: https://doi.org/10.1103/PhysRevE.96.023101

©2017 American Physical Society

Physics Subject Headings (PhySH)

• Research Areas

Authors & Affiliations

• CNR-INSEAN, Marine Technology Research Institute, Rome, Italy and Ecole Centrale Nantes, LHEEA Laboratory, Nantes, France
• CNR-INSEAN, Marine Technology Research Institute, Rome, Italy
• Department d'Enginyeria Química, ETSEQ, Universitat Rovira i Virgili, Tarragona, Spain
• CEHINAV, DMFPA, ETSIN, Universidad Politécnica de Madrid, Madrid, Spain
• * [email protected]

Article Text (Subscription Required)

References (subscription required).

Vol. 96, Iss. 2 — August 2017

Access Options

• Buy Article »
• Log in with individual APS Journal Account »
• Log in with a username/password provided by your institution »
• Get access through a U.S. public or high school library »

Authorization Required

Other options.

• Buy Article »
• Find an Institution with the Article »

Download & Share

Sign up to receive regular email alerts from Physical Review E

• Forgot your username/password?
• Create an account

Article Lookup

Paste a citation or doi, enter a citation.

A note on Stokes’ hypothesis

• Published: 09 June 2015
• Volume 226 , pages 3555–3559, ( 2015 )

Cite this article

• Guido Buresti 1  

1115 Accesses

27 Citations

Explore all metrics

The so-called Stokes’ hypothesis for a Newtonian fluid is reconsidered, and a possible explanation is given of the fact that, in spite of its evidently weak physical justification, it permits to obtain good results for the description of most compressible flows. The explanation stands upon a closer analysis of the effect of the terms of the complete stress tensor in which the viscosity coefficients appear. An alternative formulation of the hypothesis is proposed, which also permits to clearly identify the very particular flow conditions in which it cannot justify the experimental evidence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Serrin J.: Mathematical principles of classical fluid mechanics. In: Flügge, S. (ed.) Handbuch der Physik, VIII/1, pp. 125–263. Springer, Berlin (1959)

Stokes G.G.: On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids. Trans. Camb. Philos. Soc. 8 , 287–319 (1845)

Google Scholar  

Rosenhead L.: A discussion on the first and second viscosities of fluids. Proc. R. Soc. Lond. A Mat. 226 , 1–69 (1954)

Article   MathSciNet   Google Scholar  

Gad-el-Hak M.: Questions in fluid mechanics: Stokes’ hypothesis for a Newtonian, isotropic fluid. J. Fluid Eng. T. ASME 117 , 3–5 (1995)

Article   Google Scholar  

Markham J.J., Beyer R.T., Lindsay R.B.: Absorption of sound in fluids. Rev. Mod. Phys. 23 , 353–411 (1951)

Article   MathSciNet   MATH   Google Scholar  

Truesdell C.: On the viscosity of fluids according to the kinetic theory. Zeitschrift für Physik 131 , 273–289 (1952)

Rajagopal K.R.: A new development and interpretation of the Navier–Stokes fluid which reveals why the “Stokes assumption” is inapt. Int. J. Nonlinear Mech. 50 , 141–151 (2013)

Dukhin A.S., Goetz P.J.: Bulk viscosity and compressibility measurement using acoustic spectroscopy. J. Chem. Phys. 130 , 124519 (2009)

Buresti G.: Elements of Fluid Dynamics. Imperial College Press, London (2012)

MATH   Google Scholar  

Emanuel G.: Effect of bulk viscosity on a hypersonic boundary layer. Phys. Fluids A-Fluid 4 , 491–495 (1992)

Article   MATH   Google Scholar  

Emanuel G., Argrow B.M.: Linear dependence of the bulk viscosity on shock wave thickness. Phys. Fluids 6 , 3203–3205 (1994)

Tritton D.J.: Physical Fluid Dynamics. Clarendon Press, Oxford (1988)

Zonta F., Onorato M., Soldati A.: Turbulence and internal waves in stably-stratified channel flow with temperature-dependent fluid properties. J. Fluid Mech. 697 , 175–203 (2012)

Download references

Author information

Authors and affiliations.

Dipartimento di Ingegneria Civile e Industriale, University of Pisa, Pisa, Italy

Guido Buresti

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Guido Buresti .

Rights and permissions

Reprints and permissions

About this article

Buresti, G. A note on Stokes’ hypothesis. Acta Mech 226 , 3555–3559 (2015). https://doi.org/10.1007/s00707-015-1380-9

Download citation

Received : 14 January 2015

Revised : 23 April 2015

Published : 09 June 2015

Issue Date : October 2015

DOI : https://doi.org/10.1007/s00707-015-1380-9

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Stress Tensor
• Bulk Viscosity
• Viscous Stress
• Isotropic Part
• Deviatoric Part
• Find a journal
• Publish with us
• Track your research

Help | Advanced Search

Physics > Fluid Dynamics

Title: a brief introduction to bulk viscosity of fluids.

Abstract: Fluid flows are typically studied by solving the Navier--Stokes equation. One of the fundamental assumptions of this equation is Stokes' hypothesis. This hypothesis assumes bulk viscosity, to be identically zero. The Stokes' hypothesis is a reasonable approximation for commonly observed fluid flows; therefore, Navier--Stokes equation gives satisfactory results in these situations. However, there are circumstances where this hypothesis does not hold good, and therefore, the classical Navier--Stokes equation becomes inapt. These situations include the absorption of sound waves, hypersonic flows, turbulent flows, and flow of Martian air etc. Reliable analytical and computational studies of these flows requires account of bulk viscosity in the governing equations. In this article, we provide a brief review of the subject of bulk viscosity. We start with a brief background of this topic. Then we discuss the underlying microscopic mechanisms that give rise to bulk viscosity effects. It was followed by a review of methods available in the literature for estimation of this parameter. Finally, a review of the studies that analyze the effects of bulk viscosity in various fluid flows is provided.

Submission history

Access paper:.

• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

16.7: Stokes’ Theorem

• Last updated
• Save as PDF
• Page ID 2623

• Gilbert Strang & Edwin “Jed” Herman

Learning Objectives

• Explain the meaning of Stokes’ theorem.
• Use Stokes’ theorem to evaluate a line integral.
• Use Stokes’ theorem to calculate a surface integral.
• Use Stokes’ theorem to calculate a curl.

In this section, we study Stokes’ theorem, a higher-dimensional generalization of Green’s theorem. This theorem, like the Fundamental Theorem for Line Integrals and Green’s theorem, is a generalization of the Fundamental Theorem of Calculus to higher dimensions. Stokes’ theorem relates a vector surface integral over surface \(S\) in space to a line integral around the boundary of \(S\). Therefore, just as the theorems before it, Stokes’ theorem can be used to reduce an integral over a geometric object \(S\) to an integral over the boundary of \(S\). In addition to allowing us to translate between line integrals and surface integrals, Stokes’ theorem connects the concepts of curl and circulation. Furthermore, the theorem has applications in fluid mechanics and electromagnetism. We use Stokes’ theorem to derive Faraday’s law , an important result involving electric fields.

Stokes’ Theorem

Stokes’ theorem says we can calculate the flux of \( curl \,\vecs{F}\) across surface \(S\) by knowing information only about the values of \(\vecs{F}\) along the boundary of \(S\). Conversely, we can calculate the line integral of vector field \(\vecs{F}\) along the boundary of surface \(S\) by translating to a double integral of the curl of \(\vecs{F}\) over \(S\).

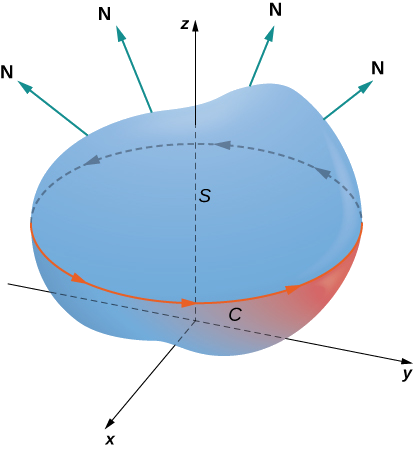
Let \(S\) be an oriented smooth surface with unit normal vector \(\vecs{N}\). Furthermore, suppose the boundary of \(S\) is a simple closed curve \(C\). The orientation of \(S\) induces the positive orientation of \(C\) if, as you walk in the positive direction around \(C\) with your head pointing in the direction of \(\vecs{N}\), the surface is always on your left. With this definition in place, we can state Stokes’ theorem .

Theorem \(\PageIndex{1}\): Stokes’ Theorem

Let \(S\) be a piecewise smooth oriented surface with a boundary that is a simple closed curve \(C\) with positive orientation (Figure \(\PageIndex{1}\)). If \(\vecs{F}\) is a vector field with component functions that have continuous partial derivatives on an open region containing \(S\), then

\[\int_C \vecs{F} \cdot d \vecs{r} = \iint_S curl \, \vecs{F} \cdot d\vecs S. \label{Stokes1} \]

Suppose surface \(S\) is a flat region in the \(xy\)-plane with upward orientation. Then the unit normal vector is \(\vecs{k}\) and surface integral

\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]

is actually the double integral

\[\iint_S curl \, \vecs{F} \cdot \vecs{k} \, dA. \nonumber \]

In this special case, Stokes’ theorem gives

\[\int_C \vecs{F} \cdot d\vecs{r} = \iint_S curl \, \vecs{F} \cdot \vecs{k} \, dA. \nonumber \]

However, this is the flux form of Green’s theorem, which shows us that Green’s theorem is a special case of Stokes’ theorem. Green’s theorem can only handle surfaces in a plane, but Stokes’ theorem can handle surfaces in a plane or in space.

The complete proof of Stokes’ theorem is beyond the scope of this text. We look at an intuitive explanation for the truth of the theorem and then see proof of the theorem in the special case that surface \(S\) is a portion of a graph of a function, and \(S\), the boundary of \(S\), and \(\vecs{F}\) are all fairly tame.

First, we look at an informal proof of the theorem. This proof is not rigorous, but it is meant to give a general feeling for why the theorem is true. Let \(S\) be a surface and let \(D\) be a small piece of the surface so that \(D\) does not share any points with the boundary of \(S\). We choose \(D\) to be small enough so that it can be approximated by an oriented square \(E\). Let \(D\) inherit its orientation from \(S\), and give \(E\) the same orientation. This square has four sides; denote them \(E_l, \, E_r, \, E_u\), and \(E_d\) for the left, right, up, and down sides, respectively. On the square, we can use the flux form of Green’s theorem:

\[\int_{E_l+E_d+E_r+E_u} \vecs{F} \cdot d \vecs{r} = \iint_E curl \, \vecs{F} \cdot \vecs{N} \, d \vecs{S} = \iint_E curl \, \vecs{F} \cdot d\vecs{S}. \nonumber \]

To approximate the flux over the entire surface, we add the values of the flux on the small squares approximating small pieces of the surface (Figure \(\PageIndex{2}\)).

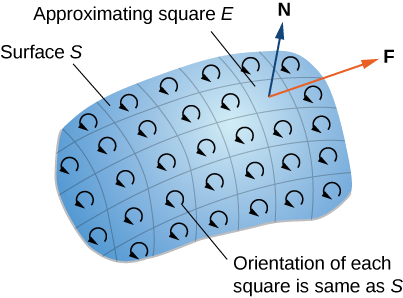
By Green’s theorem, the flux across each approximating square is a line integral over its boundary. Let \(F\) be an approximating square with an orientation inherited from \(S\) and with a right side \(E_l\) (so \(F\) is to the left of \(E\)). Let \(F_r\) denote the right side of \(F\); then, \(E_l = - F_r\). In other words, the right side of \(F\) is the same curve as the left side of \(E\), just oriented in the opposite direction. Therefore,

\[\int_{E_l} \vecs F \cdot d\vecs r = - \int_{F_r} \vecs F \cdot d\vecs r. \nonumber \]

As we add up all the fluxes over all the squares approximating surface \(S\), line integrals

\[\int_{E_l} \vecs{F} \cdot d \vecs{r} \nonumber \]

\[ \int_{F_r} \vecs{F} \cdot d\vecs{r} \nonumber \]

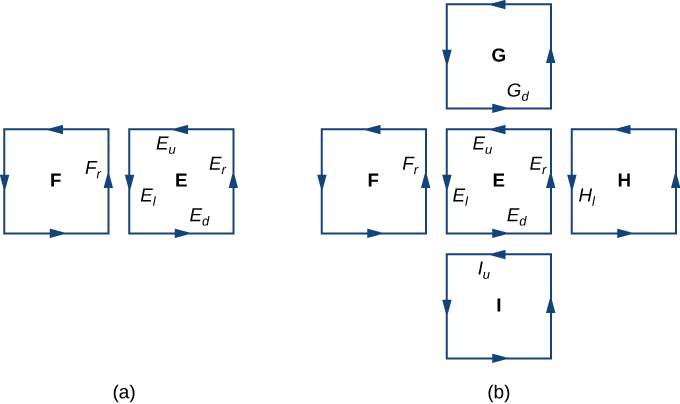
cancel each other out. The same goes for the line integrals over the other three sides of \(E\). These three line integrals cancel out with the line integral of the lower side of the square above \(E\), the line integral over the left side of the square to the right of \(E\), and the line integral over the upper side of the square below \(E\) (Figure \(\PageIndex{3}\)). After all this cancelation occurs over all the approximating squares, the only line integrals that survive are the line integrals over sides approximating the boundary of \(S\). Therefore, the sum of all the fluxes (which, by Green’s theorem, is the sum of all the line integrals around the boundaries of approximating squares) can be approximated by a line integral over the boundary of \(S\). In the limit, as the areas of the approximating squares go to zero, this approximation gets arbitrarily close to the flux.

Let’s now look at a rigorous proof of the theorem in the special case that \(S\) is the graph of function \(z = f(x,y)\), where \(x\) and \(y\) vary over a bounded, simply connected region \(D\) of finite area (Figure \(\PageIndex{4}\)). Furthermore, assume that \(f\) has continuous second-order partial derivatives. Let \(C\) denote the boundary of \(S\) and let \(C'\) denote the boundary of \(D\). Then, \(D\) is the “shadow” of \(S\) in the plane and \(C'\) is the “shadow” of \(C\). Suppose that \(S\) is oriented upward. The counterclockwise orientation of \(C\) is positive, as is the counterclockwise orientation of \(C'\). Let \(\vecs F(x,y,z) = \langle P,Q,R \rangle\) be a vector field with component functions that have continuous partial derivatives.

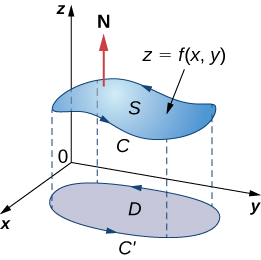
We take the standard parameterization of \(S \, : \, x = x, \, y = y, \, z = g(x,y)\). The tangent vectors are \(\vecs t_x = \langle 1,0,g_x \rangle\) and \(\vecs t_y = \langle 0,1,g_y \rangle\), and therefore \(\vecs t_x \times \vecs t_y = \langle -g_x, \, -g_y, \, 1 \rangle\).

\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} = \iint_D [- (R_y - Q_z)z_x - (P_z - R_x)z_y + (Q_x - P_y)] \, dA, \nonumber \]

where the partial derivatives are all evaluated at \((x,y,g(x,y))\), making the integrand depend on \(x\) and \(y\) only. Suppose \(\langle x (t), \, y(t) \rangle, \, a \leq t \leq b\) is a parameterization of \(C'\). Then, a parameterization of \(C\) is \(\langle x (t), \, y(t), \, g(x(t), \, y(t))\rangle, \, a \leq t \leq b\). Armed with these parameterizations, the Chain rule, and Green’s theorem, and keeping in mind that \(P\), \(Q\) and \(R\) are all functions of \(x\) and \(y\), we can evaluate line integral

\[ \begin{align*} \int_C \vecs{F} \cdot d \vecs{r} &= \int_a^b (Px'(t) + Qy'(t) + Rz'(t)) \, dt \\[4pt] &= \int_a^b \left[Px'(t) + Qy'(t) + R\left(\dfrac{\partial z}{\partial x} \dfrac{dx}{dt} + \dfrac{\partial z}{\partial y} \dfrac{dy}{dt}\right) \right] dt \\[4pt] &= \int_a^b \left[ \left(P + R \dfrac{\partial z}{\partial x} \right) x' (t) + \left(Q + R \dfrac{\partial z}{\partial y} \right) y'(t) \right] dt \\[4pt] &= \int_{C'} \left(P + R \dfrac{\partial z}{\partial x} \right)\, dx + \left(Q + R \dfrac{\partial z}{\partial y} \right) \, dy \\[4pt] &= \iint_D \left[ \dfrac{\partial}{\partial x} \left( Q + R \dfrac{\partial z}{\partial y} \right) - \dfrac{\partial}{\partial y} \left(P + R \dfrac{\partial z}{\partial x} \right) \right] \, dA \\[4pt] &=\iint_D \left(\dfrac{\partial Q}{\partial x} + \dfrac{\partial Q}{\partial z} \dfrac{\partial z}{\partial x} + \dfrac{\partial R}{\partial x} \dfrac{\partial z}{\partial y} + \dfrac{\partial R}{\partial z}\dfrac{\partial z}{\partial x} \dfrac{\partial z}{\partial y} + R \dfrac{\partial^2 z}{\partial x \partial y} \right) - \left(\dfrac{\partial P}{\partial y} + \dfrac{\partial P}{\partial z} \dfrac{\partial z}{\partial y} + \dfrac{\partial R}{\partial z} \dfrac{\partial z}{\partial y} \dfrac{\partial z}{\partial x} + R \dfrac{\partial^2 z}{\partial y \partial x} \right) \end{align*} \nonumber \]

By Clairaut’s theorem,

\[\dfrac{\partial^2 z}{\partial x \partial y} = \dfrac{\partial^2 z}{\partial y \partial x} \nonumber \]

Therefore, four of the terms disappear from this double integral, and we are left with

\[\iint_D [- (R_y - Q_z)Z_x - (P_z - R_x) z_y + (Q_x - P_y)] \, dA, \nonumber \]

which equals

\[\iint_S curl \, \vecs{F} \cdot d\vecs{S}. \nonumber \]

We have shown that Stokes’ theorem is true in the case of a function with a domain that is a simply connected region of finite area. We can quickly confirm this theorem for another important case: when vector field \(\vecs{F}\) is a conservative field. If \(\vecs{F}\) is conservative, the curl of \(\vecs{F}\) is zero, so

\[\iint_S curl \, \vecs{F} \cdot d\vecs{S} = 0. \nonumber \]

Since the boundary of \(S\) is a closed curve, the integral

\[\int_C \vecs{F} \cdot d\vecs{r}. \nonumber \]

is also zero.

Example \(\PageIndex{1}\): Verifying Stokes’ Theorem for a Specific Case

Verify that Stokes’ theorem is true for vector field \(\vecs{F}(x,y) = \langle -z,x,0 \rangle\) and surface \(S\), where \(S\) is the hemisphere, oriented outward, with parameterization \(\vecs r(\phi, \theta) = \langle \sin \phi \, \cos \theta, \, \sin \phi \, \sin \theta, \, \cos \phi \rangle, \, 0 \leq \theta \leq \pi, \, 0 \leq \phi \leq \pi\) as shown in Figure \(\PageIndex{5}\).

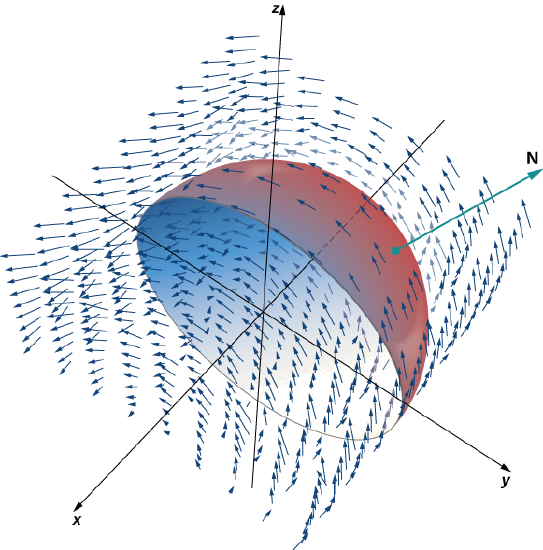
Let \(C\) be the boundary of \(S\). Note that \(C\) is a circle of radius 1, centered at the origin, sitting in plane \(y = 0\). This circle has parameterization \(\langle \cos t, \, 0, \, \sin t \rangle, \, 0 \leq t \leq 2\pi\). the equation for scalar surface integrals

\[ \begin{align*} \int_C \vecs{F} \cdot d \vecs{r} &= \int_0^{2\pi} \langle -\sin t, \, \cos t, \, 0 \rangle \cdot \langle - \sin t, \, 0, \, \cos t \rangle \, dt \\[4pt] &= \int_0^{2\pi} \sin^2 t \, dt \\[4pt] &= \pi. \end{align*}\]

By the equation for vector line integrals,

\[ \begin{align*} \iint_S \, curl \, \vecs{F} \cdot d\vecs S &= \iint_D curl \, \vecs{F} (\vecs r (\phi,\theta)) \cdot ( \vecs t_{\phi} \times \vecs t_{\theta}) \, dA \\[4pt] &= \iint_D \langle 0, -1, 1 \rangle \cdot \langle \cos \theta \, \sin^2 \phi, \, \sin \theta \, \sin^2 \phi, \, \sin \phi \, \cos \phi \rangle \, dA \\[4pt] &= \int_0^{\pi} \int_0^{\pi} (\sin \phi \, \cos \phi - \sin \theta \, \sin^2 \phi ) \, d\phi d\theta \\[4pt] &= \dfrac{\pi}{2} \int_0^{\pi} \sin \theta \, d\theta \\[4pt] &= \pi.\end{align*}\]

Therefore, we have verified Stokes’ theorem for this example.

Exercise \(\PageIndex{1}\)

Verify that Stokes’ theorem is true for vector field \(\vecs{F}(x,y,z) = \langle y,x,-z \rangle \) and surface \(S\), where \(S\) is the upwardly oriented portion of the graph of \(f(x,y) = x^2 y\) over a triangle in the \(xy\)-plane with vertices \((0,0), \, (2,0)\), and \((0,2)\).

Calculate the double integral and line integral separately.

Both integrals give \(-\dfrac{136}{45}\):

Applying Stokes’ Theorem

Stokes’ theorem translates between the flux integral of surface \(S\) to a line integral around the boundary of \(S\). Therefore, the theorem allows us to compute surface integrals or line integrals that would ordinarily be quite difficult by translating the line integral into a surface integral or vice versa. We now study some examples of each kind of translation.

Example \(\PageIndex{2}\): Calculating a Surface Integral

Calculate surface integral

\[\iint_S curl \, \vecs{F} \cdot d\vecs S, \nonumber \]

where \(S\) is the surface, oriented outward, in Figure \(\PageIndex{6}\) and \(\vecs{F} = \langle z,\, 2xy, \, x + y \rangle\).

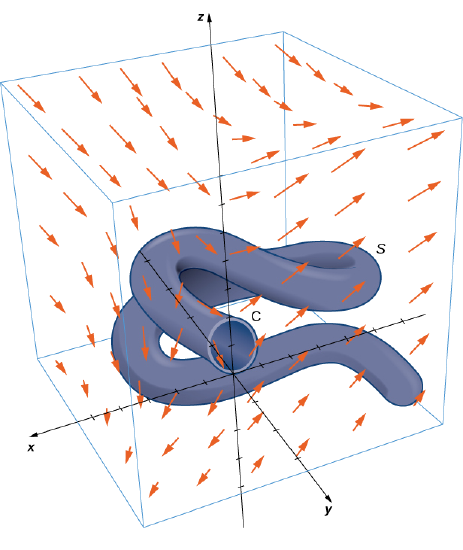
Note that to calculate

\[ \iint_S curl \, \vecs F \cdot d\vecs S \nonumber \]

without using Stokes’ theorem, we would need the equation for scalar surface integrals. Use of this equation requires a parameterization of \(S\). Surface \(S\) is complicated enough that it would be extremely difficult to find a parameterization. Therefore, the methods we have learned in previous sections are not useful for this problem. Instead, we use Stokes’ theorem, noting that the boundary \(C\) of the surface is merely a single circle with radius 1.

The curl of \(\vecs{F}\) is \(\langle 1,1,2y \rangle\). By Stokes’ theorem,

\[\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r, \nonumber \]

where \(C\) has parameterization \(\langle \cos t, \, \sin t, \, 1 \rangle, 0 \leq t \leq 2\pi\). By the equation for vector line integrals,

\[ \begin{align*} \iint_S curl \, F \cdot d\vecs S &= \int_C \vecs{F} \cdot d \vecs{r} \\[4pt] &= \int_0^2 \langle 1, \, \sin t \, \cos t, \, \cos t + \sin t \rangle \cdot \langle - \sin t, \, \cos t, \, 0 \rangle \, dt \\[4pt] &= \int_0^{2\pi} ( - \sin t + 2 \, \sin t \, \cos^2 t ) \, dt \\[4pt] &= \left[ \cos t - \dfrac{2 \, \cos^3 t}{3} \right]_0^{2\pi} \\[4pt] &= \cos (2\pi) - \dfrac{2 \, \cos^3 (2\pi)}{3} - \left(\cos (0) - \dfrac{2 \, \cos^3 (0)}{3} \right) \\[4pt] &= 0. \end{align*} \nonumber \]

An amazing consequence of Stokes’ theorem is that if \(S'\) is any other smooth surface with boundary \(C\) and the same orientation as \(S\), then \[\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r = 0 \nonumber \] because Stokes’ theorem says the surface integral depends on the line integral around the boundary only.

In Example \(\PageIndex{2}\), we calculated a surface integral simply by using information about the boundary of the surface. In general, let \(S_1\) and \(S_2\) be smooth surfaces with the same boundary \(C\) and the same orientation. By Stokes’ theorem,

\[\iint_{S_1} curl \, \vecs{F} \cdot d\vecs{S} = \int_C \vecs{F} \cdot d\vecs{r} = \iint_{S_2} curl \, \vecs{F} \cdot d\vecs{S}. \label{20} \]

Therefore, if

\[\iint_{S_1} curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]

is difficult to calculate but

\[\iint_{S_2} curl \, \vecs{F} \cdot d\vecs S \nonumber \]

is easy to calculate, Stokes’ theorem allows us to calculate the easier surface integral. In Example \(\PageIndex{2}\), we could have calculated

\[\iint_S curl \, \vecs{F} \cdot d \vecs{S} \nonumber \]

by calculating

\[\iint_{S'} curl \, \vecs{F} \cdot d\vecs{S}, \nonumber \]

where \(\vecs{S}'\) is the disk enclosed by boundary curve \(C\) (a much more simple surface with which to work).

Equation \ref{20} shows that flux integrals of curl vector fields are surface independent in the same way that line integrals of gradient fields are path independent. Recall that if \(\vecs{F}\) is a two-dimensional conservative vector field defined on a simply connected domain, \(f\) is a potential function for \(\vecs{F}\), and \(C\) is a curve in the domain of \(\vecs{F}\), then

\[\int_C \vecs{F} \cdot d\vecs{r} \nonumber \]

depends only on the endpoints of \(C\). Therefore if \(C'\) is any other curve with the same starting point and endpoint as \(C\) (that is, \(C'\) has the same orientation as \(C\)), then

\[\int_C \vecs{F} \cdot d\vecs{r} = \int_{C'} \vecs{F} \cdot d\vecs{r} \nonumber \]

In other words, the value of the integral depends on the boundary of the path only; it does not really depend on the path itself.

Analogously, suppose that \(S\) and \(S'\) are surfaces with the same boundary and same orientation, and suppose that \(\vecs{G}\) is a three-dimensional vector field that can be written as the curl of another vector field \(\vecs{F}\) (so that \(\vecs{F}\) is like a “potential field” of \(\vecs{G}\)). By Equation \ref{20},

\[ \begin{align*} \iint_S \vecs G \cdot d\vecs S = \iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r = \iint_{S'} curl \, \vecs F \cdot d\vecs S = \iint_{S'} \vecs G \cdot d\vecs S.\end{align*} \nonumber \]

Therefore, the flux integral of \(\vecs{G}\) does not depend on the surface, only on the boundary of the surface. Flux integrals of vector fields that can be written as the curl of a vector field are surface independent in the same way that line integrals of vector fields that can be written as the gradient of a scalar function are path independent.

Use Stokes’ theorem to calculate surface integral \[\iint_S curl \, \vecs{F} \cdot d\vecs{S}, \nonumber \] where \(\vecs{F} = \langle x,y,z \rangle\) and \(S\) is the surface as shown in the following figure.

Parameterize the boundary of \(S\) and translate to a line integral.

Example \(\PageIndex{3}\): Calculating a Line Integral

Calculate the line integral

\[\int_C \vecs{F} \cdot d\vecs{r}, \nonumber \]

where \(\vecs{F} = \langle xy, \, x^2 + y^2 + z^2, \, yz \rangle\) and \(C\) is the boundary of the parallelogram with vertices \((0,0,1), \, (0,1,0), \, (2,0,-1)\), and \((2,1,-2)\).

To calculate the line integral directly, we need to parameterize each side of the parallelogram separately, calculate four separate line integrals, and add the result. This is not overly complicated, but it is time-consuming.

By contrast, let’s calculate the line integral using Stokes’ theorem. Let \(S\) denote the surface of the parallelogram. Note that \(S\) is the portion of the graph of \(z = 1 - x - y\) for \((x,y)\) varying over the rectangular region with vertices \((0,0), \, (0,1), \, (2,0)\), and \((2,1)\) in the \(xy\)-plane. Therefore, a parameterization of \(S\) is \(\langle x,y, \, 1 - x - y \rangle, \, 0 \leq x \leq 2, \, 0 \leq y \leq 1\). The curl of \(\vecs{F}\) is \( \langle -z, \, 0, \, x \rangle\),and Stokes’ theorem and the equation for scalar surface integrals

\[ \begin{align*} \int_C \vecs{F} \cdot d\vecs{r} &= \iint_S curl \, \vecs{F} \cdot d\vecs{S} \\[4pt] &= \int_0^2 \int_0^1 curl \, \vecs{F} (x,y) \cdot (\vecs t_x \times \vecs t_y) \, dy\, dx \\[4pt] &= \int_0^2 \int_0^1 \langle - (1 - x - y), \, 0, \, x \rangle \cdot ( \langle 1, \, 0, -1 \rangle \times \langle 0, \, 1, \, -1 \rangle ) \, dy \,dx \\[4pt] &= \int_0^2 \int_0^1 \langle x + y - 1, \, 0, \, x \rangle \cdot \langle 1, 1, 1 \rangle \, dy \, dx \\[4pt] &= \int_0^2 \int_0^1 2x + y - 1 \, dy \, dx \\[4pt] &= 3.\end{align*} \nonumber \]

Exercise \(\PageIndex{3}\)

Use Stokes’ theorem to calculate line integral

where \(\vecs{F} = \langle z,x,y \rangle \) and \(C\) is the boundary of a triangle with vertices \((0,0,1), \, (3,0,-2)\), and \((0,1,2)\).

This triangle lies in plane \(z = 1 - x + y\).

\(\dfrac{3}{2}\)

Interpretation of Curl

In addition to translating between line integrals and flux integrals, Stokes’ theorem can be used to justify the physical interpretation of curl that we have learned. Here we investigate the relationship between curl and circulation, and we use Stokes’ theorem to state Faraday’s law—an important law in electricity and magnetism that relates the curl of an electric field to the rate of change of a magnetic field.

Recall that if \(C\) is a closed curve and \(\vecs{F}\) is a vector field defined on \(C\), then the circulation of \(\vecs{F}\) around \(C\) is line integral

If \(\vecs{F}\) represents the velocity field of a fluid in space, then the circulation measures the tendency of the fluid to move in the direction of \(C\).

Let \(\vecs{F}\) be a continuous vector field and let \(D_{\tau}\) be a small disk of radius \(r\) with center \(P_0\) (Figure \(\PageIndex{7}\)). If \(D_{\tau}\) is small enough, then \((curl \, \vecs{F})(P) \approx (curl \, \vecs F)(P_0)\) for all points \(P\) in \(D_{\tau}\) because the curl is continuous. Let \(C_{\tau}\) be the boundary circle of \(D_{\tau}\): By Stokes’ theorem,

\[\int_{C_{\tau}} \vecs{F} \cdot d\vecs{r} = \iint_{D_{\tau}} curl \, \vecs{F} \cdot \vecs{N} \, d\vecs S \approx \iint_{D_{\tau}} (curl \, \vecs{F})(P_0) \cdot \vecs{N} (P_0) \, d\vecs S. \nonumber \]

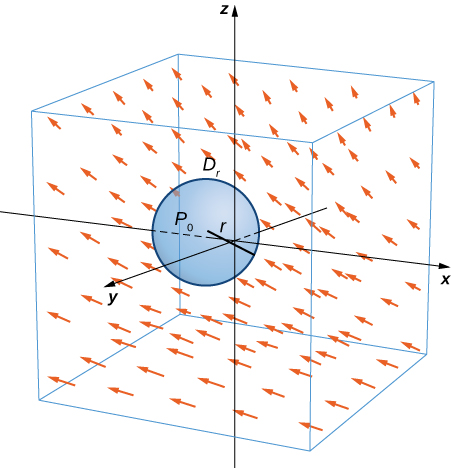
The quantity \( (curl \, \vecs F)(P_0) \cdot \vecs N (P_0) \) is constant, and therefore

\[\iint_{D_{\tau}} (curl \, \vecs F)(P_0) \cdot \vecs N (P_0) \, d\vecs S = \pi r^2 [(curl \, \vecs F)(P_0) \cdot \vecs N (P_0)]. \nonumber \]

\[\int_{C_{\tau}} \vecs F \cdot d\vecs r \approx \pi r^2 [ (curl \, \vecs F)(P_0) \cdot \vecs N (P_0)], \nonumber \]

and the approximation gets arbitrarily close as the radius shrinks to zero. Therefore Stokes’ theorem implies that

\[(curl \, \vecs F)(P_0) \cdot \vecs N (P_0) = \lim_{r\rightarrow 0^+} \dfrac{1}{\pi r^2} \int_{C_{\tau}} \vecs F \cdot d\vecs r. \nonumber \]

This equation relates the curl of a vector field to the circulation. Since the area of the disk is \(\pi r^2\), this equation says we can view the curl (in the limit) as the circulation per unit area. Recall that if \(\vecs F\) is the velocity field of a fluid, then circulation \[\oint_{C_{\tau}} \vecs F \cdot d\vecs r = \oint_{C_{\tau}} \vecs F \cdot \vecs T \, ds \nonumber \] is a measure of the tendency of the fluid to move around \(C_{\tau}\): The reason for this is that \(\vecs F \cdot \vecs T\) is a component of \(\vecs F\) in the direction of \(\vecs T\), and the closer the direction of \(\vecs F\) is to \(\vecs T\), the larger the value of \(\vecs F \cdot \vecs T\) (remember that if \(\vecs a\) and \(\vecs b\) are vectors and \(\vecs b\) is fixed, then the dot product \(\vecs a \cdot \vecs b\) is maximal when \(\vecs a\) points in the same direction as \(\vecs b\)). Therefore, if \(\vecs F\) is the velocity field of a fluid, then \(curl \, \vecs F \cdot \vecs N\) is a measure of how the fluid rotates about axis \(\vecs N\). The effect of the curl is largest about the axis that points in the direction of \(\vecs N\), because in this case \(curl \, \vecs F \cdot \vecs N\) is as large as possible.

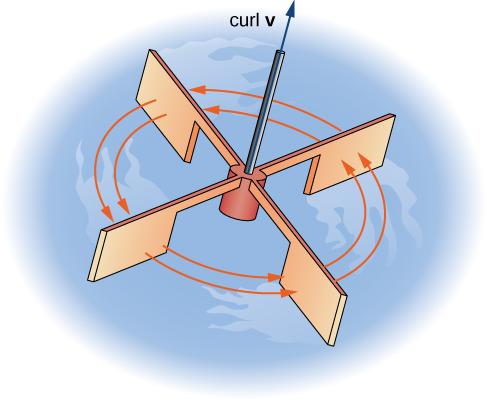
To see this effect in a more concrete fashion, imagine placing a tiny paddlewheel at point \(P_0\) (Figure \(\PageIndex{8}\)). The paddlewheel achieves its maximum speed when the axis of the wheel points in the direction of curl \(\vecs F\). This justifies the interpretation of the curl we have learned: curl is a measure of the rotation in the vector field about the axis that points in the direction of the normal vector \(\vecs N\), and Stokes’ theorem justifies this interpretation.

Now that we have learned about Stokes’ theorem, we can discuss applications in the area of electromagnetism. In particular, we examine how we can use Stokes’ theorem to translate between two equivalent forms of Faraday’s law . Before stating the two forms of Faraday’s law, we need some background terminology.

Let \(C\) be a closed curve that models a thin wire. In the context of electric fields, the wire may be moving over time, so we write \(C(t)\) to represent the wire. At a given time \(t\), curve \(C(t)\) may be different from original curve \(C\) because of the movement of the wire, but we assume that \(C(t)\) is a closed curve for all times \(t\). Let \(D(t)\) be a surface with \(C(t)\) as its boundary, and orient \(C(t)\) so that \(D(t)\) has positive orientation. Suppose that \(C(t)\)is in a magnetic field \(\vecs B(t)\) that can also change over time. In other words, \(\vecs{B}\) has the form

\[\vecs B(x,y,z) = \langle P(x,y,z), \, Q(x,y,z), \, R(x,y,z) \rangle, \nonumber \]

where \(P\), \(Q\), and \(R\) can all vary continuously over time. We can produce current along the wire by changing field \(\vecs B(t)\) (this is a consequence of Ampere’s law). Flux \(\displaystyle \phi (t) = \iint_{D(t)} \vecs B(t) \cdot d\vecs S\) creates electric field \(\vecs E(t)\) that does work. The integral form of Faraday’s law states that

\[Work = \int_{C(t)} \vecs E(t) \cdot d\vecs r = - \dfrac{\partial \phi}{\partial t}. \nonumber \]

In other words, the work done by \(\vecs{E}\) is the line integral around the boundary, which is also equal to the rate of change of the flux with respect to time. The differential form of Faraday’s law states that

\[curl \, \vecs{E} = - \dfrac{\partial \vecs B}{\partial t}. \nonumber \]

Using Stokes’ theorem, we can show that the differential form of Faraday’s law is a consequence of the integral form. By Stokes’ theorem, we can convert the line integral in the integral form into surface integral

\[-\dfrac{\partial \phi}{\partial t} = \int_{C(t)} \vecs E(t) \cdot d\vecs r = \iint_{D(t)} curl \,\vecs E(t) \cdot d\vecs S. \nonumber \]

Since \[\phi (t) = \iint_{D(t)} B(t) \cdot d\vecs S, \nonumber \] then as long as the integration of the surface does not vary with time we also have

\[- \dfrac{\partial \phi}{\partial t} = \iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S. \nonumber \]

\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \,\vecs E \cdot d\vecs S. \nonumber \]

To derive the differential form of Faraday’s law, we would like to conclude that \(curl \,\vecs E = -\dfrac{\partial \vecs B}{\partial t}\): In general, the equation

\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \,\vecs E \cdot d\vecs S \nonumber \]

is not enough to conclude that \(curl \, \vecs E = -\dfrac{\partial \vecs B}{\partial t}\): The integral symbols do not simply “cancel out,” leaving equality of the integrands. To see why the integral symbol does not just cancel out in general, consider the two single-variable integrals \(\displaystyle \int_0^1 x \, dx\) and \(\displaystyle \int_0^1 f(x)\, dx\), where

\[f(x) = \begin{cases}1, &\text{if } 0 \leq x \leq 1/2 \\ 0, & \text{if } 1/2 \leq x \leq 1. \end{cases} \nonumber \]

Both of these integrals equal \(\dfrac{1}{2}\), so \(\displaystyle \int_0^1 x \, dx = \int_0^1 f(x) \, dx\).

However, \(x \neq f(x)\). Analogously, with our equation \[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \, \vecs E \cdot d\vecs S, \nonumber \] we cannot simply conclude that \(curl \, \vecs E = -\dfrac{\partial \vecs B}{\partial t}\) just because their integrals are equal. However, in our context, equation

\[\iint_{D(t)} - \dfrac{\partial \vecs B}{\partial t} \cdot d\vecs S = \iint_{D(t)} curl \, \vecs E \cdot d\vecs S \nonumber \]

is true for any region, however small (this is in contrast to the single-variable integrals just discussed). If \(\vecs F\) and \(\vecs G\) are three-dimensional vector fields such that

\[\iint_S \vecs F \cdot d\vecs S = \iint_S \vecs G \cdot d\vecs S \nonumber \]

for any surface \(S\), then it is possible to show that \(\vecs F = \vecs G\) by shrinking the area of \(S\) to zero by taking a limit (the smaller the area of \(S\), the closer the value of \(\displaystyle \iint_S \vecs F \cdot d\vecs S\) to the value of \(\vecs F\) at a point inside \(S\)). Therefore, we can let area \(D(t)\) shrink to zero by taking a limit and obtain the differential form of Faraday’s law:

\[curl \,\vecs E = - \dfrac{\partial \vecs B}{\partial t}. \nonumber \]

In the context of electric fields, the curl of the electric field can be interpreted as the negative of the rate of change of the corresponding magnetic field with respect to time.

Example \(\PageIndex{4}\): Using Faraday’s Law

Calculate the curl of electric field \(\vecs{E}\) if the corresponding magnetic field is constant field \(\vecs B(t) = \langle 1, -4, 2 \rangle\).

Since the magnetic field does not change with respect to time, \(-\dfrac{\partial \vecs B}{\partial t} = \vecs 0\). By Faraday’s law, the curl of the electric field is therefore also zero.

A consequence of Faraday’s law is that the curl of the electric field corresponding to a constant magnetic field is always zero.

Exercise \(\PageIndex{4}\)

Calculate the curl of electric field \(\vecs{E}\) if the corresponding magnetic field is \(\vecs B(t) = \langle tx, \, ty, \, -2tz \rangle, \, 0 \leq t < \infty.\)

• Use the differential form of Faraday’s law.
• Notice that the curl of the electric field does not change over time, although the magnetic field does change over time.

\(curl \, \vecs{E} = \langle x, \, y, \, -2z \rangle\)

Key Concepts

• Stokes’ theorem relates a flux integral over a surface to a line integral around the boundary of the surface. Stokes’ theorem is a higher dimensional version of Green’s theorem, and therefore is another version of the Fundamental Theorem of Calculus in higher dimensions.
• Stokes’ theorem can be used to transform a difficult surface integral into an easier line integral, or a difficult line integral into an easier surface integral.
• Through Stokes’ theorem, line integrals can be evaluated using the simplest surface with boundary \(C\).
• Faraday’s law relates the curl of an electric field to the rate of change of the corresponding magnetic field. Stokes’ theorem can be used to derive Faraday’s law.

Key Equations

• Stokes’ theorem

\[\int_C \vecs{F} \cdot d\vecs{r} = \iint_S curl \, \vecs{F} \cdot d\vecs{S} \nonumber \]

• Previous Article
• Next Article

Questions in Fluid Mechanics: Stokes’ Hypothesis for a Newtonian, Isotropic Fluid

• Split-Screen
• Article contents
• Figures & tables
• Supplementary Data
• Peer Review
• Open the PDF for in another window
• Cite Icon Cite
• Permissions
• Search Site

Gad-el-Hak, M. (March 1, 1995). "Questions in Fluid Mechanics: Stokes’ Hypothesis for a Newtonian, Isotropic Fluid." ASME. J. Fluids Eng . March 1995; 117(1): 3–5. https://doi.org/10.1115/1.2816816

Download citation file:

• Ris (Zotero)
• Reference Manager

Article PDF first page preview

Get email alerts, related articles, related proceedings papers, related chapters, affiliations.

• Accepted Manuscripts
• About the Journal
• Editorial Board
• Information for Authors
• Call for Papers
• Rights and Permission
• Online ISSN 1528-901X
• Print ISSN 0098-2202

ASME Journals

• About ASME Journals
• Submit a Paper
• Title History

ASME Conference Proceedings

• About ASME Conference Publications and Proceedings
• Conference Proceedings Author Guidelines

ASME eBooks

• About ASME eBooks
• ASME Press Advisory & Oversight Committee
• Book Proposal Guidelines
• Frequently Asked Questions
• Publication Permissions & Reprints
• ASME Membership

Opportunities

• Faculty Positions
• ASME Community

• Accessibility
• Privacy Statement
• Terms of Use
• Get Adobe Acrobat Reader

This Feature Is Available To Subscribers Only

Sign In or Create an Account

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Published: 04 November 2019

Stoked about Stokes

Nature Reviews Physics volume  1 ,  page 637 ( 2019 ) Cite this article

1280 Accesses

9 Altmetric

Metrics details

• Fluid dynamics

This year marks the 200th anniversary of the birth of George Gabriel Stokes, a physicist and mathematician best known for his contributions to fluid dynamics, but whose work was broader than that.

November sees the 72nd annual American Physical Society Division of Fluid Dynamics Meeting. The conference brings together over 3,000 attendees from around the world and covers topics including the fluid dynamics of the interiors of stars, drug transport within the body, and ships and submarines. This variety of topics shows the many research directions and applications of fluid dynamics, a field that is indebted to the work of George Gabriel Stokes, who was born 200 years ago this year.

One of Stokes’ most famous scientific contributions is his work on the Navier–Stokes equations, which describe how incompressible fluids flow. In part, the fame of the Navier–Stokes equations derives from the fact that even the basic properties of their solutions are not well understood. A long-standing problem is to prove whether Navier–Stokes equations in 3D always have smooth and globally defined solutions, that is, that they are solved by velocity and pressure functions that can be differentiated again and again without encountering a discontinuity. This problem has stumped mathematicians for years, and is the subject of a US$1 million prize from the Clay Mathematics Institute. Although a proof that all solutions are smooth remains elusive, a possible path to a counter-example was highlighted by Terence Tao in a Comment in our July issue, involving ‘programming’ a fluid to spend a long time near equilibrium but periodically abruptly transition to a rescaled version of itself.

Apart from the interest they garner from mathematicians, the Navier–Stokes equations underlie the whole research area of fluid dynamics. One direction of that field is that of active matter, the study of ‘materials’ made up of particles that can each convert an energy supply into motion. One way to describe the collective behaviour of these particles is to invoke a new kind of hydrodynamics that includes the ‘active stresses’ that exist in the system. In a Comment in this issue, Sriram Ramaswamy discusses the history and future of active hydrodynamics, including ways that it may be used to better understand how biological tissues grow and develop.

Another aspect of biology for which fluid dynamics has a role is the study of insect flight. Whether it is a bee, a dragonfly or a mosquito, an insect in flight exerts forces on the fluid of the atmosphere around it and is itself subject to forces from that fluid. However, insects do not simply glide but control their flight. As Itai Cohen and colleagues discuss in a Comment , this control can be both passive — such as in insect wing hinges with mechanical properties that affect how the wing rotates under aerodynamic lift and drag forces — and active, controlled neuronally. Therefore, fully understanding insect flight behaviours requires an understanding of fluids, biomechanics and neuroscience.

On a much larger scale than insect flight, the fluid dynamics of the Earth’s atmosphere is experienced by all of us as weather. Weather and climate forecasts are made using numerical simulations of the atmosphere, oceans and icecaps on grids with resolution of tens of kilometres, a scale that is orders of magnitude larger than the length scale set by the viscosity of the fluids. In a Perspective earlier this year, Tim Palmer argued for weather and climate models that treat as stochastic the processes that happen on length scales shorter than the simulation grid. Such models out-perform models that impose a hard cut-off at the length scale of the grid. They also better respect the self-similarity of the Navier–Stokes equations on all length scales, a symmetry that is incompatible with a hard cut-off length scale.

The breadth of fluid dynamics research is reminiscent of the breadth of the work of Stokes himself. Although he was trained as a mathematician, Stokes made major contributions to physics problems in hydrodynamics and optics, with work spanning theory and experiment. For instance, in the field of optics, he investigated the wave theory of light in the context of diffraction and experimentally identified the phenomenon of fluorescence. Stokes also found ways to apply his research to other fields, contributing to geodesy, for example, by applying his theory for the motion of pendula in fluids to the problem of variations of gravitational acceleration at different points on the Earth’s surface.

In many ways, in the years since Stokes lived, scientific research has become more specialized, with researchers focusing on a single topic within a single discipline. Such an approach has certainly paid dividends. However, the interdisciplinary applications of fluid dynamics — and the wide-ranging research career of Stokes himself — show that crossing boundaries can pay off too.

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Stoked about Stokes. Nat Rev Phys 1 , 637 (2019). https://doi.org/10.1038/s42254-019-0124-5

Download citation

Published : 04 November 2019

Issue Date : November 2019

DOI : https://doi.org/10.1038/s42254-019-0124-5

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

• Subscriber Services
• For Authors
• Publications
• Archaeology
• Art & Architecture
• Bilingual dictionaries
• Classical studies
• Encyclopedias
• English Dictionaries and Thesauri
• Language reference
• Linguistics
• Media studies
• Medicine and health
• Names studies
• Performing arts
• Science and technology
• Social sciences
• Society and culture
• Overview Pages
• Subject Reference
• English Dictionaries
• Bilingual Dictionaries

Recently viewed (0)

• Save Search

Tony Atkins  and Marcel Escudier

• Find at OUP.com
• Google Preview
• Share This Facebook LinkedIn Twitter

Related Content

In this work.

• bulk viscosity
• Publishing Information
• Next Version

Stokes hypothesis  

Tony atkins,, marcel escudier.

The assumption that the viscosity μ and the coefficient of bulk viscosity λ for a Newtonian fluid are related by the equation ... ...

Access to the complete content on Oxford Reference requires a subscription or purchase. Public users are able to search the site and view the abstracts and keywords for each book and chapter without a subscription.

Please subscribe or login to access full text content.

If you have purchased a print title that contains an access token, please see the token for information about how to register your code.

For questions on access or troubleshooting, please check our FAQs , and if you can''t find the answer there, please contact us .

• Oxford University Press

PRINTED FROM OXFORD REFERENCE (www.oxfordreference.com). (c) Copyright Oxford University Press, 2023. All Rights Reserved. Under the terms of the licence agreement, an individual user may print out a PDF of a single entry from a reference work in OR for personal use (for details see Privacy Policy and Legal Notice ).

date: 31 March 2024

• Cookie Policy
• Privacy Policy
• Legal Notice
• Accessibility
• [66.249.64.20|109.248.223.228]
• 109.248.223.228

Character limit 500 /500

Navier-Stokes equations

From cfd-wiki.

The Navier-Stokes equations are the basic governing equations for a viscous, heat conducting fluid. It is a vector equation obtained by applying Newton's Law of Motion to a fluid element and is also called the momentum equation . It is supplemented by the mass conservation equation, also called continuity equation and the energy equation . Usually, the term Navier-Stokes equations is used to refer to all of these equations.

The instantaneous continuity equation (1), momentum equation (2) and energy equation (3) for a compressible fluid can be written as:

For a Newtonian fluid, assuming Stokes Law for mono-atomic gases, the viscous stress is given by:

Where the trace-less viscous strain-rate is defined by:

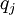
To close these equations it is also necessary to specify an equation of state. Assuming a calorically perfect gas the following relations are valid:

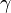
Note that the corresponding expression (15) for Favre averaged turbulent flows contains an extra term related to the turbulent energy.

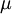
Boundary conditions

Derivation of continuity equation.

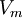
Applying the Reynolds transport theorem and divergence theorem one obtains:

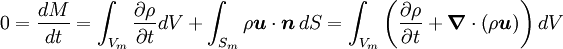
at all points of the fluid. For an incompressible fluid the change rate of density is zero. One can simplify (1) to:

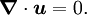
Derivation of momentum equations

All is started from Newton's law:

FORCE is equal MASS time ACCELERATION

and which is applied to the fluid parsel

Expansion, rotation and deformation of a fluid parsel

forces and stresses

There are two types of forces: body(mass) forces and surface forces. Body forces act on the entire control volume. The most common body force is that due to gravity. Electromagnetic phenomena may also create body forces, but this is a rather specialized situation.

Surface forces act on only surface of a control volume at a time and arise due to pressure or viscous stresses.

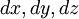
At the moment we assume this parallelepiped isolated from the rest of the fluid flow , and consider the forces acting on the faces of the parallelepiped.

Let the left forward top of a parallelepiped lies in a point O

The force due to the stress is the product of the stress and the area over which it acts.

deformation and rotation

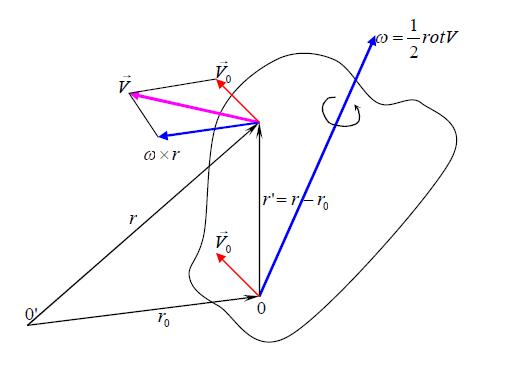
Newtonian Fluids

Newton postulated (since then experimentally verified) that the shear force or shear stress needed to deform the fluid was linearly proportional to the velocity gradient:

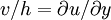
Therefore, Newton postulated:

Fluids that have a linear relationship between stress and strain rate are called Newtonian fluids . This is a property of the fluid, not the flow. Water and air are examples of Newtonian fluids, while blood is a non-Newtonian fluid.

Stokes Hypothesis

Stokes extended Newton's idea from simple 1-D flows (where only one component of velocity is present) to multidimensional flows. He developed the following relations, collectively known as Stokes relations

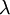
substitution

Other formulation.

Cauchy's equation of motion

The equation of motion for a Newtonian fluid is obtained by constitutive equation into Cauchy's equation to obtain

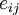
If the viscous effects are negligible, we obtain the Euler equation

Derivation of the energy equation

we follow Wesseling (2001)

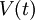
Let heat diffusion be governed by Fourier's law:

By application of the transport theorem and substitution we obtain

External links

• Navier-Stokes equations at mathworld.com
• Millenium Problem
• View source

wiki navigation

• Community portal
• Recent changes

wiki search

Wiki toolbox.

• What links here
• Related changes
• Special pages
• Printable version
• Permanent link

• This page was last modified on 28 August 2012, at 18:17.
• This page has been accessed 411,300 times.
• Content is available under GNU Free Documentation License 1.2 .
• Privacy policy
• About CFD-Wiki
• Disclaimers