t test hypothesis definition

An official website of the United States government

The .gov means it's official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you're on a federal government site.

The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Publications
Account settings
Browse Titles

NCBI Bookshelf. A service of the National Library of Medicine, National Institutes of Health.

StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

StatPearls [Internet].

Raoul R. Wadhwa ; Raghavendra Marappa-Ganeshan .

Affiliations

Last Update: January 16, 2023 .

Definition/Introduction

T-test was first described by William Sealy Gosset in 1908, when he published his article under the pseudonym 'student' while working for a brewery. [1] In simple terms, a Student's t-test is a ratio that quantifies how significant the difference is between the 'means' of two groups while taking their variance or distribution into account.

Issues of Concern

Selecting appropriate statistical tests is a critical step in conducting research. [2] Therefore, there are three forms of Student’s t-test about which physicians, particularly physician-scientists, need to be aware: (1) one-sample t-test; (2) two-sample t-test; and (3) two-sample paired t-test. The one-sample t-test evaluates a single list of numbers to test the hypothesis that a statistic of that set is equal to a chosen value, for instance, to test the hypothesis that the mean of the set of numbers is equal to zero. As an example, consider the following question: what is the average serum sodium concentration in adults? Currently, 140 mEq/L serves as an approximate center of a reference range of 135 to 145 mEq/L; thus, the null hypothesis is that the average serum sodium concentration in adults is equal to 140 mEq/L.

If you believe these numbers are wrong (alternate hypothesis) or you want to test the original hypothesis, you could collect blood from a set of subjects, measure the sodium concentration in each sample, and then take the mean of this set. If the mean is 140.1 mEq/L, you probably do not have convincing evidence that the numbers mentioned above are faulty (since 140 and 140.1 are fairly close). Thus, you would fail to reject the null hypothesis. However, if your sample has a mean of 70 mEq/L, this could be preliminary evidence (assuming, of course, rigorous methodology) and could end up rejecting the null hypothesis. The decision-making process would be trickier if the mean of the sample were 134 or 150 mEq/L. The t-test can be used to reduce subjective influence when testing a null hypothesis. Before testing a hypothesis, researchers should choose the alpha and beta values of the test. Loosely, the alpha parameter determines the threshold for false-positive results (e.g., if the actual mean serum sodium concentration is 140 mEq/L, but the t-test rejects the original hypothesis in favor of your new hypothesis), and the beta parameter determines the threshold for false-negative results (e.g., if true mean serum sodium concentration is 200 mEq/L, but the t-test fails to reject the old hypothesis). Methods of selection of alpha and beta are outside the scope of this article.

While the one-sample t-test allows you to test the statistic of a single set of numbers against a specific numeric value, the two-sample t-test allows testing the values of a statistic between two groups. In this case, a research question could be: do children and adults have the same mean serum sodium concentration? Testing this hypothesis would require sampling two groups, a group of adults and a group of children, and comparing the mean serum sodium concentrations between these two groups in a manner analogous to the one-sample t-test described above. The paired t-test is used in scenarios where measurements from the two groups have a link to one another. In the example above concerning the mean serum sodium concentration of children and adults, the implicit assumption was that all the measurements would all be completed at one point in time in a set of children and a distinct set of adults. However, it would also be possible to measure serum sodium concentrations in a set of children, wait a few years until they are adults, then measure the serum sodium concentrations again. Here, each adult sodium concentration corresponds to exactly one child sodium concentration. A paired two-sample t-test can be used to capture the dependence of measurements between the two groups.

These variations of the student's t-test use observed or collected data to calculate a test statistic, which can then be used to calculate a p-value. Often misinterpreted, the p-value is equal to the probability of collecting data that is at least as extreme as the observed data in the study, assuming that the null hypothesis is true. [3] This concept is best illustrated by examples, as in the questions that accompany this article. Often, a threshold value is set prior to the study (equal to the alpha mentioned above); if the resulting p-value is below the preset threshold, there is sufficient evidence to reject the null hypothesis.

In the above scenarios, before using any form of the t-test, one must ensure that the assumptions for the test have been met. This article does not list or explain these assumptions in detail. Please follow the guidance of a trained statistician when designing research studies and conducting data analysis.

Clinical Significance

Given the rate of research progress, disease management (medical or surgical) continuously evolves. To follow the framework of evidence-based medicine, physicians must be able to read and critically evaluate primary literature. [4] [5] The ability to do this successfully requires at least a basic foundation of knowledge in statistics, including common biases (e.g., nonresponse bias), standard study designs (e.g., randomized controlled trials), and common statistical pitfalls researchers face (e.g., statistically significant results that are not clinically significant). [6] [7] Understanding a student’s t-test is a start to clinicians gaining this necessary foundation of knowledge.

Review Questions
Access free multiple choice questions on this topic.
Comment on this article.

Disclosure: Raoul Wadhwa declares no relevant financial relationships with ineligible companies.

Disclosure: Raghavendra Marappa-Ganeshan declares no relevant financial relationships with ineligible companies.

This book is distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND 4.0) ( http://creativecommons.org/licenses/by-nc-nd/4.0/ ), which permits others to distribute the work, provided that the article is not altered or used commercially. You are not required to obtain permission to distribute this article, provided that you credit the author and journal.

Cite this Page Wadhwa RR, Marappa-Ganeshan R. T Test. [Updated 2023 Jan 16]. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2024 Jan-.

In this Page

Bulk download.

Bulk download StatPearls data from FTP

Related information

PMC PubMed Central citations
PubMed Links to PubMed

Recent Activity

T Test - StatPearls T Test - StatPearls

Your browsing activity is empty.

Activity recording is turned off.

Turn recording back on

Connect with NLM

National Library of Medicine 8600 Rockville Pike Bethesda, MD 20894

Web Policies FOIA HHS Vulnerability Disclosure

Help Accessibility Careers

JMP | Statistical Discovery.™ From SAS.

Statistics Knowledge Portal

A free online introduction to statistics

What is a t- test?

A t -test (also known as Student's t -test) is a tool for evaluating the means of one or two populations using hypothesis testing. A t-test may be used to evaluate whether a single group differs from a known value ( a one-sample t-test ), whether two groups differ from each other ( an independent two-sample t-test ), or whether there is a significant difference in paired measurements ( a paired, or dependent samples t-test ).

How are t -tests used?

First, you define the hypothesis you are going to test and specify an acceptable risk of drawing a faulty conclusion. For example, when comparing two populations, you might hypothesize that their means are the same, and you decide on an acceptable probability of concluding that a difference exists when that is not true. Next, you calculate a test statistic from your data and compare it to a theoretical value from a t- distribution. Depending on the outcome, you either reject or fail to reject your null hypothesis.

What if I have more than two groups?

You cannot use a t -test. Use a multiple comparison method. Examples are analysis of variance ( ANOVA ) , Tukey-Kramer pairwise comparison, Dunnett's comparison to a control, and analysis of means (ANOM).

t -Test assumptions

While t -tests are relatively robust to deviations from assumptions, t -tests do assume that:

The data are continuous.
The sample data have been randomly sampled from a population.
There is homogeneity of variance (i.e., the variability of the data in each group is similar).
The distribution is approximately normal.

For two-sample t -tests, we must have independent samples. If the samples are not independent, then a paired t -test may be appropriate.

Types of t -tests

There are three t -tests to compare means: a one-sample t -test, a two-sample t -test and a paired t -test. The table below summarizes the characteristics of each and provides guidance on how to choose the correct test. Visit the individual pages for each type of t -test for examples along with details on assumptions and calculations.

The table above shows only the t -tests for population means. Another common t -test is for correlation coefficients . You use this t -test to decide if the correlation coefficient is significantly different from zero.

One-tailed vs. two-tailed tests

When you define the hypothesis, you also define whether you have a one-tailed or a two-tailed test. You should make this decision before collecting your data or doing any calculations. You make this decision for all three of the t -tests for means.

To explain, let’s use the one-sample t -test. Suppose we have a random sample of protein bars, and the label for the bars advertises 20 grams of protein per bar. The null hypothesis is that the unknown population mean is 20. Suppose we simply want to know if the data shows we have a different population mean. In this situation, our hypotheses are:

$ \mathrm H_o: \mu = 20 $

$ \mathrm H_a: \mu \neq 20 $

Here, we have a two-tailed test. We will use the data to see if the sample average differs sufficiently from 20 – either higher or lower – to conclude that the unknown population mean is different from 20.

Suppose instead that we want to know whether the advertising on the label is correct. Does the data support the idea that the unknown population mean is at least 20? Or not? In this situation, our hypotheses are:

$ \mathrm H_o: \mu >= 20 $

$ \mathrm H_a: \mu < 20 $

Here, we have a one-tailed test. We will use the data to see if the sample average is sufficiently less than 20 to reject the hypothesis that the unknown population mean is 20 or higher.

See the "tails for hypotheses tests" section on the t -distribution page for images that illustrate the concepts for one-tailed and two-tailed tests.

How to perform a t -test

For all of the t -tests involving means, you perform the same steps in analysis:

Define your null ($ \mathrm H_o $) and alternative ($ \mathrm H_a $) hypotheses before collecting your data.
Decide on the alpha value (or α value). This involves determining the risk you are willing to take of drawing the wrong conclusion. For example, suppose you set α=0.05 when comparing two independent groups. Here, you have decided on a 5% risk of concluding the unknown population means are different when they are not.
Check the data for errors.
Check the assumptions for the test.
Perform the test and draw your conclusion. All t -tests for means involve calculating a test statistic. You compare the test statistic to a theoretical value from the t- distribution . The theoretical value involves both the α value and the degrees of freedom for your data. For more detail, visit the pages for one-sample t -test , two-sample t -test and paired t -test .

An open portfolio of interoperable, industry leading products

The Dotmatics digital science platform provides the first true end-to-end solution for scientific R&D, combining an enterprise data platform with the most widely used applications for data analysis, biologics, flow cytometry, chemicals innovation, and more.

Statistical analysis and graphing software for scientists

Bioinformatics, cloning, and antibody discovery software

Plan, visualize, & document core molecular biology procedures

Electronic Lab Notebook to organize, search and share data

Proteomics software for analysis of mass spec data

Modern cytometry analysis platform

Analysis, statistics, graphing and reporting of flow cytometry data

Software to optimize designs of clinical trials

The Ultimate Guide to T Tests

Get all of your t test questions answered here

The ultimate guide to t tests

The t test is one of the simplest statistical techniques that is used to evaluate whether there is a statistical difference between the means from up to two different samples. The t test is especially useful when you have a small number of sample observations (under 30 or so), and you want to make conclusions about the larger population.

The characteristics of the data dictate the appropriate type of t test to run. All t tests are used as standalone analyses for very simple experiments and research questions as well as to perform individual tests within more complicated statistical models such as linear regression. In this guide, we’ll lay out everything you need to know about t tests, including providing a simple workflow to determine what t test is appropriate for your particular data or if you’d be better suited using a different model.

What is a t test?

A t test is a statistical technique used to quantify the difference between the mean (average value) of a variable from up to two samples (datasets). The variable must be numeric. Some examples are height, gross income, and amount of weight lost on a particular diet.

A t test tells you if the difference you observe is “surprising” based on the expected difference. They use t-distributions to evaluate the expected variability. When you have a reasonable-sized sample (over 30 or so observations), the t test can still be used, but other tests that use the normal distribution (the z test) can be used in its place.

Sometimes t tests are called “Student’s” t tests, which is simply a reference to their unusual history.

Barrels at the guinness brewery museum in Dublin, Ireland |sebastiangora (Adobe Stock)

It got its name because a brewer from the Guinness Brewery, William Gosset , published about the method under the pseudonym "Student". He wanted to get information out of very small sample sizes (often 3-5) because it took so much effort to brew each keg for his samples.

When should I use a t test?

A t test is appropriate to use when you’ve collected a small, random sample from some statistical “population” and want to compare the mean from your sample to another value. The value for comparison could be a fixed value (e.g., 10) or the mean of a second sample.

For example, if your variable of interest is the average height of sixth graders in your region, then you might measure the height of 25 or 30 randomly-selected sixth graders. A t test could be used to answer questions such as, “Is the average height greater than four feet?”

How does a t test work?

Based on your experiment, t tests make enough assumptions about your experiment to calculate an expected variability, and then they use that to determine if the observed data is statistically significant. To do this, t tests rely on an assumed “null hypothesis.” With the above example, the null hypothesis is that the average height is less than or equal to four feet.

Say that we measure the height of 5 randomly selected sixth graders and the average height is five feet. Does that mean that the “true” average height of all sixth graders is greater than four feet or did we randomly happen to measure taller than average students?

To evaluate this, we need a distribution that shows every possible average value resulting from a sample of five individuals in a population where the true mean is four. That may seem impossible to do, which is why there are particular assumptions that need to be made to perform a t test.

With those assumptions, then all that’s needed to determine the “sampling distribution of the mean” is the sample size (5 students in this case) and standard deviation of the data (let’s say it’s 1 foot).

That’s enough to create a graphic of the distribution of the mean, which is:

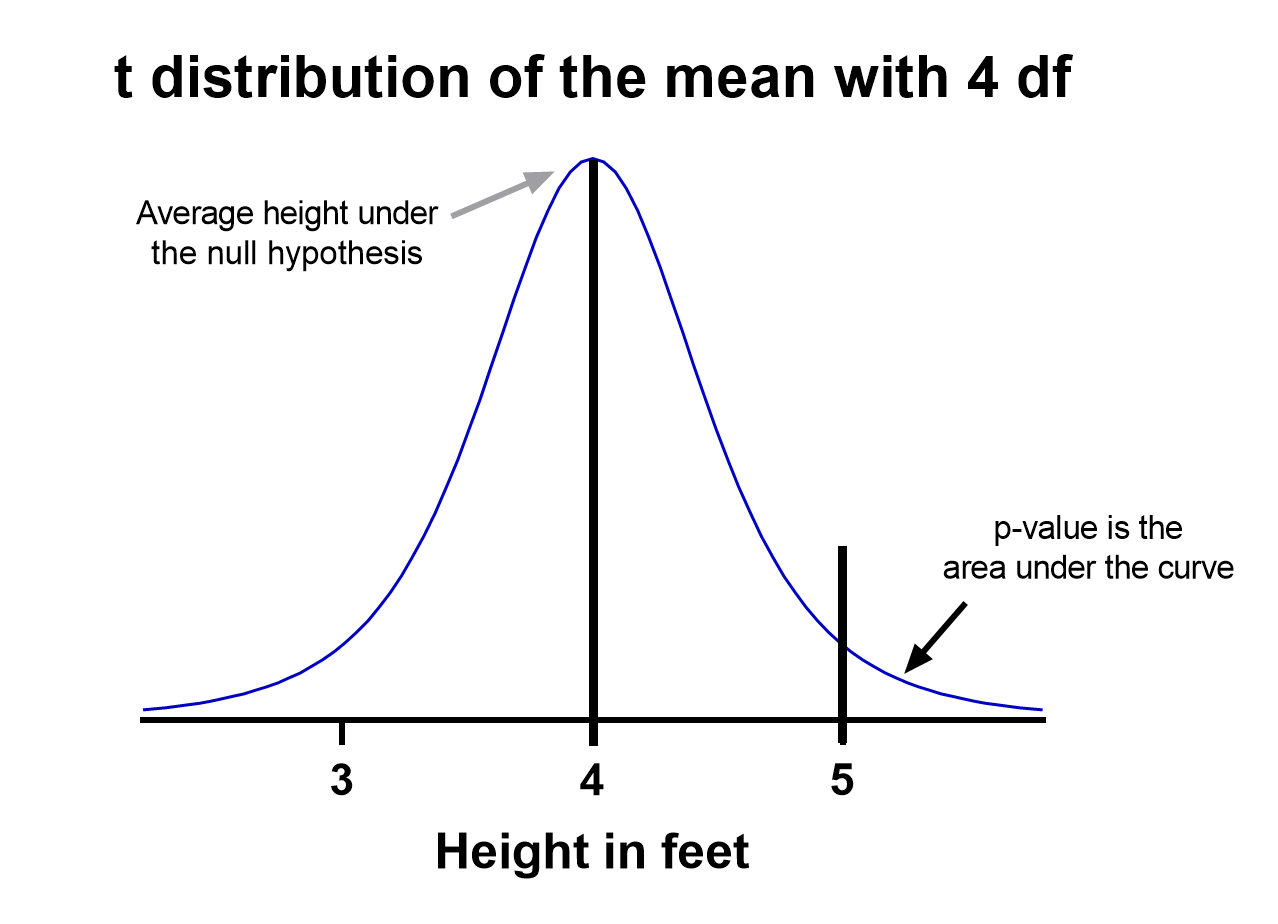
Notice the vertical line at x = 5, which was our sample mean. We (use software to) calculate the area to the right of the vertical line, which gives us the P value (0.09 in this case). Note that because our research question was asking if the average student is greater than four feet, the distribution is centered at four. Since we’re only interested in knowing if the average is greater than four feet, we use a one-tailed test in this case.

Using the standard confidence level of 0.05 with this example, we don’t have evidence that the true average height of sixth graders is taller than 4 feet.

What are the assumptions for t tests?

One variable of interest : This is not correlation or regression, where you are interested in the relationship between multiple variables. With a t test, you can have different samples, but they are all measuring the same variable (e.g., height).
Numeric data: You are dealing with a list of measurements that can be averaged. This means you aren’t just counting occurrences in various categories (e.g., eye color or political affiliation).
Two groups or less: If you have more than two samples of data, a t test is the wrong technique. You most likely need to try ANOVA.
Random sample : You need a random sample from your statistical “population of interest” in order to draw valid conclusions about the larger population. If your population is so small that you can measure everything, then you have a “census” and don’t need statistics. This is because you don’t need to estimate the truth, since you have measured the truth without variability.
Normally Distributed : The smaller your sample size, the more important it is that your data come from a normal, Gaussian distribution bell curve. If you have reason to believe that your data are not normally distributed, consider nonparametric t test alternatives . This isn’t necessary for larger samples (usually 25 or 30 unless the data is heavily skewed). The reason is that the Central Limit Theorem applies in this case, which says that even if the distribution of your data is not normal, the distribution of the mean of your data is, so you can use a z-test rather than a t test.

How do I know which t test to use?

There are many types of t tests to choose from, but you don’t necessarily have to understand every detail behind each option.

You just need to be able to answer a few questions, which will lead you to pick the right t test. To that end, we put together this workflow for you to figure out which test is appropriate for your data.

Do you have one or two samples?

Are you comparing the means of two different samples, or comparing the mean from one sample to a fixed value? An example research question is, “Is the average height of my sample of sixth grade students greater than four feet?”

If you only have one sample of data, you can click here to skip to a one-sample t test example, otherwise your next step is to ask:

Are observations in the two samples matched up or related in some way?

This could be as before-and-after measurements of the same exact subjects, or perhaps your study split up “pairs” of subjects (who are technically different but share certain characteristics of interest) into the two samples. The same variable is measured in both cases.

If so, you are looking at some kind of paired samples t test . The linked section will help you dial in exactly which one in that family is best for you, either difference (most common) or ratio.

If you aren’t sure paired is right, ask yourself another question:

Are you comparing different observations in each of the two samples?

If the answer is yes, then you have an unpaired or independent samples t test. The two samples should measure the same variable (e.g., height), but are samples from two distinct groups (e.g., team A and team B).

The goal is to compare the means to see if the groups are significantly different. For example, “Is the average height of team A greater than team B?” Unlike paired, the only relationship between the groups in this case is that we measured the same variable for both. There are two versions of unpaired samples t tests (pooled and unpooled) depending on whether you assume the same variance for each sample.

Have you run the same experiment multiple times on the same subject/observational unit?

If so, then you have a nested t test (unless you have more than two sample groups). This is a trickier concept to understand. One example is if you are measuring how well Fertilizer A works against Fertilizer B. Let’s say you have 12 pots to grow plants in (6 pots for each fertilizer), and you grow 3 plants in each pot.

In this case you have 6 observational units for each fertilizer, with 3 subsamples from each pot. You would want to analyze this with a nested t test . The “nested” factor in this case is the pots. It’s important to note that we aren’t interested in estimating the variability within each pot, we just want to take it into account.

You might be tempted to run an unpaired samples t test here, but that assumes you have 6*3 = 18 replicates for each fertilizer. However, the three replicates within each pot are related, and an unpaired samples t test wouldn’t take that into account.

What if none of these sound like my experiment?

If you’re not seeing your research question above, note that t tests are very basic statistical tools. Many experiments require more sophisticated techniques to evaluate differences. If the variable of interest is a proportion (e.g., 10 of 100 manufactured products were defective), then you’d use z-tests. If you take before and after measurements and have more than one treatment (e.g., control vs a treatment diet), then you need ANOVA.

How do I perform a t test using software?

If you’re wondering how to do a t test, the easiest way is with statistical software such as Prism or an online t test calculator .

If you’re using software, then all you need to know is which t test is appropriate ( use the workflow here ) and understand how to interpret the output. To do that, you’ll also need to:

Determine whether your test is one or two-tailed
Choose the level of significance

Is my test one or two-tailed?

Whether or not you have a one- or two-tailed test depends on your research hypothesis. Choosing the appropriately tailed test is very important and requires integrity from the researcher. This is because you have more “power” with one-tailed tests, meaning that you can detect a statistically significant difference more easily. Unless you have written out your research hypothesis as one directional before you run your experiment, you should use a two-tailed test.

Two-tailed tests

Two-tailed tests are the most common, and they are applicable when your research question is simply asking, “is there a difference?”

One-tailed tests

Contrast that with one-tailed tests, where the research questions are directional, meaning that either the question is, “is it greater than ” or the question is, “is it less than ”. These tests can only detect a difference in one direction.

Choosing the level of significance

All t tests estimate whether a mean of a population is different than some other value, and with all estimates come some variability, or what statisticians call “error.” Before analyzing your data, you want to choose a level of significance, usually denoted by the Greek letter alpha, 𝛼. The scientific standard is setting alpha to be 0.05.

An alpha of 0.05 results in 95% confidence intervals, and determines the cutoff for when P values are considered statistically significant.

One sample t test

If you only have one sample of a list of numbers, you are doing a one-sample t test. All you are interested in doing is comparing the mean from this group with some known value to test if there is evidence, that it is significantly different from that standard. Use our free one-sample t test calculator for this.

A one sample t test example research question is, “Is the average fifth grader taller than four feet?”

It is the simplest version of a t test, and has all sorts of applications within hypothesis testing. Sometimes the “known value” is called the “null value”. While the null value in t tests is often 0, it could be any value. The name comes from being the value which exactly represents the null hypothesis, where no significant difference exists.

Any time you know the exact number you are trying to compare your sample of data against, this could work well. And of course: it can be either one or two-tailed.

One sample t test formula

Statistical software handles this for you, but if you want the details, the formula for a one sample t test is:

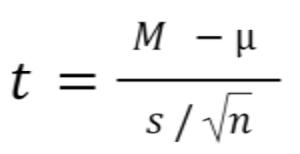
M: Calculated mean of your sample
μ: Hypothetical mean you are testing against
s: The standard deviation of your sample
n: The number of observations in your sample.

In a one-sample t test, calculating degrees of freedom is simple: one less than the number of objects in your dataset (you’ll see it written as n-1 ).

Example of a one sample t test

For our example within Prism, we have a dataset of 12 values from an experiment labeled “% of control”. Perhaps these are heights of a sample of plants that have been treated with a new fertilizer. A value of 100 represents the industry-standard control height. Likewise, 123 represents a plant with a height 123% that of the control (that is, 23% larger).

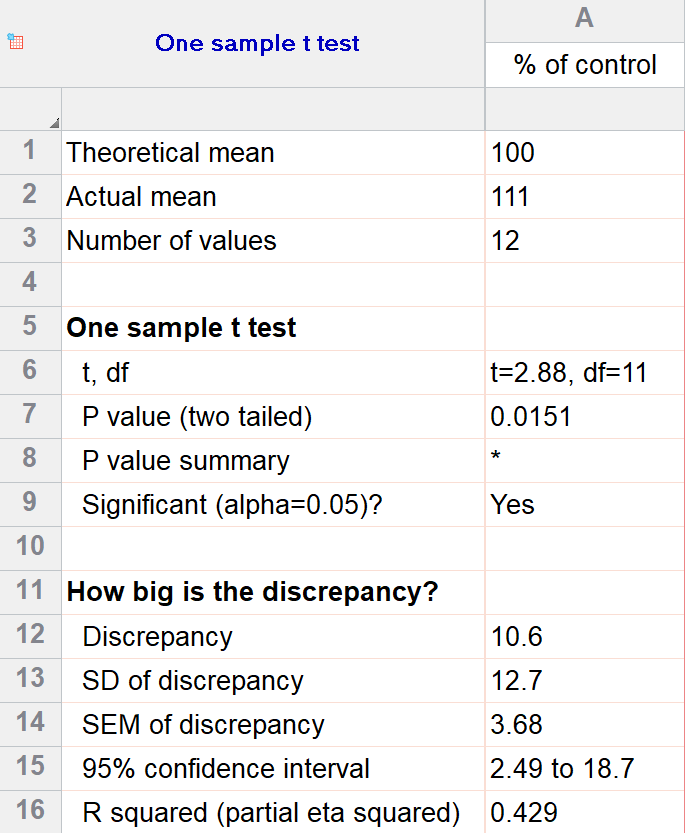
We’ll perform a two-tailed, one-sample t test to see if plants are shorter or taller on average with the fertilizer. We will use a significance threshold of 0.05. Here is the output:

You can see in the output that the actual sample mean was 111. Is that different enough from the industry standard (100) to conclude that there is a statistical difference?

The quick answer is yes, there’s strong evidence that the height of the plants with the fertilizer is greater than the industry standard (p=0.015). The nice thing about using software is that it handles some of the trickier steps for you. In this case, it calculates your test statistic (t=2.88), determines the appropriate degrees of freedom (11), and outputs a P value.

More informative than the P value is the confidence interval of the difference, which is 2.49 to 18.7. The confidence interval tells us that, based on our data, we are confident that the true difference between our sample and the baseline value of 100 is somewhere between 2.49 and 18.7. As long as the difference is statistically significant, the interval will not contain zero.

You can follow these tips for interpreting your own one-sample test.

Graphing a one-sample t test

For some techniques (like regression), graphing the data is a very helpful part of the analysis. For t tests, making a chart of your data is still useful to spot any strange patterns or outliers, but the small sample size means you may already be familiar with any strange things in your data.

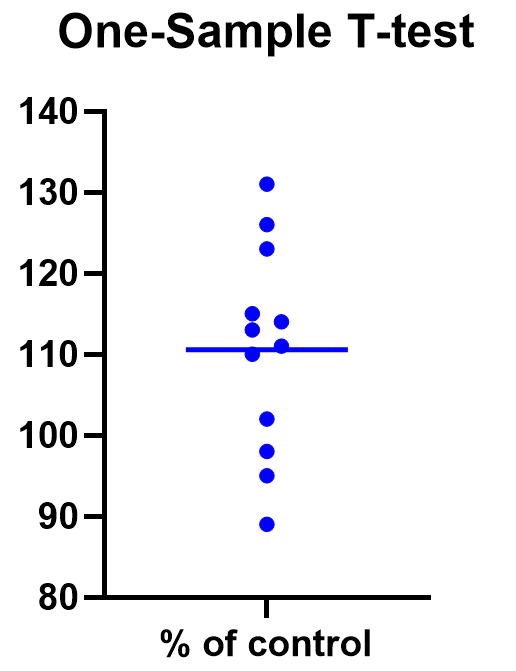
Here we have a simple plot of the data points, perhaps with a mark for the average. We’ve made this as an example, but the truth is that graphing is usually more visually telling for two-sample t tests than for just one sample.

Two sample t tests

There are several kinds of two sample t tests, with the two main categories being paired and unpaired (independent) samples.

Paired samples t test

In a paired samples t test, also called dependent samples t test, there are two samples of data, and each observation in one sample is “paired” with an observation in the second sample. The most common example is when measurements are taken on each subject before and after a treatment. A paired t test example research question is, “Is there a statistical difference between the average red blood cell counts before and after a treatment?”

Having two samples that are closely related simplifies the analysis. Statistical software, such as this paired t test calculator , will simply take a difference between the two values, and then compare that difference to 0.

In some (rare) situations, taking a difference between the pairs violates the assumptions of a t test, because the average difference changes based on the size of the before value (e.g., there’s a larger difference between before and after when there were more to start with). In this case, instead of using a difference test, use a ratio of the before and after values, which is referred to as ratio t tests .

Paired t test formula

The formula for paired samples t test is:

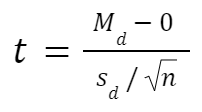
Md: Mean difference between the samples
sd: The standard deviation of the differences
n: The number of differences

Degrees of freedom are the same as before. If you’re studying for an exam, you can remember that the degrees of freedom are still n-1 (not n-2) because we are converting the data into a single column of differences rather than considering the two groups independently.

Also note that the null value here is simply 0. There is no real reason to include “minus 0” in an equation other than to illustrate that we are still doing a hypothesis test. After you take the difference between the two means, you are comparing that difference to 0.

For our example data, we have five test subjects and have taken two measurements from each: before (“control”) and after a treatment (“treated”). If we set alpha = 0.05 and perform a two-tailed test, we observe a statistically significant difference between the treated and control group (p=0.0160, t=4.01, df = 4). We are 95% confident that the true mean difference between the treated and control group is between 0.449 and 2.47.

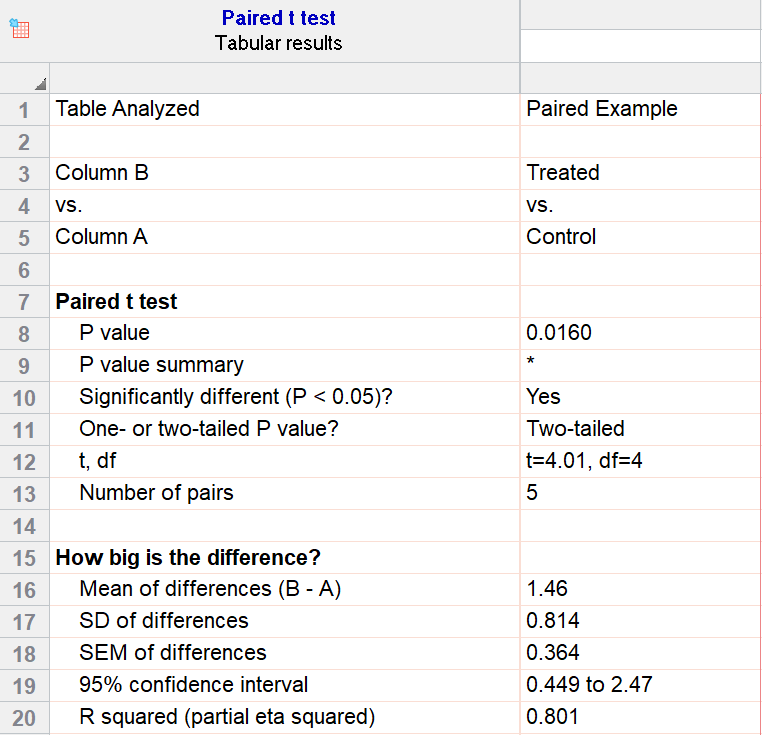
Graphing a paired t test

The significant result of the P value suggests evidence that the treatment had some effect, and we can also look at this graphically. The lines that connect the observations can help us spot a pattern, if it exists. In this case the lines show that all observations increased after treatment. While not all graphics are this straightforward, here it is very consistent with the outcome of the t test.

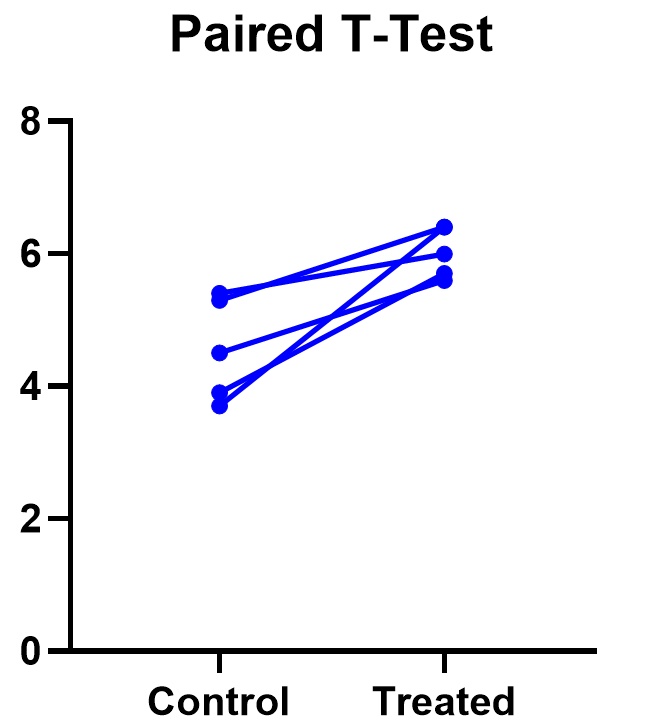
Prism’s estimation plot is even more helpful because it shows both the data (like above) and the confidence interval for the difference between means. You can easily see the evidence of significance since the confidence interval on the right does not contain zero.

Here are some more graphing tips for paired t tests .

Unpaired samples t test

Unpaired samples t test, also called independent samples t test, is appropriate when you have two sample groups that aren’t correlated with one another. A pharma example is testing a treatment group against a control group of different subjects. Compare that with a paired sample, which might be recording the same subjects before and after a treatment.

With unpaired t tests, in addition to choosing your level of significance and a one or two tailed test, you need to determine whether or not to assume that the variances between the groups are the same or not. If you assume equal variances, then you can “pool” the calculation of the standard error between the two samples. Otherwise, the standard choice is Welch’s t test which corrects for unequal variances. This choice affects the calculation of the test statistic and the power of the test, which is the test’s sensitivity to detect statistical significance.

It’s best to choose whether or not you’ll use a pooled or unpooled (Welch’s) standard error before running your experiment, because the standard statistical test is notoriously problematic. See more details about unequal variances here .

As long as you’re using statistical software, such as this two-sample t test calculator , it’s just as easy to calculate a test statistic whether or not you assume that the variances of your two samples are the same. If you’re doing it by hand, however, the calculations get more complicated with unequal variances.

Unpaired (independent) samples t test formula

The general two-sample t test formula is:

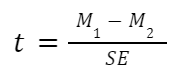
M1 and M2: Two means you are comparing, one from each dataset
SE : The combined standard error of the two samples (calculated using pooled or unpooled standard error)

The denominator (standard error) calculation can be complicated, as can the degrees of freedom. If the groups are not balanced (the same number of observations in each), you will need to account for both when determining n for the test as a whole.

As an example for this family, we conduct a paired samples t test assuming equal variances (pooled). Based on our research hypothesis, we’ll conduct a two-tailed test, and use alpha=0.05 for our level of significance. Our samples were unbalanced, with two samples of 6 and 5 observations respectively.

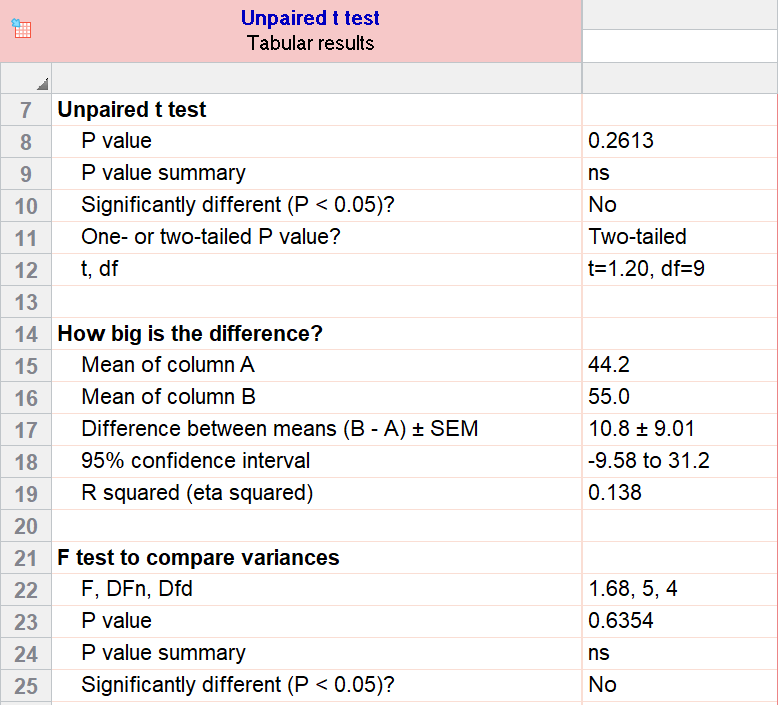
The P value (p=0.261, t = 1.20, df = 9) is higher than our threshold of 0.05. We have not found sufficient evidence to suggest a significant difference. You can see the confidence interval of the difference of the means is -9.58 to 31.2.

Note that the F-test result shows that the variances of the two groups are not significantly different from each other.

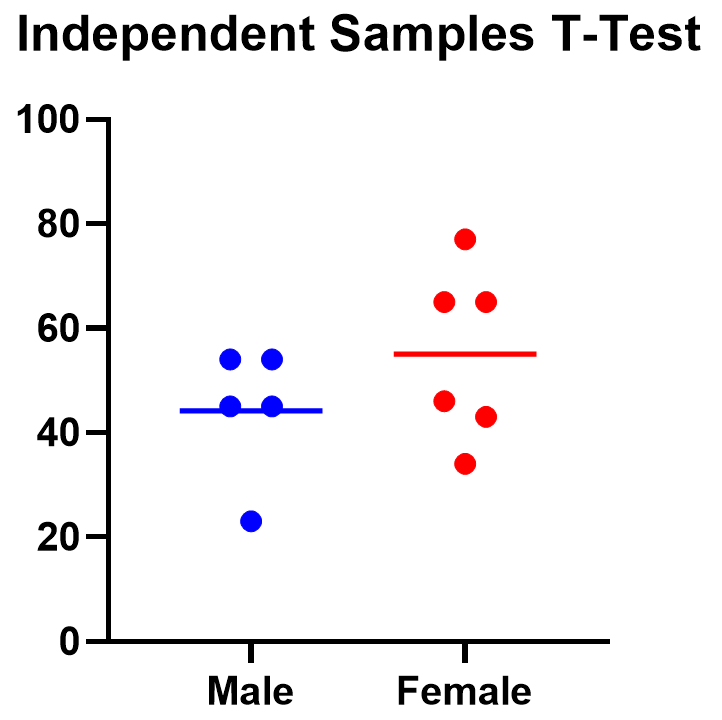
Graphing an unpaired samples t test

For an unpaired samples t test, graphing the data can quickly help you get a handle on the two groups and how similar or different they are. Like the paired example, this helps confirm the evidence (or lack thereof) that is found by doing the t test itself.

Below you can see that the observed mean for females is higher than that for males. But because of the variability in the data, we can’t tell if the means are actually different or if the difference is just by chance.

Nonparametric alternatives for t tests

If your data comes from a normal distribution (or something close enough to a normal distribution), then a t test is valid. If that assumption is violated, you can use nonparametric alternatives.

T tests evaluate whether the mean is different from another value, whereas nonparametric alternatives compare either the median or the rank. Medians are well-known to be much more robust to outliers than the mean.

The downside to nonparametric tests is that they don’t have as much statistical power, meaning a larger difference is required in order to determine that it’s statistically significant.

Wilcoxon signed-rank test

The Wilcoxon signed-rank test is the nonparametric cousin to the one-sample t test. This compares a sample median to a hypothetical median value. It is sometimes erroneously even called the Wilcoxon t test (even though it calculates a “W” statistic).

And if you have two related samples, you should use the Wilcoxon matched pairs test instead. The two versions of Wilcoxon are different, and the matched pairs version is specifically for comparing the median difference for paired samples.

Mann-Whitney and Kolmogorov-Smirnov tests

For unpaired (independent) samples, there are multiple options for nonparametric testing. Mann-Whitney is more popular and compares the mean ranks (the ordering of values from smallest to largest) of the two samples. Mann-Whitney is often misrepresented as a comparison of medians, but that’s not always the case. Kolmogorov-Smirnov tests if the overall distributions differ between the two samples.

More t test FAQs

What is the formula for a t test.

The exact formula depends on which type of t test you are running, although there is a basic structure that all t tests have in common. All t test statistics will have the form:

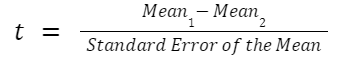
t : The t test statistic you calculate for your test
Mean1 and Mean2: Two means you are comparing, at least 1 from your own dataset
Standard Error of the Mean : The standard error of the mean , also called the standard deviation of the mean, which takes into account the variance and size of your dataset

The exact formula for any t test can be slightly different, particularly the calculation of the standard error. Not only does it matter whether one or two samples are being compared, the relationship between the samples can make a difference too.

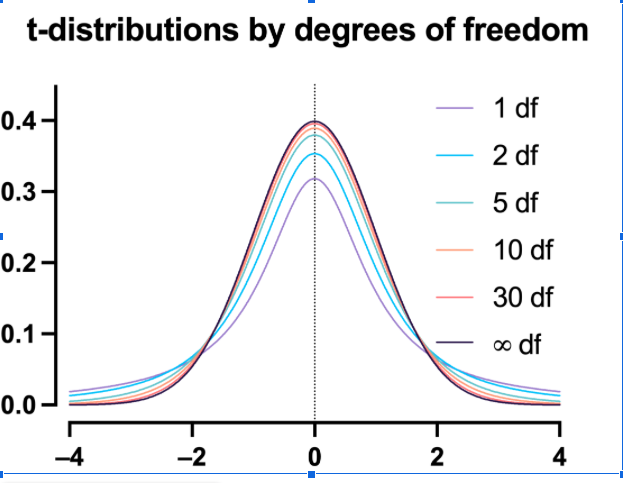
What is a t-distribution?

A t-distribution is similar to a normal distribution. It’s a bell-shaped curve, but compared to a normal it has fatter tails, which means that it’s more common to observe extremes. T-distributions are identified by the number of degrees of freedom. The higher the number, the closer the t-distribution gets to a normal distribution. After about 30 degrees of freedom, a t and a standard normal are practically the same.

What are degrees of freedom?

Degrees of freedom are a measure of how large your dataset is. They aren’t exactly the number of observations, because they also take into account the number of parameters (e.g., mean, variance) that you have estimated.

What is the difference between paired vs unpaired t tests?

Both paired and unpaired t tests involve two sample groups of data. With a paired t test, the values in each group are related (usually they are before and after values measured on the same test subject). In contrast, with unpaired t tests, the observed values aren’t related between groups. An unpaired, or independent t test, example is comparing the average height of children at school A vs school B.

When do I use a z-test versus a t test?

Z-tests, which compare data using a normal distribution rather than a t-distribution, are primarily used for two situations. The first is when you’re evaluating proportions (number of failures on an assembly line). The second is when your sample size is large enough (usually around 30) that you can use a normal approximation to evaluate the means.

When should I use ANOVA instead of a t test?

Use ANOVA if you have more than two group means to compare.

What are the differences between t test vs chi square?

Chi square tests are used to evaluate contingency tables , which record a count of the number of subjects that fall into particular categories (e.g., truck, SUV, car). t tests compare the mean(s) of a variable of interest (e.g., height, weight).

What are P values?

P values are the probability that you would get data as or more extreme than the observed data given that the null hypothesis is true. It’s a mouthful, and there are a lot of issues to be aware of with P values.

What are t test critical values?

Critical values are a classical form (they aren’t used directly with modern computing) of determining if a statistical test is significant or not. Historically you could calculate your test statistic from your data, and then use a t-table to look up the cutoff value (critical value) that represented a “significant” result. You would then compare your observed statistic against the critical value.

How do I calculate degrees of freedom for my t test?

In most practical usage, degrees of freedom are the number of observations you have minus the number of parameters you are trying to estimate. The calculation isn’t always straightforward and is approximated for some t tests.

Statistical software calculates degrees of freedom automatically as part of the analysis, so understanding them in more detail isn’t needed beyond assuaging any curiosity.

Perform your own t test

Are you ready to calculate your own t test? Start your 30 day free trial of Prism and get access to:

A step by step guide on how to perform a t test
Sample data to save you time
More tips on how Prism can help your research

With Prism, in a matter of minutes you learn how to go from entering data to performing statistical analyses and generating high-quality graphs.

Search Search Please fill out this field.

What Is a T-Test?

Understanding the t-test, using a t-test, which t-test to use.

T-Test FAQs
Fundamental Analysis

T-Test: What It Is With Multiple Formulas and When To Use Them

Read how this calculation can be used for hypothesis testing in statistics

Adam Hayes, Ph.D., CFA, is a financial writer with 15+ years Wall Street experience as a derivatives trader. Besides his extensive derivative trading expertise, Adam is an expert in economics and behavioral finance. Adam received his master's in economics from The New School for Social Research and his Ph.D. from the University of Wisconsin-Madison in sociology. He is a CFA charterholder as well as holding FINRA Series 7, 55 & 63 licenses. He currently researches and teaches economic sociology and the social studies of finance at the Hebrew University in Jerusalem.

A t-test is an inferential statistic used to determine if there is a significant difference between the means of two groups and how they are related. T-tests are used when the data sets follow a normal distribution and have unknown variances, like the data set recorded from flipping a coin 100 times.

The t-test is a test used for hypothesis testing in statistics and uses the t-statistic, the t-distribution values, and the degrees of freedom to determine statistical significance.

Key Takeaways

A t-test is an inferential statistic used to determine if there is a statistically significant difference between the means of two variables.
The t-test is a test used for hypothesis testing in statistics.
Calculating a t-test requires three fundamental data values including the difference between the mean values from each data set, the standard deviation of each group, and the number of data values.
T-tests can be dependent or independent.

Investopedia / Sabrina Jiang

A t-test compares the average values of two data sets and determines if they came from the same population. In the above examples, a sample of students from class A and a sample of students from class B would not likely have the same mean and standard deviation. Similarly, samples taken from the placebo-fed control group and those taken from the drug prescribed group should have a slightly different mean and standard deviation.

Mathematically, the t-test takes a sample from each of the two sets and establishes the problem statement. It assumes a null hypothesis that the two means are equal.

Using the formulas, values are calculated and compared against the standard values. The assumed null hypothesis is accepted or rejected accordingly. If the null hypothesis qualifies to be rejected, it indicates that data readings are strong and are probably not due to chance.

The t-test is just one of many tests used for this purpose. Statisticians use additional tests other than the t-test to examine more variables and larger sample sizes. For a large sample size, statisticians use a z-test . Other testing options include the chi-square test and the f-test.

Consider that a drug manufacturer tests a new medicine. Following standard procedure, the drug is given to one group of patients and a placebo to another group called the control group. The placebo is a substance with no therapeutic value and serves as a benchmark to measure how the other group, administered the actual drug, responds.

After the drug trial, the members of the placebo-fed control group reported an increase in average life expectancy of three years, while the members of the group who are prescribed the new drug reported an increase in average life expectancy of four years.

Initial observation indicates that the drug is working. However, it is also possible that the observation may be due to chance. A t-test can be used to determine if the results are correct and applicable to the entire population.

Four assumptions are made while using a t-test. The data collected must follow a continuous or ordinal scale, such as the scores for an IQ test, the data is collected from a randomly selected portion of the total population, the data will result in a normal distribution of a bell-shaped curve, and equal or homogenous variance exists when the standard variations are equal.

T-Test Formula

Calculating a t-test requires three fundamental data values. They include the difference between the mean values from each data set, or the mean difference, the standard deviation of each group, and the number of data values of each group.

This comparison helps to determine the effect of chance on the difference, and whether the difference is outside that chance range. The t-test questions whether the difference between the groups represents a true difference in the study or merely a random difference.

The t-test produces two values as its output: t-value and degrees of freedom . The t-value, or t-score, is a ratio of the difference between the mean of the two sample sets and the variation that exists within the sample sets.

The numerator value is the difference between the mean of the two sample sets. The denominator is the variation that exists within the sample sets and is a measurement of the dispersion or variability.

This calculated t-value is then compared against a value obtained from a critical value table called the T-distribution table. Higher values of the t-score indicate that a large difference exists between the two sample sets. The smaller the t-value, the more similarity exists between the two sample sets.

A large t-score, or t-value, indicates that the groups are different while a small t-score indicates that the groups are similar.

Degrees of freedom refer to the values in a study that has the freedom to vary and are essential for assessing the importance and the validity of the null hypothesis. Computation of these values usually depends upon the number of data records available in the sample set.

Paired Sample T-Test

The correlated t-test, or paired t-test, is a dependent type of test and is performed when the samples consist of matched pairs of similar units, or when there are cases of repeated measures. For example, there may be instances where the same patients are repeatedly tested before and after receiving a particular treatment. Each patient is being used as a control sample against themselves.

This method also applies to cases where the samples are related or have matching characteristics, like a comparative analysis involving children, parents, or siblings.

The formula for computing the t-value and degrees of freedom for a paired t-test is:

T = mean 1 − mean 2 s ( diff ) ( n ) where: mean 1 and mean 2 = The average values of each of the sample sets s ( diff ) = The standard deviation of the differences of the paired data values n = The sample size (the number of paired differences) n − 1 = The degrees of freedom \begin{aligned}&T=\frac{\textit{mean}1 - \textit{mean}2}{\frac{s(\text{diff})}{\sqrt{(n)}}}\\&\textbf{where:}\\&\textit{mean}1\text{ and }\textit{mean}2=\text{The average values of each of the sample sets}\\&s(\text{diff})=\text{The standard deviation of the differences of the paired data values}\\&n=\text{The sample size (the number of paired differences)}\\&n-1=\text{The degrees of freedom}\end{aligned} T = ( n ) s ( diff ) mean 1 − mean 2 where: mean 1 and mean 2 = The average values of each of the sample sets s ( diff ) = The standard deviation of the differences of the paired data values n = The sample size (the number of paired differences) n − 1 = The degrees of freedom

Equal Variance or Pooled T-Test

The equal variance t-test is an independent t-test and is used when the number of samples in each group is the same, or the variance of the two data sets is similar.

The formula used for calculating t-value and degrees of freedom for equal variance t-test is:

T-value = m e a n 1 − m e a n 2 ( n 1 − 1 ) × v a r 1 2 + ( n 2 − 1 ) × v a r 2 2 n 1 + n 2 − 2 × 1 n 1 + 1 n 2 where: m e a n 1 and m e a n 2 = Average values of each of the sample sets v a r 1 and v a r 2 = Variance of each of the sample sets n 1 and n 2 = Number of records in each sample set \begin{aligned}&\text{T-value} = \frac{ mean1 - mean2 }{\frac {(n1 - 1) \times var1^2 + (n2 - 1) \times var2^2 }{ n1 +n2 - 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{where:}\\&mean1 \text{ and } mean2 = \text{Average values of each} \\&\text{of the sample sets}\\&var1 \text{ and } var2 = \text{Variance of each of the sample sets}\\&n1 \text{ and } n2 = \text{Number of records in each sample set} \end{aligned} T-value = n 1 + n 2 − 2 ( n 1 − 1 ) × v a r 1 2 + ( n 2 − 1 ) × v a r 2 2 × n 1 1 + n 2 1 m e an 1 − m e an 2 where: m e an 1 and m e an 2 = Average values of each of the sample sets v a r 1 and v a r 2 = Variance of each of the sample sets n 1 and n 2 = Number of records in each sample set

Degrees of Freedom = n 1 + n 2 − 2 where: n 1 and n 2 = Number of records in each sample set \begin{aligned} &\text{Degrees of Freedom} = n1 + n2 - 2 \\ &\textbf{where:}\\ &n1 \text{ and } n2 = \text{Number of records in each sample set} \\ \end{aligned} Degrees of Freedom = n 1 + n 2 − 2 where: n 1 and n 2 = Number of records in each sample set

Unequal Variance T-Test

The unequal variance t-test is an independent t-test and is used when the number of samples in each group is different, and the variance of the two data sets is also different. This test is also called Welch's t-test.

The formula used for calculating t-value and degrees of freedom for an unequal variance t-test is:

T-value = m e a n 1 − m e a n 2 ( v a r 1 n 1 + v a r 2 n 2 ) where: m e a n 1 and m e a n 2 = Average values of each of the sample sets v a r 1 and v a r 2 = Variance of each of the sample sets n 1 and n 2 = Number of records in each sample set \begin{aligned}&\text{T-value}=\frac{mean1-mean2}{\sqrt{\bigg(\frac{var1}{n1}{+\frac{var2}{n2}\bigg)}}}\\&\textbf{where:}\\&mean1 \text{ and } mean2 = \text{Average values of each} \\&\text{of the sample sets} \\&var1 \text{ and } var2 = \text{Variance of each of the sample sets} \\&n1 \text{ and } n2 = \text{Number of records in each sample set} \end{aligned} T-value = ( n 1 v a r 1 + n 2 v a r 2 ) m e an 1 − m e an 2 where: m e an 1 and m e an 2 = Average values of each of the sample sets v a r 1 and v a r 2 = Variance of each of the sample sets n 1 and n 2 = Number of records in each sample set

Degrees of Freedom = ( v a r 1 2 n 1 + v a r 2 2 n 2 ) 2 ( v a r 1 2 n 1 ) 2 n 1 − 1 + ( v a r 2 2 n 2 ) 2 n 2 − 1 where: v a r 1 and v a r 2 = Variance of each of the sample sets n 1 and n 2 = Number of records in each sample set \begin{aligned} &\text{Degrees of Freedom} = \frac{ \left ( \frac{ var1^2 }{ n1 } + \frac{ var2^2 }{ n2 } \right )^2 }{ \frac{ \left ( \frac{ var1^2 }{ n1 } \right )^2 }{ n1 - 1 } + \frac{ \left ( \frac{ var2^2 }{ n2 } \right )^2 }{ n2 - 1}} \\ &\textbf{where:}\\ &var1 \text{ and } var2 = \text{Variance of each of the sample sets} \\ &n1 \text{ and } n2 = \text{Number of records in each sample set} \\ \end{aligned} Degrees of Freedom = n 1 − 1 ( n 1 v a r 1 2 ) 2 + n 2 − 1 ( n 2 v a r 2 2 ) 2 ( n 1 v a r 1 2 + n 2 v a r 2 2 ) 2 where: v a r 1 and v a r 2 = Variance of each of the sample sets n 1 and n 2 = Number of records in each sample set

The following flowchart can be used to determine which t-test to use based on the characteristics of the sample sets. The key items to consider include the similarity of the sample records, the number of data records in each sample set, and the variance of each sample set.

Image by Julie Bang Â© Investopedia 2019

Example of an Unequal Variance T-Test

Assume that the diagonal measurement of paintings received in an art gallery is taken. One group of samples includes 10 paintings, while the other includes 20 paintings. The data sets, with the corresponding mean and variance values, are as follows:

Though the mean of Set 2 is higher than that of Set 1, we cannot conclude that the population corresponding to Set 2 has a higher mean than the population corresponding to Set 1.

Is the difference from 19.4 to 21.6 due to chance alone, or do differences exist in the overall populations of all the paintings received in the art gallery? We establish the problem by assuming the null hypothesis that the mean is the same between the two sample sets and conduct a t-test to test if the hypothesis is plausible.

Since the number of data records is different (n1 = 10 and n2 = 20) and the variance is also different, the t-value and degrees of freedom are computed for the above data set using the formula mentioned in the Unequal Variance T-Test section.

The t-value is -2.24787. Since the minus sign can be ignored when comparing the two t-values, the computed value is 2.24787.

The degrees of freedom value is 24.38 and is reduced to 24, owing to the formula definition requiring rounding down of the value to the least possible integer value.

One can specify a level of probability (alpha level, level of significance, p ) as a criterion for acceptance. In most cases, a 5% value can be assumed.

Using the degree of freedom value as 24 and a 5% level of significance, a look at the t-value distribution table gives a value of 2.064. Comparing this value against the computed value of 2.247 indicates that the calculated t-value is greater than the table value at a significance level of 5%. Therefore, it is safe to reject the null hypothesis that there is no difference between means. The population set has intrinsic differences, and they are not by chance.

How Is the T-Distribution Table Used?

The T-Distribution Table is available in one-tail and two-tails formats. The former is used for assessing cases that have a fixed value or range with a clear direction, either positive or negative. For instance, what is the probability of the output value remaining below -3, or getting more than seven when rolling a pair of dice? The latter is used for range-bound analysis, such as asking if the coordinates fall between -2 and +2.

What Is an Independent T-Test?

The samples of independent t-tests are selected independent of each other where the data sets in the two groups don’t refer to the same values. They may include a group of 100 randomly unrelated patients split into two groups of 50 patients each. One of the groups becomes the control group and is administered a placebo, while the other group receives a prescribed treatment. This constitutes two independent sample groups that are unpaired and unrelated to each other.

What Does a T-Test Explain and How Are They Used?

A t-test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment has an effect on the population of interest, or whether two groups are different from one another.

Terms of Service
Editorial Policy
Privacy Policy
Your Privacy Choices

Independent t-test for two samples

Introduction.

The independent t-test, also called the two sample t-test, independent-samples t-test or student's t-test, is an inferential statistical test that determines whether there is a statistically significant difference between the means in two unrelated groups.

Null and alternative hypotheses for the independent t-test

The null hypothesis for the independent t-test is that the population means from the two unrelated groups are equal:

H 0 : u 1 = u 2

In most cases, we are looking to see if we can show that we can reject the null hypothesis and accept the alternative hypothesis, which is that the population means are not equal:

H A : u 1 ≠ u 2

To do this, we need to set a significance level (also called alpha) that allows us to either reject or accept the alternative hypothesis. Most commonly, this value is set at 0.05.

What do you need to run an independent t-test?

In order to run an independent t-test, you need the following:

One independent, categorical variable that has two levels/groups.
One continuous dependent variable.

Unrelated groups

Unrelated groups, also called unpaired groups or independent groups, are groups in which the cases (e.g., participants) in each group are different. Often we are investigating differences in individuals, which means that when comparing two groups, an individual in one group cannot also be a member of the other group and vice versa. An example would be gender - an individual would have to be classified as either male or female – not both.

Assumption of normality of the dependent variable

The independent t-test requires that the dependent variable is approximately normally distributed within each group.

Note: Technically, it is the residuals that need to be normally distributed, but for an independent t-test, both will give you the same result.

You can test for this using a number of different tests, but the Shapiro-Wilks test of normality or a graphical method, such as a Q-Q Plot, are very common. You can run these tests using SPSS Statistics, the procedure for which can be found in our Testing for Normality guide. However, the t-test is described as a robust test with respect to the assumption of normality. This means that some deviation away from normality does not have a large influence on Type I error rates. The exception to this is if the ratio of the smallest to largest group size is greater than 1.5 (largest compared to smallest).

What to do when you violate the normality assumption

If you find that either one or both of your group's data is not approximately normally distributed and groups sizes differ greatly, you have two options: (1) transform your data so that the data becomes normally distributed (to do this in SPSS Statistics see our guide on Transforming Data ), or (2) run the Mann-Whitney U test which is a non-parametric test that does not require the assumption of normality (to run this test in SPSS Statistics see our guide on the Mann-Whitney U Test ).

Assumption of homogeneity of variance

The independent t-test assumes the variances of the two groups you are measuring are equal in the population. If your variances are unequal, this can affect the Type I error rate. The assumption of homogeneity of variance can be tested using Levene's Test of Equality of Variances, which is produced in SPSS Statistics when running the independent t-test procedure. If you have run Levene's Test of Equality of Variances in SPSS Statistics, you will get a result similar to that below:

Levene's Test for Equality of Variances in the Independent T-Test Procedure within SPSS

This test for homogeneity of variance provides an F -statistic and a significance value ( p -value). We are primarily concerned with the significance value – if it is greater than 0.05 (i.e., p > .05), our group variances can be treated as equal. However, if p < 0.05, we have unequal variances and we have violated the assumption of homogeneity of variances.

Overcoming a violation of the assumption of homogeneity of variance

If the Levene's Test for Equality of Variances is statistically significant, which indicates that the group variances are unequal in the population, you can correct for this violation by not using the pooled estimate for the error term for the t -statistic, but instead using an adjustment to the degrees of freedom using the Welch-Satterthwaite method. In all reality, you will probably never have heard of these adjustments because SPSS Statistics hides this information and simply labels the two options as "Equal variances assumed" and "Equal variances not assumed" without explicitly stating the underlying tests used. However, you can see the evidence of these tests as below:

Differences in the t-statistic and the degrees of freedom when homogeneity of variance is not assumed

From the result of Levene's Test for Equality of Variances, we can reject the null hypothesis that there is no difference in the variances between the groups and accept the alternative hypothesis that there is a statistically significant difference in the variances between groups. The effect of not being able to assume equal variances is evident in the final column of the above figure where we see a reduction in the value of the t -statistic and a large reduction in the degrees of freedom (df). This has the effect of increasing the p -value above the critical significance level of 0.05. In this case, we therefore do not accept the alternative hypothesis and accept that there are no statistically significant differences between means. This would not have been our conclusion had we not tested for homogeneity of variances.

Reporting the result of an independent t-test

When reporting the result of an independent t-test, you need to include the t -statistic value, the degrees of freedom (df) and the significance value of the test ( p -value). The format of the test result is: t (df) = t -statistic, p = significance value. Therefore, for the example above, you could report the result as t (7.001) = 2.233, p = 0.061.

Fully reporting your results

In order to provide enough information for readers to fully understand the results when you have run an independent t-test, you should include the result of normality tests, Levene's Equality of Variances test, the two group means and standard deviations, the actual t-test result and the direction of the difference (if any). In addition, you might also wish to include the difference between the groups along with a 95% confidence interval. For example:

Inspection of Q-Q Plots revealed that cholesterol concentration was normally distributed for both groups and that there was homogeneity of variance as assessed by Levene's Test for Equality of Variances. Therefore, an independent t-test was run on the data with a 95% confidence interval (CI) for the mean difference. It was found that after the two interventions, cholesterol concentrations in the dietary group (6.15 ± 0.52 mmol/L) were significantly higher than the exercise group (5.80 ± 0.38 mmol/L) ( t (38) = 2.470, p = 0.018) with a difference of 0.35 (95% CI, 0.06 to 0.64) mmol/L.

To know how to run an independent t-test in SPSS Statistics, see our SPSS Statistics Independent-Samples T-Test guide. Alternatively, you can carry out an independent-samples t-test using Excel, R and RStudio .

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

13.3: The Independent Samples t-test (Student Test)

Last updated
Save as PDF
Page ID 4023

Danielle Navarro
University of New South Wales

Although the one sample t-test has its uses, it’s not the most typical example of a t-test 189 . A much more common situation arises when you’ve got two different groups of observations. In psychology, this tends to correspond to two different groups of participants, where each group corresponds to a different condition in your study. For each person in the study, you measure some outcome variable of interest, and the research question that you’re asking is whether or not the two groups have the same population mean. This is the situation that the independent samples t-test is designed for.

Suppose we have 33 students taking Dr Harpo’s statistics lectures, and Dr Harpo doesn’t grade to a curve. Actually, Dr Harpo’s grading is a bit of a mystery, so we don’t really know anything about what the average grade is for the class as a whole. There are two tutors for the class, Anastasia and Bernadette. There are N 1 =15 students in Anastasia’s tutorials, and N 2 =18 in Bernadette’s tutorials. The research question I’m interested in is whether Anastasia or Bernadette is a better tutor, or if it doesn’t make much of a difference. Dr Harpo emails me the course grades, in the harpo.Rdata file. As usual, I’ll load the file and have a look at what variables it contains:

As we can see, there’s a single data frame with two variables, grade and tutor . The grade variable is a numeric vector, containing the grades for all N=33 students taking Dr Harpo’s class; the tutor variable is a factor that indicates who each student’s tutor was. The first six observations in this data set are shown below:

We can calculate means and standard deviations, using the mean() and sd() functions. Rather than show the R output, here’s a nice little summary table:

To give you a more detailed sense of what’s going on here, I’ve plotted histograms showing the distribution of grades for both tutors (Figure 13.6 and 13.7). Inspection of these histograms suggests that the students in Anastasia’s class may be getting slightly better grades on average, though they also seem a little more variable.

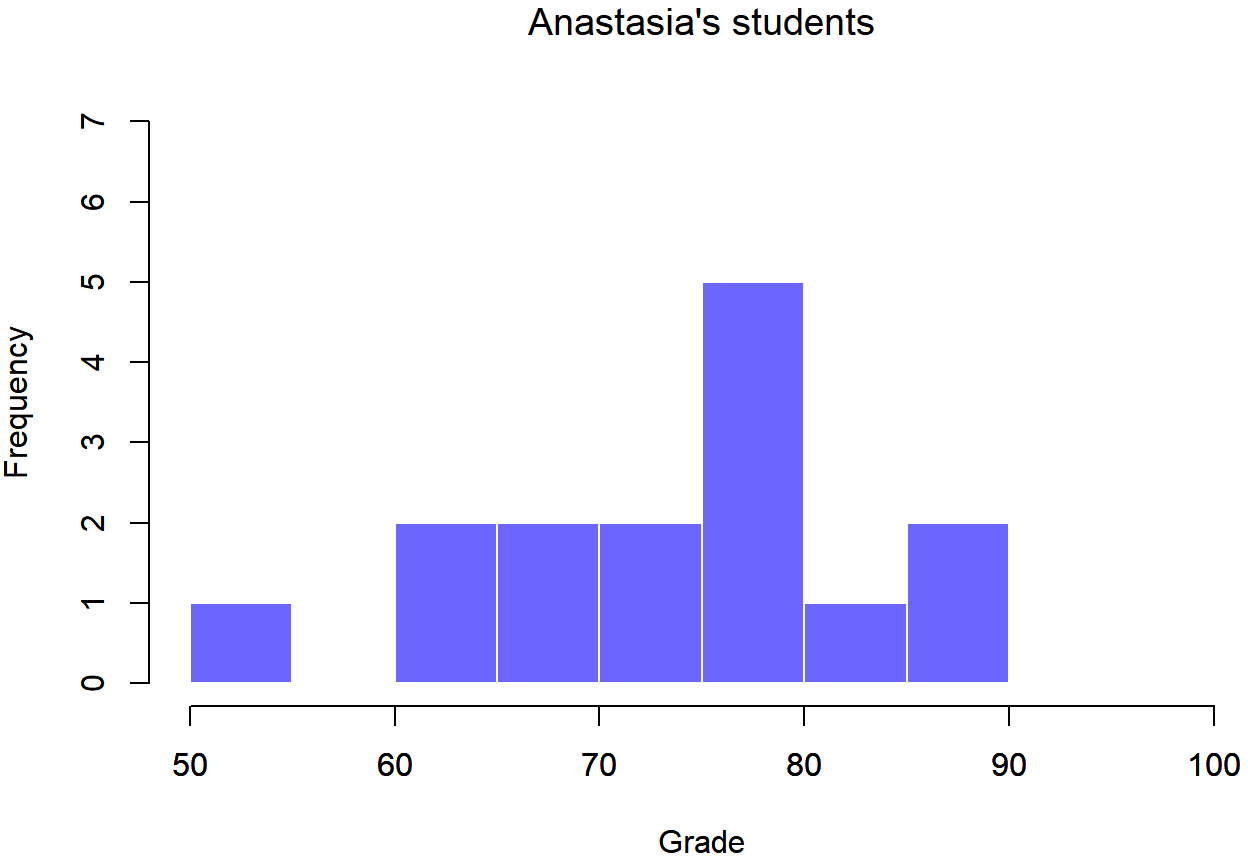
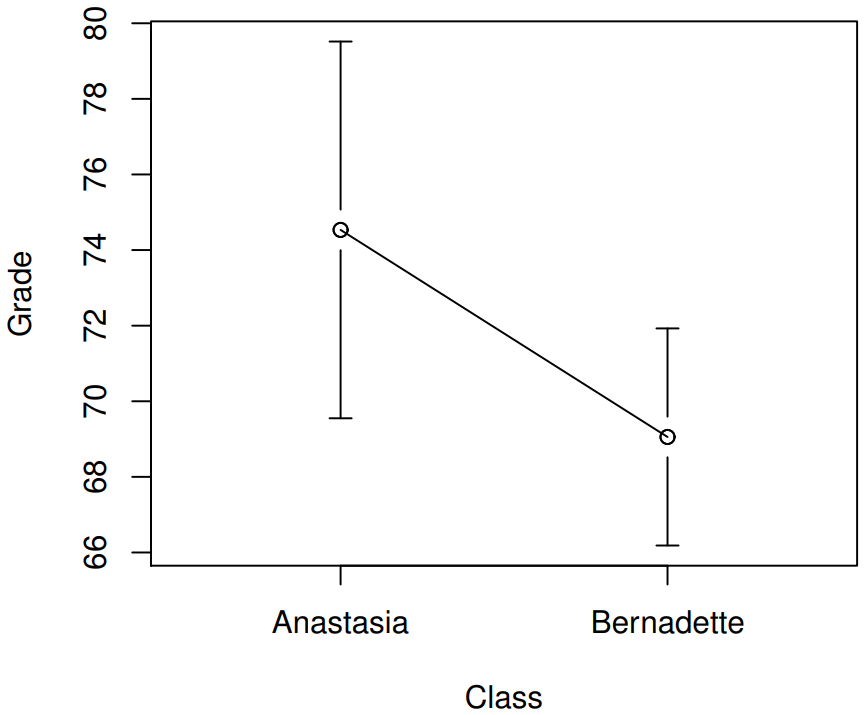
Here is a simpler plot showing the means and corresponding confidence intervals for both groups of students (Figure 13.8).

Introducing the test

The independent samples t-test comes in two different forms, Student’s and Welch’s. The original Student t-test – which is the one I’ll describe in this section – is the simpler of the two, but relies on much more restrictive assumptions than the Welch t-test. Assuming for the moment that you want to run a two-sided test, the goal is to determine whether two “independent samples” of data are drawn from populations with the same mean (the null hypothesis) or different means (the alternative hypothesis). When we say “independent” samples, what we really mean here is that there’s no special relationship between observations in the two samples. This probably doesn’t make a lot of sense right now, but it will be clearer when we come to talk about the paired samples t-test later on. For now, let’s just point out that if we have an experimental design where participants are randomly allocated to one of two groups, and we want to compare the two groups’ mean performance on some outcome measure, then an independent samples t-test (rather than a paired samples t-test) is what we’re after.

Okay, so let’s let μ 1 denote the true population mean for group 1 (e.g., Anastasia’s students), and μ 2 will be the true population mean for group 2 (e.g., Bernadette’s students), 190 and as usual we’ll let $\bar{X}_{1}$ and $\bar{X}_{2}$ denote the observed sample means for both of these groups. Our null hypothesis states that the two population means are identical (μ 1 =μ 2 ) and the alternative to this is that they are not (μ 1 ≠μ 2 ). Written in mathematical-ese, this is…

H 0 :μ 1 =μ 2

H 1 :μ 1 ≠μ 2

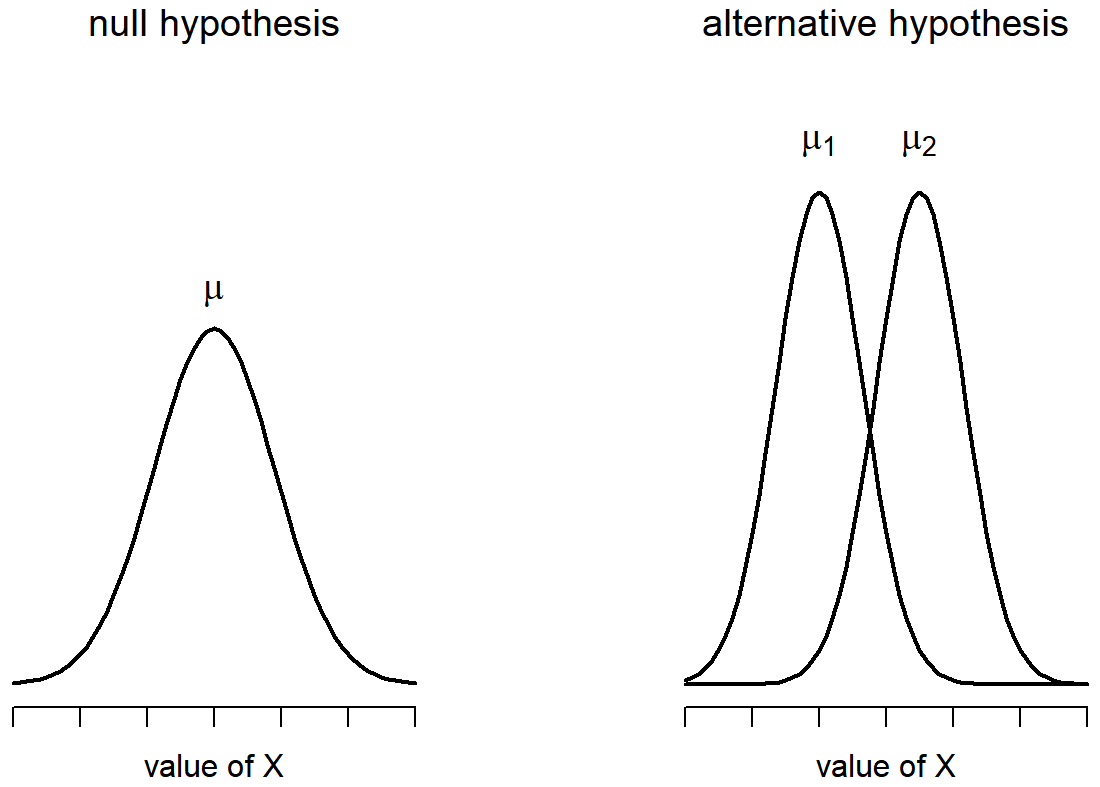
To construct a hypothesis test that handles this scenario, we start by noting that if the null hypothesis is true, then the difference between the population means is exactly zero, μ 1 −μ 2 =0 As a consequence, a diagnostic test statistic will be based on the difference between the two sample means. Because if the null hypothesis is true, then we’d expect

$\bar{X}_{1}$ - $\bar{X}_{2}$

to be pretty close to zero. However, just like we saw with our one-sample tests (i.e., the one-sample z-test and the one-sample t-test) we have to be precise about exactly how close to zero this difference

$\ t ={\bar{X}_1 - \bar{X}_2 \over SE}$

We just need to figure out what this standard error estimate actually is. This is a bit trickier than was the case for either of the two tests we’ve looked at so far, so we need to go through it a lot more carefully to understand how it works.

“pooled estimate” of the standard deviation

In the original “Student t-test”, we make the assumption that the two groups have the same population standard deviation: that is, regardless of whether the population means are the same, we assume that the population standard deviations are identical, σ 1 =σ 2 . Since we’re assuming that the two standard deviations are the same, we drop the subscripts and refer to both of them as σ. How should we estimate this? How should we construct a single estimate of a standard deviation when we have two samples? The answer is, basically, we average them. Well, sort of. Actually, what we do is take a weighed average of the variance estimates, which we use as our pooled estimate of the variance . The weight assigned to each sample is equal to the number of observations in that sample, minus 1. Mathematically, we can write this as

$\ \omega_{1}$=N 1 −1

$\ \omega_{2}$=N 2 −1

Now that we’ve assigned weights to each sample, we calculate the pooled estimate of the variance by taking the weighted average of the two variance estimates, $\ \hat{\sigma_1}^2$ and $\ \hat{\sigma_2}^2$

$\ \hat{\sigma_p}^2 ={ \omega_{1}\hat{\sigma_1}^2+\omega_{2}\hat{\sigma_2}^2 \over \omega_{1}+\omega_{2}}$

Finally, we convert the pooled variance estimate to a pooled standard deviation estimate, by taking the square root. This gives us the following formula for $\ \hat{\sigma_p}$,

$\ \hat{\sigma_p} =\sqrt{\omega_1\hat{\sigma_1}^2+\omega_2\hat{\sigma_2}^2\over \omega_1+\omega_2} $

And if you mentally substitute $\ \omega_1$=N1−1 and $\ \omega_2$=N2−1 into this equation you get a very ugly looking formula; a very ugly formula that actually seems to be the “standard” way of describing the pooled standard deviation estimate. It’s not my favourite way of thinking about pooled standard deviations, however. 191

same pooled estimate, described differently

I prefer to think about it like this. Our data set actually corresponds to a set of N observations, which are sorted into two groups. So let’s use the notation X ik to refer to the grade received by the i-th student in the k-th tutorial group: that is, X 11 is the grade received by the first student in Anastasia’s class, X 21 is her second student, and so on. And we have two separate group means $\ \bar{X_1}$ and $\ \bar{X_2}$, which we could “generically” refer to using the notation $\ \bar{X_k}$, i.e., the mean grade for the k-th tutorial group. So far, so good. Now, since every single student falls into one of the two tutorials, and so we can describe their deviation from the group mean as the difference

$\ X_{ik} - \bar{X_k}$

So why not just use these deviations (i.e., the extent to which each student’s grade differs from the mean grade in their tutorial?) Remember, a variance is just the average of a bunch of squared deviations, so let’s do that. Mathematically, we could write it like this:

$\ ∑_{ik} (X_{ik}-\bar{X}_k)^2 \over N $

where the notation “∑ ik ” is a lazy way of saying “calculate a sum by looking at all students in all tutorials”, since each “ik” corresponds to one student. 192 But, as we saw in Chapter 10, calculating the variance by dividing by N produces a biased estimate of the population variance. And previously, we needed to divide by N−1 to fix this. However, as I mentioned at the time, the reason why this bias exists is because the variance estimate relies on the sample mean; and to the extent that the sample mean isn’t equal to the population mean, it can systematically bias our estimate of the variance. But this time we’re relying on two sample means! Does this mean that we’ve got more bias? Yes, yes it does. And does this mean we now need to divide by N−2 instead of N−1, in order to calculate our pooled variance estimate? Why, yes…

$\hat{\sigma}_{p}\ ^{2}=\dfrac{\sum_{i k}\left(X_{i k}-X_{k}\right)^{2}}{N-2}$

Oh, and if you take the square root of this then you get $\ \hat{\sigma_{P}}$, the pooled standard deviation estimate. In other words, the pooled standard deviation calculation is nothing special: it’s not terribly different to the regular standard deviation calculation.

Completing the test

Regardless of which way you want to think about it, we now have our pooled estimate of the standard deviation. From now on, I’ll drop the silly p subscript, and just refer to this estimate as $\ \hat{\sigma}$. Great. Let’s now go back to thinking about the bloody hypothesis test, shall we? Our whole reason for calculating this pooled estimate was that we knew it would be helpful when calculating our standard error estimate. But, standard error of what ? In the one-sample t-test, it was the standard error of the sample mean, SE ($\ \bar{X}$), and since SE ($\ \bar{X}=\sigma/ \sqrt{N}$ that’s what the denominator of our t-statistic looked like. This time around, however, we have two sample means. And what we’re interested in, specifically, is the the difference between the two $\ \bar{X_1}$ - $\ \bar{X_2}$. As a consequence, the standard error that we need to divide by is in fact the standard error of the difference between means. As long as the two variables really do have the same standard deviation, then our estimate for the standard error is

$\operatorname{SE}\left(\bar{X}_{1}-\bar{X}_{2}\right)=\hat{\sigma} \sqrt{\dfrac{1}{N_{1}}+\dfrac{1}{N_{2}}}$

and our t-statistic is therefore

$t=\dfrac{\bar{X}_{1}-\bar{X}_{2}}{\operatorname{SE}\left(\bar{X}_{1}-\bar{X}_{2}\right)}$

(shocking, isn’t it?) as long as the null hypothesis is true, and all of the assumptions of the test are met. The degrees of freedom, however, is slightly different. As usual, we can think of the degrees of freedom to be equal to the number of data points minus the number of constraints. In this case, we have N observations (N1 in sample 1, and N2 in sample 2), and 2 constraints (the sample means). So the total degrees of freedom for this test are N−2.

Doing the test in R

Not surprisingly, you can run an independent samples t-test using the t.test() function (Section 13.7), but once again I’m going to start with a somewhat simpler function in the lsr package. That function is unimaginatively called independentSamplesTTest() . First, recall that our data look like this:

The outcome variable for our test is the student grade , and the groups are defined in terms of the tutor for each class. So you probably won’t be too surprised to see that we’re going to describe the test that we want in terms of an R formula that reads like this grade ~ tutor . The specific command that we need is:

The first two arguments should be familiar to you. The first one is the formula that tells R what variables to use and the second one tells R the name of the data frame that stores those variables. The third argument is not so obvious. By saying var.equal = TRUE , what we’re really doing is telling R to use the Student independent samples t-test. More on this later. For now, lets ignore that bit and look at the output:

The output has a very familiar form. First, it tells you what test was run, and it tells you the names of the variables that you used. The second part of the output reports the sample means and standard deviations for both groups (i.e., both tutorial groups). The third section of the output states the null hypothesis and the alternative hypothesis in a fairly explicit form. It then reports the test results: just like last time, the test results consist of a t-statistic, the degrees of freedom, and the p-value. The final section reports two things: it gives you a confidence interval, and an effect size. I’ll talk about effect sizes later. The confidence interval, however, I should talk about now.

It’s pretty important to be clear on what this confidence interval actually refers to: it is a confidence interval for the difference between the group means. In our example, Anastasia’s students had an average grade of 74.5, and Bernadette’s students had an average grade of 69.1, so the difference between the two sample means is 5.4. But of course the difference between population means might be bigger or smaller than this. The confidence interval reported by the independentSamplesTTest() function tells you that there’s a 95% chance that the true difference between means lies between 0.2 and 10.8.

In any case, the difference between the two groups is significant (just barely), so we might write up the result using text like this:

The mean grade in Anastasia’s class was 74.5% (std dev = 9.0), whereas the mean in Bernadette’s class was 69.1% (std dev = 5.8). A Student’s independent samples t-test showed that this 5.4% difference was significant (t(31)=2.1, p<.05, CI 95 =[0.2,10.8], d=.74), suggesting that a genuine difference in learning outcomes has occurred.

Notice that I’ve included the confidence interval and the effect size in the stat block. People don’t always do this. At a bare minimum, you’d expect to see the t-statistic, the degrees of freedom and the p value. So you should include something like this at a minimum: t(31)=2.1, p<.05. If statisticians had their way, everyone would also report the confidence interval and probably the effect size measure too, because they are useful things to know. But real life doesn’t always work the way statisticians want it to: you should make a judgment based on whether you think it will help your readers, and (if you’re writing a scientific paper) the editorial standard for the journal in question. Some journals expect you to report effect sizes, others don’t. Within some scientific communities it is standard practice to report confidence intervals, in other it is not. You’ll need to figure out what your audience expects. But, just for the sake of clarity, if you’re taking my class: my default position is that it’s usually worth includng the effect size, but don’t worry about the confidence interval unless the assignment asks you to or implies that you should.

Positive and negative t values

Before moving on to talk about the assumptions of the t-test, there’s one additional point I want to make about the use of t-tests in practice. The first one relates to the sign of the t-statistic (that is, whether it is a positive number or a negative one). One very common worry that students have when they start running their first t-test is that they often end up with negative values for the t-statistic, and don’t know how to interpret it. In fact, it’s not at all uncommon for two people working independently to end up with R outputs that are almost identical, except that one person has a negative t values and the other one has a positive t value. Assuming that you’re running a two-sided test, then the p-values will be identical. On closer inspection, the students will notice that the confidence intervals also have the opposite signs. This is perfectly okay: whenever this happens, what you’ll find is that the two versions of the R output arise from slightly different ways of running the t-test. What’s happening here is very simple. The t-statistic that R is calculating here is always of the form

$t=\dfrac{(\text { mean } 1)-(\text { mean } 2)}{(\mathrm{SE})}$

If “mean 1” is larger than “mean 2” the t statistic will be positive, whereas if “mean 2” is larger then the t statistic will be negative. Similarly, the confidence interval that R reports is the confidence interval for the difference “(mean 1) minus (mean 2)”, which will be the reverse of what you’d get if you were calculating the confidence interval for the difference “(mean 2) minus (mean 1)”.

Okay, that’s pretty straightforward when you think about it, but now consider our t-test comparing Anastasia’s class to Bernadette’s class. Which one should we call “mean 1” and which one should we call “mean 2”. It’s arbitrary. However, you really do need to designate one of them as “mean 1” and the other one as “mean 2”. Not surprisingly, the way that R handles this is also pretty arbitrary. In earlier versions of the book I used to try to explain it, but after a while I gave up, because it’s not really all that important, and to be honest I can never remember myself. Whenever I get a significant t-test result, and I want to figure out which mean is the larger one, I don’t try to figure it out by looking at the t-statistic. Why would I bother doing that? It’s foolish. It’s easier just look at the actual group means, since the R output actually shows them!

Here’s the important thing. Because it really doesn’t matter what R printed out, I usually try to report the t-statistic in such a way that the numbers match up with the text. Here’s what I mean… suppose that what I want to write in my report is “Anastasia’s class had higher grades than Bernadette’s class”. The phrasing here implies that Anastasia’s group comes first, so it makes sense to report the t-statistic as if Anastasia’s class corresponded to group 1. If so, I would write

Anastasia’s class had higher grades than Bernadette’s class (t(31)=2.1,p=.04).

(I wouldn’t actually emphasise the word “higher” in real life, I’m just doing it to emphasise the point that “higher” corresponds to positive t values). On the other hand, suppose the phrasing I wanted to use has Bernadette’s class listed first. If so, it makes more sense to treat her class as group 1, and if so, the write up looks like this:

Bernadette’s class had lower grades than Anastasia’s class (t(31)=−2.1,p=.04).

Because I’m talking about one group having “lower” scores this time around, it is more sensible to use the negative form of the t-statistic. It just makes it read more cleanly.

One last thing: please note that you can’t do this for other types of test statistics. It works for t-tests, but it wouldn’t be meaningful for chi-square testsm F-tests or indeed for most of the tests I talk about in this book. So don’t overgeneralise this advice! I’m really just talking about t-tests here and nothing else!

Assumptions of the test

As always, our hypothesis test relies on some assumptions. So what are they? For the Student t-test there are three assumptions, some of which we saw previously in the context of the one sample t-test (see Section 13.2.3):

Normality . Like the one-sample t-test, it is assumed that the data are normally distributed. Specifically, we assume that both groups are normally distributed. In Section 13.9 we’ll discuss how to test for normality, and in Section 13.10 we’ll discuss possible solutions.
Independence . Once again, it is assumed that the observations are independently sampled. In the context of the Student test this has two aspects to it. Firstly, we assume that the observations within each sample are independent of one another (exactly the same as for the one-sample test). However, we also assume that there are no cross-sample dependencies. If, for instance, it turns out that you included some participants in both experimental conditions of your study (e.g., by accidentally allowing the same person to sign up to different conditions), then there are some cross sample dependencies that you’d need to take into account.
Homogeneity of variance (also called “homoscedasticity”). The third assumption is that the population standard deviation is the same in both groups. You can test this assumption using the Levene test, which I’ll talk about later on in the book (Section 14.7). However, there’s a very simple remedy for this assumption, which I’ll talk about in the next section.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

AP®︎/College Statistics

Course: ap®︎/college statistics > unit 11.

Hypotheses for a two-sample t test
Example of hypotheses for paired and two-sample t tests
Writing hypotheses to test the difference of means

Two-sample t test for difference of means

Test statistic in a two-sample t test
P-value in a two-sample t test
Conclusion for a two-sample t test using a P-value
Conclusion for a two-sample t test using a confidence interval
Making conclusions about the difference of means

Want to join the conversation?

Upvote Button navigates to signup page
Downvote Button navigates to signup page
Flag Button navigates to signup page

Video transcript

Harvard Business School →
Faculty & Research →
February 2021

T-tests: Theory and Practice

Format: Video
| Language: English

About The Authors

Michael I. Parzen

Chiara Farronato

Michael W. Toffel

Driving Decarbonization at BMW

New belgium brewing and climate change.

March 2024 (Revised April 2024)

Coursera's Foray into GenAI

Driving Decarbonization at BMW By: Shirley Lu, Georgios Serafeim and Michael W. Toffel
New Belgium Brewing and Climate Change By: Michael W. Toffel, Kenneth P. Pucker and Michael Norris
Coursera's Foray into GenAI By: Suraj Srinivasan, Michael Parzen and Radhika Kak

Statistics Made Easy

Paired Samples t-test: Definition, Formula, and Example

A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.

This tutorial explains the following:

The motivation for performing a paired samples t-test.
The formula to perform a paired samples t-test.
The assumptions that should be met to perform a paired samples t-test.
An example of how to perform a paired samples t-test.

Paired Samples t-test: Motivation

A paired samples t-test is commonly used in two scenarios:

1. A measurement is taken on a subject before and after some treatment – e.g. the max vertical jump of college basketball players is measured before and after participating in a training program.

2. A measurement is taken under two different conditions – e.g. the response time of a patient is measured on two different drugs.

In both cases we are interested in comparing the mean measurement between two groups in which each observation in one sample can be paired with an observation in the other sample.

Paired Samples t-test: Formula

A paired samples t-test always uses the following null hypothesis:

H 0 : μ 1 = μ 2 (the two population means are equal)

The alternative hypothesis can be either two-tailed, left-tailed, or right-tailed:

H 1 (two-tailed): μ 1 ≠ μ 2 (the two population means are not equal)
H 1 (left-tailed): μ 1 < μ 2 (population 1 mean is less than population 2 mean)
H 1 (right-tailed): μ 1 > μ 2 (population 1 mean is greater than population 2 mean)

We use the following formula to calculate the test statistic t:

t = x diff / (s diff /√n)

x diff : sample mean of the differences
s: sample standard deviation of the differences
n: sample size (i.e. number of pairs)

If the p-value that corresponds to the test statistic t with (n-1) degrees of freedom is less than your chosen significance level (common choices are 0.10, 0.05, and 0.01) then you can reject the null hypothesis.

Paired Samples t-test: Assumptions

For the results of a paired samples t-test to be valid, the following assumptions should be met:

The participants should be selected randomly from the population.
The differences between the pairs should be approximately normally distributed.
There should be no extreme outliers in the differences.

Paired Samples t-test : Example

Suppose we want to know whether or not a certain training program is able to increase the max vertical jump (in inches) of college basketball players.

To test this, we may recruit a simple random sample of 20 college basketball players and measure each of their max vertical jumps. Then, we may have each player use the training program for one month and then measure their max vertical jump again at the end of the month.

To determine whether or not the training program actually had an effect on max vertical jump, we will perform a paired samples t-test at significance level α = 0.05 using the following steps:

Step 1: Calculate the summary data for the differences.

x diff : sample mean of the differences = -0.95
s: sample standard deviation of the differences = 1.317
n: sample size (i.e. number of pairs) = 20

Step 2: Define the hypotheses.

We will perform the paired samples t-test with the following hypotheses:

H 0 : μ 1 = μ 2 (the two population means are equal)
H 1 : μ 1 ≠ μ 2 (the two population means are not equal)

Step 3: Calculate the test statistic t .

t = x diff / (s diff /√n) = -0.95 / (1.317/ √ 20) = -3.226

Step 4: Calculate the p-value of the test statistic t .

According to the T Score to P Value Calculator , the p-value associated with t = -3.226 and degrees of freedom = n-1 = 20-1 = 19 is 0.00445 .

Step 5: Draw a conclusion.

Since this p-value is less than our significance level α = 0.05, we reject the null hypothesis. We have sufficient evidence to say that the mean max vertical jump of players is different before and after participating in the training program.

Note: You can also perform this entire paired samples t-test by simply using the Paired Samples t-test Calculator .

Additional Resources

The following tutorials explain how to perform a paired samples t-test using different statistical programs:

How to Perform a Paired Samples t-Test in Excel How to Perform a Paired Samples t-test in SPSS How to Perform a Paired Samples t-test in Stata How to Perform a Paired Samples t-test on a TI-84 Calculator How to Perform a Paired Samples t-test in R How to Perform a Paired Samples t-Test in Python How to Perform a Paired Samples t-Test by Hand

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Master of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike. My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

5 Replies to “Paired Samples t-test: Definition, Formula, and Example”

What will happen if the p-value is more than the significance level of 0.05? Does it mean it is not significant or effective?

Thank you for this. It helped me a lot.

Excellent it really helps me

Hey Zach , thanks for statology! I love this site. It helps me a lot to remember and learn new things. I have a question. What if rather then test if the difference between tests is zero or greater/lower than zero, I’d like to test if the difference is at least x? Eg: I’d like to check if the time to change tire was reduced by at least 5 seconds after a training. Not only if the time is different or less than before. Could you include this example, please? Which changes in calculation we should do? Thanks a lot. Marcelo

in paired t test are we supposed to deduct the before from the after ?

Z-test vs T-test: the differences and when to use each

What is hypothesis testing, what is a z-test, examples of a z-test, what is a t-test, examples of a t-test, how to know when to use z-test vs t-test, difference between z-test and t-test: a comparative table.

two light bulbs with inscriptions Z-test vs T-test

The EPAM Anywhere Editorial Team is an international collective of senior software engineers, managers and communications professionals who create, review and share their insights on technology, career, remote work, and the daily life here at Anywhere.

Testing is how you determine effectiveness. Whether you work as a data scientist , statistician, or software developer, to ensure quality, you must measure performance. Without tests, you could deploy flawed code, features, or data points.

With that in mind, the use cases of testing are endless. Machine learning models need statistical tests. Data analysis involves statistical tests to validate assumptions. Optimization of any kind requires evaluation. You even need to test the strength of your hypothesis before you begin an inquiry.

Let's explore two inferential statistics: the Z-test vs the T-test. That way you can understand their differences, their unique purposes, and when to use a Z-test vs T-test.

To start, imagine you have a good idea. At the moment of inception, you have no data to back up your idea. It is an unformed thought. But the idea is an excellent starting point that can launch a full investigation. We consider this starting point a hypothesis.

But what if your hypothesis is off-base? You don’t want to dive into a full-scale search if it is a pointless chase with no reward. That is a waste of resources. You need to determine if you have a workable hypothesis.

Enter hypothesis testing. It is a statistical act used to assess the viability of a hypothesis. The method discovers whether there is sufficient data to support your idea. If there is next to no significance, you do not have a very plausible hypothesis.

To confirm the validity of a hypothesis, you compare it against the status quo (also known as the null hypothesis). Your idea is something new, opposite from normal conditions (also known as the alternative hypothesis). It is zero sum: only one hypothesis between the null and alternate hypothesis can be true in a given set of parameters.

In such a comparison test, you can now determine validity. You can compare and contrast conditions to find meaningful conclusions. Whichever conditions become statistically apparent determines which hypothesis is plausible.

A Z-test is a test statistic. It works with two groups: the sample mean and the population mean. It will test whether these two groups are different.

With a Z-test, you know the population standard deviation. That is to ensure statistical accuracy as you compare one group (the sample mean) vs the second group (the population mean). In other words, you can minimize external confounding factors with a normal distribution. In addition, a defining characteristic of a Z-test is that it works with large sample sizes (typically more than 30, so we achieve normal distribution as defined by the central limit theorem). These are two crucial criteria for using a Z-test.

Within hypothesis testing, your null hypothesis states there is no difference between the two groups your Z-test will compare. Your alternative hypothesis will state there is a difference that your Z-test will expose.

How to perform a Z-test

A Z-test occurs in the following standard format:

Formulate your hypothesis: First, define the parameters of your alternative and null hypothesis.
Choose a critical value: Second, determine what you consider a viable difference between your two groups. This threshold determines when you can say the null hypothesis should be rejected. Common levels are 0.01 (1%) or 0.05 (5%) , values found to best balance Type I and Type II errors .
Collect samples: Obtain the needed data. The data must be large enough and random.
Calculate for a Z-score: Input your data into the standard Z-test statistics formula, shown below, where Z = standard score, x = observed value, mu = mean of the sample, sigma = standard deviation of the sample .
Compare: If the statistical test is greater than the critical value, you have achieved statistical significance. The sample mean is so different so you can reject the null hypothesis. Your alternative hypothesis (something other than the status quo) is at work, and that's worth investigating.

There are different variations of a Z-test. Let's explore examples of one-sample and two-sample Z-tests.

One-sample Z-test

A one-sample Z-test looks for either an increase or a decrease. There is one sample group involved, taken from a population. We want to see if there is a difference between those two means.

For example, consider a school principal who believes their students' IQ is higher than the state average. The state average is 100 points (population mean), give or take 20 (the population standard deviation). To prove this hypothesis, the principal takes 50 students (the sample size) and finds their IQ scores. To their delight, they earn an average of 110.

But does the difference offer any statistical value? The principal then plugs the numbers into a Z-test. Any Z-score greater than the critical value would state there is sufficient significance. The claim that the students have an above-average IQ is valid.

Two-sample Z-test

A two-sample test involves comparing the average of two sample groups against the population means. It is to determine a difference between two independent samples.

For example, our principal wants to compare their students' IQ scores to the school across the street. They believe their students' average IQ is higher. They don’t need to know the exact numerical increase or decrease. All they want is proof that their student's average scores are higher than the other group.

To confirm the validity of this hypothesis, the principal will search for statistical significance. They can take a 50-student sample size from their school and a 50-student sample size from the rival school. Now in possession of both sample group's average IQ (and the sample standard deviation), they hope to find a number value that is not equal. And they need them to be unequal by a significant amount.

If the test statistic comes in less than the critical value, the differences are negligible. There is not enough evidence to say the hypothesis is worth exploring, the null hypothesis is maintained. He would not have enough proof that the IQ levels between the two schools are different.

Read full story

A T-test performs the same crucial function as a Z-test: determine if there is a difference between the means of two groups. If there is a significant difference, you have achieved statistical validity for your hypothesis.

However, a T-test involves a different set of factors. Most importantly, a T-test applies when you do not know the sample variance of your values. You must generalize the normal distribution (or T-distribution). Plus, there is an expectation that you do not possess all the data in a given scenario.

These conditions better match reality, as it is often hard to collect data from entire populations or always obtain a standard normal distribution. That is why T-tests are more widely applicable than Z-tests, though they operate with less precision.

How to perform a T-test

A T-test occurs in the following standard format:

Formulate your hypothesis: First, define the parameters of your null and alternative hypothesis.
Choose a critical value: Like a Z-test, determine what you consider a viable difference between your two groups.
Collect data: Obtain the needed data. One of the key differences is degrees of freedom in the samples of a T-test, so try to define the typical values and range of values in each group.
Calculate your T-score: Input your data into the T-test formula you chose. Here is a one-sample formula:
Compare: If the statistical test is greater than the critical value, you have achieved statistical significance. The sample mean is so far from the population mean that you likely have a useful hypothesis.

There are several different kinds of T-tests as well. Let's go through the standard one-sample and two-sample T-tests.

One-sample T-test

A one-sample T-test looks for an increase or decrease compared to a population mean.

For example, your company just went through sales training. Now, the manager wants to know if the training helped improve sales.

Previous company sales data shows an average of $100 on each transaction from all workers. The null hypothesis would be no change. The alternative hypothesis (which you hope is significant), is that there is an improvement.

To test if there is significance, you take the sales average of 20 salesmen. That is the only available data, and you have no other data from nationwide stores. The average of that sample of salesmen in the past month is $130. We will also assume that the standard deviation is approximately equal .

With this set of factors, you can calculate your T-score with a T-test. You compare the sample result to the critical value. In addition, you assess it against the number of degrees of freedom. Since we know with smaller sample data sizes there is greater uncertainty, we allow more room for our data to vary.

After comparing, we may find a lot of significance. That means the data possesses enough strength to support our hypothesis that sales training likely impacted sales. Of course, this is an estimate, as we only assessed one factor with a small group. Sales could have risen for numerous other reasons. But with our set of assumptions, our hypothesis is valid.

Two-sample T-test

A two-sample T-test occurs the same as a two-sample Z-test and compares if two groups are equal when compared to a defined population parameter.

For example, consider English and non-native speakers. We want to see the effect of maternal language on test scores inside a country. To do that, we will offer both groups a reading test and compare those scores to the average.

Of course, finding the mean of an entire population of language speakers is impossible to procure. Still, we can make some assumptions and compare them with a smaller size. We take 15 English speakers and 15 non-native speakers and collect their results. We can decide on a critical score value on the reading test as well. If the average score on the test is not crucially different or outside the population standard deviation, our assumption failed. There is no significant difference between the groups, so the impact of maternal language is not worth investigating.

Both a Z-test and a T-test validate a hypothesis. Both are parametric tests that rely on assumptions. The key difference between Z-test and T-test is in their assumptions (e.g. population variance).

Key differences about the data used result in different applications. You want to use the appropriate tool, otherwise you won’t draw valid conclusions from your data.

So when should you use a Z-test vs a T-test? Here are some factors to consider:

Sample size: If the available sample size is small, opt for a T-test. Small sample sizes are more variable, so the greater spread of distribution and estimation of error involved with T-tests is ideal.
Knowledge of the population standard deviation: Z-tests are more precise and often simpler to execute. So if you know the standard deviation, use a Z-test.
Test purpose: If you are assessing the validity of a mean, a T-test is the best choice. If you are working with a hypothesized population proportion, go for a Z-test.
Assumption of normality: A Z-test assumes a normal distribution. This does not apply to all real-world scenarios. If you hope to validate a hypothesis that is not well-defined, opt for a T-test instead.
Type of data: You can only work within the constraints of the available data. The more information the better, but that is often not possible given testing and collecting conditions. If you have limited data describing means between groups, opt for a T-test. If you have large data sets comparing means between populations, you can use a Z-test.

Knowing the key differences with each statistical test makes selecting the right tool far easier. Here is a table that can help you compare:

Statistical testing lets you determine the validity of a hypothesis. You discover validity by determining if there is a significant difference between your hypothesis and the status quo. If there is, you have a possible idea worth exploring.

That process has numerous applications in the field of computer science and data analysis . You might want to determine the performance of an app with an A/B test. Or you might need to test if an application fits within the defined limits and compare performance metrics. Z-tests and T-tests can depict whether there is significant evidence in each of these scenarios. With that information, you can take the appropriate measures to fix bugs or optimize processes.

Z-test and T-test are helpful tools, especially for hypothesis testing. For data engineers of the future, knowledge of statistical testing will only help your work and overall career trajectory.

Are you a data scientist looking for a job? Check out our remote data scientist jobs available .

Explore our Editorial Policy to learn more about our standards for content creation.

step-by-step guide to creating, building, and showcasing your data analyst portfolio projects

how quantitative usability testing improves digital products

what are third-party cookies? why privacy on the web is an illusion

computer science vs data science: unraveling the differences & similarities

SDLC models: approach development the way that works for you

10 most popular programming languages for 2020 and beyond

R vs Python in data science and machine learning

red team vs blue team in cybersecurity: key roles & responsibilities

rebase vs. merge: a comprehensive guide

the future of Agile: what to expect in 2024 and beyond

best react projects for a portfolio: from ideas to standout examples

Ruby on Rails interview questions

data scientist interview questions and answers

24 unique JavaScript projects for portfolio

top resume-boosting Java projects for your portfolio

network engineer interview questions

IMAGES

Hypothesis Testing
Hypothesis Testing- Meaning, Types & Steps
Hypothesis Testing Example Two Sample t-Test
Hypothesis Testing: t
Hypothesis Testing Part-3: Two Sample t-test with tables and using
Hypothesis Testing with Two Samples

VIDEO

T- test || Hypothesis testing || t-test full concept || In just 5 steps
Z-Test for Hypothesis Testing
Hypothesis Test
#t test Independent sample
Student t-test concept
Testing of hypothesis |Part-2|statistics and numerical methods-MA3251

COMMENTS

An Introduction to t Tests
An Introduction to t Tests | Definitions, Formula and Examples. Published on January 31, 2020 by Rebecca Bevans.Revised on June 22, 2023. A t test is a statistical test that is used to compare the means of two groups. It is often used in hypothesis testing to determine whether a process or treatment actually has an effect on the population of interest, or whether two groups are different from ...
T-test and Hypothesis Testing (Explained Simply)
T-test definition, formula explanation, and assumptions. The T-test is the test, which allows us to analyze one or two sample means, depending on the type of t-test. Yes, the t-test has several types: One-sample t-test — compare the mean of one group against the specified mean generated from a population. For example, a manufacturer of mobile ...
T Test Overview: How to Use & Examples
We'll use a two-sample t test to evaluate if the difference between the two group means is statistically significant. The t test output is below. In the output, you can see that the treatment group (Sample 1) has a mean of 109 while the control group's (Sample 2) average is 100. The p-value for the difference between the groups is 0.112.
T Test
Definition/Introduction. T-test was first described by William Sealy Gosset in 1908, ... but the t-test rejects the original hypothesis in favor of your new hypothesis), and the beta parameter determines the threshold for false-negative results (e.g., if true mean serum sodium concentration is 200 mEq/L, but the t-test fails to reject the old ...
T Test (Student's T-Test): Definition and Examples
The null hypothesis for the independent samples t-test is μ 1 = μ 2. So it assumes the means are equal. With the paired t test, the null hypothesis is that the pairwise difference between the two tests is equal (H 0: µ d = 0). Paired Samples T Test By hand. Example question: Calculate a paired t test by hand for the following data:
Independent Samples T Test: Definition, Using & Interpreting
Independent Samples T Tests Hypotheses. Independent samples t tests have the following hypotheses: Null hypothesis: The means for the two populations are equal. Alternative hypothesis: The means for the two populations are not equal.; If the p-value is less than your significance level (e.g., 0.05), you can reject the null hypothesis. The difference between the two means is statistically ...
Student's t-test
Student's t-test is a statistical test used to test whether the difference between the response of two groups is statistically significant or not. It is any statistical hypothesis test in which the test statistic follows a Student's t-distribution under the null hypothesis.It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in ...
How t-Tests Work: t-Values, t-Distributions, and Probabilities
Hypothesis tests work by taking the observed test statistic from a sample and using the sampling distribution to calculate the probability of obtaining that test statistic if the null hypothesis is correct. In the context of how t-tests work, you assess the likelihood of a t-value using the t-distribution.
The t-Test
A t -test (also known as Student's t -test) is a tool for evaluating the means of one or two populations using hypothesis testing. A t-test may be used to evaluate whether a single group differs from a known value ( a one-sample t-test ), whether two groups differ from each other ( an independent two-sample t-test ), or whether there is a ...
The Ultimate Guide to T Tests
A t test is a statistical technique used to quantify the difference between the mean (average value) of a variable from up to two samples (datasets). The variable must be numeric. Some examples are height, gross income, and amount of weight lost on a particular diet. A t test tells you if the difference you observe is "surprising" based on ...
8: Introduction to t-tests
8.1: The t-statistic. The z-statistic was a useful way to link the material and ease us into the new way to looking at data, but it isn't a very common test because it relies on knowing the populations standard deviation, σ, which is rarely going to be the case. Instead, we will estimate that parameter σ using the sample statistic s in the ...
T-Test: What It Is With Multiple Formulas and When To Use Them
T-Test: A t-test is an analysis of two populations means through the use of statistical examination; a t-test with two samples is commonly used with small sample sizes, testing the difference ...
8.2: Hypothesis Testing with t
Hypothesis testing with the $t$-statistic works exactly the same way as $z$-tests did, following the four-step process of. Stating the Hypothesis; Finding the Critical Values; Computing the Test Statistic; Making the Decision. We will work though an example: let's say that you move to a new city and find a an auto shop to change your oil ...
The statistical analysis t-test explained for beginners and experts
Two- and one-tailed tests. The one-tailed test is appropriate when there is a difference between groups in a specific direction [].It is less common than the two-tailed test, so the rest of the article focuses on this one.. 3. Types of t-test. Depending on the assumptions of your distributions, there are different types of statistical tests.
Independent t-test for two samples
Reporting the result of an independent t-test. When reporting the result of an independent t-test, you need to include the t-statistic value, the degrees of freedom (df) and the significance value of the test (p-value).The format of the test result is: t(df) = t-statistic, p = significance value. Therefore, for the example above, you could report the result as t(7.001) = 2.233, p = 0.061.
13.3: The Independent Samples t-test (Student Test)
For the Student t-test there are three assumptions, some of which we saw previously in the context of the one sample t-test (see Section 13.2.3): Normality. Like the one-sample t-test, it is assumed that the data are normally distributed. Specifically, we assume that both groups are normally distributed.
How t-Tests Work: 1-sample, 2-sample, and Paired t-Tests
It's a simple calculation. In a 1-sample t-test, the sample effect is the sample mean minus the value of the null hypothesis. That's the top part of the equation. For example, if the sample mean is 20 and the null value is 5, the sample effect size is 15.
Two-sample t test for difference of means
And let's assume that we are working with a significance level of 0.05. So pause the video, and conduct the two sample T test here, to see whether there's evidence that the sizes of tomato plants differ between the fields. Alright, now let's work through this together. So like always, let's first construct our null hypothesis.
T-tests: Theory and Practice
Abstract. This video provides an introduction to hypothesis testing, sampling, t-tests, and p-values. It provides examples of A/B testing and t-testing to assess whether difference between two groups are statistically significant. This video can be assigned in conjunction with the "Comparing Two Groups: Sampling and t-Testing" technical ...
T-test: Definition, Formula, Types, Applications
The t-test is a test in statistics that is used for testing hypotheses regarding the mean of a small sample taken population when the standard deviation of the population is not known. The t-test is used to determine if there is a significant difference between the means of two groups. The t-test is used for hypothesis testing to determine ...
Paired Samples t-test: Definition, Formula, and Example
A paired samples t-test is used to compare the means of two samples when each observation in one sample can be paired with an observation in the other sample.. This tutorial explains the following: The motivation for performing a paired samples t-test. The formula to perform a paired samples t-test. The assumptions that should be met to perform a paired samples t-test.
One Sample T Test: Definition, Using & Example
One Sample T Test Hypotheses. A one sample t test has the following hypotheses: Null hypothesis (H 0): The population mean equals the hypothesized value (µ = H 0).; Alternative hypothesis (H A): The population mean does not equal the hypothesized value (µ ≠ H 0).; If the p-value is less than your significance level (e.g., 0.05), you can reject the null hypothesis.
Z-test vs T-test: the differences and when to use each
If there is a significant difference, you have achieved statistical validity for your hypothesis. However, a T-test involves a different set of factors. Most importantly, a T-test applies when you do not know the sample variance of your values. You must generalize the normal distribution (or T-distribution). Plus, there is an expectation that ...
Paired T Test: Definition & When to Use It
A paired t-test determines whether the mean change for these pairs is significantly different from zero. This test is an inferential statistics procedure because it uses samples to draw conclusions about populations. Paired t tests are also known as a paired sample t-test or a dependent samples t test. These names reflect the fact that the two ...