case study class 12 physics chapter 4

CBSE Class 12 Physics – Chapter 4 Moving Charges And Magnetism- Study Materials

NCERT Solutions Class 12 All Subjects Sample Papers Past Years Papers

Moving Charges and Magnetism : Notes and Study Materials -pdf

Concepts of Moving Charges and Magnetism
Moving Charges and Magnetism Master File
Ncert Solution
NCERT Exemplar Solution
Important Questions Moving Charges And Magnetism
Past Many Years CBSE Questions and Answer: Magnetic Fields Law
Past Many Years CBSE Questions and Answer: Magnetic force and torque
Test Paper 1
Test Paper 2

Chapter-4: Moving Charges and Magnetism of NCERT class 12 Physics note is available here.

Moving Charges and Magnetism is one of the important chapters of CBSE class 12 Physics. So, students must prepare this chapter thoroughly. The notes provided here will be very helpful for the students who are going to appear in CBSE class 12 Physics board exam .

Oersted’ Experiment

During a lecture demonstration in 1820, the Danish physicist Hans Christian Oersted noticed that a current in a straight wire caused a noticeable deflection in a nearby magnetic compass needle. He further investigated this phenomenon and confirmed the phenomenon of magnetic field around current carrying conductor.

Magnetic Field

It is the space around a magnet or current carrying conductor around which magnetic effects can be experienced. It is a vector quantity and its SI unit is tesla (T) or Wbm ‒2 .

Moving Charge & Magnetic Field

A charge can produce magnetic field if it is in motion. Magnetic field can also interact with a moving charge.

Lorentz Force

Assume a point charge q (moving with a velocity v and, located at r at a given time t ) in presence of both the electric field E ( r ) and the magnetic field B ( r ). The force on an electric charge q due to both of them is given by,

F = q [ E ( r ) + v × B ( r )] ≡ F Electric + F Magnetic

Careful analysis of this expression shows that:

• Lorentz Force depends on q , v and B (charge of the particle, the velocity and the magnetic field). Force on a negative charge is opposite to that on a positive charge.

• The magnetic force q [ v × B ] includes a vector product of velocity & magnetic field. Vector product makes the force due to magnetic field become zero if velocity and magnetic field are parallel or anti-parallel. The force acts in a (sideways) direction perpendicular to both the velocity and the magnetic field. Its direction is given by the screw rule or right hand rule for vector (or cross) product as shown in figure given below

Direction of magnetic field by right hand rule for vector

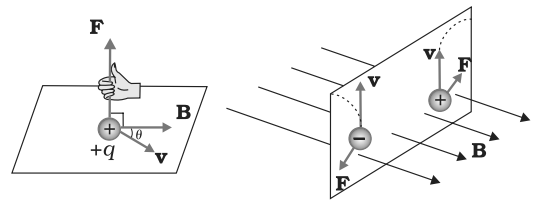
Image Source: NCERT Books

• The magnetic force is zero if charge is not moving (as then |v|= 0). Only a moving charge feels the magnetic force

F = q [ v × B ] = q |v||B| sin θ ň, where θ is angle between v and B.

Magnetic force on a current-carrying conductor

Magnetic force on a conductor of length l carrying a current I placed in a uniform magnetic field B is given by

F = I ( l × B ) or |F| = I | l| | B | sin θ.

The direction of F is perpendicular to both l and B and can be obtained with the help of Fleming’s Left hand rule.

Motion of a charged particle in Magnetic Field

A force on a particle does work if the force has a component along (or opposed to) the direction of motion of the particle.

In the case of motion of a charge in a magnetic field, the magnetic force is perpendicular to the velocity of the particle. So no work is done and no change in the magnitude of the velocity is produced (though the direction of momentum may be changed).

Generally two types of cases are possible:

Case 1 st : When v is perpendicular to B

The perpendicular force, q v × B , acts as a centripetal force and produces a circular motion perpendicular to the magnetic field. The particle will describe a circle if v and B are perpendicular to each other.

Charge particle describing a circle if v and B are mutually perpendicular

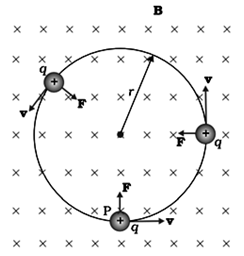
In this case, radius described by charge particle is given by, r = m v / q B

If ω is the angular frequency, then ω = 2π v = q B / m , where, v is frequency of rotation

The time taken for one revolution is T= 2π/ω ≡ 1/ν.

Case 2 nd : When v is making an angle with B other than 0 o

In this case, velocity has a component along B , this component remains unchanged as the motion along the magnetic field will not be affected by the magnetic field. The motion in a plane perpendicular to B is as before a circular one, thereby producing a helical motion

Helical Path of a moving charge particle in magnetic field

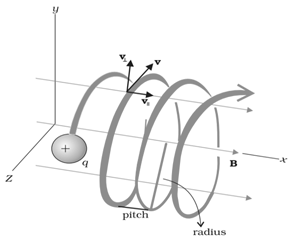
The distance moved along the magnetic field in one rotation is called pitch p and,

p = v || T = 2π m v || / q B

The radius of the circular component of motion is called the radius of the helix.

Motion of a charge in Combined Electric and Magnetic Fields

A charge q moving with velocity v in presence of both electric and magnetic fields experiences a force given by F = q ( E + v × B ) = F E + F B

Motion of a charge in Cross Electric and Magnetic Fields

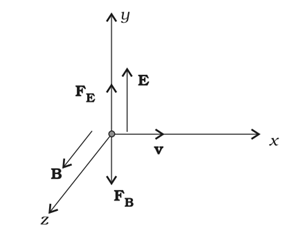
Consider the situation shown in figure given above, in this particular case we have:

Force on charge particle in cross electric and magnetic fields

Here, electric and magnetic forces are in opposite directions as shown in the figure.

If we adjust the value of E and B such that magnitude of the two forces are equal. Then, total force on the charge is zero and the charge will move in the fields undeflected.

This happens when, qE = qvB or v = E/B

This condition can be used to select charged particles of a particular velocity out of a beam containing charges moving with different speeds (irrespective of their charge and mass). The crossed E and B fields, therefore, serve as a velocity selector.

Only particles with speed E/B pass undeflected through the region of crossed fields.

It is a machine to accelerate charged particles or ions to high energies.

The cyclotron uses both electric and magnetic fields in combination to increase the energy of charged particles. As the fields are perpendicular to each other they are called crossed fields.

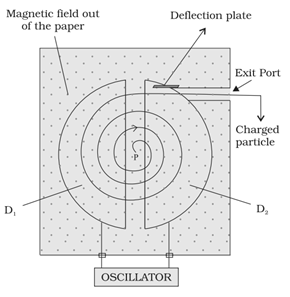
A schematic sketch of the cyclotron is shown in the figure given above. There is a source of charged particles or ions at P which move in a circular fashion in the dees, D1 and D2, on account of a uniform perpendicular magnetic field B. An alternating voltage source accelerates these ions to high speeds. The ions are eventually ‘extracted’ at the exit port.

In case of cyclotron,

cyclotron frequency and maximum kinetic energy

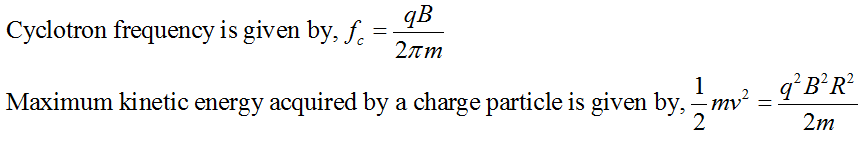
Magnetic Field Due to a Current Element: Biot-Savart Law

Image Source: NCERT Textbooks

Magnetic field strength at a point P due to a small length dl of the conductor carrying current I is given by,

CBSE Class 12th Chemistry Notes: Polymers

Magnetic Field on the Axis of a Circular Current Loop:

Magnetic field at a point on the axis of a coil, having radius R, distance x from the centre of the coil is given by,

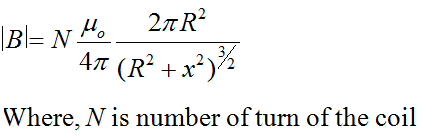
Magnetic field at the centre of a current carrying coil:

To find the magnetic field at the centre of the coil, we can put x = 0 is above equation.

So, B at the centre of a current carrying coil on N turn is given by,

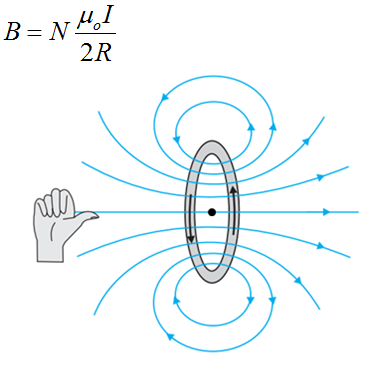
The magnetic field lines due to a circular wire form closed loops and are shown in the figure given above. The direction of the magnetic field is given by right-hand thumb rule which is if we curl the palm of our right hand around the circular wire with the fingers pointing in the direction of the current then; the right-hand thumb gives the direction of the magnetic field.

CBSE Class 12th Physics Notes: Electrostatics Potential and Capacitance

Ampere’s Circuital Law

According to this law, the line integral of magnetic field B around any closed path in vacuum is μ o times the net current ( I ) threading through the area enclosed by the curve.

Magnetic field due to a solenoid

Solenoid is a device used to generate magnetic fields. It consists of a long conducting wire wound in the form of a helix where the neighboring turns are closely spaced. When current flows in the solenoid, then each turn can be regarded as conducting circular loop. The net magnetic field is the vector sum of the fields due to all the turns. Enameled wires are used for winding so that turns are insulated from each other.

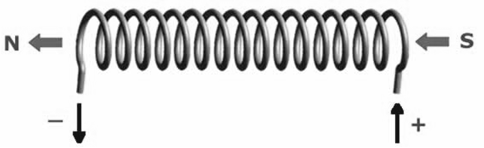
Image Source: wikipedia.org

With the help of Ampere’s circuital law we can calculate the magnetic field due to a solenoid.

Magnetic field at the centre of a long solenoid having n turns per unit length and carrying a current I is given by: B = μ o n I

The direction of the field is given by the right-hand rule. The solenoid is commonly used to obtain a uniform magnetic field.

CBSE Class 12th Chemistry Notes: Haloalkanes and Haloarenes (Part – II)

Magnetic field due to a toroid

Toroid is a hollow circular ring on which a large number of turns of a wire are closely wound. It can be viewed as a solenoid which has been bent into a circular shape to close on itself.

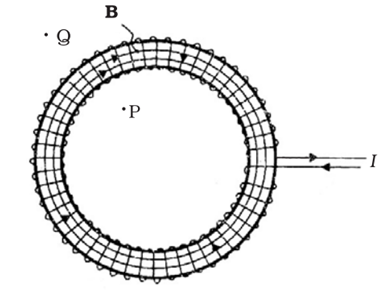
The magnetic field in the open space inside (point P) and exterior to the toroid (point Q) is zero. The field B inside the toroid is constant in magnitude for the ideal toroid of closely wound turns and is given by, B = μ o n I .

Force between two Parallel Current Carrying Wires

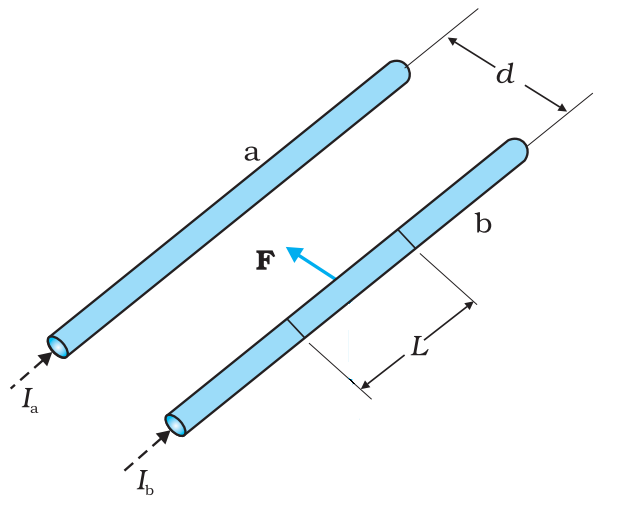
Image Source: NCERT textbooks

Two long parallel conductors a and b kept at a distance d apart in vaccum and carrying a current I a and I b respectively. The force per unit length experienced by each of them is given by

Expression for Force between two Parallel Currents

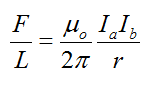
This force will be equal and opposite on both wires.

Nature of force of interaction between the current carrying conductors can be explained on the basis of Fleming’s left hand rule.

In general, two long parallel conductors carrying current

in same direction will attract each other
in different direction will repel each other

Definition of Ampere

Definition of ampere follows from the formula for force between two parallel current carrying conductors.

When 1 ampere each is passing through two long, parallel conductors kept 1 m apart in vacuum, a force of magnitude 2 × 10 ‒7 N is experienced by a meter length of each conductor.

Torque on a Rectangular Current loop in a Uniform Magnetic Field

A rectangular loop having N turns of area A each, carrying a steady current I and placed in a uniform magnetic field B such that the normal to the plane of the loop makes an angle θ with the direction of the magnetic field B, then a torque τ experienced by the loop whose magnitude is given by, τ = NIAB sin θ .

This equation can be expressed in vector form as shown below:

Here, | m | = NIA is called magnetic dipole moment of the current loop.

One can define magnetic dipole moment of the current carrying loop as product of current in the loop and total area of the loop, i.e., M = I ( NA ).

Magnetic dipole moment is a vector quantity and its direction is along the direction of magnetic field due to the current in the loop. We can also find the direction of dipole moment vector with the help of right hand grip rule.

Magnetic Dipole Moment of a Revolving Electron

Any charge in uniform circular motion would have an associated magnetic moment given by,

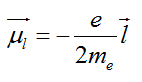
Here, e = 1.6 × 10 ‒19 C, m e = 9.1 × 10 ‒31 kg, l is the magnitude of the angular momentum of the electron about the central nucleus (“orbital” angular momentum) and | l | = ( n h )/2π, where, n is a natural number ( n = 1, 2, 3, ….) and h is a constant named after Max Planck (Planck’s constant) with a value h = 6.626 × 10 –34 J s.

The negative sign indicates that the angular momentum of the electron is opposite in direction to the magnetic moment. Instead of electron with charge (– e), if we had taken a particle with charge (+ q), the angular momentum and magnetic moment would be in the same direction.

Potential Energy of a current loop in a Magnetic Field

If a current loop of magnetic moment, M = NIA is held in a uniform magnetic field B in such a way that direction of magnetic dipole moment makes an angle θ with the direction of magnetic field, then the potential energy of the dipole is given by,

Moving Coil Galvanometer

It is an instrument used for detection and measurement of small current.

The galvanometer consists of a light rectangular coil of N turns each having area A wound on an aluminium frame.

The coil is free to rotate free to rotate about a fixed axis (as shown in figure given below), in a uniform radial magnetic field.

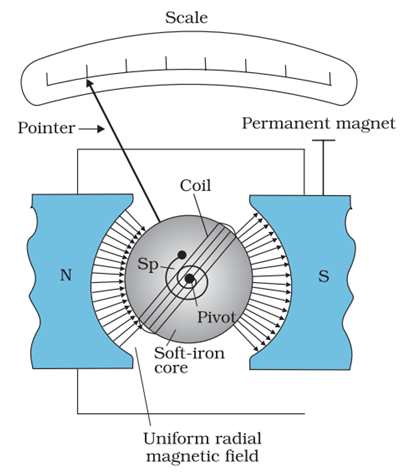
There is a cylindrical soft iron core which is used to make the field radial and also to increase the strength of the magnetic field.

When a current flows through the coil, a torque acts on it. This torque is given by, τ = NIAB where the symbols have their usual meaning.

Since the field is radial by design, we have taken sin θ = 1 in the above expression for the torque. The magnetic torque NIAB tends to rotate the coil. A spring S p provides a counter torque kϕ that balances the magnetic torque NIAB ; resulting in a steady angular deflection ϕ . In equilibrium

kϕ = NI AB

Here, k is the torsional constant of the spring; i.e. the restoring torque per unit twist.

The deflection ϕ is indicated on the scale by a pointer attached to the spring. We have

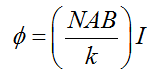
The quantity in brackets is a constant for a given galvanometer.

Sensitivity of a Galvanometer

Current Sensitivity:

Current sensitivity of a galvanometer is defined as the deflection per unit current

Mathematically,

Voltage Sensitivity:

Voltage sensitivity of a galvanometer is defined as the deflection per as the deflection per unit voltage.

Conversion of a Galvanometer into Voltmeter

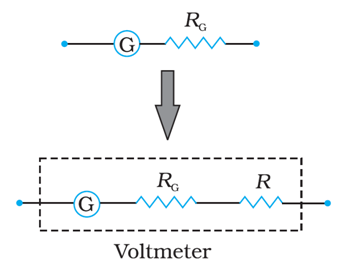
A galvanometer of coil resistance R G , showing full scale deflection for a current I G can be converted into a voltmeter for measuring potential differences having values greater than I G R G by connecting high resistance R in series with the galvanometer where,

Expression for resistance in series with the galvanometer

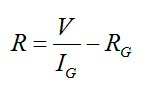
An ideal voltmeter has infinite resistance.

Conversion of a Galvanometer into Ammeter:

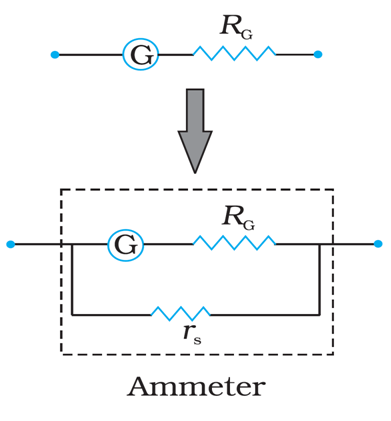
A galvanometer of coil resistance R G , showing full scale deflection for a current I G can be converted into an ammeter for measuring current having values more than I G (i.e., I > I G ) by putting a low resistance r S in parallel with the galvanometer where,

Expression for Shunt Resistance in Galvanometer

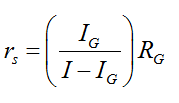
Here, r s is also called shunt resistance. An ideal ammeter has zero resistance.

CBSE Class 12 Physics Important Questions Chapter 4 – Moving Charges and Magnetism

1 mark questions.

1. State two properties of the material of the wire used for suspension of the coil in a moving coil galvanometer? Ans. (a) Non-Brittle conductor (b) Restoring Torque per unit Twist should be small.

2. What will be the path of a charged particle moving along the direction of a uniform magnetic field? Ans. The path of a charged particle will be a straight line path as no force acts on the particle.

4. A cyclotron is not suitable to accelerate electron. Why? Ans. A cyclotron is not suitable to accelerate electron because its mass is less due to which they gain speed and step out of the dee immediately.

2 Marks Questions

3. Give one difference each between diamagnetic and ferromagnetic substances. Give one example of each? Ans. Diamagnetic substances are weakly repelled by a magnet eg. Gold. Ferromagnetic materials are strongly attracted by a magnet eg. Iron.

3 Marks Questions

18. Answer the following questions: (a) A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle? (b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment? (c) An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path. Ans. (a) The initial velocity of the particle is either parallel or anti-parallel to the magnetic field. Hence, it travels along a straight path without suffering any deflection in the field. (b) Yes, the final speed of the charged particle will be equal to its initial speed. This is because magnetic force can change the direction of velocity, but not its magnitude. (c) An electron travelling from West to East enters a chamber having a uniform electrostatic field in the North-South direction. This moving electron can remain undeflected if the electric force acting on it is equal and opposite of magnetic field. Magnetic force is directed towards the South. According to Fleming’s left hand rule, magnetic field should be applied in a vertically downward direction.

5 Marks Questions

CBSE Class 10th

CBSE Class 12th

UP Board 10th
UP Board 12th
Bihar Board 10th
Bihar Board 12th
Top Schools in India
Top Schools in Delhi
Top Schools in Mumbai
Top Schools in Chennai
Top Schools in Hyderabad
Top Schools in Kolkata
Top Schools in Pune
Top Schools in Bangalore

Products & Resources

JEE Main Knockout April
Free Sample Papers
Free Ebooks
NCERT Notes

NCERT Syllabus

NCERT Books
RD Sharma Solutions
Navodaya Vidyalaya Admission 2024-25

NCERT Solutions

NCERT Solutions for Class 12
NCERT Solutions for Class 11
NCERT solutions for Class 10
NCERT solutions for Class 9
NCERT solutions for Class 8
NCERT Solutions for Class 7
JEE Main 2024
MHT CET 2024
JEE Advanced 2024
BITSAT 2024
View All Engineering Exams
Colleges Accepting B.Tech Applications
Top Engineering Colleges in India
Engineering Colleges in India
Engineering Colleges in Tamil Nadu
Engineering Colleges Accepting JEE Main
Top IITs in India
Top NITs in India
Top IIITs in India
JEE Main College Predictor
JEE Main Rank Predictor
MHT CET College Predictor
AP EAMCET College Predictor
GATE College Predictor
KCET College Predictor
JEE Advanced College Predictor
View All College Predictors
JEE Main Question Paper
JEE Main Cutoff
JEE Main Advanced Admit Card
AP EAPCET Hall Ticket
Download E-Books and Sample Papers
Compare Colleges
B.Tech College Applications
KCET Result
MAH MBA CET Exam
View All Management Exams

Colleges & Courses

MBA College Admissions
MBA Colleges in India
Top IIMs Colleges in India
Top Online MBA Colleges in India
MBA Colleges Accepting XAT Score
BBA Colleges in India
XAT College Predictor 2024
SNAP College Predictor
NMAT College Predictor
MAT College Predictor 2024
CMAT College Predictor 2024
CAT Percentile Predictor 2023
CAT 2023 College Predictor
CMAT 2024 Admit Card
TS ICET 2024 Hall Ticket
CMAT Result 2024
MAH MBA CET Cutoff 2024
Download Helpful Ebooks
List of Popular Branches
QnA - Get answers to your doubts
IIM Fees Structure
AIIMS Nursing
Top Medical Colleges in India
Top Medical Colleges in India accepting NEET Score
Medical Colleges accepting NEET
List of Medical Colleges in India
List of AIIMS Colleges In India
Medical Colleges in Maharashtra
Medical Colleges in India Accepting NEET PG
NEET College Predictor
NEET PG College Predictor
NEET MDS College Predictor
NEET Rank Predictor
DNB PDCET College Predictor
NEET Admit Card 2024
NEET PG Application Form 2024
NEET Cut off
NEET Online Preparation
Download Helpful E-books
Colleges Accepting Admissions
Top Law Colleges in India
Law College Accepting CLAT Score
List of Law Colleges in India
Top Law Colleges in Delhi
Top NLUs Colleges in India
Top Law Colleges in Chandigarh
Top Law Collages in Lucknow

Predictors & E-Books

CLAT College Predictor
MHCET Law ( 5 Year L.L.B) College Predictor
AILET College Predictor
Sample Papers
Compare Law Collages
Careers360 Youtube Channel
CLAT Syllabus 2025
CLAT Previous Year Question Paper
NID DAT Exam
Pearl Academy Exam

Predictors & Articles

NIFT College Predictor
UCEED College Predictor
NID DAT College Predictor
NID DAT Syllabus 2025
NID DAT 2025
Design Colleges in India
Top NIFT Colleges in India
Fashion Design Colleges in India
Top Interior Design Colleges in India
Top Graphic Designing Colleges in India
Fashion Design Colleges in Delhi
Fashion Design Colleges in Mumbai
Top Interior Design Colleges in Bangalore
NIFT Result 2024
NIFT Fees Structure
NIFT Syllabus 2025
Free Design E-books
List of Branches
Careers360 Youtube channel
IPU CET BJMC
JMI Mass Communication Entrance Exam
IIMC Entrance Exam
Media & Journalism colleges in Delhi
Media & Journalism colleges in Bangalore
Media & Journalism colleges in Mumbai
List of Media & Journalism Colleges in India
CA Intermediate
CA Foundation
CS Executive
CS Professional
Difference between CA and CS
Difference between CA and CMA
CA Full form
CMA Full form
CS Full form
CA Salary In India

Top Courses & Careers

Bachelor of Commerce (B.Com)
Master of Commerce (M.Com)
Company Secretary
Cost Accountant
Charted Accountant
Credit Manager
Financial Advisor
Top Commerce Colleges in India
Top Government Commerce Colleges in India
Top Private Commerce Colleges in India
Top M.Com Colleges in Mumbai
Top B.Com Colleges in India
IT Colleges in Tamil Nadu
IT Colleges in Uttar Pradesh
MCA Colleges in India
BCA Colleges in India

Diploma Colleges

Top Diploma Colleges in Maharashtra
UPSC IAS 2024
SSC CGL 2024
IBPS RRB 2024
Previous Year Sample Papers
Free Competition E-books
Sarkari Result
QnA- Get your doubts answered
UPSC Previous Year Sample Papers
CTET Previous Year Sample Papers
SBI Clerk Previous Year Sample Papers
NDA Previous Year Sample Papers

Upcoming Events

NDA Application Form 2024
UPSC IAS Application Form 2024
CDS Application Form 2024
CTET Admit card 2024
HP TET Result 2023
SSC GD Constable Admit Card 2024
UPTET Notification 2024
SBI Clerk Result 2024

Other Exams

SSC CHSL 2024
UP PCS 2024
UGC NET 2024
RRB NTPC 2024
IBPS PO 2024
IBPS Clerk 2024
IBPS SO 2024
Top University in USA
Top University in Canada
Top University in Ireland
Top Universities in UK
Top Universities in Australia
Best MBA Colleges in Abroad
Business Management Studies Colleges

Top Countries

Study in USA
Study in UK
Study in Canada
Study in Australia
Study in Ireland
Study in Germany
Study in China
Study in Europe

Student Visas

Student Visa Canada
Student Visa UK
Student Visa USA
Student Visa Australia
Student Visa Germany
Student Visa New Zealand
Student Visa Ireland
CUET PG 2024
IGNOU B.Ed Admission 2024
DU Admission 2024
UP B.Ed JEE 2024
LPU NEST 2024
IIT JAM 2024
IGNOU Online Admission 2024
Universities in India
Top Universities in India 2024
Top Colleges in India
Top Universities in Uttar Pradesh 2024
Top Universities in Bihar
Top Universities in Madhya Pradesh 2024
Top Universities in Tamil Nadu 2024
Central Universities in India
CUET Exam City Intimation Slip 2024
IGNOU Date Sheet
CUET Mock Test 2024
CUET Admit card 2024
CUET PG Syllabus 2024
CUET Participating Universities 2024
CUET Previous Year Question Paper
CUET Syllabus 2024 for Science Students
E-Books and Sample Papers
CUET Exam Pattern 2024
CUET Exam Date 2024
CUET Cut Off 2024
CUET Exam Analysis 2024
IGNOU Exam Form 2024
CUET 2024 Exam Live
CUET Answer Key 2024

Engineering Preparation

Knockout JEE Main 2024
Test Series JEE Main 2024
JEE Main 2024 Rank Booster

Medical Preparation

Knockout NEET 2024
Test Series NEET 2024
Rank Booster NEET 2024

Online Courses

JEE Main One Month Course
NEET One Month Course
IBSAT Free Mock Tests
IIT JEE Foundation Course
Knockout BITSAT 2024
Career Guidance Tool

Top Streams

IT & Software Certification Courses
Engineering and Architecture Certification Courses
Programming And Development Certification Courses
Business and Management Certification Courses
Marketing Certification Courses
Health and Fitness Certification Courses
Design Certification Courses
Specializations
Digital Marketing Certification Courses
Cyber Security Certification Courses
Artificial Intelligence Certification Courses
Business Analytics Certification Courses
Data Science Certification Courses
Cloud Computing Certification Courses
Machine Learning Certification Courses
View All Certification Courses
UG Degree Courses
PG Degree Courses
Short Term Courses
Free Courses
Online Degrees and Diplomas
Compare Courses

Top Providers

Coursera Courses
Udemy Courses
Edx Courses
Swayam Courses
upGrad Courses
Simplilearn Courses
Great Learning Courses

NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism

Eligibility
Exam Pattern
Preparation Tips
NCERT Solutions for Class 12 Physics Chapter 4 – Access and Download PDF for Free

NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism: If you're a Class 12 student in search of NCERT solutions , you've come to the right place. On this page, you'll find comprehensive class 12 physics chapter 4 ncert solutions from questions 1 to 28. Our class 12 physics ch 4 ncert solutions have been meticulously crafted by subject experts, providing detailed explanations for each step. Also, you have the option to download these solutions in PDF format, enabling you to work on them offline as well.

Latest: JEE Main high scoring chapters | JEE Main 10 year's papers

Recommended: NEET high scoring chapters | NEET question papers with solutions

New: Aakash iACST Scholarship Test. Up to 90% Scholarship. Register Now

Class 12 Physics ch 4 Exercise solutions

Moving Charges And Magnetism Class 12 Main Topics-

Ncert solutions subject wise, importance of ncert solutions for class 12 physics chapter 4 moving charges and magnetism in exams:.

A moving charge in a magnetic field can produce a force and a current-carrying conductor in a uniform magnetic field will experience a force. The solutions of NCERT Class 12 Physics Chapter 4 Moving Charges and Magnetism cover problems based on these two basic concepts. Class 12 chapter 4 physics ncert solutions will help you to boost the concepts studied in this chapter of the NCERT syllabus .

Apply to Aakash iACST Scholarship Test 2024

Applications for Admissions are open.

Two main laws discussed in the NCERT chapter Moving charges and Magnetism Class 12 are Ampere's law and Biot-savant law. Based on these laws many problems are discussed in CBSE NCERT solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism. The galvanometer is discussed in Moving charges and Magnetism Class 12 in detail with its working principle. NCERT Solutions for Class 12 Physics Chapter 4 Moving charges and Magnetism helps students for solving homework problems.

ALLEN Digital Scholarship Admission Test (ADSAT)

Aakash iACST Scholarship Test 2024

Get up to 90% scholarship on NEET, JEE & Foundation courses

The right-hand thumb rule, Flemings right-hand rule and Flemings left-hand rule are three important concepts of Moving charges and Magnetism chapter of NCERT textbook . The problems related to finding the directions can be solved using these three rules or by using the concepts of vectors. The NCERT solutions for Class 12 Physics also helps in preparing for competitive exams like NEET and JEE Mains.

Free download class 12 chapter 4 physics ncert solutions PDF for CBSE exam.

Download PDF

C lass 12 Physics ch 4 Exercise solutions

1. A circular coil of wire consisting of 100 turns, each of radius 8.0 cm carries a current of 0.40 A. What is the magnitude of the magnetic field B at the centre of the coil?

The magnitude of the magnetic field at the centre of a circular coil of radius r carrying current I is given by,

$|B|=\frac{\mu _{0}I}{2r}$

For 100 turns, the magnitude of the magnetic field will be,

$|B|=100\times \frac{\mu _{0}I}{2r}$

2. A long straight wire carries a current of 35 A. What is the magnitude of the field B at a point 20 cm from the wire?

The magnitude of the magnetic field at a distance r from a long straight wire carrying current I is given by,

$|B|=\frac{\mu _{0}I}{2\pi r}$

In this case

$|B|=\frac{4\pi \times 10^{-7}\times 35}{2\pi\times 0.2}=3.5\times 10^{-5}T$

3. A long straight wire in the horizontal plane carries a current of 50 A in north to south direction. Give the magnitude and direction of B at a point 2.5 m east of the wire.

$|B|=\frac{4\pi \times 10^{-7}\times 50}{2\pi\times 2.5}$

4. A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?

$|B|=\frac{4\pi \times 10^{-7}\times 90}{2\pi\times 1.5}=1.2\times10^{-5} T$

The current in the overhead power line is going from the East to West direction and the point lies below the power line. Applying Maxwell's right-hand thumb rule we can see that the direction of the magnetic field will be towards the South.

$30 \degree$

For a straight wire of length l in a uniform magnetic field, the Force equals to

$\\\vec{F}=\int_{0}^{l}I\vec{dl}\times \vec{B}\\ |\vec{F}|=BIlsin\theta$

In the given case the magnitude of force per unit length is equal to

$\times$

6. A 3.0 cm wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0.27 T. What is the magnetic force on the wire?

In the given case the magnitude of the force is equal to

The direction of this force depends on the orientation of the coil and the current-carrying wire and can be known using the Flemings Left-hand rule.

7. Two long and parallel straight wires A and B carrying currents of 8.0 A and 5.0 A in the same direction are separated by a distance of 4.0 cm. Estimate the force on a 10 cm section of wire A.

The magnitude of magnetic field at a distance r from a long straight wire carrying current I is given by,

In this case the magnetic field at a distance of 4.0 cm from wire B will be

$|B|=\frac{4\pi \times 10^{-7}\times 5}{2\pi\times 0.04}$

The force on a straight wire of length l carrying current I in a uniform magnetic field B is given by

$F=BIlsin\theta$

The force on a 10 cm section of wire A will be

$F=2.5\times10^{-5}\times8\times0.1 \times sin90^\circ$

8. A closely wound solenoid 80 cm long has 5 layers of windings of 400 turns each. The diameter of the solenoid is 1.8 cm. If the current carried is 8.0 A, estimate the magnitude of B inside the solenoid near its centre.

The magnitude of the magnetic field at the centre of a solenoid of length l, total turns N and carrying current I is given by

$B=\frac{\mu _{o}NI}{l}$

The magnitude of torque experienced by a current-carrying coil in a magnetic field is given by

$\tau =nBIAsin\theta$

The coil, therefore, experiences a torque of magnitude 0.96 Nm.

$M_1$

we know V=IR

$\phi k=\frac{B_{1}A_{1}N_{1}V}{R_{1}}$

Their ratio of voltage sensitivity of coil M 2 to that of coil M 1

$=\frac{B_{2}A_{2}N_{2}R_{1}}{B_{1}A_{1}N_{1}R_{2}}$

Since the velocity of the shot electron is perpendicular to the magnetic field, there is no component of velocity along the magnetic field and therefore the only force on the electron will be due to the magnetic field and will be acting as a centripetal force causing the electron to move in a circular path. (if the initial velocity of the electron had a component along the direction of the magnetic field it would have moved in a helical path)

$-1.6\times 10^{-19}C$

The angle between the direction of velocity and the magnetic field = 90 o

Since the force due to the magnetic field is the only force acting on the particle,

$\\\frac{mV^{2}}{r}=q\vec{V}\times \vec{B}\\ \frac{mV^{2}}{r}=|qVBsin\theta| \\ r=|\frac{mV}{qBsin\theta }|$

12) In Exercise 4.11 obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain

$r=\frac{eB}{mv}$

From the above equation, we can see that this frequency is independent of the speed of the electron.

$\nu =\frac{1.6\times 10^{-19}\times 4.8\times 10^{6}}{2\pi \times 9.1\times 10^{-31}}=18.2 MHz$

Number of turns in the coil(n)=30

The radius of the circular coil(r)=8.0 cm

Current flowing through the coil=6.0 A

Strength of magnetic field=1.0 T

The angle between the field lines and the normal of the coil=60 o

The magnitude of the counter-torque that must be applied to prevent the coil from turning would be equal to the magnitude of the torque acting on the coil due to the magnetic field.

$\\\tau =nBIAsin\theta\\ \tau = 30\times 1\times 6\times \pi \times (0.08)^{2}\times sin60^{o}$

A torque of magnitude 3.13 Nm must be applied to prevent the coil from turning.

13 b) Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.)

NCERT solutions for moving charges and magnetism additional exercise:

14) Two concentric circular coils X and Y of radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.

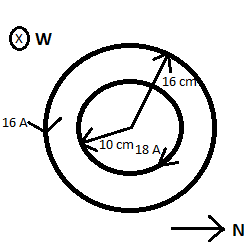
Using the right-hand thumb rule we can see that the direction of the magnetic field due to coil X will be towards the east direction and that due to coil Y will be in the West direction.

We know the magnetic field at the centre of a circular loop of radius r carrying current I is given by

$B=\frac{\mu _{o}I}{2r}$

The net magnetic field at the centre of the coils,

B net =B y - B x

The direction of the magnetic field at the centre of the coils is towards the west direction.

$100 G ( 1G = 10 ^{-4}) T$

Therefore keeping the number of turns per unit length and the value of current within the prescribed limits such that their product is approximately 8000 we can produce the required magnetic field.

e.g. n=800 and I=10 A.

16.(a) For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

$B = \frac{\mu _0 IR^2N}{2 ( x^2 + R^2 )^{3/2}}$

Show that this reduces to the familiar result for the field at the centre of the coil.

For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

For finding the field at the centre of coil we put x=0 and get the familiar result

$B = \frac{\mu _0 IN}{2R}$

16. (b) For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

$B = 0.72 \frac{\mu _0 NI}{R}$

Let a point P be at a distance of l from the midpoint of the centres of the coils.

The distance of this point from the centre of one coil would be R/2+l and that from the other would be R/2-l.

The magnetic field at P due to one of the coils would be

$B_{1}= \frac{\mu _0 IR^2N}{2 ( (R/2+l)^2 + R^2 )^{3/2}}$

The magnetic field at P due to the other coil would be

$B_{2}= \frac{\mu _0 IR^2N}{2 ( (R/2-l)^2 + R^2 )^{3/2}}$

Since the direction of current in both the coils is same the magnetic fields B 1 and B 2 due to them at point P would be in the same direction

B net =B 1 +B 2

$\\B_{net}= \frac{\mu _0 IR^2N}{2 ( (R/2-l)^2 + R^2 )^{3/2}}+\frac{\mu _0 IR^2N}{2 ( (R/2+l)^2 + R^2 )^{3/2}}\\ \\B_{net}= \frac{\mu _0 IR^2N}{2}\left [ ( (R/2-l)^2 + R^2 )^{-3/2} + ( (R/2+l)^2 + R^2 )^{-3/2}\right ]\\ \\B_{net}= \frac{\mu _0 IR^2N}{2}\left [ ( \frac{R^{2}}{4}-Rl+l^{2} + R^2 )^{-3/2} + ( \frac{R^{2}}{4}+Rl+l^{2} + R^2 )^{-3/2}\right ]\\ \\B_{net}= \frac{\mu _0 IR^2N}{2}\left [ ( \frac{5R^{2}}{4}-Rl+l^{2} )^{-3/2} + ( \frac{5R^{2}}{4}+Rl+l^{2} )^{-3/2}\right ]\\$

Since l<<R we can ignore term l 2 /R 2

$\\B_{net}= \frac{\mu _0 IN}{2R}\times (\frac{5}{4})^{-3/2}\left [ ( 1-\frac{4l}{5R} )^{-3/2} + ( 1+\frac{4l}{5R} )^{-3/2}\right ]\\$

Since the above value is independent of l for small values it is proved that about the midpoint the Magnetic field is uniform.

17.(a) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field outside the toroid

Outside the toroid, the magnetic field will be zero.

17.(b) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field inside the core of the toroid?

The magnetic field inside the core of a toroid is given by

Total number of turns(N)=3500

Current flowing in toroid =11 A

Length of the toroid, l=

$\\l=2\pi \left (\frac{ r_{1}+r_{2}}{2} \right )\\ \\l=\pi ( r_{1}+r_{2})\\ \\l=\pi (0.25+0.26)\\ \\l=0.51\pi$

17.(c) A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field in the empty space surrounded by the toroid?

The magnetic field in the empty space surrounded by the toroid is zero.

18. (a) A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?

The charged particle is not deflected by the magnetic field even while having a non zero velocity, therefore, its initial velocity must be either parallel or anti-parallel to the magnetic field i.e. It's velocity is either towards the east or the west direction.

18 b) A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?

Yes, its final speed will be equal to the initial speed if it has not undergone any collision as the work done by the magnetic field on a charged particle is always zero because it acts perpendicular to the velocity of the particle.

18 c) An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.

The electron would experience an electrostatic force towards the north direction, therefore, to nullify its force due to the magnetic field must be acting on the electron towards the south direction. By using Fleming's left-hand rule we can see that the force will be in the north direction if the magnetic field is in the vertically downward direction.

Explanation:

$q\vec{V}$

19 (a) An electron emitted by a heated cathode and accelerated through a potential difference of 2.0 kV, enters a region with uniform magnetic field of 0.15 T. Determine the trajectory of the electron if the field is transverse to its initial velocity

(a) The electron has been accelerated through a potential difference of 2.0 kV.

$1.6$

Since the electron initially has velocity perpendicular to the magnetic field it will move in a circular path.

The magnetic field acts as a centripetal force. Therefore,

$\\\frac{mv^{2}}{r}=evB\\ r=\frac{mv}{eB}\\ r=\frac{9.1\times 10^{-31}\times 2.67\times 10^{7}}{1.6\times 10^{-19}\times 0.15}=1.01mm$

The electron has been accelerated through a potential difference of 2.0 kV.

The component of velocity perpendicular to the magnetic field is

$\\v_{p}=vsin30^{o}\\ v_{p}=1.33\times 10^{7}\ ms^{-1}$

The electron will move in a helical path of radius r given by the relation,

$\\\frac{mv^{2}_{p}}{r}=ev_{p}B\\ r=\frac{mv_{p}}{eB}\\ r=\frac{9.1\times 10^{-31}\times 1.33\times 10^{7}}{1.6\times 10^{-19}\times 0.15}$

The component of velocity along the magnetic field is

$\\v_{t}=vcos30^{o}\\ v_{t}=2.31\times 10^{7}\ ms^{-1}$

The electron will move in a helical path of pitch p given by the relation,

$\\p=\frac{2\pi r}{v_{p}}\times v_{t}\\ p=\frac{2\pi \times 5\times 10^{-4}}{1.33\times 10^{7}}\times 2.31\times 10^{7}$

The electron will, therefore, move in a helical path of radius 5 mm and pitch 5.45 mm.

$9.0 \times 10 ^{-5} V m ^{-1}$

Let the beam consist of particles having charge q and mass m.

After being accelerated through a potential difference V its velocity can be found out by using the following relation,

$\\\frac{1}{2}mv^{2}=qV\\ \\v=\sqrt{\frac{2qV}{m}}$

Using the value of v from equation (ii) in (i) we have

$\\E=B\sqrt{\frac{2qV}{m}}\\ \frac{q}{m}=\frac{E^{2}}{2VB^{2}}\\ \frac{q}{m}=\frac{(9\times 10^{-5})^{2}}{2\times 15\times 10^{3}\times (0.75)^{2}}=4.8\times 10^{-13}$

21. (a) A straight horizontal conducting rod of length 0.45 m and mass 60 g is suspended by two vertical wires at its ends. A current of 5.0 A is set up in the rod through the wires. What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?

In order for the tension in the wires to be zero the force due to the magnetic field must be equal to the gravitational force on the rod.

$mg=BIl$

mass of rod=0.06 g

length of rod=0.45m

the current flowing through the rod=5 A

$\\B=\frac{mg}{Il}\\ B=\frac{0.06\times 9.8}{5\times 0.45}\\ B=0.261\ T$

A magnetic field of strength 0.261 T should be set up normal to the conductor in order that the tension in the wires is zero

$g = 9.8 m s ^{-2}$

If the direction of the current is reversed the magnetic force would act in the same direction as that of gravity.

Total tension in wires(T)=Gravitational force on rod + Magnetic force on rod

$\\T=mg+BIl\\ \\T=0.06\times 9.8+0.261\times 5\times 0.45\\ \\T=1.176\ N$

The total tension in the wires will be 1.176 N.

22. The wires which connect the battery of an automobile to its starting motor carry a current of 300 A (for a short time). What is the force per unit length between the wires if they are 70 cm long and 1.5 cm apart? Is the force attractive or repulsive?

Since the distance between the wires is much smaller than the length of the wires we can calculate the Force per unit length on the wires using the following relation.

$F=\frac{\mu _{o}I_{1}I_{2}}{2\pi d}$

Current in both wires=300 A

Distance between the wires=1.5 cm

$F=\frac{4\pi \times 10^{-7}\times 300\times 300}{2\pi \times 0.015}$

F=1.2 Nm -1

23.(a) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire intersects the axis,

The length of wire inside the magnetic field is equal to the diameter of the cylindrical region=20.0 cm=0.2 m.

Magnetic field strenth=1.5 T.

Current flowing through the wire=7.0 A

The angle between the direction of the current and magnetic field=90 o

Force on a wire in a magnetic field is calculated by relation,

$\\F=BIlsin\theta \\ F=1.5\times 7\times 0.2$

This force due to the magnetic field inside the cylindrical region acts on the wire in the vertically downward direction.

23.(b) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire is turned from N-S to northeast-northwest direction,

The angle between the direction of the current and magnetic field=45 o

The radius of the cylindrical region=10.0 cm

$\\l=\frac{2r}{sin\theta }\\$

This force will be independent of the angle between the wire and the magnetic field as we can see in the above case.

Note: There is one case in which the force will be zero and that will happen when the wire is kept along the axis of the cylindrical region.

23 c) A uniform magnetic field of 1.5 T exists in a cylindrical region of radius10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if, the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?

The wire is lowered by a distance d=6cm.

In this case, the length of the wire inside the cylindrical region decreases.

Let this length be l.

$\\(\frac{l}{2})^{2}+d^{2}=r^{2}\\ \\(\frac{l}{2})^{2}=0.1^{2}-0.06^{2}\\ \\(\frac{l}{2})^{2}=0.01-0.0036\\ \\\\(\frac{l}{2})^{2}=0.0064\\ \\\frac{l}{2}=0.08\\ \\l=0.16m$

This force acts in the vertically downward direction.

24.(a) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

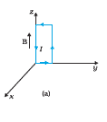
The magnetic field is

$\vec{B}=3000\ G \hat{k}=0.3\ T\hat{k}$

Current in the loop=12 A

A=0.005 m 2

$\vec{A}=0.005\ m^{2}\hat{i}$

The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-y direction. The force on the loop is zero.

24.(b) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

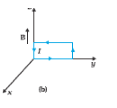
The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-y direction. The force on the loop is zero. This was exactly the case in 24. (a) as well.

24 (c). A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

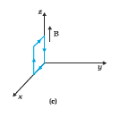
The torque on the loop has a magnitude of 0.018 Nm and acts along the negative-x-direction. The force on the loop is zero.

24 (d) . A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

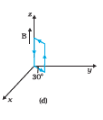
The torque on the loop has a magnitude of 0.018 Nm and at an angle of 240 o from the positive x-direction. The force on the loop is zero.

24. (e) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

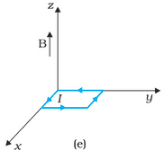
Since the area vector is along the direction of the magnetic field the torque on the loop is zero. The force on the loop is zero.

24 (f) A uniform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop in the different cases shown in Fig. 4.28? What is the force on each case? Which case corresponds to stable equilibrium?

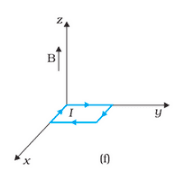
Since the area vector is in the opposite direction of the magnetic field the torque on the loop is zero. The force on the loop is zero.

The force on the loop in all the above cases is zero as the magnetic field is uniform

25. (a) A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the total torque on the coil,

As we know the torque on a current-carrying loop in a magnetic field is given by the following relation

$\\\vec{\tau }=I\vec{A}\times \vec{B}\\$

It is clear that the torque, in this case, will be 0 as the area vector is along the magnetic field only.

25. (b) A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, total force on the coil.

The total force on the coil will be zero as the magnetic field is uniform.

$10 ^{-5} m^2$

The average force on each electron in the coil due to the magnetic field will be eV d B where V d is the drift velocity of the electrons.

The current is given by

$I=neAV_{d}$

where n is the free electron density and A is the cross-sectional area.

$\\V_{d}=\frac{I}{neA}\\ \\V_{d}=\frac{5}{10^{29}\times 1.6\times 10^{-19}\times 10^{-5}}$

The average force on each electron is

$F=eV_dB$

The magnetic field inside the solenoid is given by

$B=\mu _{0}nI$

n is number of turns per unit length

$n=\frac{3\times 300}{0.6}$

n=1500 m -1

Current in the wire I w = 6 A

Mass of the wire m = 2.5 g

Length of the wire l = 2 cm

The windings of the solenoid would support the weight of the wire when the force due to the magnetic field inside the solenoid balances weight of the wire

$BI_wl=mg$

Therefore a current of 108.37 A in the solenoid would support the wire.

$12 \Omega$

The galvanometer can be converted into a voltmeter by connecting an appropriate resistor of resistance R in series with it.

At the full-scale deflection current(I) of 3 mA the voltmeter must measure a Voltage of 18 V.

$I$

The galvanometer can be converted into an ammeter by connecting an appropriate resistor of resistance R in series with it.

At the full-scale deflection current(I) of 4 mA, the ammeter must measure a current of 6 A.

Since the resistor and galvanometer coil are connected in parallel the potential difference is the same across them.

$IG=(6-I)R$

Understanding moving charges and magnetism class 12 ncert solutions is like building the foundation of a tall building. It helps you do well in your regular school exams (like the bricks at the bottom) and is also crucial for clearing tough entrance exams like JEE and NEET (like the support structure that holds up the building). So, it's important for both your regular studies and future career goals.

Class 12 physics chapter 4 exercise solutions: Important Formulas and Diagrams

Important formulas of physics chapter 4 class 12 ncert solutions are listed below:

Force Applied To A Moving Charge

Pace iit & medical, financial district, hyd.

Enrol in PACE IIT & Medical, Financial District, Hyd for JEE/NEET preparation

ALLEN NEET Coaching

Ace your NEET preparation with ALLEN Online Programs

$\vec{F}=q(\vec{v}\times \vec{B})$

Biot-Savart’s Law

Ampere Circuital Law

$\int B.dl=\mu_0I$

The following topics are covered in ch 4 Physics Class 12:

Magnetic Force- The force on a moving charge in a uniform magnetic field and also a force on a current-carrying conductor in a magnetic field are discussed in chapter 4 Physics Class 12. Some questions based on these concepts are discussed in the Class 12 Physics Chapter 4 NCERT solutions. For example questions, 5, 11, 18 and 23 of NCERT solutions for Class 12 Physics Chapter 4 uses the concepts of force on a charge/conductor in a uniform magnetic field.

Motion in a magnetic field- This part of Moving charges and Magnetism Class 12 discusses the trajectory of a charge in a magnetic field. Questions based on this are discussed in the Moving Charges and Magnetism solutions given above.

The motion of combined electric and magnetic field- The motion of charge in the presence of both electric and magnetic fields and also the topic cyclotron is discussed in this portion of Class 12 NCERT Physics.

Biot-Savart law, Amperes circuital law- These two laws and their applications are discussed in Physics chapter 4 Class 12. Other topics discussed in class 12 physics chapter 4 question answer are solenoid, toroid, the force between parallel conductors, torques on a rectangular loop in a magnetic field, the angular momentum of the electron and the concept of moving coil galvanometer and conversion of galvanometer to ammeter and voltmeter. Understanding the formulas and concepts in these topics are important to get a better idea while solving the problems.

Key Features of moving charges and magnetism class 12 ncert solutions

Comprehensive Coverage: The class 12 physics chapter 4 exercise solutions cover all the topics and questions presented in the Class 12 Physics Chapter "Moving Charges and Magnetism."

Step-by-Step Explanations: Each class 12 physics chapter 4 question answer provides detailed step-by-step explanations, helping students understand complex concepts.

Clarity and Simplicity: The physics chapter 4 class 12 ncert solutions are written in clear and simple language, making it easier for students to comprehend the content.

Practice Questions: Exercise questions are included to help students practice and assess their understanding.

Exam Preparation: These class 12 physics ch 4 exercise solutions aid students in preparing effectively for board exams and competitive exams like JEE and NEET.

Foundation for Advanced Topics: The concepts covered in this chapter are essential for more advanced topics in physics and electrical engineering.

Free Access: These solutions are available for free, ensuring accessibility to all students.

These features make the Class 12 "Moving Charges and Magnetism" solution a valuable resource for students, facilitating their success in exams and future studies.

Also Check NCERT Books and NCERT Syllabus here:

NCERT Books Class 12 Physics
NCERT Syllabus Class 12 Physics
NCERT Books Class 12
NCERT Syllabus Class 12
NCERT Exemplar Class 12 Solutions

NCERT Solutions For Class 12 Physics Chapter - Wise

NCERT solutions for Class 12 Mathematics
NCERT solutions for Class 12 Chemistry
NCERT solutions for Class 12 Physics
NCERT solutions for Class 12 Biology

As CBSE board exam is concerned, the solutions of NCERT Class 12 Physics chapter 4 Moving Charges and Magnetism is important. In 2019 CBSE board exam 12 % of questions are asked from chapter 4 and 5. Same questions discussed in the chapter 4 Physics Class 12 NCERT solutions can be expected in the board exams. NCERT Exemplar Class 12 Physics Solutions

Frequently Asked Question (FAQs)

The chapter Moving Charges and Magnetism have 8 to 10 percentage weightage. The questions asked from the chapter can be of a numerical, derivation or theory questions. CBSE board follows NCERT Syllabus. To practice problems refer to NCERT text book, NCERT syllabus and previous year board papers of Class 12 Physics.

No, you can not skip it. Since from NCERT Class 12 Physics chapter 4 you can expect 2 questions for NEET exam.

No, you have to practise more questions for doing well in JEE main exams. The questions of Moving Charges and Magnetism need a good base of vectors and a thorough understanding of concepts

Electromagnetic theory is a theory that explains the relationship between electric fields and magnetic fields. It is based on the idea that electric and magnetic fields are two different aspects of the same underlying electromagnetic field.

Magnetic resonance imaging (MRI) is a medical technique that uses a strong magnetic field and radio waves to create detailed images of the inside of the body. It is used to diagnose a wide range of medical conditions.

Latest Articles
Popular Articles

Upcoming School Exams

National institute of open schooling 12th examination.

Admit Card Date : 28 March,2024 - 22 May,2024

National Institute of Open Schooling 10th examination

Madhya pradesh board 12th examination.

Application Date : 01 May,2024 - 20 May,2024

Madhya Pradesh Board 10th Examination

Uttar pradesh board 12th examination.

Application Date : 07 May,2024 - 31 May,2024

Certifications By Top Providers

Most Viewed

Explore Top Universities Across Globe

Universities

Related E-books & Sample Papers

Cbse class 11, 12 physics syllabus 2024-25.

248 + Downloads

CBSE Class 11, 12 Economics Syllabus 2024-25

104 + Downloads

CBSE Class 11, 12 Sociology Syllabus 2024-25

112 + Downloads

CBSE Class 11, 12 Sanskrit (Elective) Syllabus 2024-25

32 + Downloads

CBSE Class 11, 12 Sanskrit (Core) Syllabus 2024-25

10 + Downloads

CBSE Class 11, 12 Psychology Syllabus 2024-25

36 + Downloads

CBSE Class 11, 12 Political Science Syllabus 2024-25

53 + Downloads

CBSE Class 11, 12 Physical Education Syllabus 2024-25

39 + Downloads

CBSE Class 11, 12 Mathematics Syllabus 2024-25

131 + Downloads

CBSE Class 11, 12 Informatics Practices Syllabus 2024-25

17 + Downloads

CBSE Class 11, 12 Home Science Syllabus 2024-25

9 + Downloads

CBSE Class 11, 12 History Syllabus 2024-25

24 + Downloads

Questions related to CBSE Class 12th

Here are some options you can explore to get admission in a good school even though admissions might be closed for many:

Waitlist: Many schools maintain waitlists after their initial application rounds close. If a student who secured a seat decides not to join, the school might reach out to students on the waitlist. So, even if the application deadline has passed, it might be worth inquiring with schools you're interested in if they have a waitlist and if they would consider adding you to it.

Schools with ongoing admissions: Some schools, due to transfers or other reasons, might still have seats available even after the main admission rush. Reach out to the schools directly to see if they have any open seats in 10th grade.

Consider other good schools: There might be other schools in your area that have a good reputation but weren't on your initial list. Research these schools and see if they have any seats available.

Focus on excelling in your current school: If you can't find a new school this year, focus on doing well in your current school. Maintain good grades and get involved in extracurricular activities. This will strengthen your application for next year if you decide to try transferring again.

Best CBSE schools in Delhi: Click Here

In India, the design and coding fields offer exciting career options that can leverage your interest in both. Here's how you can navigate this path:

Choosing Your Stream:

Graphic Design Focus: Consider a Bachelor's degree in Graphic Design or a design diploma. Build a strong portfolio showcasing your creative skills. Learn the basics of HTML, CSS, and JavaScript to understand web development better. Many online resources and bootcamps offer these introductory courses.

Coding Focus: Pursue a Computer Science degree or a coding bootcamp in India. These programs are intensive but can equip you with strong coding skills quickly. While building your coding prowess, take online courses in graphic design principles and UI/UX design.

Engineering Subjects (for a Degree):

Information Technology (IT): This offers a good mix of web development, networking, and database management, all valuable for web design/development roles.

Human-Computer Interaction (HCI): This is a specialized field that bridges the gap between design and computer science, focusing on how users interact with technology. It's a perfect choice if you're interested in both aspects.

Passing NIOS in October 2024 will make you eligible for NIT admissions in 2025 . NIT admissions are based on your performance in entrance exams like JEE Main, which typically happen in January and April. These exams consider the previous year's Class 12th board results (or equivalent exams like NIOS).

Here's why 2025 is more likely:

JEE Main 2024 Admissions: The application process for NITs through JEE Main 2024 is likely complete by now (May 2024). They consider your 2023 Class 12th marks (CBSE in this case).
NIOS Results: Since NIOS results typically come out after the NIT admission process, your October 2024 NIOS marks wouldn't be available for JEE Main 2024.

Looking Ahead (2025 Admissions):

Focus on JEE Main: Since you have a computer science background, focus on preparing for JEE Main 2025. This exam tests your knowledge in Physics, Chemistry, and Mathematics, crucial for engineering programs at NITs.
NIOS Preparation: Utilize the time between now and October 2024 to prepare for your NIOS exams.
Eligibility Criteria: Remember, NITs typically require a minimum of 75% marks in Class 12th (or equivalent) for general category students (65% for SC/ST). Ensure you meet this criteria in your NIOS exams.

Yes, scoring above 99.9 percentile in CAT significantly increases your chances of getting a call from IIM Bangalore, with your academic background. Here's why:

High CAT Score: A score exceeding 99.9 percentile is exceptional and puts you amongst the top candidates vying for admission. IIM Bangalore prioritizes CAT scores heavily in the shortlisting process.

Strong Academics: Your 96% in CBSE 12th and a B.Tech degree demonstrate a solid academic foundation, which IIM Bangalore also considers during shortlisting.

However, the shortlisting process is multifaceted:

Other Factors: IIM Bangalore considers other factors beyond CAT scores, such as your work experience (if any), XAT score (if you appear for it), academic diversity, gender diversity, and performance in the interview and Written Ability Test (WAT) stages (if shortlisted).

Here's what you can do to strengthen your application:

Focus on WAT and PI: If you receive a shortlist, prepare extensively for the Written Ability Test (WAT) and Personal Interview (PI). These stages assess your communication, soft skills, leadership potential, and suitability for the program.

Work Experience (if applicable): If you have work experience, highlight your achievements and how they align with your chosen IIM Bangalore program.

Overall, with a stellar CAT score and a strong academic background, you have a very good chance of getting a call from IIM Bangalore. But remember to prepare comprehensively for the other stages of the selection process.

Yes you can appear for the compartment paper again since CBSE gives three chances to a candidate to clear his/her exams so you still have two more attempts. However, you can appear for your improvement paper for all subjects but you cannot appear for the ones in which you have failed.

I hope this was helpful!

Colleges After 12th

JEE Main Important Physics formulas

As per latest 2024 syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters

PW JEE Coaching

Enrol in PW Vidyapeeth center for JEE coaching

PW NEET Coaching

Enrol in PW Vidyapeeth center for NEET coaching

JEE Main Important Chemistry formulas

As per latest 2024 syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters

CBSE Class 12 Syllabus 2024-25 Released - Download PDF Here

Get Latest Updates on CBSE 12th Admit Card 2024 Here

CBSE Class 12 date sheet 2024 revised: Check date sheet here

Stay up-to date with CBSE Class 12th News

Explore on careers360.

Board Exams
Navodaya Vidyalaya
Top Schools
NCERT Solutions for Class 10
NCERT Solutions for Class 9
NCERT Solutions for Class 8
NCERT Solutions for Class 6

NCERT Exemplars

NCERT Exemplar
NCERT Exemplar Class 9 solutions
NCERT Exemplar Class 10 solutions
NCERT Exemplar Class 11 Solutions
NCERT Books for class 6
NCERT Books for class 7
NCERT Books for class 8
NCERT Books for class 9
NCERT Books for Class 10
NCERT Books for Class 11
NCERT Books for Class 12
NCERT Notes for Class 9
NCERT Notes for Class 10
NCERT Notes for Class 11
NCERT Notes for Class 12
NCERT Syllabus for Class 6
NCERT Syllabus for Class 7
NCERT Syllabus for class 8
NCERT Syllabus for class 9
NCERT Syllabus for Class 10
NCERT Syllabus for Class 11
NCERT Syllabus for Class 12
CBSE Date Sheet
CBSE Syllabus
CBSE Admit Card
CBSE Result
CBSE Result Name and State Wise
CBSE Passing Marks

CBSE Class 10

CBSE Board Class 10th
CBSE Class 10 Date Sheet
CBSE Class 10 Syllabus
CBSE 10th Exam Pattern
CBSE Class 10 Answer Key
CBSE 10th Admit Card
CBSE 10th Result
CBSE 10th Toppers
CBSE Board Class 12th
CBSE Class 12 Date Sheet
CBSE Class 12 Admit Card
CBSE Class 12 Syllabus
CBSE Class 12 Exam Pattern
CBSE Class 12 Answer Key
CBSE 12th Result
CBSE Class 12 Toppers

CISCE Board 10th

ICSE 10th time table
ICSE 10th Syllabus
ICSE 10th exam pattern
ICSE 10th Question Papers
ICSE 10th Result
ICSE 10th Toppers
ISC 12th Board
ISC 12th Time Table
ISC Syllabus
ISC 12th Question Papers
ISC 12th Result
IMO Syllabus
IMO Sample Papers
IMO Answer Key
IEO Syllabus
IEO Answer Key
NSO Syllabus
NSO Sample Papers
NSO Answer Key
NMMS Application form
NMMS Scholarship
NMMS Eligibility
NMMS Exam Pattern
NMMS Admit Card
NMMS Question Paper
NMMS Answer Key
NMMS Syllabus
NMMS Result
NVS Admit Card
NTSE Application Form
NTSE Eligibility Criteria
NTSE Exam Pattern
NTSE Admit Card
NTSE Syllabus
NTSE Question Papers
NTSE Answer Key
NTSE Cutoff
Navodaya Result
Navodaya Exam Date
Navodaya Vidyalaya Admission Class 6
JNVST admit card for class 6
JNVST class 6 answer key
JNVST class 6 Result
JNVST Class 6 Exam Pattern
Navodaya Vidyalaya Admission
JNVST class 9 exam pattern
JNVST class 9 answer key
JNVST class 9 Result

Schools By Medium

Malayalam Medium Schools in India
Urdu Medium Schools in India
Telugu Medium Schools in India
Karnataka Board PUE Schools in India
Bengali Medium Schools in India
Marathi Medium Schools in India

By Ownership

Central Government Schools in India
Private Schools in India
Schools in Delhi
Schools in Lucknow
Schools in Kolkata
Schools in Pune
Schools in Bangalore
Schools in Chennai
Schools in Mumbai
Schools in Hyderabad
Schools in Gurgaon
Schools in Ahmedabad
Schools in Uttar Pradesh
Schools in Maharashtra
Schools in Karnataka
Schools in Haryana
Schools in Punjab
Schools in Andhra Pradesh
Schools in Madhya Pradesh
Schools in Rajasthan
Schools in Tamil Nadu

Download Careers360 App's

Regular exam updates, QnA, Predictors, College Applications & E-books now on your Mobile

Certifications

We Appeared in

CBSE Expert

CBSE Class 12 Physics Case Study Questions PDF Download

Case Study questions for the Class 12 Physics board exams are available here. You can read the Class 12 Physics Case Study Questions broken down by chapter. Subject matter specialists and seasoned teachers created these quizzes. You can verify the right response to each question by referring to the answer key, which is also provided. To achieve success on your final exams, practice the following questions.

CBSE (Central Board of Secondary Education) is a renowned educational board in India that designs the curriculum for Class 12 Physics with the goal of promoting a scientific temperament and nurturing critical thinking among students. As part of their Physics examination, CBSE includes case study questions to assess students’ ability to apply theoretical knowledge to real-world scenarios effectively.

Chapter-wise Solved Case Study Questions for Class 12 Physics

Before the exams, students in class 12 should review crucial Physics Case Study issues. They will gain a better understanding of the kinds of Case Study questions that may be asked in Physics exams for Grade 12. These questions were created by our highly qualified standard 12 Physics staff based on the questions that appeared most frequently in last year’s exams. The solutions have been written in a way that will make them simple to grasp and will aid students in grade 12 in understanding the topics.

Best Books for Class 12 Physics Exams

Strictly in accordance with the new term-by-term curriculum for the class 12 board exams to be held in the academic year 2023–2024, which will include multiple choice questions based on new board typologies including stand-alone MCQs and case-based MCQs with an assertion–reason. Included are inquiries from the official CBSE Question Bank that was released in April 2024. What changes have been made to the book: strictly in accordance with the term-by-term syllabus for the board exams that will be held during the 2024 academic year? Chapter- and topic-based Questions with multiple choices that are based on the unique evaluation method used for the Class 12th Physics Final Board Exams.

Key Benefits of Solving CBSE Class 12 Physics Case Study Questions

Application of Concepts: Case study questions demand the application of theoretical knowledge in practical scenarios, preparing students for real-world challenges and professional pursuits.
Critical Thinking: By evaluating and analyzing case studies, students develop critical thinking abilities, enabling them to approach complex problems with a logical mindset.
In-Depth Understanding: Addressing case study questions necessitates a thorough understanding of physics concepts, leading to a more profound comprehension of the subject matter.
Holistic Evaluation: CBSE adopts case study questions as they provide a holistic evaluation of a student’s aptitude and proficiency in physics, moving beyond rote memorization.
Preparation for Competitive Exams: Since competitive exams often include similar application-based questions, practicing case study questions equips students for various entrance tests.

How to Approach CBSE Class 12 Physics Case Study Questions

Read and Analyze Thoroughly: Carefully read the case study to grasp its context and identify the underlying physics principles involved.
Identify Relevant Concepts: Highlight the physics theories and concepts applicable to the given scenario.
Create a Systematic Solution: Formulate a step-by-step solution using the identified concepts, explaining each step with clarity.
Include Diagrams and Charts: If relevant, incorporate diagrams, charts, or graphs to visually represent the situation, aiding better comprehension.
Double-Check Answers: Always review your answers for accuracy, ensuring that they align with the principles of physics.

Tips for Excelling in CBSE Class 12 Physics

Conceptual Clarity: Focus on building a strong foundation of physics concepts, as this will enable you to apply them effectively to case study questions.
Practice Regularly: Dedicate time to solving case study questions regularly, enhancing your proficiency in handling real-world scenarios.
Seek Guidance: Don’t hesitate to seek guidance from teachers, peers, or online resources to gain additional insights into challenging concepts.
Time Management: During exams, practice efficient time management to ensure you allocate enough time to each case study question without rushing.
Stay Positive: Approach case study questions with a positive mindset, embracing them as opportunities to showcase your skills and knowledge.

CBSE Class 12 Physics case study questions play a pivotal role in promoting practical understanding and critical thinking among students. By embracing these questions as opportunities for growth, students can excel in their physics examinations and beyond.

Download India's best Exam Preparation App Now.

Key Features

Revision Notes
Important Questions
Previous Years Questions
Case-Based Questions
Assertion and Reason Questions

No thanks, I’m not interested!

CBSE Class 12 Physics Chapter 4 Revision Notes – Moving Charges and Magnetism

Moving charges and magnetism class 12 cbse revision notes.

Chapter 4 – Moving charges and magnetism, is from the class 12 textbook of physics. In this chapter, the students will learn how the magnetic field exerts forces on moving charged particles, like electrons, protons, and some wires carrying current. Moreover, various topics will be covered in moving charges and magnetism class 12 notes which will be clearing all the doubts of the students on this topic. Further, there are many derivations and exercises that will let you practice more.

Topics like a magnetic force, motion in a magnetic field, motion in a combined electric field and magnetic fields and many other topics are covered in this chapter. In addition, many laws are there through which you have to solve the derivations and the questions. Thus, there are a lot of questions in the exercise portion as well in moving charges and magnetism class 12 notes.

Download Toppr app for Android and iOS or signup for free.

Sub-topics covered under Moving Charges and Magnetism:

Ampere’s Circuital Law
Magnetic Field Due to a Current Element, Biot-Savart Law
Magnetic Force and Magnetic Field
Motion in Combined Electric and Magnetic Field
Moving Coil Galvanometer
The Solenoid and the Toroid
Torque on Current Loop, Magnetic Dipole

You can download CBSE Class 12 Physics Chapter 4 Revision Notes by clicking on the download button below

moving charges and magnetism class 12 notes

Download Toppr – Best Learning App for Class 5 to 12

Toppr is a learning platform that provides students with a chance to understand things. Furthermore, we have a team of expert subject teachers who can solve the queries and doubts of the students through our live stream program. Moreover, we have educational content for all the subjects. In addition, we provide video lectures and free pdfs also that the students can download from our website. Other than that, students can take our mock tests to check their performance and analyze their progress. Furthermore, it will also assist in identifying your strengths and weaknesses that will result in an effective learning experience.

Download Toppr app for Android and iOS or signup for free.

Customize your course in 30 seconds

Which class are you in.

CBSE Class 12 Physics Revision Notes

CBSE Class 12 Physics Chapter 14 – Semiconductor Electronic Class 12 Notes
CBSE Class 12 Physics Chapter 13 – Nuclei Class 12 Notes
CBSE Class 12 Physics Chapter 12 – Atoms Revision Notes
CBSE Class 12 Physics Chapter 11 Notes – Dual Nature of Radiation and Matter
CBSE Class 12 Physics Chapter 10 Notes – Wave Optics
CBSE Class 12 Physics Chapter 9 Notes – Ray Optics and Optical Instruments
CBSE Class 12 Physics Chapter 8 Revision Notes – Electromagnetic Waves
CBSE Class 12 Physics Chapter 7 – Alternating Current Class 12 Notes
CBSE Class 12 Physics Chapter 6 – Electromagnetic Induction Class 12 Notes
CBSE Class 12 Physics Chapter 5 Notes – Magnetism and Matter

Download the App

Physics Important Questions
Class 12 Physics
Chapter 4: Moving Charges Magnetism

Important Questions for Class 12 Physics Chapter 4 – Moving Charges and Magnetism

Magnetism is a physical characteristic caused by magnetic fields that produce attractive and repulsive effects on other objects. A magnetic field is generated by electric currents and magnetic moments of particles and influences other currents and magnetic moments. Ferromagnetic materials, which are strongly drawn to magnetic fields and can become permanent magnets themselves, are the most well-known materials that exhibit magnetism. Only a limited number of substances are ferromagnetic, including iron, cobalt, nickel and their alloys, which are the most common. The less common ferromagnetic substances include the rare-earth metals neodymium and samarium. Ferro- refers to iron as the permanent magnetism that was first found in lodestone, a type of iron ore called magnetite (Fe3O4).

A magnetic field is a field of vectors representing magnetism’s impact on moving electric charges, electric currents, and magnetic materials. A force perpendicular to both the velocity and magnetic field is experienced by a moving charge in a magnetic field. A permanent magnet’s magnetic field attracts ferromagnetic materials like iron and other magnets. Nonuniform magnetic fields can also apply tiny forces to “nonmagnetic” materials through paramagnetism, diamagnetism, and antiferromagnetism, but these forces are usually so weak that they can only be measured with laboratory equipment. Magnetised materials are surrounded by magnetic fields generated by electric currents in electromagnets and changing electric fields. As the strength and direction of magnetic fields can vary in different locations, they are described mathematically with a vector field function assigning a vector to each point in space.

Magnetic fields are produced by the movement of electric charges and the inherent magnetic moments of particles connected to their spin, a fundamental quantum property. Magnetic and electric fields are related, and both are part of the electromagnetic force, one of nature’s four fundamental forces. Magnetic fields are widely utilised in modern technology, especially in electrical engineering and electromechanics. Rotating magnetic fields are applied in electric motors and generators. The study of magnetic fields in electrical devices like transformers is called magnetic circuits. The Hall effect shows the presence of charge carriers in a material through magnetic forces. The Earth generates its own magnetic field, protecting the ozone layer from solar wind and crucial for compass navigation.

Important Questions For Class 12 – Physics – Chapter 4 – Moving Charges and Magnetism are provided here. Students must go through these questions and solve them to prepare for their Physics papers. They can also refer to these questions for quick revision. These questions are more likely to be asked in the exam; hence, students must practise them thoroughly.

Very Short Answer Type Questions

1. How does the radius of the path of a charged particle moving in a cyclotron change when the radio frequency field’s frequency is doubled?

(a) It will be halved.

(b) It will be doubled.

(d) It will be increased by four times.

Answer: (c) It will remain unchanged.

2. Which of the following statements about a cyclotron is not true?

(a) A cyclotron is a device that uses high energies to accelerate ions or charged particles.

(b) Cyclotron combines electric and magnetic fields to accelerate charged particles and increase their energy.

(c) The cyclotron works by utilising the principle that the time it takes for an ion to complete one revolution is not affected by its speed or the radius of its orbit.

(d) In a cyclotron, the path of charged particles and ions is not fixed and can be arbitrary.

Answer: (d) In a cyclotron, the path of charged particles and ions is not fixed and can be arbitrary.

3. If an electron is travelling with velocity ν, it generates a magnetic field B, then

(a) the direction of field B will align with the direction of velocity ν.

(b) the direction of field B will be in the opposite direction to the direction of velocity ν.

(d) the direction of field B is independent of the direction of velocity ν.

Answer: (c) the direction of field B will be at a right angle to the direction of velocity ν.

4. If the magnetic compass needle is brought close to a straight wire bearing current, then

(I) the straight wire results in a significant deviation of the compass needle.

(II) The needle tangentially aligns to an imaginary circle whose centre is the straight wire and whose plane is perpendicular to the wire.

(a) (II) is correct

(b) (I) is correct

(d) both (I) and (II) are correct

Answer: (d) both (I) and (II) are correct

5. Which statement about magnetic forces is correct?

(a) Magnetic forces always obey Newton’s third law.

(b) Magnetic forces do not follow Newton’s third law.

(d) Magnetic forces comply with Newton’s third law in a low magnetic field environment.

Answer: (b) Magnetic forces do not follow Newton’s third law.

6. Converting a moving coil galvanometer into a voltmeter is achieved by

(a) placing a high resistance in series.

(b) placing a low resistance in parallel.

(d) placing a low resistance in series.

Answer: (a) placing a high resistance in series.

7. Converting a moving coil galvanometer into an ammeter is done by

(a) placing a high shunt resistance in series.

(b) placing a low shunt resistance in parallel.

(d) placing a high resistance in parallel.

Answer: (b) placing a low shunt resistance in parallel.

Short Answer Type Questions

1. Verify that the cyclotron frequency = eB/m has the correct dimensions of [T] -1

When a charged particle travels normal to the magnetic field, then

$\begin{array}{l}\frac{ mv^2 }{ r } = qvB\end{array} $

$\begin{array}{l}\textup{Therefore, dimensions of } \omega = \frac{qB}{m} = \frac{v}{r} = \frac{LT^{-1}}{L} = [T^{-1}]\end{array} $

2. Show that a force that does no work and is a velocity-dependent force.

Work is a scalar product of displacement and force. Hence work done at any instant is given by the following formula:

$\begin{array}{l}dW = \vec{F}. \vec{ds}\end{array} $

Where displacement is given as:

$\begin{array}{l}\textup{Displacement, } \vec{ds} = \vec{v} dt \end{array} $

According to the question, the work done by the force is:

$\begin{array}{l}dW = 0\end{array} $

$\begin{array}{l}\Rightarrow \vec{ F }. \vec{v}dt = 0\end{array} $

$\begin{array}{l}\vec{F}.\vec{v} = 0\end{array} $

This shows that the angle between force and velocity will be 90 o . If the direction of velocity changes, then the direction of the force will also vary.

3. The magnetic force depends on v, which depends on the inertial frame of reference. Does then the magnetic force differ from inertial frame to frame? Is it reasonable that the net acceleration has a different value in different frames of reference?

The magnetic force relies on vector v, which depends on the inertial reference frame. Magnetic force on a charged particle,

$\begin{array}{l}F = q ( \vec{v} \times \vec{B} ) \end{array} $

$\begin{array}{l} F = qvBsin \theta \end{array} $

Thus, the magnetic force is velocity-dependent. It varies from one inertial frame to another inertial frame.

4. Describe the motion of a charged particle in a cyclotron if the frequency of the radio (rf) field was doubled.

When the frequency of the radio frequency (rf) field is doubled, then the resonance condition is violated, and the time period of the radio frequency (rf) field is halved.

Therefore, the duration in which a particle completes half revolution inside the dees, radio frequency completes the cycle. As a result, particles will accelerate and decelerate alternatively.

5. Two long wires carrying current I 1 and 1 2 are arranged as shown in the figure. The one carrying current I 1 is along the x-axis. The other carrying current, I 2 is along a line parallel to the y-axis given by x = 0 and z =d. Find the force exerted at 0 2 because of the wire along the x-axis.

Important Questions For Class 12 - Physics - Chapter 4 - Moving Charges and Magnetism 2

Magnetic field at the point O 2 due to current I 1 in long wire along the x-axis is

$\begin{array}{l} B_{O_{2}} = \frac{ \mu_0 }{ 4 \pi } \frac{ 2I }{ d } \end{array} $

It will be along the y-axis. Since the second wire is along the y-axis, the angle between the direction of

$\begin{array}{l} I_2 \vec{l} \textup{ and } \vec{B}_{O_{2}} \textup{ is zero.} \end{array} $

$\begin{array}{l} \theta = 0^o \end{array} $

Force on the wire existing along the y-axis is,

$\begin{array}{l} f = I_2 | \vec{ l } \times \vec{B}_{O_{2}} | = I_2 l B_{O_{2}} sin 0^o = 0 \end{array} $

Long Answer Type Questions

1. A current carrying loop consists of 3 identical quarter circles of radius R, lying in the positive quadrants of the x-y, y-z and z-x planes with their centres at the origin, joined together. Find the direction and magnitude of B at the origin.

Solution: Draw a rough diagram.

The equation used is

$\begin{array}{l}B = \frac{ \mu_0 I \theta }{ 4 \pi R }\end{array} $

It is given that

$\begin{array}{l} \textup{Quarter Circles } \theta = \frac{ \pi }{ 2 } \end{array} $

The electric current in circular arc = I, Radius = R

The magnetic field at the origin point due to the electric current carrying arc existing in x-y plane:

$\begin{array}{l} \vec{ B } _ { xy } = \frac{ \mu _ { 0 } I ( \pi / 2 ) }{ 4 \pi R } \hat{ k } \end{array} $

$\begin{array}{l} = \frac{ \mu _ { 0 } I }{ 8 R } \hat{ k } \end{array} $

Likewise, the Magnetic field at the origin point due to the electric current circular arc existing in the y-z plane:

$\begin{array}{l} \vec{ B } _ { xy } = \frac{ \mu _ { 0 } I ( \pi /2 ) } { 4 \pi R } \hat{ i } \end{array} $

$\begin{array}{l} = \frac{ \mu _ { 0 } I }{ 8 R } \hat{ i } \end{array} $

Likewise, the magnetic field at origin due to the electric current carrying a circular arc existing in the y-x plane:

$\begin{array}{l} \vec{ B } _ { zx } = \frac{ \mu _ { 0 }I ( \pi / 2 ) }{ 4 \pi R } \hat{ j } \end{array} $

$\begin{array}{l} = \frac{ \mu _ { 0 } I }{ 8R } \hat{ j } \end{array} $

The total vector sum of the magnetic field at the origin point due to each quarter circle,

$\begin{array}{l} \vec{ B } = \vec{ B } _ { xy } + \vec{ B } _ { yz } + \vec{ B } _ { zx } \end{array} $

$\begin{array}{l} \vec{ B } _ { net } = \left ( \frac{ \mu I }{ 8 R } \right ) ( \hat{ i } + \hat{ j } + \hat{ k } ) \end{array} $

2. A charged particle of charge e and mass m is moving in an electric field E, and magnetic field B. Construct dimensionless quantities and quantities of dimension [T] -1 .

No dimensionless quantity made using the given quantities. In the case of a charged particle travelling normally to the magnetic field, the magnetic Lorentz forces lend the required circular or centripetal force for revolution.

$\begin{array}{l} \frac{ mv ^ { 2 } }{ R } = qvB \end{array} $

By simplifying the equation, we get,

$\begin{array}{l} \frac{ q B }{ m } = \frac{ v }{ R } = \omega \end{array} $

The dimensional form of angular frequency

$\begin{array}{l} [\omega] = \left [ \frac{ qB }{ m } \right ] = \frac{ v } { R } = [T] ^ { -1 } \end{array} $

3. An electron enters with a velocity v = V o i into a cubical region (faces parallel to coordinate planes) in which there are uniform electric and magnetic fields. The orbit of the is found to spiral down inside the cube in the plane parallel to the x-y plane. Suggest a configuration of fields E and B that can lead to it.

If a charged particle is positioned in an electric field and magnetic field, then it begins moving in a spiral trajectory where magnetic field B and electric field E is perpendicular to the direction of motion. The electric field applies force on the charged particle, which results in the particle’s deceleration or acceleration and the centripetal force works due to the magnetic force. Assume that a magnetic field B = B 0 exists in the area, and an electron enters with a velocity of into the cubical region.

Using magnetic Lorentz force, the net force on the electron is represented by

$\begin{array}{l} \vec{ F} _ { m } = – e ( v _ { 0 } \hat{ i } \times B _ { 0 } \hat{ k } ) \end{array} $

$\begin{array}{l} = e v _ { 0 } B _ { 0 } \hat{ j } \end{array} $

The orbit of the electron circles around down inside the cube in the plane parallel to the x-y plane. So, E should be along the x-axis, and magnetic field B should be along the +z direction.

$\begin{array}{l} \vec{ B } = B _ { 0 } \hat{ k } \textup{ and } \vec{ E } = E _ { 0 } \hat{ i } \end{array} $

(where E 0 > 0)

4. Do magnetic forces obey Newton’s third law? Verify for two current elements dl 1 – dl i (unit vector) located at the origin and dl 2 = dl j (unit vector) located at (O, R, O). Both carry current I.

Here, it is required to find the magnetic field’s direction due to one wire at the point on a different wire, then the magnetic force on the current bearing wire.

As per Biot-Savart’s law, the magnetic field is parallel to idl × r, and idl is the current bearing element which has its direction along the current flow’s direction.

In the case of the magnetic field direction, at dl 2 , positioned at (0, R, 0) due to wire dl s represented by B || idl × r or i × j (point (0, r, 0) lies on the y-axis) and i × j = k. Therefore, the magnetic field at dl 2 is along the z-direction.

The magnetic force direction exerted at dl 2 due to the magnetic field of the first wire is along the x-axis.

F -i(I × ), i.e., F || (i × k) or along the -j direction.

Thus, the force due to dl 1 and dl 2 is non-zero.

Hence, magnetic forces do not follow Newton’s third law. But they follow Newton’s third law if the current carrying sections are placed parallel to each other.

5. A multirange voltmeter can be constructed by using a galvanometer circuit, as shown in the figure. We want to construct a voltmeter that can measure 2V, 20V and 200V using a galvanometer of resistance 10Ω and produce maximum deflection for a current of 1 mA. Find R 1 , R 2 , and R 3 that have to be used.

In this scenario,

$\begin{array}{l} G = 10\Omega \end{array} $

$\begin{array}{l} I _ { g } = 1 m A = 10 ^ { -3 } A \end{array} $

$\begin{array}{l} \textup{ Case (i): } V = 2V \end{array} $

$\begin{array}{l}R _ { 1 } = \frac{ V }{ I _ g } – G \end{array} $

$\begin{array}{l} \frac{ 2 }{ 10 ^ { -3 } } -10 \end{array} $

$\begin{array}{l} 1990 \Omega \approx 2\Omega \end{array} $

$\begin{array}{l} \textup{ Case (b): } V = 20V \end{array} $

$\begin{array}{l} ( R _ { 1 } + R _ { 2 } ) = \frac{ 20 }{ 10 ^ { -3 } } – 10 \end{array} $

$\begin{array}{l} 20, 000 – 10 \approx 20k\Omega \end{array} $

$\begin{array}{l} R_2 = 20k \Omega – 2 k \Omega = 18 k \Omega \end{array} $

$\begin{array}{l} \textup{ Case(c): } V = 200V \end{array} $

$\begin{array}{l} R _ { 1 } + R _ { 2 } + R _ { 3 } = \frac{ 200 }{ 10 ^ { -3 } } – 10 \end{array} $

$\begin{array}{l} \approx 200 k \Omega \end{array} $

$\begin{array}{l} \therefore R _ { 3 } = 200 k \Omega – 20 k \Omega \approx 180 k \Omega \end{array} $

6. A long straight wire carrying a current of 25A rests on a table, as shown in the figure. Another wire PQ of length 1m, mass 2.5g, carries the same current but in the opposite direction. The wire PQ is free to slide up and down. To what height will PQ rise?

In this case,

$\begin{array}{l} I _ { 1 } = 25 A \end{array} $

$\begin{array}{l} I _ { 2 } = 25 A \end{array} $

$\begin{array}{l} l = 1m \end{array} $

$\begin{array}{l} m = 2.5g = 2.5 \times 10 ^ { -3 } kg \end{array} $

In the equilibrium position,

$\begin{array}{l} m g = \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 l _ { 1 } l _ { 2 } l }{ h } \end{array} $

$\begin{array}{l} h = \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 l _ { 1 } l _ { 2 } l }{ mg } \end{array} $

$\begin{array}{l} = \frac{ 10 ^ { -7 } \times 2 \times 25 \times 25 \times 1 }{ (2.5 \times 10 ^ { -3 }) \times 9.8 } = 51 \times 10 ^ { -4 } m = 0.51 cm \end{array} $

7. A 100-turn rectangular coil, ABCD (in XY plane), is hung from one arm of a balance. A mass of 500g is added to the other arm to balance the weight of the coil. A current 4.9 A passes through the coil, and a constant magnetic field of 0.2 T acting inward (in xz plane) is switched on such that only arm CD of length 1 cm lies in the field. How much additional mass ‘m’ must be added to regain the balance?

If the magnetic field is zero and the weight is added to one balance pan, balance the rectangular coil in the other balance pan. Then

$\begin{array}{l} M g l = W _ { coil } l \textup{ or } W _ { coil } = M g = 500 \times 9.8 N \end{array} $

When the current (I) is passed through the coil and the magnetic field is switched on, let ‘m’ be the mass added in a pan to counterbalance the beam. Then

$\begin{array}{l} M g l + mgl + = W _ { coil } l + I B L \, sin 90 ^ { 0 } \, l \end{array} $

$\begin{array}{l} m g l = I B L I \textup{ or } m = \frac{ I B L }{ 9 } \end{array} $

$\begin{array}{l} \therefore m = \frac{ 4.9 \times 0.2 \times ( 1 \times 10 ^ {-2} ) }{ 9.8 } = 10 ^ {-3} kg = 1g \end{array} $

8. A rectangular conducting loop consists of two wires on two opposite sides of length ‘I’ joined together by a rod of length ‘d’. The wires are each of the same material but with cross-sections differing by a factor of 2. The thicker wire has a resistance E, and the rods are of low resistance, which in turn are connected to a constant voltage source V 0 . The loop is placed in uniform a magnetic field B at 45 o to its plane. Find τ, the torque exerted by the magnetic field on the loop about an axis through the centres of rods.

Equation used: $\begin{array}{l}B = B_0 \hat{i} \end{array} $

$\begin{array}{l} \vec{ \tau } = \vec{ r } + \vec{ F } \end{array} $

Force on current bearing wire placed in a magnetic field,

$\begin{array}{l} \vec{ F } = i ( \vec{ I } \times \vec{ B } ) \end{array} $

The force on the thicker wire (wire 1) is

$\begin{array}{l} F _ { 1 } = i _ { 1 } I B = \left ( \frac{ V _ { O } }{ R } \right ) I B \end{array} $

$\begin{array}{l} \textup{Since resistance of wire } R = \frac{ \rho I}{ A } \end{array} $

$\begin{array}{l} \textup{Each wire is of the same material } R \propto \frac{ 1 }{ A} \end{array} $

$\begin{array}{l} \textup{ Force on another wire } \vec{ F } _ { 2 } = ( \vec{ I } \times \vec{ B } ) \end{array} $

$\begin{array}{l} F _ { 2 } = i _ { 2 } I B = \left ( \frac{ V _ 0 }{ 2 R } \right ) I B \end{array} $

Torque on wire on wire 1 due to F 1 ,

$\begin{array}{l} \vec{ \tau } _ { 1 }\left ( \frac{d}{2} \right ) \left ( \frac{ V _ {0} }{ R } \right ) I B \, sin 45 ^ { o } = \left ( \frac{ V _ { 0 } d }{ 2 \sqrt{ 2 } } \right ) I B \end{array} $

Torque on the wire 2 due to F 2 ,

$\begin{array}{l} \vec{ \tau } _ { 2 } = \vec{ r } \times \vec{ F } _ { 2 } = \left ( \frac{ d }{ 2 } \right ) F _ { 2 } \, sin \theta \end{array} $

$\begin{array}{l} \tau _ { 2 } = \left ( \frac{ d }{ 2 } \right ) \left ( \frac{ V _ { 0 } }{ 2 R } \right ) I B sin 45 ^ { o } = \left ( \frac{ V _ { 0 } d }{ 4 \sqrt{ 2 } } \right ) I B \end{array} $

$\begin{array}{l} \textup{Net torque } \tau = \tau _ 1 – \tau _ 2 \end{array} $

$\begin{array}{l} \tau = \frac{ 1 }{ 4 \sqrt{ 2 } } \frac{ V _ { 0 } I d B }{ R } \end{array} $

(A = Id = Area of loop)

9. An electron and a positron are released from (0, 0, 0) and (0, 0, 1.5R), respectively, in a uniform magnetic field, each with an equal momentum of magnitude p = e BR. Under what conditions on the directions of momentum will the orbits be non-intersecting circles?

Since B is along the x-axis, for a circular orbit, the memento of the two particles is in the y-z plane. Assume p 1 and p 2 as the moment of the electron and positron, respectively. Both of them are defined as a circle of radius R. Assume p 1 makes an angle θ with the y-axis, and p 2 should make the same angle. The centre of the circles should be normal to the momenta and at a distance of R.

The circles of the two shall not overlap if the length between the two centres is more than 2R.

Let d be the length between Ce and Cp.

$\begin{array}{l} d ^ { 2 } = [ R sin \theta – ( – R sin \theta ) ^ 2 ] \left [ R cos \theta \left ( \frac{ 3 }{ 2 } – R cos \theta \right ) \right ] ^ { 2 } \end{array} $

$\begin{array}{l} d ^ { 2 } = ( 2 R sin \theta ) ^ { 2 } + \left ( \frac{ 3 }{ 2 } R – 2 R cos \theta \right ) ^ { 2 } \end{array} $

$\begin{array}{l} = 4 R ^ { 2 } sin ^ { 2 } \theta + \frac{ 9 ^ { 2 } }{ 4 } r – 6 R ^ { 2 } cos \theta + 4 R ^ 2 cos ^ 2 \theta \end{array} $

$\begin{array}{l} = 4 R ^ { 2 } + \frac{ 9 }{ 4 } R ^ { 2 } – 6 R ^ { 2 } cos \theta \end{array} $

As ‘d’ has to be larger than 2R

$\begin{array}{l} d ^ { 2 } > 4 R ^ { 2 } \end{array} $

$\begin{array}{l} \Rightarrow 4 R ^ { 2 } + \frac{ 9 }{ 4 } R ^ { 2 } – 6 R ^ { 2 } cos \theta > 4 R ^ { 2 } \end{array} $

$\begin{array}{l} \frac{ 9 }{ 4 } > 6 cos \theta \textup{ or } cos \theta < \frac{ 3 }{ 8 } \end{array} $

10. A uniform conducting wire of length 12a and resistance R is wound as a current-carrying coil in the shape of (i) an equilateral triangle of side a; (ii) a square of sides a, and (iii) a regular hexagon of sides a. The coil is connected to a voltage source V 0 . Find the magnetic moment of the coil in each case.

(i) No. of turns, n = 4

$\begin{array}{l}\textup{ Area of triangle A} = \frac{ 1 }{ 2 } a \times \alpha \, sin 60 ^ { o } \end{array} $

$\begin{array}{l} = a ^ { 2 } \sqrt{ 3 } / 4 \end{array} $

(ii) $\begin{array}{l} n = 3, \, \textup{area A} = a \times a = a ^ { 2 } \end{array} $

(iii) $\begin{array}{l} n = 2, \textup{ area A} = 6 [\frac{ a }{ 2 } \times \frac{ a }{ 2 } tan 60 ^ { o }] = \frac{ 3 \sqrt{ 3 } }{ 2 } a ^ { 2 } \end{array} $

Magnetic moment, M = nIA

$\begin{array}{l} \textup{For (i), } M _ { 1 } = 4 \times I \times a ^ { 2 } \sqrt{ 3 } / 4 = \sqrt{ 3 } a ^ { 2 } I \end{array} $

$\begin{array}{l} \textup{For (ii), } M _2 = 3 \times I \times a ^ { a } = 3 a ^ { 2 } I \end{array} $

$\begin{array}{l} \textup{For (iii), } M _ { 3 } = 2 \times \frac{ 3 \sqrt{ 3 } }{ 2 } a ^ { 2 } = 3 \sqrt{ 3 } a ^ { 2 } I \end{array} $

(a) Show that ζ(L) monotonically increases with L.

(b) Use an appropriate Amperian loop to show that ζ(∞)=μ 0 I, where I is the current in the wire.

(d) Suppose we replace the circular coil with a square coil of sides R carrying the same current I. What can you say about ζ(L) and ζ(∞)?

Since the circular loop carrying an electric current is lying in the x-y plane, the magnetic field is along the z-axis, in the line integral direction,

$\begin{array}{l} \xi ( L ) = \left| \int _ { – L } ^ { + L } \vec{ B } . \vec{ dl } \right| \end{array} $

$\begin{array}{l} = \int _ { – L } ^ { + L } B d l \cos 0 ^ { o } \end{array} $

$\begin{array}{l} = \int _ { -L } ^ { +L } B d l = 2 B L \end{array} $

So, ζ(L) is monotonically rising with L.

(b) Take a closed amperian path PQRP as represented in the figure.

As per the Ampere circuital law, the integral of B over the closed trajectory PQRP is

$\begin{array}{l} \oint _ { P Q R P } \vec{ B } . \vec{ dl } = \int _ { P Q R } \vec{ B } . \vec{d l} + \int _ { R P } \vec{ B } . \vec{ d l } \end{array} $

$\begin{array}{l} = \int _ { P Q R } \vec{ B } . \vec{ d l } + \int _ { – L } ^ { + L } \vec{ B } . \vec{ d l } = \mu _ { 0 } I \end{array} $

$\begin{array}{l} \int _ { P Q R } \vec{ B } . \vec{ d l } + \zeta ( L ) = \mu _ { 0 } I \end{array} $

If L → ∞, then the value of B → 0 (as B ∝ 1 / r3)

$\begin{array}{l} \therefore \int _ { P Q R } \vec{ B } . \vec{ d l } = 0 \textup{, from (i), } 0 + \zeta ( \infty ) = \mu _ { 0 } I \textup{ or } \zeta ( \infty ) = \mu _ { 0 } I \end{array} $

(c) Magnet field B at a point on the circular coil axis at a distance z from the centre of a circular coil of radius R bearing current I is

$\begin{array}{l} B _ { z } = \frac{ \mu _ { 0 } I R ^ { 2 } }{ 2 ( z ^ { 2 } + R ^ { 2 } ) ^ { 3/2} } \end{array} $

$\begin{array}{l} \therefore \int _ { – \infty } ^ { + \infty } B _ { z } dz = \int _ { -\infty } ^ { + \infty } \frac{ \mu _ { 0 } I R ^ { 2 } }{ 2 ( z ^ { 2 } + R ^ { 2 } ) ^ { 3/2 } } dz \end{array} $

$\begin{array}{l} \textup{Put }z = R \tan \theta, \,\, dz = R \sec ^ { 2 } \theta d \theta \end{array} $

$\begin{array}{l} \therefore \int _ { – \infty } ^ { + \infty } B _ { z } dz = \frac{ \mu _ { 0 } I }{ 2 } \int _ { \pi / 2 } ^ { + \pi / 2 } \cos \theta d \theta = \mu _ { 0 } I \end{array} $

(d) If the circular coil is replaced by a square coil of side R, bearing the same current I, then

$\begin{array}{l} B ( z ) _ { \textup{square} } < B ( z ) _ { \textup{circular coil } } \end{array} $

$\begin{array}{l} \therefore \zeta ( L ) _ { \textup{square }} < \zeta ( L ) _ { \textup{circular coil } } \end{array} $

Utilising arguments as in (b)

$\begin{array}{l} \zeta ( \infty ) _ { \textup{square } } = \zeta ( \infty ) _ { \textup{ circular } } = \mu _ { 0 } I \end{array} $

12. A multi-range current metre can be constructed by using a galvanometer circuit, as shown in the figure. We want a current metre that can measure 10mA, 100mA and 1A using a galvanometer of resistance 10Ω and that produces maximum deflection for a current of 1mA. Find S 1 , S 2 and S 3 that have to be used.

$\begin{array}{l} G = 10 \Omega \end{array} $

In order to convert a galvanometer into an ammeter of the given current range 0 to 1, the shunt resistance needed is

$\begin{array}{l} S = \frac{ I _ { g } }{ I – I _ { g } } \end{array} $

$\begin{array}{l} I = 10 m A = 10 \times 10 ^ { -3 } A \end{array} $

S = S _ { 1 } + S _ { 2 } + S _ { 3 }

$\begin{array}{l} \therefore S _ { 1 } + S _ { 2 } + S _ { 3 } = \frac{ 1 m A \times 10 \Omega }{ (10 – 1) m A } = \frac{ 10 }{ 9 } \Omega \end{array} $

$\begin{array}{l} \textup{When } I = 100 m A \end{array} $

$\begin{array}{l} S = S _ { 2 } + S _ { 3 } \end{array} $

$\begin{array}{l} \textup{Galvanometer Resistance } = G + S _ { 1 } \end{array} $

$\begin{array}{l} \therefore S _ { 2 } + S _ { 3 } = \frac{ I _ { g } (G + S _ { 1 }) }{ I – { l _ { g } } } \end{array} $

$\begin{array}{l} = \frac{ 1 m A \times ( 10 + S _ { 1 } ) }{ (100 – 1) m A } = \frac{ 10 + S _ { 1 } }{ 99 } \textup{ …. (ii)} \end{array} $

Case (iii) If I – 1A, then S = S 3

Galvanometer Resistance = (G + S 1 + S 2 )

$\begin{array}{l} \therefore S _ { 3 } = \frac{ I _ { g ( G + S + S _ { 2 } ) } }{ I – I _ { g } } \end{array} $

$\begin{array}{l} = \frac{ 1 m A [ 10 + S _ { 1 } + S _ { 2 } ] }{ ( 1000 – 1) m A } \end{array} $

$\begin{array}{l} \frac{ 10 + S _ { 1 } + S _ { 2 } }{ 999 } \textup{ …. (iii)} \end{array} $

By inserting the value (ii) in (i), we get

$\begin{array}{l} S _ { 1 } + \frac{ 10 + S _ { 1 } }{ 99 } = \frac{ 10 }{ 9 } \end{array} $

$\begin{array}{l} \textup{or } S _ { 1 } \left ( 1 + \frac{1}{99} \right ) = \frac{10}{9} – \frac{ 10 }{ 99 } = \frac{ 100 }{ 99 } \end{array} $

$\begin{array}{l} \therefore S _ { 1 } \times \frac{ 100 }{ 99 } = \frac{ 100 }{ 99 } \textup{ or } S _ { 1 } = 1 \Omega \end{array} $

From equation (ii)

$\begin{array}{l} S _ { 2 } + S _ { 3 } = \frac{ 1 }{ 99 } ( 10 + 1 ) = \frac{ 1 }{ 9 } \textup{ ….(iv)} \end{array} $

From equation (iii)

$\begin{array}{l} S _ { 3 } = \frac{ 10 + 1 + S _ { 2 } }{ 999 } = \frac{ 11 + S _ { 2 } }{ 999 } \end{array} $

$\begin{array}{l} \textup{Or } S _ { 3 } – \frac{ S _ { 2 } }{ 999 } = \frac{ 11 }{ 999 } \textup{ ….(iv)} \end{array} $

Minusing equation (v) from equation (iv), we get

$\begin{array}{l} S _ { 2 } = \frac{ S _ { 2 } }{ 999 } = \frac{ 1 }{ 9 } – \frac{ 11 }{ 999 } = \frac{ 1000 }{ 999 } \end{array} $

$\begin{array}{l} \textup{Or } \frac{ S _ { 2 } \times 1000}{ 999 } = \frac{ 1000 }{ 999 } or S _ { 2 } = \frac{1}{10} = 0.1 \Omega \end{array} $

From equation (iv)

$\begin{array}{l} \frac{1}{10} + s _ { 3 } = \frac{ 1 }{ 9 } \end{array} $

$\begin{array}{l} \textup{Or } \frac{ 1 }{ 9 } – \frac{ 1 }{ 10 } = \frac{ 1 }{ 90 } \end{array} $

$\begin{array}{l} \textup{Or } S _ { 3 } = 0.011 \omega \end{array} $

13. Five long wires, A, B, C, D, and E, each carrying current I, are arranged to form the edges of a pentagonal prism, as shown in the figure. Each carries current out of the plane of the paper.

(a) What will be magnetic induction at a point on the axis O? Axis is at a distance R from each wire.

(b) What will be the field if the current in one of the wires (say A) is switched off?

(a) The five wires A, B, C, D and E are positioned perpendicular to the plane of the paper, as shown in the figure. The total magnetic field induction at point O resulting from the current flowing through all five wires is zero, as it can be represented by the sides of a closed pentagon in the plane of the paper.

(b) The overall magnetic field induction at point O caused by the currents flowing through wires A, B, C, D, and E is the same as, but opposite in direction, to the magnetic field induction at O due to the current through wire A alone.

Therefore, the magnetic field induction at O due to the electric current flowing through wire A is

$\begin{array}{l} B = \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 I }{ R } \textup{ acting }\perp \, \, r \, \, \textup{to AO towards right. } \end{array} $

Therefore, the magnetic field induction at point O due to currents through the wires E, D, C, and B is

$\begin{array}{l} \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 I }{ R } \textup{, acting} \perp \, \, r \textup{ to AO towards left. } \end{array} $

(c) When the electric current flowing wire A is reversed, then the net magnetic field induction at point O is equal to mag. The magnetic field induction due to wires E, D, C, and B is

$\begin{array}{l} \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 I }{ R } \,\, (\textup{ acting } \perp \, \, r \,\, \textup{AO towards left}) + \frac{ \mu _ { 0 } }{ 4 \pi } \frac{ 2 I }{ R } (\textup{acting} \, \, \perp r \, \, \textup{AO towards left} ) \end{array} $

$\begin{array}{l} = \frac{ \mu _ { 0 } I }{ \pi R } \textup{ acting } \perp \,\, r \textup{ AO towards left.} \end{array} $

14. What are the applications of magnetism?

Although we frequently use computers in our daily lives, we may not have considered the presence of a magnet inside them. Magnets play a crucial role in storing data on a hard disk and allow the computer to retrieve information.
Magnets are also utilised in various electronic devices such as TVs, speakers, and radios. The combination of a small coil of wire and a magnet in a speaker converts electronic signals into sound waves.
Magnets are used within generators to convert mechanical energy into electrical energy. In contrast, certain motors also use magnets to transform electrical energy into mechanical energy.
Additionally, a powerful magnet is used by cranes to move large metal objects.
Magnet technology is utilised in various industries, including ore processing, for separating metallic materials from other substances.
Magnets also play a crucial role in medical imaging, such as MRI machines, to create detailed images of the body’s internal structures.
Magnet usage can be found in everyday household items such as refrigerator magnets and magnetic bottle openers.
A compass, which uses a magnetic needle to indicate a direction, is commonly used in outdoor activities.
Additionally, magnets are used in technology, such as credit and debit cards, as the dark strip on the back is magnetic and stores data.

15. Write an essay on Galvanometer.

A galvanometer is an instrument that measures electric current and the direction of the current. The early versions of this instrument were not precise, but later models, known as ammeters, were calibrated and able to give more accurate measurements of the current flow. A galvanometer is an instrument that uses the interaction between an electric current and a magnetic field to measure current. It deflects a pointer in reaction to the current moving through a conducting coil in a fixed magnetic field.

Galvanometers are considered a type of actuator and were the first to measure small amounts of electric current. They were discovered by Hans Christian Ørsted in 1820 and were named after Luigi Galvani, who, in 1791, observed that electric current causes the legs of a dead frog to move. André-Marie Ampère mathematically described Ørsted’s discovery and named the instrument after Galvani’s discovery. Galvanometers have been crucial in advancing science and technology across various fields. In the 19th century, they were used to establish long-distance communication via submarine cables, such as the first transatlantic telegraph cables. They also played a vital role in discovering electrical activity in the heart and brain through their precise current measurement.

Galvanometers have been utilised as display elements in other types of analogue metres, such as light and VU metres, by measuring the output of their sensors. The most commonly used galvanometer type today is the D’Arsonval/Weston type. It operates by deflecting a pointer in response to an electric current flowing through a coil in a fixed magnetic field and can be considered a type of actuator. It is important to note that ammeters, calibrated and accurate instruments for measuring current, cannot be compared with values from a galvanometer.

Moving Charges and Magnetism Class 12 Physics One Shot

Moving Charges and Magnetism Class 12 Physics Full Chapter Revision

Moving Charges and Magnetism Class 12 Physics JEE Important Questions

Stay tuned to BYJU’S and Fall in Love with Learning!

Register with BYJU'S & Download Free PDFs

Talk to our experts

1800-120-456-456

Important Questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism 2024-25

CBSE Class 12 Physics Chapter- 4 Important Questions - Free PDF Download

Important Questions of Chapter 4 Physics Class 12 PDF available on the Vedantu website will help students in their preparation for the board examinations and any entrance examinations. Among all the science subjects, Physics is always found to be difficult for most students. The only key to excelling in Physics is to study with dedication and with quality materials. Chapter 4 of Physics Class 12 deals with Moving Charges and Magnetism. The Class 12 Physics Chapter 4 important questions will be useful for students in their preparation.

Download CBSE Class 12 Physics Important Questions 2024-25 PDF

Also, check CBSE Class 12 Physics Important Questions for other chapters:

Important Topics Covered in Chapter 4

The following is a list of the important topics covered under the chapter on Moving Charges and Magnetism:

Ampere's Circuital Law

Biot-Savart Law, Magnetic Field Due to a Current Element

The Moving Coil Galvanometer

The Toroid and the Solenoid

Magnetic Field and Magnetic Force

Magnetic Field and Motion in Combined Electric

Magnetic Dipole, Torque on Current Loop

Related Chapters

Study Important Questions for Class 12 Physics Chapter 4 - Moving Charges and Magnetism

Very Short Answer Questions 1 Mark

1. State two properties of the material of the wire used for suspension of the coil in a moving coil galvanometer.

Ans: Two properties of the material of the wire used for suspension of the coil in a moving coil galvanometer are:

Non-Brittle conductor

Restoring Torque per unit twist should be small.

2. What will be the path of a charged particle moving along the direction of a uniform magnetic field?

Ans: The path of a charged particle moving along the direction of a uniform magnetic field would be a straight line path as no force would act on the particle.

3. Two wires of equal lengths are bent in the form of two loops. One of the loops is square shaped whereas the other loop is circular. These are suspended in a uniform magnetic field and the same current is passed through them. Which loop will experience greater torque? Give reasons.

Ans : We know the expression for torque as,

$\tau =\text{NIAB}$

\[\Rightarrow \tau \propto A\]

Since, we know that the area of circular loops is more than that of a square loop, torque which is directly proportional to area would experience greater torque than the square loop.

Therefore, torque experienced by a circular loop is greater.

4. A cyclotron is not suitable to accelerate electron. Why?

Ans: A cyclotron is not suitable to accelerate electron as its mass is known to be less due to which they gain speed and step out of the dee immediately.

Short Answer Questions 2 Marks

1. A steady current flows in the network shown in the figure. What will be the magnetic field at the center of the network?

Ans: The magnetic field at the center of the network is zero. This is because, the magnetic field at the center of the loop would just be equal and opposite i.e., magnetic field due \[\text{PQR}\] is equal and opposite to that due to \[\text{PSR}\].

2. An $\alpha $ - particle and a proton are moving in the plane of paper in a region where there is uniform magnetic field B directed normal to the plane of paper. If two particles have equal linear momenta, what will be the ratio of the radii of their trajectories in the field?

Ans : We know the radius of the path to be given by,

\[R=\frac{mv}{Bq}\]

\[\Rightarrow R\propto \frac{1}{q}\]

\[\Rightarrow \frac{{{R}_{\alpha }}}{{{R}_{p}}}=\frac{{{q}_{p}}}{{{q}_{\alpha }}}=\frac{e}{2e}=\frac{1}{2}\]

Where, ${{R}_{\alpha }}\text{ and }{{\text{R}}_{p}}$are radii of $\alpha $-particle and proton respectively and ${{q}_{\alpha }}\text{ and }{{\text{q}}_{p}}$ are their respective charges.

$\therefore {{R}_{\alpha }}:{{R}_{p}}=1:2$

Therefore, we find the required ratio to be 1:2.

3. Give one difference each between diamagnetic and ferromagnetic substances. Give one example of each.

Ans: Diamagnetic substances are the ones that are weakly repelled by a magnet. For example, gold. Ferromagnetic materials are the ones that are strongly attracted by a magnet. For example, iron.

4. Write the expression for the force acting on a charged particle of charge q moving with velocity is in the presence of magnetic field B. Show that in the presence of this force,

The K.E. of the particle does not change.

Ans : We know the expression for magnetic force as, $F=q(\vec{v}\times \vec{B})$

Since direction of force is perpendicular to the plane containing $(\vec{v}\times \vec{B})$,

$F=qvB\sin 90{}^\circ =qvB$

Here, we find the force and displacement to be perpendicular to each other. So,

$W=FS\cos \theta $

$\Rightarrow W=FS\cos 90{}^\circ =0$

$\Rightarrow \text{KE}=0$

Therefore, we find the kinetic energy to be constant at the given condition.

Its instantaneous power is zero.

Ans: We have the expression for instantaneous power given by,

$p=Fv\cos \theta $

When force and velocity are perpendicular to each other,

$p=Fv\cos 90{}^\circ =0$

Therefore, we find the instantaneous power to be zero.

5. An electron of kinetic energy \[25\mathbf{KeV}\]moves perpendicular to the direction of a uniform magnetic field of \[0.2\mathbf{millitesla}\]. Calculate the time period of rotation of the electron in the magnetic field.

Ans : We are given the magnetic field to be, $B=0.2T=0.2\times {{10}^{-3}}T$

We know the expression for Time Period to be, $T=\frac{2\pi M}{QB}$

Substituting the given values,

$\Rightarrow T=\frac{2\times 3.14\times 9.1\times {{10}^{-31}}}{1.6\times {{10}^{-17}}\times 0.2\times {{10}^{-3}}}$

$\Rightarrow T=1.787\times {{10}^{-7}}\text{ second}$

We find the time period of rotation of the electron in the magnetic field to be $T=1.787\times {{10}^{-7}}\text{ second}$.

6. It is desired to pass only \[10%\] of the current through a galvanometer of resistance $90\Omega $. How much shunt resistance should be connected across the galvanometer?

Ans: Current through galvanometer,

${{I}_{G}}=10%\text{ of I}=\frac{10}{100}\times I$

Galvanometer resistance is given to be, $G=90\Omega $

Now, we could find the shunt resistance as,

S $=\frac{\frac{9I}{10I-I}}{100}$

$\Rightarrow S=\frac{90I}{90I}=10$

$\Rightarrow S=10\Omega $

Therefore, we found the shunt resistance to be $S=10\Omega $.

Short Answer Question 3 Marks

1. Derive an expression for the force acting on a current carrying conductor placed in a uniform magnetic field. Name the rule which gives the direction of the force. Write the condition for which this force will have (1) maximum (2) minimum value.

Ans : Let us consider a conductor that is placed in a uniform magnetic field \[\vec{B}\]making an angle $\theta $ with \[\vec{B}\]. Let \[I\] be the current that flows through the conductor.

A conductor i.e, placed in a uniform magnetic field and making a certain angle with the field lines.

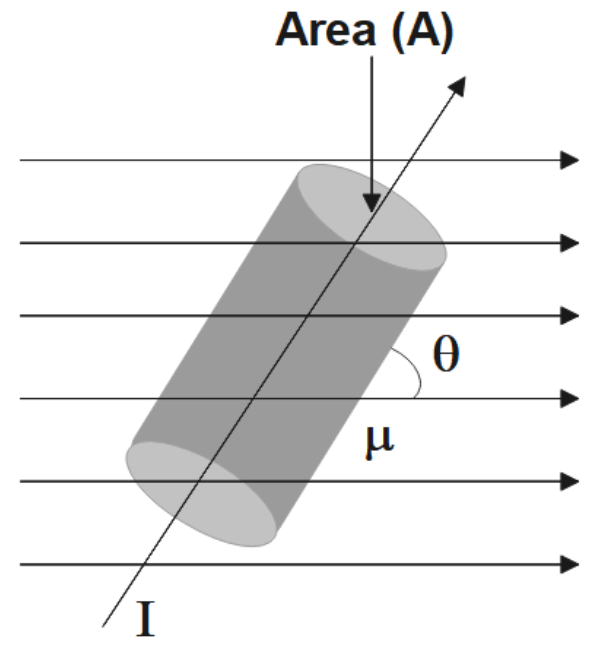
If $n$ is the number of electrons per unit volume of the conductor, then the total number of electrons in the small current element \[dl,\text{ N}=nAdl\].

We have,

$\theta =Ne$

$\Rightarrow \theta =nAdle$

Let $\vec{f}$ be the force experienced by each electron, then,

$\vec{f}=e({{\vec{v}}_{d}}\times \vec{B})$

Now, force experienced by a small current element would be,

\[d\vec{f}=neAdl({{\vec{v}}_{d}}\times \vec{B})\]

$d\vec{f}=neAdlB\sin \theta $

But we have, $I=neAvd$

$\Rightarrow d\vec{f}=IdlB\sin \theta $

Now, the total force experienced will be,

\[F=\int_{0}^{1}{df}=\int_{0}^{1}{IdlB\sin \theta }\]

$\Rightarrow F=IBl\sin \theta $

In vector form total force could be given by, $\vec{F}=I(\vec{l}\times \vec{B})$

Force will be maximum when $\theta =90{}^\circ $

Force will be minimum when $\theta =0{}^\circ $

2. A straight wire carries a current of \[\mathbf{10}\]A. An electron moving at ${{10}^{7}}\text{ m/s}$is at distance \[\mathbf{2}.\mathbf{0}\] cm from the wire. Find the force acting on the electron if its velocity is directed towards the wire.

Ans : We are given the current through the straight wire to be, \[I\text{ }=\text{ }10A\]

Speed of the electron, $v={{10}^{7}}\text{ m/s}$

Distance of electron from the wire, $R=2.0\text{ cm}=2\times {{10}^{-2}}\text{ m}$

Force acting on a moving electron would be, \[F=qVB\sin \theta \]

We have the expression for magnetic field as,

\[B=\frac{{{\mu }_{0}}}{4\pi }\frac{2I}{r}\]

$B=\frac{{{10}^{-7}}\times 2\times 10}{2\times {{10}^{-2}}}={{10}^{-4}}T$ and it is given to be $\bot $ to the plane of paper and directed towards.

Now, force acting on the electron could be given by, $\Rightarrow F=1.6\times {{10}^{-19}}\times {{10}^{7}}\times {{10}^{-4}}\sin 90{}^\circ $

$\Rightarrow F=1.6\times {{10}^{-16}}N$

Therefore, we find the force to be, $F=1.6\times {{10}^{-16}}N$.

3. State Biot-Savart's law. Derive an expression for the magnetic field at the center of a circular coil of \[\mathbf{n}\] -turns carrying current – I.

Ans: Biot – Savart law states that the magnetic field $dB$ due to a current element $\overrightarrow{dl}$ at any point would be as following:

$dB\propto I$

$dB\propto dl$

$dB\propto \sin \theta $

$dB\propto \frac{1}{{{r}^{2}}}$

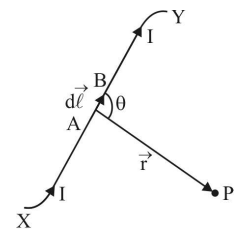
Combining all the above conditions, we get,

$dB\propto \frac{Idl\sin \theta }{{{r}^{2}}}$

\[\Rightarrow dB=\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin \theta }{{{r}^{2}}}\]

Consider a circular loop of radius $r$ that is carrying a current $I$,

Circular loop of radius r containing a current I.

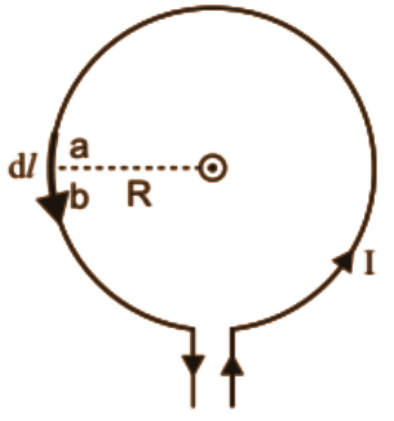
Since $dl\bot \vec{r}$ ,

$\Rightarrow \theta =90{}^\circ $

Now, on applying Biot Savart law

$dB=\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin 90{}^\circ }{{{r}^{2}}}$

For entire closed circular loop,

$B=\int_{0}^{2\pi r}{\frac{{{\mu }_{0}}}{4\pi }\frac{Idl\sin 90{}^\circ }{{{r}^{2}}}}$

$\Rightarrow B=\frac{{{\mu }_{0}}}{4\pi }\frac{I}{{{r}^{2}}}\int_{0}^{2\pi r}{dl}=\frac{{{\mu }_{0}}}{4\pi }\frac{I}{{{r}^{2}}}\times 2\pi r$

For $n$ turns of a coil we would get,

$\Rightarrow B=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nI}{r}$

Therefore, we find the expression for magnetic field at the center of a circular coil of n -turns carrying current – I to be,

$B=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nI}{r}$

4. What is a radial magnetic field? How is it obtained in a moving coil galvanometer?

Ans : A radial magnetic field is the magnetic field in which the plane of the coil always lies in the direction of the magnetic field. It can be obtained by the following ways:

Properly cutting the pole pieces concave in shape.

Placing soft iron cylindrical core between the pole pieces.

Diagram showing the soft iron core present between the pole pieces.

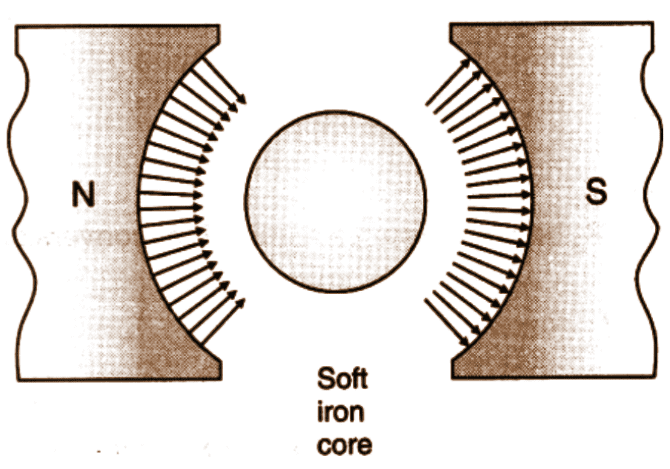
5. Two straight parallel current carrying conductors are kept at a distance r from each other in air. The direction for current in both the conductors is the same. Find the magnitude and direction of the force between them. Hence define one ampere.

Ans: Let us consider two parallel conductors carrying current ${{I}_{1}}\,\text{ and }{{I}_{2}}$ and is separated by a distance \[d\],

Force between the two straight parallel current carrying conductors.

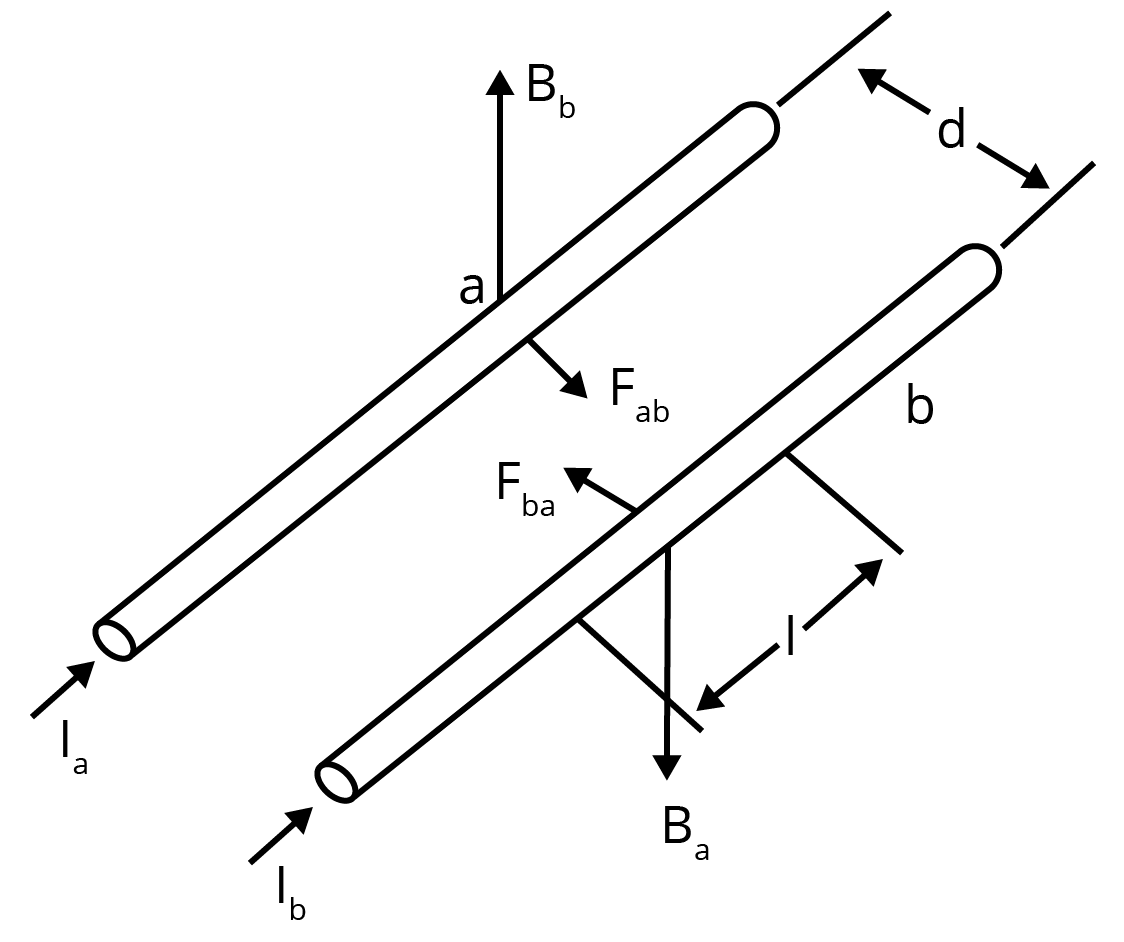
Magnetic field due to current ${{I}_{1}}$ at any point on conductor 2 could be given by,

\[{{B}_{1}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2Il}{d}\,\] ……………………….. (1)

($\bot $ to the plane and downwards $(\times )$)

Since current carrying conductor is placed at right angles with the magnetic field, we get the magnetic force to be,

$F=BIl\sin 90{}^\circ $

$\Rightarrow F=BIl$ ………………………… (2)

This would be the Force experienced per unit length of conductor.

Now, we have,

${{F}_{2}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2{{I}_{1}}{{I}_{2}}}{d}$…………………………… (3)

Fleming’s left hand Rule says ${{F}_{2}}$ is directed towards conductor 1.

Similarly, ${{F}_{1}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2{{I}_{1}}{{I}_{2}}}{d}$ (Directed Towards conductor $2$)

Since ${{F}_{1}}\text{ and }{{F}_{2}}$ are equal in magnitude and directed opposite, two parallel current carrying conductors would attract each other.

Since, $F=\frac{{{\mu }_{0}}}{4\pi }\left( \frac{2{{I}_{1}}{{I}_{2}}}{d} \right)$

If ${{I}_{1}}={{I}_{2}}=1\text{ A}$ and $d=1\text{m}$ , then,

$F=2\times {{10}^{-7}}\,\text{m}$

Hence, we found that one ampere is that current which is flowing in two infinitely long parallel conductors that are separated by a distance of $1$ meter in vacuum and experiences a force of $F=2\times {{10}^{-2}}\,\text{m}$ on each meter of the other wire.

6. A circular coil of wire consisting of $100$ turns, each of radius $8.0$ cm carries a current of $0.40\,\text{A}$. What is the magnitude of the magnetic field B at the centre of the coil?

Ans: We are given:

Number of turns on the circular coils, $n=100$

Radius of each turn, $r=8.0\text{ cm}=0.08\text{ m}$

Current flowing in the coil, $I=0.4\,\text{A}$

Magnitude of the magnetic field at the centre of the coil could be given by the relation,

$\left| B \right|=\frac{{{\mu }_{0}}}{4\pi }\frac{2\pi nl}{r}$

Where, Permeability of free space, \[{{\mu }_{0}}=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}\]

$\Rightarrow \left| B \right|=\frac{4\pi \times {{10}^{-7}}}{4\pi }\times \frac{2\pi \times 100\times 0.4}{0.08}$

$\Rightarrow \left| B \right|=3.14\times {{10}^{-4}}T$

Hence, the magnitude of the magnetic field is found to be $3.14\times {{10}^{-4}}T$.

7. A long straight wire carries a current of $35\,\text{A}$. What is the magnitude of the field B at a point $20$ cm from the wire?

Ans: We are given the following:

Current in the wire, $I=35\text{ A}$

Distance of a point from the wire, $r=20\text{ cm}=0.2\,\text{m}$

Magnitude of the magnetic field at this point could be given as:

$B=\frac{{{\mu }_{0}}}{4\pi }\frac{2l}{r}$

Where, ${{\mu }_{0}}=$ Permeability of free space $=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}$

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 35}{4\pi \times 0.2}$

$\Rightarrow B=3.5\times {{10}^{-5}}\,\text{T}$

Hence, the magnitude of the magnetic field at a point $20\,\text{cm}$ from the wire is found to be $3.5\times {{10}^{-5}}\,\text{T}$.

8. A long straight wire in the horizontal plane carries a current of \[50\text{ A}\] in the north to south direction. Give the magnitude and direction of B at a point \[2.5\]m east of the wire.

Current in the wire, \[I\text{ }=\text{ }50\text{ A}\]

A point is said to be \[2.5\]m away from the East of the wire.

Magnitude of the distance of the point from the wire is given as, \[r\text{ }=\text{ }2.5\text{ m}\].

Magnitude of the magnetic field at that point could be given by the relation, \[B=\frac{{{\mu }_{0}}2I}{4\pi r}\]

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 50}{4\pi \times 2.5}$

$\Rightarrow B=4\times {{10}^{-6}}\,\text{T}$

Since, the point is located normal to the wire length at a distance of $2.5\text{ m}$and the direction of the current in the wire is vertically downward, by using Maxwell’s right hand thumb rule we get the direction of the magnetic field at the given point as vertically upward.

9. A horizontal overhead power line carries a current of \[\mathbf{90}\text{ }\mathbf{A}\]in an east to west direction. What is the magnitude and direction of the magnetic field due to the current \[\mathbf{1}.\mathbf{5}\text{ }\mathbf{m}\] below the line?

Ans: We are given the following:

Current in the power line, \[I\text{ }=\text{ }90\,\text{A}\]

A Point is located below the power line that is at distance, \[r\text{ }=\text{ }1.5\text{ m}\]

Now, the magnetic field at that point could be given by the relation,

\[B=\frac{{{\mu }_{0}}2I}{4\pi r}\]

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 50}{4\pi \times 1.5}$

$\Rightarrow B=1.2\times {{10}^{-5}}\,\text{T}$

Since, the current is flowing from East to West and the point is given to be below the power line, by using Maxwell’s right hand thumb rule we get the direction of the magnetic field to be towards the South.

10. What is the magnitude of magnetic force per unit length on a wire carrying a current of \[8\text{ A}\] and making an angle of \[30{}^\text{o}\] with the direction of a uniform magnetic field of \[0.15\text{ T}\] ?

Current in the wire, \[I\text{ }=\text{ }8\text{ A}\]

Magnitude of the uniform magnetic field, \[B\text{ }=\text{ }0.15\text{ T}\]

Angle between the wire and magnetic field, $\theta =\text{ }30{}^\circ $

Magnetic force per unit length on the wire is given as:

$f=BI\sin \theta $

\[\Rightarrow f=0.15\times 8\times 1\times \sin 30{}^\circ \]

\[\Rightarrow f=0.6\,\text{N }{{\text{m}}^{-1}}\]

Therefore, the magnetic force per unit length on the wire is found to be $0.6\,\text{N }{{\text{m}}^{-1}}$.

11. A \[\mathbf{3}.\mathbf{0}\] cm wire carrying a current of \[\mathbf{10}\]A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be \[\mathbf{0}.\mathbf{27}\] T. What is the magnetic force on the wire?

Length of the wire, \[l\text{ }=\text{ }3\text{ cm }=\text{ }0.03\text{ m}\]

Current flowing in the wire, \[I\text{ }=\text{ }10\text{ A}\]

Magnetic field, \[B\text{ }=\text{ }0.27\text{ T}\]

Angle between the current and magnetic field, $\theta =\text{ }90{}^\circ $

Magnetic force exerted on the wire could be given as:

$F=BIl\sin \theta $

Substituting the given values, we get,

\[\Rightarrow F=0.27\times 10\times 0.03\sin 90{}^\circ \]

\[\Rightarrow F=8.1\times {{10}^{-2}}\,\text{N}\]

Therefore, the magnetic force on the wire is found to be \[8.1\times {{10}^{-2}}\,\text{N}\] and the direction of the force can be obtained using Fleming’s left-hand rule.

12. Two long and parallel straight wires A and B carrying currents of \[\mathbf{8}.\mathbf{0}\] A and \[\mathbf{5}.\mathbf{0}\] A in the same direction are separated by a distance of \[\mathbf{4}.\mathbf{0}\] cm. Estimate the force on a \[\mathbf{10}\] cm section of wire A.

Current flowing in wire A, ${{I}_{A}}=8.0\,\text{A}$

Current flowing in wire B, ${{I}_{B}}=5.0\text{ A}$

Distance between the two wires, \[r\text{ }=\text{ }4.0\text{ cm }=\text{ }0.04\text{ m}\]

Length of a section of wire A, \[l\text{ }=\text{ }10\text{ cm }=\text{ }0.1\text{ m}\]

Force exerted on length l due to the magnetic field could be given as:

$B=\frac{{{\mu }_{0}}2{{I}_{A}}{{I}_{B}}l}{4\pi r}$

Where, ${{\mu }_{0}}=$ Permeability of free space $=4\pi \times {{10}^{-7}}\,\text{T m }{{\text{A}}^{-1}}$

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 2\times 8\times 5\times 0.1}{4\pi \times 0.04}$

$\Rightarrow B=2\times {{10}^{-5}}\,\text{N}$

The magnitude of force is found to be $2\times {{10}^{-5}}\,\text{N}$. This is an attractive force that is normal to A towards B because the direction of the currents in the wires are the same.

13. A closely wound solenoid $80cm$long has $5$ layers of windings of $400$ turns each. The diameter of the solenoid is $1.8cm$. If the current carried is $8.0A$, estimate the magnitude of B inside the solenoid near its centre.

Length of the solenoid, $l=80cm=0.8m$

Since there are five layers of windings of 400 turns each on the solenoid;

Total number of turns on the solenoid would be, $N=5\times 400=2000$

Diameter of the solenoid, $D=1.8cm=0.018m$

Current carried by the solenoid, $I=8.0A$

We have the magnitude of the magnetic field inside the solenoid near its centre given by the relation,

$B=\frac{{{\mu }_{0}}NI}{l}$

Where, ${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$is the permeability of free space.

On substituting the given values we get,

$B=\frac{4\pi \times {{10}^{-7}}\times 2000\times 8}{0.8}$

$\Rightarrow B=2.512\times {{10}^{-2}}T$

Therefore, the magnitude of the magnetic field inside the solenoid near its centre is found to be $2.512\times {{10}^{-2}}T$.

14. A square coil of side $10cm$consists of 20 turns and carries a current of $12A$. The coil is suspended vertically and the normal to the plane of the coil makes an angle of $30{}^\circ $with the direction of a uniform horizontal magnetic field of magnitude $0.80T$. What is the magnitude of torque experienced by the coil?

Ans: We are given,

Length of a side of the square coil, $l=10cm=0.1m$

Area of the square, $A={{l}^{2}}={{\left( 0.1 \right)}^{2}}=0.01{{m}^{2}}$

Current flowing in the coil, $I=12A$

Number of turns on the coil, $n=20$

Angle made by the plane of the coil with magnetic field, $\theta =30{}^\circ $

Strength of magnetic field, $B=0.80T$

Magnitude of the magnetic torque experienced by the coil in the magnetic field is given by the relation,

$\tau =nIAB\sin \theta $

Substituting the given values, we get,

$\tau =20\times 0.8\times 12\times 0.01\times \sin 30{}^\circ $

$\Rightarrow \tau =0.96Nm$

Therefore, the magnitude of the torque experienced by the coil is 0.96Nm.

A circular coil of \[\mathbf{30}\] turns and radius \[\mathbf{8}.\mathbf{0}cm\] carrying a current of \[\mathbf{6}.\mathbf{0}A\] is suspended vertically in a uniform horizontal magnetic field of magnitude \[\mathbf{1}.\mathbf{0}T\]. The field lines make an angle of with the normal of the coil. Calculate the magnitude of the counter torque that must be applied to prevent the coil from turning.

Ans: Given that, number of turns on the circular coil, \[n=30\]

Radius of the coil, \[r=8.0\text{ cm}=0.08\text{ m}\]

Area of the coil $=\pi {{r}^{2}}=\pi {{(0.08)}^{2}}=0.0201\text{ }{{\text{m}}^{2}}$

Current flowing in the coil, \[I=6.0\text{ A}\]

Magnetic field strength, \[B=1\text{ T}\]

Angle between the field lines and normal with the coil surface, $\theta =60{}^\circ $

The coil experiences a torque in the magnetic field. So, it turns. The counter torque applied to prevent the coil from turning is given by the relation,

$T=nIBA\sin \theta \,$ ……………………. (1)

$\Rightarrow T=30\times 6\times 1\times 0.0201\times \sin 60{}^\circ $

$\Rightarrow T=3.133\text{Nm}$

Therefore, counter torque to be applied against coil turning is $3.133\text{Nm}$.

Would your answer change, if the circular coil in (a) were replaced by a planar coil of some irregular shape that encloses the same area? (All other particulars are also unaltered.)

Ans: It can be inferred from relation (1) that the magnitude of the applied torque is not dependent on the shape of the coil. It depends on the area of the coil. Hence, the answer would not change if the circular coil in the above case is replaced by a planar coil of some irregular shape that encloses the same area.

16. A magnetic field of $100G$$\left( where,\text{ }1G={{10}^{-4}}T \right)$ is required which is uniform in a region of linear dimension about $10cm$ and area of cross-section about${{10}^{-3}}{{m}^{2}}$. The maximum current carrying capacity of a given coil of wire is $15A$ and the number of turns per unit length that can be wound a core is at most $1000\text{ turns per m}$. Suggest some appropriate design particulars to a solenoid for the required purpose. Assume the core is not ferromagnetic.

Magnetic field strength,$B=100G=100\times {{10}^{-4}}T$

Number of turns per unit length,$n=1000turns\text{ per m}$

Current flowing in the coil,$I=15A$

Permeability of free space, ${{\mu }_{0}}=4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$

Magnetic field is given the relation,

$B={{\mu }_{0}}nI$

$\Rightarrow nI=\frac{B}{{{\mu }_{0}}}=\frac{100\times {{10}^{-4}}}{4\pi \times {{10}^{-7}}}$

$\Rightarrow nI\approx 8000A/m$

So, if the length of the coil is taken as 50 cm, radius 4 cm, number of turns 400, and current 10 A, then these values are not unique for the given purpose. There is always a Possibility of some adjustments with limits.

17. A toroid has a core (non-ferromagnetic) of inner radius 25 cm and outer radius 26 cm, around which 3500 turns of a wire are wound. If the current in the wire is 11 A, what is the magnetic field

outside the toroid

Inner radius of the toroid, ${{r}_{1}}=25cm=0.25m$

Outer radius of the toroid, ${{r}_{2}}=26cm=0.26m$

Number of turns on the coil, $N=3500$

Current in the coil, $I=11A$

So, we know, the magnetic field outside a toroid is zero. It is non-zero only inside the core of a toroid.

inside the core of the toroid.

Ans: Magnetic field inside the core of a toroid is given by the relation,

Where, Permeability of free space ${{\mu }_{0}}=4\pi \times {{10}^{-7}}Tm{{A}^{-1}}$

$l$ is the length of toroid

$l=2\pi \left( \frac{{{r}_{1}}+{{r}_{2}}}{2} \right)=\pi \left( 0.25+0.26 \right)=0.51\pi $

$\Rightarrow B=\frac{4\pi \times {{10}^{-7}}\times 3500\times 11}{0.51\pi }\approx 3.0\times {{10}^{-2}}T$

Therefore, the magnetic field inside the core of the toroid is approximately $3.0\times {{10}^{-2}}T$.

in the empty space surrounded by the toroid.

Ans: Magnetic field in the empty space that is surrounded by the toroid is zero.

18. Answer the following questions:

A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?

Ans: The initial velocity of the particle could either be parallel or be anti-parallel to the magnetic field. So, it travels along a straight path without suffering any deflection in the field.

A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?

Ans: Yes, the final speed of the charged particle would be equal to its initial speed because the magnetic force can change direction of velocity, but not its magnitude.

An electron travelling west to east enters a chamber having a uniform electrostatic field in north to south direction. Specify the direction in which a uniform magnetic field should be set up to prevent the electron from deflecting from its straight line path.

Ans: An electron travelling from West to East enters a chamber having a uniform electrostatic field along the North-South direction. This moving electron remains undeflected if the electric force acting on it is equal and opposite to the magnetic field. Magnetic force would be directed towards the South. Also, according to Fleming’s left hand rule, the magnetic field should be applied in a vertically downward direction.

19. A straight horizontal conducting rod of length $0.45m$ and mass $60g$is suspended by two vertical wires at its ends. A current of $5.0A$ is set up in the rod through the wires.

What magnetic field should be set up normal to the conductor in order that the tension in the wires is zero?

Length of the rod, $l=0.45m$

Mass suspended by the wires, $m=60g=60\times {{10}^{-3}}kg$

Acceleration due to gravity, $g=9.8m{{s}^{-2}}$

Current in the rod flowing through the wire, $I=5A$

We could say that magnetic field (B) is equal and opposite to the weight of the wire i.e.,

$\Rightarrow B=\frac{mg}{Il}=\frac{60\times {{10}^{-3}}\times 9.8}{5\times 0.45}$

$\Rightarrow B=0.26T$

Therefore, a horizontal magnetic field of 0.26 T normal to the length of the conductor should be set up.

What will be the total tension in the wires if the direction of current is reversed keeping the magnetic field same as before? (Ignore the mass of the wires.) $g=9.8m{{s}^{-2}}$

Ans: When the direction of the current is reversed, $BIl$ and $mg$ will act downwards. So, the effective tension in the wires is found to be,

$T=0.26\times 5\times 0.45+\left( 60\times {{10}^{-3}} \right)\times 9.8$

$\Rightarrow T=1.176N$

Therefore, total tension in the wires is $1.176N$.

20. The wires which connect the battery of an automobile to its starting motor carry a current of $300A$(for a short time). What is the force per unit length between the wires if they are $70cm$long and $1.5cm$ apart? Is the force attractive or repulsive?

Ans: Given that,

Current in both wires, $I=300A$

Distance between the wires, $r=1.5cm=0.015m$

Length of the two wires, $l=70cm=0.7m$

We know that, Force between the two wires is given by the relation,

$F=\frac{{{\mu }_{0}}{{I}^{2}}}{2\pi r}$

Where, Permeability of free space${{\mu }_{0}}=4\pi \times 10Tm{{A}^{-1}}$

$\Rightarrow F=\frac{4\pi \times {{10}^{-7}}\times {{300}^{2}}}{2\pi \times 0.015}$

$\Rightarrow F=1.2N$

Since the direction of the current in the wires is found to be opposite, a repulsive force exists between them.

21. A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the: (The coil is made of copper wire of cross-sectional area ${{10}^{-5}}{{m}^{2}}$, and the free electron density in copper is given to be about${{10}^{29}}{{m}^{-3}}$).

total torque on the coil?

Number of turns on the circular coil, $n=20$

Radius of the coil, $r=10cm=0.1m$

Magnetic field strength, $B=0.10T$

Current in the coil, $I=5.0A$

Since, the angle between force and the normal to the loop, the total torque on the coil is zero. So, $\tau =NIAB\sin \theta $ is zero.

total force on the coil,

Ans: The total force on the coil is zero as the field is uniform.

average force on each electron in the coil due to the magnetic field?

Ans: Number of free electrons per cubic meter in copper, $N={{10}^{29}}/{{m}^{3}}$

Charge on the electron would be, $e=1.6\times {{10}^{-19}}C$

Magnetic force, $F=Be{{v}_{d}}$

Where, ${{v}_{d}}$ is Drift velocity of electrons.

${{v}_{d}}=\frac{I}{neA}=\frac{5}{{{10}^{29}}\times 1.6\times {{10}^{-19}}\times {{10}^{-5}}}=3.125\times {{10}^{-5}}m/s$

$\Rightarrow F=0.10\times 1.6\times {{10}^{-19}}\times 3.125\times {{10}^{-5}}$

$\Rightarrow F=5\times {{10}^{-25}}N$

Therefore, the average force on each electron is found to be $5\times {{10}^{-25}}N$.

22. A galvanometer coil has a resistance of $12\Omega $and the metre shows full scale deflection for a current of $3mA$. How will you convert the metre into a voltmeter of range $0$ to $18V$?

Ans: Given that,

Resistance of the galvanometer coil, $G=12\Omega $

Current for which there is full scale deflection, ${{I}_{g}}=3mA=3\times {{10}^{-3}}A$

Range of the voltmeter needs to be converted to $18V$.

Let a resistor of resistance R be connected in series with the galvanometer to convert it into a voltmeter. This resistance can be given as:

$R=\frac{V}{{{I}_{g}}}-G$

Substituting the given values we get,

$R=\frac{18}{3\times {{10}^{-3}}}-12=6000-12$

$\Rightarrow R=5988\Omega $

Therefore, we found that a resistor of resistance $5988\Omega $ is to be connected in series with the given galvanometer.

23. A galvanometer coil has a resistance of $15\Omega $ and the metre shows full scale deflection for a current of $4mA$. How will you convert the metre into an ammeter of range $0$ to $6A$?

Resistance of the galvanometer coil, $G=15\Omega $

Current for which the galvanometer shows full scale deflection, ${{I}_{g}}=4mA=4\times {{10}^{-3}}A$

We said that, Range of the ammeter needs to be $6A$.

In order to convert the given galvanometer into an ammeter, a shunt resistor of resistance S is to be connected in parallel with the galvanometer.

The value of S could be given as:

$S=\frac{{{I}_{g}}G}{I-{{I}_{g}}}$

Substituting the values,

$S=\frac{4\times {{10}^{-3}}\times 15}{6-4\times {{10}^{-3}}}=\frac{0.06}{5.996}\approx 0.01\Omega $

$\Rightarrow S=10m\Omega $

Therefore, we found that a $10m\Omega $ shunt resistor is to be connected in parallel with the galvanometer.

Long Answer Questions 5 Marks

What is a cyclotron? Explain its working principle.

Ans: Cyclotron is a device used to accelerate charged particles like protons, deuterons, $\alpha $ - particles, etc.

It works on the basis of the principle that a charged particle can be accelerated to very high energies by making it pass through a moderate electric field a number of times and applying a strong magnetic field at the same time.

A cyclotron’s oscillator frequency is \[10\,\text{MHz}\], what should be the operating magnetic field for accelerating protons? If radius is \[20\,\text{cm}\], what is the K.E. of the proton beam produced by the accelerator? \[\left( e=1.6\times {{10}^{-19}}\text{ c},mp=1.6\times {{10}^{-27}}\text{ kg},1\text{ MeV}=1.602\times {{10}^{-13}}\text{ J} \right)\]

Ans: Given that, \[v=10\,\text{MHz}=10\times {{10}^{6}}\text{ Hz}\]

\[e=1.6\times {{10}^{-19}}\text{ c}\]

\[mp=1.6\times {{10}^{-27}}\text{ kg}\]

\[r=20\,\text{cm}=20\times {{10}^{-2}}\,\text{m}\]

We have the expression for kinetic energy,

KE $=\frac{{{q}^{2}}{{B}^{2}}{{r}^{2}}}{2m}$

Using $v=\frac{qB}{2\pi }$

$B=\frac{2\pi mV}{q}$

$\Rightarrow B=\frac{2\times 3.14\times 1.6\times {{10}^{-27}}\times {{10}^{7}}}{1.6\times {{10}^{-19}}}$

$\Rightarrow B=0.628\text{ T}$

Therefore, the operating magnetic field for accelerating protons is $0.628\text{ T}$.

KE $=\frac{{{\left( 1.6\times {{10}^{-19}} \right)}^{2}}\times {{\left( 0.66 \right)}^{2}}\times {{\left( 0.2 \right)}^{2}}}{2\times 1.67\times {{10}^{-27}}}$

KE $=13.35\times {{10}^{-13}}\text{ J}$

But we have, $1.602\times {{10}^{-13}}\text{ Joules}=1\text{ MeV}$

Since $12.02\times {{10}^{-13}}\text{ J}$ has $\frac{12.02\times {{10}^{-13}}}{1.602\times {{10}^{-13}}}\text{ MeV}$

$\Rightarrow KE=8.3\text{ MeV}$

Therefore, the K.E. of the proton beam produced by the accelerator is $8.3\text{ MeV}$.

Draw a labelled diagram of a moving coil galvanometer. Prove that in a radial magnetic field, the deflection of the coil is directly proportional to the current flowing in the coil.

Ans: When a current $I$ is passed through a coil two equal and opposite forces act on the arms of a coil to form a couple which exerts a Torque on the coil.

\[\tau =NIAB\sin \theta \]

If $\theta =90{}^\circ \left( \sin 90{}^\circ =1 \right)$

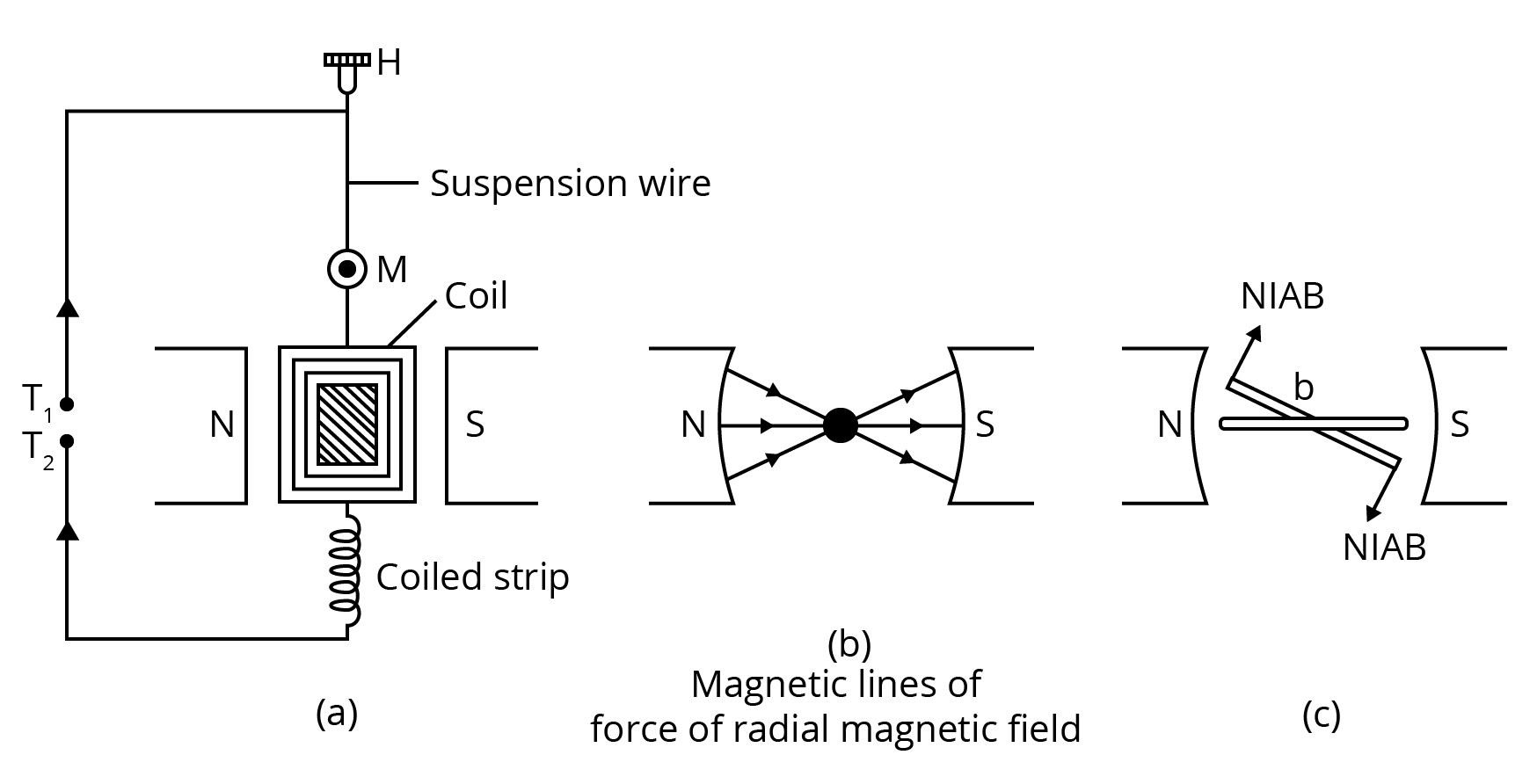
$\theta $ is the angle made by the normal to the plane of coil with B

$\tau =NIAB\text{ }$ ……………………………….. (1)

This is called as deflecting torque

As the coil deflected the spring is twisted and a restoring torque per unit twist then the restoring torque for the deflecting & is given by

${\tau }'=k\phi $ ……………………….. (2)

In equilibrium

\[\text{Deflecting Torque}=\text{Restoring Torque}\]

\[NIAB=K\phi \]

\[I=\frac{K\phi }{NAB}\phi \]

\[I=G\phi \] where \[G=\frac{K}{NAB}\] (galvanometer constant)

$\Rightarrow I\propto \phi $

Therefore, deflection of the coil is directly proportional to the current flowing in the coil.

A galvanometer can be converted into a voltmeter to measure upto

$V$ volt by connecting a resistance ${{R}_{1}}$ series with the coil

\[\frac{V}{2}\] volt by connecting a resistance ${{R}_{2}}$ in series with a coil. Find \[R\] in terms of ${{R}_{1}}\text{ and }{{R}_{2}}$ required to convert – it into a voltmeter that can read up to \['2V'\] volt.

Ans: We know that, ${{I}_{g}}=\frac{V}{R+{{R}_{G}}}$

\[\Rightarrow {{I}_{g}}\text{=}\frac{V}{{{R}_{1}}+{{R}_{G}}}\] …………………………….. (1)

And ${{I}_{g}}=\frac{\frac{V}{2}}{{{R}_{2}}+{{R}_{G}}}$ ……………………………. (2)

Equating \[\left( 1 \right)\text{ }\And \text{ }\left( 2 \right)\]

$\frac{V}{{{R}_{1}}+{{R}_{G}}}=\frac{\frac{V}{2}}{{{R}_{2}}+{{R}_{G}}}$

That is, ${{R}_{1}}+{{R}_{G}}=2\left( {{R}_{2}}+{{R}_{G}} \right)$

${{R}_{G}}=-2{{R}_{2}}+{{R}_{1}}$

For conversion ${{I}_{g}}=\frac{2V}{R+{{R}_{G}}}$

$\Rightarrow {{I}_{g}}\frac{V}{{{R}_{1}}+{{R}_{G}}}=\frac{2V}{R+{{R}_{G}}}$

$\Rightarrow {{I}_{g}}=2{{R}_{1}}+2{{R}_{G}}=R+{{R}_{G}}$

$\Rightarrow R=2{{R}_{1}}+{{R}_{G}}$

$\Rightarrow R=2{{R}_{1}}+{{R}_{1}}-2{{R}_{2}}$

$\Rightarrow R=3{{R}_{1}}-2{{R}_{2}}$

Therefore, R in the case can be written as, $R=3{{R}_{1}}-2{{R}_{2}}$.

3. Two moving coil meters, ${{M}_{1}}$ and ${{M}_{2}}$ have the following particulars:

${{R}_{1}}=10\,\Omega ,$ ${{N}_{1}}=30,$${{A}_{1}}=3.6\times {{10}^{-3}}\text{ }{{\text{m}}^{2}},$ ${{B}_{1}}=0.25\text{ T}$

\[{{R}_{2}}=14\,\Omega ,\] \[{{N}_{2}}=42\],${{A}_{2}}=1.8\times {{10}^{-3}}\text{ }{{\text{m}}^{2}},$ ${{B}_{2}}=0.50\text{ T}$

(The spring constants are identical for the two meters).

Determine the ratio of (a) current sensitivity and (b) Voltage sensitivity of ${{M}_{1}}$ and ${{M}_{2}}$.

a) current sensitivity of ${{M}_{1}}$ and ${{M}_{2}}$:

Ans: From given data, moving coil meter ${{M}_{1}}$,

Resistance, ${{R}_{1}}=10\,\Omega $

Number of turns, ${{N}_{1}}=30$

Area of cross-section, ${{A}_{1}}=3.6\times {{10}^{-3}}\text{ }{{\text{m}}^{2}}$

Magnetic field strength, ${{B}_{1}}=0.25\text{ T}$

Spring constant ${{K}_{1}}=K$

For moving coil meter ${{M}_{2}}$ :

Resistance, \[{{R}_{2}}=14\,\Omega \]

Number of turns, \[{{N}_{2}}=42\]

Area of cross-section, ${{A}_{2}}=1.8\times {{10}^{-3}}\text{ }{{\text{m}}^{2}}$

Magnetic field strength, ${{B}_{2}}=0.50\text{ T}$

Spring constant, ${{K}_{2}}=K$

Current sensitivity of ${{M}_{1}}$ is given as:

${{I}_{s1}}=\frac{{{N}_{1}}{{B}_{1}}{{A}_{1}}}{{{K}_{1}}}$

And, the current sensitivity of ${{M}_{2}}$ is given as:

${{I}_{s2}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}}{{{K}_{2}}}$

$\therefore $ Ratio $\frac{{{I}_{s2}}}{{{I}_{s1}}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}{{K}_{1}}}{{{N}_{1}}{{B}_{1}}{{A}_{1}}{{K}_{2}}}$ $=\frac{42\times 0.5\times 1.8\times {{10}^{-3}}\times K}{K\times 30\times 0.25\times 3.6\times {{10}^{-3}}}=1.4$

Hence, the ratio of current sensitivity of ${{M}_{2}}\text{ to }{{M}_{1}}$ is $1.4$.

(b) voltage sensitivity of ${{M}_{2}}\text{ and }{{M}_{1}}$

Ans: Voltage sensitivity for ${{M}_{2}}$ is given as:

${{V}_{s2}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}}{{{K}_{2}}{{R}_{2}}}$

And, voltage sensitivity for ${{M}_{1}}$ is given as:

${{V}_{s1}}=\frac{{{N}_{1}}{{B}_{1}}{{A}_{1}}}{{{K}_{1}}{{R}_{1}}}$

On taking the ratio we get,

$\frac{{{V}_{S2}}}{{{V}_{S1}}}=\frac{{{N}_{2}}{{B}_{2}}{{A}_{2}}{{K}_{1}}{{R}_{1}}}{{{K}_{2}}{{R}_{2}}{{N}_{1}}{{B}_{1}}{{A}_{1}}}$

$\therefore \frac{{{V}_{S2}}}{{{V}_{S1}}}=\frac{42\times 0.5\times 1.8\times {{10}^{-3}}\times 10\times K}{K\times 14\times 30\times 0.25\times 3.6\times {{10}^{-3}}}=1$

Therefore, the ratio of voltage sensitivity of ${{M}_{2}}\text{ and }{{\text{M}}_{1}}$is 1.

4. In a chamber, a uniform magnetic field of $6.5G\left( 1G={{10}^{-4}}T \right)$is maintained. An electron is shot into the field with a speed of $4.8\times {{10}^{6}}m{{s}^{-1}}$ normal to the field. Explain why the path of the electron is a circle. Determine the radius of the circular orbit.$\left( e=1.6\times {{10}^{-19}}C,{{m}_{e}}=9.1\times {{10}^{-31}}kg \right)$

Ans: Given that, magnetic field strength, \[B=6.5\text{ G}=6.5\times {{10}^{-4}}\text{ T}\]

Speed of the electron, \[v=4.8\times {{10}^{6}}\text{ m/s}\]

Charge on the electron, $e=1.6\times {{10}^{-19}}\text{ C}$

Mass of the electron, ${{m}_{e}}=9.1\times {{10}^{-31}}\text{ kg}$

Angle between the shot electron and magnetic field, $\theta =90{}^\circ $

Magnetic force exerted on the electron in the magnetic field is given as:

\[F=evB\sin \theta \]

This force provides centripetal force to the moving electron. Hence, the electron starts moving in a circular path of radius $r$.

Therefore, centripetal force exerted on the electron,

${{F}_{c}}=\frac{m{{v}^{2}}}{r}$

In equilibrium, the centripetal force exerted on the electron is equal to the magnetic force,

That is, ${{F}_{c}}=F$

$\frac{m{{v}^{2}}}{r}=evB\sin \theta $

$\Rightarrow r=\frac{mv}{Be\sin \theta }$

$\Rightarrow r=\frac{9.1\times {{10}^{-31}}\times 4.8\times {{10}^{6}}}{6.5\times {{10}^{-4}}\times 1.6\times {{10}^{-19}}\times \sin 90{}^\circ }$

$\Rightarrow r=4.2\times {{10}^{-2}}\text{ m}$

\[\Rightarrow r=4.2\text{ cm}\]

Therefore, the radius of the circular orbit of the electron is \[4.2\text{ cm}\].

5. In Exercise \[4.11\] obtain the frequency of revolution of the electron in its circular orbit. Does the answer depend on the speed of the electron? Explain.

Ans: Given that, magnetic field strength, $B=6.5\times {{10}^{-4}}\text{ T}$

Charge of the electron, $e=1.6\times {{10}^{-19}}\text{ C}$

Mass of the electron, ${{m}_{e}}=9.1\times {{10}^{-31}}\text{ kg}$

Velocity of the electron, \[v=4.8\times {{10}^{6}}\text{ m/s}\]

Radius of the orbit, \[r=4.2\text{ cm}=0.042\text{ m}\]

Frequency of revolution of the electron $=\upsilon $

Angular frequency of the electron, $\omega =2n\upsilon $

Velocity of the electron is related to the angular frequency as:

$v=r\omega $

In the circular orbit, the magnetic force on the electron is balanced by the centripetal force. So,

$evB=\frac{m{{v}^{2}}}{R}$

$\Rightarrow eB=\frac{m}{r}\left( r\omega \right)=\frac{m}{r}\left( r2\pi \upsilon \right)$

$\Rightarrow \upsilon =\frac{Be}{2\pi m}$

This expression for frequency is independent of the speed of the electron.

On substituting, frequency,

$\Rightarrow \upsilon =\frac{6.5\times {{10}^{-4}}\times 1.6\times {{10}^{-19}}}{2\times 3.14\times 9.1\times {{10}^{-31}}}$

$\Rightarrow \upsilon =18.2\times {{10}^{6}}\text{ Hz}$

$\Rightarrow \upsilon \approx 18\text{ MHz}$

Therefore, the frequency of the electron is around \[18\text{ MHz}\] and is independent of the speed of the electron.

6. Two concentric circular coils X and Y radii 16 cm and 10 cm, respectively, lie in the same vertical plane containing the north to south direction. Coil X has 20 turns and carries a current of 16 A; coil Y has 25 turns and carries a current of 18 A. The sense of the current in X is anticlockwise, and clockwise in Y, for an observer looking at the coils facing west. Give the magnitude and direction of the net magnetic field due to the coils at their centre.

Radius of coil X, ${{r}_{1}}=16cm=0.16m$

Radius of coil Y, ${{r}_{2}}=10cm=0.1m$

Number of turns of on coil X,${{n}_{1}}=20$

Number of turns of on coil Y,${{n}_{2}}=25$

Current in coil X, ${{I}_{1}}=16A$

Current in coil Y,${{I}_{2}}=18A$

Magnetic field due to coil X at their centre is given by the relation,

${{B}_{1}}=\frac{{{\mu }_{0}}{{n}_{1}}{{I}_{1}}}{2{{r}_{1}}}$

Where, Permeability of free space, ${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$

${{B}_{1}}=\frac{4\pi \times {{10}^{-7}}\times 20\times 16}{2\times 0.16}$

$\therefore {{B}_{1}}=4\pi \times {{10}^{-4}}T$(towards East)

Magnetic field due to coil Y at their centre is given by the relation,

${{B}_{2}}=\frac{{{\mu }_{0}}{{n}_{2}}{{I}_{2}}}{2{{r}_{2}}}$

$\Rightarrow {{B}_{2}}=\frac{4\pi \times {{10}^{-7}}\times 25\times 18}{2\times 0.10}$

$\Rightarrow {{B}_{2}}=9\pi \times {{10}^{-4}}T$(towards West)

So, net magnetic field could be obtained as,

$B={{B}_{2}}-{{B}_{1}}=9\pi \times {{10}^{-4}}-4\pi \times {{10}^{-4}}$

$\Rightarrow B=1.57\times {{10}^{-3}}T$(towards West)

Therefore, net magnetic field is $1.57\times {{10}^{-3}}T$ towards west.

7. For a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its centre is given by,

Show that this reduces to the familiar result for the field at the centre of the coil.

Radius of circular coil = R

Number of turns on the coil = N

Current in the coil = I

Magnetic field at a point on its axis at distance x is given by the relation,

Where,${{\mu }_{0}}=4\pi \times {{10}^{-4}}Tm{{A}^{-1}}$Permeability of free space

If the magnetic field at the centre of the coil is considered, then $x=0$

$\therefore B=\frac{{{\mu }_{0}}I{{R}^{2}}N}{2{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\frac{3}{2}}}}$

Therefore, this is the familiar result for the magnetic field at the centre of the coil.

Consider two parallel coaxial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the midpoint between the coils is uniform over a distance that is small as compared to R, and is given by, approximately, (Such an arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.)

Ans: Radii of two parallel coaxial circular coils = R

Number of turns on each coil = N

Current in both coils = I

Distance between both the coils = R

Let us consider point Q at distance d from the centre.

Then, one coil is at a distance of $\frac{R}{2}+d$from point Q.

Magnetic field at point Q could be given as:

$B=\frac{{{\mu }_{0}}I{{R}^{2}}N}{2{{\left( {{x}^{2}}+{{R}^{2}} \right)}^{\frac{3}{2}}}}$

Also, the other coil is at a distance of $\frac{R}{2}+d$from point Q.

Magnetic field due to this coil is given as:

${{B}_{2}}=\frac{{{\mu }_{0}}NI{{R}^{2}}}{2{{\left[ {{\left( \frac{R}{2}-d \right)}^{2}}+{{R}^{2}} \right]}^{\frac{3}{2}}}}$

Now we have the total magnetic field as,

$B={{B}_{1}}+{{B}_{2}}$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. {{\left( \frac{R}{2}-d \right)}^{2}}+{{R}^{2}} \right\} \right.}^{\frac{-3}{2}}}+{{\left. \left\{ {{\left( \frac{R}{2}+d \right)}^{2}}+{{R}^{2}} \right. \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. \frac{5{{R}^{2}}}{4}+{{d}^{2}}-Rd \right\} \right.}^{\frac{-3}{2}}}+{{\left. \left\{ \frac{5{{R}^{2}}}{4}+{{d}^{2}}+Rd \right. \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

$\Rightarrow B=\frac{{{\mu }_{0}}I{{R}^{2}}}{2}\left[ \left\{ {{\left\{ \left. 1+\frac{4{{d}^{2}}}{5{{R}^{2}}}-\frac{4d}{5R} \right\} \right.}^{\frac{-3}{2}}}+{{\left\{ 1+\frac{4{{d}^{2}}}{5{{R}^{2}}}+\frac{4d}{5R} \right\}}^{\frac{-3}{2}}}\times N \right. \right]$

Now for $d\ll R$, we could neglect the factor $\frac{{{d}^{2}}}{{{R}^{2}}}$, we get,

$B\approx \frac{{{\mu }_{0}}I{{R}^{2}}}{2}\times {{\left( \frac{5{{R}^{2}}}{4} \right)}^{\frac{-3}{2}}}\left[ {{\left( 1-\frac{4d}{5R} \right)}^{\frac{-3}{2}}}+{{\left( 1+\frac{4d}{5R} \right)}^{\frac{-3}{2}}} \right]\times N$

$\Rightarrow B\approx \frac{{{\mu }_{0}}I{{R}^{2}}}{2}\times {{\left( \frac{5{{R}^{2}}}{4} \right)}^{\frac{-3}{2}}}\left[ 1-\frac{6d}{5R}+1+\frac{6d}{5R} \right]$

$\Rightarrow B\approx {{\left( \frac{4}{5} \right)}^{\frac{3}{2}}}\frac{{{\mu }_{0}}IN}{R}=0.72\left( \frac{{{\mu }_{0}}IN}{R} \right)$

Therefore, we proved that the field along the axis around the mid-point between the coils is uniform.

8. An electron emitted by a heated cathode and accelerated through a potential difference of $2.0kV$, enters a region with a uniform magnetic field of $0.15T$. Determine the trajectory of the electron if the field

is transverse to its initial velocity.

Ans: We are given,

Magnetic field strength, $B=0.15T$

Charge on the electron, $e=1.6\times {{10}^{-19}}C$

Mass of the electron, $m=9.1\times {{10}^{-31}}kg$

Potential difference, $V=2.0kV=2\times {{10}^{3}}V$

Now we have the kinetic energy of the electron given by,

$eV=\frac{1}{2}m{{v}^{2}}$

$\Rightarrow v=\sqrt{\frac{2eV}{m}}$…………………….. (1)

Where, $v$is the velocity of the electron

Since the magnetic force on the electron provides the required centripetal force of the electron, the electron traces a circular path of radius $r$.

Now, the magnetic force on the electron is given by the relation,

Centripetal force,

${{F}_{C}}=\frac{m{{v}^{2}}}{r}$

$\Rightarrow Bev=\frac{m{{v}^{2}}}{r}$

$\Rightarrow r=\frac{mv}{Be}$………………….. (2)

From the equations (1) and (2), we get,

$r=\frac{m}{Be}{{\left[ \frac{2eV}{m} \right]}^{\frac{1}{2}}}$

$\Rightarrow r=\frac{9.1\times {{10}^{-31}}}{0.15\times 1.6\times {{10}^{-19}}}{{\left( \frac{2\times 1.6\times {{10}^{-19}}\times 2\times {{10}^{3}}}{9.1\times {{10}^{-31}}} \right)}^{\frac{1}{2}}}$

$\Rightarrow r=100.55\times {{10}^{-5}}$

$\Rightarrow r=1mm$

Therefore, we found that the electron has a circular trajectory of radius 1.0 mm normal to the magnetic field.

makes an angle of $30{}^\circ $with the initial velocity.

Ans: When the field makes an angle $\theta $ of $30{}^\circ $with initial velocity, the initial velocity will be,

${{v}_{1}}=v\sin \theta $

From equation (2), we can write the following expression:

${{r}_{1}}=\frac{m{{v}_{1}}}{Be}$

$\Rightarrow {{r}_{1}}=\frac{mv\sin \theta }{Be}$

$\Rightarrow {{r}_{1}}=\frac{9.1\times {{10}^{-31}}}{0.15\times 1.6\times {{10}^{-19}}}\left[ \frac{2\times 1.6\times {{10}^{-19}}\times 2\times {{10}^{3}}}{9\times {{10}^{-31}}} \right]\sin 30{}^\circ $

$\Rightarrow r=0.5\times {{10}^{-3}}m=0.5mm$

Therefore, we found that the electron has a helical trajectory of radius $0.5mm$, with the axis of the solenoid along the magnetic field direction.

9. A magnetic field set up using Helmholtz coils (described in Exercise $4.16$) is uniform in a small region and has a magnitude of $0.75T$. In the same region, a uniform electrostatic field is maintained in a direction normal to the common axis of the coils. A narrow beam of (single species) charged particles all accelerated through $15kV$enters this region in a direction perpendicular to both the axis of the coils and the electrostatic field. If the beam remains undeflected when the electrostatic field is $9.0\times {{10}^{-5}}V{{m}^{-1}}$ make a simple guess as to what the beam contains. Why is the answer not unique?

Magnetic field, $B=0.75T$

Accelerating voltage, $V=15kV=15\times {{10}^{3}}V$

Electrostatic field, $E=9\times {{10}^{5}}V{{m}^{-1}}$

Mass of the electron$=m$

Charge of the electron $=e$

Velocity of the electron $=v$

Kinetic energy of the electron $=eV$

Thus,

$\frac{1}{2}m{{v}^{2}}=eV$

$\Rightarrow \frac{e}{m}=\frac{{{v}^{2}}}{2V}$…………………….. (1)

Since the particle remains undeflected by electric and magnetic fields, we could infer that the electric field is balancing the magnetic field.

$\Rightarrow v=\frac{E}{B}$……………………….. (2)

Now we could substitute equation (2) in equation (1) to get,

$\Rightarrow \frac{e}{m}=\frac{1}{2}\frac{{{\left( \frac{E}{B} \right)}^{2}}}{V}=\frac{{{E}^{2}}}{2V{{B}^{2}}}$

$\Rightarrow \frac{e}{m}=\frac{{{\left( 9.0\times {{10}^{5}} \right)}^{2}}}{2\times 15000\times {{\left( 0.75 \right)}^{2}}}=4.8\times {{10}^{7}}C/kg$

This value of the specific charge $\left( \frac{e}{m} \right)$ is equal to the value of deuteron or deuterium ions. This is not a unique answer. Other possible answers are $H{{e}^{++}}$, $L{{i}^{+++}}$

10. A uniform magnetic field of $1.5T$ exists in a cylindrical region of radius $10.0cm$, its direction parallel to the axis along east to west. A wire carrying a current of $7.0A$ in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,

The wire intersects the axis,

Magnetic field strength, $B=1.5T$

Radius of the cylindrical region, $r=10cm=0.1m$

Current in the wire passing through the cylindrical region, $I=7A$

If the wire intersects the axis, then the length of the wire is the diameter of the cylindrical region. Thus, $l=2r=0.2m$

Angle between magnetic field and current, $\theta =90{}^\circ $

We know that, Magnetic force acting on the wire is given by the relation,

$F=BIl\sin \theta $

$\Rightarrow F=1.5\times 7\times 0.2\times \sin 90{}^\circ $

$\Rightarrow F=2.1N$

Therefore, a force of 2.1 N acts on the wire in a vertically downward direction.

The wire is turned from N-S to northeast-northwest direction,

Ans: New length of the wire after turning it to the northeast-northwest direction can be given as:

${{l}_{1}}=\frac{l}{\sin \theta }$

Angle between magnetic field and current, $\theta =45{}^\circ $

Force on the wire,

$F=BI{{l}_{1}}\sin \theta =BIl=1.5\times 7\times 0.2$

Therefore, a force of 2.1 N acts vertically downward on the wire. This is independent of angle $\theta $ as $l\sin \theta $ is fixed.

The wire in the N-S direction is lowered from the axis by a distance of $6.0cm$?

Ans: The wire is lowered from the axis by distance, $d=6.0cm$

Let ${{l}_{2}}$be the new length of the wire,

${{\left( \frac{{{l}_{2}}}{2} \right)}^{2}}=4\left( d+r \right)=4\left( 10+6 \right)=4\times 16$

$\Rightarrow {{l}_{2}}=8\times 2=16cm=0.16m$

Magnetic force that is exerted on the wire is,

${{F}_{2}}=BI{{l}_{2}}=1.5\times 7\times 0.16$

$\Rightarrow F=1.68N$

Therefore, a force of $1.68N$acts in a vertically downward direction on the wire.

11. A uniform magnetic field of $3000G$ is established along the positive z-direction. A rectangular loop of sides $10cm$ and $5cm$ carries a current of $12A$. What is the torque on the loop in the different cases shown in Figure? What is the force on each case? Which case corresponds to stable equilibrium?

A rectangular current carrying loop placed in a y-z plane with magnetic field in z-direction.

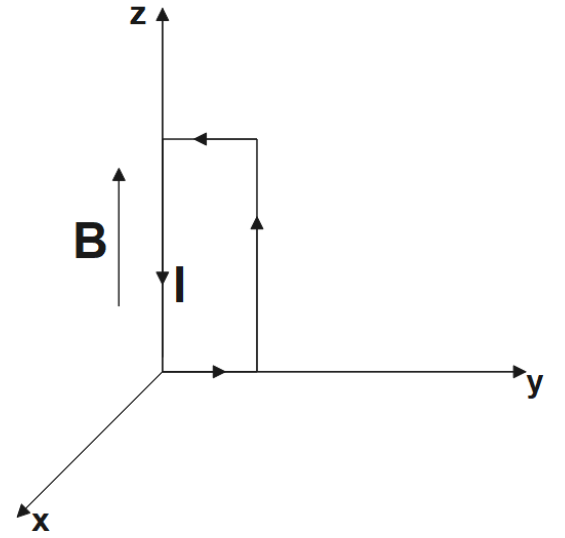
Magnetic field strength, $B=3000G=3000\times {{10}^{-4}}T=0.3T$

Length of the rectangular loop, $l=10cm$

Width of the rectangular loop, $b=5cm$

Area of the loop, $A=l\times b=\left( 10\times 5 \right)c{{m}^{2}}=50\times {{10}^{-4}}{{m}^{2}}$

Current in the loop, $I=12A$

Now, we could take the anti-clockwise direction of the current as positive and vice-versa,

We have the expression for torque given as,

\[\vec{\tau }=I\vec{A}\times \vec{B}\]

We could see from the given figure that A is normal to the y-z plane and B is directed along the z-axis. Substituting the given values,

$\tau =12\times \left( 50\times {{10}^{-4}} \right)\hat{i}\times 0.3\hat{k}$

$\Rightarrow \tau =-1.8\times {{10}^{-2}}\hat{j}Nm$

Now the torque is found to be directed along a negative y-direction. Since the external magnetic field is uniform, the force on the loop would be zero.

(Image will be uploaded soon)

Ans: This case is very similar to case (a), so, the answer here would be same as (a).

A rectangular current carrying loop placed in a x-z plane with magnetic field in z-direction.

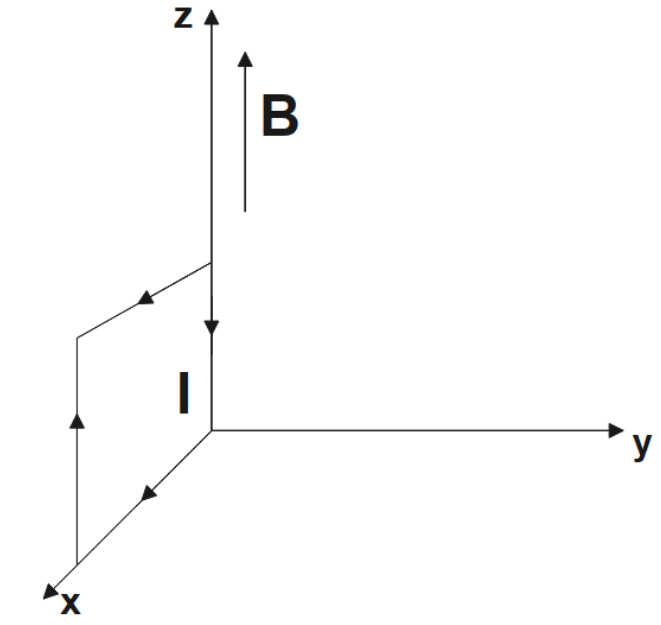
Ans: Torque here would be,

$\Rightarrow \tau =-12\left( 50\times {{10}^{-4}} \right)\hat{j}\times 0.3\hat{k}$

$\Rightarrow \tau =-1.8\times {{10}^{-2}}\hat{i}Nm$

The direction here is along the negative x direction and the force is zero.

A rectangular current carrying loop placed in a xyz plane with magnetic field in z-direction.

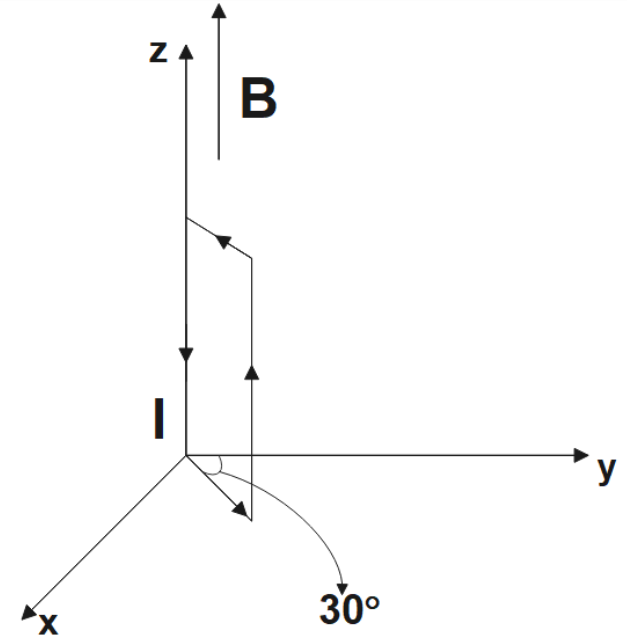
$\left| \tau \right|=IAB$

$\Rightarrow \tau =12\times \left( 50\times {{10}^{-4}} \right)\times 0.3$

$\Rightarrow \left| \tau \right|=1.8\times {{10}^{-2}}Nm$

Here, the direction is found to be at $240{}^\circ $with positive x-direction and the force is zero.

A rectangular current carrying loop placed in a xy plane with magnetic field in z-direction.

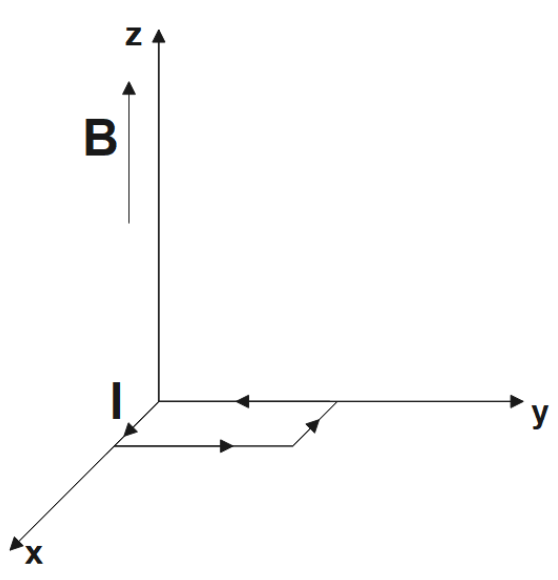
Ans: Torque,

$\tau =I\vec{A}\times \vec{B}$

$\Rightarrow \tau =\left( 50\times {{10}^{-4}}\times 12 \right)\hat{k}\times 0.3\hat{k}$

$\Rightarrow \tau =0$

Here, both torque and force are found to be zero. For this case, the direction $I\vec{A}$and $\vec{B}$is the same and the angle between them is zero. They would come back to equilibrium on being displaced and so the equilibrium is stable.

(image will be uploaded soon)

Ans: Torque is given by,

Here also both torque and force are found to be zero.

For this case, the direction of $I\vec{A}$ and $\vec{B}$ are opposite and the angle between them is $180{}^\circ $. Here it doesn’t come back to its original position on being disturbed and hence, the equilibrium is unstable.

12. A solenoid $60cm$ long and has a radius $4.0cm$ has 3 layers of windings of 300turns each. A $2.0cm$ long wire of mass $2.5g$ lies inside the solenoid (near its centre) normal to its axis; both the wire and the axis of the solenoid are in the horizontal plane. The wire is connected through two leads parallel to the axis of the solenoid to an external battery which supplies a current of $6.0A$ in the wire. What value of current (with appropriate sense of circulation) in the windings of the solenoid can support the weight of the wire? $g=9.8m{{s}^{-2}}$

Length of the solenoid, $L=60cm=0.6m$

Radius of the solenoid, $r=4.0cm=0.04m$

It is given that there are 3 layers of windings of 300 turns each.

Total number of turns, $n=3\times 300=900$

Length of the wire, $l=2cm=0.02m$

Mass of the wire, $m=2.5g=2.5\times {{10}^{-3}}kg$

Current flowing through the wire, $i=6A$

Magnetic field produced inside the solenoid, $B=\frac{{{\mu }_{0}}nI}{L}$

Current flowing through the windings of the solenoid, $I$

Magnetic force is given by the relation,

$F=Bil=\frac{{{\mu }_{0}}nI}{L}il$

Now, we have the force on the wire equal to the weight of the wire.

$mg=\frac{{{\mu }_{0}}nIil}{L}$

$\Rightarrow I=\frac{mgL}{{{\mu }_{0}}nil}=\frac{2.5\times {{10}^{-3}}\times 9.8\times 0.6}{4\pi \times {{10}^{-7}}\times 900\times 0.02\times 6}$

$\Rightarrow I=108A$

Therefore, the current flowing through the solenoid is 108 A.

Download Important Questions Of Chapter 4 Physics Class 12 PDF

Class 12 physics chapter 4 important questions.

The Class 12 Physics Chapter 4 important questions PDF is highly beneficial for the students who are targeting good grades in competitive exams. The textbook prescribed by NCERT for Class 12 Physics consists of many topics. For elevating the grades and to improve their knowledge in the subject students are suggested to download chapter wise notes available on Vedantu for detailed explanation along with exercise problems.

For thorough preparation, students should start with Chapter 4 Physics Class 12 important questions . The important questions of Chapter 4 Physics Class 12 are prepared with deep insight into the syllabus according to CBSE board exams , previous year’s questions. The Chapter 4 Physics Class 12 important questions included all the textbook exercises along with many Class 12 Physics Chapter 4 extra questions prepared by experts and the master teachers.

Chapter 4 Moving Charges and Magnetism has good marks allotment in the Board exams. The Moving charges and Magnetism include many interesting topics like magnetic forces, magnetic field, the direction of magnetic force in the current-carrying coil with different cases, etc. These concepts are not only important in the point of board exam but also for students who are aiming for IIT-JEE , NEET exams as well.

Students must start with Class 12 Physics Chapter 4 important questions after revising the chapter. Students must be thoroughly familiar with all the concepts of Chapter 4 for solving Class 12 Physics Chapter 4 extra questions. Let us have a look at some key points of Chapter 4:

The chapter consists of many direct derivations like ampere circuital law, the force between two parallel current-carrying wires, etc.

Chapter 4 mainly focused on explaining the idea that electric and magnetic fields are interrelated to one another. Because since the beginning it was assumed that electric fields and magnetic fields are independent of each other.

We come across the concepts like a magnetic force, Lorentz force which is a piece of evidence about electric and magnetic fields that are related to each other.

We study the effects of magnetic fields on current. We study a few devices that use the principle of magnetic induction.

We study cyclotrons, solenoids, moving coil galvanometers, etc.

These are a few key points to be remembered while jumping into the practice of Chapter 4 Physics Class 12 important questions .

Key Features of Vedantu’s CBSE Class 12 Important Questions for Physics Chapter 4 - Moving Charges and Magnetism

The following are the reasons why you should choose Vedantu’s Important Questions for Class 12 CBSE Physics Chapter 4 - Moving Charges and Magnetism:

Vedantu’s Important Questions for Class 12 CBSE Physics Chapter 4 - Moving Charges and Magnetism are aligned with the CBSE Board guidelines and answering pattern.

Our questions are prepared in a manner that will serve the purpose of revising the entire chapter to be able to solve any kind of question that is asked in the exam.

The questions adhere to the strict norms of the CBSE Class 12 Physics syllabus . The answers have also been framed in a straightforward manner using simple language.

The set of important questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism for the academic year 2024-25 prove to be a valuable tool for students' exam preparation. These questions cover vital concepts such as magnetic fields, Ampere's law, and applications of moving charges in magnetic fields. By practicing these questions, students can strengthen their understanding of the topic and improve problem-solving abilities. The comprehensive nature of these questions ensures thorough coverage of the chapter, enabling students to excel in their examinations. With these resources at their disposal, students can confidently approach the subject and achieve academic success in the upcoming academic year.

Important Related Links for CBSE Class 12 Physics

FAQs on Important Questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism 2024-25

1. What is Biot Savart’s law, according to Chapter 4 of Class 12 Physics?

This law is solely concerned with current sources and magnetic fields. The magnetic field is determined once the current involving vector products is spread. The distance between the field points and the current changes all the time, and this is the calculus problem. Aerodynamics and magnetic effects at the atomic and molecular levels are calculated. Visit Vedantu to learn more about this law.

2. What is Ampere's circuital law, according to Chapter 4 of Class 12 Physics?

Relation between the magnetic field and source current is discussed in ampere's circuital law. The density of a magnetic field in an imaginary path is studied in ampere's circuital law. For more information, visit Vedantu's official website. There you will find the important questions which will be helpful in your exams. These questions will cover all the important topics curated together from the exam's point of view. You can download these questions and save them on your PC for future reference free of cost from the Vedantu website and the Vedantu app.

3. What are the Different Applications of Ampere's Circuital Law, according to Chapter 4 of Class 12 Physics?

Different applications of ampere’s circuital law are:

Long current-carrying induced magnetism

Current carrying cylinder creating a magnetic field

Current carrying hollow cylinder creating magnetic fields

Vedantu has all the physics questions that are solved, so you do not have to take the pressure of solving them, especially when you have to submit the homework and have not read the chapter thoroughly. Also, in exams, you can go through these questions quickly and remember them till your exam day.

4. What is Understood by a Cyclotron, according to Chapter 4 of Class 12 Physics?

The first particle accelerator is responsible for accelerating charged particles to high energies. The charged particle accelerates outwards from the spiral routes alongside the spiral particles. Physics is a difficult topic that requires careful attention. All notes and content may be found on Vedantu. It also includes all of the practice examinations that will be useful in your board exams. Hence, if you want to get high grades, you should consult Vedantu.

5. What are the limitations to a cyclotron, according to Chapter 4 of Class 12 Physics?

The limitations of cyclotron are :

The electron cannot be accelerated by a cyclotron as they are of very small size.

Neutral particles cannot be accelerated.

Cannot accelerate large positive charged particles.

Board exams are crucial for students. For these exams, a lot of practice is required. Vedantu has previous year's question papers which you can solve and then appear for the main exams. So, visit Vedantu for all such material.

CBSE Class 12 Physics Important Questions

Cbse study materials.

Andhra Pradesh
Chhattisgarh
West Bengal
Madhya Pradesh
Maharashtra
Jammu & Kashmir
NCERT Books 2022-23
NCERT Solutions
NCERT Notes
NCERT Exemplar Books
NCERT Exemplar Solution
States UT Book
School Kits & Lab Manual
NCERT Books 2021-22
NCERT Books 2020-21
NCERT Book 2019-2020
NCERT Book 2015-2016
RD Sharma Solution
TS Grewal Solution
TR Jain Solution
Selina Solution
Frank Solution
ML Aggarwal Solution
Lakhmir Singh and Manjit Kaur Solution
I.E.Irodov solutions
ICSE - Goyal Brothers Park
ICSE - Dorothy M. Noronhe
Sandeep Garg Textbook Solution
Micheal Vaz Solution
S.S. Krotov Solution
Evergreen Science
KC Sinha Solution
ICSE - ISC Jayanti Sengupta, Oxford
ICSE Focus on History
ICSE GeoGraphy Voyage
ICSE Hindi Solution
ICSE Treasure Trove Solution
Thomas & Finney Solution
SL Loney Solution
SB Mathur Solution
P Bahadur Solution
Narendra Awasthi Solution
MS Chauhan Solution
LA Sena Solution
Integral Calculus Amit Agarwal Solution
IA Maron Solution
Hall & Knight Solution
Errorless Solution
Pradeep's KL Gogia Solution
OP Tandon Solutions
Sample Papers
Previous Year Question Paper
Value Based Questions
CBSE Syllabus
CBSE MCQs PDF
Assertion & Reason
New Revision Notes
Revision Notes
HOTS Question
Marks Wise Question
Toppers Answer Sheets
Exam Paper Aalysis
Concept Map
CBSE Text Book
Additional Practice Questions
Vocational Book
CBSE - Concept
KVS NCERT CBSE Worksheets
Formula Class Wise
Formula Chapter Wise
JEE Crash Course
JEE Previous Year Paper
Important Info
JEE Mock Test
JEE Sample Papers
SRM-JEEE Mock Test
VITEEE Mock Test
BITSAT Mock Test
Manipal Engineering Mock Test
AP EAMCET Previous Year Paper
COMEDK Previous Year Paper
GUJCET Previous Year Paper
KCET Previous Year Paper
KEAM Previous Year Paper
Manipal Previous Year Paper
MHT CET Previous Year Paper
WBJEE Previous Year Paper
AMU Previous Year Paper
TS EAMCET Previous Year Paper
SRM-JEEE Previous Year Paper
VITEEE Previous Year Paper
BITSAT Previous Year Paper
UPSEE Previous Year Paper
CGPET Previous Year Paper
CUSAT Previous Year Paper
AEEE Previous Year Paper
Crash Course
Previous Year Paper
NCERT Based Short Notes
NCERT Based Tests
NEET Sample Paper
Previous Year Papers
Quantitative Aptitude
Numerical Aptitude Data Interpretation
General Knowledge
Mathematics
Agriculture
Accountancy
Business Studies
Political science
Enviromental Studies
Mass Media Communication
Teaching Aptitude
NAVODAYA VIDYALAYA
SAINIK SCHOOL (AISSEE)
Mechanical Engineering
Electrical Engineering
Electronics & Communication Engineering
Civil Engineering
Computer Science Engineering
CBSE Board News
Scholarship Olympiad
School Admissions
Entrance Exams
All Board Updates
Miscellaneous
State Wise Books
Engineering Exam

NCERT Solutions for Class 12 Physics Chapter 4 PDF Download

Some of the students often waste their time searching for the right study material; for them, the NCERT Solutions for Class 12 Physics Chapter 4 are the right ones. It is considered to be the right one as it provides accurate answers for the Class 12 Physics Chapter 4; accordingly, students can improve their accuracy level.

NCERT Solutions for Class 12 Physics Chapter 4 PDF

To have success in Class 12 Physics Chapter 4, students need to take some effort or steps. One of the important steps is to access the NCERT Solutions for Class 12 Physics Chapter 4 PDF and need to start solving questions. Students can access the Class 12 Physics Chapter 4 questions through the Selfstudys website from their comfort zone.

How to Download the NCERT Solutions for Class 12 Physics Chapter 4?

It is important for students to download the NCERT Solutions for Class 12 Physics Chapter 4 so that they can easily refer to the answers; steps to download are:

Open the Selfstudys website.

NCERT Solutions for Class 12 Physics Chapter 4, NCERT Solutions for Class 12 Physics Chapter 4 PDF, Download NCERT Solutions for Class 12 Physics Chapter 4 PDF, NCERT Solutions for Class 12 Physics Chapter 4 Revision, NCERT Solutions for Class 12 Physics Chapter 4 Theory

Click the navigation button and select NCERT Books & Solutions.

A drop down menu will appear, select NCERT Solutions from the list.

Select Class 12th from the list

And select Physics from the list of subjects.
A new page will appear, now click Chapter 4 from the list of Chapters.

Everything Students Need to Know About NCERT Solutions for Class 12 Physics Chapter 4 PDF

The NCERT Solutions for Class 12 Physics Chapter 4 PDF are considered to be important study material for students as it provides answers to all the textbook questions; here is that students need to know:

Keywords or Formulas are Presented: Formulas provide a way to present the substance using the symbol of elements; these keywords or formulas are given in the NCERT Solutions for Class 12 Physics Chapter 4.
Explained in Step Wise Manner: The answers in the NCERT Solutions for Class 12 Physics Chapter 4 revision are explained in a stepwise manner so that students can understand each point and step.
Explained in an Easy Language: Easy language is considered to be a plain language which is easier for students to read and comprehend; the answers in the NCERT Solutions for Class 12 Physics Chapter 4 theory are explained in easy language.
Provided in a Eye Catching Format: The eye catching format contains colours in a presentable format which can attract many; the same format is followed in the Chapter 4 questions of Class 12 Physics NCERT Solutions.
Tables are Included: Inside the Class 12 Physics NCERT Solutions, tables are included for Chapter 4 so that students can have organised information about the important themes.
Available in the PDF: The Class 12 Physics questions of Chapter 4 from the NCERT Solutions are available in the PDF so that students can access accurate answers from their comfort zone.

How Can NCERT Solutions for Class 12 Physics Chapter 4 Help Students?

The NCERT Solutions for Class 12 Physics Chapter 4 can help students in various ways; those ways are discussed below:

Helps to Enhance the Learning Skills: Learning skills means the term that describes the tasks involved in the learning process; students can enhance their learning skills with the help of NCERT Solutions for Class 12 Physics Chapter 4 revision.
Offers Ample Questions to Practise: Students can only excel in the Class 12 Physics Chapter 4 only if they practise questions. Students can practise vast questions with the help of the NCERT Solutions for Class 12 Physics Chapter 4 theory.
Offers In Depth Knowledge: The NCERT Solutions for Class 12 Physics Chapter 4 PDF offers in depth knowledge about the concepts and topics so that students can build a strong and firm foundation.
Helps in Progress: Progress generally considered to be movement or improvement towards achieving something; students can judge their progress in Chapter 4 questions with the help of Class 12 Physics NCERT Solutions.
Can Get a Brief Idea About Important Questions: Through the Class 12 NCERT Physics Solutions, students can get a brief idea about the Chapter 4 questions; accordingly students can prepare for that particular Chapter.
Are Free of Cost: The Class 12 Physics NCERT Solutions are free of cost; accordingly students can access the Chapter 4 questions without paying a single penny.

How to Manage Time While Solving Questions from NCERT Solutions for Class 12 Physics Chapter 4 PDF?

Managing of time is considered to be a process in which organising and planning to divide time efficiently; there are tips to manage time while solving questions from the NCERT Solutions for Class 12 Physics Chapter 4 PDF:

Create a Plan: A study plan is defined as a time management plan that helps students in achieving their learning goals; in the same manner they need to make a study plan in order to manage time while solving questions from the NCERT Solutions for Class 12 Physics Chapter 4.
Start from the Easier Ones: Students need to start solving the easy questions for the NCERT Solutions for Class 12 Physics Chapter 4 revision so that they don’t waste much time on difficult questions and can manage time.
Set a Timer: It is advisable for students to set a timer to solve each question from the NCERT Solutions for Class 12 Physics Chapter 4 theory so that they can have enough time for each question.
Try to Avoid Distractions: Distractions are considered to be those activities which can take the attention of students; to manage time while solving Class 12 Physics Chapter 4 questions from the NCERT Solutions, students need to avoid the distractions.
Use Shortcuts and Tricks: Some Chapter 4 questions of the Class 12 Physics from the NCERT Solutions can be solved through shortcuts and tricks which can save a lot of time.
Take Breaks: To manage time while solving Class 12 Physics Chapter 4 questions from the NCERT Solutions, students can take breaks at equal intervals which can save much time in doing unnecessary activities.

What are the Challenges Faced While Solving Questions from the NCERT Solutions for Class 12 Physics Chapter 4 PDF?

Challenges are generally defined as something new or difficult that forces students to make efforts; students may face challenges while solving questions from the NCERT Solutions for Class 12 Physics Chapter 4 PDF:

Understanding of Concepts: Students may face challenges in solving questions from the NCERT Solutions for Class 12 Physics Chapter 4 if they are not able to understand the concepts properly.
Memorising Formulas or Keywords: They are formulas or keywords that students need to memorise, otherwise they may face challenges while solving questions from the NCERT Solutions for Class 12 Physics Chapter 4 revision.
Management of Time: Solving questions of NCERT Solutions for Class 12 Physics Chapter 4 theory within the given time frame is a big task for students; if they are not able to do then it may lead to challenges.
Confusing Questions: The Class 12 Physics NCERT Solutions may contain confusing questions of Chapter 4 due to difficult words; this may lead to a big challenge for students to understand what is being asked.
Fear of Failure: The fear of failure among students can lead to the challenge while solving Class 12 Physics Chapter 4 questions from the NCERT Solutions.
Lack of Clarity: Lack of clarity in the Class 12 Physics concepts can lead to big challenges in solving Chapter 4 questions from the NCERT Solutions.

How to Analyse the Mistakes After Solving Questions from NCERT Solutions for Class 12 Physics Chapter 4?

After solving questions from the NCERT Solutions for Class 12 Physics Chapter 4, it is necessary for students to analyse the mistakes so that they can assess their progress; steps to analyse are discussed below:

Identify the Patterns of Mistakes: Patterns of mistakes are considered to be those errors which are done by most students; in that case, they need to identify the pattern of mistakes while solving questions from the NCERT Solutions for Class 12 Physics Chapter 4 revision.
Keep a Record of Mistakes: In order to analyse the mistakes while solving questions from the NCERT Solutions for Class 12 Physics Chapter 4 theory, they need to keep a proper record so that they can judge the progress.
Review the Correct Questions: Students need to go through the correct Chapter 4 questions and answers in the Class 12 Physics NCERT Solutions so that they can get an idea about the pattern of correct answers; through this students can easily analyse the mistakes.
Seek Help: By seeking help from the concerned teachers, students can analyse the mistakes after solving Class 12 Physics Chapter 4 questions from the NCERT Solutions; by seeking help students can solve all their doubts.
Stay Motivated: In the process of analysing the mistakes after solving Chapter 4 questions from the Class 12 Physics NCERT Solutions, students need to stay motivated and focused.
Use Different Approaches: To analyse the mistakes of Chapter 4 questions from the Class 12 Physics NCERT Solutions, one needs to try on different approaches or strategies; through this students can get an idea of wrong approaches.

Manipal MET 2024 Application (Released) (All Pages)

NCERT Solutions for Class 12 Maths
NCERT Solutions for Class 10 Maths
CBSE Syllabus 2023-24
Social Media Channels
Login Customize Your Notification Preferences

One Last Step...

Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.

Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.

Provide prime users with access to exclusive PDF study materials that are not available to regular users.

IMAGES

NCERT Solutions For Class 12 Physics Chapter 4
NCERT Book Class 12 Physics Chapter 4 Moving Charges and Magnetism (PDF)
NCERT Solutions for Class 12 Physics Chapter 4 in Hindi and English
NCERT Exemplar Class 12 Physics Solutions Chapter 4
Ncert Solutions For Class 12 Physics Chapter 4
NCERT Book Class 12 Physics Chapter 4 Moving Charges and Magnetism

VIDEO

12th Physics
12th Physics Chapter 4 important Questions 2023
Class12 Physics Chapter 4 Introduction
Don't do these mistakes in Exam😲
Important Numerical Chapter 4 Class 12 Physics || Moving charges & Magnetism 🔥
Potential & Capacitance💥CONCEPTUAL QUESTIONS💥Class 12 Physics Board Exams 2024 @@ArvindAcademy

COMMENTS

Case Study Question for Class 12 Physics Chapter 4 Moving Charges and
Case Study Question for Class 12 Physics Chapter 4 Moving Charges and Magnetism Case Study Question 1: Moving coil galvanometer operates on Permanent Magnet Moving Coll (PMMC) mechanism and was designed by the scientist Darsonval. Moving coil galvanometers are of two types(i) Suspended coll(ii) Pivoted coil type or tangent galvanometer, Its working is based on … Continue reading Case Study ...
Class 12 Physics Case Study Questions Chapter 4 Moving Charges and
Here, we have provided case-based/passage-based questions for Class 12 Physics Chapter 4 Moving Charges and Magnetism. Case Study/Passage-Based Questions. Case Study 1: A charged particle moving in a magnetic field experiences a force that is proportional to the strength of the magnetic field, the component of the velocity that is perpendicular ...
Case Study Chapter 4 Moving Charges and Magnetism Class 12 Physics
To increase the current sensitivity of a moving coil galvanometer, we should decrease. (a) strength of magnet. (b) torsional constant of spring. (c) number of turns in coil. (d) area of coil. Answer. Please refer to below Case Study Chapter 4 Moving Charges and Magnetism Class 12 Physics. These Case Study Questions Class 12 Physics will be ...
Class 12 Physics Chapter 4 Case Study Question Moving Charges and
In Class 12 Boards there will be Case studies and Passage Based Questions will be asked, So practice these types of questions. Study Rate is always there to help you. Free PDF Download of CBSE Class 12 Physics Chapter 4 Moving Charges and Magnetism Case Study and Passage Based Questions with Answers were Prepared Based on Latest Exam Pattern.
Case Study on Moving Charges And Magnetism Class 12 Physics PDF
The PDF file of the Moving Charges And Magnetism Case Study for Class 12 Physics with Solutions is a very important study resource that can help students better prepare for the exam and boost conceptual learning. The solutions are in the hint manner as well as contain full examples too, refer to the link to access the Case Study on Moving ...
NCERT Solutions Class 12 Physics Chapter 4 Moving Charges and Magnetism
NCERT Solutions for Class 12 Physics Chapter 4 - Free PDF Download. The NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges and Magnetism is given here for the benefit of CBSE Class 12 Science students. In Chapter 4, NCERT Solutions for Class 12 Physics, students will learn the concepts of Moving Charges and Magnetism.Also, this chapter covered several topics with significant marks ...
CBSE Class 12 Physics
Chapter-4: Moving Charges and Magnetism of NCERT class 12 Physics note is available here. Moving Charges and Magnetism is one of the important chapters of CBSE class 12 Physics. So, students must prepare this chapter thoroughly. The notes provided here will be very helpful for the students who are going to appear in CBSE class 12 Physics board ...
NCERT Solutions for Class 12 Physics Chapter 4
The smallest value of M is called the Bohr magneton MB and it is MB = 9.27×10-24 J/T. Access NCERT Solutions for Class 12 Physics Chapter 4 - Moving Charges and Magnetism. 1. A Circular Coil of Wire Consisting of $100$ Turns, Each of Radius $8.0cm$ Carries a Current of $0.40A$.
NCERT Solutions for Class 12 Physics Chapter 4 Moving Charges ...
The solutions of NCERT Class 12 Physics Chapter 4 Moving Charges and Magnetism cover problems based on these two basic concepts. Class 12 chapter 4 physics ncert solutions will help you to boost the concepts studied in this chapter of the NCERT syllabus. Apply to Aakash iACST Scholarship Test 2024.
CBSE Class 12 Physics Case Study Questions PDF Download
Chapter-wise Solved Case Study Questions for Class 12 Physics. Chapter 1 Electric Charges and Fields. Chapter 2 Electrostatic Potential and Capacitance. Chapter 3 Current Electricity. Chapter 4 Moving Charges and Magnetism. Chapter 5 Magnetism and Matter. Chapter 6 Electromagnetic Induction. Chapter 7 Alternating Current.
Class 12 Physics Chapter 4 Notes
Chapter 4 - Moving charges and magnetism, is from the class 12 textbook of physics. In this chapter, the students will learn how the magnetic field exerts forces on moving charged particles, like electrons, protons, and some wires carrying current. Moreover, various topics will be covered in moving charges and magnetism class 12 notes which ...
NCERT Exemplar for Class 12 Physics Chapter-4 (Book Solutions)
The topics that are covered in the Class 12 Physics Chapter 4 moving charges and magnetism can be provided as follows: Magnetic force. Source and fields. Magnetic field and lorentz force. Motion in a magnetic field. Magnetic force on a current carrying conductor. Motion in a combined electric and magnetic fields.
Moving Charges and Magnetism Class 12 Notes CBSE Physics Chapter 4
PDF Summary - Class 12 Physics Moving Charges and Magnetism Notes (Chapter 4) 1. Force on a moving charge: The source of the magnetic field is a moving charge. Suppose a positive charge q is in motion in a uniform magnetic field →B with velocity →v . n. ∴ F α qBvsin θ ⇒ F=kqBvsin θ [k = constant]
Important Questions for Class 12 Physics Chapter 4
Important Questions for Class 12 Physics Chapter 4 - Moving Charges and Magnetism. Magnetism is a physical characteristic caused by magnetic fields that produce attractive and repulsive effects on other objects. A magnetic field is generated by electric currents and magnetic moments of particles and influences other currents and magnetic moments.
CBSE Class 12 Physics Case Study Questions With Solutions
CBSE Class 12 Physics Case Study Download PDF. CBSE Class 12 Physics Case Study Questions will help students this year to score good marks. Because such types of problems are a bit easier compared to other types of questions. Also, Class 12th Physics is a bit complex so having case-based problems, assertion and reason and Multiple Choice ...
CBSE NCERT Solutions for CBSE Class 12 Physics
These NCERT solutions are designed as per the latest CBSE Class 12 syllabus. Class 12 Physics chapter 4 NCERT solutions contain answers to all the in-text questions at the end of the chapter. Embibe has over 300 practice questions for the sub-topics included in chapter 4 of Physics to help students achieve their desired results.
Physics Case Study for Class 12 (Download Free PDF)
Physics Case Study for Class 12: Here, you will get class 12 case study questions and answers for Physics pdf at free of cost. Along with you can also download Physics case study questions for class 12 chapter wise for getting higher marks in board exams.
CBSE Class 12 Physics Chapter 4
The set of important questions for CBSE Class 12 Physics Chapter 4 - Moving Charges and Magnetism for the academic year 2024-25 prove to be a valuable tool for students' exam preparation. These questions cover vital concepts such as magnetic fields, Ampere's law, and applications of moving charges in magnetic fields.
NCERT Solutions for Class 12 Physics Chapter 4 PDF Download
It is important for students to download the NCERT Solutions for Class 12 Physics Chapter 4 so that they can easily refer to the answers; steps to download are: Open the Selfstudys website. Click the navigation button and select NCERT Books & Solutions. A drop down menu will appear, select NCERT Solutions from the list.