homework 5 adding and subtracting fractions with unlike bases

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Adding Subtracting Fractions Worksheets

Welcome to our Adding Subtracting Fractions Worksheets page. Here you will find a wide range of 5th Grade Fraction Worksheets which will help your child to learn to add and subtract fractions with unlike denominators.

If you are looking for help, we also have a how-to add and subtract fractions video and links to our support pages about adding and subtracting fractions.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Quicklinks to...

• How to Add and Subtract Fractions support

Adding Subtracting Fractions Calculator

• All Adding Subtracting Fractions Worksheets
• Adding Subtracting Fractions Like Denominators
• Adding Subtracting Fractions Like Denominators Quiz
• Adding Subtracting Fractions Unlike Denominators
• Adding Subtracting Fractions Unlike Denominators Quiz
• More related Math resources

Adding Subtracting Fractions

How to add and subtract fractions.

Formula for adding two fractions

\[{a \over b} + {c \over d} = {ad + bc \over bd} \]

Formula for subtracting two fractions

\[{a \over b} - {c \over d} = {ad - bc \over bd} \]

Here you will find support pages about how to add and subtract fractions.

• How do you Add Fractions
• Steps to Subtract Fractions

Adding and Subtracting Fractions Video

This video clip shows you how to add and subtract fractions.

There are several different examples including adding and subtracting fractions with both like and unlike denominators, and also examples where one denominator is a multiple of the other.

If you want to use our Free Fraction Calculator to do the work for you then use the link below.

Our Fraction calculator will allow you to add or subtract fractions and show you the steps to work it out.

Otherwise, for more detailed support, keep reading!

• Free Fraction Calculator

Adding and Subtracting Fractions Worksheets

Here you will find a selection of Fraction worksheets designed to help your child understand how to add and subtract 2 fractions.

The sheets have been split into sections so that you can easily select the right one for your needs.

Within each section the sheets get gradually harder and bring in different skills such as simplifying.

Before your child tackles adding and subtracting fractions with unlike denominators, they should be confident with equivalent fractions.

Using these sheets will help your child to:

• add and subtract 2 fractions with the same denominator;
• add and subtract 2 fractions with different denominators;
• add and subtract improper fractions;
• apply their understanding of equivalent fractions;
• simplify fractions;
• convert an improper fraction to a mixed number.

Adding & Subtracting Fractions with Like Denominators Worksheets

Sheet 1: like denominators; no simplifying needed.

• Adding Subtracting Fractions Like Denominators 1
• PDF version

Sheet 2: like denominators; some simplifying of fractions needed.

• Adding Subtracting Fractions Like Denominators 2

Adding and Subtracting Improper Fractions (like denominators)

Sheet 1: like denominators; some simplifying but no converting needed.

• Adding and Subtracting Improper Fractions Like Denominators 1

Sheet 2: like denominators; simplifying and converting to mixed numbers needed.

• Adding and Subtracting Improper Fractions Like Denominators 2

Adding & Subtracting Fractions with Like Denominators Online Quiz

Our quizzes have been created using Google Forms.

At the end of the quiz, you will get the chance to see your results by clicking 'See Score'.

This will take you to a new webpage where your results will be shown. You can print a copy of your results from this page, either as a pdf or as a paper copy.

For incorrect responses, we have added some helpful learning points to explain which answer was correct and why.

We do not collect any personal data from our quizzes, except in the 'First Name' and 'Group/Class' fields which are both optional and only used for teachers to identify students within their educational setting.

We also collect the results from the quizzes which we use to help us to develop our resources and give us insight into future resources to create.

For more information on the information we collect, please take a look at our Privacy Policy

We would be grateful for any feedback on our quizzes, please let us know using our Contact Us link, or use the Facebook Comments form at the bottom of the page.

This quick quiz tests your understanding and skill at adding and subtracting fractions with like denominators.

Adding Subtracting Fractions with Unlike Denominators Worksheets

Sheet 1: easier denominators with one denominator a multiple of the other; no simplifying needed.

• Adding Subtracting Fractions Sheet 1

Sheet 2: easier denominators with one denominator a multiple of the other; some simplifying needed.

• Adding Subtracting Fractions Sheet 2

Sheet 3: harder denominators - supported; no simplifying needed.

• Adding Subtracting Fractions Sheet 3

Sheet 3: harder denominators; simplifying needed.

• Adding Subtracting Fractions Sheet 4

Adding and Subtracting Improper Fractions (unlike denominators)

Sheet 1: easy denominators - one denominator is a multiple of the other; simplifying and converting needed.

• Adding and Subtracting Improper Fractions 1

Sheet 2: harder denominators; simplifying and converting needed.

• Adding and Subtracting Improper Fractions 2

Sheet 3: harder denominators; simplifying and converting needed.

• Adding and Subtracting Improper Fractions 3

Adding & Subtracting Fractions with Unlike Denominators Quiz

This quick quiz tests your understanding and skill at adding and subtracting fractions with unlike denominators.

Fun Quiz Facts

• This quiz attempted a total of 738 times in the last academic year.
• The average (mean) score was 9.8 out of 15 marks.
• Can you beat the mean score?

More Recommended Math Resources

Take a look at some more of our resources similar to these.

Fractions Adding and Subtracting Generated Sheets

We have created a random generator for making your own adding and subtracting fractions worksheets.

You can change your fraction values, choose whether you want like or unlike denominators or change from proper to improper fractions.

• Fractions Adding and Subtracting Worksheets (randomly generated)
• Add Subtract Multiply Divide Fractions (Randomly Generated)

Separate Adding and Subtracting Fractions Worksheets

The sheets in this section will help you practice just adding fractions.

Some of the sheets also involve simplifying the fractions and converting the answers to mixed fractions.

• Adding Fractions Worksheets
• Adding Improper Fractions
• Subtracting Fractions Worksheets

Equivalent Fractions

Equivalent fractions are fractions which have the same value as each other.

We have a support page to help you understand all about equivalent fractions, and also some equivalent fractions worksheets.

• Finding Equivalent Fractions support page
• Equivalent Fractions Worksheets

Multiplying and Dividing Fractions

Here you will find a selection of Fraction Worksheets based on multiplying and dividing fractions.

• multiply and divide fractions by whole numbers and other fractions;
• multiply and divide mixed fractions.

All the printable fraction worksheets in this section support the Elementary Math benchmarks for 5th Grade.

• Multiplying Fractions Worksheets
• Multiplying Mixed Fractions
• How to Divide Fractions
• Dividing Fractions by whole numbers
• How to Divide Mixed Numbers
• Least Common Multiple Calculator

Our Least Common Multiple Calculator will find the lowest common multiple of 2 or more numbers.

It will tell you the best multiple to convert the denominators of the fractions you are adding or subtracting into.

There are also some worked examples.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to 5th Grade Math Worksheets

Return to Fraction Worksheets

Return from Adding Subtracting Fractions to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.5: Adding and Subtracting Fractions

• Last updated
• Save as PDF
• Page ID 22483

• David Arnold
• College of the Redwoods

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Paul and Tony order a pizza which has been cut into eight equal slices. Thus, each slice is 1/8 of the whole pizza. Paul eats two slices (shaded in light gray in Figure \(\PageIndex{1}\)), or 2/8 of the whole pizza. Tony eats three slices (shaded in light red (or a darker shade of gray in black-and-white printing) in Figure \(\PageIndex{1}\)), or 3/8 of the whole pizza.

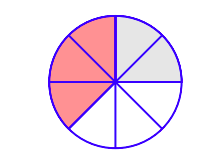
It should be clear that together Paul and Tony eat five slices, or 5/8 of the whole pizza. This reflects the fact that

\[ \frac{2}{8} + \frac{3}{8} = \frac{5}{8}.\nonumber \]

This demonstrates how to add two fractions with a common (same) denominator. Keep the common denominator and add the numerators. That is,

\[ \begin{align*} \frac{2}{8} + \frac{3}{8} &= \frac{2 + 3}{8} ~ && \textcolor{red}{ \text{ Keep denominator; add numerators.}} \\ &= \frac{5}{8} ~ && \textcolor{red}{ \text{ Simplify numerator.}} \end{align*} \]

Adding Fractions with Common Denominators

Let a/c and b/c be two fractions with a common (same) denominator. Their sum is defined as

\[ \frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\nonumber \]

That is, to add two fractions having common denominators, keep the common denominator and add their numerators.

A similar rule holds for subtraction.

Subtracting Fractions with Common Denominators

Let a/c and b/c be two fractions with a common (same) denominator. Their difference is defined as

\[ \frac{a}{c} - \frac{b}{c} = \frac{a-b}{c}.\nonumber \]

That is, to subtract two fractions having common denominators, keep the common denominator and subtract their numerators.

Example \(\PageIndex{1}\)

Find the sum of 4/9 and 3/9.

Keep the common denominator and add the numerators.

\[ \begin{aligned} \frac{4}{9} + \frac{3}{9} &= \frac{4+3}{9} ~ & \textcolor{red}{ \text{ Keep denominator; add numerators.}} \\ &= \frac{7}{9} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Exercise \(\PageIndex{1}\)

\[ \frac{1}{8} + \frac{2}{8}\nonumber \]

Example \(\PageIndex{2}\)

Subtract 5/16 from 13/16.

Keep the common denominator and subtract the numerators.

\[ \begin{aligned} \frac{13}{16} - \frac{5}{16} &= \frac{13-5}{16} ~ & \textcolor{red}{ \text{ Keep denominator; subtract numerators.}} \\ &=\frac{8}{16} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Of course, as we learned in Section 4.1, we should always reduce our final answer to lowest terms. One way to accomplish that in this case is to divide numerator and denominator by 8, the greatest common divisor of 8 and 16.

\[ \begin{aligned} = \frac{8 \div 8}{16 \div 8} ~ & \textcolor{red}{ \text{ Divide numerator and denominator by 8.}} \\ = \frac{1}{2} ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

Exercise \(\PageIndex{2}\)

\[ \frac{11}{12} - \frac{7}{12}\nonumber \]

Example \(\PageIndex{3}\)

\[ \frac{3}{x} - \left( - \frac{7}{x} \right) .\nonumber \]

Both fractions share a common denominator.

\[ \begin{aligned} \frac{3}{x} - \left( - \frac{7}{x} \right) &= \frac{3}{x} + \frac{7}{x} ~ & \textcolor{red}{ \text{ Add the opposite.}} \\ &= \frac{3+7}{x} ~ & \textcolor{red}{ \text{ Keep denominator, add numerators.}} \\ &= \frac{10}{x} ~ & \textcolor{red}{ \text{ Simplify.}} \end{aligned}\nonumber \]

Adding Fractions with Different Denominators

Consider the sum

\[ \frac{4}{9} + \frac{1}{6}.\nonumber \]

We cannot add these fractions because they do not have a common denominator. So, what to do?

In order to add two fractions with different denominators, we need to:

• Find a common denominator for the given fractions.
• Make fractions with the common denominator that are equivalent to the original fractions.

If we accomplish the two items in the “Goal,” we will be able to find the sum of the given fractions.

So, how to start? We need to find a common denominator, but not just any common denominator. Let’s agree that we want to keep the numbers as small as possible and find a least common denominator .

Definition: Least Common Denominator

The least common denominator (LCD) for a set of fractions is the smallest number divisible by each of the denominators of the given fractions.

Consider again the sum we wish to find:

\[ \frac{4}{9} + \frac{1}{6} .\nonumber \]

The denominators are 9 and 6. We wish to find a least common denominator, the smallest number that is divisible by both 9 and 6. A number of candidates come to mind: 36, 54, and 72 are all divisible by 9 and 6, to name a few. But the smallest number that is divisible by both 9 and 6 is 18. This is the least common denominator for 9 and 6.

We now proceed to the second item in “Goal.” We need to make fractions having 18 as a denominator that are equivalent to 4/9 and 1/6. In the case of 4/9, if we multiply both numerator and denominator by 2, we get

\[ \begin{aligned} \frac{4}{9} &= \frac{4 \cdot 2}{9 \cdot 2} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 2.}} \\ &= \frac{8}{18}. ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

In the case of 1/6, if we multiply both numerator and denominator by 3, we get

\[ \begin{aligned} \frac{1}{6} &= \frac{1 \cdot 3}{6 \cdot 3} ~ & \textcolor{red}{ \text{ Multiply numerator and denominator by 3.}} \\ &= \frac{3}{18}. ~ & \textcolor{red}{ \text{ Simplify numerator and denominator.}} \end{aligned}\nonumber \]

Typically, we’ll arrange our work as follows.

\[ \begin{aligned} \frac{4} + \frac{1}{6} &= \frac{4 \cdot \textcolor{red}{2}}{9 \cdot \textcolor{red}{2}} + \frac{1 \cdot \textcolor{red}{3}}{6 \cdot \textcolor{red}{3}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 18.}} \\ &= \frac{8}{18} + \frac{3}{18} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{8+3}{18} ~ & \textcolor{red}{ \text{ Keep common denominator; add numerators.}} \\ &= \frac{11}{18} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Let’s summarize the procedure.

Adding or Subtracting Fractions with Different Denominators

• Find the LCD, the smallest number divisible by all the denominators of the given fractions.
• Create fractions using the LCD as the denominator that are equivalent to the original fractions.
• Add or subtract the resulting equivalent fractions. Simplify, including reducing the final answer to lowest terms.

Example \(\PageIndex{4}\)

Simplify: \( \displaystyle \frac{3}{5} - \frac{2}{3}\).

The smallest number divisible by both 5 and 3 is 15.

\[ \begin{aligned} \frac{3}{5} - \frac{2}{3} &= \frac{3 \cdot \textcolor{red}{3}}{5 \cdot \textcolor{red}{3}} - \frac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 15.}} \\ &= \frac{9}{15} - \frac{10}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{9-10}{15} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ &= \frac{-1}{15} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Although this answer is perfectly acceptable, negative divided by positive gives us a negative answer, so we could also write

\[ = - \frac{1}{15}.\nonumber \]

Exercise \(\PageIndex{4}\)

\[ \frac{3}{4} - \frac{7}{5}\nonumber \]

Example \(\PageIndex{5}\)

Simplify: \(-\frac{1}{4} - \frac{5}{6}\).

The smallest number divisible by both 4 and 6 is 12.

\[ \begin{aligned} -\frac{1}{4} - \frac{5}{6} &= - \frac{1 \cdot \textcolor{red}{3}}{4 \cdot \textcolor{red}{3}} - \frac{5 \cdot \textcolor{red}{2}}{6 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD =12.}} \\ &= - \frac{3}{12} - \frac{10}{12} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ &= \frac{-3-10}{12} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ &= \frac{-13}{12} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Exercise \(\PageIndex{5}\)

Subtract: \(-\frac{3}{8} - \frac{1}{12}\)

Example \(\PageIndex{6}\)

Simplify: \(\frac{5}{x} + \frac{3}{4}\).

The smallest number divisible by both 4 and x is 4x.

\[ \begin{aligned} \frac{5}{x} + \frac{3}{4} = \frac{5 \cdot \textcolor{red}{4}}{x \cdot \textcolor{red}{4}} + \frac{3 \cdot \textcolor{red}{x}}{4 \cdot \textcolor{red}{x}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = }4x.} \\ = = \frac{20}{4x} + \frac{3x}{4x} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{20 + 3x}{4x} ~ & \textcolor{red}{ \text{ Keep LCD; add numerators.}} \end{aligned}\nonumber \]

Exercise \(\PageIndex{6}\)

\[ \frac{5}{z} + \frac{2}{3}\nonumber \]

\[ \frac{15+2z}{3z}\nonumber \]

Example \(\PageIndex{7}\)

Simplify: \(\frac{2}{3}- \frac{x}{5}\).

The smallest number divisible by both 3 and 5 is 15.

\[ \begin{aligned} \frac{2}{3} - \frac{x}{5} = \frac{2 \cdot \textcolor{red}{5}}{3 \cdot \textcolor{red}{5}} - \frac{x \cdot \textcolor{red}{3}}{5 \cdot \textcolor{red}{3}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 15.}} \\ = \frac{10}{15} - \frac{3x}{15} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{10 - 3x}{15} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \end{aligned}\nonumber \]

Least Common Multiple

First we define the multiple of a number.

Definition: Multiples

The multiples of a number d are 1 d , 2 d , 3 d , 4 d , etc. That is, the multiples of d are the numbers nd , where n is a natural number.

For example, the multiples of 8 are 1 · 8, 2 · 8, 3 · 8, 4 · 8, etc., or equivalently, 8, 16, 24, 32, etc.

Definition: Least Common Multiple

The least common multiple (LCM) of a set of numbers is the smallest number that is a multiple of each number of the given set. The procedure for finding an LCM follows:

• List all of the multiples of each number in the given set of numbers.
• List the multiples that are in common.
• Pick the least of the multiples that are in common.

Find the least common multiple (LCM) of 12 and 16.

List the multiples of 12 and 16.

Multiples of 12 : 12, 24, 36, 48, 60, 72, 84, 96,...

Multiples of 16 : 16, 32, 48, 64, 80, 96, 112,...

Pick the common multiples.

Common Multiples : 48, 96,...

The LCM is the least of the common multiples.

LCM(12,16) = 48

Exercise \(\PageIndex{7}\)

Find the least common denominator of 6 and 9.

Important Observation

The least common denominator is the least common multiple of the denominators.

For example, suppose your problem is 5/12 + 5/16. The LCD is the smallest number divisible by both 12 and 16. That number is 48, which is also the LCM of 12 and 16. Therefore, the procedure for finding the LCM can also be used to find the LCD.

Least Common Multiple Using Prime Factorization

You can also find the LCM using prime factorization.

LCM By Prime Factorization

To find an LCM for a set of numbers, follow this procedure:

• Write down the prime factorization for each number in compact form using exponents.
• The LCM is found by writing down every factor that appears in step 1 to the highest power of that factor that appears.

Example \(\PageIndex{8}\)

Use prime factorization to find the least common multiple find the least common denominator of 18 and 24. (LCM) of 12 and 16.

Prime factor 12 and 16.

\[ \begin{aligned} 12 = 2 \cdot 2 \cdot 3 \\ 16 = 2 \cdot 2 \cdot 2 \cdot 2 \end{aligned}\nonumber \]

Write the prime factorizations in compact form using exponents.

\[ \begin{aligned} 12 = 2^2 \cdot 3^1 \\ 16 = 2^4 \end{aligned}\nonumber \]

To find the LCM, write down each factor that appears to the highest power of that factor that appears. The factors that appear are 2 and 3. The highest power of 2 that appears is 2 4 . The highest power of 3 that appears is 3 1 .

\[ \begin{aligned} \text{LCM} = 2^4 \cdot 3^1 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \end{aligned}\nonumber \]

Now we expand this last expression to get our LCM.

\[ \begin{aligned} = 16 \cdot 3 ~ & \textcolor{red}{ \text{ Expand: } 2^4 = 16 \text{ and } 3^1 = 3.} \\ = 48. ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Note that this answer is identical to the LCM found in Example 8 that was found by listing multiples and choosing the smallest multiple in common.

Exercise \(\PageIndex{8}\)

Use prime factorization to find the least common denominator of 18 and 24.

Example \(\PageIndex{10}\)

Simplify: \(\frac{5}{28} + \frac{11}{42}\).

Prime factor the denominators in compact form using exponents.

28 = 2 · 2 · 7=2 2 · 7

42 = 2 · 3 · 7=2 1 · 3 1 · 7 1

To find the LCD, write down each factor that appears to the highest power of that factor that appears. The factors that appear are 2, 3, and 7. The highest power of 2 that appears is 2 2 . The highest power of 3 that appears is 3 1 . The highest power of 7 that appears is 7 1 .

\[ \begin{aligned} \text{LCM} = 2^2 \cdot 3^1 \cdot 7^1 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \\ = 4 \cdot 3 \cdot 7 ~ & \textcolor{red}{ \text{ Expand: } 2^2 = 4, ~ 3^1 = 3, ~ 7^1 = 7.} \\ = 84 ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Create equivalent fractions with the new LCD, then add.

\[ \begin{aligned} \frac{5}{28} + \frac{11}{42} = \frac{5 \cdot \textcolor{red}{3}}{28 \cdot \textcolor{red}{3}} + \frac{11 \cdot \textcolor{red}{2}}{42 \cdot \textcolor{red}{2}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 84.}} \\ = \frac{15}{84} + \frac{22}{84} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{37}{84} ~ & \textcolor{red}{ \text{ Keep LCD; add numerators.}} \end{aligned}\nonumber \]

Exercise \(\PageIndex{10}\)

Simplify: \( \frac{5}{24} + \frac{5}{36}\)

Example \(\PageIndex{11}\)

Simplify: \(- \frac{11}{24} - \frac{1}{18}\).

24 = 2 · 2 · 2 · 3=2 3 · 3 1

18 = 2 · 3 · 3=2 1 · 3 2

To find the LCD, write down each factor that appears to the highest power of that factor that appears. The factors that appear are 2 and 3. The highest power of 2 that appears is 2 3 . The highest power of 3 that appears is 3 2 .

\[ \begin{aligned} \text{LCM} = 2^3 \cdot 3^2 ~ & \textcolor{red}{ \text{ Keep highest power of each factor.}} \\ = 8 \cdot 9 ~ & \textcolor{red}{ \text{ Expand: } 2^3 = 8 \text{ and } 3^2 = 9.} \\ = 72. ~ & \textcolor{red}{ \text{ Multiply.}} \end{aligned}\nonumber \]

Create equivalent fractions with the new LCD, then subtract.

\[ \begin{aligned} - \frac{11}{24} - \frac{1}{18} = - \frac{11 \cdot \textcolor{red}{3}}{24 \cdot \textcolor{red}{3}} - \frac{1 \cdot \textcolor{red}{4}}{18 \cdot \textcolor{red}{4}} ~ & \textcolor{red}{ \text{ Equivalent fractions with LCD = 72.}} \\ = - \frac{33}{72} - \frac{4}{72} ~ & \textcolor{red}{ \text{ Simplify numerators and denominators.}} \\ = \frac{-33-4}{72} ~ & \textcolor{red}{ \text{ Keep LCD; subtract numerators.}} \\ = \frac{-37}{72} ~ & \textcolor{red}{ \text{ Simplify numerator.}} \end{aligned}\nonumber \]

Of course, negative divided by positive yields a negative answer, so we can also write our answer in the form

\[ - \frac{11}{24} - \frac{1}{18} = - \frac{37}{72}.\nonumber \]

Exercise \(\PageIndex{11}\)

Simplify: \( - \frac{5}{24} - \frac{11}{36}\)

−37/72

Comparing Fractions

The simplest way to compare fractions is to create equivalent fractions.

Example \(\PageIndex{12}\)

Arrange the fractions −1/2 and −4/5 on a number line, then compare them by using the appropriate inequality symbol.

The least common denominator for 2 and 5 is the number 10. First, make equivalent fractions with a LCD equal to 10.

\[ \begin{array}{c} - \frac{1}{2} = - \frac{1 \cdot \textcolor{red}{5}}{2 \cdot \textcolor{red}{5}} = - \frac{5}{10} \\ - \frac{4}{5} = - \frac{4 \cdot \textcolor{red}{2}}{5 \cdot \textcolor{red}{2}} = - \frac{8}{10} \end{array}\nonumber \]

To plot tenths, subdivide the interval between −1 and 0 into ten equal increments.

Because −4/5 lies to the left of −1/2, we have that −4/5 is less than −1/2, so we write

\[ - \frac{4}{5} < - \frac{1}{2}.\nonumber \]

Exercise \(\PageIndex{12}\)

Compare −3/8 and −1/2.

\[ - \frac{1}{2} < - \frac{3}{8}\nonumber \]

In Exercises 1-10, list the multiples the given numbers, then list the common multiples. Select the LCM from the list of common multiples.

1. 9 and 15

2. 15 and 20

3. 20 and 8

4. 15 and 6

5. 16 and 20

6. 6 and 10

7. 20 and 12

8. 12 and 8

9. 10 and 6

10. 10 and 12

In Exercises 11-20, for the given numbers, calculate the LCM using prime factorization.

11. 54 and 12

12. 108 and 24

13. 18 and 24

14. 36 and 54

15. 72 and 108

16. 108 and 72

17. 36 and 24

18. 18 and 12

19. 12 and 18

20. 12 and 54

In Exercises 21-32, add or subtract the fractions, as indicated, and simplify your result.

21. \(\frac{7}{12} − \frac{1}{12}\)

22. \(\frac{3}{7} − \frac{5}{7}\)

23. \(\frac{1}{9} + \frac{1}{9}\)

24. \(\frac{1}{7} + \frac{3}{7}\)

25. \(\frac{1}{5} − \frac{4}{5}\)

26. \(\frac{3}{5} − \frac{2}{5}\)

27. \(\frac{3}{7} − \frac{4}{7}\)

28. \(\frac{6}{7} − \frac{2}{7}\)

29. \(\frac{4}{11} + \frac{9}{11}\)

30. \(\frac{10}{11} + \frac{4}{11}\)

31. \(\frac{3}{11} + \frac{4}{11}\)

32. \(\frac{3}{7} + \frac{2}{7}\)

In Exercises 33-56, add or subtract the fractions, as indicated, and simplify your result.

33. \(\frac{1}{6} − \frac{1}{8}\)

34. \(\frac{7}{9} − \frac{2}{3}\)

35. \(\frac{1}{5} + \frac{2}{3}\)

36. \(\frac{7}{9} + \frac{2}{3}\)

37. \(\frac{2}{3} + \frac{5}{8}\)

38. \(\frac{3}{7} + \frac{5}{9}\)

39. \(\frac{4}{7} − \frac{5}{9}\)

40. \(\frac{3}{5} − \frac{7}{8}\)

41. \(\frac{2}{3} − \frac{3}{8}\)

42. \(\frac{2}{5} − \frac{1}{8\)

43. \(\frac{6}{7} − \frac{1}{6}\)

44. \(\frac{1}{2} − \frac{1}{4}\)

45. \(\frac{1}{6} + \frac{2}{3}\)

46. \(\frac{4}{9} + \frac{7}{8}\)

47. \(\frac{7}{9} + \frac{1}{8}\)

48. \(\frac{1}{6} + \frac{1}{7}\)

49. \(\frac{1}{3} + \frac{1}{7}\)

50. \(\frac{5}{6} + \frac{1}{4}\)

51. \(\frac{1}{2} − \frac{2}{7}\)

52. \(\frac{1}{3} − \frac{1}{8}\)

53. \(\frac{5}{6} − \frac{4}{5}\)

54. \(\frac{1}{2} − \frac{1}{9}\)

55. \(\frac{1}{3} + \frac{1}{8}\)

56. \(\frac{1}{6} + \frac{7}{9}\)

In Exercises 57-68, add or subtract the fractions, as indicated, by first using prime factorization to find the least common denominator.

57. \(\frac{7}{36} + \frac{11}{54}\)

58. \(\frac{7}{54} + \frac{7}{24}\)

59. \(\frac{7}{18} − \frac{5}{12}\)

60. \(\frac{5}{54} − \frac{7}{12}\)

61. \(\frac{7}{36} + \frac{7}{54}\)

62. \(\frac{5}{72} + \frac{5}{108}\)

63. \(\frac{7}{24} − \frac{5}{36}\)

64. \(\frac{11}{54} + \frac{7}{72}\)

65. \(\frac{11}{12} + \frac{5}{18}\)

66. \(\frac{11}{24} + \frac{11}{108}\)

67. \(\frac{11}{54} − \frac{5}{24}\)

68. \(\frac{7}{54} − \frac{5}{24}\)

In Exercises 69-80, add or subtract the fractions, as indicated, and simplify your result.

69. \(\frac{−3}{7} + \left( \frac{−3}{7} \right)\)

70. \(\frac{−5}{9} + \left( \frac{−1}{9} \right)\)

71. \(\frac{7}{9} − \left( \frac{−1}{9} \right) \)

72. \(\frac{8}{9} − \left( \frac{−4}{9} \right)\)

73. \(\frac{7}{9} + \left( \frac{−2}{9} \right)\)

74. \( \frac{2}{3} + \left( \frac{−1}{3} \right)\)

75. \(\frac{−3}{5} − \frac{4}{5}\)

76. \(\frac{−7}{9} − \frac{1}{9}\)

77. \(\frac{−7}{8} + \frac{1}{8}\)

78. \(\frac{−2}{3} + \(\frac{1}{3}\)

79. \(\frac{−1}{3} − \left( \frac{−2}{3} \right)\)

80. \(\frac{−7}{8} − \left( \frac{−5}{8} \right)\)

In Exercises 81-104, add or subtract the fractions, as indicated, and simplify your result.

81. \(\frac{−2}{7}\) + \frac{4}{5}\)

82. \(\frac{−1}{4} + \frac{2}{7}\)

83. \(\frac{−1}{4} − \left( \frac{−4}{9} \right)\)

84. \(\frac{−3}{4} −left( \frac{−1}{8} \right)\)

85. \(\frac{−2}{7} + \frac{3}{4}\)

86. \(\frac{−1}{3} + \frac{5}{8}\)

87. \(\frac{−4}{9} − \frac{1}{3}\)

88. \(\frac{−5}{6} − \frac{1}{3}\)

89. \(\frac{−5}{7} − \left( \frac{−1}{5} \right)\)

90. \(\frac{−6}{7} − \left( \frac{−1}{8} \right)\)

91. \(\frac{1}{9} + \left( \frac{−1}{3} \right)\)

92. \(\frac{1}{8} + \left( \frac{−1}{2} \right)\)

93. \(\frac{2}{3} + \left( \frac{−1}{9} \right)\)

94. \(\frac{3}{4} + \left( \frac{−2}{3} \right)\)

95. \(\frac{−1}{2} + \left( \frac{−6}{7} \right)\)

96. \(\frac{−4}{5} + \left( \frac{−1}{2} \right)\)

97. \(\frac{−1}{2} + \left( \frac{−3}{4} \right)\)

98. \(\frac{−3}{5} + \left( \frac{−1}{2} \right)\)

99. \(\frac{−1}{4} − \frac{1}{2}\)

100. \(\frac{−8}{9} − \frac{2}{3}\)

101. \(\frac{5}{8} − \left( \frac{−3}{4} \right)\)

102. \(\frac{3}{4} − \left( \frac{−3}{8} \right)\)

103. \(\frac{1}{8} − \left( \frac{−1}{3} \right)\)

104. \(\frac{1}{2} − \left( \frac{−4}{9} \right)\)

In Exercises 105-120, add or subtract the fractions, as indicated, and write your answer is lowest terms.

105. \(\frac{1}{2} + \frac{3q}{5}\)

106. \(\frac{4}{7} − \frac{b}{3}\)

107. \(\frac{4}{9} − \frac{3a}{4}\)

108. \(\frac{4}{9} − \frac{b}{2}\)

109. \(\frac{2}{s} + \frac{1}{3}\)

110. \(\frac{2}{s} + \frac{3}{7}\)

111. \(\frac{1}{3} − \frac{7}{b}\)

112. \(\frac{1}{2} − \frac{9}{s}\)

113. \(\frac{4b}{7} + \frac{2}{3}\)

114. \(\frac{2a}{5} + \frac{5}{8}\)

115. \(\frac{2}{3} − \frac{9}{t}\)

116. \(\frac{4}{7} − \frac{1}{y}\)

117. \(\frac{9}{s} + \frac{7}{8}\)

118. \(\frac{6}{t} − \frac{1}{9}\)

119. \(\frac{7b}{8} − \frac{5}{9}\)

120. \(\frac{3p}{4} − \frac{1}{8}\)

In Exercises 121-132, determine which of the two given statements is true.

121. \(\frac{−2}{3} < \frac{−8}{7}\) or \(\frac{− 2}{3} > \frac{−8}{7}\)

122. \(\frac{−1}{7} < \frac{−8}{9}\) or \(\frac{− 1}{7} > \frac{−8}{9}\)

123. \(\frac{6}{7} < \frac{7}{3}\) or \(\frac{6}{7} > \frac{7}{3}\)

124. \(\frac{1}{2} < \frac{2}{7}\) or \(\frac{1}{2} > \frac{2}{7}\)

125. \(\frac{−9}{4} < \frac{−2}{3}\) or \frac{− 9}{4} > \frac{−2}{3}\)

126. \(\frac{−3}{7} < \frac{−9}{2}\) or \(\frac{− 3}{7} > \frac{−9}{2}\)

127. \(\frac{5}{7} < \frac{5}{9}\) or \frac{5}{7} > \frac{5}{9}\)

128. \(\frac{1}{2} < \frac{1}{3}\) or \(\frac{1}{2} > \frac{1}{3}\)

129. \(\frac{−7}{2} < \frac{−1}{5}\) or \(\frac{− 7}{2} > \frac{−1}{5}\)

130. \(\frac{−3}{4} < \frac{−5}{9}\) or \(\frac{− 3}{4} > \frac{−5}{9}\)

131. \(\frac{5}{9} < \frac{6}{5}\) or \(\frac{5}{9} > \frac{6}{5}\)

132. \(\frac{3}{2} < \frac{7}{9}\) or \(\frac{3}{2} > \frac{7}{9}\)

21. \(\frac{1}{2}\)

23. \(\frac{2}{9}\)

25. \(\frac{−3}{5}\)

27. \(\frac{−1}{7}\)

29. \(\frac{13}{11}\)

31. \(\frac{7}{11}\)

33. \(\frac{1}{24}\)

35. \(\frac{13}{15}\)

37. \(\frac{31}{24}\)

39. \(\frac{1}{63}\)

41. \(\frac{7}{24}\)

43. \(\frac{29}{42}\)

45. \(\frac{5}{6}\)

47. \(\frac{65}{72}\)

49. \(\frac{10}{21}\)

51. \(\frac{3}{14}\)

53. \(\frac{1}{30}\)

55. \(\frac{11}{24}\)

57. \(\frac{43}{108}\)

59. \(\frac{−1}{36}\)

61. \(\frac{35}{108}\)

63. \(\frac{11}{72}\)

65. \(\frac{43}{36}\)

67. \(\frac{−1}{216}\)

69. \(\frac{−6}{7}\)

71. \(\frac{8}{9}\)

73. \(\frac{5}{9}\)

75. \(\frac{− 7}{5}\)

77. \(\frac{− 3}{4}\)

79. \(\frac{1}{3}\)

81. \(\frac{18}{35}\)

83. \(\frac{7}{36}\)

85. \(\frac{13}{28}\)

87. \(\frac{− 7}{9}\)

89. \(\frac{−18}{35}\)

91. \(\frac{− 2}{9}\)

93. \(\frac{5}{9}\)

95. \(\frac{−19}{14}\)

97. \(\frac{− 5}{4}\)

99. \(\frac{− 3}{4}\)

101. \(\frac{11}{8}\)

103. \(\frac{11}{24}\)

105. \(\frac{5+6 q}{10}\)

107. \(\frac{16 − 27 a}{36}\)

109. \(\frac{6 + s}{3 s}\)

111. \(\frac{b − 21}{3b}\)

113. \(\frac{12 b + 14}{21}\)

115. \(\frac{2 t − 27}{3t}\)

117. \(\frac{72 + 7 s}{8 s}\)

119. \(\frac{63 b − 40}{72}\)

121. \(\frac{− 2}{3} > \(\frac{− 8}{7}\)

123. \(\frac{6}{7} < \frac{7}{3}\)

125. \(\frac{− 9}{4} < \frac{− 2}{3}\)

127. \(\frac{5}{7} > \frac{5}{9}\)

129. \(\frac{− 7}{2 } < \frac{− 1}{5}\)

131. \(\frac{5}{9} < \frac{6}{5}\)

• → Resources
• → 6th Grade
• → Fractions

Add and Subtract Fractions with Unlike Denominators Lesson Plan

Get the lesson materials.

Add and Subtract Fractions with Unlike Denominators Guided Notes with Doodles

Ever wondered how to teach adding and subtracting fractions with unlike denominators in an engaging way to your 5th or 6th-grade students?

In this lesson plan, students will learn about fraction addition and subtraction and their real-life applications. Through artistic, interactive guided notes, check for understanding, a practice activity that includes a doodle & color by number worksheet, and a maze worksheet, students will gain a comprehensive understanding of adding and subtracting fractions with unlike denominators.

The lesson culminates with a real-life example that explores how this math skill can be applied in practical situations. Students will read and write about real-life uses of adding and subtracting fractions.

• Standards : CCSS 5.NF.A.1 , CCSS 5.NF.A.2
• Topic : Fractions
• Grade : 6th Grade
• Type : Lesson Plans

Learning Objectives

After this lesson, students will be able to:

Add and subtract fractions with unlike denominators

Use visual aids and doodles to enhance understanding of fraction addition and subtraction

Explain real life applications of fractions in real life

Prerequisites

Before this lesson, students should be familiar with:

Basic addition and subtraction skills of whole numbers

Understand how to generate equivalent fractions

Knowledge of how to find common multiples and factors

Colored pencils or markers

Add and Subtract Fractions with Unlike Denominators Guided Notes

Key Vocabulary

Unlike Denominators

Common Denominator

Visual Models

Introduction

As a hook, ask students why it is important to know how to add and subtract fractions with unlike denominators in real-life situations.

Use the first page of the guided notes to introduce the concept of adding and subtracting fractions with unlike denominators. Walk through the steps of finding a common denominator, adding or subtracting the numerators, and simplifying the fraction. Emphasize the importance of finding a common denominator to make the fractions compatible.

Use the second page of the guided notes to introduce how to use visual models to solve fractions addition and subtracting with unlike denominators. Walk through the steps of finding a common denominator, subtracting the numerators, and simplifying the fraction.

Based on student responses, reteach concepts that students need extra help with. If your class has a wide range of proficiency levels, you can pull out students for reteaching, and have more advanced students begin work on the practice exercises.

Have students practice adding and subtracting fractions with unlike denominators using the practice worksheet provided in the resource in the first two pages of the guided notes. Walk around the classroom to answer any questions students may have.

Fast finishers can continue practicing with the maze activities (page 3) or color by number (page 4) included in the resource. You can assign these activities as extra practice or as homework for the remainder of the class.

Real-Life Application

Use the last page of the guided notes to bring the class back together, and introduce the concept of real-life application of adding and subtracting fractions with unlike denominators. Explain to the students that understanding how to add and subtract fractions is important in many real-life situations.

Some examples of real-life applications of adding and subtracting fractions include:

Recipes: Fractions are commonly used in cooking and baking. When following a recipe, you often have to adjust the measurements based on the number of servings or the size of the dish. Adding or subtracting fractions allows you to adjust the quantities of ingredients accordingly.

Measurements: Fractions are also used in various measurements, such as measuring ingredients for a recipe or calculating distances. For example, if you want to measure a distance that is less than a whole unit, you may need to add or subtract fractions to get an accurate measurement.

Discuss these examples with the students and encourage them to brainstorm other situations where adding and subtracting fractions might be useful in their daily lives. This discussion will help them see the relevance and practical application of the skills they are learning.

Additional Self-Checking Digital Practice

If you’re looking for digital practice for adding and subtracting fractions with unlike denominators, try my Pixel Art activities in Google Sheets. Every answer is automatically checked, and correct answers unlock parts of a mystery picture. It’s incredibly fun, and a powerful tool for differentiation.

Here are some activities to explore:

Adding Fractions with Unlike Denominators Pixel Art

Subtracting Fractions with Unlike Denominators Pixel Art

Fractions Operations Pixel Art

Additional Print Practice

A fun, no-prep way to practice adding and subtracting fractions with unlike denominators is Doodle Math — they’re a fresh take on color by number or color by code. It includes multiple levels of practice, perfect for a review day or sub plan.

Here are some activities to try:

Adding and Subtracting Unlike Fractions | Doodle Math: Twist on Color by Number

What are unlike denominators in fractions? Open

Unlike denominators are denominators that are different from each other in a fraction. In other words, when the numbers at the bottom of two or more fractions are not the same, they have unlike denominators.

Examples of unlike denominators:

1/3 and 1/4

2/5 and 3/8

5/6 and 7/9

How do I add fractions with unlike denominators? Open

To add fractions with unlike denominators, you need to find a common denominator. Once you have a common denominator, you can add the numerators together and keep the common denominator.

Steps to add fractions with unlike denominators:

Find a common denominator.

Rewrite each fraction with the common denominator.

Add the numerators together.

Write the sum over the common denominator.

How do I subtract fractions with unlike denominators? Open

Subtracting fractions with unlike denominators is similar to adding fractions with unlike denominators. You need to find a common denominator first, and then subtract the numerators while keeping the common denominator.

Steps to subtract fractions with unlike denominators:

Subtract the numerators.

Write the difference over the common denominator.

What is a common denominator? Open

A common denominator is a number that is divisible by all the denominators in a set of fractions. It is used to make the fractions have the same denominator so that they can be added or subtracted easily.

Example of finding a common denominator: Let's say we have the fractions 1/2 and 3/4. The common denominator for these fractions is 4 because it is divisible by both 2 and 4.

How do I find the common denominator for fractions? Open

To find the common denominator for fractions, you can use the least common multiple (LCM) of the denominators. The LCM is the smallest multiple that both denominators have in common.

Steps to find the common denominator for fractions:

Find the least common multiple (LCM) of the denominators.

Use the LCM as the common denominator for the fractions.

Can fractions with unlike denominators be simplified? Open

Yes, fractions with unlike denominators can be simplified. However, simplifying fractions is not necessary when adding or subtracting fractions with unlike denominators. Simplifying is done to express the fraction in its simplest form.

Example of simplifying a fraction: Let's say we have the fraction 4/8. It can be simplified by dividing both the numerator and denominator by their greatest common factor (GCF), which in this case is 4. So, 4/8 simplifies to 1/2.

How can I practice adding and subtracting fractions with unlike denominators? Open

You can practice adding and subtracting fractions with unlike denominators by using worksheets, online math activities, or interactive games. These resources provide practice problems and allow you to check your answers.

Available resources for practicing adding and subtracting fractions with unlike denominators:

Online math games

Interactive websites

Are there any real-life applications for adding and subtracting fractions with unlike denominators? Open

Yes, there are many real-life applications for adding and subtracting fractions with unlike denominators. Some examples include:

Calculating ingredients in a recipe

Determining discount percentages during shopping

Estimating time and distances in travel

Calculating portions and servings in food preparation

Adding and subtracting fractions with unlike denominators is a valuable skill that can help in various real-life situations where fractions are involved.

Want more ideas and freebies?

Get my free resource library with digital & print activities—plus tips over email.

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

• Fractions: add / subtract
• Unlike mixed numbers

Download & Print Only $4.10

Adding mixed numbers

Unlike denominators.

In these fractions worksheets, students add mixed numbers where the fractional parts of the numbers have different denominators. 

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

More fractions worksheets

Explore all of our fractions worksheets , from dividing shapes into "equal parts" to multiplying and dividing improper fractions and mixed numbers.

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

• Forgot Password?

Adding or Subtracting 2 Fractions Calculator for Like or Unlike Denominators

This calculator will add one fraction to another, or subtract one fraction from another -- regardless of whether or not the two fractions have the same or different denominators -- and give the result in simplest form.

Plus, unlike other online fraction calculators, this calculator will show its work and give a detailed step-by-step explanation as to how it arrived at the answer.

Also, be sure to check out my other online math calculators for help with fractions:

• Multiplying

Also on this page:

• How do you add fractions with same denominators?
• How do you add fractions with different denominators?
• What are the steps to subtract fractions?

Add or Subtract 2 Fractions Calculator

Add or subtract 2 fractions with like or unlike denominators.

Selected Data Record:

A Data Record is a set of calculator entries that are stored in your web browser's Local Storage. If a Data Record is currently selected in the "Data" tab, this line will list the name you gave to that data record. If no data record is selected, or you have no entries stored for this calculator, the line will display "None".

Addend/Subtrahend:

Enter the numerator and denominator for the Addend (addition) or Subtrahend (subtraction) for the second fraction in the equation. If you would like the fraction to be a whole number, simply enter the desired whole number in the numerator field and enter a 1 in the denominator field (4/1 = 4).

This is the result of the addition or subtraction of the two fractions. After calculating the addition or subtraction, the calculator will show its work and give a detailed explanation of each step it took to arrive at this answer.

If you would like to save the current entries to the secure online database, tap or click on the Data tab, select "New Data Record", give the data record a name, then tap or click the Save button. To save changes to previously saved entries, simply tap the Save button. Please select and "Clear" any data records you no longer need.

Related Calculators

Help and tools, how to add and subtract fractions., how do you add fractions.

The answer to that question depends on whether you are adding fractions with like denominators or adding fractions with unlike denominators.

Adding Fractions with Like Denominators

Adding fractions with like denominators is easy. All you do is add the numerators together and keep the denominator the same, like this:

Adding Fractions with Unlike Denominators

Adding fractions with unlike denominators requires a little more work (unless you use the calculator on this page), because in order to add the fractions you must first turn their unlike denominators into like denominators. You do that by finding the lowest common multiple (LCM) of the denominators.

To illustrate how you use LCM to turn unlike denominators into like denominators, let's suppose you want to add the fraction 1/3 to the fraction 2/5.

The first step is to find the lowest number that both 3 and 5 will divide into evenly (the LCM). According to my calculations, the LCM of the two denominators (3 & 5) is 15.

Once we have found the LCM for the two denominators, the next step is to multiply the top and bottom of each fraction by the number of times each fraction's denominator goes into the LCM.

Since 3 goes into 15 a total of 5 times, you would multiply the top and bottom of 1/3 by 5, which results in 5/15.

Next, since 5 goes into 15 a total of 3 times, you would multiply the top and bottom of 2/5 by 3, which results in 6/15.

Finally, since both denominators are now the same, you simply add the numerators (5 + 6) while keeping the denominator (15) the same -- giving you a result of 11/15. Here is how our example of adding fractions with unlike denominators might appear on paper:

What About the Steps to Subtract Fractions?

The steps to subtract fractions are the same as the steps to add fractions.

If you are subtracting fractions with like denominators, you simply subtract the second numerator from the first numerator and keep the denominator the same.

If you are subtracting fractions with unlike denominators, you go through the same process as when adding fractions with unlike denominators.

So for like denominators you simply add or subtract the numerators, and for unlike denominators you multiply the top and bottom by the least common multiple of each denominator, and then add or subtract the numerators.

Happy adding and subtracting!

Adjust Calculator Width:

Move the slider to left and right to adjust the calculator width. Note that the Help and Tools panel will be hidden when the calculator is too wide to fit both on the screen. Moving the slider to the left will bring the instructions and tools panel back into view.

Also note that some calculators will reformat to accommodate the screen size as you make the calculator wider or narrower. If the calculator is narrow, columns of entry rows will be converted to a vertical entry form, whereas a wider calculator will display columns of entry rows, and the entry fields will be smaller in size ... since they will not need to be "thumb friendly".

Show/Hide Popup Keypads:

Select Show or Hide to show or hide the popup keypad icons located next to numeric entry fields. These are generally only needed for mobile devices that don't have decimal points in their numeric keypads. So if you are on a desktop, you may find the calculator to be more user-friendly and less cluttered without them.

Stick/Unstick Tools:

Select Stick or Unstick to stick or unstick the help and tools panel. Selecting "Stick" will keep the panel in view while scrolling the calculator vertically. If you find that annoying, select "Unstick" to keep the panel in a stationary position.

If the tools panel becomes "Unstuck" on its own, try clicking "Unstick" and then "Stick" to re-stick the panel.

8.4 Add and Subtract Rational Expressions with Unlike Denominators

Learning objectives.

By the end of this section, you will be able to:

• Find the least common denominator of rational expressions
• Find equivalent rational expressions
• Add rational expressions with different denominators
• Subtract rational expressions with different denominators

Be Prepared 8.4

Before you get started, take this readiness quiz.

If you miss a problem, go back to the section listed and review the material.

• Add: 7 10 + 8 15 . 7 10 + 8 15 . If you missed this problem, review Example 1.81 .
• Subtract: 6 ( 2 x + 1 ) − 4 ( x − 5 ) . 6 ( 2 x + 1 ) − 4 ( x − 5 ) . If you missed this problem, review Example 1.139 .
• Find the Greatest Common Factor of 9 x 2 y 3 9 x 2 y 3 and 12 x y 5 12 x y 5 . If you missed this problem, review Example 7.3 .
• Factor completely −48 n − 12 −48 n − 12 . If you missed this problem, review Example 7.11 .

Find the Least Common Denominator of Rational Expressions

When we add or subtract rational expressions with unlike denominators we will need to get common denominators. If we review the procedure we used with numerical fractions, we will know what to do with rational expressions.

Let’s look at the example 7 12 + 5 18 7 12 + 5 18 from Foundations . Since the denominators are not the same, the first step was to find the least common denominator (LCD). Remember, the LCD is the least common multiple of the denominators. It is the smallest number we can use as a common denominator.

To find the LCD of 12 and 18, we factored each number into primes, lining up any common primes in columns. Then we “brought down” one prime from each column. Finally, we multiplied the factors to find the LCD.

We do the same thing for rational expressions. However, we leave the LCD in factored form.

Find the least common denominator of rational expressions.

• Step 1. Factor each expression completely.
• Step 2. List the factors of each expression. Match factors vertically when possible.
• Step 3. Bring down the columns.
• Step 4. Multiply the factors.

Remember, we always exclude values that would make the denominator zero. What values of x should we exclude in this next example?

Example 8.38

Find the LCD for 8 x 2 − 2 x − 3 , 3 x x 2 + 4 x + 3 8 x 2 − 2 x − 3 , 3 x x 2 + 4 x + 3 .

Find the LCD for 8 x 2 − 2 x − 3 , 3 x x 2 + 4 x + 3 . Factor each expression completely, lining up common factors. Bring down the columns. x 2 − 2 x − 3 = ( x + 1 ) ( x − 2 ) x 2 + 4 x + 3 = ( x + 1 ) ( x + 3 ) LCD = ( x + 1 ) ( x − 2 ) ( x + 3 ) Multiply the factors. The LCD is ( x + 1 ) ( x − 3 ) ( x + 3 ) . Find the LCD for 8 x 2 − 2 x − 3 , 3 x x 2 + 4 x + 3 . Factor each expression completely, lining up common factors. Bring down the columns. x 2 − 2 x − 3 = ( x + 1 ) ( x − 2 ) x 2 + 4 x + 3 = ( x + 1 ) ( x + 3 ) LCD = ( x + 1 ) ( x − 2 ) ( x + 3 ) Multiply the factors. The LCD is ( x + 1 ) ( x − 3 ) ( x + 3 ) .

Try It 8.75

Find the LCD for 2 x 2 − x − 12 , 1 x 2 − 16 2 x 2 − x − 12 , 1 x 2 − 16 .

Try It 8.76

Find the LCD for x x 2 + 8 x + 15 , 5 x 2 + 9 x + 18 x x 2 + 8 x + 15 , 5 x 2 + 9 x + 18 .

Find Equivalent Rational Expressions

When we add numerical fractions, once we find the LCD, we rewrite each fraction as an equivalent fraction with the LCD.

We will do the same thing for rational expressions.

Example 8.39

Rewrite as equivalent rational expressions with denominator ( x + 1 ) ( x − 3 ) ( x + 3 ) ( x + 1 ) ( x − 3 ) ( x + 3 ) : 8 x 2 − 2 x − 3 , 3 x x 2 + 4 x + 3 . 8 x 2 − 2 x − 3 , 3 x x 2 + 4 x + 3 .

Try It 8.77

Rewrite as equivalent rational expressions with denominator ( x + 3 ) ( x − 4 ) ( x + 4 ) ( x + 3 ) ( x − 4 ) ( x + 4 ) : 2 x 2 − x − 12 , 1 x 2 − 16 . 2 x 2 − x − 12 , 1 x 2 − 16 .

Try It 8.78

Rewrite as equivalent rational expressions with denominator ( x + 3 ) ( x + 5 ) ( x + 6 ) ( x + 3 ) ( x + 5 ) ( x + 6 ) : x x 2 + 8 x + 15 , 5 x 2 + 9 x + 18 . x x 2 + 8 x + 15 , 5 x 2 + 9 x + 18 .

Add Rational Expressions with Different Denominators

Now we have all the steps we need to add rational expressions with different denominators. As we have done previously, we will do one example of adding numerical fractions first.

Example 8.40

Add: 7 12 + 5 18 . 7 12 + 5 18 .

Try It 8.79

Add: 11 30 + 7 12 . 11 30 + 7 12 .

Try It 8.80

Add: 3 8 + 9 20 . 3 8 + 9 20 .

Now we will add rational expressions whose denominators are monomials.

Example 8.41

Add: 5 12 x 2 y + 4 21 x y 2 . 5 12 x 2 y + 4 21 x y 2 .

Try It 8.81

Add: 2 15 a 2 b + 5 6 a b 2 . 2 15 a 2 b + 5 6 a b 2 .

Try It 8.82

Add: 5 16 c + 3 8 c d 2 . 5 16 c + 3 8 c d 2 .

Now we are ready to tackle polynomial denominators.

Example 8.42

How to add rational expressions with different denominators.

Add: 3 x − 3 + 2 x − 2 . 3 x − 3 + 2 x − 2 .

Try It 8.83

Add: 2 x − 2 + 5 x + 3 . 2 x − 2 + 5 x + 3 .

Try It 8.84

Add: 4 m + 3 + 3 m + 4 . 4 m + 3 + 3 m + 4 .

The steps to use to add rational expressions are summarized in the following procedure box.

Add rational expressions.

• Step 1. Determine if the expressions have a common denominator. Yes – go to step 2. No – Rewrite each rational expression with the LCD. Find the LCD. Rewrite each rational expression as an equivalent rational expression with the LCD.
• Step 2. Add the rational expressions.
• Step 3. Simplify, if possible.

Example 8.43

Add: 2 a 2 a b + b 2 + 3 a 4 a 2 − b 2 . 2 a 2 a b + b 2 + 3 a 4 a 2 − b 2 .

Try It 8.85

Add: 5 x x y − y 2 + 2 x x 2 + y 2 . 5 x x y − y 2 + 2 x x 2 + y 2 .

Try It 8.86

Add: 7 2 m + 6 + 4 m 2 + 4 m + 3 . 7 2 m + 6 + 4 m 2 + 4 m + 3 .

Avoid the temptation to simplify too soon! In the example above, we must leave the first rational expression as 2 a ( 2 a − b ) b ( 2 a + b ) ( 2 a − b ) 2 a ( 2 a − b ) b ( 2 a + b ) ( 2 a − b ) to be able to add it to 3 a · b ( 2 a + b ) ( 2 a − b ) · b 3 a · b ( 2 a + b ) ( 2 a − b ) · b . Simplify only after you have combined the numerators.

Example 8.44

Add: 8 x 2 − 2 x − 3 + 3 x x 2 + 4 x + 3 . 8 x 2 − 2 x − 3 + 3 x x 2 + 4 x + 3 .

Try It 8.87

Add: 1 m 2 − m − 2 + 5 m m 2 + 3 m + 2 . 1 m 2 − m − 2 + 5 m m 2 + 3 m + 2 .

Try It 8.88

Add: 2 n n 2 − 3 n − 10 + 6 n 2 + 5 n + 6 . 2 n n 2 − 3 n − 10 + 6 n 2 + 5 n + 6 .

Subtract Rational Expressions with Different Denominators

The process we use to subtract rational expressions with different denominators is the same as for addition. We just have to be very careful of the signs when subtracting the numerators.

Example 8.45

How to subtract rational expressions with different denominators.

Subtract: x x − 3 − x − 2 x + 3 . x x − 3 − x − 2 x + 3 .

Try It 8.89

Subtract: y y + 4 − y − 2 y − 5 . y y + 4 − y − 2 y − 5 .

Try It 8.90

Subtract: z + 3 z + 2 − z z + 3 . z + 3 z + 2 − z z + 3 .

The steps to take to subtract rational expressions are listed below.

Subtract rational expressions.

• Step 1. Determine if they have a common denominator. Yes – go to step 2. No – Rewrite each rational expression with the LCD. Find the LCD. Rewrite each rational expression as an equivalent rational expression with the LCD.
• Step 2. Subtract the rational expressions.

Example 8.46

Subtract: 8 y y 2 − 16 − 4 y − 4 . 8 y y 2 − 16 − 4 y − 4 .

Try It 8.91

Subtract: 2 x x 2 − 4 − 1 x + 2 . 2 x x 2 − 4 − 1 x + 2 .

Try It 8.92

Subtract: 3 z + 3 − 6 z z 2 − 9 . 3 z + 3 − 6 z z 2 − 9 .

There are lots of negative signs in the next example. Be extra careful!

Example 8.47

Subtract: −3 n − 9 n 2 + n − 6 − n + 3 2 − n . −3 n − 9 n 2 + n − 6 − n + 3 2 − n .

Try It 8.93

Subtract: 3 x − 1 x 2 − 5 x − 6 − 2 6 − x . 3 x − 1 x 2 − 5 x − 6 − 2 6 − x .

Try It 8.94

Subtract: −2 y − 2 y 2 + 2 y − 8 − y − 1 2 − y . −2 y − 2 y 2 + 2 y − 8 − y − 1 2 − y .

When one expression is not in fraction form, we can write it as a fraction with denominator 1.

Example 8.48

Subtract: 5 c + 4 c − 2 − 3 . 5 c + 4 c − 2 − 3 .

Try It 8.95

Subtract: 2 x + 1 x − 7 − 3 . 2 x + 1 x − 7 − 3 .

Try It 8.96

Subtract: 4 y + 3 2 y − 1 − 5 . 4 y + 3 2 y − 1 − 5 .

Add or subtract rational expressions.

• Step 2. Add or subtract the rational expressions.

We follow the same steps as before to find the LCD when we have more than two rational expressions. In the next example we will start by factoring all three denominators to find their LCD.

Example 8.49

Simplify: 2 u u − 1 + 1 u − 2 u − 1 u 2 − u . 2 u u − 1 + 1 u − 2 u − 1 u 2 − u .

Try It 8.97

Simplify: v v + 1 + 3 v − 1 − 6 v 2 − 1 . v v + 1 + 3 v − 1 − 6 v 2 − 1 .

Try It 8.98

Simplify: 3 w w + 2 + 2 w + 7 − 17 w + 4 w 2 + 9 w + 14 . 3 w w + 2 + 2 w + 7 − 17 w + 4 w 2 + 9 w + 14 .

Section 8.4 Exercises

Practice makes perfect.

In the following exercises, find the LCD.

5 x 2 − 2 x − 8 , 2 x x 2 − x − 12 5 x 2 − 2 x − 8 , 2 x x 2 − x − 12

8 y 2 + 12 y + 35 , 3 y y 2 + y − 42 8 y 2 + 12 y + 35 , 3 y y 2 + y − 42

9 z 2 + 2 z − 8 , 4 z z 2 − 4 9 z 2 + 2 z − 8 , 4 z z 2 − 4

6 a 2 + 14 a + 45 , 5 a a 2 − 81 6 a 2 + 14 a + 45 , 5 a a 2 − 81

4 b 2 + 6 b + 9 , 2 b b 2 − 2 b − 15 4 b 2 + 6 b + 9 , 2 b b 2 − 2 b − 15

5 c 2 − 4 c + 4 , 3 c c 2 − 10 c + 16 5 c 2 − 4 c + 4 , 3 c c 2 − 10 c + 16

2 3 d 2 + 14 d − 5 , 5 d 3 d 2 − 19 d + 6 2 3 d 2 + 14 d − 5 , 5 d 3 d 2 − 19 d + 6

3 5 m 2 − 3 m − 2 , 6 m 5 m 2 + 17 m + 6 3 5 m 2 − 3 m − 2 , 6 m 5 m 2 + 17 m + 6

In the following exercises, write as equivalent rational expressions with the given LCD.

5 x 2 − 2 x − 8 , 2 x x 2 − x − 12 5 x 2 − 2 x − 8 , 2 x x 2 − x − 12 LCD ( x − 4 ) ( x + 2 ) ( x + 3 ) ( x − 4 ) ( x + 2 ) ( x + 3 )

8 y 2 + 12 y + 35 , 3 y y 2 + y − 42 8 y 2 + 12 y + 35 , 3 y y 2 + y − 42 LCD ( y + 7 ) ( y + 5 ) ( y − 6 ) ( y + 7 ) ( y + 5 ) ( y − 6 )

9 z 2 + 2 z − 8 , 4 z z 2 − 4 9 z 2 + 2 z − 8 , 4 z z 2 − 4 LCD ( z − 2 ) ( z + 4 ) ( z + 2 ) ( z − 2 ) ( z + 4 ) ( z + 2 )

6 a 2 + 14 a + 45 , 5 a a 2 − 81 6 a 2 + 14 a + 45 , 5 a a 2 − 81 LCD ( a + 9 ) ( a + 5 ) ( a − 9 ) ( a + 9 ) ( a + 5 ) ( a − 9 )

4 b 2 + 6 b + 9 , 2 b b 2 − 2 b − 15 4 b 2 + 6 b + 9 , 2 b b 2 − 2 b − 15 LCD ( b + 3 ) ( b + 3 ) ( b − 5 ) ( b + 3 ) ( b + 3 ) ( b − 5 )

5 c 2 − 4 c + 4 , 3 c c 2 − 10 c + 10 5 c 2 − 4 c + 4 , 3 c c 2 − 10 c + 10 LCD ( c − 2 ) ( c − 2 ) ( c − 8 ) ( c − 2 ) ( c − 2 ) ( c − 8 )

2 3 d 2 + 14 d − 5 , 5 d 3 d 2 − 19 d + 6 2 3 d 2 + 14 d − 5 , 5 d 3 d 2 − 19 d + 6 LCD ( 3 d − 1 ) ( d + 5 ) ( d − 6 ) ( 3 d − 1 ) ( d + 5 ) ( d − 6 )

3 5 m 2 − 3 m − 2 , 6 m 5 m 2 + 17 m + 6 3 5 m 2 − 3 m − 2 , 6 m 5 m 2 + 17 m + 6 LCD ( 5 m + 2 ) ( m − 1 ) ( m + 3 ) ( 5 m + 2 ) ( m − 1 ) ( m + 3 )

In the following exercises, add.

5 24 + 11 36 5 24 + 11 36

7 30 + 13 45 7 30 + 13 45

9 20 + 11 30 9 20 + 11 30

8 27 + 7 18 8 27 + 7 18

7 10 x 2 y + 4 15 x y 2 7 10 x 2 y + 4 15 x y 2

1 12 a 3 b 2 + 5 9 a 2 b 3 1 12 a 3 b 2 + 5 9 a 2 b 3

1 2 m + 7 8 m 2 n 1 2 m + 7 8 m 2 n

5 6 p 2 q + 1 4 p 5 6 p 2 q + 1 4 p

3 r + 4 + 2 r − 5 3 r + 4 + 2 r − 5

4 s − 7 + 5 s + 3 4 s − 7 + 5 s + 3

8 t + 5 + 6 t − 5 8 t + 5 + 6 t − 5

7 v + 5 + 9 v − 5 7 v + 5 + 9 v − 5

5 3 w − 2 + 2 w + 1 5 3 w − 2 + 2 w + 1

4 2 x + 5 + 2 x − 1 4 2 x + 5 + 2 x − 1

2 y y + 3 + 3 y − 1 2 y y + 3 + 3 y − 1

3 z z − 2 + 1 z + 5 3 z z − 2 + 1 z + 5

5 b a 2 b − 2 a 2 + 2 b b 2 − 4 5 b a 2 b − 2 a 2 + 2 b b 2 − 4

4 c d + 3 c + 1 d 2 − 9 4 c d + 3 c + 1 d 2 − 9

2 m 3 m − 3 + 5 m m 2 + 3 m − 4 2 m 3 m − 3 + 5 m m 2 + 3 m − 4

3 4 n + 4 + 6 n 2 − n − 2 3 4 n + 4 + 6 n 2 − n − 2

3 n 2 + 3 n − 18 + 4 n n 2 + 8 n + 12 3 n 2 + 3 n − 18 + 4 n n 2 + 8 n + 12

6 q 2 − 3 q − 10 + 5 q q 2 − 8 q + 15 6 q 2 − 3 q − 10 + 5 q q 2 − 8 q + 15

3 r r 2 + 7 r + 6 + 9 r 2 + 4 r + 3 3 r r 2 + 7 r + 6 + 9 r 2 + 4 r + 3

2 s s 2 + 2 s − 8 + 4 s 2 + 3 s − 10 2 s s 2 + 2 s − 8 + 4 s 2 + 3 s − 10

In the following exercises, subtract.

t t − 6 − t − 2 t + 6 t t − 6 − t − 2 t + 6

v v − 3 − v − 6 v + 1 v v − 3 − v − 6 v + 1

w + 2 w + 4 − w w − 2 w + 2 w + 4 − w w − 2

x − 3 x + 6 − x x + 3 x − 3 x + 6 − x x + 3

y − 4 y + 1 − 1 y + 7 y − 4 y + 1 − 1 y + 7

z + 8 z − 3 − z z − 2 z + 8 z − 3 − z z − 2

5 a a + 3 − a + 2 a + 6 5 a a + 3 − a + 2 a + 6

3 b b − 2 − b − 6 b − 8 3 b b − 2 − b − 6 b − 8

6 c c 2 − 25 − 3 c + 5 6 c c 2 − 25 − 3 c + 5

4 d d 2 − 81 − 2 d + 9 4 d d 2 − 81 − 2 d + 9

6 m + 6 − 12 m m 2 − 36 6 m + 6 − 12 m m 2 − 36

4 n + 4 − 8 n n 2 − 16 4 n + 4 − 8 n n 2 − 16

−9 p − 17 p 2 − 4 p − 21 − p + 1 7 − p −9 p − 17 p 2 − 4 p − 21 − p + 1 7 − p

7 q + 8 q 2 − 2 q − 24 − q + 2 4 − q 7 q + 8 q 2 − 2 q − 24 − q + 2 4 − q

−2 r − 16 r 2 + 6 r − 16 − 5 2 − r −2 r − 16 r 2 + 6 r − 16 − 5 2 − r

2 t − 30 t 2 + 6 t − 27 − 2 3 − t 2 t − 30 t 2 + 6 t − 27 − 2 3 − t

5 v − 2 v + 3 − 4 5 v − 2 v + 3 − 4

6 w + 5 w − 1 + 2 6 w + 5 w − 1 + 2

2 x + 7 10 x − 1 + 3 2 x + 7 10 x − 1 + 3

8 y − 4 5 y + 2 − 6 8 y − 4 5 y + 2 − 6

In the following exercises, add and subtract.

5 a a − 2 + 9 a − 2 a + 18 a 2 − 2 a 5 a a − 2 + 9 a − 2 a + 18 a 2 − 2 a

2 b b − 5 + 3 2 b − 2 b − 15 2 b 2 − 10 b 2 b b − 5 + 3 2 b − 2 b − 15 2 b 2 − 10 b

c c + 2 + 5 c − 2 − 11 c c 2 − 4 c c + 2 + 5 c − 2 − 11 c c 2 − 4

6 d d − 5 + 1 d + 4 − 7 d − 5 d 2 − d − 20 6 d d − 5 + 1 d + 4 − 7 d − 5 d 2 − d − 20

In the following exercises, simplify.

6 a 3 a b + b 2 + 3 a 9 a 2 − b 2 6 a 3 a b + b 2 + 3 a 9 a 2 − b 2

2 c 2 c + 10 + 7 c c 2 + 9 c + 20 2 c 2 c + 10 + 7 c c 2 + 9 c + 20

6 d d 2 − 64 − 3 d − 8 6 d d 2 − 64 − 3 d − 8

5 n + 7 − 10 n n 2 − 49 5 n + 7 − 10 n n 2 − 49

4 m m 2 + 6 m − 7 + 2 m 2 + 10 m + 21 4 m m 2 + 6 m − 7 + 2 m 2 + 10 m + 21

3 p p 2 + 4 p − 12 + 1 p 2 + p − 30 3 p p 2 + 4 p − 12 + 1 p 2 + p − 30

−5 n − 5 n 2 + n − 6 + n + 1 2 − n −5 n − 5 n 2 + n − 6 + n + 1 2 − n

−4 b − 24 b 2 + b − 30 + b + 7 5 − b −4 b − 24 b 2 + b − 30 + b + 7 5 − b

7 15 p + 5 18 p q 7 15 p + 5 18 p q

3 20 a 2 + 11 12 a b 2 3 20 a 2 + 11 12 a b 2

4 x − 2 + 3 x + 5 4 x − 2 + 3 x + 5

6 m + 4 + 9 m − 8 6 m + 4 + 9 m − 8

2 q + 7 y + 4 − 2 2 q + 7 y + 4 − 2

3 y − 1 y + 4 − 2 3 y − 1 y + 4 − 2

z + 2 z − 5 − z z + 1 z + 2 z − 5 − z z + 1

t t − 5 − t − 1 t + 5 t t − 5 − t − 1 t + 5

3 d d + 2 + 4 d − d + 8 d 2 + 2 d 3 d d + 2 + 4 d − d + 8 d 2 + 2 d

2 q q + 5 + 3 q − 3 − 13 q + 15 q 2 + 2 q − 15 2 q q + 5 + 3 q − 3 − 13 q + 15 q 2 + 2 q − 15

Everyday Math

Decorating cupcakes Victoria can decorate an order of cupcakes for a wedding in t t hours, so in 1 hour she can decorate 1 t 1 t of the cupcakes. It would take her sister 3 hours longer to decorate the same order of cupcakes, so in 1 hour she can decorate 1 t + 3 1 t + 3 of the cupcakes.

• ⓐ Find the fraction of the decorating job that Victoria and her sister, working together, would complete in one hour by adding the rational expressions 1 t + 1 t + 3 . 1 t + 1 t + 3 .
• ⓑ Evaluate your answer to part (a) when t = 5 . t = 5 .

Kayaking When Trina kayaks upriver, it takes her 5 3 − c 5 3 − c hours to go 5 miles, where c c is the speed of the river current. It takes her 5 3 + c 5 3 + c hours to kayak 5 miles down the river.

• ⓐ Find an expression for the number of hours it would take Trina to kayak 5 miles up the river and then return by adding 5 3 − c + 5 3 + c . 5 3 − c + 5 3 + c .
• ⓑ Evaluate your answer to part (a) when c = 1 c = 1 to find the number of hours it would take Trina if the speed of the river current is 1 mile per hour.

Writing Exercises

Felipe thinks 1 x + 1 y 1 x + 1 y is 2 x + y . 2 x + y .

• ⓐ Choose numerical values for x and y and evaluate 1 x + 1 y . 1 x + 1 y .
• ⓑ Evaluate 2 x + y 2 x + y for the same values of x and y you used in part (a).
• ⓒ Explain why Felipe is wrong.
• ⓓ Find the correct expression for 1 x + 1 y . 1 x + 1 y .

Simplify the expression 4 n 2 + 6 n + 9 − 1 n 2 − 9 4 n 2 + 6 n + 9 − 1 n 2 − 9 and explain all your steps.

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/elementary-algebra/pages/1-introduction

• Authors: Lynn Marecek, MaryAnne Anthony-Smith
• Publisher/website: OpenStax
• Book title: Elementary Algebra
• Publication date: Feb 22, 2017
• Location: Houston, Texas
• Book URL: https://openstax.org/books/elementary-algebra/pages/1-introduction
• Section URL: https://openstax.org/books/elementary-algebra/pages/8-4-add-and-subtract-rational-expressions-with-unlike-denominators

© Feb 9, 2022 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Adding and Subtracting Fractions with Unlike Bases Homework| Distance Learning

Also included in

Description

Includes word problems and a digital link.

Questions & Answers

The distracted teacher.

• We're hiring
• Help & FAQ
• Privacy policy
• Student privacy
• Terms of service
• Tell us what you think