riemann hypothesis progress

Subscribe or renew today

Every print subscription comes with full digital access

Science News

Mathematicians report possible progress on proving the riemann hypothesis.

A new study of Jensen polynomials revives an old approach

STILL ELUSIVE   Researchers may have edged closer to a proof of the Riemann hypothesis — a statement about the Riemann zeta function, plotted here — which could help mathematicians understand the quirks of prime numbers.

Jan Homann/Wikimedia Commons

Share this:

By Emily Conover

May 24, 2019 at 12:03 pm

Researchers have made what might be new headway toward a proof of the Riemann hypothesis, one of the most impenetrable problems in mathematics. The hypothesis, proposed 160 years ago, could help unravel the mysteries of prime numbers.

Mathematicians made the advance by tackling a related question about a group of expressions known as Jensen polynomials, they report May 21 in Proceedings of the National Academy of Sciences . But the conjecture is so difficult to verify that even this progress is not necessarily a sign that a solution is near ( SN Online: 9/25/18 ).

At the heart of the Riemann hypothesis is an enigmatic mathematical entity known as the Riemann zeta function. It’s intimately connected to prime numbers — whole numbers that can’t be formed by multiplying two smaller numbers — and how they are distributed along the number line. The Riemann hypothesis suggests that the function’s value equals zero only at points that fall on a single line when the function is graphed, with the exception of certain obvious points. But, as the function has infinitely many of these “zeros,” this is not easy to confirm. The puzzle is considered so important and so difficult that there is a $1 million prize for a solution , offered up by the Clay Mathematics Institute.

But Jensen polynomials might be a key to unlocking the Riemann hypothesis. Mathematicians have previously shown that the Riemann hypothesis is true if all the Jensen polynomials associated with the Riemann zeta function have only zeros that are real, meaning the values for which the polynomial equals zero are not imaginary numbers — they don’t involve the square root of negative 1. But there are infinitely many of these Jensen polynomials.

Studying Jensen polynomials is one of a variety of strategies for attacking the Riemann hypothesis. The idea is more than 90 years old, and previous studies have proved that a small subset of the Jensen polynomials have real roots. But progress was slow, and efforts had stalled.

Now, mathematician Ken Ono and colleagues have shown that many of these polynomials indeed have real roots, satisfying a large chunk of what’s needed to prove the Riemann hypothesis.

“Any progress in any direction related to the Riemann hypothesis is fascinating,” says mathematician Dimitar Dimitrov of the State University of São Paulo. Dimitrov thought “it would be impossible that anyone will make any progress in this direction,” he says, “but they did.”

It’s hard to say whether this progress could eventually lead to a proof. “I am very reluctant to predict anything,” says mathematician George Andrews of Penn State, who was not involved with the study. Many strides have been made on the Riemann hypothesis in the past, but each advance has fallen short. However, with other major mathematical problems that were solved in recent decades, such as Fermat’s last theorem ( SN: 11/5/94, p. 295 ), it wasn’t clear that the solution was imminent until it was in hand. “You never know when something is going to break.”

The result supports the prevailing viewpoint among mathematicians that the Riemann hypothesis is correct. “We’ve made a lot of progress that offers new evidence that the Riemann hypothesis should be true,” says Ono, of Emory University in Atlanta.

If the Riemann hypothesis is ultimately proved correct, it would not only illuminate the prime numbers, but would also immediately confirm many mathematical ideas that have been shown to be correct assuming the Riemann hypothesis is true.

In addition to its Riemann hypothesis implications, the new result also unveils some details of what’s known as the partition function , which counts the number of possible ways to create a number from the sum of positive whole numbers ( SN: 6/17/00, p. 396 ). For example, the number 4 can be made in five different ways: 3+1, 2+2, 2+1+1, 1+1+1+1, or just the number 4 itself.

The result confirms an earlier proposition about the details of how that partition function grows with larger numbers. “That was an open question … for a long time,” Andrews says. The real prize would be proving the Riemann hypothesis, he notes. That will have to wait.

More Stories from Science News on Math

How two outsiders tackled the mystery of arithmetic progressions

A predicted quasicrystal is based on the ‘einstein’ tile known as the hat.

Here’s how much fruit you can take from a display before it collapses

Here are some astounding scientific firsts of 2023

‘Is Math Real?’ asks simple questions to explore math’s deepest truths

An enduring Möbius strip mystery has finally been solved

Non-Western art and design can reveal alternate ways of thinking about math

Seen Bigfoot or the Loch Ness Monster? Data suggest the odds are low

From the nature index.

Subscribers, enter your e-mail address for full access to the Science News archives and digital editions.

Not a subscriber? Become one now .

A new approach to a $1 million mathematical enigma

Physicist translates the riemann zeta function into quantum field theory.

Numbers like π, e and φ often turn up in unexpected places in science and mathematics. Pascal's triangle and the Fibonacci sequence also seem inexplicably widespread in nature. Then there's the Riemann zeta function, a deceptively straightforward function that has perplexed mathematicians since the 19th century. The most famous quandary, the Riemann hypothesis, is perhaps the greatest unsolved question in mathematics, with the Clay Mathematics Institute offering a $1 million prize for a correct proof.

UC Santa Barbara physicist Grant Remmen believes he has a new approach for exploring the quirks of the zeta function. He has found an analogue that translates many of the function's important properties into quantum field theory. This means that researchers can now leverage the tools from this field of physics to investigate the enigmatic and oddly ubiquitous zeta function. His work could even lead to a proof of the Riemann hypothesis. Remmen lays out his approach in the journal Physical Review Letters.

"The Riemann zeta function is this famous and mysterious mathematical function that comes up in number theory all over the place," said Remmen, a postdoctoral scholar at UCSB's Kavli Institute for Theoretical Physics. "It's been studied for over 150 years."

An outside perspective

Remmen generally doesn't work on cracking the biggest questions in mathematics. He's usually preoccupied chipping away at the biggest questions in physics. As the fundamental physics fellow at UC Santa Barbara, he normally devotes his attention to topics like particle physics, quantum gravity, string theory and black holes. "In modern high-energy theory, the physics of the largest scales and smallest scales both hold the deepest mysteries," he remarked.

One of his specialties is quantum field theory, which he describes as a "triumph of 20 th century physics." Most people have heard of quantum mechanics (subatomic particles, uncertainty, etc.) and special relativity (time dilation, E=mc 2 , and so forth). "But with quantum field theory, physicists figured out how to combine special relativity and quantum mechanics into a description of how particles moving at or near the speed of light behave," he explained.

Quantum field theory is not exactly a single theory. It's more like a collection of tools that scientists can use to describe any set of particle interactions.

Remmen realized one of the concepts therein shares many characteristics with the Riemann zeta function. It's called a scattering amplitude, and it encodes the quantum mechanical probability that particles will interact with each other. He was intrigued.

Scattering amplitudes often work well with momenta that are complex numbers. These numbers consist of a real part and an imaginary part -- a multiple of √-1, which mathematicians call i . Scattering amplitudes have nice properties in the complex plane. For one, they're analytic (can be expressed as a series) around every point except a select set of poles, which all lie along a line.

"That seemed similar to what's going on with the Riemann zeta function's zeros, which all seem to lie on a line," said Remmen. "And so I thought about how to determine whether this apparent similarity was something real."

The scattering amplitude poles correspond to particle production, where a physical event happens that generates a particle with a momentum. The value of each pole corresponds with the mass of the particle that's created. So it was a matter of finding a function that behaves like a scattering amplitude and whose poles correspond to the non-trivial zeros of the zeta function.

With pen, paper and a computer to check his results, Remmen set to work devising a function that had all the relevant properties. "I had had the idea of connecting the Riemann zeta function to amplitudes in the back of my mind for a couple years," he said. "Once I set out to find such a function, it took me about a week to construct it, and fully exploring its properties and writing the paper took a couple months."

Deceptively simple

At its core, the zeta function generalizes the harmonic series:

This series blows up to infinity when x ≤ 1, but it converges to an actual number for every x > 1.

In 1859 Bernhard Riemann decided to consider what would happen when x is a complex number. The function, now bearing the name Riemann zeta, takes in one complex number and spits out another.

Riemann also decided to extend the zeta function to numbers where the real component was not greater than 1 by defining it in two parts: the familiar definition holds in places where the function behaves, and another, implicit definition covers the places where it would normally blow up to infinity.

Thanks to a theorem in complex analysis, mathematicians know there is only one formulation for this new area that smoothly preserves the properties of the original function. Unfortunately, no one has been able to represent it in a form with finitely many terms, which is part of the mystery surrounding this function.

Given the function's simplicity, it should have some nice features. "And yet, those properties end up being fiendishly complicated to understand," Remmen said. For example, take the inputs where the function equals zero. All the negative even numbers are mapped to zero, though this is apparent -- or "trivial" as mathematicians say -- when the zeta function is written in certain forms. What has perplexed mathematicians is that all of the other, non-trivial zeros appear to lie along a line: Each of them has a real component of ½.

Riemann hypothesized that this pattern holds for all of these non-trivial zeros, and the trend has been confirmed for the first few trillion of them. That said, there are conjectures that work for trillions of examples and then fail at extremely large numbers. So mathematicians can't be certain the hypothesis is true until it's proven.

But if it is true, the Riemann hypothesis has far-reaching implications. "For various reasons it crops up all over the place in fundamental questions in mathematics," Remmen said. Postulates in fields as distinct as computation theory, abstract algebra and number theory hinge on the hypothesis holding true. For instance, proving it would provide an accurate account of the distribution of prime numbers.

A physical analogue

The scattering amplitude that Remmen found describes two massless particles interacting by exchanging an infinite set of massive particles, one at a time. The function has a pole -- a point where it cannot be expressed as a series -- corresponding to the mass of each intermediate particle. Together, the infinite poles line up with the non-trivial zeros of the Riemann zeta function.

What Remmen constructed is the leading component of the interaction. There are infinitely more that each account for smaller and smaller aspects of the interaction, describing processes involving the exchange of multiple massive particles at once. These "loop-level amplitudes" would be the subject of future work.

The Riemann hypothesis posits that the zeta function's non-trivial zeros all have a real component of ½. Translating this into Remmen's model: All of the amplitude's poles are real numbers. This means that if someone can prove that his function describes a consistent quantum field theory -- namely, one where masses are real numbers, not imaginary -- then the Riemann hypothesis will be proven.

This formulation brings the Riemann hypothesis into yet another field of science and mathematics, one with powerful tools to offer mathematicians. "Not only is there this relation to the Riemann hypothesis, but there's a whole list of other attributes of the Riemann zeta function that correspond to something physical in the scattering amplitude," Remmen said. For instance, he has already discovered unintuitive mathematical identities related to the zeta function using methods from physics.

Remmen's work follows a tradition of researchers looking to physics to shed light on mathematical quandaries. For instance, physicist Gabriele Veneziano asked a similar question in 1968: whether the Euler beta function could be interpreted as a scattering amplitude. "Indeed it can," Remmen remarked, "and the amplitude that Veneziano constructed was one of the first string theory amplitudes."

Remmen hopes to leverage this amplitude to learn more about the zeta function. "The fact that there are all these analogues means that there's something going on here," he said.

And the approach sets up a path to possibly proving the centuries-old hypothesis. "The innovations necessary to prove that this amplitude does come from a legitimate quantum field theory would, automatically, give you the tools that you need to fully understand the zeta function," Remmen said. "And it would probably give you more as well."

• Math Puzzles
• Mathematics
• Quantum Computers
• Mathematical Modeling
• Spintronics Research
• Computer Modeling
• Computers and Internet
• Trigonometry
• Symmetry in mathematics
• Algebraic geometry
• Probability distribution
• Bioinformatics

Story Source:

Materials provided by University of California - Santa Barbara . Original written by Harrison Tasoff. Note: Content may be edited for style and length.

Related Multimedia :

• Remmen’s scattering amplitude translates the Riemann zeta function into the language of quantum field theory.

Journal Reference :

• Grant N. Remmen. Amplitudes and the Riemann Zeta Function . Physical Review Letters , 2021; 127 (24) DOI: 10.1103/PhysRevLett.127.241602

Cite This Page :

Explore More

• Illuminating Oxygen's Journey in the Brain
• DNA Study IDs Descendants of George Washington
• Heart Disease Risk: More Than One Drink a Day
• Unlocking Supernova Stardust Secrets
• Why Do Some Memories Become Longterm?
• Cell Division Quality Control 'Stopwatch'
• What Controls Sun's Differential Rotation?
• Robot, Can You Say 'Cheese'?
• Researchers Turn Back the Clock On Cancer Cells
• Making Long-Term Memories: Nerve-Cell Damage

Trending Topics

Strange & offbeat.

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• 11 November 2022
• Correction 14 November 2022

Mathematician who solved prime-number riddle claims new breakthrough

• Davide Castelvecchi

You can also search for this author in PubMed   Google Scholar

A mathematician who went from obscurity to luminary status in 2013 for cracking a century-old question about prime numbers now claims to have solved another. The problem is similar to — but distinct from — the Riemann hypothesis, which is considered one of the most important problems in mathematics.

Access options

Access Nature and 54 other Nature Portfolio journals

Get Nature+, our best-value online-access subscription

24,99 € / 30 days

cancel any time

Subscribe to this journal

Receive 51 print issues and online access

185,98 € per year

only 3,65 € per issue

Rent or buy this article

Prices vary by article type

Prices may be subject to local taxes which are calculated during checkout

Nature 611 , 645-646 (2022)

doi: https://doi.org/10.1038/d41586-022-03689-2

Updates & Corrections

Correction 14 November 2022 : This article has been amended to clarify that the formula Zhang claims to have proved is not the Landau-Siegel zeros conjecture, but a weaker version of it.

Zhang, Y. Preprint at https://arxiv.org/abs/2211.02515 (2022).

Zhang, Y. Preprint at https://arxiv.org/abs/0705.4306 (2007).

Zhang, Y. Ann. Math. 179 , 1121–1174 (2014).

Article   Google Scholar  

Download references

Reprints and permissions

Related Articles

First proof that prime numbers pair up into infinity

• Mathematics and computing

How scientists are making the most of Reddit

Career Feature 01 APR 24

A global timekeeping problem postponed by global warming

Article 27 MAR 24

Climate change has slowed Earth’s rotation — and could affect how we keep time

News 27 MAR 24

Senior Scientist, Research

Be part of something altogether life-changing!  Working at Cytiva means being at the forefront of providing new solutions to transform human heal...

Vancouver, British Columbia (CA)

Postdoctoral positions in the integrative structural biology of cancer and immunity

Postdoctoral positions in the integrative structural biology study of signaling complexes important in cancer and the immune system

Farmington, Connecticut (US)

University of Connecticut Health Center (UCHC)

Faculty Positions & Postdocs at Institute of Physics (IOP), Chinese Academy of Sciences

IOP is the leading research institute in China in condensed matter physics and related fields. Through the steadfast efforts of generations of scie...

Beijing, China

Institute of Physics (IOP), Chinese Academy of Sciences (CAS)

Postdoctoral Scholar - PHAST Alzheimer

Memphis, Tennessee

The University of Tennessee Health Science Center (UTHSC)

Postdoctoral Associate- Neurodevelopmental Disease

Houston, Texas (US)

Baylor College of Medicine (BCM)

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Has one of math’s greatest mysteries, the Riemann hypothesis, finally been solved?

Professor of Mathematics, University of Richmond

Disclosure statement

William Ross does not work for, consult, own shares in or receive funding from any company or organisation that would benefit from this article, and has disclosed no relevant affiliations beyond their academic appointment.

University of Richmond provides funding as a member of The Conversation US.

View all partners

Over the past few days, the mathematics world has been abuzz over the news that Sir Michael Atiyah, the famous Fields Medalist and Abel Prize winner, claims to have solved the Riemann hypothesis .

If his proof turns out to be correct, this would be one of the most important mathematical achievements in many years. In fact, this would be one of the biggest results in mathematics, comparable to the proof of Fermat’s Last Theorem from 1994 and the proof of the Poincare Conjecture from 2002 .

Besides being one of the great unsolved problems in mathematics and therefore garnishing glory for the person who solves it, the Riemann hypothesis is one of the Clay Mathematics Institute’s “Million Dollar Problems.” A solution would certainly yield a pretty profitable haul: one million dollars.

The Riemann hypothesis has to do with the distribution of the prime numbers, those integers that can be divided only by themselves and one, like 3, 5, 7, 11 and so on. We know from the Greeks that there are infinitely many primes. What we don’t know is how they are distributed within the integers.

The problem originated in estimating the so-called “prime pi” function, an equation to find the number of primes less than a given number. But its modern reformulation, by German mathematician Bernhard Riemann in 1858, has to do with the location of the zeros of what is now known as the Riemann zeta function.

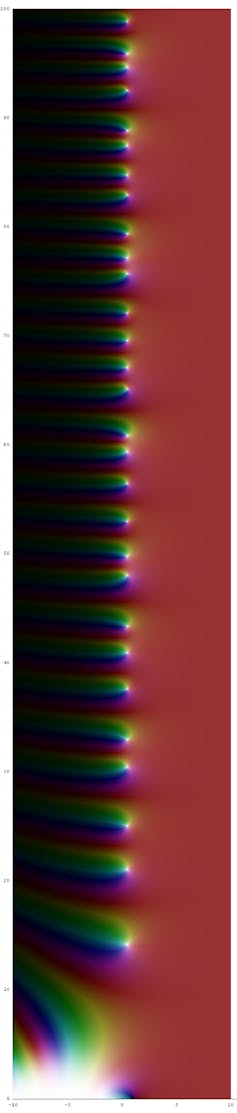
The technical statement of the Riemann hypothesis is “the zeros of the Riemann zeta function which lie in the critical strip must lie on the critical line.” Even understanding that statement involves graduate-level mathematics courses in complex analysis.

Most mathematicians believe that the Riemann hypothesis is indeed true. Calculations so far have not yielded any misbehaving zeros that do not lie in the critical line. However, there are infinitely many of these zeros to check, and so a computer calculation will not verify all that much. Only an abstract proof will do.

If, in fact, the Riemann hypothesis were not true, then mathematicians’ current thinking about the distribution of the prime numbers would be way off, and we would need to seriously rethink the primes.

The Riemann hypothesis has been examined for over a century and a half by some of the greatest names in mathematics and is not the sort of problem that an inexperienced math student can play around with in his or her spare time. Attempts at verifying it involve many very deep tools from complex analysis and are usually very serious ones done by some of the best names in mathematics.

Atiyah gave a lecture in Germany on Sept. 25 in which he presented an outline of his approach to verify the Riemann hypothesis. This outline is often the first announcement of the solution but should not be taken that the problem has been solved – far from it. For mathematicians like me, the “proof is in the pudding,” and there are many steps that need to be taken before the community will pronounce Atiyah’s solution as correct. First, he will have to circulate a manuscript detailing his solution. Then, there is the painstaking task of verifying his proof. This could take quite a lot of time, maybe months or even years.

Is Atiyah’s attempt at the Riemann hypothesis serious? Perhaps. His reputation is stellar, and he is certainly capable enough to pull it off. On the other hand, there have been several other serious attempts at this problem that did not pan out. At some point, Atiyah will need to circulate a manuscript that experts can check with a fine-tooth comb.

• Mathematics
• Prime numbers
• Quick reads

Lecturer (Hindi-Urdu)

Initiative Tech Lead, Digital Products COE

Director, Defence and Security

Opportunities with the new CIEHF

School of Social Sciences – Public Policy and International Relations opportunities

• Math Drudge blog (older)
• Experimental math site
• Math Investor blog
• Jon Borwein memorial site
• About Math Scholar
• Book reviews

Note that the real part of these zeroes is always 1/2. Riemann’s famous hypothesis is that all nontrivial zeroes of the zeta function lie along the line ${\rm Re}(z) = 1/2$. The Riemann hypothesis is widely regarded as the most significant outstanding unsolved problem in mathematics. For instance, the Clay Mathematics Institute lists the Riemann hypothesis as one of its “millennium problems,” the solution to which would qualify for an award of one million U.S. dollars. For some additional background on the Riemann hypothesis, see this article written by Peter Sarnak for the Clay Institute.

Consequences of the Riemann hypothesis

If the Riemann hypothesis is true, many important results would hold. Here are just two:

• The Mobius function : Define the Mobius function of a positive integer $n$ as: $1$ if $n$ is a square-free positive integer with an even number of prime factors; $-1$ if $n$ is a square-free positive integer with an odd number of prime factors; and $0$ if $n$ has a squared prime factor. Then the statement that $$\frac{1}{\zeta(s)} \; = \; \sum_{n=1}^\infty \frac{\mu(n)}{n^s}$$ is valid for every s with ${\rm Re}(s) \gt 1/2$, with the sum converging, is equivalent to the Riemann hypothesis.
• The prime-counting function : For real $x \gt 0$, let $\pi(x)$ denote the number of primes less than $x$, and let ${\rm Li}(x) = \int_2^x 1/\log(t) \, {\rm d}t$. The “prime number theorem,” proven by Hadamard and de la Vallee Poussin in 1896, asserts that $\pi(x) / {\rm Li}(x)$ tends to one for large $x$. But if one assumes the Riemann hypothesis, a stronger result can be proved, namely $$|\pi(x) – {\rm Li}(x)| \lt \frac{\sqrt{x} \log(x)}{8 \pi}$$ for all sufficiently large $x$ (in fact, for all $x \ge 2657$).

For details and some other examples, see this Wikipedia article .

The Griffin-Ono-Rolen-Zagier result

In a remarkable new paper , published in the Proceedings of the National Academy Of Sciences , the four mathematicians have resurrected a line of reasoning, long thought to be dead, originally developed by Johan Jensen and George Polya . The proof relies on “Jensen polynomials,” which for an arbitrary real sequence $(\alpha(0), \alpha(1), \alpha(2), \ldots)$, integer degree $d$ and shift $n$ are defined as: $$J_\alpha^{d,n} (x) = \sum_{j=0}^d {d \choose j} \alpha(n+j) x^j.$$ We say that a polynomial with real coefficients is hyperbolic if all of its zeroes are real. Define $\Lambda( s) = \pi^{-s/2} \Gamma(s/2) \zeta(s) = \Lambda(1-s)$. Consider now the sequence of Taylor coefficients $(\gamma(n), n \geq 1)$ defined implicitly by $$(4z^2 – 1) \Lambda(z+1/2) \; = \; \sum_{n=0}^\infty \frac{\gamma(n) z^{2n}}{n!}.$$

Polya proved that the Riemann hypothesis is equivalent to the assertion that the Jensen polynomials associated with the sequence $(\gamma(n))$ are hyperbolic for all nonnegative integers $d$ and $n$.

What Griffin, Ono, Rolen and Zagier have shown is that for $d \geq 1$, the associated Jensen polynomials $J_\gamma^{d,n}$ are hyperbolic for all sufficiently large $n$. This is not the same as for every $n$, but it certainly is a remarkable advance. In addition, the four authors proved that for $1 \leq d \leq 8$, that the associated Jensen polynomials are indeed hyperbolic for all $n \geq 0$. Previous to this result, the best result was for $1 \leq d \leq 3$ and all $n \geq 0$.

Ken Ono emphasizes that he and the other authors did not invent any new techniques or new mathematical objects. Instead, the advantage of their proof is its simplicity (the paper is only eight pages long!). The idea for the paper was a “toy problem” that Ono presented for entertainment to Zagier during a recent conference celebrating Zagier’s 65th birthday. Ono thought that the problem was essentially intractable and did not expect Zagier to make much headway with it, but Zagier was enthused by the challenge and soon had sketched a solution. Together with the other authors, they fleshed out the solution and then extended it to a more general theory.

Kannan Soundararajan, a Stanford mathematician who has studied the Riemann Hypothesis, said “The result established here may be viewed as offering further evidence toward the Riemann Hypothesis, and in any case, it is a beautiful stand-alone theorem.”

How much longer?

The authors emphasize that their work definitely falls short of a full proof of the Riemann hypothesis. For all they know, the hypothesis may still turn out to be false, or that what remains in this or any other proposed proof outline is so difficult that it may defy efforts to prove for many years to come. But the result is definitely encouraging.

It should be mentioned that some other manuscripts have circulated with authors claiming proofs, at least a few of which are by mathematicians with very solid credentials. However, none of these has ever gained any traction, so the only safe conclusion is that the Riemann hypothesis remains unproven and may be as difficult as ever.

Will it still be unproven 100 years from now? Stay tuned (if any of us are still around in 2119).

Comments are closed.

Recent Posts

• Pi Day 2024 crossword puzzle
• Using network theory to analyze Bach’s music
• Overcoming experimenter bias in scientific research
• Progress in troubled times: Good news in science, medicine and society
• Aliens made this rock: The post-hoc probability fallacy in biology, finance and cosmology
• DeepMind program discovers new sorting algorithms
• Is modern science socially constructed and forever tentative?
• Peter Borwein: A visionary mathematician
• PiDay 2023 crossword puzzle
• Can ChatGPT prove math theorems?
• Entries feed
• Comments feed
• WordPress.org

Distribution of large values of the argument of the Riemann zeta function on short intervals

• Brief Communications
• Published: 16 January 2011
• Volume 65 , pages 261–263, ( 2010 )

Cite this article

• R. N. Boyarinov 1  

33 Accesses

Explore all metrics

An upper bound for the measure of the set of values t ∈ ( T,T + H ] for H = T 27/82+ ɛ for which | S ( t )| ≥ λ is obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

A. A. Karatsuba and M. A. Korolev, “The Argument of the Riemann Zeta Function,” Uspekhi Matem. Nauk 60 (3(363)), 41 (2005) [Russ. Math. Surveys 60 (3), 433 (2005)].

MathSciNet   Google Scholar  

M. A. Korolev, “On Large Values of the Function S ( t ) on Short Intervals,” Izvestiya Russ. Akad. Nauk, Matem. 69 (1), 115 (2005) [Izvestiya: Math. 69 (1), 113 (2005)].

E. Trost, Primzahlen (Basel, 1953; Fizmatlit, Moscow, 1959).

A. A. Karatsuba and M. A. Korolev, “Behavior of the Argument of the Riemann Zeta Function on the Critical Line,” Uspekhi Matem. Nauk 61 (3(369)), 3 (2006) [Russ. Math. Surveys 61 (3), 389 (2006)].

Download references

Author information

Authors and affiliations.

Faculty of Mechanics and Mathematics, Moscow State University, Leninskie Gory, Moscow, 119899, Russia

R. N. Boyarinov

You can also search for this author in PubMed   Google Scholar

Additional information

Original Russian Text © R. N. Boyarinov, 2010, published in Vestnik Moskovskogo Universiteta, Matematika. Mekhanika, 2010, Vol. 65, No. 6, pp. 55–58.

About this article

Boyarinov, R.N. Distribution of large values of the argument of the Riemann zeta function on short intervals. Moscow Univ. Math. Bull. 65 , 261–263 (2010). https://doi.org/10.3103/S0027132210060100

Download citation

Received : 31 May 2010

Published : 16 January 2011

Issue Date : December 2010

DOI : https://doi.org/10.3103/S0027132210060100

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Short Interval
• Prime Number
• Lower Estimate
• Integer Number
• Find a journal
• Publish with us
• Track your research

We apologize for the inconvenience...

To ensure we keep this website safe, please can you confirm you are a human by ticking the box below.

If you are unable to complete the above request please contact us using the below link, providing a screenshot of your experience.

https://ioppublishing.org/contacts/

Vladimir Ilyich Lenin

The right of nations to self-determination.

Written: February-May 1914 Published: April-June 1914 in the journal Prosveshcheniye Nos. 4, 5 and 6. Signed: V. Ilyin . Published according to the text in the journal. Source: Lenin’s Collected Works , Progress Publishers, 1972, Moscow, Volume 20 , pp. 393-454. Translated: Bernard Isaacs and The Late Joe Fineberg Transcription\Markup: B. Baggins , D. Walters , & K. Goins (2008) Public Domain: Lenin Internet Archive (2000). You may freely copy, distribute, display and perform this work; as well as make derivative and commercial works. Please credit “Marxists Internet Archive” as your source.