case study on inverse trigonometric functions

CBSE Case Study Questions for Class 12 Maths Inverse Trigonometric Functions Free PDF

Mere Bacchon, you must practice the CBSE Case Study Questions Class 12 Maths Inverse Trigonometric Functions  in order to fully complete your preparation . They are very very important from exam point of view. These tricky Case Study Based Questions can act as a villain in your heroic exams!

I have made sure the questions (along with the solutions) prepare you fully for the upcoming exams. To download the latest CBSE Case Study Questions , just click ‘ Download PDF ’.

CBSE Case Study Questions for Class 12 Maths Inverse Trigonometric Functions PDF

Mcq set 1 -, mcq set 2 -, checkout our case study questions for other chapters.

• Chapter 1 Relations and Functions Case Study Questions
• Chapter 3 Matrices Case Study Questions
• Chapter 4 Determinants Case Study Questions
• Chapter 5 Continuity and Differentiability Case Study Questions

How should I study for my upcoming exams?

First, learn to sit for at least 2 hours at a stretch

Solve every question of NCERT by hand, without looking at the solution.

Solve NCERT Exemplar (if available)

Sit through chapter wise FULLY INVIGILATED TESTS

Practice MCQ Questions (Very Important)

Practice Assertion Reason & Case Study Based Questions

Sit through FULLY INVIGILATED TESTS involving MCQs. Assertion reason & Case Study Based Questions

After Completing everything mentioned above, Sit for atleast 6 full syllabus TESTS.

Comments are closed.

Contact Form

Privacy Policy

Class 12 Maths: Case Study of Chapter 2 Inverse Trigonometric Functions PDF Download

• Post author: studyrate
• Post published:
• Post category: 12 board / Class 12
• Post comments: 0 Comments

In Class 12 Boards there will be Case studies and Passage Based Questions will be asked, So practice these types of questions. Study Rate is always there to help you. Free PDF Download of CBSE Class 12 Mathematics Chapter 2 Inverse Trigonometric Functions Case Study and Passage Based Questions with Answers were Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 12 Maths Inverse Trigonometric Functions  to know their preparation level.

Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 12 Maths Paper, There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.

Inverse Trigonometric Functions Case Study Questions With answers

Here, we have provided case-based/passage-based questions for Class 12 Mathematics  Chapter 2 Inverse Trigonometric Functions

Case Study/Passage-Based Questions

Case Study 1:

Two men on either side of a temple of 30 meters high observe its top at the angles of elevation α and β respectively. (as shown in the figure above). The distance between the two men is 40√3 metres and the distance between the first person A and the temple is 30√3 meters. ∠CAB = α =

• A.sin -1 (2/√3)
• B.sin -1 (1/2)
• C.sin −1 (2)
• D.sin −1 (√3/2)

Answer: (B)

Hope the information shed above regarding Case Study and Passage Based Questions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 12 Mathematics Inverse Trigonometric Functions Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible. By Team Study Rate

You Might Also Like

Class 12 chemistry case study question chapter 12 aldehydes ketones and carboxylic acids, mcq class 12 english indigo questions with answers english chapter 5, class 12 chemistry case study questions chapter 11 alcohols, phenols, and ethers, leave a reply cancel reply.

Save my name, email, and website in this browser for the next time I comment.

This site uses Akismet to reduce spam. Learn how your comment data is processed .

The Topper Combo Flashcards

• Contains the Latest NCERT in just 350 flashcards.
• Colourful and Interactive
• Summarised Important reactions according to the latest PYQs of NEET(UG) and JEE

No thanks, I’m not interested!

Gurukul of Excellence

Classes for Physics, Chemistry and Mathematics by IITians

Join our Telegram Channel for Free PDF Download

Case Study Questions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions

• Last modified on: 1 year ago
• Reading Time: 4 Minutes

Case Study Questions:

Question 1:

The Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. ‘A’ is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby, Ram Robert and Rahim suggested to the film to place the hoarding board at three different locations namely C, D and E. ‘C’ is at the height of 10 metres from the ground level. For the viewer ‘A’, the angle of elevation of ‘D’ is double the angle of elevation of ‘C’. The angle of elevation of ‘E’ is triple the angle of elevation of ‘C’ for the same viewer.

Look at the figure given and based on the above information answer the following:

(i) Measure of ∠CAB = (a) tan –1 (2) (b) tan –1 (1/2) (c) tan– 1 (1) (d) tan –1 (3)

(ii) Measure of ∠DAB = (a) tan –1 (3/4) (b) tan –1 (3) (c) tan –1 (4/3) (d) tan –1 (4)

(iii) Measure of ∠EAB (a) tan –1 (11) (b) tan –1 (3) (c) tan –1 (2/11) (d) tan –1 (11/2)

(iv) A’ is another viewer standing on the same line of observation across the road. If the width of the road is 5 meters, then the difference between ∠CAB and ∠CA’B is (a) tan –1 (1/12) (b) tan –1 (1/8) (c) tan –1 (2/5) (d) tan –1 (11/21)

Related Posts

Category lists (all posts).

All categories of this website are listed below with number of posts in each category for better navigation. Visitors can click on a particular category to see all posts related to that category.

• Full Form (1)
• Biography of Scientists (1)
• Assertion Reason Questions in Biology (37)
• Case Study Questions for Class 12 Biology (14)
• DPP Biology for NEET (12)
• Blog Posts (35)
• Career Guidance (1)
• Assertion Reason Questions for Class 10 Maths (14)
• Case Study Questions for Class 10 Maths (15)
• Extra Questions for Class 10 Maths (12)
• Maths Formulas for Class 10 (1)
• MCQ Questions for Class 10 Maths (15)
• NCERT Solutions for Class 10 Maths (4)
• Quick Revision Notes for Class 10 Maths (14)
• Assertion Reason Questions for Class 10 Science (16)
• Case Study Questions for Class 10 Science (14)
• Evergreen Science Book Solutions for Class 10 (17)
• Extra Questions for Class 10 Science (23)
• HOTS for Class 10 Science (17)
• Important Questions for Class 10 Science (10)
• Lakhmir Singh Class 10 Biology Solutions (4)
• Lakhmir Singh Class 10 Chemistry Solutions (5)
• Lakhmir Singh Class 10 Physics Solutions (5)
• MCQ Questions for Class 10 Science (20)
• NCERT Exemplar Solutions for Class 10 Science (16)
• NCERT Solutions for Class 10 Science (15)
• Quick Revision Notes for Class 10 Science (4)
• Study Notes for Class 10 Science (17)
• Assertion Reason Questions for Class 10 Social Science (14)
• Case Study Questions for Class 10 Social Science (24)
• MCQ Questions for Class 10 Social Science (3)
• Topicwise Notes for Class 10 Social Science (4)
• CBSE CLASS 11 (1)
• Assertion Reason Questions for Class 11 Chemistry (14)
• Case Study Questions for Class 11 Chemistry (11)
• Free Assignments for Class 11 Chemistry (1)
• MCQ Questions for Class 11 Chemistry (8)
• Very Short Answer Questions for Class 11 Chemistry (7)
• Assertion Reason Questions for Class 11 Entrepreneurship (8)
• Important Questions for CBSE Class 11 Entrepreneurship (1)
• Assertion Reason Questions for Class 11 Geography (24)
• Case Study Questions for Class 11 Geography (24)
• Assertion Reason Questions for Class 11 History (12)
• Case Study Questions for Class 11 History (12)
• Assertion and Reason Questions for Class 11 Maths (16)
• Case Study Questions for Class 11 Maths (16)
• Formulas for Class 11 Maths (6)
• MCQ Questions for Class 11 Maths (17)
• NCERT Solutions for Class 11 Maths (8)
• Case Study Questions for Class 11 Physical Education (11)
• Assertion Reason Questions for Class 11 Physics (15)
• Case Study Questions for Class 11 Physics (12)
• Class 11 Physics Study Notes (5)
• Concept Based Notes for Class 11 Physics (2)
• Conceptual Questions for Class 11 Physics (10)
• Derivations for Class 11 Physics (3)
• Extra Questions for Class 11 Physics (13)
• MCQ Questions for Class 11 Physics (16)
• NCERT Solutions for Class 11 Physics (16)
• Numerical Problems for Class 11 Physics (4)
• Physics Formulas for Class 11 (7)
• Revision Notes for Class 11 Physics (11)
• Very Short Answer Questions for Class 11 Physics (11)
• Assertion Reason Questions for Class 11 Political Science (20)
• Case Study Questions for Class 11 Political Science (20)
• CBSE CLASS 12 (8)
• Extra Questions for Class 12 Biology (14)
• MCQ Questions for Class 12 Biology (13)
• Case Studies for CBSE Class 12 Business Studies (13)
• MCQ Questions for Class 12 Business Studies (1)
• Revision Notes for Class 12 Business Studies (10)
• Assertion Reason Questions for Class 12 Chemistry (15)
• Case Study Based Questions for Class 12 Chemistry (14)
• Extra Questions for Class 12 Chemistry (5)
• Important Questions for Class 12 Chemistry (15)
• MCQ Questions for Class 12 Chemistry (8)
• NCERT Solutions for Class 12 Chemistry (16)
• Revision Notes for Class 12 Chemistry (7)
• Assertion Reason Questions for Class 12 Economics (9)
• Case Study Questions for Class 12 Economics (9)
• MCQ Questions for Class 12 Economics (1)
• MCQ Questions for Class 12 English (2)
• Assertion Reason Questions for Class 12 Entrepreneurship (7)
• Case Study Questions for Class 12 Entrepreneurship (7)
• Case Study Questions for Class 12 Geography (18)
• Assertion Reason Questions for Class 12 History (8)
• Case Study Questions for Class 12 History (13)
• Assertion Reason Questions for Class 12 Informatics Practices (13)
• Case Study Questions for Class 12 Informatics Practices (11)
• MCQ Questions for Class 12 Informatics Practices (5)
• Assertion and Reason Questions for Class 12 Maths (14)
• Case Study Questions for Class 12 Maths (13)
• Maths Formulas for Class 12 (5)
• MCQ Questions for Class 12 Maths (14)
• Problems Based on Class 12 Maths (1)
• RD Sharma Solutions for Class 12 Maths (1)
• Assertion Reason Questions for Class 12 Physical Education (11)
• Case Study Questions for Class 12 Physical Education (11)
• MCQ Questions for Class 12 Physical Education (10)
• Assertion Reason Questions for Class 12 Physics (16)
• Case Study Based Questions for Class 12 Physics (14)
• Class 12 Physics Conceptual Questions (16)
• Class 12 Physics Discussion Questions (1)
• Class 12 Physics Latest Updates (2)
• Derivations for Class 12 Physics (8)
• Extra Questions for Class 12 Physics (4)
• Important Questions for Class 12 Physics (8)
• MCQ Questions for Class 12 Physics (14)
• NCERT Solutions for Class 12 Physics (18)
• Numerical Problems Based on Class 12 Physics (16)
• Physics Class 12 Viva Questions (1)
• Revision Notes for Class 12 Physics (7)
• Assertion Reason Questions for Class 12 Political Science (16)
• Case Study Questions for Class 12 Political Science (16)
• Notes for Class 12 Political Science (1)
• Assertion Reason Questions for Class 6 Maths (13)
• Case Study Questions for Class 6 Maths (13)
• Extra Questions for Class 6 Maths (1)
• Worksheets for Class 6 Maths (1)
• Assertion Reason Questions for Class 6 Science (16)
• Case Study Questions for Class 6 Science (16)
• Extra Questions for Class 6 Science (1)
• MCQ Questions for Class 6 Science (9)
• Assertion Reason Questions for Class 6 Social Science (1)
• Case Study Questions for Class 6 Social Science (26)
• NCERT Exemplar for Class 7 Maths (13)
• NCERT Exemplar for Class 7 Science (19)
• NCERT Exemplar Solutions for Class 7 Maths (12)
• NCERT Exemplar Solutions for Class 7 Science (18)
• NCERT Notes for Class 7 Science (18)
• Assertion Reason Questions for Class 7 Maths (14)
• Case Study Questions for Class 7 Maths (14)
• Extra Questions for Class 7 Maths (5)
• Assertion Reason Questions for Class 7 Science (18)
• Case Study Questions for Class 7 Science (17)
• Extra Questions for Class 7 Science (19)
• Assertion Reason Questions for Class 7 Social Science (1)
• Case Study Questions for Class 7 Social Science (30)
• Assertion Reason Questions for Class 8 Maths (7)
• Case Study Questions for Class 8 Maths (17)
• Extra Questions for Class 8 Maths (1)
• MCQ Questions for Class 8 Maths (6)
• Assertion Reason Questions for Class 8 Science (16)
• Case Study Questions for Class 8 Science (11)
• Extra Questions for Class 8 Science (2)
• MCQ Questions for Class 8 Science (4)
• Numerical Problems for Class 8 Science (1)
• Revision Notes for Class 8 Science (11)
• Assertion Reason Questions for Class 8 Social Science (27)
• Case Study Questions for Class 8 Social Science (23)
• CBSE Class 9 English Beehive Notes and Summary (2)
• Assertion Reason Questions for Class 9 Maths (14)
• Case Study Questions for Class 9 Maths (14)
• MCQ Questions for Class 9 Maths (11)
• NCERT Notes for Class 9 Maths (6)
• NCERT Solutions for Class 9 Maths (12)
• Revision Notes for Class 9 Maths (3)
• Study Notes for Class 9 Maths (10)
• Assertion Reason Questions for Class 9 Science (16)
• Case Study Questions for Class 9 Science (15)
• Evergreen Science Book Solutions for Class 9 (15)
• Extra Questions for Class 9 Science (22)
• MCQ Questions for Class 9 Science (11)
• NCERT Solutions for Class 9 Science (15)
• Revision Notes for Class 9 Science (1)
• Study Notes for Class 9 Science (15)
• Topic wise MCQ Questions for Class 9 Science (2)
• Topicwise Questions and Answers for Class 9 Science (15)
• Assertion Reason Questions for Class 9 Social Science (15)
• Case Study Questions for Class 9 Social Science (19)
• CHEMISTRY (8)
• Chemistry Articles (2)
• Daily Practice Problems (DPP) (3)
• Books for CBSE Class 9 (1)
• Books for ICSE Class 10 (3)
• Editable Study Materials (8)
• Exam Special for CBSE Class 10 (3)
• H. C. Verma (Concepts of Physics) (13)
• Study Materials for ICSE Class 10 Biology (14)
• Extra Questions for ICSE Class 10 Chemistry (1)
• Study Materials for ICSE Class 10 Chemistry (5)
• Study Materials for ICSE Class 10 Maths (16)
• Important Questions for ICSE Class 10 Physics (13)
• MCQ Questions for ICSE Class 10 Physics (4)
• Study Materials for ICSE Class 10 Physics (8)
• Study Materials for ICSE Class 9 Maths (7)
• Study Materials for ICSE Class 9 Physics (10)
• Topicwise Problems for IIT Foundation Mathematics (4)
• Challenging Physics Problems for JEE Advanced (2)
• Topicwise Problems for JEE Physics (1)
• DPP for JEE Main (1)
• Integer Type Questions for JEE Main (1)
• Integer Type Questions for JEE Chemistry (6)
• Chapterwise Questions for JEE Main Physics (1)
• Integer Type Questions for JEE Main Physics (8)
• Physics Revision Notes for JEE Main (4)
• JEE Mock Test Physics (1)
• JEE Study Material (1)
• JEE/NEET Physics (6)
• CBSE Syllabus (1)
• Maths Articles (2)
• NCERT Books for Class 12 Physics (1)
• NEET Chemistry (13)
• Important Questions for NEET Physics (17)
• Topicwise DPP for NEET Physics (5)
• Topicwise MCQs for NEET Physics (32)
• NTSE MAT Questions (1)
• Physics (1)
• Alternating Current (1)
• Electrostatics (6)
• Fluid Mechanics (2)
• PowerPoint Presentations (13)
• Previous Years Question Paper (3)
• Products for CBSE Class 10 (15)
• Products for CBSE Class 11 (10)
• Products for CBSE Class 12 (6)
• Products for CBSE Class 6 (2)
• Products for CBSE Class 7 (5)
• Products for CBSE Class 8 (1)
• Products for CBSE Class 9 (3)
• Products for Commerce (3)
• Products for Foundation Courses (2)
• Products for JEE Main & Advanced (10)
• Products for NEET (6)
• Products for ICSE Class 6 (1)
• Electrostatic Potential and Capacitance (1)
• Topic Wise Study Notes (Physics) (2)
• Topicwise MCQs for Physics (2)
• Uncategorized (138)

Test series for students preparing for Engineering & Medical Entrance Exams are available. We also provide test series for School Level Exams. Tests for students studying in CBSE, ICSE or any state board are available here. Just click on the link and start test.

Download CBSE Books

Exam Special Series:

• Sample Question Paper for CBSE Class 10 Science (for 2024)
• Sample Question Paper for CBSE Class 10 Maths (for 2024)
• CBSE Most Repeated Questions for Class 10 Science Board Exams
• CBSE Important Diagram Based Questions Class 10 Physics Board Exams
• CBSE Important Numericals Class 10 Physics Board Exams
• CBSE Practical Based Questions for Class 10 Science Board Exams
• CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
• Sample Question Papers for CBSE Class 12 Physics (for 2024)
• Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
• Sample Question Papers for CBSE Class 12 Maths (for 2024)
• Sample Question Papers for CBSE Class 12 Biology (for 2024)
• CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
• Master Organic Conversions CBSE Class 12 Chemistry Board Exams
• CBSE Important Numericals Class 12 Physics Board Exams
• CBSE Important Definitions Class 12 Physics Board Exams
• CBSE Important Laws & Principles Class 12 Physics Board Exams
• 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
• 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
• ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
• ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
• ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
• ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
• ICSE Important Functions and Locations Based Questions Class 10 Biology
• ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)

✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year

✨ Join our Online NEET Test Series for 499/- Only for 1 Year

Leave a Reply Cancel reply

Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs

Study Guides > Precalculus II

Inverse trigonometric functions, understanding and using the inverse sine, cosine, and tangent functions.

• Since [latex]\sin\left(\frac{\pi}{6}\right)=\frac{1}{2}[/latex], then [latex]\frac{\pi}{6}=\sin^{−1}(\frac{1}{2})[/latex].
• Since [latex]\cos(\pi)=−1[/latex], then [latex]\pi=\cos^{−1}(−1)[/latex].
• Since [latex]\tan\left(\frac{\pi}{4}\right)=1[/latex], then [latex]\frac{\pi}{4}=\tan^{−1}(1)[/latex].

Figure 2. (a) Sine function on a restricted domain of [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]; (b) Cosine function on a restricted domain of [0, π]

Figure 3.  Tangent function on a restricted domain of [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex]

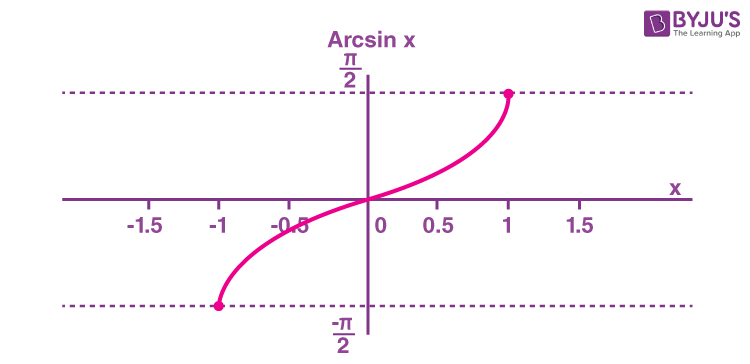
• The inverse sine function  [latex]y=\sin^{−1}x[/latex] means [latex]x=\sin y[/latex]. The inverse sine function is sometimes called the arcsine function, and notated arcsin x . [latex]y=\sin^{−1}x[/latex] has domain [−1, 1] and range [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]
• The inverse cosine function  [latex]y=\cos^{−1}x[/latex] means [latex]x=\cos y[/latex]. The inverse cosine function is sometimes called the arccosine function, and notated arccos x . [latex]y=\cos^{−1}x[/latex] has domain [−1, 1] and range [0, π]
• The inverse tangent function  [latex]y=\tan^{−1}x[/latex] means [latex]x=\tan y[/latex]. The inverse tangent function is sometimes called the arctangent function, and notated arctan x . [latex]y=\tan^{−1}x[/latex] has domain (−∞, ∞) and range [latex]\left(−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right)[/latex]

A General Note: Relations for Inverse Sine, Cosine, and Tangent Functions

Example 1: writing a relation for an inverse function.

[latex]\sin^{−1}(0.96593)\approx \frac{5\pi}{12}[/latex]

Finding the Exact Value of Expressions Involving the Inverse Sine, Cosine, and Tangent Functions

How to: given a “special” input value, evaluate an inverse trigonometric function..

• Find angle  x  for which the original trigonometric function has an output equal to the given input for the inverse trigonometric function.
• If  x  is not in the defined range of the inverse, find another angle  y  that is in the defined range and has the same sine, cosine, or tangent as  x , depending on which corresponds to the given inverse function.

Example 2: Evaluating Inverse Trigonometric Functions for Special Input Values

a. [latex]\sin−1\left(\frac{1}{2}\right)[/latex]

b. [latex]\sin−1\left(−\frac{2}{\sqrt{2}}\right)[/latex]

c. [latex]\cos−1\left(−\frac{3}{\sqrt{2}}\right)[/latex]

d. [latex]\tan^{− 1}(1)[/latex]

a. Evaluating [latex]\sin^{−1}(\frac{1}{2})[/latex] is the same as determining the angle that would have a sine value of [latex]\frac{1}{2}[/latex]. In other words, what angle x would satisfy [latex]\sin(x)=\frac{1}{2}[/latex]? There are multiple values that would satisfy this relationship, such as [latex]\frac{\pi}{6} and \frac{5\pi}{6}[/latex], but we know we need the angle in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex], so the answer will be [latex]\sin^{−1}(\frac{1}{2})=\frac{\pi}{6}[/latex]. Remember that the inverse is a function, so for each input, we will get exactly one output.

b. To evaluate [latex]\sin^{−1}\left(−\frac{\sqrt{2}}{2}\right)[/latex], we know that [latex]\frac{5\pi}{4}[/latex] and [latex]\frac{7\pi}{4}[/latex] both have a sine value of [latex]−\frac{\sqrt{2}}{2}[/latex], but neither is in the interval [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right][/latex]. For that, we need the negative angle coterminal with [latex]\frac{7\pi}{4}:\sin^{−1}\left(−\frac{\sqrt{2}}{2}\right)=−\frac{\pi}{4}[/latex].

c. To evaluate [latex]cos^{−1}\left(−\frac{\sqrt{3}}{2}\right)[/latex], we are looking for an angle in the interval [0,π] with a cosine value of [latex]−\frac{\sqrt{3}}{2}[/latex]. The angle that satisfies this is [latex]\cos^{−1}\left(−\frac{\sqrt{3}}{2}\right)=\frac{5\pi}{6}[/latex].

d. Evaluating [latex]tan^{−1}(1)[/latex], we are looking for an angle in the interval [latex](−\frac{\pi}{2}\text{, }\frac{\pi}{2})[/latex] with a tangent value of 1. The correct angle is [latex]\tan^{−1}(1)=\frac{\pi}{4}[/latex].

• [latex]\sin^{−1}(−1)[/latex]
• [latex]\tan^{−1}(−1)[/latex]
• [latex]\cos^{−1}(−1)[/latex]
• [latex]\cos^{−1}(\frac{1}{2})[/latex]

Using a Calculator to Evaluate Inverse Trigonometric Functions

Example 3: evaluating the inverse sine on a calculator, how to: given two sides of a right triangle like the one shown in figure 7, find an angle..

• If one given side is the hypotenuse of length h and the side of length a adjacent to the desired angle is given, use the equation [latex]\theta=\cos^{−1}\left(\frac{a}{h}\right)[/latex].
• If one given side is the hypotenuse of length h and the side of length p opposite to the desired angle is given, use the equation [latex]\theta=\sin^{−1}\left(\frac{p}{h}\right)[/latex].
• If the two legs (the sides adjacent to the right angle) are given, then use the equation [latex]\theta=\tan^{−1}\left(\frac{p}{a}\right)[/latex].

Example 4: Applying the Inverse Cosine to a Right Triangle

[latex]\begin{array}  \cos\theta=\frac{9}{12} \hfill& \\ \theta=\cos^{−1}\left(\frac{9}{12}\right) \hfill& \text{Apply definition of the inverse.} \\ \theta\approx0.7227\text{ or about }41.4096^{\circ} \hfill& \text{Evaluate.} \end{array}[/latex]

Finding Exact Values of Composite Functions with Inverse Trigonometric Functions

Evaluating compositions of the form [latex]f\left(f^{−1}(y)\right)\\[/latex] and [latex]f^{−1}(f(x))\\[/latex], a general note: compositions of a trigonometric function and its inverse.

[latex]\begin{array} \hfill \sin(\sin^{−1}x)=x\text{ for }−1\leq x\leq1 \hfill \\ \cos(\cos^{−1}x)=x\text{ for }−\infty\leq x\leq1 \\ \tan(\tan^{−1}x)=x\text{ for }−\infty\text{ < }x\text{ < }\infty \end{array}\\[/latex]

[latex]\begin{array} \hfill \sin^{−1}(\sin x)=x\text{ only for }−\frac{\pi}{2} \leq x \leq \frac{\pi}{2} \hfill \\ \cos^{−1}(\cos x)=x\text{ only for }0\leq x\leq\pi \hfill \\ \tan^{−1}(\tan x)=x\text{ only for }−\frac{\pi}{2}\text{ < }x\text{ < }\frac{\pi}{2} \end{array}\\[/latex]

Is it correct that [latex]\sin^{−1}(\sin x)=x\\[/latex]?

• If θ is in the restricted domain of f , then [latex]f^{−1}(f(\theta))=\theta[/latex].
• If not, then find an angle ϕ within the restricted domain of f such that [latex]f(\phi)=f(\theta)\\[/latex]. Then [latex]f^{−1}(f(\theta))=\phi\\[/latex].

Example 5: Using Inverse Trigonometric Functions

• [latex]\sin^{−1}(\sin(\frac{\pi}{3}))\\[/latex]
• [latex]\sin^{−1}(\sin(\frac{2\pi}{3}))\\[/latex]
• [latex]\cos^{−1}(\cos(\frac{2\pi}{3}))\\[/latex]
• [latex]\cos^{−1}(\cos(−\frac{\pi}{3}))\\[/latex]
• [latex]\frac{\pi}{3}\\[/latex] is in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right]\\[/latex], so [latex]\sin^{−1}(\sin(\frac{\pi}{3}))=\frac{\pi}{3}\\[/latex].
• [latex]\frac{2\pi}{3}\\[/latex] is not in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right]\\[/latex], but [latex]\sin\left(\frac{2\pi}{3}\right)=\sin\left(\frac{\pi}{3}\right)\\[/latex], so [latex]\sin^{−1}\left(\sin\left(\frac{2\pi}{3}\right)\right)=\frac{\pi}{3}\\[/latex].
• [latex]\frac{2\pi}{3}\\[/latex] is in [0,π], so [latex]\cos^{−1}\left(\cos\left(\frac{2\pi}{3}\right)\right)=\frac{2\pi}{3}\\[/latex].
• [latex]−\frac{\pi}{3}\\[/latex] is not in [0,π], but [latex]\cos(−\frac{\pi}{3})=\cos\left(\frac{\pi}{3}\right)\\[/latex] because cosine is an even function.
• [latex]\frac{\pi}{3}[/latex] is in [0,π], so [latex]\cos^{−1}\left(\cos\left(−\frac{\pi}{3}\right)\right)=\frac{\pi}{3}\\[/latex].

Evaluating Compositions of the Form [latex]f^{−1}(g(x))\\[/latex]

How to: given functions of the form [latex]\sin^{−1}(\cos x)\text{ and }\cos^{−1}(\sin x)\\[/latex], evaluate them..

• If x  is in [0,π], then [latex]\sin^{−1}(\cos x)=\frac{\pi}{2}−x\\[/latex].
• If x  is not in [0,π], then find another angle y  in [0,π] such that [latex]\cos y=\cos x\\[/latex]. [latex]\sin^{−1}(\cos x)=\frac{\pi}{2}−y\\[/latex]
• If x  is in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right]\\[/latex], then [latex]\cos^{−1}(\sin x)=\frac{\pi}{2}−x\\[/latex].
• If x  is not in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right]\\[/latex], then find another angle y  in [latex]\left[−\frac{\pi}{2}\text{, }\frac{\pi}{2}\right]\\[/latex] such that [latex]\sin y=\sin x\\[/latex]. [latex]\cos^{−1}(\sin x)=\frac{\pi}{2}−y\\[/latex]

Example 6: Evaluating the Composition of an Inverse Sine with a Cosine

• by direct evaluation.
• by the method described previously.
• Here, we can directly evaluate the inside of the composition. [latex]\begin{array}\cos\left(\frac{13\pi}{6}\right)=\cos\left(\frac{\pi}{6}+2\pi\right) \\ \hfill =\cos\left(\frac{\pi}{6}\right) \\ \hfill =\frac{\sqrt{3}}{2} \end{array}\\[/latex] Now, we can evaluate the inverse function as we did earlier. [latex]\sin^{−1}\left(\frac{\sqrt{3}}{2}\right)=\frac{\pi}{3}\\[/latex]
• We have [latex]x=\frac{13\pi}{6}\\[/latex], [latex]y=\frac{\pi}{6}\\[/latex], and [latex]\begin{array} \hfill \sin^{−1}\left(\cos\left(\frac{13\pi}{6}\right)\right)=\frac{\pi}{2}−\frac{\pi}{6} \\ \hfill =\frac{\pi}{3} \hfill \end{array}\\[/latex]

Evaluating Compositions of the Form [latex]f(g^{−1}(x))\\[/latex]

Example 7: evaluating the composition of a sine with an inverse cosine.

[latex]\begin{array} \hfill \sin^{2}\theta+\cos^{2}\theta=1 \hfill& \text{Use our known value for cosine.} \\ \sin^{2}\theta+\left(\frac{4}{5}\right)^{2}=1 \hfill& \text{Solve for sine.} \\ \sin^{2}\theta=1−\frac{16}{25} \\ \sin\theta=\pm\sqrt{\frac{9}{25}}=\pm\frac{3}{5} \end{array}[/latex]

Figure 11. Right triangle illustrating that if [latex]\cos\theta=\frac{4}{5}[/latex], then [latex]\sin\theta=\frac{3}{5}\\[/latex]

Example 8: Evaluating the Composition of a Sine with an Inverse Tangent

[latex]\begin{array}\hfill 4^{2}+7^{2}=\text{hypotenuse}^{2} \\ \text{hypotenuse}=\sqrt{65} \end{array}\\[/latex]

Example 9: Finding the Cosine of the Inverse Sine of an Algebraic Expression

[latex]\begin{array}\hfill\sin^{2}\theta+\cos^{2}\theta=1 \hfill& \text{Use the Pythagorean Theorem.} \\ \left(\frac{x}{3}\right)^{2}+\cos^{2}+\cos^2\theta=1 \hfill& \text{Solve for cosine.} \\ \cos^{2}\theta=1−\frac{x^{2}}{9} \\ \cos\theta=\pm\sqrt{\frac{9−x^{2}}{9}}=\pm\frac{\sqrt{9−x^{2}}}{3} \end{array}\\[/latex]

[latex]\cos\left(\sin^{−1}\left(\frac{x}{3}\right)\right)=\frac{\sqrt{9−x^{2}}}{3}\\[/latex]

Key Concepts

• An inverse function is one that “undoes” another function. The domain of an inverse function is the range of the original function and the range of an inverse function is the domain of the original function.
• Because the trigonometric functions are not one-to-one on their natural domains, inverse trigonometric functions are defined for restricted domains.
• For any trigonometric function [latex]f(x)[/latex], if [latex]x=f^{−1}(y)[/latex], then [latex]f(x)=y[/latex]. However, [latex]f(x)=y[/latex] only implies [latex]x=f^{−1}(y)[/latex] if x is in the restricted domain of f .
• Special angles are the outputs of inverse trigonometric functions for special input values; for example, [latex]\frac{\pi}{4}=\tan^{−1}( 1 )\text{ and }\frac{\pi}{6}=\sin^{−1}(\frac{1}{2})[/latex].
• A calculator will return an angle within the restricted domain of the original trigonometric function.
• Inverse functions allow us to find an angle when given two sides of a right triangle.
• In function composition, if the inside function is an inverse trigonometric function, then there are exact expressions; for example, [latex]\sin\left(\cos^{−1}\left(x\right)\right)=\sqrt{1−x^{2}}[/latex].
• If the inside function is a trigonometric function, then the only possible combinations are [latex]\sin^{−1}\left(\cos x\right)=\frac{\pi}{2}−x[/latex] if [latex]0\leq x\leq\pi[/latex] and [latex]\cos^{−1}\left(\sin x\right)=\frac{\pi}{2}−x[/latex] if [latex]−\frac{\pi}{2}\leq x \leq\frac{\pi}{2}[/latex].
• When evaluating the composition of a trigonometric function with an inverse trigonometric function, draw a reference triangle to assist in determining the ratio of sides that represents the output of the trigonometric function.
• When evaluating the composition of a trigonometric function with an inverse trigonometric function, you may use trig identities to assist in determining the ratio of sides.

Section Exercises

Licenses & attributions, cc licensed content, specific attribution.

• Precalculus. Provided by: OpenStax Authored by: OpenStax College. Located at: https://cnx.org/contents/ [email protected] :1/Preface. License: CC BY: Attribution .

Please add a message.

Message received. Thanks for the feedback.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Inverse trigonometric functions

Intro to inverse trigonometric functions.

• Intro to arcsine (Opens a modal)
• Intro to arctangent (Opens a modal)
• Intro to arccosine (Opens a modal)
• Restricting domains of functions to make them invertible (Opens a modal)
• Domain & range of inverse tangent function (Opens a modal)
• Using inverse trig functions with a calculator (Opens a modal)
• Inverse trigonometric functions review (Opens a modal)
• Evaluate inverse trig functions Get 3 of 4 questions to level up!
• Principal value of inverse trig function Get 3 of 4 questions to level up!
• Shifting angle to principal value branch Get 3 of 4 questions to level up!
• Simplify inverse trig function Get 3 of 4 questions to level up!

Chapter 8: More Functions and Identities

Exercises: 8.2 Inverse Trigonometric Functions Exercises

Practice each skill in the Homework Problems listed.

• Decide whether a function has an inverse function #1–8
• Evaluate the inverse trig functions #9–20
• Model problems with inverse trig functions #21–24
• Solve formulas #25–30
• Simplify expressions involving the inverse trig functions #31–42, 51–68
• Graph the inverse trig functions #43–50, 69 and 70

Suggested Homework

Exercises for 8.2 Inverse Trigonometric Functions

Exercise group.

In Problems 1–4, which functions have an inverse function? Explain your answer.

For Problems 5–8, graph the function and decide if it has an inverse function.

[latex]f(x)=\sin 2x - \cos x[/latex]

[latex]g(x)=4e^{-(x/4)^2}[/latex]

[latex]G(x)=\sqrt{25-x^2}[/latex]

[latex]F(x)=\ln(x^3+8)[/latex]

For Problems 9–14, use a calculator to evaluate. Round your answers to the nearest tenth of a degree.

[latex]\sin^{-1}(0.2838)[/latex]

[latex]\tan^{-1}(4.8972)[/latex]

[latex]\cos^{-1}(0.6894)[/latex]

[latex]\arccos(-0.8134)[/latex]

[latex]\arctan(-1.2765)[/latex]

[latex]\arcsin(-07493)[/latex]

For Problems 15–20, give exact values in radians.

[latex]\cos^{-1} \dfrac{-1}{\sqrt{2}}[/latex]

[latex]\tan^{-1}(-1)[/latex]

[latex]\sin^{-1}\dfrac{-1}{2}[/latex]

[latex]\arccos\dfrac{\sqrt{3}}{2}[/latex]

[latex]\arctan \dfrac{1}{\sqrt{3}}[/latex]

[latex]\arcsin (-1)[/latex]

For Problems 21–26, sketch a figure to help you model each problem.

Delbert is watching the launch of a satellite at Cape Canaveral. The viewing area is 500 yards from the launch site. The angle of elevation, [latex]\theta{,}[/latex] of Delbert’s line of sight increases as the booster rocket rises.

• Write a formula for the height, [latex]h{,}[/latex] of the rocket as a function of [latex]\theta{.}[/latex]
• Write a formula for [latex]\theta[/latex] as a function of [latex]h{.}[/latex]
• Evaluate the formula in part (b) for [latex]h=1000{,}[/latex] and interpret the result.

Francine’s house lies under the flight path from the city airport, and commercial airliners pass overhead at an altitude of 35,000 feet. As Francine watches an airplane recede, its angle of elevation, [latex]\theta{,}[/latex] decreases.

• Write a formula for the horizontal distance, [latex]d{,}[/latex] to the airplane as a function of [latex]\theta{.}[/latex]
• Write a formula for [latex]\theta[/latex] as a function of [latex]d{.}[/latex]
• Evaluate the formula in part (b) for [latex]d=20,000{,}[/latex] and interpret the result.

While driving along the interstate, you approach an enormous 50-foot-wide billboard that sits just beside the road. Your viewing angle, [latex]\theta{,}[/latex] increases as you get closer to the billboard.

• Write a formula for your distance, [latex]d{,}[/latex] from the billboard as a function of [latex]\theta{.}[/latex]
• Evaluate the formula in part (b) for [latex]d=200{,}[/latex] and interpret the result.

Emma is walking along the bank of a straight river toward a 20-meter-long bridge over the river. Let [latex]\theta[/latex] be the angle subtended horizontally by Emma’s view of the bridge.

• Write a formula for Emma’s distance from the bridge, [latex]d{,}[/latex] as a function of [latex]\theta{.}[/latex]
• Evaluate the formula in part (b) for [latex]d=500{,}[/latex] and interpret the result.

Martin is viewing a 4-meter-tall painting whose base is 1 meter above his eye level.

• Write a formula for [latex]\alpha{,}[/latex] the angle subtended from Martin’s eye level to the bottom of the painting, when he stands [latex]x[/latex] meters from the wall.
• Write a formula for [latex]\beta{,}[/latex] the angle subtended by the painting, in terms of [latex]x{.}[/latex]
• Evaluate the formula in part (b) for [latex]x=5{,}[/latex] and interpret the result.

A 5-foot mirror is positioned so that its bottom is 1.5 feet below Jane’s eye level.

• Write a formula for [latex]\alpha{,}[/latex] the angle subtended by the section of mirror below Jane’s eye level, when she stands [latex]x[/latex] feet from the mirror.
• Write a formula for [latex]\theta{,}[/latex] the angle subtended by the entire mirror, in terms of [latex]x{.}[/latex]
• Evaluate the formula in part (b) for [latex]x=10{,}[/latex] and interpret the result.

For Problems 27–32, solve the formula for the given variable.

[latex]V=V_0 \sin(2\pi\omega t+\phi){,}[/latex] for [latex]t[/latex]

[latex]R=\dfrac{1}{32} v_0^2\sin (2\theta){,}[/latex] for [latex]\theta[/latex]

[latex]\dfrac{a}{\sin A}= \dfrac{b}{\sin B}{,}[/latex] for [latex]A[/latex]

[latex]c^2=a^2 + b^2 - 2ab\cos C{,}[/latex] for [latex]C[/latex]

[latex]P=\dfrac{k}{R^4\cos \theta}[/latex] for [latex]\theta[/latex]

[latex]\dfrac{r}{z}=\dfrac{1}{\tan (\alpha + \beta)}{,}[/latex] for [latex]\alpha[/latex]

For Problems 33–38, find exact values without using a calculator.

[latex]\tan\left(\sin^{-1}\left(\dfrac{2}{3}\right)\right)[/latex]

[latex]\tan\left(\cos^{-1}\left(\dfrac{3}{4}\right)\right)[/latex]

[latex]\cos\left[\tan^{-1}(-2)\right][/latex]

[latex]\sin \left[\tan^{-1}\left(\dfrac{-3}{\sqrt{5}}\right)\right][/latex]

[latex]\sin\left[\cos^{-1}\left(\dfrac{-2\sqrt{6}}{7}\right)\right][/latex]

[latex]\cos\left[\sin^{-1}\left(\dfrac{-2}{7}\right)\right][/latex]

For Problems 39–44, simplify the expression.

[latex]\tan(\cos^{-1}x)[/latex]

[latex]\cos(\tan^{-1}a)[/latex]

[latex]\cos(\sin^{-1}h)[/latex]

[latex]\sin(\cos^{-1}v)[/latex]

[latex]\sin(\tan^{-1}2t)[/latex]

[latex]\tan(\sin^{-1}3b)[/latex]

For Problems 45–47, complete the table of values and sketch the function.

Use a graphing calculator to answer each of the following questions. Then explain the results.

• Does [latex]\cos^{-1}x=\dfrac{1}{\cos x}{?}[/latex]
• Does [latex]\sin^{-1}x=\dfrac{1}{\sin x}{?}[/latex]
• Does [latex]\tan^{-1}x=\dfrac{1}{\tan x}{?}[/latex]
• Sketch a graph of [latex]y=\cos^{-1}x{,}[/latex] and label the scales on the axes.
• Use transformations to sketch graphs of [latex]y=2\cos^{-1}x[/latex] and [latex]y=\cos^{-1}(2x){.}[/latex]

Does [latex]2\cos^{-1}x=\cos^{-1}(2x){?}[/latex]

• Sketch a graph of [latex]y=\sin^{-1}x{,}[/latex] and label the scales on the axes.
• Use transformations to sketch graphs of [latex]y=\dfrac{1}{2}\sin^{-1}x[/latex] and [latex]y=\cos^{-1}\left(\dfrac{1}{2}x\right){.}[/latex]
• Does [latex]\dfrac{1}{2}\sin^{-1}x=\cos^{-1}\left(\dfrac{1}{2}x\right){?}[/latex]
• Sketch a graph of [latex]y=\tan^{-1}x{,}[/latex] and label the scales on the axes.
• Use your calculator to graph [latex]y=\dfrac{\sin^{-1}x}{\cos^{-1}x}[/latex] on a suitable domain.
• Does [latex]\tan^{-1}x=\dfrac{\sin^{-1}x}{\cos^{-1}x}{?}[/latex]
• Use your calculator to sketch [latex]y=\sqrt[3]{x}[/latex] and [latex]\tan^{-1}x[/latex] on [latex][-10, 10]{.}[/latex]
• Describe the similarities and differences in the two graphs.

Use the identities from Section 8.1 to help you find exact values for the expressions in Problems 53–58.

[latex]\sin (2\tan^{-1}4)[/latex]

[latex]\cos\left(2\sin^{-1}\left(\dfrac{5}{13}\right)\right)[/latex]

[latex]\tan\left(2\cos^{-1}\left(\dfrac{3}{4}\right)\right)[/latex]

[latex]\sin\left(2\cos^{-1}\left(\dfrac{-4}{5}\right)\right)[/latex]

[latex]\tan\left(2\sin^{-1}\left(\dfrac{1}{3}\right)\right)[/latex]

[latex]\cos\left(2\tan^{-1}\left(\dfrac{3}{2}\right)\right)[/latex]

Let [latex]\alpha= \cos^{-1}\left(\dfrac{-4}{5}\right),~\beta=\sin^{-1}\left(\dfrac{5}{13}\right){.}[/latex] Find exact values for the following:

[latex]\displaystyle \sin (\alpha+\beta)[/latex]

[latex]\displaystyle \cos (\alpha-\beta)[/latex]

[latex]\displaystyle \sin (\alpha-\beta)[/latex]

Let [latex]\alpha= \sin^{-1}\left(\dfrac{-15}{17}\right),~\beta=\tan^{-1}\left(\dfrac{4}{3}\right){.}[/latex] Find exact values for the following:

Find an exact value for [latex]\sin\left(\tan^{-1}\left(\dfrac{3}{4}\right)-\sin^{-1}\left(\dfrac{-4}{5}\right)\right){.}[/latex]

Find an exact value for [latex]\cos\left(\tan^{-1}\left(\dfrac{5}{12}\right)+\sin^{-1}\left(\dfrac{-3}{5}\right)\right){.}[/latex]

Express in terms of [latex]x[/latex] without trigonometric functions.

[latex]\displaystyle \cos(2\sin^{-1}x)[/latex]

Express in terms of [latex]w[/latex] without trigonometric functions.

[latex]\displaystyle \cos(2\tan^{-1}w)[/latex]

If [latex]x=5\sin \theta,~0° \lt \theta \lt 90°{,}[/latex] express [latex]\sin 2\theta[/latex] and [latex]\cos 2\theta[/latex] in terms of [latex]x{.}[/latex]

If [latex]x-1=2\cos \theta,~0° \lt \theta \lt 90°{,}[/latex] express [latex]\sin 2\theta[/latex] and [latex]\cos 2\theta[/latex] in terms of [latex]x{.}[/latex]

If [latex]x=3\tan \theta{,}[/latex] write [latex]\theta +\dfrac{1}{4}\sin 2\theta[/latex] in terms of [latex]x{.}[/latex]

If [latex]x=5\cos \theta{,}[/latex] write [latex]\dfrac{\theta}{2}-\cos 2\theta[/latex] in terms of [latex]x{.}[/latex]

• For what values of [latex]x[/latex] is the function [latex]f(x)=\sin (\arcsin x)[/latex] defined?
• Is [latex]\sin (\arcsin x)=x[/latex] for all [latex]x[/latex] where it is defined? If not, for what values of [latex]x[/latex] is the equation false?
• For what values of [latex]x[/latex] is the function [latex]g(x)=\arcsin(\sin x)[/latex] defined?
• Is [latex]\arcsin (\sin x)=x[/latex] for all [latex]x[/latex] where it is defined? If not, for what values of [latex]x[/latex] is the equation false?
• For what values of [latex]x[/latex] is the function [latex]f(x)=\cos (\arccos x)[/latex] defined?
• Is [latex]\cos (\arccos x)=x[/latex] for all [latex]x[/latex] where it is defined? If not, for what values of [latex]x[/latex] is the equation false?
• For what values of [latex]x[/latex] is the function [latex]g(x)=\arccos(\cos x)[/latex] defined?
• Is [latex]\arccos (\cos x)=x[/latex] for all [latex]x[/latex] where it is defined? If not, for what values of [latex]x[/latex] is the equation false?

Use your calculator to graph [latex]y=\sin^{-1}x+\cos^{-1}x{.}[/latex]

• State the domain and range of the graph.
• Explain why the graph looks as it does.

Use your calculator to graph [latex]y=\tan^{-1}x+\tan^{-1}(\dfrac{1}{x}){.}[/latex]

In Problems 73–74, we find a formula for the area under part of a semicircle.

• Write an expression for the area of the shaded sector in terms of [latex]\theta{.}[/latex]
• How are [latex]\theta[/latex] and [latex]t[/latex] related in the figure? (Hint: Write an expression for [latex]\sin \theta{.}[/latex])
• Combine your answers to (a) and (b) to write an expression for the area of the sector in terms of [latex]t{.}[/latex]
• Write an expression for the height of the shaded triangle in terms of [latex]t{.}[/latex] (Hint: Use the Pythagorean theorem.)
• Write an expression for the area of the triangle in terms of [latex]t{.}[/latex]
• Combine your answers to (b) and to Problem 73 to write an expression for the area bounded above by the upper semicircle, below by the [latex]x[/latex]-axis, on the left by the [latex]y[/latex]-axis, and on the right by [latex]x=t{,}[/latex] when [latex]0 \le t \le 1{.}[/latex]

Trigonometry Copyright © 2024 by Bimal Kunwor; Donna Densmore; Jared Eusea; and Yi Zhen. All Rights Reserved.

Share This Book

• Math Article

Inverse Trigonometric Functions

Inverse trigonometric functions are defined as the inverse functions of the basic trigonometric functions, which are sine, cosine, tangent, cotangent, secant and cosecant functions. They are also termed arcus functions, antitrigonometric functions or cyclometric functions. These inverse functions in trigonometry are used to get the angle with any of the trigonometry ratios . The inverse trigonometry functions have major applications in the field of engineering, physics, geometry and navigation.

Table of Contents

• Derivatives

What Are Inverse Trigonometric Functions?

Inverse trigonometric functions are also called “ arc functions ” since, for a given value of trigonometric functions, they produce the length of arc needed to obtain that particular value. The inverse trigonometric functions perform the opposite operation of the trigonometric functions such as sine, cosine, tangent, cosecant, secant and cotangent. We know that trigonometric functions are applicable, especially to the right-angle triangle. These six important functions are used to find the angle measure in the right-angle triangle when two sides of the triangle measures are known.

The basic inverse trigonometric formulas are as follows:

Inverse Trigonometric  Functions Graphs

There are particularly six inverse trig functions for each trigonometry ratio . The inverse of six important trigonometric functions are

• Arccotangent
• Arccosecant

Let us discuss all six important types of inverse trigonometric functions, along with its definition, formulas, graphs, properties and solved examples.

Arcsine Function

The arcsine function is an inverse of the sine function denoted by sin -1 x . It is represented in the graph as shown below.

Arccosine Function

The arccosine function is the inverse of the cosine function denoted by cos -1 x . It is represented in the graph as shown below.

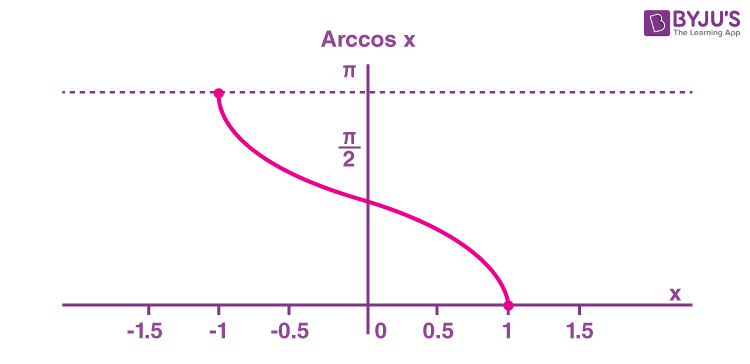
Therefore, the inverse of the cos function can be expressed as y = cos -1 x (arccosine x )

Domain and range of arcsine function are as follows:

Arctangent Function

The arctangent function is the inverse of the tangent function denoted by tan -1 x . It is represented in the graph as shown below.

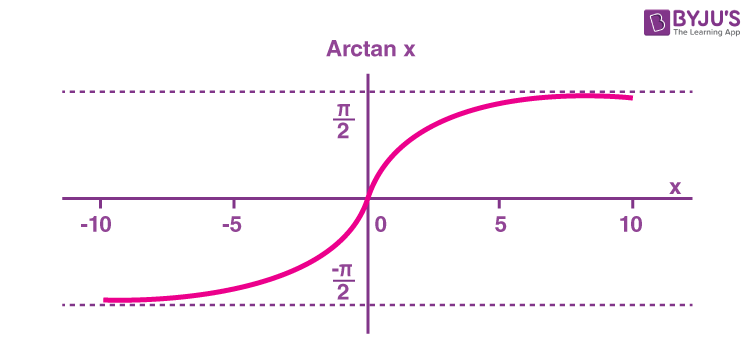
Therefore, the inverse of the tangent function can be expressed as y = tan -1 x (arctangent x )

Domain and range of arctangent are as follows:

Arccotangent (Arccot) Function

The arccotangent function is the inverse of the cotangent function denoted by cot -1 x .

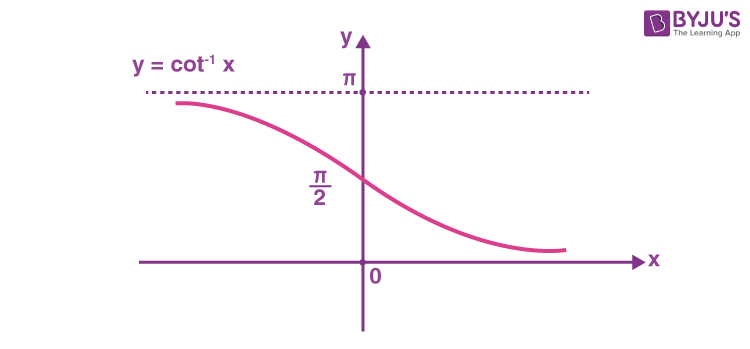
Therefore, the inverse of the cotangent function can be expressed as y = cot -1 x (arccotangent x )

Domain and range of arccotangent are as follows:

Arcsecant Function

What is the arcsecant (arcsec) function? The arcsecant function is the inverse of the secant function denoted by sec -1 x . It is represented in the graph as shown below.

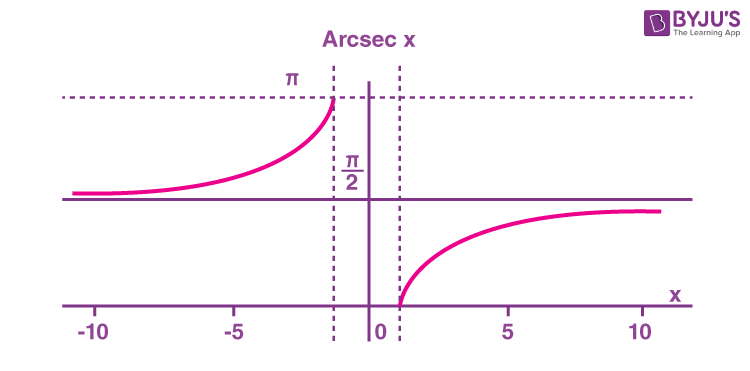
Therefore, the inverse of the secant function can be expressed as y = sec -1 x (arcsecant x )

Domain and range of arcsecant are as follows:

Arccosecant Function

What is the arccosecant (arccsc x ) function? The arccosecant function is the inverse of the cosecant function denoted by cosec -1 x . It is represented in the graph as shown below.

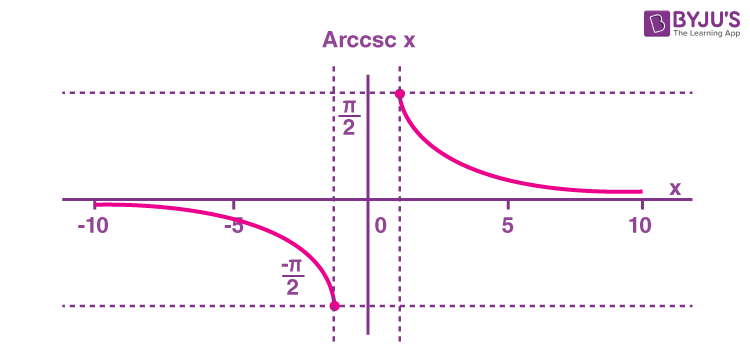
Therefore, the inverse of the cosecant function can be expressed as y = cosec -1 x (arccosecant x )

Domain and range of arccosecant are:

Inverse Trigonometric Functions Table

Let us look at all the inverse trigonometric functions with their notation, definition, domain and range.

Inverse Trigonometric Functions Derivatives

The derivatives of inverse trigonometric functions are first-order derivatives. Let us check out the derivatives of all six inverse functions here.

Learn in detail the derivation of these functions here:  Derivative Inverse Trigonometric Functions

Inverse Trigonometric Functions Properties

The inverse trigonometric functions are also known as arc functions. Inverse trigonometric functions are defined in a certain interval (under restricted domains). Read more on inverse trigonometric properties here .

Trigonometry Basics

Trigonometry basics include the basic trigonometry and trigonometric ratios, such as sin x, cos x, tan x, cosec x, sec x and cot x.

Video Lessons on Inverse Trigonometric Functions

Multiple Angles

Inverse Trigonometric Functions Problems

Example 1: Find the value of x for sin(x) = 2.

Solution:  Given: sin x = 2

x =sin -1 (2), which is not possible.

Hence, there is no value of x for which sin x = 2, so the domain of sin -1 x is -1 to 1 for the values of x.

Example 2: Find the value of sin -1 (sin (π/6)).

sin -1 (sin (π/6) = π/6 (Using identity sin -1 (sin (x) ) = x)

Example 3: Find sin (cos -1 3/5).

Suppose that, cos -1 3/5 = x

So, cos x = 3/5

This implies, sin x = sin (cos -1 3/5) = 4/5

Example 4: 

Practice Problems

Problem 1: Solve: tan(arcsin 12/13)

Problem 2: Find the value of x, cos(arccos 1) = cos x

Learn more about inverse trigonometric functions at BYJU’S. Download BYJU’S – The Learning App for other Maths-related articles and access various interactive videos to make the subject easy.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Case study inverse trigonometry 2 chapter 2 class 12

Case study chapter 2 (inverse trigonometry).

Case study 2:- Read the following and answer the question.(Case study inverse trigonometry 1)

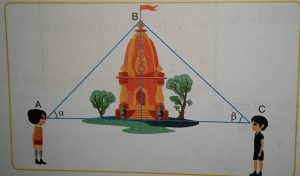
  Two men on either side of a temple 30 metres high observes its top at the angles of elevation α and β respectively. (as shown in the figure above). the distance between the two men is 40√3 metres and the distance between the first person A and the temple is 30√3 metres.

(i) ∠CAB = α =

(ii) ∠CAB = α =

(iii) ∠BCA = β = 

(iv) ∠ABC = 

(a) π/4                       (b) π/6

(c) π/2                         (d) π/3

(a) (-1, 1), (0, π)                (b) [-1, 1], (0, π)

(c) [-1, 1], [0, π]                 (d) (-1, 1), [-π/2, π/2]

Solution :We have

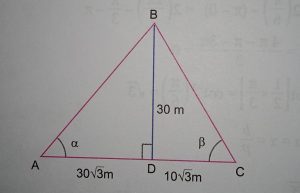
(i) Answer (b)

Now in ΔABD (right angled)

(ii) Answer (c) 

We have from (i)

(iii) Answer (d)

In right ΔBCD, we have

(iv) Answer (c)

ΔABC, we have,

∠ABC + ∠BAC  +  ∠ACB = 180°

⇒  ∠ABC + α + β = 180°

⇒  ∠ABC + 30 + 60 = 180

⇒  ∠ABC = 90

⇒  ∠ABC = π/2

(v) Answer (c)

Domain =[-1, 1]

Range = [0, π]

Some other Case study problem

Case study 1:-  The government of India is planning to fix a hoarding board at the face of a building on yhe road of bisy market for awaeeness on COVID-19 protocol. Ram , Robert and Rahim are the three engineers who are working on this project. “A” is considered to be person viewing the hoarding board 20 metres away from the building , standing at the edge of a pathwaynearby . Ram , Robert and Rahim suggested to the firm to place the hoarding board at three different locations namely C, D and E. “C” is at the height of  10 metres from the ground level. for the viewer A, the angle of elevation of “D” is double the angle of elevation of “C” the angle of elevation of “E” is triple the angle of elevation of “C” for the same viewer.(Case study inverse trigonometric 1 )

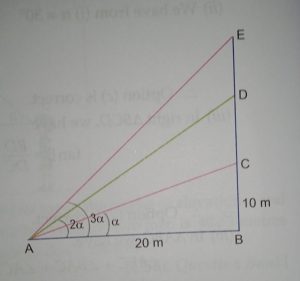
Solution: For solution click here

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

The Site is down as we are performing important server maintenance, during which time the server will be unavailable for approximately 24 hours. Please hold off on any critical actions until we are finished. As always your feedback is appreciated.

• Study Packages
• NCERT Solutions
• Sample Papers
• Online Test

• Questions Bank
• Mathematics
• Inverse Trigonometric Functions
• Test Series
• Ncert Solutions
• Solved Papers
• Current Affairs
• JEE Main & Advanced
• Pre-Primary
• MP State Exams
• UP State Exams
• Rajasthan State Exams
• Jharkhand State Exams
• Chhattisgarh State Exams
• Bihar State Exams
• Haryana State Exams
• Gujarat State Exams
• MH State Exams
• Himachal State Exams
• Delhi State Exams
• Uttarakhand State Exams
• Punjab State Exams
• J&K State Exams

12th Class Mathematics Inverse Trigonometric Functions Question Bank

Done case based (mcqs) - inverse trigonometric functions total questions - 10.

A) \[{{\sin }^{-1}}\left( \frac{2}{\sqrt{3}} \right)\] done clear

B) \[{{\sin }^{-1}}\left( \frac{1}{2} \right)\] done clear

C) \[{{\sin }^{-1}}\left( 2 \right)\] done clear

D) \[{{\sin }^{-1}}\left( \frac{\sqrt{3}}{2} \right)\] done clear

question_answer 2) \[\angle CAB=\alpha =\]

A) \[{{\cos }^{-1}}\left( \frac{1}{5} \right)\] done clear

B) \[{{\cos }^{-1}}\left( \frac{2}{5} \right)\] done clear

C) \[{{\cos }^{-1}}\left( \frac{\sqrt{3}}{2} \right)\] done clear

D) \[{{\cos }^{-1}}\left( \frac{4}{5} \right)\] done clear

question_answer 3) \[\angle BCA=\beta =\]

A) \[{{\tan }^{-1}}\left( \frac{1}{2} \right)\] done clear

B) \[{{\tan }^{-1}}\left( 2 \right)\] done clear

C) \[{{\tan }^{-1}}\left( \frac{1}{\sqrt{3}} \right)\] done clear

D) \[{{\tan }^{-1}}\left( \sqrt{3} \right)\] done clear

question_answer 4) \[\angle ABC=\]

A) \[\frac{\pi }{4}\] done clear

B) \[\frac{\pi }{6}\] done clear

C) \[\frac{\pi }{2}\] done clear

D) \[\frac{\pi }{3}\] done clear

question_answer 5) Domain and Range of \[{{\cos }^{-1}}x=\]

A) \[\left( -1,\,\,1 \right),\,\left( 0,\,\,\pi  \right)\] done clear

B) \[\left[ -1,\,\,1 \right],\,\left( 0,\,\pi  \right)\] done clear

C) \[\left[ -1,\,1 \right],\,\left[ 0,\,\,\pi  \right]\] done clear

D) \[\left( -1,\,\,1 \right),\,\left[ -\frac{\pi }{2},\frac{\pi }{2} \right]\] done clear

A) \[{{\tan }^{-1}}\left( 2 \right)\] done clear

B) \[{{\tan }^{-1}}\left( \frac{1}{2} \right)\] done clear

C) \[{{\tan }^{-1}}\left( 1 \right)\] done clear

D) \[{{\tan }^{-1}}\left( 3 \right)\] done clear

question_answer 7) Measure of \[\angle DAB=\]

A) \[{{\tan }^{-1}}\left( \frac{3}{4} \right)\] done clear

B) \[{{\tan }^{-1}}\left( 3 \right)\] done clear

C) \[{{\tan }^{-1}}\left( \frac{4}{3} \right)\] done clear

D) \[{{\tan }^{-1}}(4)\] done clear

question_answer 8) Measure of \[\angle EAB=\]

A) \[{{\tan }^{-1}}\left( 11 \right)\] done clear

B) \[{{\tan }^{-1}}3\] done clear

C) \[{{\tan }^{-1}}\left( \frac{2}{11} \right)\] done clear

D) \[{{\tan }^{-1}}\left( \frac{11}{2} \right)\] done clear

question_answer 9) A' is another viewer standing on the same line of observation across the road. If the width of the road is 5 meters, then the difference between \[\angle CAB\]and \[\angle CA'B\]is

A) \[{{\tan }^{-1}}\left( 1/2 \right)\] done clear

B) \[{{\tan }^{-1}}\left( \frac{1}{12} \right)\] done clear

C) \[{{\tan }^{-1}}\left( \frac{2}{5} \right)\] done clear

D) \[{{\tan }^{-1}}\left( \frac{11}{21} \right)\] done clear

question_answer 10) Domain and Range of \[{{\tan }^{-1}}x=\]

A) \[{{R}^{+}},\,\left( -\frac{\pi }{2},\,\frac{\pi }{2} \right)\] done clear

B) \[{{R}^{-}},\,\left( -\frac{\pi }{2},\,\frac{\pi }{2} \right)\] done clear

C) \[R,\,\left( -\frac{\pi }{2},\,\frac{\pi }{2} \right)\] done clear

D) \[R,\,\left( 0,\,\frac{\pi }{2} \right)\] done clear

Study Package

Case Based (MCQs) - Inverse Trigonometric Functions

Related question.

Reset Password.

OTP has been sent to your mobile number and is valid for one hour

Mobile Number Verified

Your mobile number is verified.

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

2.2: The Inverse Trigonometric Functions

• Last updated
• Save as PDF
• Page ID 113912

• Carl Stitz & Jeff Zeager
• Lakeland Community College & Lorain County Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

As the title indicates, in this section we concern ourselves with finding inverses of the (circular) trigonometric functions. Our immediate problem is that, owing to their periodic nature, none of the six circular functions is one-to-one. To remedy this, we restrict the domains of the circular functions in the same way we restricted the domain of the quadratic function in Example 5.2.3 in Section 5.2 to obtain a one-to-one function. We first consider \(f(x) = \cos(x)\). Choosing the interval \([0,\pi]\) allows us to keep the range as \([-1,1]\) as well as the properties of being smooth and continuous.

Restricting the domain of \(f(x)=\cos (x) \text { to }[0, \pi]\).

Recall from Section 5.2 that the inverse of a function \(f\) is typically denoted \(f^{-1}\). For this reason, some textbooks use the notation \(f^{-1}(x) = \cos^{-1}(x)\) for the inverse of \(f(x) = \cos(x)\). The obvious pitfall here is our convention of writing \((\cos(x))^2\) as \(\cos^{2}(x)\), \((\cos(x))^3\) as \(\cos^{3}(x)\) and so on. It is far too easy to confuse \(\cos^{-1}(x)\) with \(\frac{1}{\cos(x)} = \sec(x)\) so we will not use this notation in our text. 1 Instead, we use the notation \(f^{-1}(x) = \arccos(x)\), read ‘arc-cosine of \(x\)’. To understand the ‘arc’ in ‘arccosine’, recall that an inverse function, by definition, reverses the process of the original function. The function \(f(t) = \cos(t)\) takes a real number input \(t\), associates it with the angle \(\theta = t\) radians, and returns the value \(\cos(\theta)\). Digging deeper, 2 we have that \(\cos(\theta) = \cos(t)\) is the \(x\)-coordinate of the terminal point on the Unit Circle of an oriented arc of length \(|t|\) whose initial point is \((1, 0)\). Hence, we may view the inputs to \(f(t) = \cos(t)\) as oriented arcs and the outputs as \(x\)-coordinates on the Unit Circle. The function \(f^{-1}\), then, would take \(x\)-coordinates on the Unit Circle and return oriented arcs, hence the ‘arc’ in arccosine. Below are the graphs of \(f(x) = \cos(x)\) and \(f^{-1}(x) = \arccos(x)\), where we obtain the latter from the former by reflecting it across the line \(y=x\), in accordance with Theorem5.3 .

We restrict \(g(x) = \sin(x)\) in a similar manner, although the interval of choice is \(\left[ -\frac{\pi}{2}, \frac{\pi}{2}\right]\).

It should be no surprise that we call \(g^{-1}(x) = \arcsin(x)\), which is read ‘arc-sine of \(x\)’.

We list some important facts about the arccosine and arcsine functions in the following theorem.

Theorem 10.26. Properties of the Arccosine and Arcsine Functions

• Domain: \([-1,1]\)
• Range: \([0,\pi]\)
• \(\arccos(x) = t\) if and only if \(0 \leq t \leq \pi\) and \(\cos(t) = x\)
• \(\cos(\arccos(x)) = x\) provided \(-1 \leq x \leq 1\)
• \(\arccos(\cos(x)) = x\) provided \(0 \leq x \leq \pi\)
• Range: \(\left[ -\frac{\pi}{2}, \frac{\pi}{2}\right]\)
• \(\arcsin(x) = t\) if and only if \(-\frac{\pi}{2} \leq t \leq \frac{\pi}{2}\) and \(\sin(t) = x\)
• \(\sin(\arcsin(x)) = x\) provided \(-1 \leq x \leq 1\)
• \(\arcsin(\sin(x)) = x\) provided \(-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}\)
• additionally, arcsine is odd

Everything in Theorem 10.26 is a direct consequence of the facts that \(f(x) = \cos(x)\) for \(0 \leq x \leq \pi\) and \(F(x) = \arccos(x)\) are inverses of each other as are \(g(x) = \sin(x)\) for \(-\frac{\pi}{2} \leq x \leq \frac{\pi}{2}\) and \(G(x) = \arcsin(x)\). It’s about time for an example.

Example 10.6.1

• \(\arccos\left(\frac{1}{2}\right)\)
• \(\arcsin\left(\frac{\sqrt{2}}{2}\right)\)
• \(\cos\left(\arccos\left(-\frac{3}{5}\right)\right)\)
• \(\sin\left(\arccos\left(-\frac{3}{5}\right)\right)\)
• \(\arccos\left(-\frac{\sqrt{2}}{2}\right)\)
• \(\arcsin\left(-\frac{1}{2}\right)\)
• \(\arccos\left( \cos\left(\frac{\pi}{6}\right)\right)\)
• \(\arccos\left( \cos\left(\frac{11\pi}{6}\right)\right)\)
• \(\tan\left(\arccos\left(x \right)\right)\)
• \(\cos\left(2 \arcsin(x)\right)\)
• To find \(\arccos\left(\frac{1}{2}\right)\), we need to find the real number \(t\) (or, equivalently, an angle measuring \(t\) radians) which lies between \(0\) and \(\pi\) with \(\cos(t) = \frac{1}{2}\). We know \(t = \frac{\pi}{3}\) meets these criteria, so \(\arccos\left(\frac{1}{2}\right)= \frac{\pi}{3}\).
• The value of \(\arcsin\left(\frac{\sqrt{2}}{2}\right)\) is a real number \(t\) between \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\) with \(\sin(t) = \frac{\sqrt{2}}{2}\). The number we seek is \(t = \frac{\pi}{4}\). Hence, \(\arcsin\left(\frac{\sqrt{2}}{2}\right) = \frac{\pi}{4}\).
• The number \(t = \arccos\left(-\frac{\sqrt{2}}{2}\right)\) lies in the interval \([0,\pi]\) with \(\cos(t) = -\frac{\sqrt{2}}{2}\). Our answer is \(\arccos\left(-\frac{\sqrt{2}}{2}\right) = \frac{3\pi}{4}\).
• To find \(\arcsin\left(-\frac{1}{2}\right)\), we seek the number \(t\) in the interval \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) with \(\sin(t) = -\frac{1}{2}\). The answer is \(t = -\frac{\pi}{6}\) so that \(\arcsin\left(-\frac{1}{2}\right) = -\frac{\pi}{6}\).
• Since \(0 \leq \frac{\pi}{6} \leq \pi\), we could simply invoke Theorem 10.26 to get \(\arccos\left( \cos\left(\frac{\pi}{6}\right)\right) = \frac{\pi}{6}\). However, in order to make sure we understand why this is the case, we choose to work the example through using the definition of arccosine. Working from the inside out, \(\arccos\left( \cos\left(\frac{\pi}{6}\right)\right) = \arccos\left( \frac{\sqrt{3}}{2}\right)\). Now, \(\arccos\left( \frac{\sqrt{3}}{2}\right)\) is the real number \(t\) with \(0 \leq t \leq \pi\) and \(\cos(t) = \frac{\sqrt{3}}{2}\). We find \(t = \frac{\pi}{6}\), so that \(\arccos\left( \cos\left(\frac{\pi}{6}\right)\right) = \frac{\pi}{6}\).
• Since \(\frac{11\pi}{6}\) does not fall between \(0\) and \(\pi\), Theorem 10.26 does not apply. We are forced to work through from the inside out starting with \(\arccos\left( \cos\left(\frac{11\pi}{6}\right)\right) = \arccos\left(\frac{\sqrt{3}}{2}\right)\). From the previous problem, we know \(\arccos\left(\frac{\sqrt{3}}{2}\right) = \frac{\pi}{6}\). Hence, \(\arccos\left( \cos\left(\frac{11\pi}{6}\right)\right) = \frac{\pi}{6}\).
• One way to simplify \(\cos\left(\arccos\left(-\frac{3}{5}\right)\right)\) is to use Theorem 10.26 directly. Since \(-\frac{3}{5}\) is between \(-1\) and \(1\), we have that \(\cos\left(\arccos\left(-\frac{3}{5}\right)\right) = -\frac{3}{5}\) and we are done. However, as before, to really understand why this cancellation occurs, we let \(t = \arccos\left(-\frac{3}{5}\right)\). Then, by definition, \(\cos(t) = -\frac{3}{5}\). Hence, \(\cos\left(\arccos\left(-\frac{3}{5}\right)\right) = \cos(t) = -\frac{3}{5}\), and we are finished in (nearly) the same amount of time.
• As in the previous example, we let \(t = \arccos\left(-\frac{3}{5}\right)\) so that \(\cos(t) = -\frac{3}{5}\) for some \(t\) where \(0 \leq t \leq \pi\). Since \(\cos(t) < 0\), we can narrow this down a bit and conclude that \(\frac{\pi}{2} < t < \pi\), so that \(t\) corresponds to an angle in Quadrant II. In terms of \(t\), then, we need to find \(\sin\left(\arccos\left(-\frac{3}{5}\right)\right) = \sin(t)\). Using the Pythagorean Identity \(\cos^{2}(t) + \sin^{2}(t) = 1\), we get \(\left(-\frac{3}{5}\right)^2 + \sin^{2}(t) = 1\) or \(\sin(t) = \pm \frac{4}{5}\). Since \(t\) corresponds to a Quadrants II angle, we choose \(\sin(t) = \frac{4}{5}\). Hence, \(\sin\left(\arccos\left(-\frac{3}{5}\right)\right) = \frac{4}{5}\).
• We begin this problem in the same manner we began the previous two problems. To help us see the forest for the trees, we let \(t = \arccos(x)\), so our goal is to find a way to express \(\tan\left(\arccos\left(x \right)\right) = \tan(t)\) in terms of \(x\). Since \(t = \arccos(x)\), we know \(\cos(t) = x\) where \(0 \leq t \leq \pi\), but since we are after an expression for \(\tan(t)\), we know we need to throw out \(t = \frac{\pi}{2}\) from consideration. Hence, either \(0 \leq t < \frac{\pi}{2}\) or \(\frac{\pi}{2} < t \leq \pi\) so that, geometrically, \(t\) corresponds to an angle in Quadrant I or Quadrant II. One approach 3 to finding \(\tan(t)\) is to use the quotient identity \(\tan(t) = \frac{\sin(t)}{\cos(t)}\). Substituting \(\cos(t) = x\) into the Pythagorean Identity \(\cos^{2}(t) + \sin^{2}(t) = 1\) gives \(x^2 + \sin^{2}(t) = 1\), from which we get \(\sin(t) = \pm \sqrt{1-x^2}\). Since \(t\) corresponds to angles in Quadrants I and II, \(\sin(t) \geq 0\), so we choose \(\sin(t) = \sqrt{1-x^2}\). Thus, \[\tan(t) = \dfrac{\sin(t)}{\cos(t)} = \dfrac{\sqrt{1-x^2}}{x}\nonumber\] To determine the values of \(x\) for which this equivalence is valid, we consider our substitution \(t = \arccos(x)\). Since the domain of \(\arccos(x)\) is \([-1,1]\), we know we must restrict \(-1 \leq x \leq 1\). Additionally, since we had to discard \(t = \frac{\pi}{2}\), we need to discard \(x = \cos\left(\frac{\pi}{2}\right) = 0\). Hence, \(\tan\left(\arccos\left(x \right)\right) =\frac{\sqrt{1-x^2}}{x}\) is valid for \(x\) in \([-1,0)\cup(0,1]\).
• We proceed as in the previous problem by writing \(t = \arcsin(x)\) so that \(t\) lies in the interval \(\left[ -\frac{\pi}{2}, \frac{\pi}{2}\right]\) with \(\sin(t) = x\). We aim to express \(\cos\left(2 \arcsin(x)\right) = \cos(2t)\) in terms of \(x\). Since \(\cos(2t)\) is defined everywhere, we get no additional restrictions on \(t\) as we did in the previous problem. We have three choices for rewriting \(\cos(2t)\): \(\cos^{2}(t) - \sin^{2}(t)\), \(2\cos^{2}(t) - 1\) and \(1 - 2\sin^{2}(t)\). Since we know \(x = \sin(t)\), it is easiest to use the last form: \[\cos\left(2 \arcsin(x)\right) = \cos(2t) = 1 - 2\sin^{2}(t) = 1 - 2x^2\nonumber\] To find the restrictions on \(x\), we once again appeal to our substitution \(t = \arcsin(x)\). Since \(\arcsin(x)\) is defined only for \(-1 \leq x \leq 1\), the equivalence \(\cos\left(2 \arcsin(x)\right) = 1-2x^2\) is valid only on \([-1,1]\).

A few remarks about Example 10.6.1 are in order. Most of the common errors encountered in dealing with the inverse circular functions come from the need to restrict the domains of the original functions so that they are one-to-one. One instance of this phenomenon is the fact that \(\arccos\left( \cos\left(\frac{11\pi}{6}\right)\right) = \frac{\pi}{6}\) as opposed to \(\frac{11\pi}{6}\). This is the exact same phenomenon discussed in Section 5.2 when we saw \(\sqrt{(-2)^2} = 2\) as opposed to \(-2\). Additionally, even though the expression we arrived at in part 2b above, namely \(1 - 2x^2\), is defined for all real numbers, the equivalence \(\cos\left(2 \arcsin(x)\right) = 1-2x^2\) is valid for only \(-1 \leq x \leq 1\). This is akin to the fact that while the expression \(x\) is defined for all real numbers, the equivalence \(\left( \sqrt{x} \right)^2 = x\) is valid only for \(x \geq 0\). For this reason, it pays to be careful when we determine the intervals where such equivalences are valid.

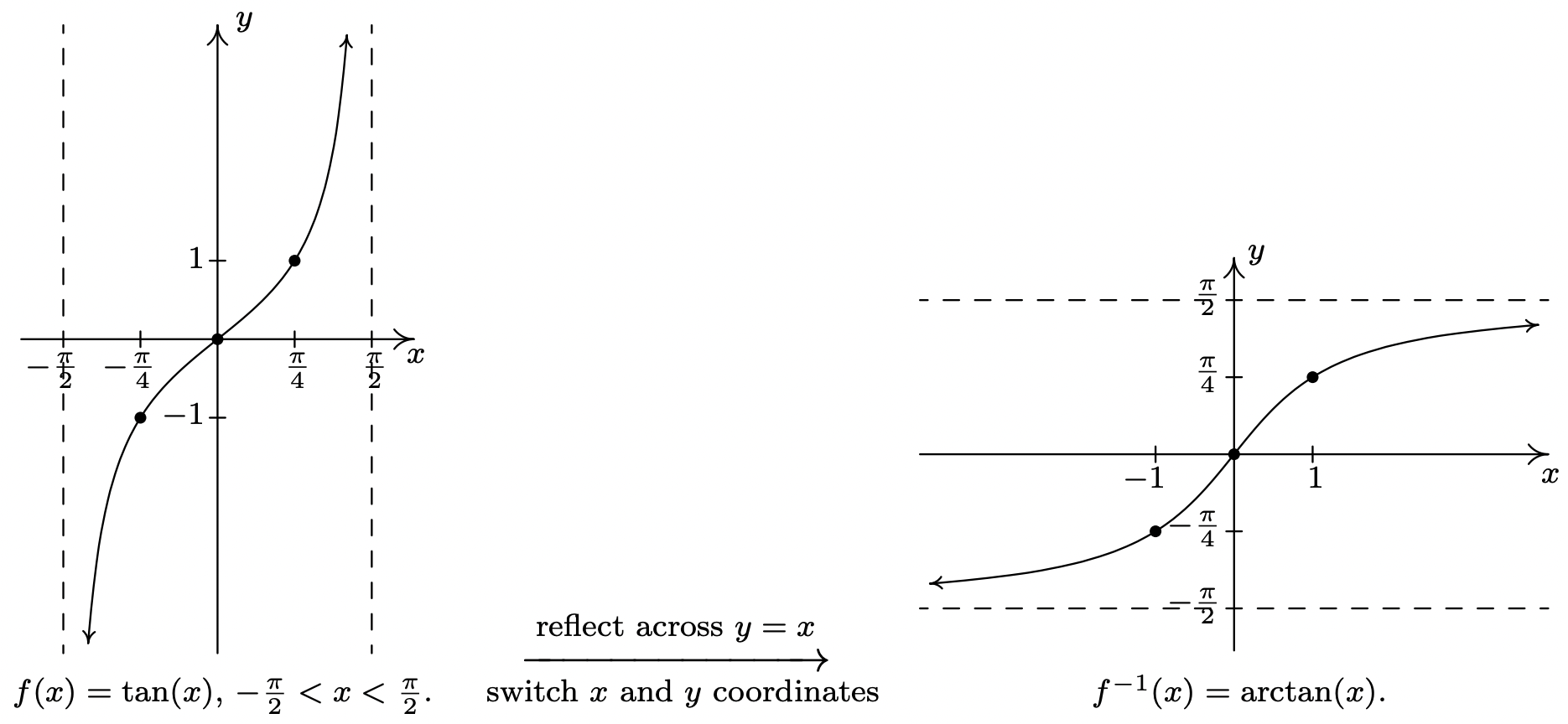
The next pair of functions we wish to discuss are the inverses of tangent and cotangent, which are named arctangent and arccotangent, respectively. First, we restrict \(f(x) = \tan(x)\) to its fundamental cycle on \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) to obtain \(f^{-1}(x) = \arctan(x)\). Among other things, note that the vertical asymptotes \(x = -\frac{\pi}{2}\) and \(x = \frac{\pi}{2}\) of the graph of \(f(x) = \tan(x)\) become the horizontal asymptotes \(y = -\frac{\pi}{2}\) and \(y = \frac{\pi}{2}\) of the graph of \(f^{-1}(x) = \arctan(x)\).

Next, we restrict \(g(x) = \cot(x)\) to its fundamental cycle on \((0,\pi)\) to obtain \(g^{-1}(x) = \mbox{arccot}(x)\). Once again, the vertical asymptotes \(x=0\) and \(x=\pi\) of the graph of \(g(x) = \cot(x)\) become the horizontal asymptotes \(y = 0\) and \(y = \pi\) of the graph of \(g^{-1}(x) = \mbox{arccot}(x)\). We show these graphs on the next page and list some of the basic properties of the arctangent and arccotangent functions.

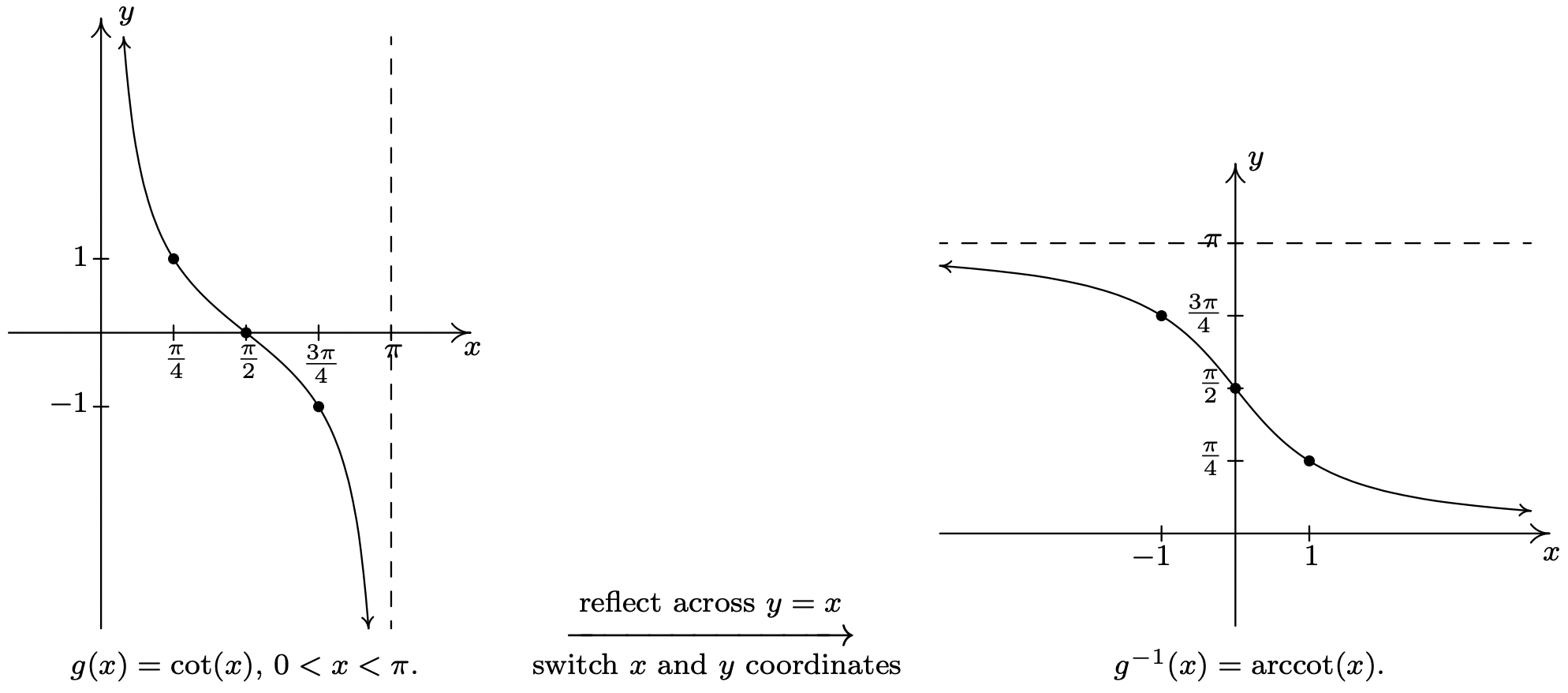
Theorem 10.27. Properties of the Arctangent and Arccotangent Functions

• Domain: \((-\infty, \infty)\)
• Range: \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\)
• as \(x \rightarrow -\infty\), \(\arctan(x) \rightarrow -\frac{\pi}{2}^{+}\); as \(x \rightarrow \infty\), \(\arctan(x) \rightarrow \frac{\pi}{2}^{-}\)
• \(\arctan(x) = t\) if and only if \(-\frac{\pi}{2} < t < \frac{\pi}{2}\) and \(\tan(t) = x\)
• \(\arctan(x) = \mbox{arccot}\left(\frac{1}{x}\right)\) for \(x > 0\)
• \(\tan\left(\arctan(x)\right) = x\) for all real numbers \(x\)
• \(\arctan(\tan(x)) = x\) provided \(-\frac{\pi}{2} < x < \frac{\pi}{2}\)
• additionally, arctangent is odd
• Range: \((0, \pi)\)
• as \(x \rightarrow -\infty\), \(\mbox{arccot}(x) \rightarrow \pi^{-}\); as \(x \rightarrow \infty\), \(\mbox{arccot}(x) \rightarrow 0^{+}\)
• \(\mbox{arccot}(x) = t\) if and only if \(0 < t < \pi\) and \(\cot(t) = x\)
• \(\mbox{arccot}(x) =\arctan\left(\frac{1}{x}\right)\) for \(x > 0\)
• \(\cot\left(\mbox{arccot}(x)\right) = x\) for all real numbers \(x\)
• \(\mbox{arccot}(\cot(x)) = x\) provided \(0 < x < \pi\)

Example 10.6.2

• \(\arctan(\sqrt{3})\)
• \(\mbox{arccot}(-\sqrt{3})\)
• \(\cot(\mbox{arccot}(-5))\)
• \(\sin\left(\arctan\left(-\frac{3}{4}\right)\right)\)
• \(\tan(2 \arctan(x))\)
• \(\cos(\mbox{arccot}(2x))\)
• We know \(\arctan(\sqrt{3})\) is the real number \(t\) between \(-\frac{\pi}{2}\) and \(\frac{\pi}{2}\) with \(\tan(t) = \sqrt{3}\). We find \(t = \frac{\pi}{3}\), so \(\arctan(\sqrt{3}) = \frac{\pi}{3}\).
• The real number \(t = \mbox{arccot}(-\sqrt{3})\) lies in the interval \((0,\pi)\) with \(\cot(t) = -\sqrt{3}\). We get \(\mbox{arccot}(-\sqrt{3}) = \frac{5\pi}{6}\).
• We can apply Theorem 10.27 directly and obtain \(\cot(\mbox{arccot}(-5)) = -5\). However, working it through provides us with yet another opportunity to understand why this is the case. Letting \(t = \mbox{arccot}(-5)\), we have that \(t\) belongs to the interval \((0,\pi)\) and \(\cot(t)=-5\). Hence, \(\cot(\mbox{arccot}(-5)) = \cot(t)=-5\).
• We start simplifying \(\sin\left(\arctan\left(-\frac{3}{4}\right)\right)\) by letting \(t = \arctan\left(-\frac{3}{4}\right)\). Then \(\tan(t) = -\frac{3}{4}\) for some \(-\frac{\pi}{2} < t < \frac{\pi}{2}\). Since \(\tan(t) < 0\), we know, in fact, \(-\frac{\pi}{2} < t < 0\). One way to proceed is to use The Pythagorean Identity, \(1 + \cot^{2}(t) = \csc^{2}(t)\), since this relates the reciprocals of \(\tan(t)\) and \(\sin(t)\) and is valid for all \(t\) under consideration. 4 From \(\tan(t) = -\frac{3}{4}\), we get \(\cot(t) = -\frac{4}{3}\). Substituting, we get \(1 + \left(-\frac{4}{3}\right)^2 = \csc^{2}(t)\) so that \(\csc(t) = \pm \frac{5}{3}\). Since \(-\frac{\pi}{2} < t < 0\), we choose \(\csc(t) = -\frac{5}{3}\), so \(\sin(t) = -\frac{3}{5}\). Hence, \(\sin\left(\arctan\left(-\frac{3}{4}\right)\right) = -\frac{3}{5}\).
• If we let \(t = \arctan(x)\), then \(-\frac{\pi}{2} < t < \frac{\pi}{2}\) and \(\tan(t) = x\). We look for a way to express \(\tan(2 \arctan(x)) = \tan(2t)\) in terms of \(x\). Before we get started using identities, we note that \(\tan(2t)\) is undefined when \(2t = \frac{\pi}{2} + \pi k\) for integers \(k\). Dividing both sides of this equation by \(2\) tells us we need to exclude values of \(t\) where \(t = \frac{\pi}{4} + \frac{\pi}{2} k\), where \(k\) is an integer. The only members of this family which lie in \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) are \(t = \pm \frac{\pi}{4}\), which means the values of \(t\) under consideration are \(\left(-\frac{\pi}{2}, -\frac{\pi}{4}\right) \cup \left(-\frac{\pi}{4}, \frac{\pi}{4}\right) \cup \left(\frac{\pi}{4}, \frac{\pi}{2}\right)\). Returning to \(\arctan(2t)\), we note the double angle identity \(\tan(2t) = \frac{2 \tan(t)}{1 - \tan^{2}(t)}\), is valid for all the values of \(t\) under consideration, hence we get \[\tan(2 \arctan(x)) = \tan(2t) = \frac{2 \tan(t)}{1 - \tan^{2}(t)}= \frac{2x}{1-x^2}\nonumber\] To find where this equivalence is valid we check back with our substitution \(t = \arctan(x)\). Since the domain of \(\arctan(x)\) is all real numbers, the only exclusions come from the values of \(t\) we discarded earlier, \(t = \pm \frac{\pi}{4}\). Since \(x =\tan(t)\), this means we exclude \(x = \tan\left(\pm \frac{\pi}{4}\right) = \pm 1\). Hence, the equivalence \(\tan(2 \arctan(x)) = \frac{2x}{1-x^2}\) holds for all \(x\) in \((-\infty, -1) \cup (-1,1) \cup (1,\infty)\).
• To get started, we let \(t = \mbox{arccot}(2x)\) so that \(\cot(t) = 2x\) where \(0 < t < \pi\). In terms of \(t\), \(\cos(\mbox{arccot}(2x)) = \cos(t)\), and our goal is to express the latter in terms of \(x\). Since \(\cos(t)\) is always defined, there are no additional restrictions on \(t\), so we can begin using identities to relate \(\cot(t)\) to \(\cos(t)\). The identity \(\cot(t) = \frac{\cos(t)}{\sin(t)}\) is valid for \(t\) in \((0,\pi)\), so our strategy is to obtain \(\sin(t)\) in terms of \(x\), then write \(\cos(t) = \cot(t) \sin(t)\). The identity \(1 + \cot^{2}(t) = \csc^{2}(t)\) holds for all \(t\) in \((0,\pi)\) and relates \(\cot(t)\) and \(\csc(t) = \frac{1}{\sin(t)}\). Substituting \(\cot(t) =2x\), we get \(1 + (2x)^2 = \csc^{2}(t)\), or \(\csc(t) = \pm \sqrt{4x^2+1}\). Since \(t\) is between \(0\) and \(\pi\), \(\csc(t) > 0\), so \(\csc(t) =\sqrt{4x^2+1}\) which gives \(\sin(t) = \frac{1}{\sqrt{4x^2+1}}\). Hence, \[\cos(\mbox{arccot}(2x)) = \cos(t) = \cot(t) \sin(t) = \frac{2x}{\sqrt{4x^2+1}}\nonumber\] Since \(\mbox{arccot}(2x)\) is defined for all real numbers \(x\) and we encountered no additional restrictions on \(t\), we have \(\cos\left(\mbox{arccot}(2x)\right) = \frac{2x}{\sqrt{4x^2+1}}\) for all real numbers \(x\).

The last two functions to invert are secant and cosecant. A portion of each of their graphs, which were first discussed in Subsection 10.5.2 , are given below with the fundamental cycles highlighted.

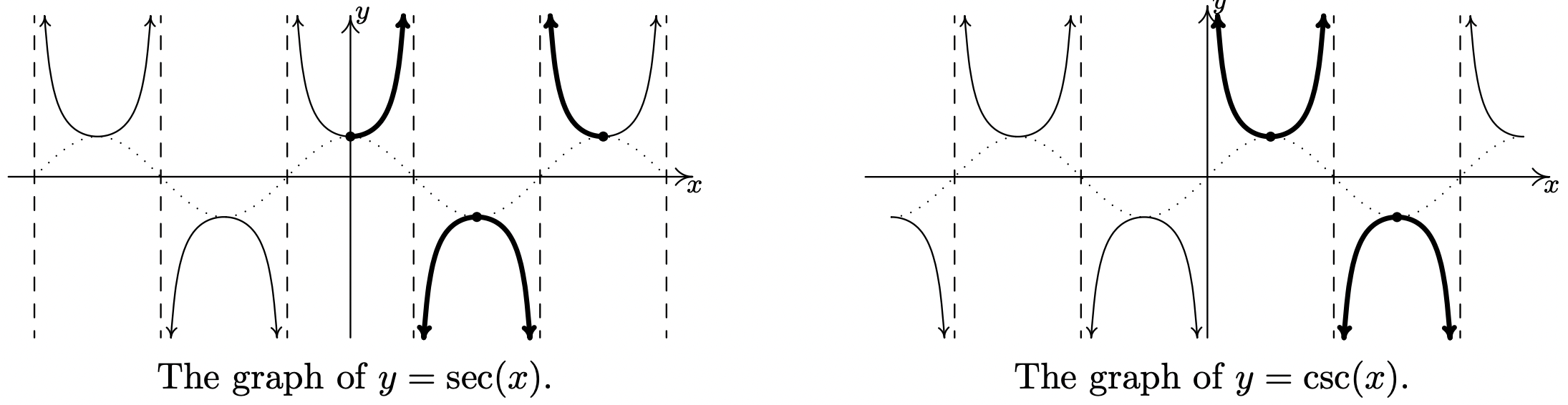
It is clear from the graph of secant that we cannot find one single continuous piece of its graph which covers its entire range of \((-\infty, -1] \cup [1, \infty)\) and restricts the domain of the function so that it is one-to-one. The same is true for cosecant. Thus in order to define the arcsecant and arccosecant functions, we must settle for a piecewise approach wherein we choose one piece to cover the top of the range, namely \([1, \infty)\), and another piece to cover the bottom, namely \((-\infty, -1]\). There are two generally accepted ways make these choices which restrict the domains of these functions so that they are one-to-one. One approach simplifies the Trigonometry associated with the inverse functions, but complicates the Calculus; the other makes the Calculus easier, but the Trigonometry less so. We present both points of view.

10.6.1. Inverses of Secant and Cosecant: Trigonometry Friendly Approach

In this subsection, we restrict the secant and cosecant functions to coincide with the restrictions on cosine and sine, respectively. For \(f(x) = \sec(x)\), we restrict the domain to \(\left[0, \frac{\pi}{2}\right) \cup \left( \frac{\pi}{2}, \pi\right]\)

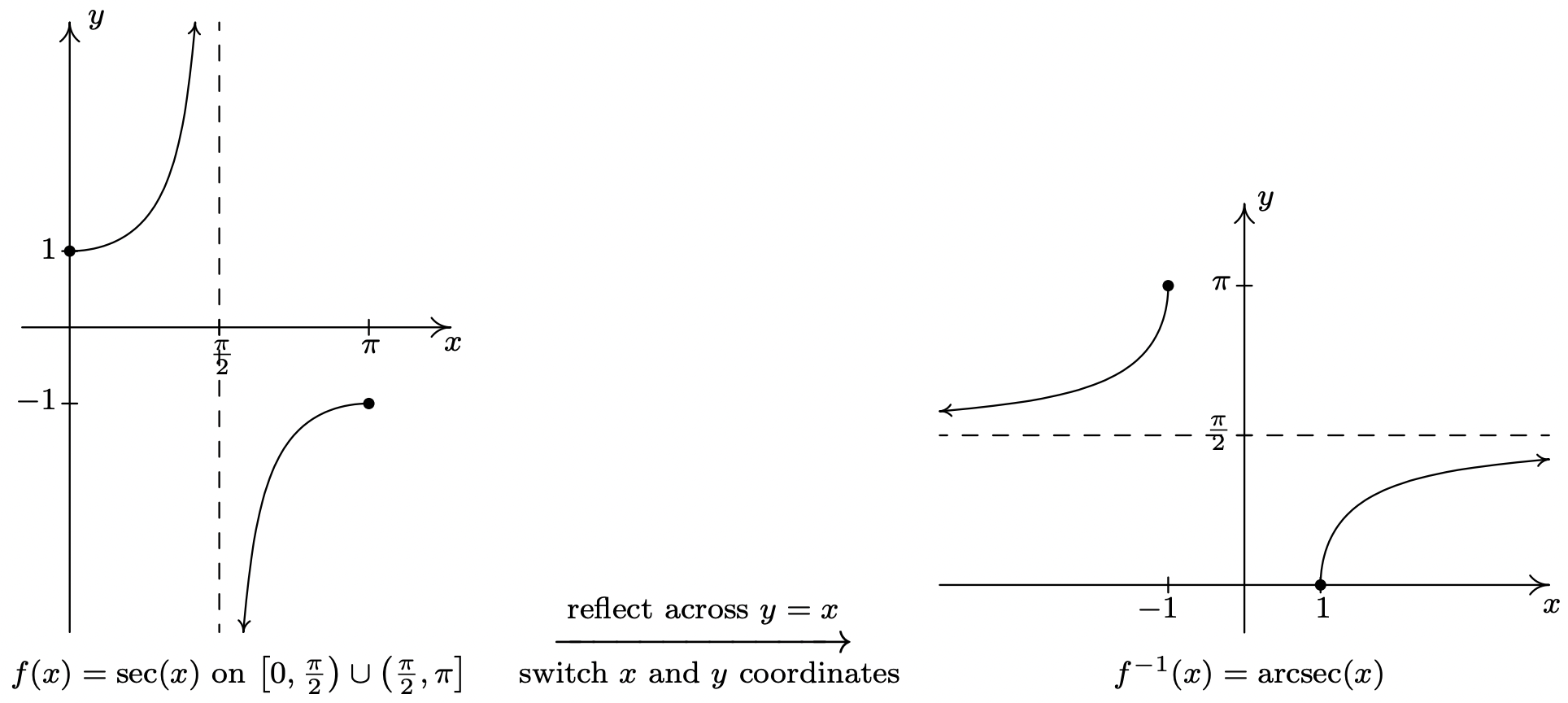
and we restrict \(g(x) = \csc(x)\) to \(\left[-\frac{\pi}{2}, 0\right) \cup \left(0, \frac{\pi}{2}\right]\).

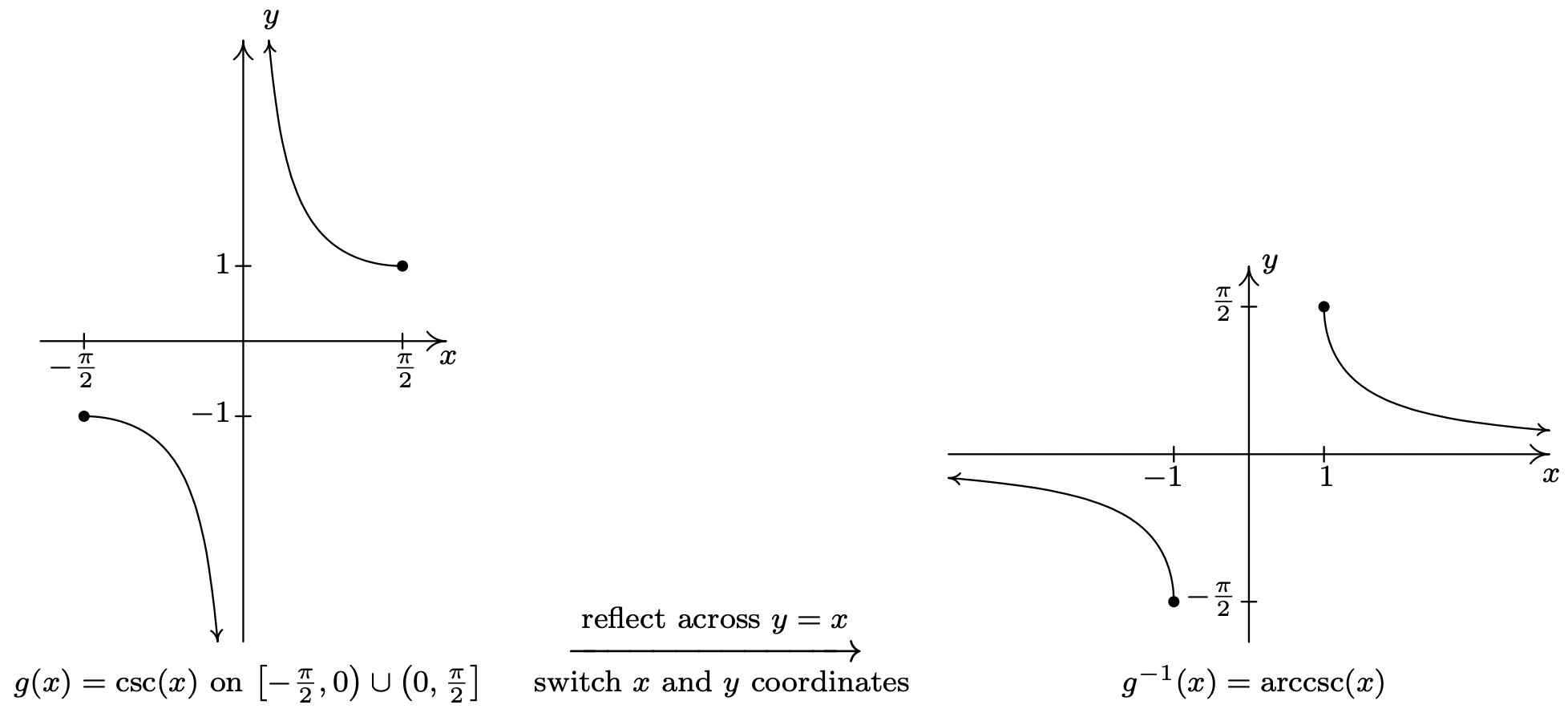
Note that for both arcsecant and arccosecant, the domain is \((-\infty, -1] \cup [1, \infty)\). Taking a page from Section 2.2 , we can rewrite this as \(\left\{ x : |x| \geq 1\right\}\). This is often done in Calculus textbooks, so we include it here for completeness. Using these definitions, we get the following properties of the arcsecant and arccosecant functions.

Theorem 10.28. Properties of the Arcsecant and Arccosecant Function a

• Domain: \(\left\{ x : |x| \geq 1 \right\} = (-\infty, -1] \cup [1,\infty)\)
• Range: \(\left[0, \frac{\pi}{2} \right) \cup \left(\frac{\pi}{2}, \pi\right]\)
• as \(x \rightarrow -\infty\), \(\mbox{arcsec}(x) \rightarrow \frac{\pi}{2}^{+}\); as \(x \rightarrow \infty\), \(\mbox{arcsec}(x) \rightarrow \frac{\pi}{2}^{-}\)
• \(\mbox{arcsec}(x) = t\) if and only if \(0 \leq t < \frac{\pi}{2}\) or \(\frac{\pi}{2} < t \leq \pi\) and \(\sec(t) = x\)
• \(\mbox{arcsec}(x) = \arccos\left(\frac{1}{x}\right)\) provided \(|x| \geq 1\)
• \(\sec\left(\mbox{arcsec}(x)\right) = x\) provided \(|x| \geq 1\)
• \(\mbox{arcsec}(\sec(x)) = x\) provided \(0 \leq x < \frac{\pi}{2}\) or \(\frac{\pi}{2} < x \leq \pi\)
• Range: \(\left[-\frac{\pi}{2}, 0 \right) \cup \left(0, \frac{\pi}{2} \right]\)
• as \(x \rightarrow -\infty\), \(\mbox{arccsc}(x) \rightarrow 0^{-}\); as \(x \rightarrow \infty\), \(\mbox{arccsc}(x) \rightarrow 0^{+}\)
• \(\mbox{arccsc}(x) = t\) if and only if \(-\frac{\pi}{2} \leq t < 0\) or \(0 < t \leq \frac{\pi}{2}\) and \(\csc(t) = x\)
• \(\mbox{arccsc}(x) = \arcsin\left(\frac{1}{x}\right)\) provided \(|x| \geq 1\)
• \(\csc\left(\mbox{arccsc}(x)\right) = x\) provided \(|x| \geq 1\)
• \(\mbox{arccsc}(\csc(x)) = x\) provided \(-\frac{\pi}{2} \leq x < 0\) or \(0 < x \leq \frac{\pi}{2}\)
• additionally, arccosecant is odd

Example 10.6.3.

• \(\mbox{arcsec}(2)\)
• \(\mbox{arccsc}(-2)\)
• \(\mbox{arcsec}\left( \sec\left( \frac{5\pi}{4} \right) \right)\)
• \(\cot\left(\mbox{arccsc}\left(-3\right)\right)\)
• \(\tan(\mbox{arcsec}(x))\)
• \(\cos(\mbox{arccsc}(4x))\)
• Using Theorem 10.28 , we have \(\mbox{arcsec}(2) = \arccos\left(\frac{1}{2}\right) = \frac{\pi}{3}\).
• Once again, Theorem 10.28 comes to our aid giving \(\mbox{arccsc}(-2) = \arcsin\left(-\frac{1}{2}\right) = -\frac{\pi}{6}\).
• Since \(\frac{5\pi}{4}\) doesn’t fall between \(0\) and \(\frac{\pi}{2}\) or \(\frac{\pi}{2}\) and \(\pi\), we cannot use the inverse property stated in Theorem 10.28 . We can, nevertheless, begin by working ‘inside out’ which yields \(\mbox{arcsec}\left( \sec\left( \frac{5\pi}{4} \right) \right) = \mbox{arcsec}(-\sqrt{2}) = \arccos\left(-\frac{\sqrt{2}}{2}\right) = \frac{3\pi}{4}\).
• One way to begin to simplify \(\cot\left(\mbox{arccsc}\left(-3\right)\right)\) is to let \(t = \mbox{arccsc}(-3)\). Then, \(\csc(t) = -3\) and, since this is negative, we have that \(t\) lies in the interval \(\left[ -\frac{\pi}{2},0\right)\). We are after \(\cot\left(\mbox{arccsc}\left(-3\right)\right) = \cot(t)\), so we use the Pythagorean Identity \(1 + \cot^{2}(t) = \csc^{2}(t)\). Substituting, we have \(1 + \cot^{2}(t) = (-3)^2\), or \(\cot(t) = \pm \sqrt{8} = \pm 2 \sqrt{2}\). Since \(-\frac{\pi}{2} \leq t < 0\), \(\cot(t) < 0\), so we get \(\cot\left(\mbox{arccsc}\left(-3\right)\right) = -2\sqrt{2}\).

\[\tan(t) = \left\{ \begin{array}{rr} \sqrt{x^2-1}, & \text{if $0 \leq t < \frac{\pi}{2}$} \\[4pt] -\sqrt{x^2-1}, & \text{if $\frac{\pi}{2} < t \leq \pi$} \end{array}\right.\nonumber\]

Now we need to determine what these conditions on \(t\) mean for \(x\). Since \(x = \sec(t)\), when \(0 \leq t < \frac{\pi}{2}\), \(x \geq 1\), and when \(\frac{\pi}{2} < t \leq \pi\), \(x \leq -1\). Since we encountered no further restrictions on \(t\), the equivalence below holds for all \(x\) in \((-\infty, -1] \cup [1, \infty)\).

\[\tan(\mbox{arcsec}(x)) = \left\{ \begin{array}{rr} \sqrt{x^2-1}, & \text{if $x \geq 1$} \\[5pt] -\sqrt{x^2-1}, & \text{if $x \leq -1$} \end{array}\right.\nonumber\]

• To simplify \(\cos(\mbox{arccsc}(4x))\), we start by letting \(t = \mbox{arccsc}(4x)\). Then \(\csc(t) = 4x\) for \(t\) in \(\left[-\frac{\pi}{2}, 0 \right) \cup \left(0, \frac{\pi}{2}\right]\), and we now set about finding an expression for \(\cos(\mbox{arccsc}(4x)) = \cos(t)\). Since \(\cos(t)\) is defined for all \(t\), we do not encounter any additional restrictions on \(t\). From \(\csc(t) = 4x\), we get \(\sin(t) = \frac{1}{4x}\), so to find \(\cos(t)\), we can make use if the identity \(\cos^{2}(t) + \sin^{2}(t) = 1\). Substituting \(\sin(t) = \frac{1}{4x}\) gives \(\cos^{2}(t) + \left(\frac{1}{4x}\right)^2 = 1\). Solving, we get \[\cos(t) = \pm \sqrt{\frac{16x^2-1}{16x^2}} = \pm \frac{\sqrt{16x^2-1}}{4|x|}\nonumber\] Since \(t\) belongs to \(\left[-\frac{\pi}{2}, 0 \right) \cup \left(0, \frac{\pi}{2}\right]\), we know \(\cos(t) \geq 0\), so we choose \(\cos(t) = \frac{\sqrt{16-x^2}}{4|x|}\). (The absolute values here are necessary, since \(x\) could be negative.) To find the values for which this equivalence is valid, we look back at our original substution, \(t = \mbox{arccsc}(4x)\). Since the domain of \(\mbox{arccsc}(x)\) requires its argument \(x\) to satisfy \(|x| \geq 1\), the domain of \(\mbox{arccsc}(4x)\) requires \(|4x| \geq 1\). Using Theorem 2.4 , we rewrite this inequality and solve to get \(x \leq -\frac{1}{4}\) or \(x \geq \frac{1}{4}\). Since we had no additional restrictions on \(t\), the equivalence \(\cos(\mbox{arccsc}(4x)) = \frac{\sqrt{16x^2-1}}{4|x|}\) holds for all \(x\) in \(\left(-\infty, -\frac{1}{4} \right] \cup \left[\frac{1}{4}, \infty \right)\).

10.6.2. Inverses of Secant and Cosecant: Calculus Friendly Approach

In this subsection, we restrict \(f(x) = \sec(x)\) to \(\left[0, \frac{\pi}{2}\right) \cup \left[\pi, \frac{3\pi}{2}\right)\)

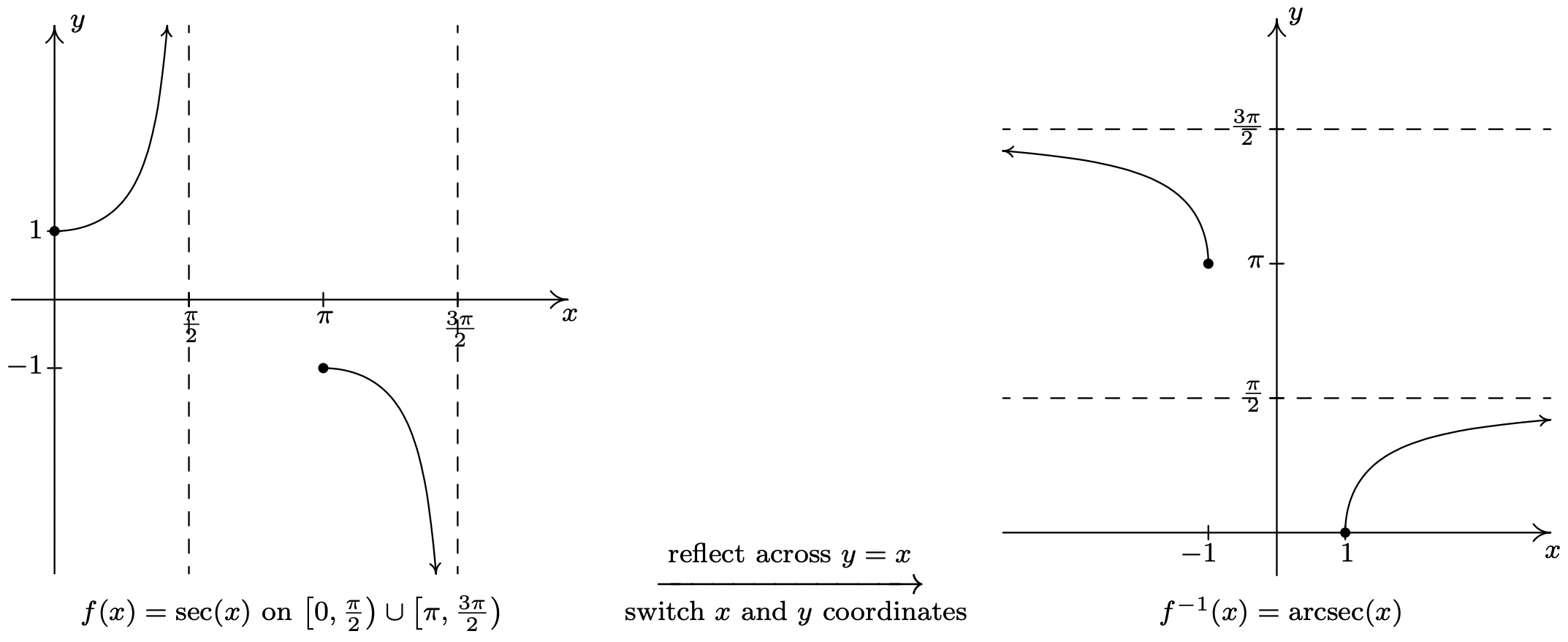
and we restrict \(g(x) = \csc(x)\) to \(\left(0, \frac{\pi}{2}\right] \cup \left( \pi, \frac{3\pi}{2}\right]\).

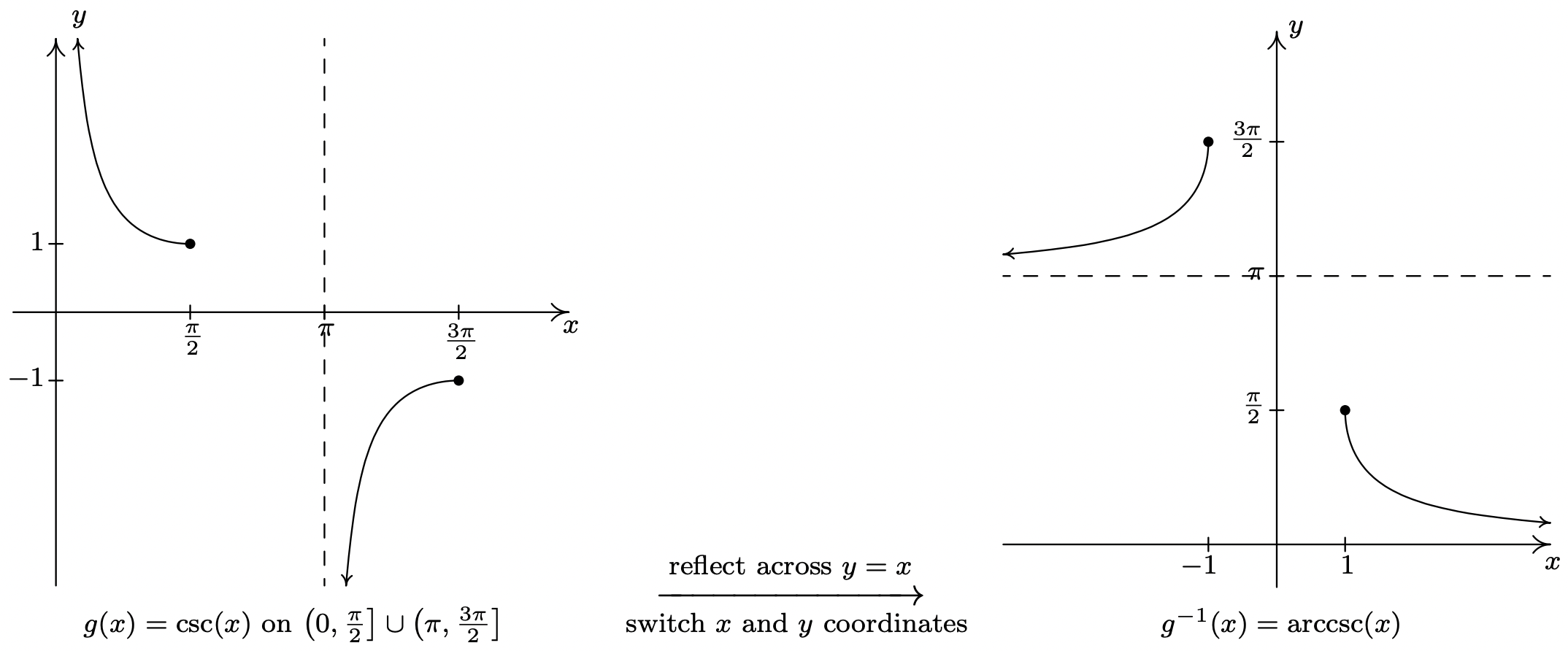
Using these definitions, we get the following result.

Theorem 10.29. Properties of the Arcsecant and Arccosecant Function a

• Range: \(\left[0, \frac{\pi}{2} \right) \cup \left[\pi, \frac{3\pi}{2} \right)\)
• as \(x \rightarrow -\infty\), \(\mbox{arcsec}(x) \rightarrow \frac{3\pi}{2}^{-}\); as \(x \rightarrow \infty\), \(\mbox{arcsec}(x) \rightarrow \frac{\pi}{2}^{-}\)
• \(\mbox{arcsec}(x) = t\) if and only if \(0 \leq t < \frac{\pi}{2}\) or \(\pi \leq t < \frac{3\pi}{2}\) and \(\sec(t) = x\)
• \(\mbox{arcsec}(x) = \arccos\left(\frac{1}{x}\right)\) for \(x \geq 1\) only b
• \(\mbox{arcsec}(\sec(x)) = x\) provided \(0 \leq x < \frac{\pi}{2}\) or \(\pi \leq x < \frac{3\pi}{2}\)
• Range: \(\left(0, \frac{\pi}{2} \right] \cup \left( \pi, \frac{3\pi}{2} \right]\)
• as \(x \rightarrow -\infty\), \(\mbox{arccsc}(x) \rightarrow \pi^{+}\); as \(x \rightarrow \infty\), \(\mbox{arccsc}(x) \rightarrow 0^{+}\)
• \(\mbox{arccsc}(x) = t\) if and only if \(0 < t \leq \frac{\pi}{2}\) or \(\pi < t \leq \frac{3\pi}{2}\) and \(\csc(t) = x\)
• \(\mbox{arccsc}(x) = \arcsin\left(\frac{1}{x}\right)\) for \(x \geq 1\) only c
• \(\mbox{arccsc}(\csc(x)) = x\) provided \(0 < x \leq \frac{\pi}{2}\) or \(\pi < x \leq \frac{3\pi}{2}\)

a . . . assuming the “Calculus Friendly” ranges are used.

b Compare this with the similar result in Theorem 10.28 .

c Compare this with the similar result in Theorem 10.28 .

Our next example is a duplicate of Example 10.6.3 . The interested reader is invited to compare and contrast the solution to each.

Example 10.6.4.

• Since \(2 \geq 1\), we may invoke Theorem 10.29 to get \(\mbox{arcsec}(2) = \arccos\left(\frac{1}{2}\right) = \frac{\pi}{3}\).
• Unfortunately, \(-2\) is not greater to or equal to \(1\), so we cannot apply Theorem 10.29 to \(\mbox{arccsc}(-2)\) and convert this into an arcsine problem. Instead, we appeal to the definition. The real number \(t = \mbox{arccsc}(-2)\) lies in \(\left(0,\frac{\pi}{2} \right] \cup \left(\pi, \frac{3\pi}{2}\right]\) and satisfies \(\csc(t) = -2\). The \(t\) we’re after is \(t = \frac{7\pi}{6}\), so \(\mbox{arccsc}(-2) = \frac{7\pi}{6}\).
• Since \(\frac{5\pi}{4}\) lies between \(\pi\) and \(\frac{3\pi}{2}\), we may apply Theorem 10.29 directly to simplify \(\mbox{arcsec}\left( \sec\left( \frac{5\pi}{4} \right) \right) = \frac{5\pi}{4}\). We encourage the reader to work this through using the definition as we have done in the previous examples to see how it goes.
• To simplify \(\cot\left(\mbox{arccsc}\left(-3\right)\right)\) we let \(t = \mbox{arccsc}\left(-3\right)\) so that \(\cot\left(\mbox{arccsc}\left(-3\right)\right) = \cot(t)\). We know \(\csc(t) = -3\), and since this is negative, \(t\) lies in \(\left( \pi, \frac{3\pi}{2}\right]\). Using the identity \(1 + \cot^{2}(t) = \csc^{2}(t)\), we find \(1 + \cot^{2}(t) = (-3)^2\) so that \(\cot(t) = \pm \sqrt{8} = \pm 2 \sqrt{2}\). Since \(t\) is in the interval \(\left(\pi, \frac{3\pi}{2}\right]\), we know \(\cot(t) > 0\). Our answer is \(\cot\left(\mbox{arccsc}\left(-3\right)\right) = 2 \sqrt{2}\).
• We begin simplifying \(\tan(\mbox{arcsec}(x))\) by letting \(t = \mbox{arcsec}(x)\). Then, \(\sec(t) = x\) for \(t\) in \(\left[0, \frac{\pi}{2} \right) \cup \left[\pi, \frac{3\pi}{2} \right)\), and we seek a formula for \(\tan(t)\). Since \(\tan(t)\) is defined for all \(t\) values under consideration, we have no additional restrictions on \(t\). To relate \(\sec(t)\) to \(\tan(t)\), we use the identity \(1 + \tan^{2}(t) = \sec^{2}(t)\). This is valid for all values of \(t\) under consideration, and when we substitute \(\sec(t) = x\), we get \(1 + \tan^{2}(t) = x^2\). Hence, \(\tan(t) = \pm \sqrt{x^2-1}\). Since \(t\) lies in \(\left[0, \frac{\pi}{2} \right) \cup \left[\pi, \frac{3\pi}{2} \right)\), \(\tan(t) \geq 0\), so we choose \(\tan(t) = \sqrt{x^2-1}\). Since we found no additional restrictions on \(t\), the equivalence \(\tan(\mbox{arcsec}(x)) = \sqrt{x^2-1}\) holds for all \(x\) in the domain of \(t = \mbox{arcsec}(x)\), namely \((-\infty, -1] \cup [1,\infty)\).

\[\cos(t) = \left\{ \begin{array}{rr} \dfrac{\sqrt{16x^2-1}}{4|x|}, & \text{if $0 \leq t \leq \frac{\pi}{2}$} \\[4pt] -\dfrac{\sqrt{16x^2-1}}{4|x|}, & \text{if $\pi < t \leq \frac{3\pi}{2}$} \end{array}\right.\nonumber\]

We now see what these restrictions mean in terms of \(x\). Since \(4x = \csc(t)\), we get that for \(0 \leq t \leq \frac{\pi}{2}\), \(4x \geq 1\), or \(x \geq \frac{1}{4}\). In this case, we can simplify \(|x| = x\) so \[\cos(t) = \frac{\sqrt{16x^2-1}}{4|x|} = \frac{\sqrt{16x^2-1}}{4x}\] Similarly, for \(\pi < t \leq \frac{3\pi}{2}\), we get \(4x \leq -1\), or \(x \leq -\frac{1}{4}\). In this case, \(|x| = -x\), so we also get \[\cos(t) = -\frac{\sqrt{16x^2-1}}{4|x|} = -\frac{\sqrt{16x^2-1}}{4(-x)} = \frac{\sqrt{16x^2-1}}{4x}\] Hence, in all cases, \(\cos(\mbox{arccsc}(4x)) = \frac{\sqrt{16x^2-1}}{4x}\), and this equivalence is valid for all \(x\) in the domain of \(t = \mbox{arccsc}(4x)\), namely \(\left(-\infty, -\frac{1}{4}\right] \cup \left[ \frac{1}{4}, \infty \right)\)

10.6.3. Calculators and the Inverse Circular Functions.

In the sections to come, we will have need to approximate the values of the inverse circular functions. On most calculators, only the arcsine, arccosine and arctangent functions are available and they are usually labeled as \(\sin^{-1}, \cos^{-1}\) and \(\tan^{-1}\), respectively. If we are asked to approximate these values, it is a simple matter to punch up the appropriate decimal on the calculator. If we are asked for an arccotangent, arcsecant or arccosecant, however, we often need to employ some ingenuity, as our next example illustrates.

Example 10.6.5

• \(\mbox{arccot}(2)\)
• \(\mbox{arcsec}(5)\)
• \(\mbox{arccot}(-2)\)
• \(\mbox{arccsc}\left(-\dfrac{3}{2}\right)\)
• \(f(x) = \dfrac{\pi}{2} - \arccos\left(\dfrac{x}{5}\right)\)
• \(f(x) = 3\arctan\left(4x \right)\).
• \(f(x) = \text{arccot}\left(\dfrac{x}{2} \right) + \pi\)
• Since \(2 > 0\), we can use the property listed in Theorem 10.27 to rewrite \(\mbox{arccot}(2)\) as \(\mbox{arccot}(2) = \arctan\left(\frac{1}{2}\right)\). In ‘radian’ mode, we find \(\mbox{arccot}(2) = \arctan\left(\frac{1}{2}\right) \approx 0.4636\).

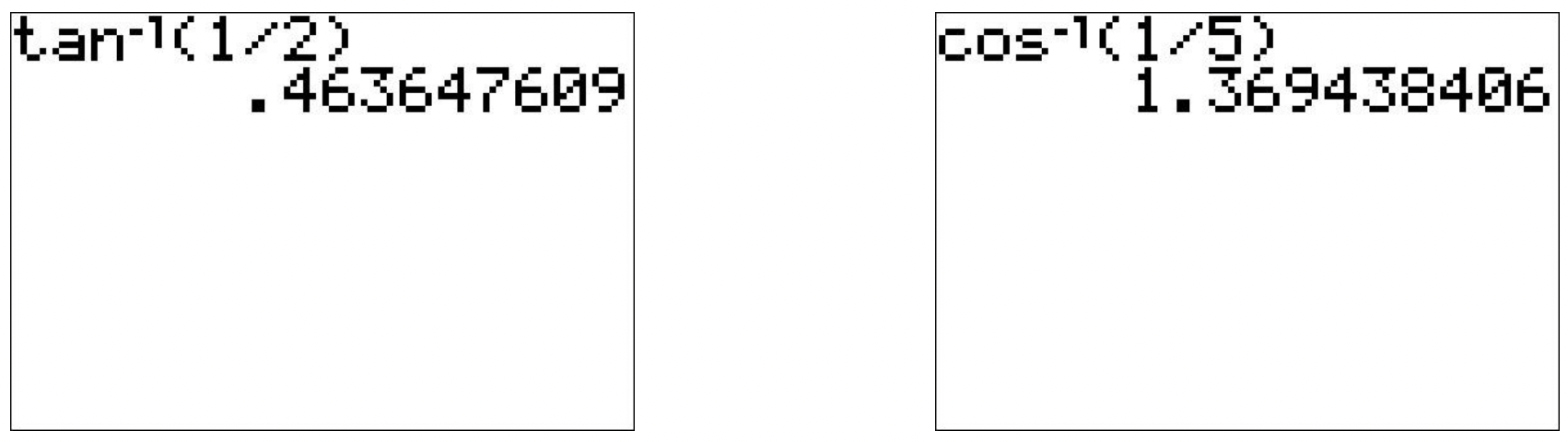
Another way to attack the problem is to use \(\arctan\left(-\frac{1}{2}\right)\). By definition, the real number \(t = \arctan\left(-\frac{1}{2}\right)\) satisfies \(\tan(t) = -\frac{1}{2}\) with \(-\frac{\pi}{2} < t < \frac{\pi}{2}\). Since \(\tan(t)<0\), we know more specifically that \(-\frac{\pi}{2} < t < 0\), so \(t\) corresponds to an angle \(\beta\) in Quadrant IV. To find the value of \(\mbox{arccot}(-2)\), we once again visualize the angle \(\theta = \mbox{arccot}(-2)\) radians and note that it is a Quadrant II angle with \(\tan(\theta) = -\frac{1}{2}\). This means it is exactly \(\pi\) units away from \(\beta\), and we get \(\theta = \pi + \beta = \pi + \arctan\left(-\frac{1}{2}\right) \approx 2.6779\) radians. Hence, as before, \(\mbox{arccot}(-2) \approx 2.6779\).

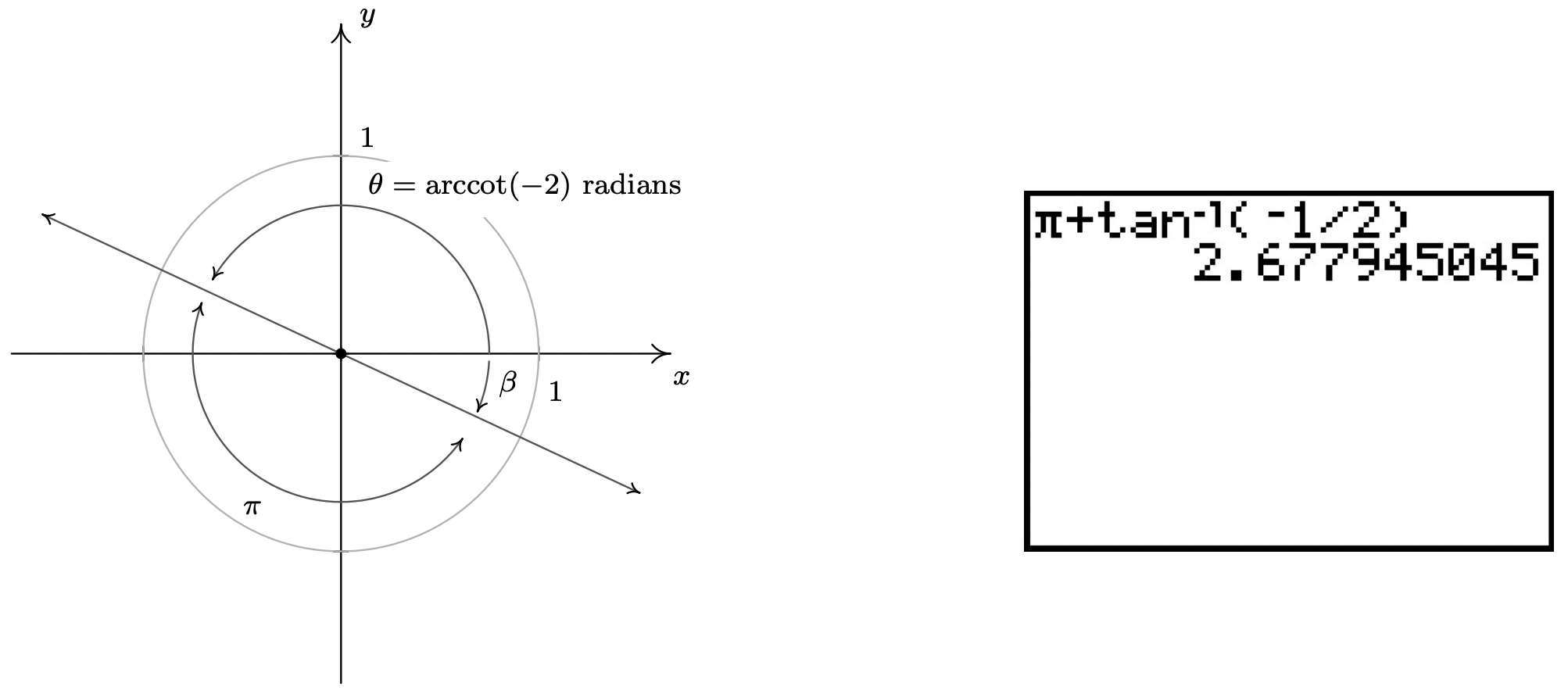
• Since the domain of \(F(x) = \arccos(x)\) is \(-1 \leq x \leq 1\), we can find the domain of \(f(x) = \frac{\pi}{2} - \arccos\left(\frac{x}{5}\right)\) by setting the argument of the arccosine, in this case \(\frac{x}{5}\), between \(-1\) and \(1\). Solving \(-1 \leq \frac{x}{5} \leq 1\) gives \(-5 \leq x \leq 5\), so the domain is \([-5,5]\). To determine the range of \(f\), we take a cue from Section 1.7 . Three ‘key’ points on the graph of \(F(x) = \arccos(x)\) are \((-1, \pi)\), \(\left(0, \frac{\pi}{2}\right)\) and \((1,0)\). Following the procedure outlined in Theorem 1.7 , we track these points to \(\left(-5, -\frac{\pi}{2}\right)\), \((0, 0)\) and \(\left(5, \frac{\pi}{2}\right)\). Plotting these values tells us that the range 5 of \(f\) is \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\). Our graph confirms our results.

\[g(x) = \text{arccot}\left(\frac{x}{2}\right) + \pi = \left\{ \begin{array}{rr} \arctan\left(\frac{2}{x}\right) + 2\pi, & \text{if $x<0$} \\[4pt] \pi, & \text{if $x=0$} \\[4pt] \arctan\left(\frac{2}{x}\right) + \pi, & \text{if $x>0$} \end{array}\right.\nonumber\]

We show the input and the result below.

The inverse trigonometric functions are typically found in applications whenever the measure of an angle is required. One such scenario is presented in the following example.

Example 10.6.6

7 The roof on the house below has a ‘\(6/12\) pitch’. This means that when viewed from the side, the roof line has a rise of 6 feet over a run of 12 feet. Find the angle of inclination from the bottom of the roof to the top of the roof. Express your answer in decimal degrees, rounded to the nearest hundredth of a degree.

If we divide the side view of the house down the middle, we find that the roof line forms the hypotenuse of a right triangle with legs of length \(6\) feet and \(12\) feet. Using Theorem 10.10 , we find the angle of inclination, labeled \(\theta\) below, satisfies \(\tan(\theta) = \frac{6}{12} = \frac{1}{2}\). Since \(\theta\) is an acute angle, we can use the arctangent function and we find \(\theta = \arctan\left(\frac{1}{2}\right)\, \text{radians} \, \approx 26.56^{\circ}\).

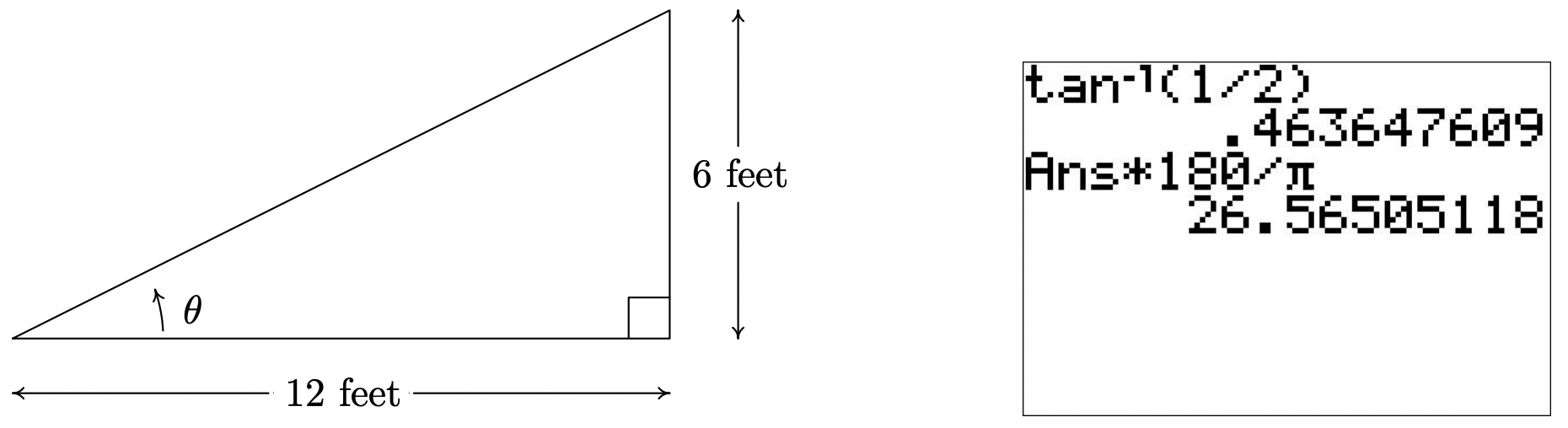
10.6.4. Solving Equations Using the Inverse Trigonometric Functions.

In Sections 10.2 and 10.3 , we learned how to solve equations like \(\sin(\theta) = \frac{1}{2}\) for angles \(\theta\) and \(\tan(t) = -1\) for real numbers \(t\). In each case, we ultimately appealed to the Unit Circle and relied on the fact that the answers corresponded to a set of ‘common angles’ listed on page 724. If, on the other hand, we had been asked to find all angles with \(\sin(\theta) = \frac{1}{3}\) or solve \(\tan(t) = -2\) for real numbers \(t\), we would have been hard-pressed to do so. With the introduction of the inverse trigonometric functions, however, we are now in a position to solve these equations. A good parallel to keep in mind is how the square root function can be used to solve certain quadratic equations. The equation \(x^2 = 4\) is a lot like \(\sin(\theta) = \frac{1}{2}\) in that it has friendly, ‘common value’ answers \(x = \pm 2\). The equation \(x^2 = 7\), on the other hand, is a lot like \(\sin(\theta) = \frac{1}{3}\). We know 8 there are answers, but we can’t express them using ‘friendly’ numbers. 9 To solve \(x^2 = 7\), we make use of the square root function and write \(x = \pm \sqrt{7}\). We can certainly approximate these answers using a calculator, but as far as exact answers go, we leave them as \(x = \pm \sqrt{7}\). In the same way, we will use the arcsine function to solve \(\sin(\theta) = \frac{1}{3}\), as seen in the following example.

Example 10.6.7

Solve the following equations

• Find all angles \(\theta\) for which \(\sin(\theta) = \frac{1}{3}\).
• Find all real numbers \(t\) for which \(\tan(t) = -2\)
• Solve \(\, \sec(x) = -\frac{5}{3} \,\) for \(x\).

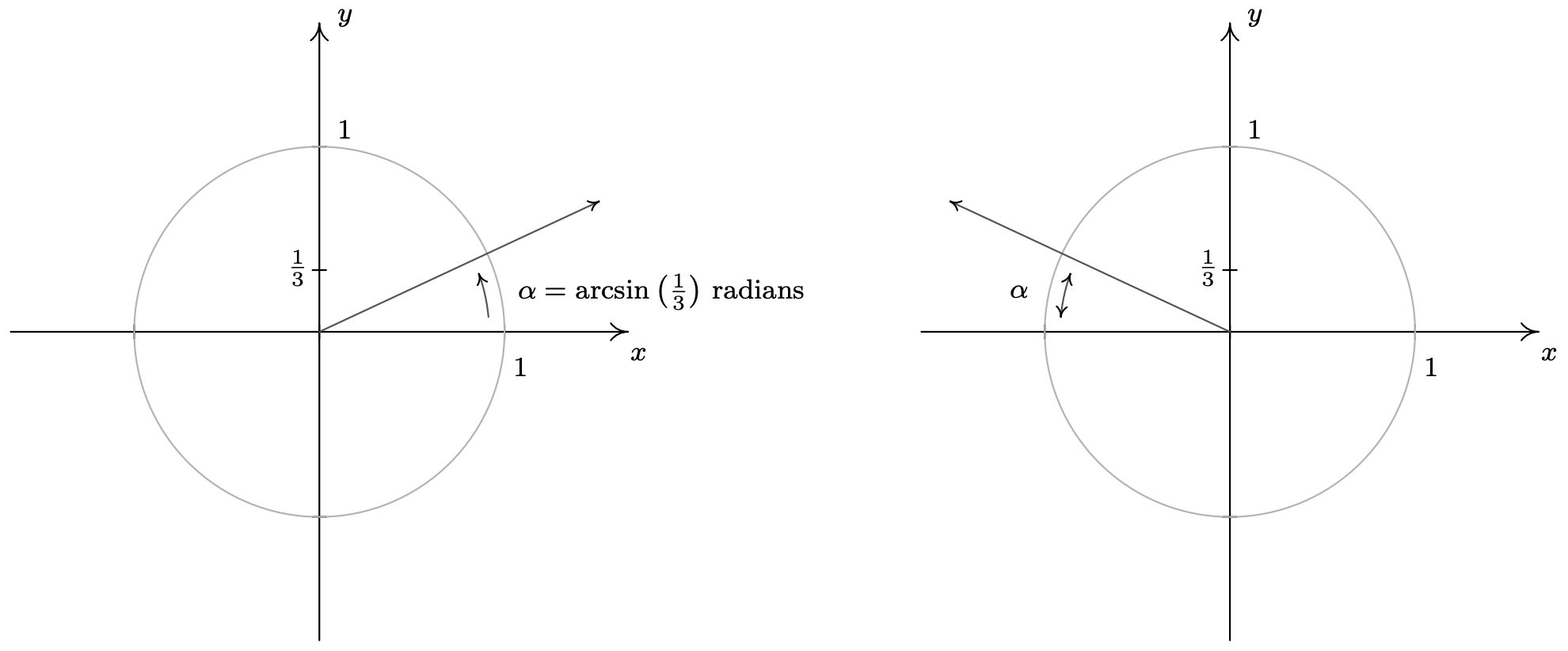
Since \(\frac{1}{3}\) isn’t the sine of any of the ‘common angles’ discussed earlier, we use the arcsine functions to express our answers. The real number \(t = \arcsin\left(\frac{1}{3}\right)\) is defined so it satisfies \(0 < t < \frac{\pi}{2}\) with \(\sin(t) = \frac{1}{3}\). Hence, \(\alpha = \arcsin\left(\frac{1}{3}\right)\) radians. Since the solutions in Quadrant I are all coterminal with \(\alpha\), we get part of our solution to be \(\theta = \alpha + 2\pi k = \arcsin\left(\frac{1}{3}\right) + 2\pi k\) for integers \(k\). Turning our attention to Quadrant II, we get one solution to be \(\pi - \alpha\). Hence, the Quadrant II solutions are \(\theta = \pi - \alpha + 2\pi k = \pi - \arcsin\left(\frac{1}{3}\right) + 2\pi k\), for integers \(k\).

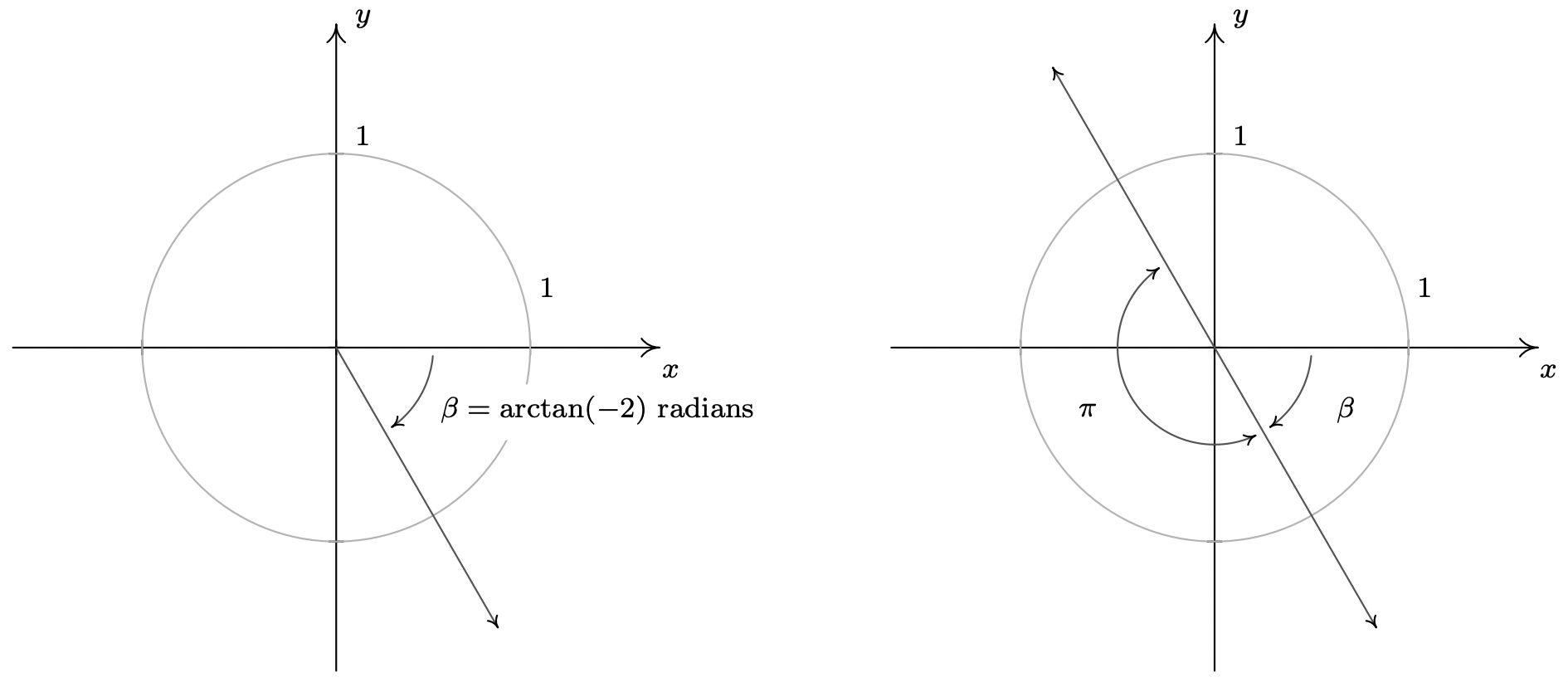
Since \(-2\) isn’t the tangent of any of the ‘common angles’, we need to use the arctangent function to express our answers. The real number \(t = \arctan(-2)\) satisfies \(\tan(t)=-2\) and \(-\frac{\pi}{2} < t < 0\). If we let \(\beta = \arctan(-2)\) radians, we see that all of the Quadrant IV solutions to \(\tan(\theta) = -2\) are coterminal with \(\beta\). Moreover, the solutions from Quadrant II differ by exactly \(\pi\) units from the solutions in Quadrant IV, so all the solutions to \(\tan(\theta) = -2\) are of the form \(\theta = \beta + \pi k = \arctan(-2) + \pi k\) for some integer \(k\). Switching back to the variable \(t\), we record our final answer to \(\tan(t) = -2\) as \(t = \arctan(-2) + \pi k\) for integers \(k\).

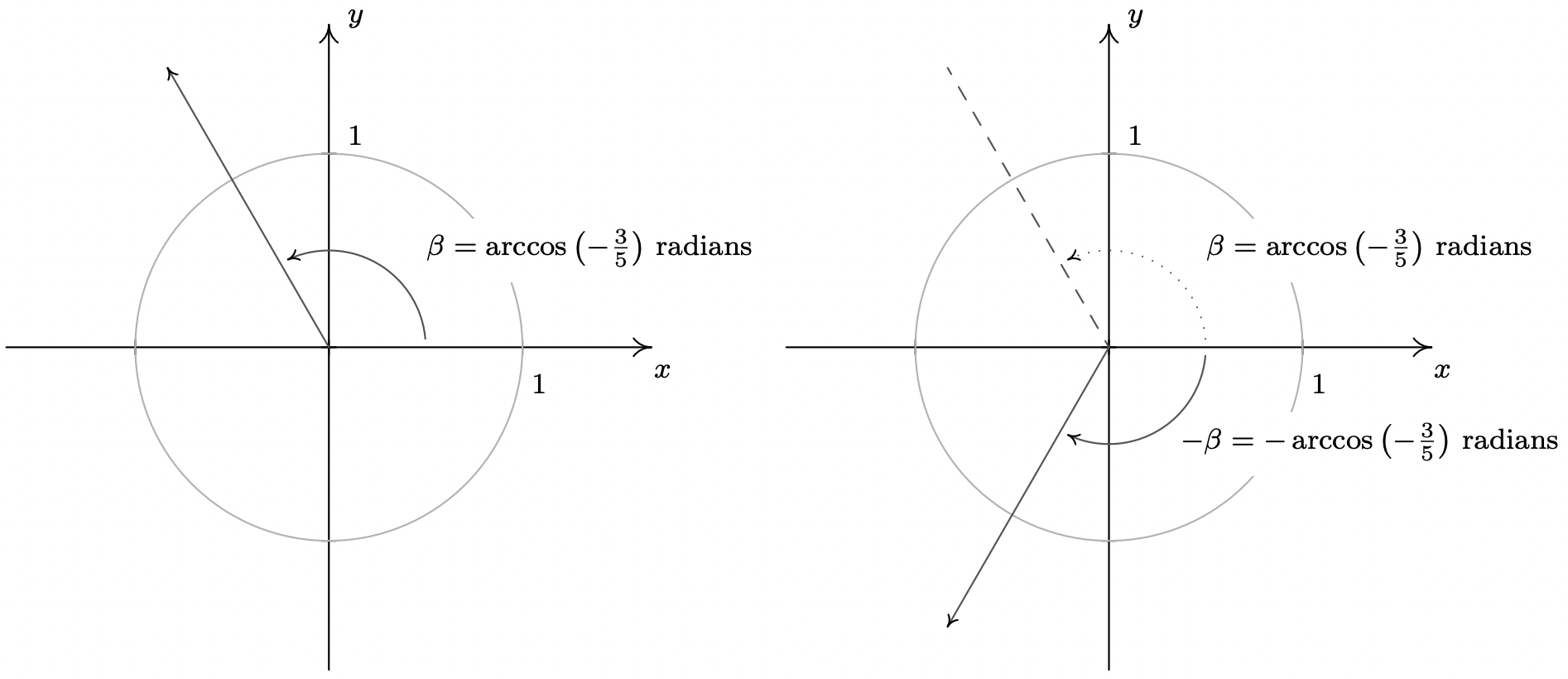
The reader is encouraged to check the answers found in Example 10.6.7 - both analytically and with the calculator (see Section 10.6.3 ). With practice, the inverse trigonometric functions will become as familiar to you as the square root function. Speaking of practice …

10.6.5. Exercises

In Exercises 1 - 40, find the exact value.

• \(\arcsin \left( -1 \right)\)
• \(\arcsin \left( -\dfrac{\sqrt{3}}{2} \right)\)
• \(\arcsin \left( -\dfrac{\sqrt{2}}{2} \right)\)
• \(\arcsin \left( -\dfrac{1}{2} \right)\)
• \(\arcsin \left( 0 \right)\)
• \(\arcsin \left( \dfrac{1}{2} \right)\)
• \(\arcsin \left( \dfrac{\sqrt{2}}{2} \right)\)
• \(\arcsin \left( \dfrac{\sqrt{3}}{2} \right)\)
• \(\arcsin \left( 1 \right)\)
• \(\arccos \left( -1 \right)\)
• \(\arccos \left( -\dfrac{\sqrt{3}}{2} \right)\)
• \(\arccos \left( -\dfrac{\sqrt{2}}{2} \right)\)
• \(\arccos \left( -\dfrac{1}{2} \right)\)
• \(\arccos \left( 0 \right)\)
• \(\arccos \left( \dfrac{1}{2} \right)\)
• \(\arccos \left( \dfrac{\sqrt{2}}{2} \right)\)
• \(\arccos \left( \dfrac{\sqrt{3}}{2} \right)\)
• \(\arccos \left( 1 \right)\)
• \(\arctan \left( -\sqrt{3} \right)\)
• \(\arctan \left( -1 \right)\)
• \(\arctan \left( -\dfrac{\sqrt{3}}{3} \right)\)
• \(\arctan \left( 0 \right)\)
• \(\arctan \left( \dfrac{\sqrt{3}}{3} \right)\)
• \(\arctan \left( 1 \right)\)
• \(\arctan \left( \sqrt{3} \right)\)
• \(\mbox{arccot} \left( -\sqrt{3} \right)\)
• \(\mbox{arccot} \left( -1 \right)\)
• \(\mbox{arccot} \left( -\dfrac{\sqrt{3}}{3} \right)\)
• \(\mbox{arccot} \left( 0 \right)\)
• \(\mbox{arccot} \left( \dfrac{\sqrt{3}}{3} \right)\)
• \(\mbox{arccot} \left( 1 \right)\)
• \(\mbox{arccot} \left( \sqrt{3} \right)\)
• \(\mbox{arcsec} \left( 2 \right)\)
• \(\mbox{arccsc} \left( 2 \right)\)
• \(\mbox{arcsec} \left( \sqrt{2} \right)\)
• \(\mbox{arccsc} \left( \sqrt{2} \right)\)
• \(\mbox{arcsec} \left( \dfrac{2\sqrt{3}}{3} \right)\)
• \(\mbox{arccsc} \left( \dfrac{2\sqrt{3}}{3} \right)\)
• \(\mbox{arcsec} \left( 1 \right)\)
• \(\mbox{arccsc} \left( 1 \right)\)

In Exercises 41 - 48, assume that the range of arcsecant is \(\left[0, \frac{\pi}{2} \right) \cup \left[\pi, \frac{3\pi}{2} \right)\) and that the range of arccosecant is \(\left(0, \frac{\pi}{2} \right] \cup \left( \pi, \frac{3\pi}{2} \right]\) when finding the exact value.

• \(\mbox{arcsec} \left( -2 \right)\)
• \(\mbox{arcsec} \left( -\sqrt{2} \right)\)
• \(\mbox{arcsec} \left( -\dfrac{2\sqrt{3}}{3} \right)\)
• \(\mbox{arcsec} \left( -1 \right)\)
• \(\mbox{arccsc} \left( -2 \right)\)
• \(\mbox{arccsc} \left( -\sqrt{2} \right)\)
• \(\mbox{arccsc} \left( -\dfrac{2\sqrt{3}}{3} \right)\)
• \(\mbox{arccsc} \left( -1 \right)\)

In Exercises 49 - 56, assume that the range of arcsecant is \(\left[0, \frac{\pi}{2} \right) \cup \left( \frac{\pi}{2}, \pi \right]\) and that the range of arccosecant is \(\left[ -\frac{\pi}{2}, 0 \right) \cup \left(0, \frac{\pi}{2} \right]\) when finding the exact value.

In Exercises 57 - 86, find the exact value or state that it is undefined.

• \(\sin\left(\arcsin\left(\dfrac{1}{2}\right)\right)\)
• \(\sin\left(\arcsin\left(-\dfrac{\sqrt{2}}{2}\right)\right)\)
• \(\sin\left(\arcsin\left(\dfrac{3}{5}\right)\right)\)
• \(\sin\left(\arcsin\left(-0.42\right)\right)\)
• \(\sin\left(\arcsin\left(\dfrac{5}{4}\right)\right)\)
• \(\cos\left(\arccos\left(\dfrac{\sqrt{2}}{2}\right)\right)\)
• \(\cos\left(\arccos\left(-\dfrac{1}{2}\right)\right)\)
• \(\cos\left(\arccos\left(\dfrac{5}{13}\right)\right)\)
• \(\cos\left(\arccos\left(-0.998\right)\right)\)
• \(\cos\left(\arccos\left(\pi \right)\right)\)
• \(\tan\left(\arctan\left(-1\right)\right)\)
• \(\tan\left(\arctan\left(\sqrt{3}\right)\right)\)
• \(\tan\left(\arctan\left(\dfrac{5}{12}\right)\right)\)
• \(\tan\left(\arctan\left(0.965\right)\right)\)
• \(\tan\left(\arctan\left( 3\pi \right)\right)\)
• \(\cot\left(\text{arccot}\left(1\right)\right)\)
• \(\cot\left(\text{arccot}\left(-\sqrt{3}\right)\right)\)
• \(\cot\left(\text{arccot}\left(-\dfrac{7}{24}\right)\right)\)
• \(\cot\left(\text{arccot}\left(-0.001\right)\right)\)
• \(\cot\left(\text{arccot}\left( \dfrac{17\pi}{4} \right)\right)\)
• \(\sec\left(\text{arcsec}\left(2\right)\right)\)
• \(\sec\left(\text{arcsec}\left(-1\right)\right)\)
• \(\sec\left(\text{arcsec}\left(\dfrac{1}{2}\right)\right)\)
• \(\sec\left(\text{arcsec}\left(0.75\right)\right)\)
• \(\sec\left(\text{arcsec}\left( 117\pi \right)\right)\)
• \(\csc\left(\text{arccsc}\left(\sqrt{2}\right)\right)\)
• \(\csc\left(\text{arccsc}\left(-\dfrac{2\sqrt{3}}{3}\right)\right)\)
• \(\csc\left(\text{arccsc}\left(\dfrac{\sqrt{2}}{2}\right)\right)\)
• \(\csc\left(\text{arccsc}\left(1.0001\right)\right)\)
• \(\csc\left(\text{arccsc}\left( \dfrac{\pi}{4} \right)\right)\)

In Exercises 87 - 106, find the exact value or state that it is undefined.

• \(\arcsin\left(\sin\left(\dfrac{\pi}{6}\right) \right)\)
• \(\arcsin\left(\sin\left(-\dfrac{\pi}{3}\right) \right)\)
• \(\arcsin\left(\sin\left(\dfrac{3\pi}{4}\right) \right)\)
• \(\arcsin\left(\sin\left(\dfrac{11\pi}{6}\right) \right)\)
• \(\arcsin\left(\sin\left(\dfrac{4\pi}{3}\right) \right)\)
• \(\arccos\left(\cos\left(\dfrac{\pi}{4}\right) \right)\)
• \(\arccos\left(\cos\left(\dfrac{2\pi}{3}\right) \right)\)
• \(\arccos\left(\cos\left(\dfrac{3\pi}{2}\right) \right)\)
• \(\arccos\left(\cos\left(-\dfrac{\pi}{6}\right) \right)\)
• \(\arccos\left(\cos\left(\dfrac{5\pi}{4}\right) \right)\)
• \(\arctan\left(\tan\left(\dfrac{\pi}{3}\right) \right)\)
• \(\arctan\left(\tan\left(-\dfrac{\pi}{4}\right) \right)\)
• \(\arctan\left(\tan\left(\pi\right) \right)\)
• \(\arctan\left(\tan\left(\dfrac{\pi}{2}\right) \right)\)
• \(\arctan\left(\tan\left(\dfrac{2\pi}{3}\right) \right)\)
• \(\text{arccot}\left(\cot\left(\dfrac{\pi}{3}\right) \right)\)
• \(\text{arccot}\left(\cot\left(-\dfrac{\pi}{4}\right) \right)\)
• \(\text{arccot}\left(\cot\left(\pi\right) \right)\)
• \(\text{arccot}\left(\cot\left(\dfrac{\pi}{2}\right) \right)\)
• \(\text{arccot}\left(\cot\left(\dfrac{2\pi}{3}\right) \right)\)

In Exercises 107 - 118, assume that the range of arcsecant is \(\left[0, \frac{\pi}{2} \right) \cup \left[\pi, \frac{3\pi}{2} \right)\) and that the range of arccosecant is \(\left(0, \frac{\pi}{2} \right] \cup \left( \pi, \frac{3\pi}{2} \right]\) when finding the exact value.

• \(\text{arcsec}\left(\sec\left(\dfrac{\pi}{4}\right) \right)\)
• \(\text{arcsec}\left(\sec\left(\dfrac{4\pi}{3}\right) \right)\)
• \(\text{arcsec}\left(\sec\left( \dfrac{5\pi}{6} \right) \right)\)
• \(\text{arcsec}\left(\sec\left(-\dfrac{\pi}{2} \right) \right)\)
• \(\text{arcsec}\left(\sec\left(\dfrac{5\pi}{3}\right) \right)\)
• \(\text{arccsc}\left(\csc\left(\dfrac{\pi}{6}\right) \right)\)
• \(\text{arccsc}\left(\csc\left(\dfrac{5\pi}{4}\right) \right)\)
• \(\text{arccsc}\left(\csc\left( \dfrac{2\pi}{3} \right) \right)\)
• \(\text{arccsc}\left(\csc\left(-\dfrac{\pi}{2} \right) \right)\)
• \(\text{arccsc}\left(\csc\left(\dfrac{11\pi}{6}\right) \right)\)
• \(\text{arcsec}\left(\sec\left(\dfrac{11\pi}{12}\right) \right)\)
• \(\text{arccsc}\left(\csc\left(\dfrac{9\pi}{8}\right) \right)\)

In Exercises 119 - 130, assume that the range of arcsecant is \(\left[0, \frac{\pi}{2} \right) \cup \left( \frac{\pi}{2}, \pi \right]\) and that the range of arccosecant is \(\left[ -\frac{\pi}{2}, 0 \right) \cup \left(0, \frac{\pi}{2} \right]\) when finding the exact value.

In Exercises 131 - 154, find the exact value or state that it is undefined.

• \(\sin\left(\arccos\left(-\dfrac{1}{2}\right)\right)\)
• \(\sin\left(\arccos\left(\dfrac{3}{5}\right)\right)\)
• \(\sin\left(\arctan\left(-2\right)\right)\)
• \(\sin\left(\text{arccot}\left(\sqrt{5}\right)\right)\)
• \(\sin\left(\text{arccsc}\left(-3\right)\right)\)
• \(\cos\left(\arcsin\left(-\dfrac{5}{13}\right)\right)\)
• \(\cos\left(\arctan\left(\sqrt{7} \right)\right)\)
• \(\cos\left(\text{arccot}\left( 3 \right)\right)\)
• \(\cos\left(\text{arcsec}\left( 5 \right)\right)\)
• \(\tan\left(\arcsin\left(-\dfrac{2\sqrt{5}}{5}\right)\right)\)
• \(\tan\left(\arccos\left(-\dfrac{1}{2}\right)\right)\)
• \(\tan\left(\text{arcsec}\left(\dfrac{5}{3}\right)\right)\)
• \(\tan\left(\text{arccot}\left( 12 \right)\right)\)
• \(\cot\left(\arcsin\left(\dfrac{12}{13}\right)\right)\)
• \(\cot\left(\arccos\left(\dfrac{\sqrt{3}}{2}\right)\right)\)
• \(\cot\left(\text{arccsc}\left(\sqrt{5}\right)\right)\)
• \(\cot\left(\arctan \left( 0.25 \right)\right)\)
• \(\sec\left(\arccos\left(\dfrac{\sqrt{3}}{2}\right)\right)\)
• \(\sec\left(\arcsin\left(-\dfrac{12}{13}\right)\right)\)
• \(\sec\left(\arctan\left(10\right)\right)\)
• \(\sec\left(\text{arccot}\left(-\dfrac{\sqrt{10}}{10}\right)\right)\)
• \(\csc\left(\text{arccot}\left(9 \right)\right)\)
• \(\csc\left(\arcsin\left(\dfrac{3}{5}\right)\right)\)
• \(\csc\left(\arctan\left(-\dfrac{2}{3}\right)\right)\)

In Exercises 155 - 164, find the exact value or state that it is undefined.

• \(\sin\left(\arcsin\left( \dfrac{5}{13} \right) + \dfrac{\pi}{4}\right)\)
• \(\cos\left( \text{arcsec}(3) + \arctan(2) \right)\)
• \(\tan\left( \arctan(3) + \arccos\left(-\dfrac{3}{5}\right) \right)\)
• \(\sin\left(2\arcsin\left(-\dfrac{4}{5}\right)\right)\)
• \(\sin\left(2\text{arccsc}\left(\dfrac{13}{5}\right)\right)\)
• \(\sin\left(2\arctan\left(2\right)\right)\)
• \(\cos\left(2 \arcsin\left(\dfrac{3}{5}\right)\right)\)
• \(\cos\left(2 \text{arcsec}\left(\dfrac{25}{7}\right)\right)\)
• \(\cos\left(2 \text{arccot}\left(-\sqrt{5}\right)\right)\)
• \(\sin\left( \dfrac{\arctan(2)}{2} \right)\)

In Exercises 165 - 184, rewrite the quantity as algebraic expressions of \(x\) and state the domain on which the equivalence is valid.

• \(\sin \left( \arccos \left( x \right) \right)\)
• \(\cos \left( \arctan \left( x \right) \right)\)
• \(\tan \left( \arcsin \left( x \right) \right)\)
• \(\sec \left( \arctan \left( x \right) \right)\)
• \(\csc \left( \arccos \left( x \right) \right)\)
• \(\sin \left( 2\arctan \left( x \right) \right)\)
• \(\sin \left( 2\arccos \left( x \right) \right)\)
• \(\cos \left( 2\arctan \left( x \right) \right)\)
• \(\sin(\arccos(2x))\)
• \(\sin\left(\arccos\left(\dfrac{x}{5}\right)\right)\)
• \(\cos\left(\arcsin\left(\dfrac{x}{2}\right)\right)\)
• \(\cos\left(\arctan\left(3x\right)\right)\)
• \(\sin(2\arcsin(7x))\)
• \(\sin\left(2 \arcsin\left( \dfrac{x\sqrt{3}}{3} \right) \right)\)
• \(\cos(2 \arcsin(4x))\)
• \(\sec(\arctan(2x))\tan(\arctan(2x))\)
• \(\sin \left( \arcsin(x) + \arccos(x) \right)\)
• \(\cos \left( \arcsin(x) + \arctan(x) \right)\)
• \(\tan \left( 2\arcsin(x) \right)\)
• \(\sin \left( \dfrac{1}{2}\arctan(x) \right)\)
• If \(\sin(\theta) = \dfrac{x}{2}\) for \(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\), find an expression for \(\theta + \sin(2\theta)\) in terms of \(x\).
• If \(\tan(\theta) = \dfrac{x}{7}\) for \(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\), find an expression for \(\dfrac{1}{2}\theta - \dfrac{1}{2}\sin(2\theta)\) in terms of \(x\).
• If \(\sec(\theta) = \dfrac{x}{4}\) for \(0 < \theta < \dfrac{\pi}{2}\), find an expression for \(4\tan(\theta) - 4\theta\) in terms of \(x\).

In Exercises 188 - 207, solve the equation using the techniques discussed in Example 10.6.7 then approximate the solutions which lie in the interval \([0, 2\pi)\) to four decimal places.

• \(\sin(x) = \dfrac{7}{11}\)
• \(\cos(x) = -\dfrac{2}{9}\)
• \(\sin(x) = -0.569\)
• \(\cos(x) = 0.117\)
• \(\sin(x) = 0.008\)
• \(\cos(x) = \dfrac{359}{360}\)
• \(\tan(x) = 117\)
• \(\cot(x) = -12\)
• \(\sec(x) = \dfrac{3}{2}\)
• \(\csc(x) = -\dfrac{90}{17}\)
• \(\tan(x) = -\sqrt{10}\)
• \(\sin(x) = \dfrac{3}{8}\)
• \(\cos(x) = -\dfrac{7}{16}\)
• \(\tan(x) = 0.03\)
• \(\sin(x) = 0.3502\)
• \(\sin(x) = -0.721\)
• \(\cos(x) = 0.9824\)
• \(\cos(x) = -0.5637\)
• \(\cot(x) = \dfrac{1}{117}\)
• \(\tan(x) = -0.6109\)

In Exercises 208 - 210, find the two acute angles in the right triangle whose sides have the given lengths. Express your answers using degree measure rounded to two decimal places.

• 5, 12 and 13
• 336, 527 and 625
• A guy wire 1000 feet long is attached to the top of a tower. When pulled taut it touches level ground 360 feet from the base of the tower. What angle does the wire make with the ground? Express your answer using degree measure rounded to one decimal place.
• At Cliffs of Insanity Point, The Great Sasquatch Canyon is 7117 feet deep. From that point, a fire is seen at a location known to be 10 miles away from the base of the sheer canyon wall. What angle of depression is made by the line of sight from the canyon edge to the fire? Express your answer using degree measure rounded to one decimal place.
• Shelving is being built at the Utility Muffin Research Library which is to be 14 inches deep. An 18-inch rod will be attached to the wall and the underside of the shelf at its edge away from the wall, forming a right triangle under the shelf to support it. What angle, to the nearest degree, will the rod make with the wall?
• A parasailor is being pulled by a boat on Lake Ippizuti. The cable is 300 feet long and the parasailor is 100 feet above the surface of the water. What is the angle of elevation from the boat to the parasailor? Express your answer using degree measure rounded to one decimal place.
• A tag-and-release program to study the Sasquatch population of the eponymous Sasquatch National Park is begun. From a 200 foot tall tower, a ranger spots a Sasquatch lumbering through the wilderness directly towards the tower. Let \(\theta\) denote the angle of depression from the top of the tower to a point on the ground. If the range of the rifle with a tranquilizer dart is 300 feet, find the smallest value of \(\theta\) for which the corresponding point on the ground is in range of the rifle. Round your answer to the nearest hundreth of a degree.

In Exercises 216 - 221, rewrite the given function as a sinusoid of the form \(S(x) = A\sin(\omega x + \phi)\) using Exercises 35 and 36 in Section 10.5 for reference. Approximate the value of \(\phi\) (which is in radians, of course) to four decimal places.

• \(f(x) = 5\sin(3x) + 12\cos(3x)\)
• \(f(x) = 3\cos(2x) + 4\sin(2x)\)
• \(f(x) = \cos(x) - 3\sin(x)\)
• \(f(x) = 7\sin(10x) - 24\cos(10x)\)
• \(f(x) = -\cos(x) - 2\sqrt{2} \sin(x)\)
• \(f(x) = 2\sin(x) - \cos(x)\)

In Exercises 222 - 233, find the domain of the given function. Write your answers in interval notation.

• \(f(x) = \arcsin(5x)\)
• \(f(x) = \arccos\left(\dfrac{3x-1}{2} \right)\)
• \(f(x) = \arcsin\left(2x^2\right)\)
• \(f(x) = \arccos\left(\dfrac{1}{x^2-4}\right)\)
• \(f(x) = \arctan(4x)\)
• \(f(x) = \text{arccot}\left(\dfrac{2x}{x^2-9}\right)\)
• \(f(x) =\arctan(\ln(2x-1))\)
• \(f(x) = \text{arccot}(\sqrt{2x-1})\)
• \(f(x) = \text{arcsec}(12x)\)
• \(f(x) = \text{arccsc}(x+5)\)
• \(f(x) = \text{arcsec}\left(\dfrac{x^3}{8}\right)\)
• \(f(x) = \text{arccsc}\left(e^{2x}\right)\)
• Show that \(\mbox{arcsec}(x) = \arccos \left( \dfrac{1}{x} \right)\) for \(|x| \geq 1\) as long as we use \(\left[0, \dfrac{\pi}{2} \right) \cup \left( \dfrac{\pi}{2}, \pi \right]\) as the range of \(f(x) = \mbox{arcsec}(x)\).
• Show that \(\mbox{arccsc}(x) = \arcsin \left( \dfrac{1}{x} \right)\) for \(|x| \geq 1\) as long as we use \(\left[ -\dfrac{\pi}{2}, 0 \right) \cup \left(0, \dfrac{\pi}{2} \right]\) as the range of \(f(x) = \mbox{arccsc}(x)\).
• Show that \(\arcsin(x) + \arccos(x) = \dfrac{\pi}{2}\) for \(-1 \leq x \leq 1\).
• Discuss with your classmates why \(\arcsin\left(\dfrac{1}{2}\right) \neq 30^{\circ}\).

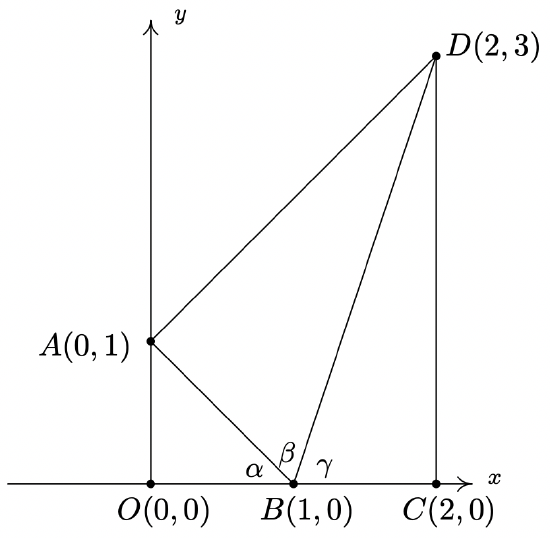
• Clearly \(\triangle AOB\) and \(\triangle BCD\) are right triangles because the line through \(O\) and \(A\) and the line through \(C\) and \(D\) are perpendicular to the \(x\)-axis. Use the distance formula to show that \(\triangle BAD\) is also a right triangle (with \(\angle BAD\) being the right angle) by showing that the sides of the triangle satisfy the Pythagorean Theorem.
• Use \(\triangle AOB\) to show that \(\alpha = \arctan(1)\)
• Use \(\triangle BAD\) to show that \(\beta = \arctan(2)\)
• Use \(\triangle BCD\) to show that \(\gamma = \arctan(3)\)
• Use the fact that \(O\), \(B\) and \(C\) all lie on the \(x\)-axis to conclude that \(\alpha + \beta + \gamma = \pi\). Thus \(\arctan(1) + \arctan(2) + \arctan(3) = \pi\).

10.6.6 Answers

• \(\arcsin \left( -1 \right) = -\dfrac{\pi}{2}\)
• \(\arcsin \left( -\dfrac{\sqrt{3}}{2} \right) = -\dfrac{\pi}{3}\)
• \(\arcsin \left( -\dfrac{\sqrt{2}}{2} \right) = -\dfrac{\pi}{4}\)
• \(\arcsin \left( -\dfrac{1}{2} \right) = -\dfrac{\pi}{6}\)
• \(\arcsin \left( 0 \right) = 0\)
• \(\arcsin \left( \dfrac{1}{2} \right) = \dfrac{\pi}{6}\)
• \(\arcsin \left( \dfrac{\sqrt{2}}{2} \right) = \dfrac{\pi}{4}\)
• \(\arcsin \left( \dfrac{\sqrt{3}}{2} \right) = \dfrac{\pi}{3}\)
• \(\arcsin \left( 1 \right) = \dfrac{\pi}{2}\)
• \(\arccos \left( -1 \right) = \pi\)
• \(\arccos \left( -\dfrac{\sqrt{3}}{2} \right) = \dfrac{5\pi}{6}\)
• \(\arccos \left( -\dfrac{\sqrt{2}}{2} \right) = \dfrac{3\pi}{4}\)
• \(\arccos \left( -\dfrac{1}{2} \right) = \dfrac{2\pi}{3}\)
• \(\arccos \left( 0 \right) = \dfrac{\pi}{2}\)
• \(\arccos \left( \dfrac{1}{2} \right) = \dfrac{\pi}{3}\)
• \(\arccos \left( \dfrac{\sqrt{2}}{2} \right) = \dfrac{\pi}{4}\)
• \(\arccos \left( \dfrac{\sqrt{3}}{2} \right) = \dfrac{\pi}{6}\)
• \(\arccos \left( 1 \right) = 0\)
• \(\arctan \left( -\sqrt{3} \right) = -\dfrac{\pi}{3}\)
• \(\arctan \left( -1 \right) = -\dfrac{\pi}{4}\)
• \(\arctan \left( -\dfrac{\sqrt{3}}{3} \right) = -\dfrac{\pi}{6}\)
• \(\arctan \left( 0 \right) = 0\)
• \(\arctan \left( \dfrac{\sqrt{3}}{3} \right) = \dfrac{\pi}{6}\)
• \(\arctan \left( 1 \right) = \dfrac{\pi}{4}\)
• \(\arctan \left( \sqrt{3} \right) = \dfrac{\pi}{3}\)
• \(\mbox{arccot} \left( -\sqrt{3} \right) = \dfrac{5\pi}{6}\)
• \(\mbox{arccot} \left( -1 \right) = \dfrac{3\pi}{4}\)
• \(\mbox{arccot} \left( -\dfrac{\sqrt{3}}{3} \right) = \dfrac{2\pi}{3}\)
• \(\mbox{arccot} \left( 0 \right) = \dfrac{\pi}{2}\)
• \(\mbox{arccot} \left( \dfrac{\sqrt{3}}{3} \right) = \dfrac{\pi}{3}\)
• \(\mbox{arccot} \left( 1 \right) = \dfrac{\pi}{4}\)
• \(\mbox{arccot} \left( \sqrt{3} \right) = \dfrac{\pi}{6}\)
• \(\mbox{arcsec} \left( 2 \right) = \dfrac{\pi}{3}\)
• \(\mbox{arccsc} \left( 2 \right) = \dfrac{\pi}{6}\)
• \(\mbox{arcsec} \left( \sqrt{2} \right) = \dfrac{\pi}{4}\)
• \(\mbox{arccsc} \left( \sqrt{2} \right) = \dfrac{\pi}{4}\)
• \(\mbox{arcsec} \left( \dfrac{2\sqrt{3}}{3} \right) = \dfrac{\pi}{6}\)
• \(\mbox{arccsc} \left( \dfrac{2\sqrt{3}}{3} \right) = \dfrac{\pi}{3}\)
• \(\mbox{arcsec} \left( 1 \right) = 0\)
• \(\mbox{arccsc} \left( 1 \right) = \dfrac{\pi}{2}\)
• \(\mbox{arcsec} \left( -2 \right) = \dfrac{4\pi}{3}\)
• \(\mbox{arcsec} \left( -\sqrt{2} \right) = \dfrac{5\pi}{4}\)
• \(\mbox{arcsec} \left( -\dfrac{2\sqrt{3}}{3} \right) = \dfrac{7\pi}{6}\)
• \(\mbox{arcsec} \left( -1 \right) = \pi\)
• \(\mbox{arccsc} \left( -2 \right) = \dfrac{7\pi}{6}\)
• \(\mbox{arccsc} \left( -\sqrt{2} \right) = \dfrac{5\pi}{4}\)
• \(\mbox{arccsc} \left( -\dfrac{2\sqrt{3}}{3} \right) = \dfrac{4\pi}{3}\)
• \(\mbox{arccsc} \left( -1 \right) = \dfrac{3\pi}{2}\)
• \(\mbox{arcsec} \left( -2 \right) = \dfrac{2\pi}{3}\)
• \(\mbox{arcsec} \left( -\sqrt{2} \right) = \dfrac{3\pi}{4}\)
• \(\mbox{arcsec} \left( -\dfrac{2\sqrt{3}}{3} \right) = \dfrac{5\pi}{6}\)
• \(\mbox{arccsc} \left( -2 \right) = -\dfrac{\pi}{6}\)
• \(\mbox{arccsc} \left( -\sqrt{2} \right) = -\dfrac{\pi}{4}\)
• \(\mbox{arccsc} \left( -\dfrac{2\sqrt{3}}{3} \right) = -\dfrac{\pi}{3}\)
• \(\mbox{arccsc} \left( -1 \right) = -\dfrac{\pi}{2}\)
• \(\sin\left(\arcsin\left(\dfrac{1}{2}\right)\right) = \dfrac{1}{2}\)
• \(\sin\left(\arcsin\left(-\dfrac{\sqrt{2}}{2}\right)\right) = -\dfrac{\sqrt{2}}{2}\)
• \(\sin\left(\arcsin\left(\dfrac{3}{5}\right)\right) = \dfrac{3}{5}\)
• \(\sin\left(\arcsin\left(-0.42\right)\right) = -0.42\)
• \(\sin\left(\arcsin\left(\dfrac{5}{4}\right)\right)\) is undefined.
• \(\cos\left(\arccos\left(\dfrac{\sqrt{2}}{2}\right)\right) = \dfrac{\sqrt{2}}{2}\)
• \(\cos\left(\arccos\left(-\dfrac{1}{2}\right)\right) = -\dfrac{1}{2}\)
• \(\cos\left(\arccos\left(\dfrac{5}{13}\right)\right) = \dfrac{5}{13}\)
• \(\cos\left(\arccos\left(-0.998\right)\right) = -0.998\)
• \(\cos\left(\arccos\left(\pi \right)\right)\) is undefined.
• \(\tan\left(\arctan\left(-1\right)\right) = -1\)
• \(\tan\left(\arctan\left(\sqrt{3}\right)\right) = \sqrt{3}\)
• \(\tan\left(\arctan\left(\dfrac{5}{12}\right)\right) = \dfrac{5}{12}\)
• \(\tan\left(\arctan\left(0.965\right)\right) = 0.965\)
• \(\tan\left(\arctan\left( 3\pi \right)\right) = 3\pi\)
• \(\cot\left(\text{arccot}\left(1\right)\right) = 1\)
• \(\cot\left(\text{arccot}\left(-\sqrt{3}\right)\right) = -\sqrt{3}\)
• \(\cot\left(\text{arccot}\left(-\dfrac{7}{24}\right)\right) = -\dfrac{7}{24}\)
• \(\cot\left(\text{arccot}\left(-0.001\right)\right) = -0.001\)
• \(\cot\left(\text{arccot}\left( \dfrac{17\pi}{4} \right)\right) = \dfrac{17\pi}{4}\)
• \(\sec\left(\text{arcsec}\left(2\right)\right) = 2\)
• \(\sec\left(\text{arcsec}\left(-1\right)\right) = -1\)
• \(\sec\left(\text{arcsec}\left(\dfrac{1}{2}\right)\right)\) is undefined.
• \(\sec\left(\text{arcsec}\left(0.75\right)\right)\) is undefined.
• \(\sec\left(\text{arcsec}\left( 117\pi \right)\right)= 117\pi\)
• \(\csc\left(\text{arccsc}\left(\sqrt{2}\right)\right) = \sqrt{2}\)
• \(\csc\left(\text{arccsc}\left(-\dfrac{2\sqrt{3}}{3}\right)\right) = -\dfrac{2\sqrt{3}}{3}\)
• \(\csc\left(\text{arccsc}\left(\dfrac{\sqrt{2}}{2}\right)\right)\) is undefined.
• \(\csc\left(\text{arccsc}\left(1.0001\right)\right) = 1.0001\)
• \(\csc\left(\text{arccsc}\left( \dfrac{\pi}{4} \right)\right)\) is undefined.
• \(\arcsin\left(\sin\left(\dfrac{\pi}{6}\right) \right) = \dfrac{\pi}{6}\)
• \(\arcsin\left(\sin\left(-\dfrac{\pi}{3}\right) \right) = -\dfrac{\pi}{3}\)
• \(\arcsin\left(\sin\left(\dfrac{3\pi}{4}\right) \right) = \dfrac{\pi}{4}\)
• \(\arcsin\left(\sin\left(\dfrac{11\pi}{6}\right) \right) = -\dfrac{\pi}{6}\)
• \(\arcsin\left(\sin\left(\dfrac{4\pi}{3}\right) \right) = -\dfrac{\pi}{3}\)
• \(\arccos\left(\cos\left(\dfrac{\pi}{4}\right) \right) = \dfrac{\pi}{4}\)
• \(\arccos\left(\cos\left(\dfrac{2\pi}{3}\right) \right) = \dfrac{2\pi}{3}\)
• \(\arccos\left(\cos\left(\dfrac{3\pi}{2}\right) \right) = \dfrac{\pi}{2}\)
• \(\arccos\left(\cos\left(-\dfrac{\pi}{6}\right) \right) = \dfrac{\pi}{6}\)
• \(\arccos\left(\cos\left(\dfrac{5\pi}{4}\right) \right) = \dfrac{3\pi}{4}\)
• \(\arctan\left(\tan\left(\dfrac{\pi}{3}\right) \right) = \dfrac{\pi}{3}\)
• \(\arctan\left(\tan\left(-\dfrac{\pi}{4}\right) \right) = -\dfrac{\pi}{4}\)
• \(\arctan\left(\tan\left(\pi\right) \right) = 0\)
• \(\arctan\left(\tan\left(\dfrac{\pi}{2}\right) \right)\) is undefined
• \(\arctan\left(\tan\left(\dfrac{2\pi}{3}\right) \right) = -\dfrac{\pi}{3}\)
• \(\text{arccot}\left(\cot\left(\dfrac{\pi}{3}\right) \right) = \dfrac{\pi}{3}\)
• \(\text{arccot}\left(\cot\left(-\dfrac{\pi}{4}\right) \right) = \dfrac{3\pi}{4}\)
• \(\text{arccot}\left(\cot\left(\pi\right) \right)\) is undefined
• \(\text{arccot}\left(\cot\left(\dfrac{3\pi}{2}\right) \right) = \dfrac{\pi}{2}\)
• \(\text{arccot}\left(\cot\left(\dfrac{2\pi}{3}\right) \right) = \dfrac{2\pi}{3}\)
• \(\text{arcsec}\left(\sec\left(\dfrac{\pi}{4}\right) \right) = \dfrac{\pi}{4}\)
• \(\text{arcsec}\left(\sec\left(\dfrac{4\pi}{3}\right) \right) = \dfrac{4\pi}{3}\)
• \(\text{arcsec}\left(\sec\left( \dfrac{5\pi}{6} \right) \right) = \dfrac{7\pi}{6}\)
• \(\text{arcsec}\left(\sec\left(-\dfrac{\pi}{2} \right) \right)\) is undefined.
• \(\text{arcsec}\left(\sec\left(\dfrac{5\pi}{3}\right) \right) = \dfrac{\pi}{3}\)
• \(\text{arccsc}\left(\csc\left(\dfrac{\pi}{6}\right) \right) = \dfrac{\pi}{6}\)
• \(\text{arccsc}\left(\csc\left(\dfrac{5\pi}{4}\right) \right) = \dfrac{5\pi}{4}\)
• \(\text{arccsc}\left(\csc\left( \dfrac{2\pi}{3} \right) \right) = \dfrac{\pi}{3}\)
• \(\text{arccsc}\left(\csc\left(-\dfrac{\pi}{2} \right) \right) = \dfrac{3\pi}{2}\)
• \(\text{arccsc}\left(\csc\left(\dfrac{11\pi}{6}\right) \right) = \dfrac{7\pi}{6}\)
• \(\text{arcsec}\left(\sec\left(\dfrac{11\pi}{12}\right) \right) = \dfrac{13\pi}{12}\)
• \(\text{arccsc}\left(\csc\left(\dfrac{9\pi}{8}\right) \right) = \dfrac{9\pi}{8}\)
• \(\text{arcsec}\left(\sec\left(\dfrac{4\pi}{3}\right) \right) = \dfrac{2\pi}{3}\)
• \(\text{arcsec}\left(\sec\left( \dfrac{5\pi}{6} \right) \right) = \dfrac{5\pi}{6}\)
• \(\text{arccsc}\left(\csc\left(\dfrac{5\pi}{4}\right) \right) = -\dfrac{\pi}{4}\)
• \(\text{arccsc}\left(\csc\left(-\dfrac{\pi}{2} \right) \right) = -\dfrac{\pi}{2}\)
• \(\text{arccsc}\left(\csc\left(\dfrac{11\pi}{6}\right) \right) = -\dfrac{\pi}{6}\)
• \(\text{arcsec}\left(\sec\left(\dfrac{11\pi}{12}\right) \right) = \dfrac{11\pi}{12}\)
• \(\text{arccsc}\left(\csc\left(\dfrac{9\pi}{8}\right) \right) = -\dfrac{\pi}{8}\)
• \(\sin\left(\arccos\left(-\dfrac{1}{2}\right)\right) = \dfrac{\sqrt{3}}{2}\)
• \(\sin\left(\arccos\left(\dfrac{3}{5}\right)\right) = \dfrac{4}{5}\)
• \(\sin\left(\arctan\left(-2\right)\right) = -\dfrac{2\sqrt{5}}{5}\)
• \(\sin\left(\text{arccot}\left(\sqrt{5}\right)\right) = \dfrac{\sqrt{6}}{6}\)
• \(\sin\left(\text{arccsc}\left(-3\right)\right) = -\dfrac{1}{3}\)
• \(\cos\left(\arcsin\left(-\dfrac{5}{13}\right)\right) = \dfrac{12}{13}\)
• \(\cos\left(\arctan\left(\sqrt{7} \right)\right) = \dfrac{\sqrt{2}}{4}\)
• \(\cos\left(\text{arccot}\left( 3 \right)\right) = \dfrac{3\sqrt{10}}{10}\)
• \(\cos\left(\text{arcsec}\left( 5 \right)\right) = \dfrac{1}{5}\)
• \(\tan\left(\arcsin\left(-\dfrac{2\sqrt{5}}{5}\right)\right)=-2\)
• \(\tan\left(\arccos\left(-\dfrac{1}{2}\right)\right) = -\sqrt{3}\)
• \(\tan\left(\text{arcsec}\left(\dfrac{5}{3}\right)\right) = \dfrac{4}{3}\)
• \(\tan\left(\text{arccot}\left( 12 \right)\right) = \dfrac{1}{12}\)
• \(\cot\left(\arcsin\left(\dfrac{12}{13}\right)\right) = \dfrac{5}{12}\)
• \(\cot\left(\arccos\left(\dfrac{\sqrt{3}}{2}\right)\right) = \sqrt{3}\)
• \(\cot\left(\text{arccsc}\left(\sqrt{5}\right)\right) = 2\)
• \(\cot\left(\arctan \left( 0.25 \right)\right) = 4\)
• \(\sec\left(\arccos\left(\dfrac{\sqrt{3}}{2}\right)\right) = \dfrac{2\sqrt{3}}{3}\)
• \(\sec\left(\arcsin\left(-\dfrac{12}{13}\right)\right) = \dfrac{13}{5}\)
• \(\sec\left(\arctan\left(10\right)\right) = \sqrt{101}\)
• \(\sec\left(\text{arccot}\left(-\dfrac{\sqrt{10}}{10}\right)\right) = -\sqrt{11}\)
• \(\csc\left(\text{arccot}\left(9 \right)\right) = \sqrt{82}\)
• \(\csc\left(\arcsin\left(\dfrac{3}{5}\right)\right) = \dfrac{5}{3}\)
• \(\csc\left(\arctan\left(-\dfrac{2}{3}\right)\right) = -\dfrac{\sqrt{13}}{2}\)
• \(\sin\left(\arcsin\left( \dfrac{5}{13} \right) + \dfrac{\pi}{4}\right) = \dfrac{17\sqrt{2}}{26}\)
• \(\cos\left( \text{arcsec}(3) + \arctan(2) \right) = \dfrac{\sqrt{5} - 4\sqrt{10}}{15}\)
• \(\tan\left( \arctan(3) + \arccos\left(-\dfrac{3}{5}\right) \right) = \dfrac{1}{3}\)
• \(\sin\left(2\arcsin\left(-\dfrac{4}{5}\right)\right)= -\dfrac{24}{25}\)
• \(\sin\left(2\text{arccsc}\left(\dfrac{13}{5}\right)\right) = \dfrac{120}{169}\)
• \(\sin\left(2\arctan\left(2\right)\right) = \dfrac{4}{5}\)
• \(\cos\left(2 \arcsin\left(\dfrac{3}{5}\right)\right) = \dfrac{7}{25}\)
• \(\cos\left(2 \text{arcsec}\left(\dfrac{25}{7}\right)\right) = -\dfrac{527}{625}\)
• \(\cos\left(2 \text{arccot}\left(-\sqrt{5}\right)\right) = \dfrac{2}{3}\)
• \(\sin\left( \dfrac{\arctan(2)}{2} \right) = \sqrt{\dfrac{5-\sqrt{5}}{10}}\)
• \(\sin \left( \arccos \left( x \right) \right) = \sqrt{1 - x^{2}}\) for \(-1 \leq x \leq 1\)
• \(\cos \left( \arctan \left( x \right) \right) = \dfrac{1}{\sqrt{1 + x^{2}}}\) for all \(x\)
• \(\tan \left( \arcsin \left( x \right) \right) = \dfrac{x}{\sqrt{1 - x^{2}}}\) for \(-1 < x < 1\)
• \(\sec \left( \arctan \left( x \right) \right) = \sqrt{1 + x^{2}}\) for all \(x\)
• \(\csc \left( \arccos \left( x \right) \right) = \dfrac{1}{\sqrt{1 - x^{2}}}\) for \(-1 < x < 1\)
• \(\sin \left( 2\arctan \left( x \right) \right) = \dfrac{2x}{x^{2} + 1}\) for all \(x\)
• \(\sin \left( 2\arccos \left( x \right) \right) = 2x\sqrt{1-x^2}\) for \(-1 \leq x \leq 1\)
• \(\cos \left( 2\arctan \left( x \right) \right) = \dfrac{1 - x^{2}}{1 + x^{2}}\) for all \(x\)
• \(\sin(\arccos(2x)) = \sqrt{1-4x^2}\) for \(-\frac{1}{2} \leq x \leq \frac{1}{2}\)
• \(\sin\left(\arccos\left(\dfrac{x}{5}\right)\right) = \dfrac{\sqrt{25-x^2}}{5}\) for \(-5 \leq x \leq 5\)
• \(\cos\left(\arcsin\left(\dfrac{x}{2}\right)\right) = \dfrac{\sqrt{4-x^2}}{2}\) for \(-2 \leq x \leq 2\)
• \(\cos\left(\arctan\left(3x\right)\right) = \dfrac{1}{\sqrt{1+9x^{2}}}\) for all \(x\)
• \(\sin(2\arcsin(7x)) = 14x \sqrt{1-49x^2}\) for \(-\dfrac{1}{7} \leq x \leq \dfrac{1}{7}\)
• \(\sin\left(2 \arcsin\left( \dfrac{x\sqrt{3}}{3} \right) \right) = \dfrac{2x\sqrt{3-x^2}}{3}\) for \(-\sqrt{3} \leq x \leq \sqrt{3}\)
• \(\cos(2 \arcsin(4x)) = 1 - 32x^2\) for \(-\dfrac{1}{4} \leq x \leq \dfrac{1}{4}\)
• \(\sec(\arctan(2x))\tan(\arctan(2x)) = 2x \sqrt{1+4x^2}\) for all \(x\)
• \(\sin \left( \arcsin(x) + \arccos(x) \right) = 1\) for \(-1 \leq x \leq 1\)
• \(\cos \left( \arcsin(x) + \arctan(x) \right) = \dfrac{\sqrt{1 - x^{2}} - x^{2}}{\sqrt{1 + x^{2}}}\) for \(-1 \leq x \leq 1\)
• 10 \(\tan \left( 2\arcsin(x) \right) = \dfrac{2x\sqrt{1 - x^{2}}}{1 - 2x^{2}}\) for \(x\) in \(\left(-1, -\dfrac{\sqrt{2}}{2}\right) \cup \left(-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2} \right) \cup \left(\dfrac{\sqrt{2}}{2}, 1\right)\)
• \(\sin \left(\frac{1}{2} \arctan (x)\right)=\left\{\begin{array}{cl} \sqrt{\frac{\sqrt{x^{2}+1}-1}{2 \sqrt{x^{2}+1}}} & \text { for } x \geq 0 \\-\sqrt{\frac{\sqrt{x^{2}+1}-1}{2 \sqrt{x^{2}+1}}} & \text { for } x<0 \end{array}\right.\)
• If \(\sin(\theta) = \dfrac{x}{2}\) for \(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\), then \(\theta + \sin(2\theta) = \arcsin \left( \dfrac{x}{2} \right) + \dfrac{x\sqrt{4 - x^{2}}}{2}\)
• If \(\tan(\theta) = \dfrac{x}{7}\) for \(-\dfrac{\pi}{2} < \theta < \dfrac{\pi}{2}\), then \(\dfrac{1}{2}\theta - \dfrac{1}{2}\sin(2\theta) = \dfrac{1}{2} \arctan \left( \dfrac{x}{7} \right) - \dfrac{7x}{x^{2} + 49}\)
• If \(\sec(\theta) = \dfrac{x}{4}\) for \(0 < \theta < \dfrac{\pi}{2}\), then \(4\tan(\theta) - 4\theta = \sqrt{x^{2} - 16} - 4\mbox{arcsec} \left( \dfrac{x}{4} \right)\)
• \(x = \arcsin\left(\dfrac{7}{11}\right) + 2\pi k\) or \(x = \pi - \arcsin\left(\dfrac{7}{11}\right) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 0.6898, \, 2.4518\)
• \(x = \arccos\left(-\dfrac{2}{9}\right) + 2\pi k\) or \(x = - \arccos\left(-\dfrac{2}{9}\right) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 1.7949, \, 4.4883\)
• \(x = \pi + \arcsin(0.569) + 2\pi k\) or \(x = 2\pi - \arcsin(0.569) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 3.7469, \, 5.6779\)
• \(x = \arccos(0.117) + 2\pi k\) or \(x = 2\pi - \arccos(0.117) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 1.4535, \, 4.8297\)
• \(x = \arcsin(0.008) + 2\pi k\) or \(x = \pi - \arcsin(0.008) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 0.0080, \, 3.1336\)
• \(x = \arccos\left(\dfrac{359}{360}\right) + 2\pi k\) or \(x = 2\pi - \arccos\left(\dfrac{359}{360}\right) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 0.0746, \, 6.2086\)
• \(x = \arctan(117) + \pi k\), in \([0, 2\pi)\), \(x \approx 1.56225, \, 4.70384\)
• \(x = \arctan\left(-\dfrac{1}{12}\right) + \pi k\), in \([0, 2\pi)\), \(x \approx 3.0585, \, 6.2000\)
• \(x = \arccos\left(\dfrac{2}{3}\right) + 2\pi k\) or \(x = 2\pi - \arccos\left(\dfrac{2}{3}\right) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 0.8411, \, 5.4422\)
• \(x = \pi + \arcsin\left(\dfrac{17}{90}\right) + 2\pi k\) or \(x = 2\pi - \arcsin\left(\dfrac{17}{90}\right) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 3.3316, \, 6.0932\)
• \(x = \arctan\left(-\sqrt{10}\right) + \pi k\), in \([0, 2\pi)\), \(x \approx 1.8771, \, 5.0187\)
• \(x = \arcsin\left(\dfrac{3}{8}\right) + 2\pi k\) or \(x = \pi - \arcsin\left(\dfrac{3}{8}\right) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 0.3844, \, 2.7572\)
• \(x = \arccos\left(-\dfrac{7}{16}\right) + 2\pi k\) or \(x = - \arccos\left(-\dfrac{7}{16}\right) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 2.0236, \, 4.2596\)
• \(x = \arctan(0.03) + \pi k\), in \([0, 2\pi)\), \(x \approx 0.0300, \, 3.1716\)
• \(x = \arcsin(0.3502) + 2\pi k\) or \(x = \pi - \arcsin(0.3502) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 0.3578, \,2.784\)
• \(x = \pi + \arcsin(0.721) + 2\pi k\) or \(x = 2\pi - \arcsin(0.721) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 3.9468, \, 5.4780\)
• \(x = \arccos(0.9824) + 2\pi k\) or \(x = 2\pi - \arccos(0.9824) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 0.1879, \, 6.0953\)
• \(x = \arccos(-0.5637) + 2\pi k\) or \(x = - \arccos(-0.5637) + 2\pi k\), in \([0, 2\pi)\), \(x \approx 2.1697, \, 4.1135\)
• \(x = \arctan(117) + \pi k\), in \([0, 2\pi)\), \(x \approx 1.5622, \, 4.7038\)
• \(x = \arctan(-0.6109) + \pi k\), in \([0, 2\pi)\), \(x \approx 2.5932, \, 5.7348\)
• \(36.87^{\circ}\) and \(53.13^{\circ}\)
• \(22.62^{\circ}\) and \(67.38^{\circ}\)
• \(32.52^{\circ}\) and \(57.48^{\circ}\)
• \(68.9^{\circ}\)
• \(7.7^{\circ}\)
• \(51^{\circ}\)
• \(19.5^{\circ}\)
• \(41.81^{\circ}\)
• \(f(x) = 5\sin(3x) + 12\cos(3x) = 13\sin\left(3x + \arcsin\left(\dfrac{12}{13}\right)\right) \approx 13\sin(3x + 1.1760)\)
• \(f(x) = 3\cos(2x) + 4\sin(2x) = 5\sin\left(2x+\arcsin\left(\dfrac{3}{5}\right) \right) \approx 5\sin(2x+0.6435)\)
• \(f(x) = \cos(x) - 3\sin(x) = \sqrt{10} \sin\left(x + \arccos\left(-\dfrac{3\sqrt{10}}{10} \right)\right) \approx \sqrt{10} \sin(x + 2.8198)\)
• \(f(x) = 7\sin(10x) - 24\cos(10x) = 25\sin\left( 10x + \arcsin\left(-\dfrac{24}{25}\right)\right) \approx 25 \sin(10x-1.2870)\)
• \(f(x) = -\cos(x) - 2\sqrt{2} \sin(x) = 3\sin\left(x+\pi + \arcsin\left(\dfrac{1}{3}\right)\right) \approx 3\sin(x+3.4814)\)
• \(f(x) = 2\sin(x) - \cos(x) = \sqrt{5}\sin\left(x + \arcsin\left(-\dfrac{\sqrt{5}}{5}\right)\right) \approx \sqrt{5}\sin(x -0.4636)\)
• \(\left[-\dfrac{1}{5}, \dfrac{1}{5}\right]\)
• \(\left[-\dfrac{1}{3}, 1 \right]\)
• \(\left[-\dfrac{\sqrt{2}}{2}, \dfrac{\sqrt{2}}{2}\right]\)
• \((-\infty, -\sqrt{5}] \cup [-\sqrt{3}, \sqrt{3}] \cup [\sqrt{5}, \infty)\)
• \((-\infty, \infty)\)
• \((-\infty, -3) \cup (-3,3) \cup (3, \infty)\)
• \(\left(\dfrac{1}{2}, \infty \right)\)
• \(\left[\dfrac{1}{2}, \infty \right)\)
• \(\left(-\infty, -\dfrac{1}{12}\right] \cup \left[\dfrac{1}{12}, \infty\right)\)
• \((-\infty, -6] \cup [-4, \infty)\)
• \((-\infty, -2] \cup [2, \infty)\)
• \([0, \infty)\)

1 But be aware that many books do! As always, be sure to check the context!

2 See page 704 if you need a review of how we associate real numbers with angles in radian measure.

3 Alternatively, we coul duse the identity: \(1+\tan ^{2}(t)=\sec ^{2}(t)\). Since \(x=\cos (t), \sec (t)=\frac{1}{\cos (t)}=\frac{1}{x}\). The reader is invited to work through this approach to see what, if any, difficulties arise.

4 It’s always a good idea to make sure the identities used in these situations are valid for all values t under consideration. Check our work back in Example 10.6.1 . Were the identities we used there valid for all t under consideration? A pedantic point, to be sure, but what else do you expect from this book?

5 It also confirms our domain!

6 Without Calculus, of course . . .

7 The authors would like to thank Dan Stitz for this problem and associated graphics.

8 How do we know this again?

9 This is all, of course, a matter of opinion. For the record, the authors find \(\pm \sqrt{7}\) just as ‘nice’ as \(\pm 2\).

10 The equivalence for \(x=\pm 1\) can be verified independently of the derivation of the formula, but Calculus is required to fully understand what is happening at those \(x\) values. You’ll see what we mean when you work through the details of the identity for \(\tan (2 t)\). For now, we exclude \(x=\pm 1\) from our answer.

• Class 6 Maths
• Class 6 Science
• Class 6 Social Science
• Class 6 English
• Class 7 Maths
• Class 7 Science
• Class 7 Social Science
• Class 7 English
• Class 8 Maths
• Class 8 Science
• Class 8 Social Science
• Class 8 English
• Class 9 Maths
• Class 9 Science
• Class 9 Social Science
• Class 9 English
• Class 10 Maths
• Class 10 Science
• Class 10 Social Science
• Class 10 English
• Class 11 Maths
• Class 11 Computer Science (Python)
• Class 11 English
• Class 12 Maths
• Class 12 English
• Class 12 Economics
• Class 12 Accountancy
• Class 12 Physics
• Class 12 Chemistry
• Class 12 Biology
• Class 12 Computer Science (Python)
• Class 12 Physical Education
• GST and Accounting Course
• Excel Course
• Tally Course
• Finance and CMA Data Course
• Payroll Course

Interesting

• Learn English
• Learn Excel
• Learn Tally
• Learn GST (Goods and Services Tax)
• Learn Accounting and Finance
• GST Tax Invoice Format
• Accounts Tax Practical
• Tally Ledger List
• GSTR 2A - JSON to Excel

Are you in school ? Do you love Teachoo?

We would love to talk to you! Please fill this form so that we can contact you

You are learning...

Chapter 2 Class 12 Inverse Trigonometric Functions

Click on any of the links below to start learning from Teachoo ...

Get NCERT Solutions of Chapter 2 Class 12 Inverse Trigonometry free at teachoo . Solutions of all exercise questions, examples are given, with detailed explanation.

In this chapter, first we learn

• What are inverse trigonometry functions, and what is their domain and range
• How are trigonometry and inverse trigonometry related - with triangles, and a cool explanation
• Finding principal value of inverse trigonometry functions like sin -1 , cos -1 , tan -1 , cot -1 , cosec -1 , sec -1
• Solving inverse trigonometry questions using formulas
• Then, solving by changing trigonometric variables ... like sin -1 to cos -1  or sec -1 to tan -1 and then applying formulas
• Also, there are some questions where we do not know if it can be solved via formula, it is not clear. So, we do them. Please look at them before the exams.

Important questions are also marked. You can check the Sample papers as well.

Serial order wise

Concept wise.

What's in it?

Hi, it looks like you're using AdBlock :(

Please login to view more pages. it's free :), solve all your doubts with teachoo black.